A szilárdtestfizika alapjai
Tartalomjegyzék[elrejtés] |
Általános adatok
- Kód: BMETE11AF05;
- Követelmény: 2/0/0/V/2;
- Félév: ősz;
- Nyelv: magyar;
- Előadó: Mihály György, egyetemi tanár
- Jelenléti követelmények: A félév végi aláírás feltétele előadások legalább 70%-án való részvétel. Az előadásokon jelenléti ívet vezetünk.
- Félévközi számonkérések: azonosak a Szilárdtestfizika gyakorlat számonkéréseivel.
- Félév végi osztályzat: írásbeli és szóbeli vizsga. A vizsga feltétele az aláírás, valamint a gyakorlati jegy megszerzése.
Időbeosztás (2016 ősz)
- Előadások: kedd 14-16, F. épület III. lépcsőház 2.emelet 13.
- Konzultációk: hétfő 14-18 (előzetes bejelentkezés alapján a mihaly.gyorgy@mail.bme.hu email címen);
Az előadások rövid kivonata - jegyzetelésre alkalmas formában - letölthető az előadás címére kattintva. A kivonatok önmagukban nem alkalmasak a tananyag elsajátítására, de megkönnyítik a jegyzetelést (tartalmazzák az összes lényeges formulát), így elősegítik az előadásra való koncentrálást.
szept. 5. Szilárd testek
szept. 13. Szerkezetmeghatározás, szóráskísérletek
szept. 20. [[Média: | Kristályok szimmetriái ]]
szept. 27. [[Média: | Szimmetriák szerepe a szilárdtestfizikában ]]
okt. 4. [[Média: | Rácsrezgések ]]
okt. 11. Fononfajhő
okt. 18. Szabad elektronok kvantummechanikája
okt. 25. Periodikus potenciál
nov. 7. Szoros kötésű közelítés
nov. 14. Fémek, félrevezetők
nov. 21.
nov. 28. Fermi-felület kísérleti meghatározása
dec. 05. Fonon diszperzió, Összefoglalás
Részletes tematika
Kristálytan - Szerkezetvizsgálat
Kristály: elemi cella, Wigner-Seitz cella; kristály síkok, Miller-index; reciprok rács, Brillouin-zóna
Kristályrendszerek (eltolás + egy definiáló szimmetria); Bravais-rácsok (élhossz és szögek szerinti osztályozás); pontcsoportok és tércsoportok
Diffrakció elmélete: Bragg-feltétel; Laue féle leírás; szerkezeti tényező és atomi alaktényző
Rugalmas szóráskisérletek: Ewald szerkesztés, Debye-Scherrer- és Laue-módszer; Röntgen-, elektron- és neutron-szórási mechanizmus; szinkrotron-sugárzás; kvázikristályok
Rácsrezgések - fononok
Klasszikus leírás: lineáris lánc rezgései; rácsrezgések 3 dimenzióban (Dinamikus mátrix sajátérték-egyenlete); diszperziós reláció; állapotsűrűség
Kvantummechanikai leírás: Fonon-energia és impulzus; Bose-Einstein statisztika; a fonongáz fajhője
A diszperziós reláció kisérleti meghatározása: megmaradási tételek részecske-fonon, ill. foton-fonon kölcsönhatáskor; rugalmatlan neutron-szórás
Elektronok
Szabad elektrongáz kvantummechanikai leírása: Fermi-Dirac statisztika; Sommerfeld-sorfejtés; fajhő, mágneses szuszceptibilitás
Elektronok periodikus potenciálban: Bloch-tétel; diszperziós reláció perturbációs számolása; szoros-kötésű közelítés
Sávszerkezet: kváziklasszikus közelítés, effektív tömeg; Fermi-felület kísérleti meghatározása; fémek-félvezetők-szigetelők
Drude-modell: vezetőképesség, Hall-állandó, fémek optikai tulajdonságai
Tételek
- Kristályrács definíciója. Reciprok-rács, kristálysíkok, Miller-index. Szimmetriaműveletek, kristályrendszerek, Bravais-rácsok.
- Diffrakció elmélete. Szerkezeti tényező, atomi szórási tényező. Röntgen-, elektron- és neutron-szórási kísérletek.
- Rácsrezgések diszperziós relációja. A dinamikus mátrix sajátérték-egyenlete. Akusztikus és optikai ágak. A diszperziós reláció kísérleti meghatározása.
- Szilárd testek fajhőjének kvantummechanikai leírása. Bose-Einstein eloszlás. Az állapotsűrűség számolása. Debye-modell.
- Szabad elektrongáz kvantummechanikai leírása. Fermi-Dirac eloszlás. Elektron-fajhő, fémek mágneses szuszceptibilitása (Sommerfeld-sorfejtés).
- Bloch-tétel. Közel szabad elektron modell. Sávszerkezet. Fermi-felület kísérleti meghatározása.
- Wannier-függvények. Szoros kötésű közelítés. Lokalizált és kiterjedt elektronállapotok.
- Hullámcsomag. Effektív tömeg, fémek-félvezetők. Drude-modell: Hall-állandó,
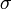 (
(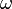 ),
),  (
(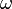 ).
).
Irodalom
Sólyom Jenő: A modern szilárdtestfizika alapjai I-II (második kiadás), Eötvös Kiadó, Budapest (2009).
Ajánlott olvasmány: Kivonatok "bevezető" kvantummechanika jegyzetből,