Nagyfrekvenciás jelek terjedésének fizikai alapjai
Tartalomjegyzék[elrejtés] |
Bevezetés
A laborgyakorlat célja, hogy a nagyfrekvenciás (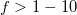 MHz) méréstechika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére.
MHz) méréstechika és jelátvitel területén felmerülő alapfogalmakat és jelenségeket bemutassa. A legfontosabb amit érdemes megjegyezni az, hogy az alacsony frekvenciás hálózatok vizsgálatakor megszokott leírásmódok nagyobb frekvenciákon érvényüket vesztik, és a hagyományos áramköri jelenségeken túlmutató, szokatlan jelenségek lépnek fel, mint pl. a jelek reflexiója. A fizika szempontjából itt a Maxwell-egyenletek nagyfrekvenciás, azaz hullámjelenségeket is figyelembe vevő alkalmazásáról van szó kábelek esetére.
A XIX. század közepén felmerült az igény a nagy távolságokra történő adattovábbításra, akár kontinensnyi távolságokban, pl. tenger alatti kábelek segítségével. (Az első transzatlanti kábelt 1858-ban helyezték üzembe.) Hamar kiderült, hogy a vezetékben történő jeltovábbításánál lényeges a hullámjelenségek figyelembevétele. Ez a technológiai fejlődés és igény az elméleti leírásra időben közel volt a Maxwell-egyenletek (1861) megszületéséhez. A vezetékben terjedő hullámjelenségek leírását ma mint az ún. távíróegyenleteket ismerjük. Ez a Maxwell-egyenletek által megjósolt elektromágneses hullámjelenségek egyik gyakorlati alkalmazása, és e leírás gyakorlati sikere is inspirálóan hatott az elektromágneses sugárzás későbbi felfedezésére (Hertz, 1886).
A fizikus tanulmányok során eddigiekben felmerült egyenáramú (DC) és alacsony frekvenciás váltóáramú (AC) hálózatok vizsgálatakor nem törődtünk azzal, hogy a jel terjedési sebessége véges. Feltételeztük, hogy adott ponton feszültséget kapcsolva egy áramkörre az pillanatszerűen megjelenik minden azonos potenciálú helyen. Mindez nyilvánalóan érvényét veszíti, amikor a jel számára szükséges terjedési idő, 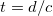 (itt
(itt  a kábel hossza,
a kábel hossza,  a közegben érvényes fénysebesség), összemérhető a jel periódusidejével:
a közegben érvényes fénysebesség), összemérhető a jel periódusidejével: 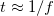 (a gyakorlatban inkább a
(a gyakorlatban inkább a 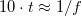 feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia
feltétel a használatos). Például a transzatlanti kábel esetére az így kapott frekvencia 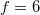 Hz. Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb.
Hz. Ez az eredmény azt jelenti, hogy a hullámjelenségek figyelembe vétele nélkül a transzatlanti kommunikáció csak ennél lényegesen alacsonyabb frekvencián, mai szóhasználattal kb. 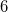 Hz sávszélességen (azaz 6 bit/sec) mehetne csak végbe.
Hz sávszélességen (azaz 6 bit/sec) mehetne csak végbe.
A hullámjelenségek figyelembevétele a modern kommunikációs eszközöknél még fontosabb, mivel pl. 9 GHz-es vivőfrekvenciára (ami egy elterjedt kommunikációs sáv) a hullámhossz mindössze 3 cm. Egy másik gyakorlati példánk a számítógépek, melyek tipikusan 2-3 GHz-es jelekkel dolgoznak (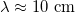 ), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az Önálló labor tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.
), melyeket 10-20 cm távolságra juttatnak el, így itt nyilvánvalóan szükséges a hullámjelenségek figyelembevétele az áramkörök tervezésekor. A későbbi tanulmányaink során hasonló jelenségekkel találkozhatunk az Önálló labor tárgy NMR (magmágneses-rezonancia) és ESR (elektronspin-rezonancia) laborgyakorlatain.
Elméleti háttér
A távíróegyenletek
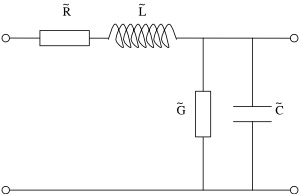
Tekintsük a jelet továbbító vezeték egy infinitezimálisan kicsi darabját, ami az 1. ábrán látható. Ezt legáltalánosabban egy soros, ún. elosztott ellenállás, 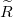 (egysége Ohm per méter), elosztott induktivitás,
(egysége Ohm per méter), elosztott induktivitás, 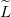 (egysége Henry per méter), elosztott kapacitás,
(egysége Henry per méter), elosztott kapacitás, 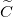 (egysége Farád per méter), és a két drót közti elosztott vezetés,
(egysége Farád per méter), és a két drót közti elosztott vezetés, 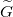 (egysége Siemens per méter) jellemzi.
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A
(egysége Siemens per méter) jellemzi.
A soros ellenállás oka a vezetékdarabokban lévő veszteség, az induktivitás oka pedig az, hogy az egyes drótdarabokat mágneses tér veszi körbe, ezért lesz egyetlen drótszálnak is önindukciója. A 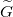 írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a
írja le a két vezetékdarab közti elektromos vezetést, ami akkor is jelen van, ha nagyon jó dielektrikum választja el a két vezetőt egymástól. Mivel a két drót nincs azonos potenciálon, ezért lesz köztük a 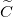 kapacitás.
kapacitás.
| 1. ábra: A jelterjedésben vizsgált vezeték egy darabjának áramköri modellje. |
Látható, hogy a fenti értékek közül 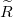 értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a skin-effektus miatt megnő), azonban
értéke elsősorban a vezető anyagi minőségétől függ (értéke nagyfrekvencián a skin-effektus miatt megnő), azonban 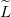 ,
, 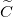 és
és 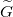 értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra
értéke nagyban függ attól, hogy a két drót egymáshoz képest hogyan helyezkedik el (pl. sodort érpárra 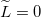 , de
, de 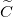 értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére
értéke nagy). Egymástól adott távolságra elhelyezkedő drótpár esetére 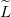 értéke fix, viszont
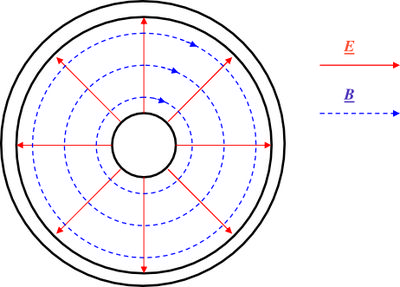
értéke fix, viszont 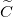 nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan
nagyban függ a környező dielektrikumtól (utóbbi probléma a sós víz miatt a transzatlanti kábelnél merült fel). Mindezen problémákra kínál megoldást a koaxiális kábel (Heaviside, 1880), amiben a földelt külső vezetéken belül helyezkedik el a másik drót. Ennek előnye, hogy minden paramétere jól definiált, mind az elektromos, mind a mágneses erővonalak belül a két koaxiális vezeték között helyezkednek el, amint azt a 2. ábra mutatja. A korábbi merev falú, levegővel kitöltött koaxiális kábeleket mára a rugalmas dielektrikummal kitöltött kábelek váltották fel (tipikusan 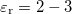 és
és 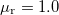 ).
).
2. ábra: A koaxiális vezeték keresztmetszete az elektromos és mágneses tér 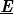 , ill. , ill. 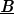 vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve. vonalaival a kábel alapvető, ún. TEM00 módusára. A belső vezetéken változó feszültség van, míg a külső leggyakrabban le van földelve.
|
A koaxiális kábelek hosszegységre eső kapacitására és önindukciós együtthatójára e két paraméter definiciójából adódik:
![\[ \widetilde{C}=\frac{2 \pi \varepsilon_0 \varepsilon_{\text{r}}}{\ln(D/d)}, \qquad \widetilde{L}=\frac{\mu_0 \mu_{\text{r}}\ln(D/d)}{2\pi}, \]](/images/math/6/9/0/690a2bceed2cc1530ee78e457e0c9a56.png)
\noindent ahol  az árnyékolás belső átmérője és
az árnyékolás belső átmérője és  a kábel belső vezetőjének külső átmérője,
a kábel belső vezetőjének külső átmérője, 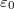 és
és 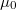 az ismert fizika állandók,
az ismert fizika állandók, 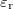 és
és 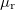 az anyagra jellemző paraméterek.
az anyagra jellemző paraméterek.
A távíróegyenletek bemutatásához a legegyszerűbb eset tárgyalásához feltesszük, hogy mindkét drót tökéletes vezető (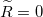 ) és tökéletesen szigetelt egymástól (
) és tökéletesen szigetelt egymástól (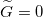 ), tehát a jelenség csak
), tehát a jelenség csak 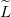 és
és 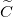 -től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség (
-től fog függeni. (A teljesen általános eset is megoldható, csak bonyolultabb eredményekre vezet.) Ekkor mind a feszültség (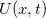 ), mind az áram (
), mind az áram (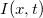 ) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880):
) hely- és időfüggő lesz, és leírásukra a következő két csatolt, lineáris, elsőrendű parciális-differenciálegyenlet adódik (Heaviside, 1880):
![\[ \begin{aligned} \frac{\partial U(x,t)}{\partial x}=-\widetilde{L} \frac{\partial I(x,t)}{\partial t}\\ \frac{\partial I(x,t)}{\partial x}=-\widetilde{C} \frac{\partial U(x,t)}{\partial t}. \end{aligned} \]](/images/math/b/4/2/b42c7453324b14212652250b1c030ea8.png)
Ezek a távíróegyenletek a Maxwell-egyenletekből véges differenciák segítségével elemi úton levezethetők. További összevonással két ekvivalens hullámegyenletet kapunk mind az áramra, mind a feszültségre:
![\[ \begin{aligned} \frac{\partial^2 U(x,t)}{\partial t^2}=\frac{1}{\widetilde{L}\widetilde{C}}\frac{\partial^2 U(x,t)}{\partial x^2}\\ \frac{\partial^2 I(x,t)}{\partial t^2}=\frac{1}{\widetilde{L}\widetilde{C}}\frac{\partial^2 I(x,t)}{\partial x^2}. \end{aligned} \]](/images/math/7/b/2/7b2d296fb325fdba98591229785c26e2.png)
Az ismert alakú hullámegyenletekből leolvasható, hogy a kábelben terjedő zavar sebessége 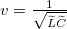 , és a legáltalánosabb megoldás a feszültségre és áramra:
, és a legáltalánosabb megoldás a feszültségre és áramra:
![\[ \begin{aligned} U(x,t)=U^+ f(\omega t- k x)+U^-f(\omega t+ k x)\\ I(x,t)=I^+ f(\omega t- k x)+I^-f(\omega t+ k x), \end{aligned} \]](/images/math/c/d/d/cdd1833774e27b35ce35085d1bddd450.png)
ahol  a terjedő hullám körfrekvenciája,
a terjedő hullám körfrekvenciája, 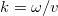 pedig a hullámszáma.
pedig a hullámszáma. 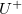 és
és 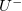 a pozitív, illetve negatív
a pozitív, illetve negatív  irányba terjedő jel amplitúdója,
irányba terjedő jel amplitúdója,  egy tetszőleges függvény. Vegyük észre, hogy a
egy tetszőleges függvény. Vegyük észre, hogy a  mennyiség dimenziója valóban m/s.
mennyiség dimenziója valóban m/s.
Egy speciális eset az, amikor a kábelen csak egy irányba haladó hullám van jelen. Ez a megoldás:
![\[ \begin{aligned} U(x,t)=U_0 e^{i(\omega t- k x)}\\ I(x,t)=I_0 e^{i(\omega t- k x)}. \end{aligned} \]](/images/math/1/7/b/17bda5e19986fa1b178bd4606ac94bcb.png)
Ezt a speciális megoldást a távíróegyenletekbe visszaírva azt kapjuk, hogy a feszültség és áram aránya a haladó hullámra:
![\[ \frac{U(x,t)}{I(x,t)}=\sqrt{\frac{\widetilde{L}}{\widetilde{C}}}=Z_0, \]](/images/math/4/2/0/42092ec1c6d0285584f917e078fd290a.png)
ahol a 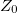 ellenállás dimenziójú mennyiséget a kábel hullámimpendaciájának nevezzük.
ellenállás dimenziójú mennyiséget a kábel hullámimpendaciájának nevezzük.
Visszaverődések a kábel végéről
A hullámegyenlet konkrét megoldását a kezdeti és peremfeltételek (pl. a drót végén előírt amplitúdó) ismeretében kaphatjuk meg. Középiskolás hangtani jelenségekkel analóg a következő két eset: amikor a koax kábel végét rövidre zárjuk (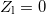 ), ill. amikor a koax kábel végén szakadás van (
), ill. amikor a koax kábel végén szakadás van (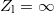 ). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn (
). E két esetet szemlélteti a 3. ábra. Amennyiben a vezeték hossza és a gerjesztő hullám frekvenciája között jól meghatározható összefüggések állnak fenn (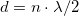 a zárt végre és
a zárt végre és 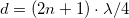 nyitott végre,
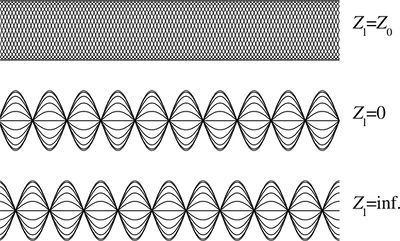
nyitott végre,  egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a rövidrezárt drótpárban végig 0, míg a szakadásos végű drótpárra végig a meghajtó generátor feszültségét veszi fel.
egész), a vezeték mentén feszültség állóhullámok alakulnak ki. A csomó- és duzzadóhelyeket a jól ismert bezárt illetve nyitott végű síppal való analógia alapján kaphatjuk meg. E két esetet a hanghullámokra vonatkozó analógia alapján úgy érthetjük meg, hogy mind a lezárt, mind a nyitott végről visszaverődik a hullám, és a kábelmenti feszültségben látható állóhullám kép az odafelé haladó és visszavert hullámok interferenciájának eredménye. A DC áramköröknél szerzett ismeretek azt mondanák, hogy a feszültség a rövidrezárt drótpárban végig 0, míg a szakadásos végű drótpárra végig a meghajtó generátor feszültségét veszi fel.
3. ábra: Sematikus áramkör szinuszos meghajtó generátorral aminek 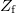 kimenő ellenállása van, koaxiális vezeték aminek a végén kimenő ellenállása van, koaxiális vezeték aminek a végén 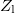 lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha lezáró impedancia van. A generátorból jön ki a teljes teljesítmény ha 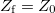 . A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor . A lezárás három értékére vonatkozó vezetékbeli feszültség eloszlást is mutatjuk 20 pillanatfelvételre, amikor 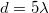 . Vegyük észre, hogy . Vegyük észre, hogy 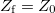 esetén a vezetékben homogén a feszültség maximuma, esetén a vezetékben homogén a feszültség maximuma, 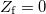 esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és esetén mindkét végén csomópont van (ekkor forráson is 0 feszültséget mérünk), és 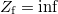 esetén mindkét végén duzzadóhely van. esetén mindkét végén duzzadóhely van.
|
A nagyfrekvenciás adat- vagy energiaátvitel nyilvánvalóan azt követeli meg, hogy a kábel végéről ne legyen visszaverődés. Az A. függelékben megmutatjuk, hogy ez akkor lép fel, amennyiben a lezáró impedanciára fennáll:
![\[ Z_{\text{l}}=Z_0\,, \]](/images/math/1/d/6/1d645ae2a5758b9be2e2e9eabed95f2b.png)
ahol 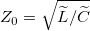 a vezeték hullámimpedanciája. Amennyiben ez a feltétel nem teljesül, akkor a visszavert és a kábel végére érkező hullámok amplitúdójának arányára fennáll:
a vezeték hullámimpedanciája. Amennyiben ez a feltétel nem teljesül, akkor a visszavert és a kábel végére érkező hullámok amplitúdójának arányára fennáll:
![\[ \Gamma=\frac{Z_{\text{l}}-Z_0}{Z_{\text{l}}+Z_0}, \]](/images/math/e/7/0/e70ce2a45531aa4098b85dbb1e85ffd7.png)
ahol 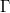 az ún. reflexiós tényező;
az ún. reflexiós tényező; 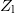 komplex értéke mellett
komplex értéke mellett 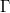 is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse
is komplex, ami azt fejezi ki, hogy a visszavert hullám fázisa nem többszöröse 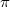 -nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben,
-nek. Vegyük észre, hogy a két fentebb tárgyalt határesetben, 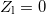 és
és 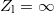 , amikor is maximális a reflexió
, amikor is maximális a reflexió 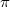 ill. 0 fokos fázistolással visszavert hullámmal.
ill. 0 fokos fázistolással visszavert hullámmal.
A leggyakrabban használt koaxiális kábelek hullámimpedanciája 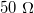 . Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még
. Ez az érték megállapodásból született, és a 60-as évektől kezdve elterjedt ipari sztenderd lett. Néhány helyen találkozhatunk még 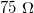 -os koaxiális kábelekkel is. Érdekességképp ezen értékek és az
-os koaxiális kábelekkel is. Érdekességképp ezen értékek és az 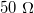 történeti hátteréről olvashatunk a B. függelékben.
történeti hátteréről olvashatunk a B. függelékben.
A DC és alacsony frekvenciájú (néhány kHz-es AC) eszközöknél megszokhattuk, hogy egy ideális feszültség forrás belső ellenállása 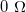 , míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása
, míg ideális feszültségmérő bemenő ellenállása végtelen. A nagyfrekvenciás hálózatoknál minden mérőeszköz bemenő és kimenő ellenállása 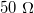 , mivel ekkora hullámimpdanciájú kábeleket csatlakoztatunk hozzájuk. Amennyiben egy adott hullámimpedanciájú vezetéket az ennek megfelelő ellenállással zárunk le, úgy nem alakulnak ki állóhullámok (hiszen nincs reflexió a végről), és a teljes vezeték hosszában azonos feszültséget mérhetünk.
, mivel ekkora hullámimpdanciájú kábeleket csatlakoztatunk hozzájuk. Amennyiben egy adott hullámimpedanciájú vezetéket az ennek megfelelő ellenállással zárunk le, úgy nem alakulnak ki állóhullámok (hiszen nincs reflexió a végről), és a teljes vezeték hosszában azonos feszültséget mérhetünk.
A lezáró impedancia
Visszaverődések vizsgálata
A Smith chart
Mérési feladatok
A mérést két alkalomra bontva fogjuk elvégezni.
Kábelvégi reflexió vizsgálata (első mérési alkalom)
Oszcilloszkóppal
Itt oszcilloszkóppal mérjük meg a kábelvégi reflexió hatását a forrás kimenetére.
- Vegyük fel oszcilloszkóp segítségével a nagyfrekvenciás jelgenerátor kimenetének feszültségét a lezáró impedancia három esetére (0, 50
 és szakadás) a frekvencia (0.001 MHz-15 MHz) függvényében a mérőprogrammal. (Segítség: BNC T a forrás kimenetén, egyik vége oszcilloszkópon minél rövidebb dróttal 50 Ohmmal lezárva, másik végén egy ismert hosszúságú BNC kábel, mérőeszköz leírás \aref{muszer_fuggelek}. függelékben. A forrás 2-es kimenetére triggereljük az oszcilloszkópot. A mérőprogramban a rflabor <startfreq> <stopfreq> <numberofpoints> paranccsal tudjuk a frekvencia változtatása mellett felvenni az oszcilloszkóp 1-es csatornáján mért jel nagyságát és az 1-es és 2-es csatornán mért jel egymáshoz viszonyított fázisát. A save paranccsal tudjuk elmenteni a mérésünk eredményét. A readscope paranccsal fel tudjuk venni az oszcilloszkópon éppen látható jelet.)
és szakadás) a frekvencia (0.001 MHz-15 MHz) függvényében a mérőprogrammal. (Segítség: BNC T a forrás kimenetén, egyik vége oszcilloszkópon minél rövidebb dróttal 50 Ohmmal lezárva, másik végén egy ismert hosszúságú BNC kábel, mérőeszköz leírás \aref{muszer_fuggelek}. függelékben. A forrás 2-es kimenetére triggereljük az oszcilloszkópot. A mérőprogramban a rflabor <startfreq> <stopfreq> <numberofpoints> paranccsal tudjuk a frekvencia változtatása mellett felvenni az oszcilloszkóp 1-es csatornáján mért jel nagyságát és az 1-es és 2-es csatornán mért jel egymáshoz viszonyított fázisát. A save paranccsal tudjuk elmenteni a mérésünk eredményét. A readscope paranccsal fel tudjuk venni az oszcilloszkópon éppen látható jelet.)