Experiments with microwaves
Aim of the experiment
- To deepen the knowledge related to wave phenomena,
- To verify the relationships in wave physics experimentally,
- To model phenomena and devices in wave optics.
For the purpose:
- We summarize the basic knowledge on wave phenomena,
- We examine reflection, refraction, interference and diffraction of microwaves,
- We assemble some experimental setups (which are also useful in optics) based on interference of waves, and measure the wavelength of the used microwave.
Tartalomjegyzék |
Theoretical summary
In the experiment we use microwaves to study wave phenomena. Microwaves - as well as light - are electromagnetic waves of wavelength about 1 mm - 30 cm (correspondingly, the frequency of microwaves is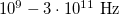 
).
Polarization of waves
In a transversal wave the vector related to the changing quantity is in the plane perpendicular to the direction of propagation but within this plane its direction is arbitrary. A certain direction of oscillation can be selected by putting a block in the path of the wave. This way behind the block a wave can be observed in which the oscillation takes place in the plane determined by the selected direction of the block and the direction of propagation. This type of wave is plane polarized wave, and the method is called polarization of waves. The selected plane is the plane of polarization, the block which creates the polarized wave is called polarizer, and usually for the selected direction direction of polarization is said. Different kind of waves can be polarized by using different methods: Transversal waves on a string or rope with a slit, electromagnetic waves with a mirror or with an equipment made of special material, microwaves with metal grating. Polarized waves have a characteristic property, namely they can be canceled out by using a polarizer of direction perpendicular to the plane of the oscillation. In case of electromagnetic waves the above definition of polarization is not unambiguous since in the plane perpendicular to the direction of propagation there are two vectors perpendicular to each other. By agreement in this case the plane of polarization is the plane containing the electric field vector.
Reflection and refraction of waves
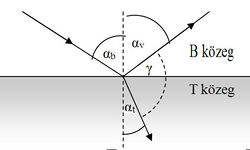
Waves propagate in finite sized medium, sooner or later they reach the boundary of the medium (for electromagnetic waves the madium can be vacuum). According to experience waves are partially reflected by the boundary, and partially refracted by the boundary, penetrating in the other medium generally by changing its direction of propagation. By using the notations of Fig. 1 laws of reflection and refraction are as follows.
In case of refection the angle of incidence (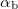
), which is the angle between the direction of incident plane wave and the normal of the reflected surface, is equal to the angle of reflection (
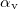), which is the angle between the direction of reflected wave and the surface normal:
![\[ \alpha_\text b = \alpha_\text v. \]](/images/math/9/8/9/989b253ff375166dfe1cd758784bd9aa.png)
In case of refraction Snell's law is valid:
![\[ \frac{\sin \alpha_\text b}{\sin \alpha_\text t}= \frac{c_\text b}{c_\text t}=n_\text{tb},\]](/images/math/3/4/b/34bf15ac3f77c4770dc2f1e425c2881e.png)
where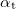 
is the angle of refraction, which is the included angle of the direction of refracted wave and the surface normal. In the medium in which the incident wave propagates (medium B in Fig. 1) the speed of propagation is 
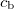, and that in the medium of the refracted wave is 
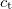(medium T in Fig. 1). The ratio of these speeds (
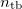) is the relative refractive index, the refractive index of medium T if the wave comes from medium B. If medium B is vacuum, the absolute refractive index is used. If the absolute refractive indices are 
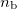and 
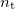for media B and T, respectively, it can be shown that:
![\[ n_\text{tb} = \frac{n_\text t}{n_\text b}.\]](/images/math/7/1/d/71dbd6901c7aba75a835d87155305515.png)
When 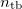is smaller than 1 (
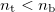), increasing the angle of incidence the angle of refraction becomes 
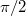. Further increasing the angle of incidence the boundary behaves like a mirror, the wave is reflected according to the law of reflection. This is called total internal reflection, and the angle of incidence 
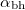belonging to the angle of refraction 
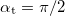is the critical angle:
![\[ \sin \alpha_\text{bh} = n_\text{tb}.\]](/images/math/d/6/d/d6ddc391d19ab5a36f932ef97a197403.png)
On reflection and refraction the phase of the wave may change, in case of electromagnetic wave even its polarization. It is an important experience in practice that for a certain angle of incidence the reflected electromagnetic wave becomes plane polarized. The plane of polarization of the reflected wave is perpendicular to the plane of incidence, which is determined by the direction of the incident and the reflected waves and the surface normal (electric field vector of the reflected wave is parallel to the reflected surface). It can be shown that this happens if the directions of the refracted and the incident waves are perpendicular to each other (in Fig. 1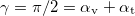 
), from which it follows that
![\[\tan \alpha_\text{b,B}= n_\text{tb}.\]](/images/math/e/6/2/e62f03e98ce0b67c198258e5cf4efc06.png)
This is called Brewster's law, and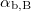 
is Brewster's angle.
Interference of waves
In the examined part of space simultaneously more waves can propagate. In this case the resultant oscillation pattern can be determined mostly by means of superposition principle: the instantaneous values of the wave functions should be added. This is called interference, which depends on the phases of the meeting waves. In the extreme case the amplitudes can add if the phases of the waves are the same (constructive interference), or they can subtract, moreover in case of equal amplitudes they can cancel out each other, if the phases of the waves are opposite (destructive interference). If the phase of the wave sources does not change in time, and uninterrupted, regular traveling waves of equal frequencies are examined (called coherent waves), the phase difference at the location of summation is determined by the phase difference of the wave sources and the path difference between the waves until reaching that location. This means that for coherent waves the amplitude of the wave at any any locations is constant in time, which results in a steady spatial amplitude distribution (for visible waves the interference pattern can be observed by eye). For instance in case of two in-phase sources the phase difference in the interference of two harmonic waves is specified by the path difference only. If the wave sources are at distances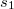 
and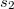 
from the location of the examined point, constructive interference is observed in those points for which the path difference is an integer number multiple of the wavelength:
![\[ \Delta s_n = n \lambda \quad \left( n=1,2,3,...\right),\]](/images/math/a/0/c/a0ce2203acde2add10b6573b7bc3e590.png)
destructive interference is observed in those points for which the path difference is an odd number multiple of the half wavelength:
![\[ \Delta s_n = \left( 2n-1 \right) \frac{\lambda }{2} \quad \left( n=1,2,3,...\right).\]](/images/math/7/1/7/717879d651af8b704c2527206a2742ba.png)
Standing waves
Formation of standing waves is an important special case of interference of waves: it is due to the fact that the wave is at least partially reflected at the boundary of a medium. Under certain circumstances interference of waves traveling to the boundary and being reflected from it results in a specific steady waveform, standing wave. Characteristics of standing waves is that at certain points of the medium oscillation takes place in the same phase, the amplitude depends on the location only.
Standing wave can be formed for example in a medium between two planes perpendicular to the direction of the reflected harmonic plane wave only if its wavelength (frequency) fulfills certain conditions. The possible wavelengths of the standing wave is determined by the distance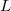 
between the two reflecting planes and by the boundary conditions at the locations of reflection. The physical conditions at the boundary are such that oscillation cannot be formed there (for example elastic string with fixed ends, an oscillating air column between solid walls, or a metal surface reflecting the electric component of the electromagnetic wave). In other cases there is no restriction (or hardly any) for the formation of oscillation at the boundary (for example at the free ends of an elastic string, at the open end of a gas column, on the magnetic component of the electromagnetic wave at a reflecting metal surface).
It can be shown if the oscillation is restricted or unrestricted on both ends of a medium of length 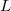, the possible wavelengths is given by
![\[ \lambda_n = \frac{2L}{n} \quad \left( n=1,2,3,...\right).\]](/images/math/1/2/a/12a538cec4e2371ae72adcf9095e7a26.png)
If it is restricted on one of the ends and the other is free
![\[ \lambda_n = \frac{4L}{2n-1} \quad \left( n=1,2,3,...\right)\]](/images/math/9/e/1/9e1086f5fa3c91fd92a1e157177ee2b7.png)
