1. Mérés: Egyenáramú mérések, multiméter használata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Ideális feszültség- és áramgenerátor
| Az ideális feszültséggenerátor egy olyan ideális feszültségforrás, amelynek kapcsain állandó feszültség mérhető függetlenül a terhelő áramkörben folyó áramtól. Ilyen eszköz a valóságban nem létezhet, hiszen az áramot minden határon túl növelve tetszőlegesen nagy teljesítményt adna. Azonban valós feszültségforrásokat lentebb tárgyalt esetben jól modellezi ez az idealizáció, ezért gyakran ezt az egyszerűbb képet használjuk. |
| Az ideális áramgenerátor egy olyan ideális áramforrás, mely állandó áramot hajt át a terhelő körön függetlenül a kapcsain mérhető feszültségtől. Hasonlóan az ideális feszültséggenerátorhoz a valódi áramgenerátorok csak bizonyos tartományban közelíthetőek az idealizációjukkal. |
Valós telep
Egy valós telepet egy  feszültséget szolgáltató feszültséggenerátor és egy azzal sorosan kapcsolt feszültséget szolgáltató feszültséggenerátor és egy azzal sorosan kapcsolt 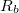 belső ellenállással modellezhetünk. Galván elemek esetén az elektródák illetve a közöttük lévő elektrolit véges ellenállása okozza a belső ellenállást. Ha a telep kapcsait belső ellenállással modellezhetünk. Galván elemek esetén az elektródák illetve a közöttük lévő elektrolit véges ellenállása okozza a belső ellenállást. Ha a telep kapcsait  terhelő ellenálláson keresztül zárjuk, akkor a körben terhelő ellenálláson keresztül zárjuk, akkor a körben  áram indul el: áram indul el:
![\[ U_0=U+IR_b \]](/images/math/2/9/2/2923ac1ef18c91068d4a36606fe93d07.png) Ha az |
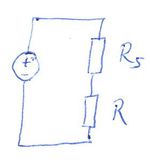
Áramgenerátoros meghajtás
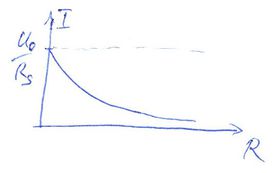
Gyakori feladat, hogy forrásunk feszültséggenerátoként működik, de áramgenerátorra lenne szükségünk. Ezt egy a feszültséggenerátorral sorba kapcsolt 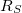 söntellenállással érhető el. Ekkor a körben folyó áramot az alábbi összefüggés adja söntellenállással érhető el. Ekkor a körben folyó áramot az alábbi összefüggés adja  terhelő ellenállás esetén: terhelő ellenállás esetén:
![\[ I=\frac{U_0}{R_S+R} \]](/images/math/c/6/a/c6a21165c65ea6622d23c4e0e7e64fd7.png) Az áram maximális értéke limitált |
Volt- és árammérő
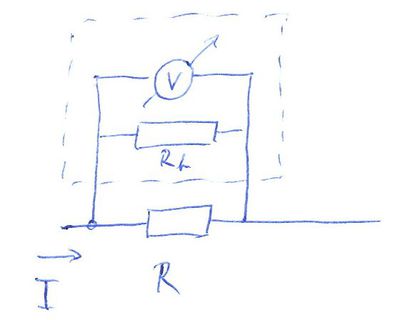
Egy ideális voltmérő  ellenállással párhuzamosan kapcsolva megméri az ellenálláson áthaladó ellenállással párhuzamosan kapcsolva megméri az ellenálláson áthaladó  áram hatására eső áram hatására eső 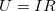 feszültséget. Egy valós műszeren az áram egy kis része átfolyik, melyet egy nagy, de véges feszültséget. Egy valós műszeren az áram egy kis része átfolyik, melyet egy nagy, de véges 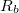 belsőellenállással modellezhetünk. Látható, hogy az eszköz által mért belsőellenállással modellezhetünk. Látható, hogy az eszköz által mért 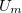 feszültség értéke: feszültség értéke:
![\[ U_{m}=\frac{RR_b}{R_b+R}I=\frac{RI}{1+R/R_b}, \]](/images/math/c/5/b/c5b92676faa617ee6cdeaec2308277f2.png) tehát az eszköz által mért feszültség, akkor közelíti meg az ideális |
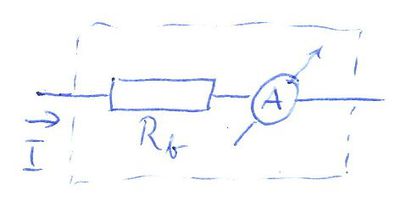
Az ideális árammérő az áramkörbe sorosan kapcsolva megméri a rajta átfolyó áramot. Ezek az eszközök is rendelkeznek véges 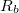 belsőellenállással, mely erősen függ a műszer érzékenységétől (értéke kb. 1..1000 belsőellenállással, mely erősen függ a műszer érzékenységétől (értéke kb. 1..1000  között változik kézi műszerek esetén). között változik kézi műszerek esetén).
|
Ellenállásmérés
Mérésben használt műszerek
MAS-830 3.5 digites kézi multiméter
| Méréshatár | Felbontás | Pontosság |
|---|---|---|
| 200 mV | 100  V V
|
±0.5% of rdg ± 2 digits |
| 2 V | 1 mV | ±0.5% of rdg ± 2 digits |
| 20 V | 10 mV | ±0.5% of rdg ± 2 digits |
| 200 V | 100 mV | ±0.5% of rdg ± 2 digits |
| 600 V | 1 V | ±0.8% of rdg ± 2 digits |
| Méréshatár | Felbontás | Pontosság |
|---|---|---|
| 200 mA | 0,1  A A
|
±1% of rdg ± 2 digits |
| 2 mA | 1  A A
|
±1% of rdg ± 2 digits |
| 20 mA | 10  A A
|
±1% of rdg ± 2 digits |
| 200 mA | 100  A A
|
±1.5% of rdg ± 2 digits |
| 10 A | 10 mA | ±3% of rdg ± 2 digits |
National Instruments myDAQ digitalizálókártya
Mérési feladatok
1. Feladat Kézi multiméter segítségével mérjük meg a 10 db 5%-os, névlegesen 3,3 k -os ellenállást (vastag, zöld ellenállások 3k3, 5% felirattal) majd a 10 db névlegesen 4,7
-os ellenállást (vastag, zöld ellenállások 3k3, 5% felirattal) majd a 10 db névlegesen 4,7  -os ellenállást is (vastag, zöld ellenállások 4R7, 5% felirattal). Jegyezzük fel a használt mérőműszer beállításait, felbontását, soroljuk fel a lehetséges hibaforrásokat, és becsüljük meg az okozott hiba nagyságát. A mért ellenállás értékeket táblázatban foglaljuk össze. Végezetül addjuk meg az átlagos ellenállást és a mért értékek szórását. Írásban értékeljük a tapasztaltakat!
-os ellenállást is (vastag, zöld ellenállások 4R7, 5% felirattal). Jegyezzük fel a használt mérőműszer beállításait, felbontását, soroljuk fel a lehetséges hibaforrásokat, és becsüljük meg az okozott hiba nagyságát. A mért ellenállás értékeket táblázatban foglaljuk össze. Végezetül addjuk meg az átlagos ellenállást és a mért értékek szórását. Írásban értékeljük a tapasztaltakat!
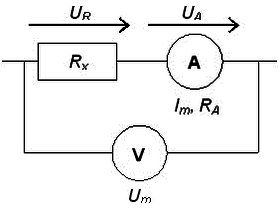
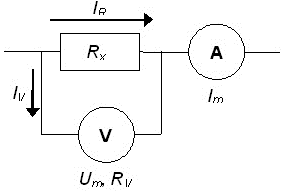
2. Feladat A 4,7  -os ellenállásokat mérjük meg négypont módszerrel is. A mérésekhez használjuk a myDAQ 5 V-os kimenetét, az áramot mérjük a kézi multiméterrel, -os ellenállásokat mérjük meg négypont módszerrel is. A mérésekhez használjuk a myDAQ 5 V-os kimenetét, az áramot mérjük a kézi multiméterrel,
az ellenálláson eső feszültséget pedig a myDAQ multiméterével. Használjunk áramgenerátoros meghajtást ( |
3. Feladat Az előző feladatban leírt négypontos mérést ismételjük meg az ismeretlen fémszálon, majd számítsuk ki annak fajlagos ellenállását. Elemezzük a különböző hibákat, azok terjedését. A mért fajlagos ellenállás hogyan viszonyul ismert vezetőanyagok, pl. réz, arany, fajlagos ellenállásához? Mi lehet a vezeték anyaga és vajon mire használható ez a drót?
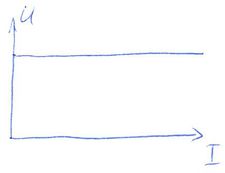

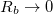 Ezzel szemben ha kis ellenállással terheljük a telepet, "rövidre zárjuk", akkor a kapocsfeszültség leesik.
Ezzel szemben ha kis ellenállással terheljük a telepet, "rövidre zárjuk", akkor a kapocsfeszültség leesik.

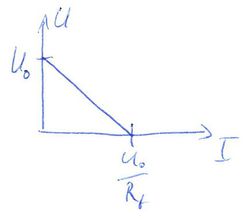
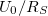 értéken, melyet kis terhelő ellenállás esetén közelít meg a körben folyó áram.
értéken, melyet kis terhelő ellenállás esetén közelít meg a körben folyó áram.
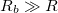 . A belsőellenállás értéke egyszerű kéziműszereknél kb. 10
. A belsőellenállás értéke egyszerű kéziműszereknél kb. 10 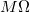 , drágább eszközökben több nagyságrenddel nagyobb is lehet.
, drágább eszközökben több nagyságrenddel nagyobb is lehet.