RLC körök mérése
A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul.
Ebben a mérésben elektromos rezgőköröket (és frekvenciafüggő áramköri elemeken alapuló szűrőket) fog tanulmányozni. Az ezzel teljesen analóg módon leírható mechanikai rezgéseket a kényszerrezgés vizsgálata mérésében tanulmányozza. A két mérésből közös jegyzőkönyvet kell készítenie.
Tartalomjegyzék |
Elméleti összefoglaló
A felhasznált áramköri elemek:
Ohmos ellenállás
Az ellenálláson eső feszültséget az
![\[u(t)=R i(t)\]](/images/math/5/b/3/5b3eacca33f2f21f61fce5be60d9610c.png)
összefüggés írja le. Szinuszos gerjesztés [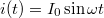
] esetén
![\[u(t) = R I_0 \sin\omega t,\]](/images/math/4/a/0/4a04c0999406f97c01969c2d879e1a60.png)
azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.
Tekercs
A tekercsben indukálódó feszültséget az
![\[u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}\]](/images/math/7/0/d/70d81694316981734d9306478ac2b228.png)
egyenlet írja le. Szinuszos gerjesztés [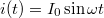] esetén
![\[u(t) = L \omega I_0 \cos\omega t = L \omega I_0 \sin( \omega t + 90^\circ),\]](/images/math/c/a/0/ca02809dd30cc558785d3acc3350868b.png)
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.
Kondenzátor
A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:
![\[i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.\]](/images/math/2/a/d/2ad4b9dbaa6debb8b51c07b374b84fdf.png)
Szinuszos gerjesztés [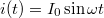] esetén:
![\[u(t) = -\frac{I_0}{C\omega}\cos\omega t = \frac{I_0}{C\omega}\sin(\omega t - 90^\circ),\]](/images/math/8/1/f/81fa0ed654e843707afa632e20ebdc64.png)
azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.
Komplex jelölés
Színuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos 
körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az ábrán egy soros RLC-kör fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.
Szűrő áramkörök
Szűrők segítségével egy különböző frekvenciájú rezgésekből álló elektromos jelből ki lehet szűrni bizonyos frekvenciatartományokat. Ezen a mérésen csak RC alul- és felüláteresztő szűrőket fog mérni, de itt néhány más kapcsolást is bemutatunk.
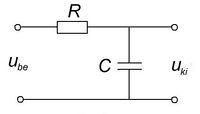
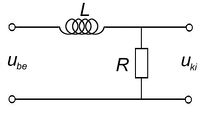
Aluláteresztő szűrők
A 3/a és 3/b ábrákon látható kapcsolások kimenő feszültségeit a komplexjelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, 
a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!
 |
 |
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega RC} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega RC}\right|=\frac{1}{\sqrt{1+(\omega RC)^2}} \end{array} \]](/images/math/9/4/3/943854eb463ad63e4d67664743f7e96e.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{R}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega L/R} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega L/R}\right|=\frac{1}{\sqrt{1+(\omega L/R)^2}} \end{array} \]](/images/math/5/f/1/5f1da1dd24d313e4abefdadb0d7af81c.png) |
A kimeneti és bemeneti feszültségek hányadosa, a hálózatra jellemző, frekvenciafüggő kifejezés.
A két kifejezés formailag azonos, tehát a két kapcsolás azonos jellegű viselkedést mutat. Ameddig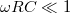 
vagy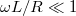 
, a kifejezések értéke 1; ha 
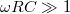vagy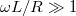 
, a hányados értéke 
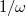szerint csökken. Ez azt jelenti, hogy adott 
, 
és 
esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
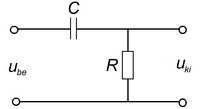
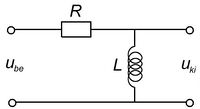
Felüláteresztő szűrő
A 4/a és a 4/b ábrákon látható kapcsolásokat leíró egyenletek az előző pontban követett eljárás alapján az alábbiak szerint alakulnak.
 |
 |
![\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{R}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + 1/j\omega RC} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + 1/j\omega RC}\right|=\frac{1}{\sqrt{1+(1/\omega RC)^2}} \end{array} \]](/images/math/6/7/e/67eb7285e8d93596127be6e7771a16c0.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{j\omega L}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + R/j\omega L} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + R/j\omega L}\right| \end{array} \]](/images/math/6/3/d/63ddfbd96b23b34081ca19c03ece4da2.png) |
A kifejezésekből jól látszik, hogy a kapcsolások a kisfrekvenciás jeleket nem engedik a kimenetre, míg a nagyfrekvenciás jelek csillapítás nélkül jelennek meg a kimeneti pontokon.
Sávzáró és sáváteresztő szűrő
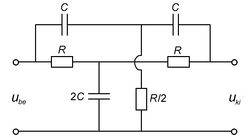
Alul és felüláteresztő szűrők egymás után kapcsolásával és az áteresztési tartományok helyes megválasztásával előállítható olyan szűrő, amelyik csak egy meghatározott tartományban csillapítja a jelet. Az ilyen kapcsolást nevezik sávzáró szűrőnek. Ennek egy realizálása a 3. ábrán látható kettős T szűrő.
A kapcsolás részletes elemzése nélkül is megállapítható, hogy alacsony frekvenciákon a hosszági ellenállásokon, magas frekvenciákon a hosszági kondenzátorokon jut jel a kimenetre.
Ehhez hasonlóan alul- és felüláteresztő szűrőkből összeállítható olyan kapcsolás is, amely csak egy meghatározott tartományban engedi át a jeleket. Ezek a sáváteresztő szűrök.
Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. műveleti erősítő) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.
Soros rezgőkör
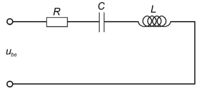
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (4. ábra).
A hálózat eredő impedanciája:
![\[\mathbf{Z}(\omega) = R + j\omega L + 1/j\omega C\]](/images/math/6/0/4/60452012ac73440dd34795ed2669eae4.png)
Az impedancia abszolút értéke és fázisszöge:
![\[Z(\omega) = \sqrt{R^2 + (\omega L-1/\omega C)^2}\]](/images/math/5/5/5/55535c841c82dfc3c1deb89925ebde9f.png)
![\[\tan\varphi = \frac{\omega L - 1/\omega C}{R}\]](/images/math/9/8/7/9874e1a562fd3e9e0266d10c87eff028.png)
A körben folyó áram:
![\[I(\omega) = \frac{U_{be}}{\sqrt{R^2 + (\omega L-1/\omega C)^2}}\]](/images/math/1/f/c/1fc5af577ff9a60e6ead580ec5662da9.png)
A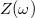 
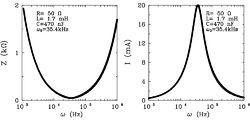
és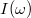 
függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (5. ábra).
Látható, hogy az eredő impedanciának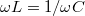 
esetén az
![\[\omega_0 = \frac{1}{\sqrt{LC}}\]](/images/math/a/d/4/ad4a43ecaf657200d72e8c141af15534.png)
körfrekvencián minimuma van, értéke valós, a veszteségi ellenállással egyezik meg. A jelenséget rezonanciának, 
-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, úgynevezett áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.
Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymással 180°-os szöget zárnak be, abszolút értékük megegyezik, hiszen azonos áram folyik át rajtuk (6. ábra).
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
- Általános megjegyzések:
- A méréshez szükséges alkatrészek egy átlátszó plexidobozban találhatók, banánhüvelyes kivezetésekkel. Az alkatrészek körülbelüli értékei a dobozról leolvashatók, illetve a mellékelt lapon is megtalálhatók.
- Az egyes mérési feladatok elvégzésekor azokban a frekvenciatartományokban, ahol jelentős a kimenő jel változása, sűrűbben vegyen fel mérési pontokat!
- Az oszcilloszkópot csak esetleges ellenőrzésre használja, a frekvenciákat és a feszültségeket a digitális műszerekkel kell mérni.
1. Mérje meg a dobozban található ellenállások értékét valamint a tekercsek ohmos ellenállását multiméterrel!
- Az ellenállásmérést csak hálózatba be nem kötött elemeken szabad végezni!
2. Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget függvényében! Ábrázolja a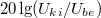 
– 
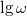függvényt! Illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző 
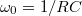körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor (mért) kapacitását! (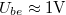
legyen!)
- A multiméterekkel mérhető frekvenciatartomány: 5 Hz – 100 kHz. Az és (névleges) értékeket úgy kell kiválasztani a panelen lévők közül, hogy
lehetőleg ennek a tartománynak a közepe táján (0,5-1 kHz körül) legyen. Figyelem! A képletekből -t számolunk, de a műszerek 
-et mérnek!
- A mérési naplóban írja le, hogy milyen elemeket használt fel a kapcsolás összeállításához! Válaszát számítással indokolja.
- Mivel az eredményeket logaritmikus skálán fogja ábrázolni, érdemes nagyjából logaritmikusan egyenletes sűrűséggel felvenni az adatokat. Pl.: 5 Hz, 10 Hz, 20 Hz, 50 Hz, 100 Hz, ...
3. Állítson össze felüláteresztő szűrőt kondenzátor felhasználásával! A feladatokat az 2. pont szerint végezze el!
- Vegye észre, hogy az alul- és felüláteresztő szűrő ugyanaz a kapcsolás, csak az egyiknél az ellenálláson, a másiknál a kondenzátoron mérjük a kimenő feszültséget. Mivel három műszer van, az egyikkel a bemenő feszültséget ellenőrizze, a másik kettővel pedig egyszerre lehet mérni az ellenálláson és kondenzátoron eső feszültséget, így a két karakterisztika egyszerre felvehető.
4. Állítson össze soros rezgőkört! külön elemként legyen bekötve, mert a kör áramát az ellenálláson eső feszültségből fogja meghatározni! A frekvencia függvényében mérje meg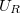 
, 
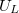, és 
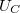értékeit! Számítsa ki és ábrázolja a körben folyó 
áramot és a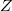 
eredő impedanciát függvényében. A mért adatokra illesszen megfelelő függvényeket, és az illesztésből határozza meg -t. Az eredmény (és a korábban megmért , 
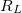és értékek) alapján határozza meg a tekercs induktivitását!
- Melyik ellenállást célszerű választani az RLC-kör összeállításához, ha azt szeretné, hogy a rezonanciagörbe minél élesebb legyen? Válaszát indokolja!
- Az illesztésnél vegye figyelembe a tekercs (korábban megmért) ohmos ellenállását is!
5. Végezze el az előző mérést egy nagyobb sorbakötött ellenállással is! Végezze el most is az illesztést! Ábrázolja a két mérésnél kapott 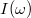rezonanciagörbéket közös garfikonban!
FONTOS! Ebből a mérésból és a kényszerrezgés vizsgálata mérésből közös jegyzőkönyvet kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!
Vissza a Fizika laboratórium 1. tárgyoldalára.
