Számítógépes mérések

A mérés célja:

- megismerkedni laboratóriumban használt Vernier LabPro számítógépes adatgyűjtő rendszerrel, és gyakorlatot szerezni a számítógéppel gyűjtött adatok feldolgozásában.

Ennek érdekében:

- egyszerű méréseket végzünk a számítógépes adatgyűjtő rendszerrel (RC kör időállandójának mérése az exponenciális kisülés vizsgálatával, ill. hangtani mérések mikrofonnal).

- kiértékeljük a mérési eredményeket Origin szoftver segítségével.

Elméleti összefoglaló

Bevezetés

A laboratóriumi gyakorlat során személyi számítógéphez csatlakoztatott mérési adatgyűjtő interfész segítségével végzünk méréseket. A számítógépek felépítéséről és működésük alapelveiről hasznos információkat tartalmaz egy korábbi mérésleírás „Rakjunk össze számítógépet!” címmel. A következőkben két számítógépes mérési feladatot, illetve a méréshez használt Vernier LabPro interfész használatát ismertetjük.

Kondenzátor kapacitásának mérése exponenciális kisülés vizsgálatával

1.ábra: Kapcsolási rajz

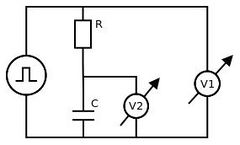
Tekintsük az 1. ábrán vázolt kapcsolást, melyen egy soros RC kört egy négyszögjel segítségével hajtunk meg. A négyszögjel feszültsége U₀ és 0 feszültség között váltakozik. A négyszögjelet biztosító generátor kimenetére kötjük a vizsgált rendszerünket, mely egy sorba kapcsolt kapacitásból (C) és ellenállásból (R) áll. A jelgenerátor kimenő feszültségét (V₁(t)) ill. a kondenzátoron eső feszültséget (V₂(t)) számítógépes adatgyűjtő rendszerrel mérjük.

A négyszögjel ráadásakor a kapacitás feltöltődik U₀ feszültségre, majd mikor a generátor feszültsége 0-ra esik, a kondenzátor kisül az ellenálláson keresztül. Az R ellenállás értékét úgy választjuk, hogy lényegesen nagyobb legyen a függvénygenerátor belső ellenállásánál (50 Ω-nál), így a kisülés sebességét csak R és C értéke határozza meg. A kondenzátor feszültsége:

$\[ U = \frac{1}{C} Q \]$

(1)

így a feszültség deriváltja:

$\[ \dot U = \frac{1}{C} \dot Q = \frac{1}{C} I = - \frac{U}{R C} \]$

(2)

Ez alapján a kondenzátor feszültségének időfüggése a kisülés közben:

$\[ U(t) = U_0 \cdot e^{-\frac{t}{RC} } \]$

(3)

A kisülés karakterisztikus idejét a 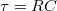$\setbox0\hbox{$ \tau = RC $}% \message{//depth:\the\dp0//}% \box0%$ időállandó jellemzi. Az exponenciális kisülést számítógéppel felvéve az időállandó, ill. ismert ellenállás esetén a kapacitás értéke meghatározható.

Hangtani mérések mikrofon segítségével

A mérés során egy hangvilla ill. egy fújással megszólaltatott kémcső által kiadott hangokat rögzítjük és analizáljuk számítógéphez csatlakoztatott mikrofon segítségével.

Egy hangszer által kiadott tiszta hang egy $\setbox0\hbox{$ \nu $}% \message{//depth:\the\dp0//}% \box0%$ frekvenciájú periodikus jelnek felel meg, melyben az alaphangnak megfelelő $\setbox0\hbox{$ \nu $}% \message{//depth:\the\dp0//}% \box0%$ frekvenciás szinuszos rezgés mellett az alaphang felharmonikusai is szerepelnek. Ez matematikailag a Fourier-sorfejtés segítségével fogalmazható meg. Vegyünk egy tetszőleges $\setbox0\hbox{$ \nu $}% \message{//depth:\the\dp0//}% \box0%$ frekvenciás f(t) jelet, melyre:

$\[ f ( t ) = f \left( t + \frac{n}{\nu} \right) \]$

(4)

tetszőleges n egész számra. Ez a függvény kifejthető a következő ún. Fourier-sorral:

$\[ f ( t ) = \displaystyle\sum\limits_{n=1}^{\infty} A_n \sin \left( 2 \pi n \nu t + \varphi_n \right) \]$

(5)

ahol az A_n ill. φ_n megadják, hogy a jelben milyen amplitúdóval és milyen fázistolással szerepel az 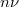$\setbox0\hbox{$n \nu$}% \message{//depth:\the\dp0//}% \box0%$ frekvenciájú felharmonikus. Azonos hangmagasságon megszólaltatott különböző hangszerek a felharmonikusok eltérő amplitúdói és fázisai miatt szólnak másként.

Ha a jelünk nem periodikus, akkor is felbonthatjuk különböző frekvenciájú komponensekre. Ezt a műveletet hívjuk Fourier-transzformációnak:

$\[ F(\nu)=\int\limits_{-\infty}^{\infty} f(t) e^{-{\rm i}2\pi\nu t} {\rm d}t \]$

(6)

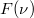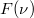ahol $\setbox0\hbox{$F(\nu)$}% \message{//depth:\the\dp0//}% \box0%$ megadja, hogy egy adott $\setbox0\hbox{$\nu$}% \message{//depth:\the\dp0//}% \box0%$ frekvenciájú komponens mekkora járulékot ad a jelünkhöz. ($\setbox0\hbox{$F(\nu)$}% \message{//depth:\the\dp0//}% \box0%$ komplex szám, melynek abszolút értéke adja meg a $\setbox0\hbox{$\nu$}% \message{//depth:\the\dp0//}% \box0%$ frekvenciás komponens amplitúdóját, fázisa pedig a fázistolást.) Ha a Fourier-transzformációt egy periodikus jelre alkalmazzuk, akkor az alapfrekvenciánál ($\setbox0\hbox{$\nu$}% \message{//depth:\the\dp0//}% \box0%$), és a felharmonikusoknál ($\setbox0\hbox{$n \nu$}% \message{//depth:\the\dp0//}% \box0%$) 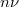kapunk csúcsokat, melyek nagysága megadja a különböző felharmonikusok amplitúdóját.

Mérésekben a jelünket csak diszkrét pontokban ismerjük ( f(t_n) ), így a fenti folytonos Fourier-integrált is ún. diszkrét Fourier-transzformáció (DFT) helyettesíti:

$\[ F(\nu)=\displaystyle\sum\limits_{n=1}^{N} f(t_n) e^{-{\rm i}2\pi\nu t_n} \cdot\Delta t_n \]$

(7)

A diszkrét Fourier-transzformáció hatékony kiszámítására különböző algoritmusokat használhatunk, melyek közül kiemelkedően fontos az ún. FFT, „Fast Fourier Transformation”.

A diszkrét Fourier-transzformáció fontos összefüggése a Nyquist-Shannon-féle mintavételezési tétel. Ha egy időfüggő jelből t idő alatt N-szer veszünk mintát ekvidisztáns Δt = t/N időközönként, akkor a vett mintából a teljes spektrum csak f_max=N/(2t) maximális frekvenciáig, Δf =1/t feloldással rekonstruálható. Másként kimondva, ha egy f_max frekvenciánál nagyobb frekvenciakomponenst nem tartalmazó (sávkorlátozott) jelet akarunk mintavételezni, akkor legalább 2f_max mintavételi frekvenciával kell mérni. A mérés hossza pedig a frekvenciafölbontást javítja.

A mérésben egy hangvilla és egy kémcsőben levő levegőoszlop rezgéseit vizsgáljuk. A hangvillára jellemző, hogy rezgési spektrumában csak az alaphang szerepel, nincsenek felharmonikusok. A kémcsövet egy egyik oldalán zárt sípnak tekinthetjük, melyben ideális esetben λ=4L/(2n+1) hullámhosszú állóhullámok alakulhatnak ki, ahol L a kémcső hossza, n pedig egy egész szám. A fenti feltétel abból ered, hogy a kémcső szájánál az állóhullámok duzzadóhelyei, a kémcső alján pedig csomópontok találhatók. Az így kialakuló rezgések frekvenciái:

$\[ \nu=\frac{c}{\lambda}=\frac{c}{4L}(2n+1) \]$

(8)

ahol c a hang terjedési sebessége levegőben. Látszik, hogy félig zárt síp hangjában csak az alaphang páratlan felharmonikusai szerepelnek. A kémcsőben kialakuló rezgések frekvenciáit, illetve a kémcső hosszát megmérve meghatározható a hang terjedési sebessége.

A Vernier LabPro interfész használata

2.ábra: Vernier LabPro interfész

A méréseket a 2. ábrán látható Vernier LabPro interfész segítségével végezzük, melyhez különböző szenzorok csatlakoztathatók. A mérés során két feszültségszenzort ill. egy mikrofont használunk. Az interfész soros vagy USB porton keresztül csatlakoztatható a számítógéphez, és a szenzorok jelét a Logger Pro szoftver segítségével rögzítjük.

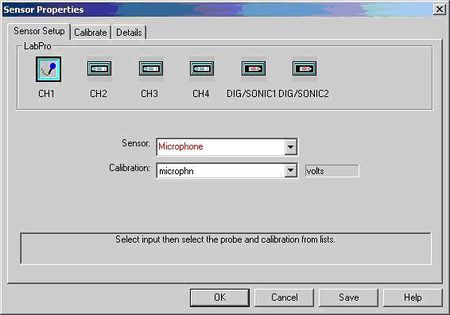
A szoftver elindítása után először be kell állítani, hogy milyen szenzorral (szenzorokkal) kívánunk mérni. Az 3. ábrán látható ablakhoz a Setup/Sensors gombokkal juthatunk el. Az ábrán látható beállításban az interfész CH1-es bemenetéhez a mikrofont társítottuk.

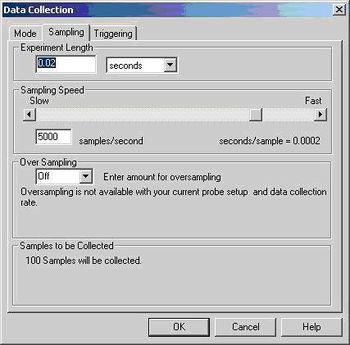
3.ábra: A szenzorok beállítása	4.ábra: Az adatgyűjtés beállítása

A következő feladat az adatgyűjtés paramétereinek megadása. A Setup/Data Collection/Sampling gombokkal a 4. ábrán látható ablakhoz jutunk. Itt állíthatjuk be a mérés hosszát és a mintavételezési frekvenciát. (A többi beállítást hagyjuk alapértéken!)

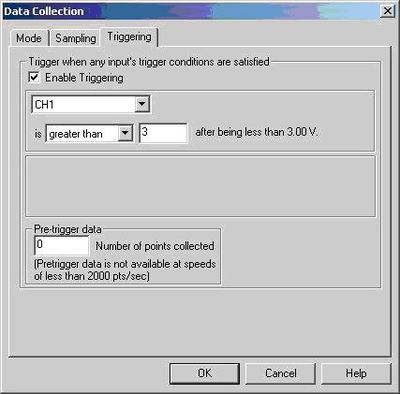
Mindkét mérésnél célszerű a mérőrendszert oszcilloszkóphoz hasonló üzemmódban használni. Ehhez a Setup/Data Collection/Mode menüben állítsunk be ismétlődő mintavételezést (repeat), melynek hatására a Sampling menüben beállított mérési hossz eltelte után újra kezdi a mérést a rendszer. A mintavételezést Setup/Data Collection/Triggering menü segítségével szinkronizálhatjuk a mért jel periódusával. Az 5. ábrán látható beállítás esetén a mintavételezés mindig akkor kezdődik, mikor a mért jel (CH1) értéke pozitív meredekséggel átlépi a beállított 3 V-os küszöbszintet.

5.ábra: Trigger beállítása	6.ábra: A grafikon beállítása

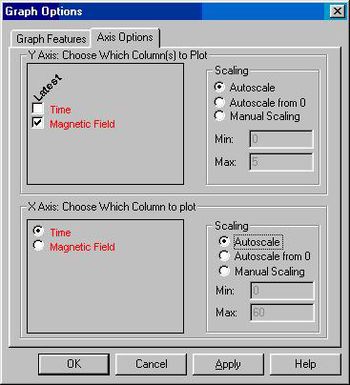
A View/Graph Options/Axis Options gombok segítségével jeleníthetjük meg a 6. ábrán látható ablakot, ahol a grafikon tulajdonságait állíthatjuk be.

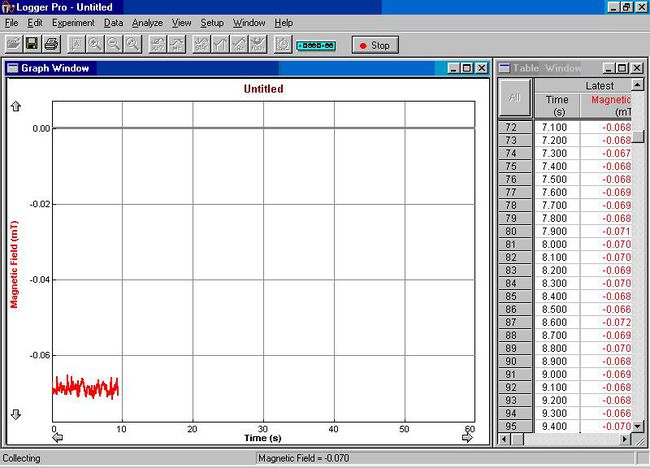
A mérést a fő ablakban (7. ábra) található Collect/Stop gombbal indíthatjuk el, ill. állíthatjuk le.

7.ábra: Logger Pro főmenü

A mérés végén az adatokat nem a Save utasítással kell elmenteni (ekkor olyan fájlt kapnánk, amit később is csak ezzel a programmal tudnánk megnyitni), hanem exportálni kell (File/Export Data)! Az így elmentett textfájlokat később bármely más adatkezelő programmal (Origin, Excel, stb.) meg lehet nyitni.

Mérési feladatok

RC kör időállandójának meghatározása

Állítsuk össze a 1. ábrán szereplő kapcsolást. A jelgenerátor kimenő feszültségét és a kondenzátoron eső feszültséget kössük a VernierPro interfész bemeneteire. A LoggerPro adatgyűjtő szoftverben az interfész megfelelő bemeneteit állítsuk feszültségmérő üzemmódba. (Setup → Sensors → Voltage (-10 – 10V)). Állítsunk be megfelelő mintavételezési sebességet (Setup → data collection → sampling), és állítsunk be oszcilloszkóp-szerű ismétlődő adatgyűjtést (Setup → data collection → mode → repeat). A jelgenerátor kimenő feszültségét használjuk trigger jelnek (Setup → data collection → triggering).

A jelgenerátor amplitúdójának és offset értékének beállításával érjük el, hogy a négyszögjel platói 5 V ill. 0 V feszültségértékeknél helyezkedjenek el. Keressünk megfelelő ellenállásértéket, mellyel a mérendő kapacitás kisülésének időállandója összemérhető a négyszögjel periódusidejének ~1/10 részével, és így az exponenciális kisülés jól látható.

Rögzítsük az exponenciális kisülést számítógéppel, vigyük át az adatokat Originbe, határozzuk meg a kisülés időállandóját. Ehhez válasszuk ki a kisüléshez tartozó görbeszakaszt, és erre illesszünk 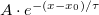$\setbox0\hbox{$ A \cdot e^{-(x-x_0)/ \tau } $}% \message{//depth:\the\dp0//}% \box0%$ függvényt. Az ismert ellenállásértéket behelyettesítve számítsuk ki a mérésben használt kondenzátor ismeretlen kapacitását, és becsüljük meg a meghatározott kapacitásérték hibáját.

A (2) képlet alapján a kondenzátor feszültségének a deriváltja arányos a kondenzátor feszültségével, és az arányossági tényező a rendszer időállandója. Ezt az összefüggést ellenőrizzük a kisülési görbe numerikus deriválásával.

A fenti mérési feladatokat végezzük el mind a C₁, mind a C₂ jelzésű kondenzátorokon. (A kondenzátorok bekötésénél ügyeljünk a polaritásra!) Az első kondenzátoron végzett méréseket még a mérési gyakorlat során értékeljük ki, felmerülő problémák esetén kérjük a gyakorlatvezető segítségét.

Hangtani mérések mikrofonnal

Csatlakoztassuk a mikrofont a VernierPro interfészhez, és a Logger Pro szoftverben állítsuk a megfelelő bemenetet „microphone” üzemmódba.

Szólaltassuk meg a hangvillát, és vegyük fel a hangját a mikrofon segítségével. Vigyük át az adatokat Originbe, és határozzuk meg a hangvilla sajátfrekvenciáját. Ehhez először nemlineáris görbeillesztés segítségével illesszünk 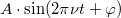$\setbox0\hbox{$ A \cdot \sin (2\pi \nu t+\varphi) $}% \message{//depth:\the\dp0//}% \box0%$ függvényt a mért adatokra. Ezután Fourier-transzformáljuk az adatokat, és a Fourier-transzformáltból olvassuk le a sajátfrekvenciát. Az illesztéssel és a Fourier-transzformációval kapott frekvenciákat hasonlítsuk össze.

Válasszunk olyan mintavételi paramétereket, hogy a hangvilla sajátfrekvenciáját a lehető legpontosabban tudjuk mérni (a Nyquist-Shannon-féle mintavételezési tételt figyelembe véve). Mekkora a legkisebb mintavételi frekvencia, amellyel a hangvilla sajátfrekvenciája meghatározható? Határozzuk meg a sajátfrekvenciát a lehető legkisebb hibával! Mekkora ez a hiba?

Szólaltassuk meg a kémcsövet (fújjunk bele!), és vegyük fel a rezgéseit mikrofonnal. Fourier-transzformációval határozzuk meg az alaphang ill. a felharmonikusok frekvenciáit és relatív amplitúdóit. Az így kapott frekvenciákat hasonlítsuk össze az elméleti várakozásokkal. Az alaphang frekvenciáját és a kémcső hosszát megmérve határozzuk meg a hang terjedési sebességét. Itt is törekedjünk a mintavételezés olyan beállítására (mérési idő, mintavételezési frekvencia), hogy a legkisebb hibával meghatározhatóak legyenek az alaphang és a felharmonikusok (az első öt) frekvenciái!

A kémcsőbe vizet töltve határozzuk meg az alapfrekvencia függését a kémcső hosszától (az üres kémcső mellett vizsgáljunk három különböző vízszintet), és hasonlítsuk össze eredményeinket az elméleti összefüggésekkel!