Egyszerű RL, RC, RLC körök megoldásai
Tartalomjegyzék[elrejtés] |
Váltakozó áram, váltakozó feszültség
Mint azt az indukció tárgyalásánál láttuk, az effektus egyik – talán legfontosabb – alkalmazása a váltakozó feszültségű generátor. A generátor által biztosított váltakozó feszültség:
![\[ U(t) = U_0 sin(\omega t) \]](/images/math/c/5/f/c5fee7df0b393c7e6eb6e3c40c7305fc.png) |
(1.1) |
ahol 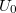 a maximális feszültségérték vagy feszültségamplitúdó, és
a maximális feszültségérték vagy feszültségamplitúdó, és  a körfrekvencia.
Az áramkörök válasza erre a gerjesztésre általában a váltakozó áram:
a körfrekvencia.
Az áramkörök válasza erre a gerjesztésre általában a váltakozó áram:
![\[ I(t) = I_0 sin(\omega t - \varphi) \]](/images/math/b/b/4/bb4e62a6a1c4cd35a10f311f330d8fbe.png) |
(1.2) |
Itt 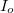 a maximális áramerősség és
a maximális áramerősség és 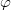 azt mutatja, hogy az áram mennyit késik (vagy siet) a feszültséghez képest.
azt mutatja, hogy az áram mennyit késik (vagy siet) a feszültséghez képest.
Nézzük meg először, hogy mi történik, ha az 1.1 szerint megadott váltófeszültséget kapcsolunk egy ohmikus terhelésre vagy fogyasztóra, mondjuk egy merülőforralóra (1.1 ábra).
| 1.1 ábra |
A huroktörvény alkalmazásával, vagy talán kevésbé elegánsan, az Ohm-törvény segítségével kapjuk az ellenálláson átfolyó áram értékét:
![\[ I(t) = \frac {U_0}{R} sin(\omega t) \]](/images/math/8/3/9/8392a3321ec9144c309ed8989d85c211.png) |
(1.3) |
Jól látszik, hogy az áramerősség maximális értékét az 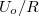 hányados adja, azaz
hányados adja, azaz 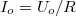 és hogy az áram ”nem késik” a feszültséghez képest. Arra a kérdésre pedig, hogy mekkora teljesítmény disszipálódik az
és hogy az áram ”nem késik” a feszültséghez képest. Arra a kérdésre pedig, hogy mekkora teljesítmény disszipálódik az  ellenállású fogyasztón, kétféle választ adhatunk. Először is megadhatjuk a pillanatnyi veszteséget, a Joule-törvény segítségével:
ellenállású fogyasztón, kétféle választ adhatunk. Először is megadhatjuk a pillanatnyi veszteséget, a Joule-törvény segítségével:
![\[ P(t)=I(t)U(t) = \frac {U^2_0}{R} sin^2(\omega t) \]](/images/math/d/d/8/dd83ae649f7aea99933493092b242a1f.png) |
(1.4) |
Minthogy az általunk használt váltakozó feszültség frekvenciája 50 Hz, ezért a disszipált teljesítmény időfüggésével – legtöbbször, pl. egy merülőforraló esetében – értelmetlen dolog foglalkozni. Jobban használható adat egy fogyasztó esetében az átlagteljesítmény:
![\[ P_{\acute{a}tl}= \left< I(t)U(t) \right > = \frac{1}{T} \int\limits_0^T P(t)dt \]](/images/math/e/f/e/efe58325d63211d785c272ceaa24061c.png) |
(1.5) |
Ebben a konkrét példában:
![\[ P_{\acute{a}tl}= \frac{1}{T} \int\limits_0^T \frac {U^2_0}{R} sin^2(\omega t)dt \]](/images/math/3/6/8/36874ff7145ec58d38dd38f60ac90d46.png) |
(1.6) |
Nem nehéz megmutatni, hogy:
![\[ P_{\acute{a}tl}= \frac {U^2_0}{2R} \]](/images/math/c/6/3/c63c1dd627cd7ddf873ed3bad526f8cf.png) |
(1.7) |
A kapott eredményt írhatjuk így is:
![\[ P_{\acute{a}tl}= \frac {1}{R} \left( \frac {U_0}{\sqrt {2}} \right)^2 \]](/images/math/c/2/c/c2cdc3a624bcd57db6d0b8e583e36492.png) |
(1.8) |
Ennek pedig a következő az olvasata: a fogyasztón disszipált átlagteljesítmény akkorának adódik, mintha egy olyan egyenfeszültség-forrást kapcsoltunk volna a fogyasztóra, amelynek az elektromotoros ereje 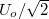 , ezt hívjuk effektív feszültségnek:
, ezt hívjuk effektív feszültségnek:
![\[ U_{eff} = \frac {U_0}{\sqrt {2}} \]](/images/math/9/7/5/97500ce03d32e275cb78bc0ac4bb92ac.png) |
(1.9) |
Hasonló módon bevezethetjük az effektív áramerősséget is:
![\[ I_{eff} = \frac {I_0}{\sqrt {2}} \]](/images/math/1/3/c/13c2fb6625a8791dec9a0a0b41c47e60.png) |
(1.10) |
Az effektív feszültség és áramerősség segítségével az átlagteljesítmény - ohmikus ellenállás esetén - a szokásos módon számítható:
![\[ P_{\acute{a}tl}= RI^2_{eff} = I_{eff} U_{eff} = \frac {U^2_{eff}}{R} \]](/images/math/b/f/1/bf1faa1439c9ecfb4922c0b4a68c0b5d.png) |
(1.11) |
Mint azt a bemutatott példán láttuk, az ohmikus fogyasztó esetében az áram és a feszültség "fázisban vannak", azaz nincs köztük fáziskülönbség.
Most rugaszkodjunk el az előző egyszerű példától és tegyük fel, hogy a váltakozó feszültség és áram között fáziskülönbség van, azaz:
![\[U(t) = U_0 sin(\omega t) \qquad {\rm {\acute{e}}s} \qquad I(t) = I_0 sin(\omega t - \varphi) \]](/images/math/4/9/f/49fcbd669e261bd75e7adb2dee2c9583.png) |
(1.12) |
Számítsuk ki az átlagteljesítményt ebben az esetben:
![\[ P_{\acute{a}tl}= \frac{1}{T} \int\limits_0^T P(t)dt = \frac{1}{T} \int\limits_0^T U_0 I_0 sin(\omega t)sin(\omega t - \varphi)dt \]](/images/math/4/a/2/4a29fb43ad51895e66c153f1f55122d9.png) |
(1.13) |
Könnyű belátni, hogy:
![\[ P_{\acute{a}tl}= U_{eff} I_{eff} cos(\varphi) \]](/images/math/0/4/b/04b8847696b1c970ca17ee9cfa94139f.png) |
(1.14) |
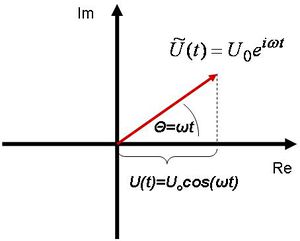
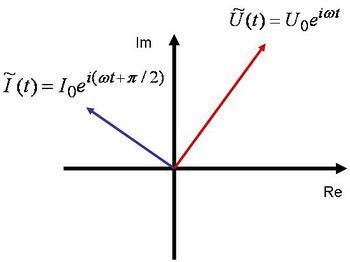
A váltakozó áram és feszültség időfüggését szemléletesen lehet bemutatni a komplex síkon. Ezt a következőképpen tehetjük meg; legyen, mondjuk a feszültség a következő formában megadva:
![\[ U(t) = U_0 cos(\omega t) \]](/images/math/3/2/6/326dab122555dcdc11d3b034765e4707.png) |
(1.15) |
Ezt át lehet írni a következő alakba:
![\[ U(t) = Re [ U_0 e^{i\omega t} ] \]](/images/math/3/3/e/33e6561061423f52dd4caa192e3cc6d5.png) |
(1.16) |
A feszültséget tehát komplex alakban is felvehetjük:
![\[ \widetilde{U}(t) = U_0 e^{i\omega t} \]](/images/math/a/0/a/a0a8785e47bd64c366545e9f1fc55b7e.png) |
(1.17) |
Ez pedig egy 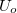 abszolút-értékű vektor, amely
abszolút-értékű vektor, amely  körfrekvenciával forog a komplex számsíkon, amint ez az 1.2 ábrán látható.
körfrekvenciával forog a komplex számsíkon, amint ez az 1.2 ábrán látható.
| 1.2 ábra |
Természetesen az áramot is megadhatjuk komplex alakban (az áram késik a feszültséghez képest):
![\[ \widetilde{I}(t) = I_0 e^{i\omega t - \varphi} \]](/images/math/4/e/6/4e606f5647965f0a5f6bd82525b31ff7.png) |
(1.18) |
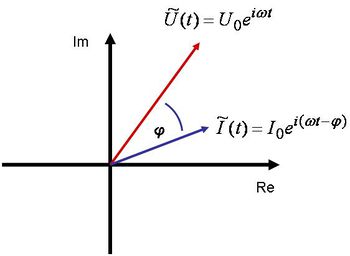
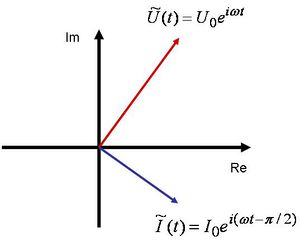
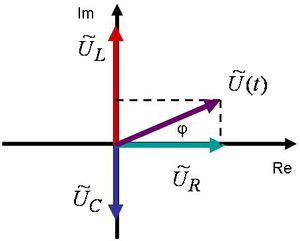
Az ábrázolásmód haszna abban rejlik, hogy a komplex síkon egyszerre ábrázolhatjuk a feszültséget és az áramot:
| 1.3 ábra |
Természetesen az 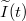 és az
és az  komplex vektorok ω szögsebességgel forognak, miközben
komplex vektorok ω szögsebességgel forognak, miközben 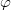 szöget zárnak be egymással. Az
szöget zárnak be egymással. Az  szögsebességű forgást azonban könnyen leválaszthatjuk az
szögsebességű forgást azonban könnyen leválaszthatjuk az 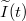 és az
és az  komplex vektorokról, amennyiben midkét tagot elosztjuk az
komplex vektorokról, amennyiben midkét tagot elosztjuk az 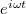 -vel.
-vel.
Most nézzük meg, hogy mi történik, ha egy kondenzátorra váltófeszültséget kapcsolunk (1.4 ábra).
| 1.4 ábra |
A huroktörvény alkalmazásával kapjuk a következő összefüggést:
![\[ \frac {Q}{C} = U_0 sin(\omega t) \]](/images/math/3/5/2/3520d2d63c173ecffd2176b17be4014c.png) |
(1.19) |
Az áram definíciójának felhasználásával:
![\[ \frac {1}{C} \int I(t)dt = U_0 sin(\omega t) \]](/images/math/8/f/c/8fced729c7511cce4a6c0649da2ac120.png) |
(1.20) |
Mindkét oldalt deriválva kifejezhetjük 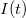 – t:
– t:
![\[I(t) = C \omega U_0 cos(\omega t) \qquad {\rm {azaz}} \qquad I(t) = \frac {U_0}{X_C} cos(\omega t) = \frac {U_0}{X_C} sin(\omega t + \frac {\pi}{2}) \]](/images/math/1/8/d/18d0a9a48eea3728c9f0f5ff312aa1d4.png) |
(1.21) |
ahol 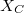 a kapacitív ellenállás, más néven kapacitív reaktancia:
a kapacitív ellenállás, más néven kapacitív reaktancia:
![\[ X_C = \frac {1}{C\omega} \]](/images/math/2/4/8/248cf6c5b94aab1451f4dcd9708985de.png) |
(1.22) |
Az áramot megadó 1.21-ből két dolog is következik; egyrészt a kondenzátor úgy viselkedik, mint egy olyan eszköz, amelynek az ellenállása frekvenciafüggő, másrészt pedig az áram  -ot siet a feszültséghez képest (1.5 ábra).
-ot siet a feszültséghez képest (1.5 ábra).
| 1.5 ábra |
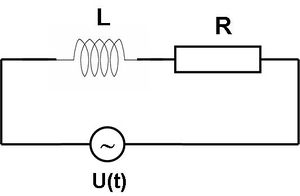
Hasonlóképpen megvizsgálhatjuk azt is, hogy miként reagál egy szolenoid vagy egy toroid (egy olyan eszköz, amelynek önindukciós tényezője L), ha rá váltakozó feszültséget kapcsolunk (1.6 ábra). Az egyszerűség kedvéért feltesszük, hogy az ohmikus ellenállás elhanyagolható.
| 1.6 ábra |
Most is alkalmazhatjuk a huroktörvényt:
![\[ U(t) - L \frac {dI}{dt} = 0 \]](/images/math/0/e/3/0e33ca274c9ad7d9a3c633f42365a501.png) |
(1.23) |
Ezt kissé átrendezhetjük és beírhatjuk a feszültség időfüggését:
![\[ \frac {dI}{dt} = \frac {1}{L} U_0 sin(\omega t) \]](/images/math/d/4/d/d4d707eb71d4a2ae89e5ae965700ae83.png) |
(1.24) |
Az 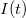 áramot megkaphatjuk, ha mindkét oldalt integráljuk a
áramot megkaphatjuk, ha mindkét oldalt integráljuk a 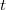 szerint:
szerint:
![\[ I(t) = - \frac {U_0}{L \omega} cos(\omega t) = \frac {U_0}{X_L} sin(\omega t - \frac {\pi}{2}) \]](/images/math/a/8/f/a8feed9eb70062e84ea295fa82725470.png) |
(1.25) |
ahol 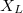 a tekercs induktív ellenállása (más néven: induktív reaktancia):
a tekercs induktív ellenállása (más néven: induktív reaktancia):
![\[ X_L = L\omega \]](/images/math/4/4/6/446f301b88dfafda93c23b99e8d71885.png) |
(1.26) |
Az 1.25 formula egyrészt megadja azt, hogy az induktív ellenállás hogyan függ a frekvenciától, másrészt pedig, hogy az áram fázisban éppen 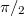 -vel marad le a feszültségtől (1.7 ábra). Ez utóbbi állítást természetesen fordítva is meg lehet fogalmazni, azaz hogy a feszültség siet az áramhoz képest.
-vel marad le a feszültségtől (1.7 ábra). Ez utóbbi állítást természetesen fordítva is meg lehet fogalmazni, azaz hogy a feszültség siet az áramhoz képest.
| 1.7 ábra |
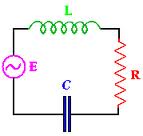
Most próbáljuk meg alkalmazni a tanult módszert a soros RLC kör esetén. Először tekintsük a következő ábrán látható elrendezést.
| 1.8 ábra |
A Kirchhhoff-féle huroktörvény alkalmazásával – figyelembe véve, hogy az áramerősség az áramkörben mindenhol ugyanazt az értéket veszi fel egyidejűleg – természetesen felírható egy differenciálegyenlet:
![\[ U(t)-L \frac {dI}{dt} - RI - \frac {Q}{C} = 0 \]](/images/math/f/a/d/fadaf9770e108f3bfe1dc741f5fb9474.png) |
(1.27) |
Ezzel most az a probléma, hogy két változó is szerepel benne, de az áram definícióját felhasználva felírható az előbbi egyenlet egyszerűbb alakban is:
![\[ L \frac {d^2 Q}{dt^2} + R\frac {dQ}{dt} + \frac {Q}{C} = U(t) \]](/images/math/f/f/9/ff988a32cbd7d9efeeba20d729898e8e.png) |
(1.28) |
ahol 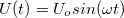 vagy
vagy 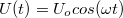 . Ez az egyenlet már megoldható, de mi most egyelőre nem így keressük a megoldást.
. Ez az egyenlet már megoldható, de mi most egyelőre nem így keressük a megoldást.
Használjuk fel az előzőekben tanultakat. Láttuk, hogy az áramhoz képest a kapacitív ellenálláson a feszültség késik  -ot és annak maximális értéke:
-ot és annak maximális értéke: 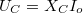 . Azt is megmutattuk, hogy az induktív ellenálláson a feszültség siet
. Azt is megmutattuk, hogy az induktív ellenálláson a feszültség siet  -ot és maximális értéke
-ot és maximális értéke 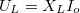 . Az ohmikus ellenálláson mérhető feszültség fázisban van az árammal és maximális értéke:
. Az ohmikus ellenálláson mérhető feszültség fázisban van az árammal és maximális értéke: 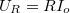 . Most csak annyit kell tennünk, hogy a komplex számsíkon ábrázoljuk a valós tengelyen felvett
. Most csak annyit kell tennünk, hogy a komplex számsíkon ábrázoljuk a valós tengelyen felvett 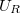 feszültséggel együtt a másik két feszültségértéket az említett fázistolásokkal, és venni kell ezek vektori eredőjét, hiszen a huroktörvény alapján:
feszültséggel együtt a másik két feszültségértéket az említett fázistolásokkal, és venni kell ezek vektori eredőjét, hiszen a huroktörvény alapján:
![\[ \widetilde{U}_R + \widetilde{U}_L + \widetilde{U}_C = \widetilde{U}(t) \]](/images/math/3/0/6/306beacaf2a124be9c33501f0da1b336.png) |
(1.29) |
Ugyanez a komplex síkon ábrázolva:
| 1.9 ábra |
Az ábráról leolvasható, hogy az áram a feszültséghez képest 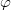 fázissal késik. Elemi geometriai megfontolások alapján:
fázissal késik. Elemi geometriai megfontolások alapján:
![\[ tg \varphi = \frac {\left|\widetilde{U}_L \right| - \left|\widetilde{U}_C \right| }{\left|\widetilde{U}_R \right|} \]](/images/math/a/5/6/a56762ab47d302332e9292a394444de2.png) |
(1.30) |
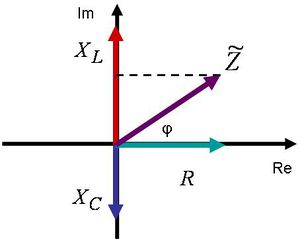
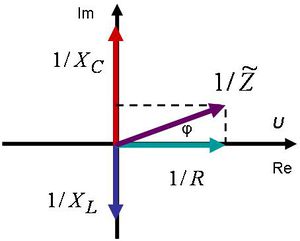
A második lépésben 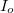 – val egyszerűsíthetünk. Most szükséges bevezetni egy új fogalmat a feszültség és az áram hányadosára, hiszen most már ez is egy komplex mennyiség lesz. Ez az új mennyiség a komplex impedancia, és jele:
– val egyszerűsíthetünk. Most szükséges bevezetni egy új fogalmat a feszültség és az áram hányadosára, hiszen most már ez is egy komplex mennyiség lesz. Ez az új mennyiség a komplex impedancia, és jele:  . Amennyiben
. Amennyiben 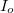 – val elosztjuk a 1.9 ábrán szereplő összes tagot, felrajzolható a soros RLC kör fazor ábrája:
– val elosztjuk a 1.9 ábrán szereplő összes tagot, felrajzolható a soros RLC kör fazor ábrája:
| 1.10 ábra |
Erről az ábráról egyrészt leolvasható, hogy mekkora az áram fáziskésése a feszültséghez képest. Másrészt pedig meghatározható az impedancia abszolút értéke, amely megadja a maximális feszültség és maximális áramerősség hányadosát, vagy – ami ugyanaz – az effektív feszültség és effektív áram hányadosának értékét. A komplex impedancia tehát:
![\[ \widetilde{Z} = R + i(X_L - X_C) \]](/images/math/8/f/2/8f2ee77eb40396a44122bf35d18f7f68.png) |
(1.31) |
és annak abszolút értéke:
![\[ \left|\widetilde{Z} \right| = Z = \frac {U_0}{I_0} = \sqrt {R^2 + (X_L - X_C)^2} = \sqrt {R^2 + \left( L\omega - \frac {1}{C\omega} \right)^2} \]](/images/math/4/5/1/4512c5795befd89f74c45997243a33ed.png) |
(1.32) |
Az áramkörben kialakuló áramerősség maximális értéke - és természetesen az effektív áramerősség is - tehát frekvenciafüggést mutat:
![\[ I_{eff} = \frac {U_{eff}}{Z(\omega)} \]](/images/math/e/9/2/e9220eaf217998d918f3db6ac6284510.png) |
(1.33) |
Az impedancia értékét megadó 1.32-ből következik, hogy abban az esetben lesz maximális az áramerősség, ha 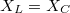 , azaz a váltakozó feszültség - és az áram - körfrekvenciája:
, azaz a váltakozó feszültség - és az áram - körfrekvenciája:
![\[ \omega_o = \frac {1}{\sqrt{CL}} \]](/images/math/5/9/4/5946dd526adb8b3056bb18a0976f77c6.png) |
(1.34) |
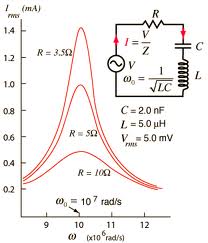
ahol 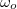 a soros RLC kör rezonanciafrekvenciája. Az áram rezonanciagörbéjét mutatja a következő ábra:
a soros RLC kör rezonanciafrekvenciája. Az áram rezonanciagörbéjét mutatja a következő ábra:
| 1.11 ábra |
Az 1.32 formulából következik az is, hogy az áramerősség maximális értékét rezonancia esetén az  ellenállás értéke határozza meg; ezt jól mutatják a 1.11 ábra rezonanciagörbéi. Az 1.30-ból pedig közvetlenül adódik, hogy a rezonancia megvalósulásánál az áram és a feszültség között nincs fáziskülönbség, valamint ilyenkor maximális az áram amplitúdója.
ellenállás értéke határozza meg; ezt jól mutatják a 1.11 ábra rezonanciagörbéi. Az 1.30-ból pedig közvetlenül adódik, hogy a rezonancia megvalósulásánál az áram és a feszültség között nincs fáziskülönbség, valamint ilyenkor maximális az áram amplitúdója.
A 1.10 ábráról az is leolvasható, hogy:
![\[ R = Z cos (\varphi) \]](/images/math/9/3/8/9386cd484d5ac9ea2d9f3857465c072d.png) |
(1.35) |
Most már viszonylag egyszerűen megadhatjuk az előző két összefüggés felhasználásával a soros RLC körön disszipált átlagteljesítményt:
![\[ P_{\acute{a}tl}= U_{eff}I_{eff}cos(\varphi) = U_{eff}I_{eff} \frac{R}{Z} = R I^2_{eff} \]](/images/math/e/8/2/e82b820bc53f96a96fd5a5adf11dfed5.png) |
(1.36) |
Ez az eredmény rávilágít arra a tényre is, hogy a veszteséget az ellenállás okozza. Az induktivitásra és a kapacitásra számítható átlagteljesítmény – ideális esetben – zérus, hiszen a rájuk eső feszültség és az átfolyó áram között 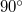 – os fáziskülönbség van.
A rezgőkört szokás még jellemezni az úgynevezett jósági tényező segítségével is. Ez a paraméter azt adja meg, hogy milyen arányban áll a rendszer energiája az egy periódus alatt történő energiaveszteséggel a rezonanciafrekvencián:
– os fáziskülönbség van.
A rezgőkört szokás még jellemezni az úgynevezett jósági tényező segítségével is. Ez a paraméter azt adja meg, hogy milyen arányban áll a rendszer energiája az egy periódus alatt történő energiaveszteséggel a rezonanciafrekvencián:
![\[ Q = 2 \pi \frac {\rm {a\, rendszerben \, t\acute {a} rolt \, energia}}{\rm {egy \, peri\acute{o}dus \, alatt \, disszip\acute{a}lt \, energia}} \]](/images/math/9/5/d/95dec2e1c92a93416e6ce0a1f3e7eb71.png) |
(1.37) |
Könnyen kiszámítható a definíció alapján, hogy soros rezgőkör esetében:
![\[ Q = \frac {L\omega_o}{R} \]](/images/math/0/c/8/0c8bab3ebd19135039a0ca8c17e7f76b.png) |
(1.38) |
A csillapított kényszerrezgés dinamikája és az RLC kör feszültség- valamint áramviszonyai hasonlóképpen tárgyalhatók. Tegyük fel, hogy egy Hooke-törvényt követő rugó végére kötünk egy 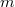 tömegű testet, amelyre egyrészt – a rugóerőn kívül – hat az
tömegű testet, amelyre egyrészt – a rugóerőn kívül – hat az 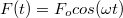 kényszererő, másrészt pedig a sebességgel arányos nagyságú, de azzal ellentétes irányú
kényszererő, másrészt pedig a sebességgel arányos nagyságú, de azzal ellentétes irányú 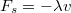 súrlódási erő (1.12 ábra).
súrlódási erő (1.12 ábra).
| 1.12 ábra |
A mozgásegyenletet a következő formában adhatjuk tehát meg:
![\[ ma = -kx-\lambda v + F_o cos(\omega t) \]](/images/math/e/d/8/ed803af4ebae1426936d6c179c5d43cb.png) |
(1.39) |
Elosztjuk mindkét oldalt a tömeggel és bevezetjük a 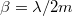 új paramétert, így kapjuk a jól ismert egyenletet:
új paramétert, így kapjuk a jól ismert egyenletet:
![\[ \ddot{x} + 2\beta \dot{x} + \omega^2_o x = f_o cos(\omega t) \]](/images/math/0/7/d/07d107a1d8ac18bb1bb55dbf236a3731.png) |
(1.40) |
ahol természetesen 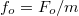 és
és 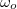 az oszcillátor saját (kör)frekvenciája. A differenciálegyenlet szembetűnő hasonlóságot mutat a 1.28 formulával; ebből következően a két egyenlet megoldása matematikailag hasonló. Az 1.40 egyenlet jobb oldalán álló tag írható a következő formába is:
az oszcillátor saját (kör)frekvenciája. A differenciálegyenlet szembetűnő hasonlóságot mutat a 1.28 formulával; ebből következően a két egyenlet megoldása matematikailag hasonló. Az 1.40 egyenlet jobb oldalán álló tag írható a következő formába is: ![\setbox0\hbox{$f_o cos(\omega t) = f_o Re \left[ exp(i\omega t) \right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/b/b/1/bb1450a8f6b12da29bf61582bd221802.png) . Most már megtehetjük, hogy a változót is komplexnek vesszük, de közben észben tartjuk, hogy csak a valós értéknek van fizikai jelentése. Ezután a megoldást a következő alakban keressük:
. Most már megtehetjük, hogy a változót is komplexnek vesszük, de közben észben tartjuk, hogy csak a valós értéknek van fizikai jelentése. Ezután a megoldást a következő alakban keressük:
![\[ x (t) = A e^{i\omega t} \]](/images/math/6/d/8/6d8e22cb6678f3c617f5e59042d594d4.png) |
(1.41) |
Helyettesítsünk be 1.40-be:
![\[ \left(\omega^2_o - \omega^2 + 2i\beta \omega \right) \widetilde {A} e^{i\omega t} = f_o e^{i\omega t} \]](/images/math/c/2/7/c27da368329e04db24c040b9a9513e48.png) |
(1.42) |
A komplex amplitúdó könnyen kifejezhető:
![\[ \widetilde {A} = \frac {f_o}{\left(\omega^2_o - \omega^2 + 2i\beta \omega \right)} = A e^{i\varphi} \]](/images/math/1/3/d/13db9ce7ff4347ea09731f20bce3992b.png) |
(1.43) |
ahol a rezgés 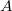 amplitúdója és
amplitúdója és 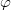 fázisa a következőféleképpen számítható:
fázisa a következőféleképpen számítható:
![\[ A = \frac {f_o}{\sqrt{\left(\omega^2_o - \omega^2 \right)^2 + 4\beta^2 \omega^2 }} \qquad {\rm {\acute{e}}s} \qquad tg(\varphi) = \frac {2\beta \omega}{\omega^2_o - \omega^2} \]](/images/math/5/0/6/5068b990d13ef9dbdfa020726d8118f7.png) |
(1.44) |
A mozgásegyenlet megoldása tehát:
![\[ x(t) = A cos ( \omega t - \varphi) \]](/images/math/9/9/1/991620bbf303c488956e38b66176291d.png) |
(1.45) |
Hasonlóképpen a soros RLC kör esetében is követhetnénk az itt bemutatott módszert, és akkor 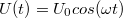 gerjesztés esetén írhatnánk, hogy:
gerjesztés esetén írhatnánk, hogy:
![\[ I(t) = I_o cos ( \omega t - \varphi) \]](/images/math/a/1/3/a1300974db4e820363de3145e9e76c78.png) |
(1.46) |
ahol a maximális áramerősség, azaz az áram-amplitúdó:
![\[ I_o = \frac {U_o}{\sqrt{R^2 + \left( L\omega - \frac {1}{C\omega} \right)^2}} \]](/images/math/8/f/d/8fd22c92c274c46d129585559f1fab0a.png) |
(1.47) |
Könnyű észrevenni a hasonlóságot 1.44 első formulája és 1.47 között. Azonban nemcsak a megoldás hasonló, hanem a levonható következtetések is; mindkét esetben fellép a rezonancia jelensége és a fáziskésés frekvenciafüggése is egy hasonló függvénnyel írható le, sőt még a jósági tényező meghatározása is ugyanazon definíció alapján történik. Meg lehet mutatni mindkét esetben, hogy ha a csillapítás nem erős, azaz például 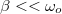 esetén, akkor a rezonanciagörbe félérték-szélessége arányos a csillapítással, vagyis
esetén, akkor a rezonanciagörbe félérték-szélessége arányos a csillapítással, vagyis 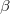 -val illetve az
-val illetve az  ellenállással.
Láttuk, hogy a fazorábra segítségével hogyan adható meg a soros RLC kör impedanciája valamit a feszültség és az áram közötti fázis.
ellenállással.
Láttuk, hogy a fazorábra segítségével hogyan adható meg a soros RLC kör impedanciája valamit a feszültség és az áram közötti fázis.
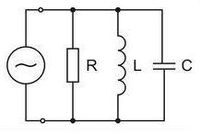
A módszer jól használható a párhuzamos RLC kör esetében is.
| 1.13 ábra |
Mint az 1.13 ábrán jól látszik, most a feszültség lesz mindegyik áramköri elemen ugyanaz minden pillanatban. Alkalmazhatjuk a csomóponti törvényt, azaz 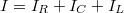 , azaz ugyanezt komplex alakban felírva és a feszültséggel osztva:
, azaz ugyanezt komplex alakban felírva és a feszültséggel osztva:
![\[ \frac {1}{\widetilde {Z}} = \frac {1}{R} + \frac {1}{iL\omega} - \frac {C\omega}{i} \]](/images/math/0/a/d/0ad715d90593e83a9b9fe834117ebee6.png) |
(1.48) |
Az ehhez tartozó fazorábra:
| 1.13 ábra |
Innen leolvasható, hogy az áram és a feszültség közötti fázis meghatározható a következő összefüggésből:
![\[ tg(\varphi) = \frac {\frac {1}{L\omega} - C\omega}{\frac {1}{R}} \]](/images/math/6/1/5/6152bfd4649fa15784b7495464ef9b85.png) |
(1.49) |
ahol az áram:
![\[ I(t) = \frac {U_o}{\widetilde {Z}} sin (\omega t - \varphi) \qquad {\rm {\acute{e}}s} \qquad I_{eff} = \frac {U_{eff}}{\left|\widetilde{Z} \right|} \]](/images/math/7/7/9/779b763ed6f98a2165ea26c0fc350cf8.png) |
(1.50) |
alakban adható meg.
Lineáris rendszer állapotváltozós leírása időtartományban
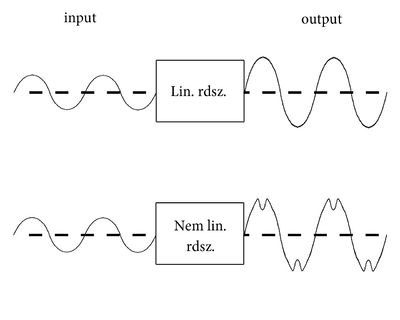
Ezidáig arra láthattunk példákat, hogy mi történik, ha egy RC, egy RL, egy soros RLC kör vagy az azzal analóg gerjesztett csillapított oszcillátor hogyan reagál az egyszerű szinuszos gerjesztésre. A mérnöki gyakorlatban azonban gyakran előfordul, hogy a gerjesztés egy aperiodikus jel. Annak vizsgálata, hogy ebben az általános esetben mi történik, igen fontos, hiszen a különböző áramkörökkel, oszcillátorral megvalósított rendszer egy általános leírását kaphatjuk meg. A matematikai leírás természetesen nem csak elméleti szempontból fontos, hanem számos gyakorlati haszna is van. A mérnöki gyakorlatban is használt eljárások közül talán a legfontosabb a zajszűrés, de még számos érdekes probléma megoldható az alábbiakban vázlatosan bevezetésre kerülő módszerek alkalmazásával, mint például az alakfelismerés, homályos képek ”visszaállítása”, 3D-s képfeldolgozás, stb. Az általunk idáig vizsgált áramkörök és oszcillátorok úgynevezett lineáris rendszerek. Ez azt jelenti, hogy például "kétszer erősebb" (kétszeres amplitúdójú) gerjesztésre kétszer nagyobb választ ad a rendszer, azaz a bejövő jel (input) és a rendszer válasza között lineáris kapcsolat áll fenn. Arról, hogy az input és az output közötti kapcsolat nemlineáris szinte mindenkinek van némi tapasztalata: amennyiben egy rádiónak vagy akár egy HiFi berendezésnek (erősítő, hangfal, stb.) a hangerő szabályozóját maximálisra állítjuk, akkor a legtöbb esetben igen erős hangminőség romlás észlelhető. Erre általában azt mondjuk, hogy az eszköz torzít. Mit is jelent ez egyszerűen modellezve? Tegyük fel, hogy van két HiFi berendezésünk; az egyiken a jelátvitel lineáris, míg a másikon nem, ez utóbbi esetben érezzük azt, hogy a hang nem tiszta. Mindezt igen szemléletesen mutatja a következő ábra.
| 2.1 ábra |
Mindkét esetben egy tiszta szinuszos bemenő jel volt az input, azonban a nemlineáris rendszer válasza, amit mi torzítottnak hallunk, tartalmazza az egyik felharmonikust is. A bemutatott egyszerű példa is rávilágít arra, hogy érdemes lehet a jelátvitel problémáját a frekvencia-tartományban vizsgálni. Ez három lépésben valósítható meg. Először meg kell határozni a gerjesztés (vagy input) különböző frekvenciájú komponenseinek amplitúdóját és fázisát, vagyis fel kell venni a spektrumát. A második lépésben valahogyan meg kell adni, hogy a különböző komponensek hogyan mennek át a rendszeren, azaz miként változik az amplitúdójuk és a fázisuk. Végül a szuperpozíció elvét alkalmazva, a komponensek összegeként előáll a rendszer válasza. A következőkben azt fogjuk megmutatni, hogy ez a három lépés hogyan valósítható meg, és néhány példát látunk majd az alkalmazásukra is. A most körvonalazott módszer segítségével – mint azt majd látni fogjuk – ráadásul lineáris differenciálegyenletek megoldása is viszonylag könnyen megadható.
Periódikus jel Fourier sora
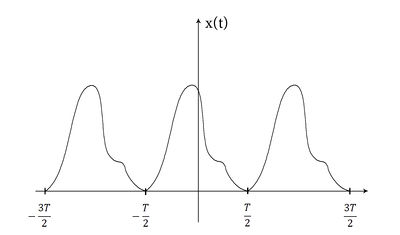
Egy periodikus jel megadható a Fourier sorával, illetve közelíthető a Fourier sor véges tagjának összegével. Legyen a periodikus jel  és a periódusa
és a periódusa 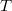 . A
. A 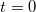 időpontot válasszuk meg úgy, hogy éppen egy ciklus közepére essen, azaz az ismétlődő jelsorozat egy periódusa tartson
időpontot válasszuk meg úgy, hogy éppen egy ciklus közepére essen, azaz az ismétlődő jelsorozat egy periódusa tartson 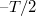 -től
-től 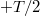 -ig (lásd a 2.1.1 ábrát).
-ig (lásd a 2.1.1 ábrát).
| 2.1.1 ábra |
A jel periódusából adódó legalacsonyabb frekvencia 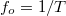 , a felharmonikusok:
, a felharmonikusok: 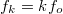 és természetesen
és természetesen 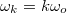 , ahol
, ahol 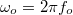 . Az
. Az  periodikus jel tehát megadható a (már tanult) Fourier sor segítségével:
periodikus jel tehát megadható a (már tanult) Fourier sor segítségével:
![\[ x(t) = \sum^{\infty}_{i=1} a_k cos (\omega_k t)+ \sum^{\infty}_{i=1} b_k sin (\omega_k t) + a_0\]](/images/math/2/f/5/2f509ccf6d77fca37e7fa384bd9b80b8.png) |
(2.1.1) |
Az 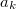 és
és 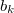 Fourier együtthatókat a következőképen számíthatjuk ki:
Fourier együtthatókat a következőképen számíthatjuk ki:
![\[ a_0 = \frac{1}{T}\int\limits_{-\frac{T}{2}}^{+\frac{T}{2}} x(t)dt \]](/images/math/8/0/e/80edfebb204766b1d4cf2e6db862d12b.png) |
(2.1.2) |
![\[ a_k = \frac{2}{T}\int\limits_{-\frac{T}{2}}^{+\frac{T}{2}} x(t)cos(\omega_k t)dt \]](/images/math/3/7/9/379085057bd88a27cc6d1291ec19543a.png) |
(2.1.3) |
![\[ b_k = \frac{2}{T}\int\limits_{-\frac{T}{2}}^{+\frac{T}{2}} x(t)sin(\omega_k t)dt \]](/images/math/5/a/1/5a14394b0b7b4f5d631d423037030fa7.png) |
(2.1.4) |
ahol k = 1, 2, 3, …
Természetesen vannak feltételek, melyek teljesülése szükséges ahhoz, hogy az  függvény megadható legyen a Fourier sorával, például legyen a tartományon Riemann integrálható, stb. Most ezekkel a feltételekkel nem foglalkozunk; fogadjuk el, hogy az általunk vizsgált függvények "jól viselkedő függvények" (folytonosak, deriválhatók, végesek, stb.), amelyek esetében nem lép fel probléma az együtthatók kiszámításánál.
Példaként tekintsünk egy periodikus négyszögjelet, pontosabban ennek egy periódusát:
függvény megadható legyen a Fourier sorával, például legyen a tartományon Riemann integrálható, stb. Most ezekkel a feltételekkel nem foglalkozunk; fogadjuk el, hogy az általunk vizsgált függvények "jól viselkedő függvények" (folytonosak, deriválhatók, végesek, stb.), amelyek esetében nem lép fel probléma az együtthatók kiszámításánál.
Példaként tekintsünk egy periodikus négyszögjelet, pontosabban ennek egy periódusát:
![\[ x(t)= \begin{cases} -1 &ha \quad -\frac{T}{2}<t<0 \\ 0 &ha \quad t= 0 \\ +1 &ha \quad 0<t<\frac{T}{2} \end{cases} \]](/images/math/8/0/4/8047941b644c0c3b9eec976775f682f1.png) |
(2.1.5) |
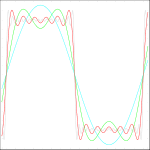
A Fourier együtthatók kiszámítása után kapjuk, hogy
![\[ x(t) = \frac{4}{\pi}\left(sin(\omega t)+ \frac {1}{3}sin(3\omega t) + \frac {1}{5}sin(5\omega t)+...\right) \]](/images/math/9/5/0/9500baa3a3deef8f4bd09e6009ec9021.png) |
(2.1.6) |
Az eredményt jól mutatja a 2.1.2 ábra, ahol a sor első három tagjának összege látszik.
| 2.1.2 ábra |
Amennyiben a 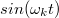 és a
és a 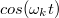 tagokat az Euler összefüggés segítségével átírjuk exponenciális alakra, akkor – mint az egyszerűen belátható – az
tagokat az Euler összefüggés segítségével átírjuk exponenciális alakra, akkor – mint az egyszerűen belátható – az  Fourier sora megadható egy általánosabb formában is:
Fourier sora megadható egy általánosabb formában is:
![\[ x(t) = \sum^{\infty}_{k=1} c_k e^{i\omega_k t}+ \sum^{\infty}_{k=1} c_{-k} e^{-i\omega_k t} + a_0\]](/images/math/0/f/9/0f9c62a74581ea6587ebf321a74e2c2c.png) |
(2.1.7) |
Az általánosításban még tovább mehetünk:
![\[ x(t) = \sum^{\infty}_{-\infty} c_k e^{i\omega_k t} \]](/images/math/f/0/1/f0116958dd89a6ca05fee078f69936f2.png) |
(2.1.8) |
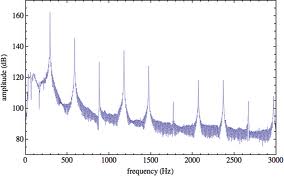
A Fourier együtthatókat azonban nemcsak kiszámítani lehet, hanem megfelelő szűrőkkel az együtthatók értékét, vagy egymáshoz való arányukat is megváltoztathatjuk. Egy sávszűrővel könnyen elnyomható a zaj, ha az valamely frekvencia-tartományban jelentkezik, amely a jel spektrumán kívül jelentkezik. Egy koncertfelvételt például véletlenszerűen megzavaró vonatfütty hangja szinte teljesen eltüntethető. Az említett módszerrel azonban nemcsak a zajszűrés oldható meg, hanem akár a dobpergés vagy a hegedű hangja is kiemelhető egy együttes zenéjéből. Lássunk erre egy szemléletes példát! A következő ábrán egy gitár megpendített húrjának rezgési spektruma látható.
| 2.1.3 ábra |
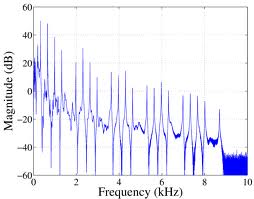
Ha azonban a gitár húrját megérintjük a hosszának 1/3 – ánál, vagyis egy "természetes sávszűrő"-t alkalmazunk, a spektrum is természetesen ennek megfelelően változni fog (az alapharmonikus frekvenciája most más érték):
| 2.1.4 ábra |
Aperiodikus jel spektruma
Amennyiben egy lineáris rendszer inputja, illetve gerjesztése egy aperiodikus jel, akkor a Fourier-sor már nem alkalmazható arra, hogy áttérjünk a frekvencia-tartományba, hiszen a jelet nem lehet előállítani egy alapharmonikus és felharmonikusai összegével; már az alapharmonikus meghatározása sem lehetséges. Az aperiodikus jel spektrumának kiszámításához a 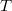 periódusidőt minden határon túl növeljük, ennek következtében a két szomszédos harmonikus közötti távolság, azaz
periódusidőt minden határon túl növeljük, ennek következtében a két szomszédos harmonikus közötti távolság, azaz 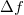 (ami eredetileg
(ami eredetileg 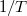 -vel volt egyenlő) egyre kisebb lesz, azaz
-vel volt egyenlő) egyre kisebb lesz, azaz 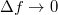 . Mindez azt sugallja, hogy a 2.1.14 kifejezésben összegzés helyett integrálnunk kell. Az általánosítás tehát a következő: az
. Mindez azt sugallja, hogy a 2.1.14 kifejezésben összegzés helyett integrálnunk kell. Az általánosítás tehát a következő: az 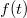 aperiodikus jel Fourier transzformáltja az
aperiodikus jel Fourier transzformáltja az 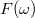 komplex függvény (komplex, mert minden frekvencia-komponenshez tartozik egy fázis):
komplex függvény (komplex, mert minden frekvencia-komponenshez tartozik egy fázis):
![\[ F(\omega)= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty} f(t)e^{-i\omega t}dt \]](/images/math/1/1/7/117416dfbfa7a04d7aaac9e3466b7837.png) |
(2.2.1) |
Az 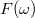 -ból pedig az inverz Fourier transzformáció segítségével kaphatjuk meg időtartományban az
-ból pedig az inverz Fourier transzformáció segítségével kaphatjuk meg időtartományban az 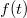 jelet:
jelet:
![\[ f(t)= \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty} F(\omega)e^{i\omega t}dt \]](/images/math/6/8/0/6801c4897004d8e75bd96cb5ebfbf2d7.png) |
(2.2.2) |
A módszer egyik nagy előnye a már említett zajszűrés. (Például zajos, szemcsés képek is megtisztíthatók bizonyos frekvencia-tartományok elnyomásával; ekkor kettős integrált és 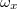 ,
, 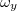 komponenseket kell használni áttérve 2D-re.)
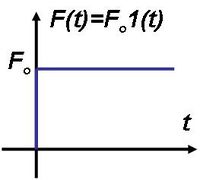
Ahhoz, hogy egy másik, igen fontos alkalmazási lehetőséget is megmutathassunk, tekintsünk egy egyszerű mechanikai példát. Legyen egy csillapítatlan harmonikus oszcillátor eredetileg nyugalomban
komponenseket kell használni áttérve 2D-re.)
Ahhoz, hogy egy másik, igen fontos alkalmazási lehetőséget is megmutathassunk, tekintsünk egy egyszerű mechanikai példát. Legyen egy csillapítatlan harmonikus oszcillátor eredetileg nyugalomban 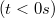 , de a
, de a  – ban bekapcsolunk egy
– ban bekapcsolunk egy 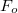 állandó erőt. Ezt a gerjesztést másféleképpen is jelölhetjük:
állandó erőt. Ezt a gerjesztést másféleképpen is jelölhetjük: 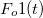 , ahol
, ahol 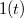 az ún. egységugrás függvény:
az ún. egységugrás függvény:
| 2.2.1 ábra |
Az oszcillátor mozgásegyenlete:
![\[ m\ddot{x} + Dx = F_o 1(t) \]](/images/math/6/d/4/6d45f1cb98be241ebd4c5b5fd6a49498.png) |
(2.2.3) |
Könnyen meggyőződhetünk róla és szemléletesen is egyszerű belátni, hogy a megoldás (jelöljük ezt most 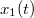 -vel):
-vel):
![\[ x_1 (t) = \frac{F_o}{D}\left[1-cos(\omega_o t)\right] \]](/images/math/f/c/a/fca58dd21fd3cd85da09be0eafc6d2f3.png) |
(2.2.4) |
ahol természetesen:
![\[ \omega_o = \sqrt {\frac{D}{m}} \]](/images/math/3/d/c/3dc304879d7203b8983360cd5a4b6433.png) |
(2.2.5) |
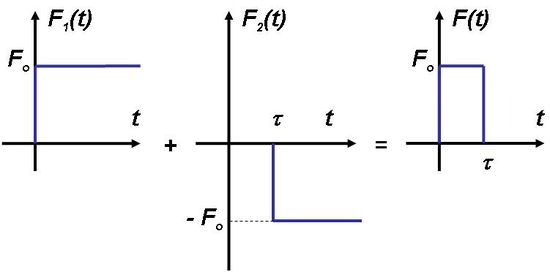
Ezután szeretnénk meghatározni, hogy egy erőlökésre hogyan reagál a rendszer, vagyis a csillapítatlan harmonikus oszcillátor. Az erőlökés  ideig tart és ezen időtartam alatt állandó
ideig tart és ezen időtartam alatt állandó 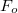 erő hat:
erő hat:
| 2.2.2 ábra |
Az erőlökést megadó 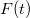 függvény – mint az a 2.2.3 ábrán látható – összerakható két egységugrás függvény összegeként:
függvény – mint az a 2.2.3 ábrán látható – összerakható két egységugrás függvény összegeként:
| 2.2.3 ábra |
A második 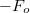 erőt t =
erőt t =  időpontban kapcsoljuk be. Most vizsgáljuk meg azt, hogy mi történne, ha az eredetileg nyugalomban lévő oszcillátorra csak az
időpontban kapcsoljuk be. Most vizsgáljuk meg azt, hogy mi történne, ha az eredetileg nyugalomban lévő oszcillátorra csak az  erő hatna. A mozgásegyenlet megoldása hasonló 2.2.4 - hez, de most figyelembe kell venni, hogy a
erő hatna. A mozgásegyenlet megoldása hasonló 2.2.4 - hez, de most figyelembe kell venni, hogy a 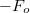 erő csak a t =
erő csak a t =  időpontban kezd el hatni:
időpontban kezd el hatni:
![\[ x_2 (t) = - \frac{F_o}{D}\left[1-cos(\omega_o (t-\tau))\right] \]](/images/math/2/2/2/2220025b3cb79b3298eb80217d2b9351.png) |
(2.2.6) |
Láttuk, hogy a  ideig tartó erőlökés előáll az
ideig tartó erőlökés előáll az 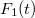 és
és 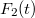 összegeként. Minthogy a csillapítatlan oszcillátor lineáris rendszer és
összegeként. Minthogy a csillapítatlan oszcillátor lineáris rendszer és  , ezért az erőlökésre, mint gerjesztésre a rendszer az
, ezért az erőlökésre, mint gerjesztésre a rendszer az 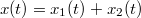 megoldással "válaszol":
megoldással "válaszol":
![\[ x(t) = \frac{F_o}{D}\left[1-cos(\omega_o t)\right] - \frac{F_o}{D}\left[1-cos(\omega_o (t-\tau))\right] \]](/images/math/0/6/1/06183841231ca8d5b1cc01b629946e98.png) |
(2.2.7) |
A zárójeleket felbontva egyszerűbb alakot nyerhetünk:
![\[ x(t) = \frac{F_o}{D}\left[cos(\omega_o t)cos(\omega_o \tau) + sin(\omega_o t)sin(\omega_o \tau) - cos(\omega_o t) \right] \]](/images/math/3/a/7/3a7edc0069bb2ee489973113c6ee5203.png) |
(2.2.8) |
Ezután végezzünk el egy előremutató általánosítást: tegyük fel, hogy az erőlökés pillanatszerű. Az erőlökés pillanatszerűsége gyakorlati szempontból azt jelenti, hogy  << T, ahol T az oszcillátor periódusideje. Most tartson az erőhatás egyre rövidebb ideig, azaz
<< T, ahol T az oszcillátor periódusideje. Most tartson az erőhatás egyre rövidebb ideig, azaz 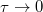 , de közben az erőlökés nagysága - vagyis az oszcillátornak átadott impulzus:
, de közben az erőlökés nagysága - vagyis az oszcillátornak átadott impulzus: 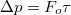 - maradjon állandó. Ebből azonnal adódik, hogy
- maradjon állandó. Ebből azonnal adódik, hogy 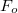 minden határon túl tart a
minden határon túl tart a 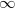 - be. Ez a speciális erőlökés a
- be. Ez a speciális erőlökés a  - vel megszorzott Dirac-delta, amiről tudjuk, hogy:
- vel megszorzott Dirac-delta, amiről tudjuk, hogy:
![\[ \int\limits_{-\infty}^{+\infty} \delta(t)dt = 1 \qquad {\rm {\acute{e}}s} \qquad \delta(t) = 0 \qquad {\rm ha} \qquad t \neq 0 \]](/images/math/8/a/f/8af28c2e711e0ab4142877f65b7fb912.png) |
(2.2.9) |
A 2.2.8 formulából megkaphatjuk a választ arra a kérdésre, hogy miként reagál a csillapítatlan harmonikus oszcillátor egy pillanatnyi erőlökésre, ha elvégezzük a 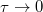 közelítést. Könnyen belátható, hogy a
közelítést. Könnyen belátható, hogy a 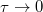 esetben:
esetben:
![\[ x(t) = \frac{F_o \tau \omega_o}{D}sin(\omega_o t)= \frac{\Delta p \omega_o}{D}sin(\omega_o t) \]](/images/math/3/5/6/356a436990805b39f4c0b86c53d4d7ce.png) |
(2.2.10) |
Kérdés, hogy mi történik akkor, ha a pillanatnyi erőlökés nem a 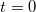 , hanem valamely
, hanem valamely 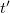 időpontban történik. A válasz egyszerű;
időpontban történik. A válasz egyszerű; 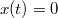 ha
ha 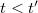 , viszont a
, viszont a 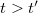 esetén:
esetén:
![\[ x(t) = \frac{F_o \tau \omega_o}{D}sin \left[\omega_o (t-t')\right] \]](/images/math/d/a/e/dae7d7fdc21d3b96da8c261701ed28b9.png) |
(2.2.11) |
Most már elég sokat tudunk ahhoz, hogy megvizsgálhassuk egy általános 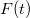 gerjesztés problémáját. Tegyük fel tehát, hogy a csillapítatlan oszcillátorra hat egy
gerjesztés problémáját. Tegyük fel tehát, hogy a csillapítatlan oszcillátorra hat egy 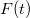 erő (vagy erőlökés):
erő (vagy erőlökés):
| 2.2.4 ábra |
A véges ideig ható 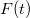 erőt felbonthatjuk "pillanatszerű" erőlökések összegére (2.2.5 ábra).
erőt felbonthatjuk "pillanatszerű" erőlökések összegére (2.2.5 ábra).
| 2.2.5 ábra |
A rendszernek a ráható  ,
, 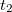 ,
, 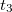 , stb. időpontokban bekövetkező erőlökésekre adott válaszait össze kell adni, hiszen egy lineáris rendszer esetén alkalmazható a szuperpozíció, tehát:
, stb. időpontokban bekövetkező erőlökésekre adott válaszait össze kell adni, hiszen egy lineáris rendszer esetén alkalmazható a szuperpozíció, tehát:
![\[ x(t) = \frac{F_1 \tau \omega_o}{D}sin \left[\omega_o (t-t_1)\right]+ \frac{F_2 \tau \omega_o}{D}sin \left[\omega_o (t-t_2)\right]+...= \frac{\omega_o}{D}\sum^{n}_{i=1} F_n sin \left[\omega_o (t-t_n)\Delta t \right] \]](/images/math/6/5/9/659ed1fb9aa399cef975e2c41cf5f077.png) |
(2.2.12) |
Ha ránézünk az összegzésre és tudjuk, hogy  , akkor az
, akkor az  megadható egy könnyebben kezelhető formában is:
megadható egy könnyebben kezelhető formában is:
![\[ x(t)= \frac{\omega_o}{D}\int\limits_{-\infty}^{t}F(t')sin \left[\omega_o (t-t')\right] dt' \]](/images/math/8/3/6/836870149e60fabf563a464890ebb891.png) |
(2.2.13) |
Ezt a formulát írhatjuk egy másik – jóval általánosabb – alakba is:
![\[ x(t)= \int\limits_{-\infty}^{t}F(t')G(t-t') dt' \]](/images/math/4/c/1/4c159666fc9718d11c8e35503bd71e5e.png) |
(2.2.14) |
ahol a 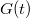 az ún. Green-függvény, amelynek jelentése a következő: megadja, hogy a lineáris rendszer milyen választ ad egy
az ún. Green-függvény, amelynek jelentése a következő: megadja, hogy a lineáris rendszer milyen választ ad egy 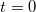 időpontban bekövetkezett
időpontban bekövetkezett 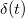 gerjesztésre. Most már jól látszik tehát, hogy egy általános
gerjesztésre. Most már jól látszik tehát, hogy egy általános 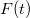 gerjesztésre úgy számíthatjuk ki a rendszer
gerjesztésre úgy számíthatjuk ki a rendszer  válaszát, hogy először meghatározzuk a rendszer Green-függvényét, majd a (2.2.14) integrál segítségével kiszámítjuk
válaszát, hogy először meghatározzuk a rendszer Green-függvényét, majd a (2.2.14) integrál segítségével kiszámítjuk  -t. A módszer sok esetben jól működik, azonban a (2.2.14) integrál (vagyis az
-t. A módszer sok esetben jól működik, azonban a (2.2.14) integrál (vagyis az 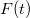 és a
és a 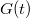 konvolúciója) kiszámítása néha nem egyszerű. Ennek a problémának az orvoslására felhasználhatunk egy igen gyakran alkalmazott tételt:
konvolúciója) kiszámítása néha nem egyszerű. Ennek a problémának az orvoslására felhasználhatunk egy igen gyakran alkalmazott tételt:
![\[ F(f {*} g)= F(f)F(g) \]](/images/math/3/3/0/33086afd4117824cc21b6a67fc5433f0.png) |
(2.2.15) |
ahol  az
az 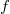 és a
és a  függvény konvolúcióját jelenti, az
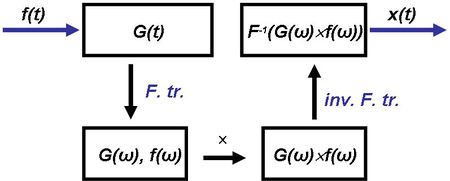
függvény konvolúcióját jelenti, az  pedig a Fourier transzformációt. Ha tehát a két függvény konvolúciójának kiszámítása nehézkesen megy, akkor áttérünk frekvencia-tartományba és egyszerűen összeszorozzuk a két függvény Fourier transzformáltját, majd egy inverz Fourier-transzformációval visszatérünk az időtartományba és megkapjuk a rendszer gerjesztésre adott válaszát. Mindezt egy egyszerű ábrán sematikusan is összefoglalhatjuk:
pedig a Fourier transzformációt. Ha tehát a két függvény konvolúciójának kiszámítása nehézkesen megy, akkor áttérünk frekvencia-tartományba és egyszerűen összeszorozzuk a két függvény Fourier transzformáltját, majd egy inverz Fourier-transzformációval visszatérünk az időtartományba és megkapjuk a rendszer gerjesztésre adott válaszát. Mindezt egy egyszerű ábrán sematikusan is összefoglalhatjuk:
| 2.2.6 ábra |
Az itt bemutatott módszer természetesen nem csak oszcillátorra, hanem lineáris áramkörökre, hálózatokra is alkalmazható. Az eljárás azonban csak abban az esetben használható, ha a Fourier transzformáció elvégezhető, azaz négyzetesen vagy abszolút értékre integrálható függvényekkel megadott gerjesztések lépnek fel. A mérnöki gyakorlatban azonban előfordul, hogy modellezni kell a bekapcsolási (vagy kisütés) jelenségeket is, ahol az említett feltételek nem teljesülnek.
Laplace transzformáció
A rendszertechnikai gyakorlatban előfordulnak olyan gerjesztések is, amelyek Fourier-transzformáltját nem lehet megadni. Ezeket olyan függvények írják le, amelyek nem négyzetesen integrálhatók ill. nem abszolút integrálhatók; ilyenek például a egységugrás függvény, az exponenciális függvény, az egységnyi sebességugrás függvény, stb.
Az előző fejezetben tanult módszer azonban a Fourier-transzformáció egy kis módosításával az említett gerjesztések esetén is használható. Az ötlet a következő: szorozzuk be a nem integrálható függvényeket a 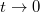 esetben gyorsan lecsengő
esetben gyorsan lecsengő 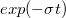 – vel; ekkor elvárásaink szerint már egy konvergens megoldást kapunk a Fourier integrálra, amennyiben azt csak a t ≥ 0 tartományon számítjuk ki. A nem integrálható
– vel; ekkor elvárásaink szerint már egy konvergens megoldást kapunk a Fourier integrálra, amennyiben azt csak a t ≥ 0 tartományon számítjuk ki. A nem integrálható 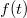 jel transzformáltját az említett módosítással a következőképpen kapjuk:
jel transzformáltját az említett módosítással a következőképpen kapjuk:
![\[ F(s)= \int\limits_{0}^{+\infty} f(t)e^{-\sigma t}e^{-i\omega t}dt = \int\limits_{0}^{+\infty} f(t)e^{-(\sigma + i\omega)t}dt = \int\limits_{0}^{+\infty} f(t)e^{-st}dt \]](/images/math/0/1/1/011956f923e96d66a63ac2da4a5c1648.png) |
(2.3.1) |
Az eljárást Laplace francia matematikus dolgozta ki, az ő tiszteletére a javított transzformációs formulát Laplace-transzformációnak hívják és jelölése:
![\[ L \left( f(t)\right ) = F(s)= \int\limits_{0}^{+\infty} f(t)e^{-st}dt \]](/images/math/4/4/7/447ccbcf45115c1170aa78ca872f1588.png) |
(2.3.2) |
A következő táblázatban összefoglaltuk néhány függvény Laplace-transzformáltját:
| Idő-tartományban: f(t) | Laplace-transzformáltja: L(f(t))=F(s) |
|---|---|
|
|
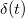
|
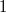
|
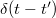
|
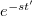
|
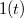
|
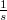
|
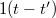
|
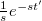
|
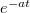
|
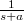
|
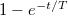
|
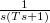
|

|
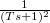
|
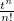
|
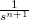
|
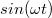
|

|
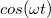
|
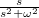
|
Van még néhány – az integrálszámítás módszereivel könnyen bizonyítható – szabály, amelyeket érdemes megemlíteni:
1. Linearitás: ha 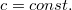 :
:
![\[ L(cf(t)) = cL(f(t)) = cF(s) \qquad {\rm {\acute{e}}s} \qquad L\left[ f_1 (t) + f_2 (t)\right] = L(f_1 (t))+ L(f_2 (t)) \]](/images/math/0/4/1/04114439a9603c4fa2a7a8eaace59007.png) |
(2.3.3) |
2. Eltolás:
![\[ L(f(t-\tau)) = e^{-\tau s}L(f(t))=e^{-\tau s}F(s) \]](/images/math/6/0/5/605a8ce6b618e60e4fc1ef14e04563cd.png) |
(2.3.4) |
3. Hasonlóság:
![\[ L(f(at) = \frac {1}{a}F\left(\frac{s}{a}\right) \]](/images/math/5/1/4/5148978f8f85efd332ae314b58389695.png) |
(2.3.5) |
4. Differenciálás:
![\[ L(f'(t)) = sF(s) \]](/images/math/5/a/4/5a4b5d27655cfaab37b49432cef001a0.png) |
(2.3.6) |
(a kezdeti feltételeket zérusnak választottuk)
5. Integrálás:
![\[ L\left( \int\limits_{0}^{t} f(t)dt \right) = \frac {1}{s}F(s) \]](/images/math/0/d/1/0d1ebc55ca6e2bdcbf9f47d031e2ef84.png) |
(2.3.7) |
(a kezdeti feltételeket zérusnak választottuk)
Megjegyzés: az inverz-Laplace-transzformációt végezhetjük úgy is, hogy a fenti táblázatot visszafelé olvassuk.
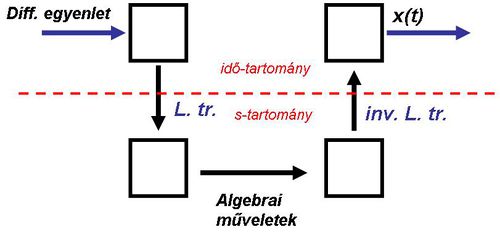
Problémák megoldására a 2.2.6 ábrán látható sémához némileg hasonló módszert követhetünk. A követendő lépések: 1. felírjuk a probléma differenciálegyenletét… 2. végrehajtjuk a Laplace-transzformációt… 3. elvégezzük a szükséges algebrai átalakításokat… 4. inverz-Laplace-transzformációval kapjuk a probléma megoldását. Mindez egy sémában összefoglalva:
| 2.3.1 ábra |
A tanultak alkalmazására keressük meg két ismert probléma megoldását!
Az RL-kör bekapcsolási jelensége
| 2.3.2 ábra |
A probléma matematikai felírása már ismert:
![\[ L\frac{dI}{dt}+RI = U_o 1(t) \]](/images/math/4/4/d/44d0afe412a8953dbdd1b9e80d25b9e9.png) |
(2.3.8) |
Most végezzük el a Laplace-transzformációt az egyenlet mindkét oldalán, ezzel áttértünk az  - térbe:
- térbe:
![\[ sLI(s)+RI(s) = \frac{1}{s}U_o \]](/images/math/1/0/c/10cbcda9bf712247c58512c63d89aa2f.png) |
(2.3.9) |
Ezután kifejezzük 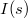 –t:
–t:
![\[ I(s)= U_o\frac{1}{s} \frac{1}{Ls+R}=\frac {U_o}{R}\frac{1}{s} \frac{1}{\frac {L}{R}s+1} \]](/images/math/e/0/c/e0c2d1f56ce67b036b076cc249bba398.png) |
(2.3.10) |
A táblázat segítségével elvégezhetjük az inverz-Laplace-transzformációt és megkapjuk az ismert megoldást:
![\[ I(t)= \frac {U_o}{R}\left(1-e^{-\frac{L}{R}t}\right) \]](/images/math/2/f/2/2f2b5be087aff6ab3db2c77f1ea51c43.png) |
(2.3.11) |
Hasonlóan járhatunk el az RC-kör esetén is.
| 2.3.3 ábra |
A probléma matematikai modellje – csakúgy, mint az előbbi esetnél – ismert:
![\[ R\frac{dQ}{dt}+\frac{1}{C}Q = U_o 1(t) \]](/images/math/c/9/3/c93e00d1a4888df1c0b39f2312f32793.png) |
(2.3.12) |
Az egyenletet átírva az áramra azt kapjuk, hogy:
![\[ RI+\frac{1}{C}\int I(t)dt = U_o 1(t) \]](/images/math/9/6/8/9684ff2ce0b35803385eb6af0ba5c4e0.png) |
(2.3.13) |
A Laplace-transzformációt elvégezve:
![\[ RI(s)+\frac{1}{C}\frac{1}{s}I(s) = U_o \frac{1}{s} \]](/images/math/c/e/b/ceb557f8c127063fb5cb8520aaf5c0cc.png) |
(2.3.14) |
Az egyenletből I(s)-t kifejezve:
![\[ I(s)= \frac{U_o}{Rs+ \frac{1}{C}}=\frac{U_o}{R} \frac{1}{s+\frac{1}{RC}} \]](/images/math/0/b/1/0b141e00dbb4381dc517f74dde3c3a25.png) |
(2.3.15) |
Végezzük el az inverz-Laplace-transzformációt a táblázat segítségével:
![\[ I(t)= \frac{U_o}{R} e^{-\frac{1}{RC}t} \]](/images/math/3/a/0/3a07bcf663cbb2f500151c97add2e684.png) |
(2.3.16) |
Megmutatható, hogy a Fourier-transzformációt alkalmazó konvolúciós tétel a Laplace-transzformációra is alkalmazható; tehát egy általános 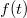 gerjesztés esetén (megszorítás:
gerjesztés esetén (megszorítás:  ha
ha 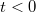 ).
).
![\[ L(f {*} g)= L(f)L(g)=f(s)g(s) \]](/images/math/4/b/8/4b8affab8b03015161c6498228ea23a6.png) |
(2.2.15) |
A rendszer által adott választ most már a 2.2.6 ábrán látható sémának megfelelően kaphatjuk meg azzal a különbséggel, hogy a Fourier és inverz Fourier-transzformációk helyett a Laplace és inverz-Laplace-transzformációt kell alkalmazni.
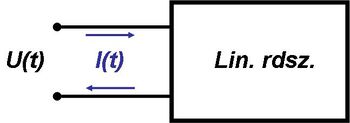
Az általunk vizsgált egyszerű, lineáris áramkörök, valamint az alkalmazott módszerek – ahogy azt az előzőekben láthattuk – egy egyszerű sémával jellemezhetők (2.3.4 ábra).
| 2.3.4 ábra |
Mint azt az ábra is mutatja, az 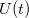 feszültségre – vagyis a gerjesztésre – a lineáris rendszer az
feszültségre – vagyis a gerjesztésre – a lineáris rendszer az 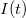 árammal reagál.
árammal reagál.