Szilárdtestfizika gyakorlat

Általános adatok (2012 ősz)

• Kód: BMETE11AF06;
• Követelmény: 0/2/0/F/2;
• Félév: ősz;
• Nyelv: magyar;
• Tárgyfelelős: Dr. Készmárki István egyetemi docens
• Gyakorlatvezetők: Dr. Kézsmárki István, Bácsi Ádám, Kanász-Nagy Márton
• A gyakorlatok időpontja: csütörtök 14:15-16:00
• Helyszín: T606 (K.I. csoportja), T604 (B.Á. csoportja), T601/2 (K-N.M. csoportja)

• Jelenléti követelmények: A félév végi aláírás feltétele előadások legalább 70%-án való részvétel. Az előadásokon jelenléti ívet vezetünk.
• Félévközi számonkérések: azonosak a [Szilárdtestfizika gyakorlat] számonkéréseivel.
• Félév végi osztályzat: írásbeli és szóbeli vizsga. A vizsga feltétele az aláírás, valamint a gyakorlati jegy megszerzése.

Tematika

• Kristályok szimmetriái Nevezetes rácsok és reciprok rácsaik. Miller index, kristály síkok, reciprok rácsvektorok kapcsolata. Neumann-elv.

Röntgen-diffrakció tökéletes kristályon Rácsösszeg. Atomi alaktényezõ számítása különbözõ töltéseloszlások esetén. Röntgen-diffrakció nem-tökéletes kristályon Rácsrezgések figyelembe vétele. Véletlen ötvözetek. Rácsrezgések dinamikája Két dimenziós rácsok rugós modelljei. Rezgési módusok és frekvenciájuk. Rácsfajhõ és állapotsûrûség Az állapotsûrûség viselkedése különbözõ dimenziókban izotrop és anizotrop hangsebesség esetén. Debye-modell. Debye-Waller faktor. Lindemann kritérium az olvadáspontra. Elektronok szoros kötésû közelítésben Atomi hullámfüggvények egydimenziós Dirac-delta potenciál esetén. Elektronok kétdimenziós ferdeszögû rácsban. S- és p-típusú pályák. Kváziszabad elektron közelítés Tilos sáv számítása egydimenziós Dirac-delta potenciál esetén. Elektronsávok négyzetrács esetén. Elektronok állapotsûrûsége és fajhõje Fermi-hullámszám számítása. Állapotsûrûség kétdimenziós derékszögû tight-binding modellben kis betöltés esetén.

• Előadások: kedd 14-16, F. épület III. lépcsőház 2.emelet 13.
• Konzultációk: hétfő 14-18 (előzetes bejelentkezés alapján a email címen);

Az előadások rövid kivonata - jegyzetelésre alkalmas formában - letölthető az előadás címére kattintva. A kivonatok önmagukban nem alkalmasak a tananyag elsajátítására, de megkönnyítik a jegyzetelést (tartalmazzák az összes lényeges formulát), így elősegítik az előadásra való koncentrálást.

1. szept. 4. Szilárd testek
2. szept. 11. Kristályok szimmetriái
3. szept. 18. Szerkezetmeghatározás (elmélet)
4. szept. 25. Szóráskísérletek
5. okt. 2. Rácsrezgések (klasszikus)
6. okt. 9. Fononok (kvantummechanikai leírás)
7. okt. 16. Szilárd testek fajhője
8. okt. 30. Fonon diszperziós reláció mérése
9. nov. 6. Elektronok Drude-modellje (klasszikus)
10. nov. 13. Sommerfeld-modell (kvantummechanikai leírás)
11. nov. 20. Közel szabad elektron modell (periódikus potenciál)
12. dec. 27. Sávszerkezet, szoros kötésű közelítés
13. dec. 4. Fermi felület és diszperziós relációk kísérleti meghatározása

Részletes tematika

Kristálytan - Szerkezetvizsgálat

Kristály = Rács + Bázis

Kristályrendszerek (eltolás + egy definiáló szimmetria) Bravais-rácsok (élhossz és szögek szerinti osztályozás) Pontcsoportok, Tércsoportok

Elemi cella, Wigner-Seitz cella Kristály síkok, Miller-index Reciprok rács, Brillouin-zóna

Diffrakció elmélete: Bragg-feltétel, Laue féle leírás, Szerkezeti tényező, atomi alaktényző

Rugalmas szóráskisérletek: Ewald szerkesztés, Debye-Scherrer- és Laue-módszer Röntgen-, elektron- és neutron-szórási mechanizmus Szinkrotron-sugárzás

Kvázikristályok Nem-kristályos szilárd testek (páreloszlási függvény) Ponthibák, vonalhibák (diszlokációk)

Rácsrezgések - fononok

Szilárd testek fajhőjének Einstein- és Debye-modellje

Lineáris lánc rezgései Rácsrezgések 3 dimenzióban (Dinamikus mátrix sajátérték-egyenlete) Rugalmas hullámok

Diszperziós reláció Állapotsűrűség, Van Hove szingularitás

Kvantummechanikai leírás Fonon-energia és impulzus, a fonongáz fajhője

A diszperziós reláció kisérleti meghatározása: Megmaradási tételek részecske-fonon, ill. foton-fonon kölcsönhatáskor

Rugalmatlan neutron-szórás

Elektronok

Szabad elektrongáz kvantummechanikai leírása: A Fermi-statisztika, Sommerfeld-sorfejtés Fajhő, szuszceptibilitás

Elektronok periodikus potenciálban: Bloch-tétel, Energiaspektrum perturbációs számolása Szoros kötésű közelítés Sávszerkezet, diszperziós reláció

Elektronok propagálása mágneses térben:

Kváziklasszikus közelítés

Ciklotron frekvencia

Drude-modell: vezetőképesség, Hall-állandó diszperziós reláció, optikai tulajdonságok

Tételek

• Kristályrács definíciója. Reciprok-rács, kristálysíkok, Miller-index. Szimmetriaműveletek, kristályrendszerek, Bravais-rácsok.
• Diffrakció elmélete. Szerkezeti tényező, atomi szórási tényező. Röntgen-, elektron- és neutron-szórási kísérletek. Kvázikristályos és amorf anyagok.
• Rácsrezgések diszperziós relációja. A dinamikus mátrix sajátérték-egyenlete. Akusztikus és optikai ágak. A diszperziós reláció kísérleti meghatározása.
• Szilárd testek fajhőjének kvantummechanikai leírása. Bose-Einstein eloszlás. Az állapotsűrűség számolása. Debye-modell.
• Szabad elektrongáz kvantummechanikai leírása. Elektron-fajhő, fémek mágneses szuszceptibilitása (Sommerfeld-sorfejtés).
• Bloch-tétel. Közel szabad elektron modell. Sávszerkezet. $\epsilon$(k) kísérleti meghatározása: szögfelbontású fotoelektron-spektroszkópia (ARPES).
• Wannier-függvények. Szoros kötésű közelítés. Lokalizált és kiterjedt elektronállapotok. Effektív tömeg.
• Hullámcsomag. Elektronok mágneses térben:ciklotron frekvencia. Landau-nívók. Drude-modell: Hall-állandó, $\sigma$($\omega$), $\epsilon$($\omega$).

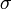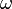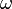Irodalom

Charles Kittel: Introduction to Solid State Physics, 6th edition, John Wiley & Sons, New York (1986). Neil W. Aschcroft and N.David Mermin: Solid State Physics, Sauders Collage, Philadelphia (1976). Sólyom Jenő: A modern szilárdtestfizika alapjai I, A szilárd testek szerkezete és dinamikája, ELTE Eötvös Kiadó, Budapest (2002).