Folyadék szabad felszínének vizsgálata
A szabad folyadékfelszín viselkedését egyenletes körmozgás esetén vizsgáljuk. A problémát alkalmas koordináta rendszer választásával visszavezetjük a szabad, nyugvó folyadékfelszín viselkedésére.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A nyugvó folyadék szabad (az edénnyel nem érintkező) felszíne mindenütt merőleges a külső erők eredőjére. Ha ugyanis a felszín valahol nem lenne merőleges az eredő erőre, akkor az utóbbi felszínnel párhuzamos összetevőjének hatására a felszín közelében áramlás jönne létre, vagyis a folyadékot nem tekinthetnénk nyugvónak.
Ha egy folyadékot tartalmazó hengeres edényt függőleges tengelye körül  szögsebességgel forgatunk, akkor a folyadék felszíne felülről nézve homorú forgásfelület lesz. A folyadék az azonos tengely körül
szögsebességgel forgatunk, akkor a folyadék felszíne felülről nézve homorú forgásfelület lesz. A folyadék az azonos tengely körül  szögsebességgel forgó koordinátarendszerben nyugalomban van. Ebben a rendszerben a felszínen lévő
szögsebességgel forgó koordinátarendszerben nyugalomban van. Ebben a rendszerben a felszínen lévő  tömegű folyadékrészre kétféle erő hat: az
tömegű folyadékrészre kétféle erő hat: az 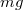 nagyságú, függőleges
nagyságú, függőleges 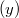 irányú nehézségi erő, valamint a forgó rendszerben fellépő tehetetlenségi erők. Esetünkben az utóbbiak közül csak az
irányú nehézségi erő, valamint a forgó rendszerben fellépő tehetetlenségi erők. Esetünkben az utóbbiak közül csak az 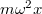 nagyságú, a forgástengelyre merőleges és attól sugárirányban elfelé mutató centrifugális erő játszik szerepet (
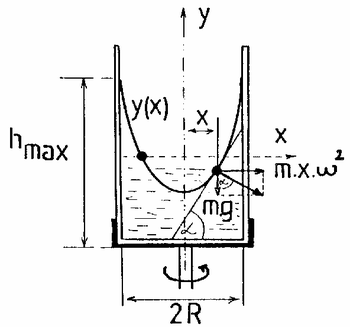
nagyságú, a forgástengelyre merőleges és attól sugárirányban elfelé mutató centrifugális erő játszik szerepet ( a folyadékrésznek a forgástengelytől mért távolsága). A folyadékfelszín mindenhol a két erő eredőjére merőleges helyzetet vesz fel (1. ábra). A kialakuló felület egy forgási paraboloid. A kísérletben ennek a forgási paraboloidnak egy, a forgástengelyen átmenő metszetét határozzuk meg.
a folyadékrésznek a forgástengelytől mért távolsága). A folyadékfelszín mindenhol a két erő eredőjére merőleges helyzetet vesz fel (1. ábra). A kialakuló felület egy forgási paraboloid. A kísérletben ennek a forgási paraboloidnak egy, a forgástengelyen átmenő metszetét határozzuk meg.
Kísérleti berendezés
A folyadékot két egymáshoz közeli párhuzamos síklap által alkotott (téglatest alakú) edényben helyeztük el. (Továbbiakban a síklapokat egymáshoz végtelen közelinek tekintjük.) A forgástengely a téglatest egyik szimmetriatengelye. A forgó edényben kialakuló folyadékfelszín vizsgálatát egy olyan koordináta rendszerben végezzük, melynek  tengelye az
tengelye az 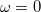 szögsebességhez tartozó (vízszintes) folyadékfelszínnel esik egybe,
szögsebességhez tartozó (vízszintes) folyadékfelszínnel esik egybe,  tengelye pedig a függőleges forgástengely.
tengelye pedig a függőleges forgástengely.
Az 1. ábráról leolvasható, hogy
![\[\tan\alpha=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{mx\omega^2}{mg}=\frac{\omega^2}{g}x,\]](/images/math/a/9/9/a99dec45bde449ca3da93b49c9e7862b.png)
azaz
![\[\mathrm{d}y=\frac{\omega^2}{g}x\mathrm{d}x,\]](/images/math/a/9/7/a97adf140a3c86b9c945442508556639.png)
ahonnan integrálással az
![\[y=\frac{\omega^2}{2g}x^2+C\]](/images/math/2/d/1/2d1dea864bf53b6d28fe195b9900ebd0.png)
összefüggés adódik. A kifejezés egy parabola egyenlete, ahol a  integrálási állandó értéke a parabola csúcspontjának ordinátája.
integrálási állandó értéke a parabola csúcspontjának ordinátája.  -t abból a feltételből kaphatjuk meg, hogy az állandó folyadéktérfogat miatt a
-t abból a feltételből kaphatjuk meg, hogy az állandó folyadéktérfogat miatt a 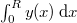 határozott integrálnak nullát kell adnia, azaz
határozott integrálnak nullát kell adnia, azaz
![\[0=\int_0^R \left(\frac{\omega^2}{2g}x^2+C\right)\,\mathrm{d}x=\frac{\omega^2}{6g}R^3+CR,\]](/images/math/7/8/0/780a6b5712c02b46fd5bf3ece9e31457.png)
ahonnét
![\[C=-\frac{\omega R}{6g}.\]](/images/math/9/0/c/90c9cd7a3b444497d06a4715d538f6fc.png)
Így a folyadékfelszín egyenlete:
![\[y=\frac{\omega^2}{2g}\left(x^2-\frac{R^2}{3}\right).\]](/images/math/f/c/6/fc60a7151f61e5f466d3fc57d92aa14b.png)
A (1) kifejezésből az alábbi következtetések vonhatók le:
- A parabola csúcspontjának ordinátája
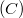 arányos
arányos 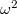 -tel, ami alapján fordulatszámmérő készíthető.
-tel, ami alapján fordulatszámmérő készíthető.
- A különböző szögsebességekhez tartozó parabolák átmennek a
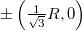 pontokon. [Az utóbbi állítás könnyen belátható, ha (1)-be
pontokon. [Az utóbbi állítás könnyen belátható, ha (1)-be 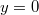 -t helyettesítünk és
-t helyettesítünk és 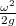 -vel egyszerűsítünk.]
-vel egyszerűsítünk.]
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
1. Igazolja kísérletileg, hogy a forgó folyadék felszíne által kialakított parabola csúcspontjának süllyedése a szögsebesség négyzetével arányos!
Vegye fel a 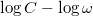 függvényt és a grafikon segítségével állapítsa meg
függvényt és a grafikon segítségével állapítsa meg  kitevőjét! (Használja a
kitevőjét! (Használja a 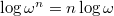 összefüggést! A szögsebességet fordulatszámméréssel határozza meg!)
összefüggést! A szögsebességet fordulatszámméréssel határozza meg!)
2. Határozza meg a nehézségi gyorsulás értékét!
Rajzolja fel a 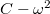 függvényt, majd határozza meg a mérési pontokon át fektetett egyenes meredekségét, ami
függvényt, majd határozza meg a mérési pontokon át fektetett egyenes meredekségét, ami 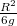 értékét adja meg. Ennek ismeretében számítsa ki a nehézségi gyorsulást!
értékét adja meg. Ennek ismeretében számítsa ki a nehézségi gyorsulást!