A zaj mint jel
SZERKESZTÉS ALATT!
A mérés célja
Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség "zaja" több információt hordoz a rendszerről mint maga a várható érték. A mérési gyakorlaton különböző zajjelenségeket vizsgálunk egy spektrumanalizátor segítségével. Először ellenállások termikus zajának mérése alapján meghatározzuk a Boltzmann állandó értékét. Ezután egy félvezető dióda zajának méréséből az elektrontöltés értékét határozzuk meg. Végül a Barkhausen zaj jelenségét tanulmányozzuk.
Elméleti összefoglalás
A zaj definíciója
| 1. ábra |
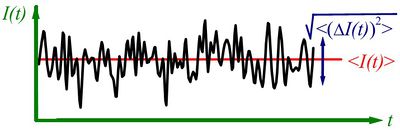
Egy időben változó mennyiség (pl. 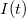 áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát,
áram, lásd 1. ábra) mérésekor definiálhatjuk a mért mennyiség időbeli átlagát, 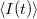 , illetve az átlagtól vett eltérést,
, illetve az átlagtól vett eltérést, 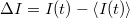 . A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével,
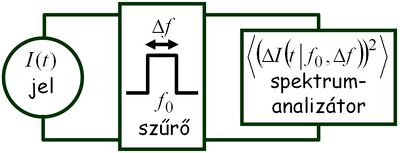
. A zajt jellemezhetnénk egyszerűen az áram szórásnégyzetével, 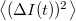 , azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az
, azonban ekkor nem vennénk figyelembe hogy mérőrendszerünk csak véges sávszélességgel tud mérni, azaz egy bizonyos határfrekvencia fölött már nem tudjuk felbontani a jel időbeli fluktuációit. Ezért célszerű a zaj értékét a 2. ábrán szemléltetett módon egy bizonyos frekvenciasávra vonatkoztatni: az 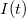 jelet egy
jelet egy  középfrekvencia körüli
középfrekvencia körüli  szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző
szélességű sáváteresztő szűrőn keresztül mérjük, azaz csak az adott frekvenciasávra jellemző 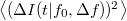 szórásnégyzetet mérünk.
szórásnégyzetet mérünk.
| 2. ábra |
Az így kapott szórásnégyzet kis  esetén arányos a
esetén arányos a  sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
sávszélességgel, az arányossági tényezőt pedig a zaj spektrális sűrűségének nevezzük:
![\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]](/images/math/3/3/f/33ff88a562de7a830d972009efd5d850.png)
Áramzaj esetén az 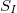 spektrális sűrűség mértékegysége
spektrális sűrűség mértékegysége 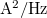 . A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját
. A mérnöki gyakorlatban gyakran a spektrális sűrűség négyzetgyökével jellemzik egy eszköz zaját 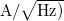 mértékegységgel.
mértékegységgel.
![\[\left<(\Delta V(t|f_0,\Delta f))^2\right>=S_V(f_0)\Delta f.\]](/images/math/8/9/a/89add176c6c234d68ca1a7b6097619e0.png)
Egy egyszerű ellenállás esetén 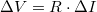 , azaz
, azaz 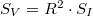 . Egy nemlineáris eszköznél, pl. egy diódánál
. Egy nemlineáris eszköznél, pl. egy diódánál 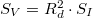 , ahol
, ahol 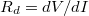 az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
az eszköz differenciális ellenállása a mérésnél alkalmazott munkapontban.
A fenti definíciók megismerése után érdemes megnézni a mérésnél használt Stanford Research Systems 770 típusú spektrumanalizátor specificációit, melyek szerint a műszer bemeneti zaja a legkisebb méréshatárban 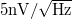 . Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása
. Ez azt jelenti, hogy a műszer bemenetét rövidre zárva a várt zérus feszültség helyett a bemeneti erősítő feszültségzaját látjuk, melynek a szórása 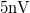
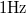 -es sávszélességű mérés esetén.
-es sávszélességű mérés esetén.
Puskalövések zaja
A zaj fogalma egy klasszikus példával is jól szemléltethető, nézzük meg hogy mi történik ha egy puskából véletlenszerűen lövöldözünk, úgy hogy a lövések időpontja egymástól teljesen független. Ha a szomszédos lövések között eltelt átlagos idő  akkor
akkor  idő alatt a lövések átlagos száma értelemszerűen
idő alatt a lövések átlagos száma értelemszerűen 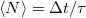 . A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a
. A tényleges lövésszám azonban nyilvánvalóan fluktuálni fog az átlagérték körül. A szórásnégyzet meghatározásához érdemes kiszámolni a 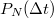 valószínűséget, azaz annak a valószínűségét, hogy
valószínűséget, azaz annak a valószínűségét, hogy  idő alatt
idő alatt  lövés dördül. Ha
lövés dördül. Ha 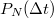 értékét ismerjük, akkor
értékét ismerjük, akkor 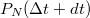 értéke a
értéke a
![\[P_N(\Delta t+dt)=P_{N-1}(\Delta t)\frac{dt}{\tau}+P_N(\Delta t)\left(1-\frac{dt}{\tau}\right)\]](/images/math/3/f/4/3f4062d58cc637d85054d98f2b6b3f49.png)
egyenlettel írható fel, azaz a kezdeti  és az utána következő
és az utána következő 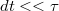 idő alatt vagy
idő alatt vagy 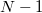 ill.
ill.  vagy
vagy  ill.
ill.  lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
lövés dördül. A megfelelő valószínűségeket a lövések függetlensége miatt szorozhatjuk össze.
A fenti egyenlet átrendezésével a
![\[\frac{dP_N(\Delta t)}{dt}=\frac{P_{N-1}(\Delta t)-P_N(\Delta t)}{\tau}\]](/images/math/b/6/4/b64ef404ea69d3816419cfebef01952b.png)
differenciálegyenletet kapjuk. Megmutatható, hogy ezen feltételt a
![\[P_N(\Delta t)=\frac{(\Delta t)^N}{\tau^N N!}e^{-\Delta t/\tau}\]](/images/math/f/b/b/fbb852541ecee469bb9e8e91c30241fe.png)
Poisson eloszlás elégíti ki. A Poisson eloszlás speciális tulajdonsága, hogy a szórásnégyzet megegyezik a várható értékkel, azaz
![\[\left< (\Delta N)^2 \right>=\left< N \right>=\frac{\Delta t}{\tau}.\]](/images/math/c/9/2/c925d13d542008c08786e26fc2259b03.png)
Elektronok sörétzaja
A fenti gondolatmenetet vonatkoztathatjuk elektronokra is ha teljesül az, hogy az elektronok véletlenszerűen, egymástól függetlenül jutnak át az egyik elektródából a másikba. Tegyük fel, hogy mérőrendszerünkkel az elektromos áramot  időbeli felbontással tudjuk mérni. Egy
időbeli felbontással tudjuk mérni. Egy  szélességű mintavételezési intervallum alatt
szélességű mintavételezési intervallum alatt 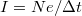 áramot detektálunk ahol a
áramot detektálunk ahol a  idő alatt áthaladó eletronok
idő alatt áthaladó eletronok  számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke
számának eloszlását a fenti Poisson eloszlás adja meg. Így a mért áram várható értéke 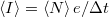 , míg az áram szórásnégyzete
, míg az áram szórásnégyzete 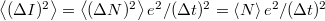 .
A Nyquist - Shannon mintavételezési törvény szerint
.
A Nyquist - Shannon mintavételezési törvény szerint  időfelbontás esetén a mért jelet
időfelbontás esetén a mért jelet 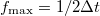 maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áramzaj spektrális sűrűsége:
maximális frekvenciáig tudjuk rekonstruálni. Ez alapján a mért áramzaj spektrális sűrűsége:
![\[S_I=\frac{\left< (\Delta I)^2 \right>}{f_{\mathrm{max}}}=2e\left< I \right>.\]](/images/math/b/8/9/b897997349b4a8f111d035c2c475d355.png)
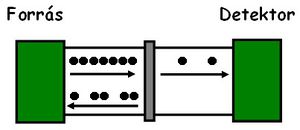
A puskagolyós analógia alapján az elektronok diszkrét töltéséből adódó áramzajt sörétzajnak szokták nevezni. Fontos megemlíteni, hogy a sörétzaj fehér zaj, azaz a spektrális sűrűség frekvenciafüggetlen. Az előbbiekben levezetett zajformula a sörétzajnak is egyik speciális esetét írja le, az ún. Poisson zajt, mely egymástól független elektronok detektálására vonatkozik. A kvantummechanikából ismert Pauli elv szerint (lásd a laborgyakorlattel párhuzamosan futó Kvantummechanika tárgy anyagát) két elektron nem lehet ugyan abban az állapotban, azaz egy adott időpontban nem tudunk két teljesen egyforma állapotú elektront detektálni. Egy makroszkópikus vezetőben az elektronok nem egymástól függetlenül, hanem inkább sorban egymást követve érkeznek az árammérőhöz, így a fenti zajformula nem érvényes, a Poisson zajnál lényegesen kisebb sörétzajt tapasztalunk. Azonban a Poisson zaj feltételét megvalósíthatjuk akkor, ha az elektronok útjába egy olyan akadályt helyezünk, melyen véletlenszerűen az elektronoknak csak egy kis része tud keresztüljutni (3a ábra).
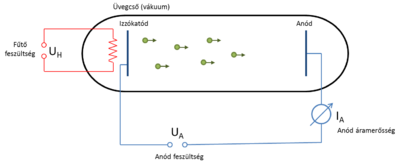
Az első sörétzaj mérést Walter Schottky végezte 1918-ban [1]: híres kísérletében egy vákuumdióda anódáramának zaját vizsgálta. A vákuumdióda felépítését a 3b. ábra szemlélteti. Egy fűtött katódból véletlenszerűen kilépő elektronok a katód és anód közé kapcsolt feszültség hatására eljutnak az anódba, ahol áramot detektálunk. A vákuumdióda ideális eszköz a sörétzaj tanulmányozásához, hiszen az elektronok valóban véletlenül, és egymástól függetlenül emittálódnak, így a mért zajsűrűség és az áram hányadosából az elektrontöltés a Poisson zaj formulája meghatározható.
| 3a. ábra | 3b. ábra |
Poisson zajt modern elektronikai eszközökben is tapasztalhatunk, például egy diódát alkotó félvezető p-n átmenet is biztosítja az elektronok véletlen és független emisszióját megfelelően kicsi áram esetén.
Termikus zaj
Az előbbiekben bemutatott sörétzaj egy nemegyensúlyi zaj, melyet csak akkor tapasztalunk, ha a vizsgált áramköri elemen áramot folyatunk keresztül. Zajt azonban egensúlyi állapotban is tapasztalhatunk pusztán az elektronok termikus fluktuációi miatt. A termikus zaj megértése komolyabb elméleti hátteret igényel, azonban maga a jelenség egy nagyon egyszerű formulával leírható: egy  elektromos ellenállással rendelkező áramköri elemen
elektromos ellenállással rendelkező áramköri elemen
![\[S_V=4k_B T\cdot R\]](/images/math/8/5/0/8500771d360277ebaf7f4f7c0a6fef77.png)
feszültségzaj-sűrűséget mérhetünk attól függetlenül, hogy pontosan milyen fizikai rendszer adja az  ellenállást.
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
Ezen jelenség segítségével a
ellenállást.
A termikus zaj szintén fehér zaj, azaz a zajsűrűség nem függ a frekvenciától.
Ezen jelenség segítségével a  hőmérséklet és az
hőmérséklet és az  ellenállás ismeretében a feszültségzaj méréséből a Boltzmann állandó meghatározható.
ellenállás ismeretében a feszültségzaj méréséből a Boltzmann állandó meghatározható.
Egyéb zajforrások
A termikus zaj és a sörétzaj mellett még a szennyezők és rácshibák véletlen mozgásából adódó ún. 1/f zajról is érdemes megemlékezni, mely alacsony frekvenciákon dominál, és a nevét is a zajsűrűség tipikus frekvenciafüggéséről kapta. Az 1/f zaj a sörétzajhoz hasonlóan nemegyensúlyi zaj, a spektrális sűrűség a feszültség négyzetével skálázódik.
Az eddigiekben csak vizsgált rendszerünk belső zajáról beszéltünk, azonban zajmérésnél mindig fontos a külső forráspokból felvett zajokra is gondolni. Az egyik legfontosabb zavaró tényező az elektromos hálózat 50Hz-es váltakozó feszültségéból felvett zaj, de a mérőrendszerünk könnyen felvesz zajt monitorok képernyőjének frissítési frekvenciájánál, kapcsoló üzemű tápok frissítési frekvenciájánál, vagy akár rádióállomások, mobiltelefonok sugárzási frekvenciájánál.
Mágneses anyagok speciális zaja: Barkhausen zaj
Mérési elrendezés
A méréshez használt eszközök
A méréshez egy Stanford Reserch Systems 770 típusú spektrumanalizátort használunk. A későbbiekben csak a műszer legfontosabb funkcióit ismertetjük, részletes specifikációk és leírás a műszer [adatlapjában és használati utasításában érhető el.
A spektrumanalizátor jele egy saját fejlesztésű szoftverrel (SRS770_beolvasas.exe) számítógépbe beolvasható illetve fájlba kimenzhető.
A termikus és a sörétzaj méréséhez egy lezárható alumínium dobozba helyezett ún. breadboard panel áll rendelkezésre, melyben forrasztás nélkül könnyen összeállítható egy elektromos áramkör (4. ábra). A dobozon két BNC csatlakozó található. A méréshez különböző áramköri elemek állnak rendelkezésre: ellenállások, alacsony zajú tranzisztor, kondenzátorok, 9V-os elem csatlakozóval, BNC-BNC toldó, BNC csatlakozós koax kábel.
| 4. ábra |
A termikus zaj mérésének elve
A termikus zaj mérésénél a doboz egyik BNC csatlakozójának belső pontja és földpontja közé egy ellenállást kötünk, a BNC csatlakozót pedig egy BNC-BNC toldó segítségével (lásd 4. ábra felső csatlakozó) közvetlenül a spektrumanalizátor Signal in (A) bemenetére kötjük és ebben az elrendezésben mérjük az ellenállás feszültségzaját. Mivel a mért termikus zaj összemérhető a műszer bemeneti zajával (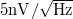 ) ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz:
) ezért a mért zaj a termikus zaj és a műszer bemeneti zajának összege lesz:
![\[S_V=4k_B T\cdot R + S_0.\]](/images/math/a/b/d/abd2e7c79dbc44dd178c08da8a388ecc.png)
Ha a mérést több ellenálláson is megismételjük akkor az 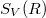 függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann állandó értékét.
függvény meredekségéből a szobahőmérséklet ismeretében megkapjuk a Boltzmann állandó értékét.
| 5. ábra |
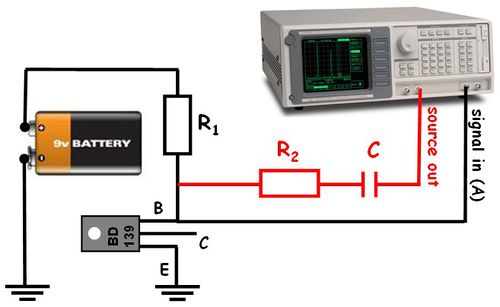
A sörétzaj mérésének elve
A sörétzaj mérésekor az 5. ábrán bemutatott kapcsolást érdemes alkalmazni. Tápegységként használjunk egy 9V-os elemet, így a meghajtó feszültségünk zaja kisebb lesz mint ha bármilyen elektromos hálózatra kötött tápegységet használnánk. A teleppel kössünk sorba egy nagy ellenállást ( ) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk.
) és egy félvezető diódát. Diódaként érdemes egy alacsony zajszintű tranzisztort használni úgy, hogy azt a bázis és emitter kontaktusokon keresztül kötjük az áramkörbe és a kollektor elektródát nem használjuk.
A körben folyó egyenáramot könnyen meghatározhatjuk az  ellenálláson eső feszültség mérése alapján (a biztonság kedvéért érdemes az
ellenálláson eső feszültség mérése alapján (a biztonság kedvéért érdemes az  ellenállás értékét is pontosan megmérni, és ezzel számolni a névleges érték helyett.) A feszültség- és ellenállás-méréshez használjunk 4.5 digites Goodwill digitális multimétert.
ellenállás értékét is pontosan megmérni, és ezzel számolni a névleges érték helyett.) A feszültség- és ellenállás-méréshez használjunk 4.5 digites Goodwill digitális multimétert.
Az áram meghatározása után mérjük meg a spektrumanalizátorral a diódán jelentkező feszültségzajt. (Ennél a mérésnél az ábrán pirossal jelölt  ellenállást és
ellenállást és  kondenzátort ne kössük az áramkörbe!) Az így mért feszültségzaj
kondenzátort ne kössük az áramkörbe!) Az így mért feszültségzaj
![\[S_V=2e\left< I \right> \cdot R_d^2 +S_0,\]](/images/math/c/b/b/cbb0b32f6c711a3163b5c6a7e91a8bc6.png)
ahol 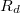 a dióda differenciális ellenállása a beállított munkapontban,
a dióda differenciális ellenállása a beállított munkapontban, 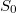 pedig a műszer bemeneti zaja.
pedig a műszer bemeneti zaja.
A következő lépés a dióda differenciális ellenállásának a meghatározása. Ehhez a spektrumanalizátor source out kimenetéről egy  ellenálláson és egy
ellenálláson és egy  kondenzátoron keresztül hozzákevetrünk egy váltóáramot a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a vátóáramú feszültségesést a meghajtó jellel azonos frekvencián. A spektrumanalizátor kimeneti feszültségszintjét és az
kondenzátoron keresztül hozzákevetrünk egy váltóáramot a telepből jövő egyenáramhoz, és a spektrumanalizátorral megmérjük a vátóáramú feszültségesést a meghajtó jellel azonos frekvencián. A spektrumanalizátor kimeneti feszültségszintjét és az  ellenállást úgy kell megválasztani hogy a diódán folyó váltóáram az egyenáramnál lényegesen kisebb legyen. A
ellenállást úgy kell megválasztani hogy a diódán folyó váltóáram az egyenáramnál lényegesen kisebb legyen. A  kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a spektrumanalizátor kimenete felé elfolyni. Célszerű
kapacitás azt a célt szolgálja, hogy a telepből jövő egyenáramból semennyi ne tudjon a spektrumanalizátor kimenete felé elfolyni. Célszerű  értékét úgy megválasztani hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen
értékét úgy megválasztani hogy a meghajtó frekvencián vett impedancia lényegesen kisebb legyen  -nél. Így a differenciális ellenállást
-nél. Így a differenciális ellenállást
![\[R_d=\frac{\Delta U_{\mathrm{rms}}}{\Delta I_{\mathrm{rms}}}\]](/images/math/5/f/f/5ffcd9e91b4c5ee0332e3c1527333e8c.png)
képlet szerint számoljuk, ahol 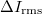 a source out kimeneten kiadott váltófeszültség rms értékének és
a source out kimeneten kiadott váltófeszültség rms értékének és  ellenállásnak a hányadosa,
ellenállásnak a hányadosa, 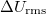 pedig a diódán mért váltóáramú feszültség rms értéke.
pedig a diódán mért váltóáramú feszültség rms értéke.
Ha különböző  ellenállásokkal megmérjük
ellenállásokkal megmérjük 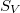 ,
, 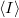 és
és 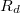 értékét akkor az
értékét akkor az 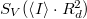 függvényre egyenest illesztve megkapjuk az elektron töltésének értékét.
függvényre egyenest illesztve megkapjuk az elektron töltésének értékét.
Mérési feladatok
Kitekintés
Ujkisnano, szilfiz, kvantum, statfiz. Zaj hőmérő, kvázirészecskék töltésének meghatározása, bozon fermion, kvantumos vagy klasszikus viselkedés
Hivatkozások
[1] Schottky, W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern, Annalen der Physik 57 p541–567 (1918).