Sztatikus mágneses mező vizsgálata
Szerkesztés alatt!
A mérés célja
- a Helmholtz-tekercs mágneses terének vizsgálata és az Ampére-féle gerjesztési törvény kísérleti igazolása.
Ennek érdekében:
- megismerkedünk a mágneses térerősség mérésére szolgáló magnetorezisztív szenzorral, és az Universal Lab Interface (ULI) adatgyűjtő rendszerrel;
- feltérképezzük a mágneses térerősség komponensei-nek helyfüggését a Helmholtz-tekercs körül.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Egyes sztatikus mágnességgel kapcsolatos jelenségek (pl. az, hogy bizonyos vasércek a kisméretű vasdarabokat magukhoz vonzzák) már az ókorban ismertek voltak. A Föld mágneses terét évezredek óta használjuk tájékozódásra. Ezen mérés keretében állandó mágneses terek vizsgálatával foglalkozunk.
Szemben a Naprendszerünk hasonló méretű bolygóinak többségével, a Föld erős mágneses térrel rendelkezik, amely a Föld belsejében található anyag/töltés áramlásokkal hozható kapcsolatba. A Föld mágneses tere fontos szerepet játszik a földfelszín nagyenergiás kozmikus részecskékkel szembeni védelmében (1. ábra), és jelenléte alapvető lehetett a földi élet kialakulása szempontjából is.
A földmágneses tér eloszlása a Föld felszínén első közelítésben olyan, mintha egy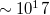 Vsm momentumú dipólus helyezkedne el a Föld közepe táján, melynek tengelye hozzávetőleg a
Vsm momentumú dipólus helyezkedne el a Föld közepe táján, melynek tengelye hozzávetőleg a 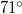 É,
É, 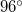 NY ill.
NY ill. 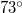 D,
D, 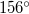 K ponto-ban metszi a felszínt. A súlypontjában felfüggesztett mágnestű (feltéve, hogy nincsenek a környezetében mágneses vagy mágnesezhető anyagok ill. áramjárta vezetők) a Föld LaTex syntax error
K ponto-ban metszi a felszínt. A súlypontjában felfüggesztett mágnestű (feltéve, hogy nincsenek a környezetében mágneses vagy mágnesezhető anyagok ill. áramjárta vezetők) a Föld LaTex syntax error\setbox0\hbox{$\mathhit{\mathbf{B_F}}$}%
\message{//depth:\the\dp0//}%
\box0%
mágneses terének (mágneses indukciójának) irányába áll be.
BF-et általában a mágneses elhajlás vagy deklináció szögével (térerősség vektoron átmenő függőleges ún. mágneses meridiánsík és az adott helyen átmenő földrajzi meridiánsík vagy hosszúsági kör által bezárt szög), ill. a lehajlás vagy inklináció szöge (BF-nek a vízszintessel bezárt szöge), valamint a horizontális intenzitás (BF vízszintes vetülete) segítségével adják meg, melyekkel kifejezhető a teljes intenzitás (a vektor abszolút értéke) és a vertikális intenzitás (a függőleges komponens).