Optika és információ
Tartalomjegyzék[elrejtés] |
A fény szerepe a földi élet kialakulásában és az azt követő biológiai evolúcióban alapvető jelentőségű volt. Az emberi agy számára a "látás" közvetíti a legtöbb információt a világról. Gondoljunk arra, hogy csupán egy pillantást vetve a környezetünkre utólag milyen sok mindent fel tudunk idézni a látottakból. Az ember már igen korán megpróbálta a vizuális élményeit rögzíteni. A sziklarajzoktól a 3D moziig terjed a sikeres technikák vonulata. Tapasztalatból tudjuk, hogy egy fénykép információtartalma korlátozott, ugyanakkor holografikus módon sokkal több információt tudunk rögzíteni. Vajon mi akadályoz minket abban, hogy az oly sikeres litográfiás technikával a mainál sokkal nagyobb alkatrészsűrűséget érjünk el? Mitől függ egy digitális kamera felbontása?
Az informatikában igen fontos a gyors és nagymennyiségű adatforgalom. Az optikai szálak használata ugrásszerűen megnövelte az átviteli csatornák kapacitását. Az optika megjelent az adatrögzítés területén is. Vajon miként növelhető (egyáltalán növelhető-e tovább) a DVD lemezek adatsűrűsége? Ebben a fejezetben választ kapunk olyan érdekes kérdésekre is, mint például: hogyan lehet az, hogy egy távcsővel figyelve egy távoli tárgyat mégsem látjuk élesen annak részeit, annak ellenére, hogy a nagyítás megfelelő, vagy miért nem lehet egy optikai mikroszkóppal lefényképezni az atomokat?
Geometriai optika
A geometriai optika elvei
Az optika az elektromágneses hullámok elméletéhez tartozik, hiszen a látható tartomány (400 nm <  < 750 nm) az elektromágneses spektrum része. Különleges fontossággal bír ez a tudományterület, mert számos optikai mérést illetve berendezést fejlesztettek ki, amelyek segítségével információt kaphatunk – eredetileg esetleg szemmel nem, vagy nem jól látható – tárgyakról illetve folyamatokról, amelyek a minket körülvevő világ pontosabb leírását adhatják.
< 750 nm) az elektromágneses spektrum része. Különleges fontossággal bír ez a tudományterület, mert számos optikai mérést illetve berendezést fejlesztettek ki, amelyek segítségével információt kaphatunk – eredetileg esetleg szemmel nem, vagy nem jól látható – tárgyakról illetve folyamatokról, amelyek a minket körülvevő világ pontosabb leírását adhatják.
Az elektromágneses hullámok tárgyalása során tett megállapítások, valamint bizonyítások az optikában is jól használhatók. Ismételjük át ezeket:
| 1. | A síkhullám egy olyan transzverzális hullám, amelyben az elektromos és mágneses térerősség-komponensek merőlegesek egymásra és a hullám terjedési irányára. |
| 2. | A síkhullám szabad térben (vákuumban vagy levegőben, akadálymentes tartományban) egyenes vonalban terjed  fénysebességgel. fénysebességgel.
|
| 3. | Sík felületről úgy verődik vissza, hogy a beesési és a visszaverődési szög megegyezik. |
Az egyenes vonalú terjedésről, valamint a beesési és visszaverődési szög megegyezéséről csaknem mindenkinek vannak tapasztalatai; elég csak arra gondolni, hogy milyennek is látjuk a lézer-mutató nyalábját, amint egy sima felületről pl. egy sima asztallapról, üvegről, vagy egy tükörről verődik vissza (1.1.1.a és b ábra).
| 1.1.1.a ábra | 1.1.1.b ábra |
Idáig nem beszéltünk arról, hogy az EMH miként terjed különböző közegekben. Ezen jegyzet kereteibe nem fér be jó néhány igen érdekes és fontos eset, mint például az EMH és plazma kölcsönhatása, stb. Ezért most korlátozzuk vizsgálatainkat – ha "közegről" vagy "anyagról" van szó – dielektrikumokra. Mérések segítségével kimutatták, hogy a fény a dielektrikumokban (pl. a vízben) lassabban halad a vákuumbeli  fénysebességnél. Az anyagot jellemezhetjük a két sebességérték hányadosával, ez az anyagra jellemző törésmutató (egy adott hullámhosszon):
fénysebességnél. Az anyagot jellemezhetjük a két sebességérték hányadosával, ez az anyagra jellemző törésmutató (egy adott hullámhosszon):
![\[ n = \frac {c}{v} \]](/images/math/9/8/7/987ee51ae0a9f610f6c53bdce94eb008.png) |
(1.1.1) |
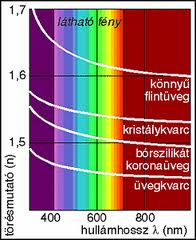
Igen sok mérés alapján megállapítható, hogy a legtöbb anyag törésmutatója függ a hullámhossztól; mint az az 1.1.2. ábrán is látható.
| 1.1.2 ábra |
Az előzőekből következik, hogy a vákuumban eredetileg  hullámhosszúságú síkhullám hullámhossza – minthogy a fény frekvenciája nem változik – a dielektrikumban:
hullámhosszúságú síkhullám hullámhossza – minthogy a fény frekvenciája nem változik – a dielektrikumban:
![\[ \lambda' = v T = \frac {c}{n}T = \frac{\lambda}{n} \]](/images/math/f/3/3/f33b6d89baba3240ec8a0c08b6b9a7f3.png) |
(1.1.2) |
Ezután megvizsgáljuk, hogy miként is törik meg a fény, ha vákuumból (vagy levegőből) valamely dielektrikumba lép be. Tekintsük a következő ábrát, amelynek alapján megmagyarázhatjuk a fénytörés jelenségét a Huygens-elv felhasználásával.
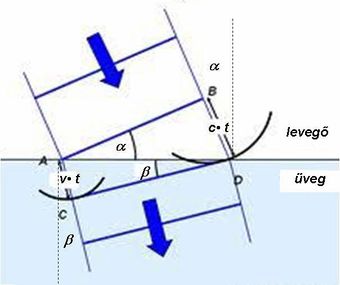
| 1.1.3 ábra |
Az 1.1.3 ábrán látható, hogy a felső, levegőt tartalmazó tartományból érkező síkhullám 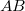 hullámfrontja miként változtatja meg terjedési irányát. A beeső síkhullám terjedési iránya
hullámfrontja miként változtatja meg terjedési irányát. A beeső síkhullám terjedési iránya  szöget zár be a felületi normálissal. Amint a síkhullám
szöget zár be a felületi normálissal. Amint a síkhullám  pontot tartalmazó része eléri a dielektrikumot, akkor ez a rész (az egyszerűség kedvéért az
pontot tartalmazó része eléri a dielektrikumot, akkor ez a rész (az egyszerűség kedvéért az  pont) Huygens-elvéből következően a dielektrikumban maga is egy hullámforrás lesz, azaz egy gömbhullám kiindulópontja. Amíg
pont) Huygens-elvéből következően a dielektrikumban maga is egy hullámforrás lesz, azaz egy gömbhullám kiindulópontja. Amíg  időtartam alatt a levegőben a hullámfront a
időtartam alatt a levegőben a hullámfront a  pontból eléri a közeghatárt, ugyanazon
pontból eléri a közeghatárt, ugyanazon  idő alatt az
idő alatt az  pontból kiinduló gömbhullám sugara
pontból kiinduló gömbhullám sugara 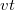 értékre növekszik. Ekkor a gömbhullámok alkotta hullámfront – az ábrán a
értékre növekszik. Ekkor a gömbhullámok alkotta hullámfront – az ábrán a 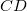 szakasz – meghatározza a síkhullám terjedési irányát a dielektrikumban; ez azt jelenti, hogy a hullámterjedés iránya
szakasz – meghatározza a síkhullám terjedési irányát a dielektrikumban; ez azt jelenti, hogy a hullámterjedés iránya  szöget zár be a felületi normálissal. Az ábráról leolvasható:
szöget zár be a felületi normálissal. Az ábráról leolvasható:
![\[ vt = AD sin(\beta) \qquad {\rm \acute{e}s} \qquad ct = AD sin(\alpha) \]](/images/math/6/f/f/6ffef834d66b9a5d6e25c2b655f1b1a9.png) |
(1.1.3) |
Ebből következik – a 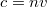 felhasználásával – a Schnellius-Descartes törvény:
felhasználásával – a Schnellius-Descartes törvény:
![\[ n = \frac {sin \alpha}{sin \beta} \]](/images/math/f/5/6/f5609b66e75262b49e8afd78d8b4e0ad.png) |
(1.1.4) |
Könnyű belátni, hogy amennyiben a fény nem levegőből vagy vákuumból érkezik a határfelülethez, hanem egy másik dielektrikumból, akkor a Schnellius-Descartes törvény általános alakja:
![\[ n_1 sin \alpha_1 = n_2 sin \alpha_2 \]](/images/math/1/7/8/1788f09980eb8528aba6c23de801894a.png) |
(1.1.5) |
A most bemutatott – és többek által már a középiskolában tanult – törvénynek van egy fontos következménye. Ennek szemléltetésére tekintsük a következő ábrát!
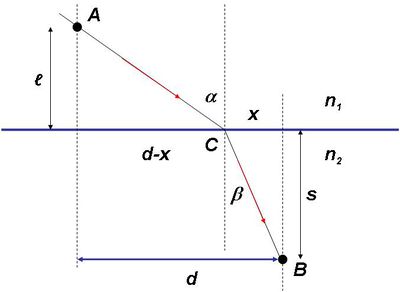
| 1.1.4 ábra |
A fény az  pontból indulva a
pontból indulva a  ponton keresztül (ott megtörve) halad a
ponton keresztül (ott megtörve) halad a  pontba. A felső régióban
pontba. A felső régióban 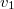 , míg az alsóban
, míg az alsóban 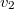 sebességgel halad. Most egy kis időre felejtsük el a törési törvényt. Kérdés, hogy
sebességgel halad. Most egy kis időre felejtsük el a törési törvényt. Kérdés, hogy  milyen értékénél ér a fénysugár a legrövidebb idő alatt az
milyen értékénél ér a fénysugár a legrövidebb idő alatt az  pontból a
pontból a  -be? A fény az
-be? A fény az 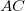 távolságot
távolságot 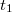 , míg a
, míg a 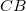 távolságot
távolságot 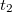 időtartam alatt teszi meg, azaz:
időtartam alatt teszi meg, azaz:
![\[ t_1 = \frac {AC}{v_1} \qquad {\rm \acute{e}s} \qquad t_2 = \frac {CB}{v_2} \]](/images/math/9/3/1/9317921b0a523a76d29e04bfa2d5c3bc.png) |
(1.1.6) |
vagyis:
![\[ t_1 = \frac {\sqrt{\ell^2 + (d-x)^2}}{v_1} \qquad {\rm \acute{e}s} \qquad t_2 = \frac {\sqrt{s^2 + x^2}}{v_2} \]](/images/math/9/a/6/9a68199c8b9b3f6c8912522142656107.png) |
(1.1.7) |
A teljes  időtartam tehát ezek szerint
időtartam tehát ezek szerint  -től függ:
-től függ:
![\[ t = \frac {\sqrt{\ell^2 + (d-x)^2}}{v_1} + \frac {\sqrt{s^2 + x^2}}{v_2} \]](/images/math/a/1/e/a1e45fa558da8792355b92c17781df47.png) |
(1.1.8) |
Azt, hogy mely  érték mellett lesz a
érték mellett lesz a  minimális, megkaphatjuk az
minimális, megkaphatjuk az  szerinti deriválással:
szerinti deriválással:
![\[ \frac {dt}{dx} = \frac {x-d}{v_1 \sqrt{\ell^2 + (d-x)^2}} + \frac {x}{v_2 \sqrt{s^2 + x^2}}= 0 \]](/images/math/0/d/a/0dafaba367670faf180f5c3b7d084d48.png) |
(1.1.9) |
Az 1.1.4 ábráról leolvasható, hogy:
![\[ sin \alpha = \frac {d-x}{\sqrt{\ell^2 + (d-x)^2}} \qquad {\rm \acute{e}s} \qquad sin \beta = \frac {x}{\sqrt{s^2 + x^2}} \]](/images/math/d/9/3/d93d1d87993bb709696b23c47d6a20ef.png) |
(1.1.10) |
Ez utóbbi két összefüggés felhasználásával 1.1.9 a következő alakba írható:
![\[ \frac {sin\alpha}{v_1} = \frac {sin\beta}{v_2} \]](/images/math/9/f/0/9f0fb78773c5ed37bddaf1016f459b33.png) |
(1.1.11) |
Amennyiben a terjedési sebességeket megadjuk a törésmutatókkal, azaz 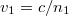 és
és 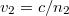 , akkor az 1.1.11 formulát megkaphatjuk a következő alakban:
, akkor az 1.1.11 formulát megkaphatjuk a következő alakban:
![\[ n_1 sin \alpha = n_2 sin \beta \]](/images/math/d/f/7/df725de16bb15e12c2e37e731a690e04.png) |
(1.1.12) |
Ez pedig éppen a most megismert Schnellius-Descartes törvény általános alakja. Megállapíthatjuk tehát, hogy a fény olyan pályán terjed az egyik pontból a másikba, amelyre az jellemző, hogy a hullámterjedéshez szükséges időtartam a legrövidebb. Ez az elv természetesen általános esetben is megfogalmazható. Amennyiben a közeg törésmutatója helyfüggő, azaz 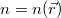 , akkor az előbb szóban megfogalmazott elv matematikai alakban is megadható:
, akkor az előbb szóban megfogalmazott elv matematikai alakban is megadható:
![\[ \int\limits_a^b dt = \int\limits_a^b \frac{1}{v} ds = \int\limits_a^b \frac{n(\vec r)}{c} ds = min. \]](/images/math/6/e/8/6e8956bfe80747a07f841426b0157da5.png) |
(1.1.13) |
Mivel a fénysebesség állandó, így elhagyható és kapjuk a Fermat-elvet:
![\[ \int\limits_a^b n(\vec r) ds = min. \]](/images/math/5/c/e/5ce696ca495142ac0d2a034343073701.png) |
(1.1.14) |
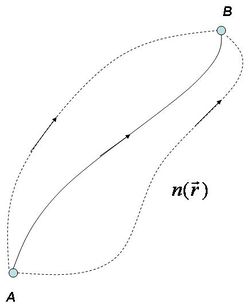
Ennek a formulának a következő az olvasata: az összes olyan pálya közül, amelyen a fénynyaláb az  pontból a
pontból a  pontba juthat, az 1.1.14 feltétel által kiválasztott útvonalon fog a fény terjedni. (A fizikailag megvalósuló, az 1.1.14-ből meghatározható fényutat folytonos vonallal, míg a virtuális pályákat szaggatott vonallal jelöltük a következő ábrán.) Itt csak megjegyezzük, hogy a mechanika és az elektrodinamika törvényei is megfogalmazhatók variációs elv segítségével.
pontba juthat, az 1.1.14 feltétel által kiválasztott útvonalon fog a fény terjedni. (A fizikailag megvalósuló, az 1.1.14-ből meghatározható fényutat folytonos vonallal, míg a virtuális pályákat szaggatott vonallal jelöltük a következő ábrán.) Itt csak megjegyezzük, hogy a mechanika és az elektrodinamika törvényei is megfogalmazhatók variációs elv segítségével.
| 1.1.5 ábra |
Az említett elv segítségével, az elemi geometria alkalmazásával könnyen bizonyítható például, hogy reflexiónál a beesési szög megegyezik a visszaverődési szöggel.
A Fermat-elv alkalmazásával meghatározhatjuk például egy fénynyaláb pályáját olyan esetekben is, amikor például a törésmutató folytonosan változik.
A geometriai optika törvényei fénysugarakra és azok terjedésére vonatkoznak. Az elektromágneses hullámokról tanultak a 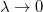 határátmenetben visszaadják a geometriai optika szabályait. Az előzőekben bemutatott példák alapján a geometriai optika törvényeit a következőkben foglalhatjuk össze:
határátmenetben visszaadják a geometriai optika szabályait. Az előzőekben bemutatott példák alapján a geometriai optika törvényeit a következőkben foglalhatjuk össze:
| 1. | A fény(sugár) egyenes vonalban terjed. |
| 2. | Különböző közegek határfelületein a fénysugár egy része reflektálódik, más része fénytörést szenvedve behatol a másik közegbe. |
| 3. | A szuperpozíció elvéből következően két vagy több fénynyaláb áthaladhat a tér egy pontján (tartományán) anélkül, hogy zavarnák egymást. |
| 4. | Ha a fénysugár az egyik pontból a másikba egy meghatározott pályán halad, akkor visszafelé a második pontból az eredetibe ugyanazon az úton terjed a fény. |
A geometriai optika törvényeinek alkalmazásával tárgyalhatjuk gömbtükrök és lencsék, illetve lencserendszerek, stb. leképezési tulajdonságait.
Képalkotás gömbtükörrel
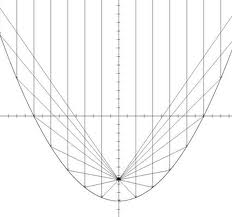
A parabolatükörre az optikai tengellyel párhuzamosan érkező fénysugarak - mint az az elemi geometriából ismert – a parabola fókuszpontján mennek át (1.2.1 ábra).
| 1.2.1 ábra |
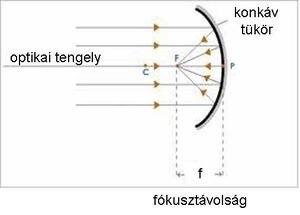
Hasonló jelenséget észlelhetünk, ha egy tükröző, homorú gömbfelülettel szeretnénk a párhuzamosan érkező fénysugarakat összegyűjteni, fókuszálni (1.2.2 ábra).
| 1.2.2 ábra |
Vizsgáljuk meg ezt a fókuszálási jelenséget kissé részletesebben! Ehhez tekintsük a következő ábrát!
| 1.2.3 ábra |
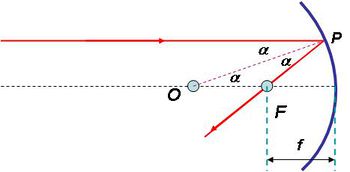
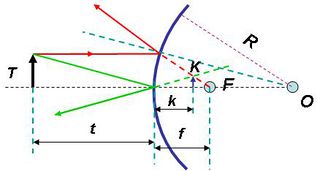
Az optikai tengellyel (szaggatott vonal) párhuzamosan érkező fénysugár az  görbületi sugarú gömbtükörről a
görbületi sugarú gömbtükörről a  pontban reflektálódik, majd az
pontban reflektálódik, majd az  fókuszponton megy át. A beesési és a visszaverődési szög megegyezik. Ez azt jelenti, hogy a fénysugár az
fókuszponton megy át. A beesési és a visszaverődési szög megegyezik. Ez azt jelenti, hogy a fénysugár az 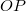 szakasszal ugyanakkora szöget zár be, mint az
szakasszal ugyanakkora szöget zár be, mint az 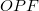 szög, ez viszont megegyezik a
szög, ez viszont megegyezik a 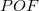 szöggel, tehát az
szöggel, tehát az 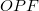 egy egyenlő szárú háromszög, vagyis
egy egyenlő szárú háromszög, vagyis 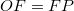 . Az ábráról leolvasható, hogy
. Az ábráról leolvasható, hogy 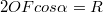 . Amennyiben
. Amennyiben 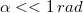 és ennek következtében
és ennek következtében 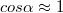 , ebből következik, hogy
, ebből következik, hogy 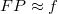 , azaz a gömbtükör fókusztávolsága:
, azaz a gömbtükör fókusztávolsága:
![\[ f \approx \frac {R}{2} \]](/images/math/6/3/e/63ea5791977f39a4a185ef6791319e5a.png) |
(1.2.1) |
Egy gömbtükörrel azonban nem csak a végtelenből (gyakorlatilag a tükör görbületi sugaránál sokkal nagyobb távolságból) érkező fénysugarak fókuszálása oldható meg, hanem egy tárgy leképezése is. A képalkotás folyamatának megértésében segíthet a következő ábra.
| 1.2.4 ábra |
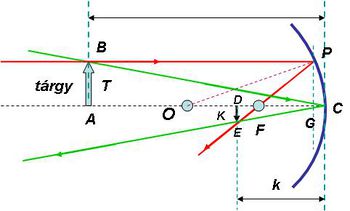
A tükörtől  távolságban lévő,
távolságban lévő,  magasságú
magasságú 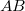 tárgy
tárgy  pontjából kiinduló két jellegzetes fénysugár közül az egyik (pirossal jelölt) az optikai tengellyel párhuzamosan halad, majd a tükörről visszaverődve áthalad a fókuszponton. A másik (zöld vonallal jelölt) fénysugár a tükör közepén, a
pontjából kiinduló két jellegzetes fénysugár közül az egyik (pirossal jelölt) az optikai tengellyel párhuzamosan halad, majd a tükörről visszaverődve áthalad a fókuszponton. A másik (zöld vonallal jelölt) fénysugár a tükör közepén, a  pontban reflektálódik. A két fénysugár az
pontban reflektálódik. A két fénysugár az  pontban metszi egymást, azaz a tárgy
pontban metszi egymást, azaz a tárgy  pontját a tükör az
pontját a tükör az  pontba képezi le. Minthogy a tárgy méretére – azon kívül, hogy az
pontba képezi le. Minthogy a tárgy méretére – azon kívül, hogy az 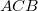 szög legyen kicsi ( << 1 rad) – semmilyen megkötést nem tettünk, így nyugodtan mondhatjuk, hogy az
szög legyen kicsi ( << 1 rad) – semmilyen megkötést nem tettünk, így nyugodtan mondhatjuk, hogy az  pontban lévő tárgyat a tükör az attól
pontban lévő tárgyat a tükör az attól  távolságban lévő,
távolságban lévő,  méretű
méretű 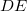 -be képezi le. A leképezés azt jelenti, hogy a tükörtől
-be képezi le. A leképezés azt jelenti, hogy a tükörtől  távolságban lévő ernyőn a tárgy – leképező optika, vagy lencse nélkül is látható - valódi képe jelenik meg, azaz a tárgy egy pontjának képe ideális esetben egy képpont lesz, nem pedig egy fényfolt (ekkor homályos képet kapunk). A leképezés törvényét a geometria módszereinek alkalmazásával adhatjuk meg. Az
távolságban lévő ernyőn a tárgy – leképező optika, vagy lencse nélkül is látható - valódi képe jelenik meg, azaz a tárgy egy pontjának képe ideális esetben egy képpont lesz, nem pedig egy fényfolt (ekkor homályos képet kapunk). A leképezés törvényét a geometria módszereinek alkalmazásával adhatjuk meg. Az 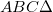 hasonló a
hasonló a 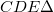 -höz, vagyis:
-höz, vagyis:
![\[ \frac {K}{T} = \frac {k}{t} \]](/images/math/3/d/1/3d191e49d7b46f0439a01ea85541b5f5.png) |
(1.2.2) |
Hasonlóképpen felhasználhatjuk azt is, hogy az 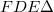 hasonló a
hasonló a 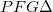 -höz (A
-höz (A 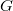 pont az optikai tengely és a
pont az optikai tengely és a  pontban a tengelyre állított merőleges egyenes metszéspontja. Kis szögeket feltételezve a
pontban a tengelyre állított merőleges egyenes metszéspontja. Kis szögeket feltételezve a 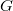 és a
és a  pont csaknem egybeesik.) Ebből következik, hogy:
pont csaknem egybeesik.) Ebből következik, hogy:
![\[ \frac {K}{T} = \frac {k-f}{f} \]](/images/math/a/2/f/a2f1e4f823123b947292f321c3a643ba.png) |
(1.2.3) |
Az 1.2.2 és 1.2.3 jobb oldalát egyenlővé téve és a kapott egyenletet átrendezve kapjuk az 1/f szabályt:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f} \]](/images/math/5/d/8/5d859b74de084110d14edc1fb0a417a9.png) |
(1.2.4) |
Az 1.2.4 – ből adódik (és az 1.2.4 ábrán is látszik), hogy ha a 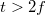 , akkor a kép a tükörtől mérve a fókuszpont és a gömb középpontja közé esik:
, akkor a kép a tükörtől mérve a fókuszpont és a gömb középpontja közé esik: 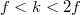 . Ebben az esetben a tárgynak egy valódi, fordított állású, kicsinyített képe jelenik meg. A nagyítás mértékét a kép és a tárgy méretének arányával, vagy a képtávolság és a tárgytávolság hányadosával adhatjuk meg:
. Ebben az esetben a tárgynak egy valódi, fordított állású, kicsinyített képe jelenik meg. A nagyítás mértékét a kép és a tárgy méretének arányával, vagy a képtávolság és a tárgytávolság hányadosával adhatjuk meg:
![\[ N = \frac {K}{T} = \frac {k}{t} \]](/images/math/a/6/2/a62d7060d483ee3e83ebd1b925708cc2.png) |
(1.2.5) |
A gömbtükör előzőekben tárgyalt leképezései esetében a nagyítást egyértelműen meghatározza a tárgytávolság; az 1.2.4 - ből kifejezve  – t és behelyettesítve 1.2.5 - be kapjuk:
– t és behelyettesítve 1.2.5 - be kapjuk:
![\[ N = \frac {f}{t-f} \]](/images/math/8/c/9/8c95d9239b4375535b3ccd02355000f0.png) |
(1.2.6) |
A fénysugarak megfordíthatóságának elvéből következik, hogy ha 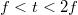 , akkor
, akkor 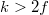 , és a tárgy valódi, fordított állású, nagyított képe jelenik meg. Amennyiben
, és a tárgy valódi, fordított állású, nagyított képe jelenik meg. Amennyiben 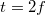 , akkor természetesen
, akkor természetesen 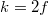 , és
, és 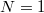 . Már csak azt az esetet nem néztük meg, hogy miként valósul meg a képalkotás, ha
. Már csak azt az esetet nem néztük meg, hogy miként valósul meg a képalkotás, ha 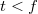 . Ehhez tekintsük a következő ábrát:
. Ehhez tekintsük a következő ábrát:
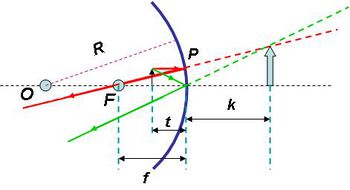
| 1.2.5 ábra |
A háromszögek hasonlóságát felhasználva, az előzőekben bemutatott módon, könnyen megkaphatjuk a leképezési törvényt a borotválkozó tükör esetén is:
![\[ \frac {1}{t} - \frac {1}{k} = \frac {1}{f} \]](/images/math/f/8/7/f8773ab926afaebe97041f0dd7b4ed13.png) |
(1.2.7) |
Az 1.2.5 ábrán látható, hogy miként lehet megszerkeszteni a tárgy (fekete nyíl) képét (kék nyíl) a tárgy egy pontjából kiinduló két jellegzetes sugárral. Ebben az esetben a tárgy egyenes állású virtuális képe (ernyőn fel nem fogható) áll elő, hiszen a tárgy egy pontjából kiinduló fénysugarak a tükörről visszaverődve széttartók (divergensek) lesznek. Borotválkozás (vagy szépítkezés) közben a képet csak azért látjuk, mert a szemünk lencséje a képet, mint egy másodlagos tárgyat, leképezi a retinánkra.
| 1.2.6.a ábra | 1.2.6.b ábra |
A nagyítás az 1.2.7 felhasználásával:
![\[ N = \frac {f}{f-t} \]](/images/math/3/7/2/372466c35d2c6bdd9a0e56b7421eb587.png) |
(1.2.8) |
Egy gömbtükörnek természetesen a domború oldala is használható tükörként; lásd a következő két képet.
| 1.2.7.a ábra | 1.2.7.b ábra |
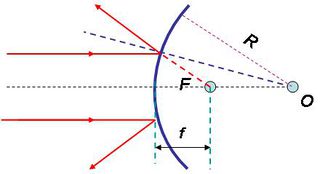
A következő ábra alapján könnyen belátható, hogy a domború gömbtükörre érkező, az optikai tengellyel párhuzamos fénysugarak a reflexió után széttartóvá válnak, és úgy terjednek, mintha az  fókuszpontból indultak volna.
fókuszpontból indultak volna.
| 1.2.8 ábra |
Kis szögek esetén itt is használhatjuk az 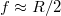 közelítést. A leképezést megszerkeszthetjük az 1.2.9 ábrán látható módon:
közelítést. A leképezést megszerkeszthetjük az 1.2.9 ábrán látható módon:
| 1.2.9 ábra |
Az előzőekben már bemutatott hasonló háromszögek módszerével kapjuk az 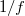 szabály domború gömbtükörre alkalmazható alakját:
szabály domború gömbtükörre alkalmazható alakját:
![\[ \frac {1}{t} - \frac {1}{k} = -\frac {1}{f} \]](/images/math/d/2/c/d2cc3e3c3f3a6462f07a9f36e7aa2e51.png) |
(1.2.9) |
Az 1.2.9 segítségével bizonyítható és az 1.2.9 ábráról is leolvasható, hogy domború (konvex) gömbtükör használatával egyenes állású, virtuális képet kapunk. A legtöbb esetben egy ilyen tükör erősen torzított képet ad, mégis széleskörűen alkalmazzák a közlekedési eszközökön visszapillantó tükörként, illetve a közlekedést segítendő útkereszteződésekben, mert bár a kép torz, viszont nagy látószögű.
| 1.2.10.a ábra | 1.2.10.b ábra |
A most bemutatott, gömbtükörrel megvalósítható leképezések esetében felállíthatunk egy gyakorlati szabályt: amennyiben a kép vagy (és) a fókuszpont a tükör "másik oldalán" van, akkor  vagy (és)
vagy (és)  helyett
helyett 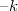 -t vagy (és)
-t vagy (és) 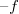 –t kell behelyettesíteni az
–t kell behelyettesíteni az 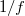 formulába.
formulába.
Lencse és lencserendszer képalkotása
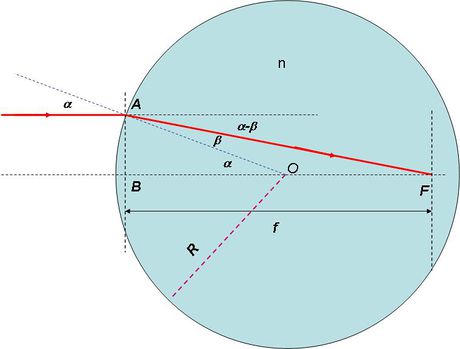
Mielőtt lencsékkel és lencsékből összerakható leképező eszközökkel foglalkoznánk, először tekintsünk egy egyszerű modellt. Vizsgáljuk meg, hogy mi történik, ha egy  törésmutatójú,
törésmutatójú,  sugarú, átlátszó dielektrikum gömbre síkhullám esik. A síkhullám terjedését egy fénysugár nyomon követésével modellezzük:
sugarú, átlátszó dielektrikum gömbre síkhullám esik. A síkhullám terjedését egy fénysugár nyomon követésével modellezzük:
| 1.3.1 ábra |
A beeső fénysugár az  pontban éri el a gömbfelszínt, majd ott megtörik, és az optikai tengelyt az
pontban éri el a gömbfelszínt, majd ott megtörik, és az optikai tengelyt az  fókuszpontban metszi. Próbáljuk most megadni a fókusztávolságot a sugárral és a törésmutatóval! Vizsgálatainkat kis szögekre korlátozzuk, vagyis
fókuszpontban metszi. Próbáljuk most megadni a fókusztávolságot a sugárral és a törésmutatóval! Vizsgálatainkat kis szögekre korlátozzuk, vagyis 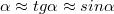 és
és 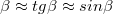 . Az
. Az  fókusztávolság meghatározásához induljunk ki a következő összefüggésből:
fókusztávolság meghatározásához induljunk ki a következő összefüggésből:
![\[ \frac {AB}{f}= tg(\alpha - \beta) \approx \alpha - \beta \]](/images/math/6/1/3/6132b4ea96f201039ef8bd22172820ed.png) |
(1.3.1) |
A fénytörési törvény megadja  és
és  hányadosát:
hányadosát:
![\[ \frac {sin \alpha}{sin \beta}= n \approx \frac{\alpha}{\beta} \]](/images/math/8/9/5/895f15911c23082c45967a1d04e6794f.png) |
(1.3.2) |
Az 1.3.1 és 1.3.2 formulákból kapjuk az 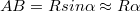 közelítés (az 1.3.1 ábráról leolvasható) felhasználásával a fókusztávolságot:
közelítés (az 1.3.1 ábráról leolvasható) felhasználásával a fókusztávolságot:
![\[ f= \frac{Rn}{n-1} \]](/images/math/8/6/8/8688532528bca10a59494e0ebd925568.png) |
(1.3.3) |
Az  sugarú,
sugarú,  törésmutatójú dielektrikum gömb, mint a legegyszerűbb leképező eszköz a természetben is megtalálható. A híradásokban néha hallani, hogy az erdőtüzet esetleg a napfényt fókuszáló vízcsepp okozhatta. Az 1.3.2 ábrán jól látszik egyrészt, hogy a vízcsepp, ha nem is egy pontba (nem tökéletes gömb), de egy kisebb területre fókuszálja a fényt; másrészt pedig mint egy nagyító (lencse) "működik".
törésmutatójú dielektrikum gömb, mint a legegyszerűbb leképező eszköz a természetben is megtalálható. A híradásokban néha hallani, hogy az erdőtüzet esetleg a napfényt fókuszáló vízcsepp okozhatta. Az 1.3.2 ábrán jól látszik egyrészt, hogy a vízcsepp, ha nem is egy pontba (nem tökéletes gömb), de egy kisebb területre fókuszálja a fényt; másrészt pedig mint egy nagyító (lencse) "működik".
| 1.3.2 ábra |
(Az evolúció ellenzői - Darwin elméletének tarthatatlanságát bizonyítandó - a szem összetett szerkezetét (is) felemlegették. Érvelésük lényege az volt, hogy a fajok folyamatos változása során nem alakulhatott ki egy ilyen bonyolult optikai eszköz lépésről lépésre. Az előzőekben bemutatott modell jól mutatja, hogy egy - a környezetétől eltérő törésmutatójú - dielektrikum gömb is alkalmas optikai leképezésre, csakúgy, mint a fényképezőgép őse, a camera obscura. Mindkét optikai jelenség részét képezi a szem evolúcióját bizonyító magyarázatoknak.)
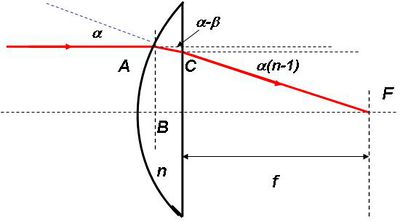
Ezután képzeljük el, hogy lencsét készítünk a gömb alakú dielektrikumból úgy, hogy annak nagy részét leválasztjuk róla (1.3.3 ábra).
| 1.3.3 ábra |
Most határozzuk meg a lencse fókusztávolságát! Az előző modell vizsgálatából már tudjuk, hogy a dielektrikumon belül a fénysugár az optikai tengellyel 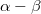 szöget zár be, de ugyanekkora szöget zár be a lencsét határoló sík felületi normálisával is. A lencséből kilépve a fénysugár ismét törést szenved (a
szöget zár be, de ugyanekkora szöget zár be a lencsét határoló sík felületi normálisával is. A lencséből kilépve a fénysugár ismét törést szenved (a  pontban); ekkor újra felírhatjuk a Schnellius-Descartes törési törvényt:
pontban); ekkor újra felírhatjuk a Schnellius-Descartes törési törvényt:
![\[ \frac {sin\gamma}{sin(\alpha - \beta)} \approx \frac {\gamma}{\alpha - \beta} \approx n \quad \Longrightarrow \quad \gamma \approx n (\alpha - \beta) \approx n(\alpha - \frac {\alpha}{n})\approx \alpha (n-1) \]](/images/math/a/8/b/a8b871d19ce500f0d88648bc471eb282.png) |
(1.3.4) |
ahol a kilépő nyaláb  szöget (ezt külön nem jelöltük az ábrán) zár be az optikai tengellyel. A lencséről feltesszük, hogy annyira vékony, hogy a vastagságából adódó eltolással nem kell foglalkozni. Ekkor a fókusztávolság így számítható:
szöget (ezt külön nem jelöltük az ábrán) zár be az optikai tengellyel. A lencséről feltesszük, hogy annyira vékony, hogy a vastagságából adódó eltolással nem kell foglalkozni. Ekkor a fókusztávolság így számítható:
![\[ f \approx \frac {AB}{\alpha (n-1)} \approx \frac {R\alpha}{\alpha (n-1)} \approx \frac {R}{n-1} \]](/images/math/0/9/4/0942a89d796eca5b9ae12034c88312dd.png) |
(1.3.5) |
Ebből már meghatározhatjuk, hogy hány dioptriás egy vékony sík-domború lencse; a dioptria-szám a fókusztávolság reciproka:
![\[ D = \frac {1}{f}=(n-1)\frac {1}{R} \]](/images/math/c/4/0/c40cc8938279f6a01e437f608fdfe9f1.png) |
(1.3.6) |
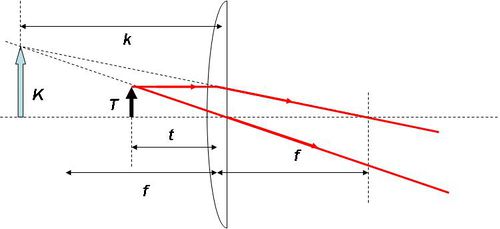
A jellegzetes fénysugarak által megszerkeszthető leképezés segítségével felírható a lencse leképezési törvénye. A tárgy egy pontjából kiinduló, az optikai tengellyel párhuzamosan haladó fénynyaláb a lencse másik oldalán átmegy a fókuszponton. A lencse közepén átmenő fénysugár pedig nem szenved törést (úgy tekinthetjük, mintha egy vékony plánparalell lemezen menne át).
| 1.3.4 ábra |
A lencse vastagságával nem törődve felírhatók a hasonló háromszögek közötti arányok. Könnyű belátni, hogy egy ilyen lencse esetén is leírható a leképezés az 1/f szabály alkalmazásával:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f} \]](/images/math/5/d/8/5d859b74de084110d14edc1fb0a417a9.png) |
(1.3.7) |
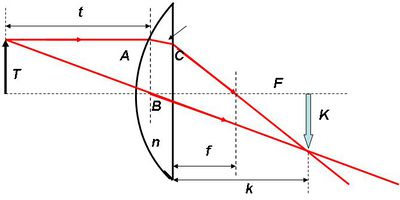
Itt most nem diszkutáljuk a különböző eseteket, de kitérünk a nagyító (lupe) esetére. Amennyiben a tárgytávolság kisebb a fókusztávolságnál, akkor is megszerkeszthetjük az említett módszerek segítségével a képet:
| 1.3.5 ábra |
A megfelelő háromszögek hasonlóságát felhasználva nem nehéz bizonyítani, hogy:
![\[ \frac {1}{t} - \frac {1}{k} = \frac {1}{f} \]](/images/math/f/8/7/f8773ab926afaebe97041f0dd7b4ed13.png) |
(1.3.8) |
Ennek segítségével a nagyítás is megadható:
![\[ N = \frac {f}{f-t} \]](/images/math/3/7/2/372466c35d2c6bdd9a0e56b7421eb587.png) |
(1.3.9) |
Vagyis a nagyítás – természetesen – függ a tárgytávolságtól. A lencsék nagyítását mégis valahogyan jellemezni kell. Megállapodás szerint a tisztánlátás távolsága 0.25m; ezt képtávolságnak választva a 1.3.9 segítségével belátható, hogy:
![\[ N = \frac {f+0.25}{f} \]](/images/math/4/9/f/49fc33a34296598914c4529cb6a26b24.png) |
(1.3.10) |
amennyiben a fókusztávolságot méterben számítják. Ha bemegyünk egy optikai szaküzletbe, láthatjuk, hogy a lupék nagyítása egy számmal van megadva; ez az 1.3.10-nek megfelelően lett meghatározva. Egy ilyen gyűjtőlencse nagyítása jellemzően 2 és 8 közötti érték.
Ezután vizsgáljuk meg, hogy mi történik, ha az 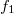 fókusztávolságú lencse után közvetlenül odahelyezünk még egy másik
fókusztávolságú lencse után közvetlenül odahelyezünk még egy másik 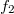 fókusztávolságút. Számítsuk ki a két lencséből álló "lencserendszer" fókuszának hosszát. Tegyük fel, hogy mindkét lencse követi az 1/f szabályt. Ekkor az első lencse által a kép a lencse mögött
fókusztávolságút. Számítsuk ki a két lencséből álló "lencserendszer" fókuszának hosszát. Tegyük fel, hogy mindkét lencse követi az 1/f szabályt. Ekkor az első lencse által a kép a lencse mögött  képtávolságban képeződne le, amelyre:
képtávolságban képeződne le, amelyre:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f_1} \quad \Longrightarrow \quad \frac {1}{k} = \frac {1}{f_1} - \frac {1}{t} \]](/images/math/1/0/7/1072b96e032fe6b72431f211855fd120.png) |
(1.3.11) |
Viszont a második lencsénél ennek a képtávolságnak a 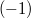 - szerese lesz a tárgytávolság. Most megint alkalmazható a leképezési szabály:
- szerese lesz a tárgytávolság. Most megint alkalmazható a leképezési szabály:
![\[ \frac {1}{t} - \frac {1}{f_1} + \frac {1}{k'} = \frac {1}{f_2} \quad \Longrightarrow \quad \frac {1}{t} + \frac {1}{k'} = \frac {1}{f_1} + \frac {1}{f_2} = D_1 + D_2 = D_e \]](/images/math/1/f/a/1fa608d68f04af20dc9dda54fdda7d4e.png) |
(1.3.12) |
ahol 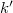 a második lencse után kialakult képtávolság. Az eredő fókusztávolság tehát:
a második lencse után kialakult képtávolság. Az eredő fókusztávolság tehát:
![\[ f = \frac {1}{D_e} \quad \Longrightarrow \quad f = \frac {f_1 f_2}{f_1 + f_2} \]](/images/math/0/c/b/0cb4891155438f09d7f70daab3b67dde.png) |
(1.3.13) |
Az 1.3.12 összefüggés ( 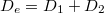 ), a "dioptriák törvénye" csak vékony lencsékre alkalmazható; vékonynak tekinthetünk egy lencsét, ha a vastagsága (középen) jóval kisebb az átmérőjénél.
), a "dioptriák törvénye" csak vékony lencsékre alkalmazható; vékonynak tekinthetünk egy lencsét, ha a vastagsága (középen) jóval kisebb az átmérőjénél.
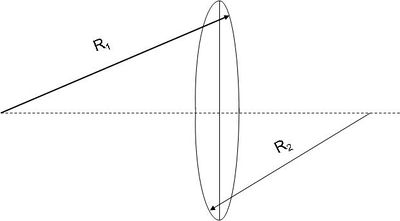
A sík-domború lencsére kapott 1.3.6 eredményt és a dioptriák összeadásának szabályát felhasználhatjuk arra, hogy meghatározzuk egy olyan lencse fókusztávolságát, amelyet két  és
és  görbületi sugarú felület határol. Úgy is tekinthetünk egy ilyen lencsére, mintha két sík-domború lencséből lenne összeragasztva.
görbületi sugarú felület határol. Úgy is tekinthetünk egy ilyen lencsére, mintha két sík-domború lencséből lenne összeragasztva.
| 1.3.6 ábra |
A dioptriákat összeadva adódik az eredő fókusztávolság az 1.3.6 segítségével:
![\[ \frac {1}{f_1}=(n-1)\frac {1}{R_1} \qquad {\rm \acute{e}s} \qquad \frac {1}{f_2}=(n-1)\frac {1}{R_2} \]](/images/math/4/6/d/46daf77088afa9569044d97dee4df89c.png) |
(1.3.14) |
tehát:
![\[ \frac {1}{f}= \frac {1}{f_1} + \frac {1}{f_2} = (n-1) \left( \frac {1}{R_1} + \frac {1}{R_2} \right) \]](/images/math/a/c/5/ac564374abc9cb16f015c2d8e7a0e9b5.png) |
(1.3.15) |
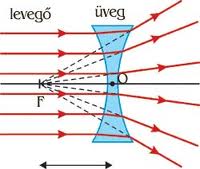
Ez a formula megadja nemcsak a gyűjtőlencse (a közepe vastagabb a szélénél), hanem a szórólencse (a közepe vékonyabb a szélénél) fókusztávolságának képletét is. Azonban vegyük észre, hogy egy szórólencse fókusztávolsága negatív érték (a homorú oldalhoz tartozó görbületi sugár 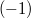 -szeresét kell venni). Ez érthető is, hiszen a szórólencsén az optikai tengellyel párhuzamosan érkező fénysugarak úgy szóródnak, mintha a belépő oldalon lévő fókuszpontból mint forrásból lépnének ki:
-szeresét kell venni). Ez érthető is, hiszen a szórólencsén az optikai tengellyel párhuzamosan érkező fénysugarak úgy szóródnak, mintha a belépő oldalon lévő fókuszpontból mint forrásból lépnének ki:
| 1.3.7 ábra |
A távcső
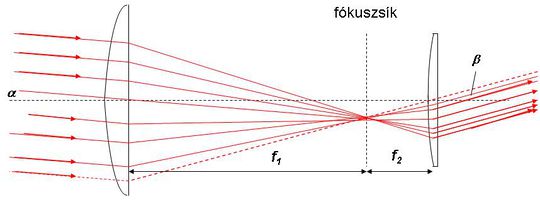
A távoli tárgyak minél pontosabb megfigyelése iránti igény már évszázadokkal ezelőtt felvetődött. A távcső megjelenése a csillagászatban forradalmi változásokat hozott. Ugyanígy a tengeri navigációban is. A legegyszerűbb optikai távcsövet fogjuk elemezni. A Kepler-féle távcső két – eltérő fókusztávolságú – lencséből áll. A lencsék egy optikai tengelyre vannak "felfűzve", és közös fókuszsíkkal rendelkeznek, azaz a két lencse közötti távolság a fókusztávolságok összege. A nagy távolságban lévő tárgy egy pontjából kiinduló fénysugarak gyakorlatilag párhuzamosnak tekinthetők, ezért a fókuszsík egy pontján mennek át.
| 1.4.1 ábra |
A távcső nagyítását az első lencsére (objektív) beeső és a második lencsét (okulár) elhagyó párhuzamos sugárnyalábok optikai tengellyel bezárt szögeik arányával adjuk meg:
![\[ N = \frac {\beta}{\alpha} \approx \frac {tg(\beta)}{tg(\alpha)} = \frac {f_1}{f_2} \]](/images/math/4/c/5/4c55e03a6098333dff98afa3671203c4.png) |
(1.4.1) |
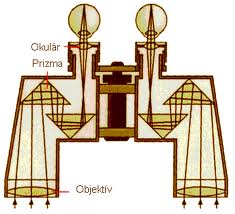
A Kepler-féle távcső fordított állású képet ad, ezért a földi megfigyelésre használatos távcsövek a képet két prizma segítségével "visszafordítják" (az objektív és okulár lencséket egy-egy összetett lencserendszer helyettesíti a jobb képminőség érdekében).
| 1.4.2.a ábra | 1.4.2.b ábra | 1.4.2.c ábra |
A Newton-féle távcsőben az objektívet egy konkáv tükörrel helyettesítik (a 0.5 m-nél nagyobb átmérőjű távcsövek szinte kivétel nélkül Newton rendszerűek):
| 1.4.3.a ábra | 1.4.3.b ábra |
Egy ilyen távcső vázlatos képe látható az 1.4.3.a ábrán; a nyalábot általában egy síktükörrel oldalra kivezetik az okulárhoz a könnyebb kezelhetőség érdekében. Ma már gyakran nem szemmel néznek a távcsőbe, hanem egy megfelelően átalakított CCD kamerát használnak az okulároldalon, majd csatlakoztatják számítógéphez és a monitoron láthatók a megfigyelni kívánt objektumok. Az itt felsorolt távcső típusokon kívül még számos egyéb elrendezésű "messzelátó" berendezést építettek.
A mikroszkóp
A mikroszkóp használatával a szabad szemmel nem látható tárgyakat, élőlényeket tudjuk láthatóvá tenni. A mikroszkóp fejlődése az egyre nagyobb felbontású optikai mikroszkópok fejlesztésével kezdődött. A mikroszkóp segítségével a biológusok egy új, addig nem látott világba nyertek bepillantást. A botanikus Brown mikroszkópjával felfedezte a virágpollen darabkák véletlenszerű mozgását, amelyet azóta Brow-mozgásnak neveznek. Ezt az effektust végül Albert Einstein tudta megmagyarázni; ez volt az első komoly bizonyíték az atomok létezésére.
A legegyszerűbb mikroszkóp szintén két lencséből áll, az objektívből és az okulárból.
| 1.5.1 ábra |
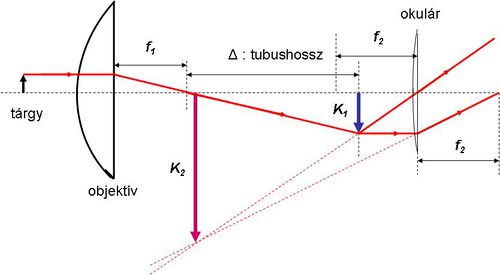
A mikroszkóp működésének megértéséhez tekintsük a következő ábrát:
| 1.5.2 ábra |
A tárgyat az objektívlencse leképezi a 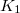 közbenső képbe. Az ábráról leolvasható, hogy az első leképezés nagyítása a tubushossz és az
közbenső képbe. Az ábráról leolvasható, hogy az első leképezés nagyítása a tubushossz és az 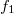 fókusz hányadosa:
fókusz hányadosa:
![\[ N_{obj.} = \frac {\Delta}{f_1} \]](/images/math/a/c/5/ac5aa9c19ea6d0379c7013874d058ffc.png) |
(1.5.1) |
Az okulár nagyítását megadhatjuk 1.3.10 formula segítségével, kihasználva, hogy 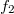 általában jóval kisebb
általában jóval kisebb 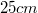 -nél (fókusztávolság méterben számítandó):
-nél (fókusztávolság méterben számítandó):
![\[ N_{ok.} = \frac {f_2 + 0.25}{f_2} \approx \frac {0.25}{f_2} \]](/images/math/f/5/7/f573b6f9803dee6baaa635fe0a74fd2c.png) |
(1.5.2) |
A mikroszkóp nagyítása az objektív és az okulár nagyításának szorzata:
![\[ N_{obj.} N_{ok.} = \frac {0.25 \Delta}{f_1 f_2} \]](/images/math/c/d/6/cd6ae38540754097e5f7bb5b2d7ec769.png) |
(1.5.3) |
A fénymikroszkópok nagyítása jellemzően 50 és 3000 közé esik. Arról majd a későbbiekben lesz szó, hogy a mikroszkóp nagyítását miért nem lehet egy bizonyos határ fölé növelni. Ezt akkor sem lehetne megtenni, ha a lencsékkel illetve lencserendszerekkel torzításmentes leképezést lehetne megvalósítani.
Lencsehibák
A lencsével történő képalkotás általában nem tökéletes. Ennek például az az oka, hogy a tárgy egy pontjából kiinduló fénysugarak az ernyőn, vagy a szemünkben nem egy pontban találkoznak, hanem egy foltot hoznak létre; ezáltal lesz a kép homályos. Más típusú lencsehibák is előfordulhatnak. A szférikus felületekkel határolt lencsék hibái közül itt csak néhányat említünk meg.
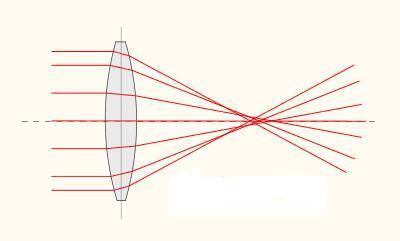
A szférikus aberráció abból fakad, hogy az optikai tengellyel párhuzamosan futó, de attól kissé távolabbi sugarak az optikai tengelyt más-más pontban érik el (1.6.1 ábra). A szférikus aberráció kiküszöbölésére aszférikus felülettel határolt lencséket használnak.
| 1.6.1 ábra |
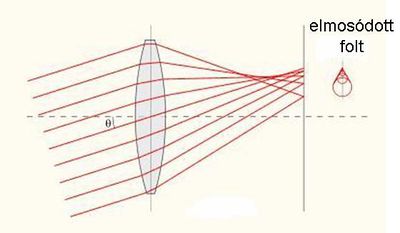
A lencsével történő képalkotás esetében fellépő kóma (vagy üstököshiba) azért jön létre, mert a ferde sugarak nem találkoznak a fókuszsíkon illetve a leképezés síkjában (1.6.2 ábra). Ez a típusú hiba általában a kép szélén okoz problémát; főként nagy látószögű objektívek alkalmazásánál lehet jelentős a hatása.
| 1.6.2 ábra |
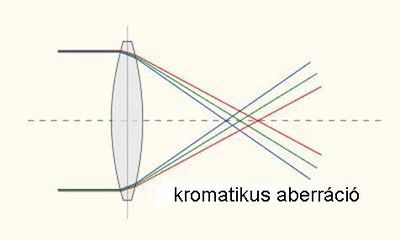
Idáig nem foglalkoztunk azzal, hogy milyen hullámhosszú fénnyel is dolgozunk. A tükrökkel megvalósítható leképezésnél ez nem is lényeges. A lencsék esetében azonban a színes tárgyak képalkotásánál kromatikus aberráció léphet fel a törésmutató hullámhosszfüggése miatt. Láttuk, hogy a fókusztávolság függ a törésmutatótól; ez azt eredményezi, hogy a különböző színű fénysugarakra más fókusztávolság adódik (1.6.3 ábra).
| 1.6.3 ábra |
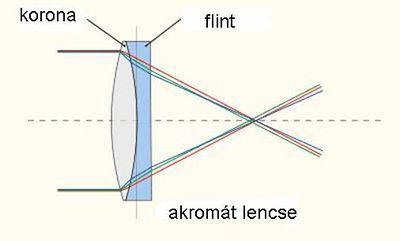
A kromatikus aberráció (színhiba) csökkentését általában két, különböző törésmutatójú üvegből (pl. korona és flint üveg) készült lencse együttes alkalmazásával érik el (1.6.4 ábra).
| 1.6.4 ábra |
Joggal kérdezhetné valaki, hogy ha ennyi fajta lencsehiba léphet fel, miért alkalmazunk üveglencséket. Erre az lehetne a válasz, hogy ugyan ma már széleskörűen alkalmaznak fröccsöntéssel készült műanyag lencséket, amelyeket aszférikus felületek határolnak kiküszöbölendő a lencsehibák egy része, azonban a szférikus felületekkel határolt lencséket még mindig sokkal pontosabban lehet megmunkálni. A lencsehibákat pedig lencserendszerek alkalmazásával korrigálni lehet, ezért például egy "tökéletes", azaz lencsehibáktól csaknem mentes (diffrakciólimitált) objektív általában jó néhány lencséből áll (1.6.5 ábra). Egy-egy ilyen lencserendszer tervezése többnyire igen bonyolult számítógépes feladat.
| 1.6.5 ábra |
Teljes visszaverődés (totálreflexió)
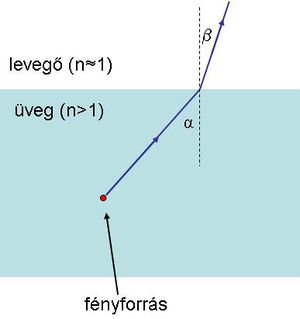
Idáig részletesebben nem foglalkoztunk azzal az esettel, hogy mi történik akkor, ha egy fénysugár a nagyobb törésmutatójú közegből az optikailag ritkább felé halad. Egy ilyen fénysugár fénytörését szintén a Schnellius-Descartes törvénnyel tudjuk leírni (1.7.1 ábra).
| 1.7.1 ábra |
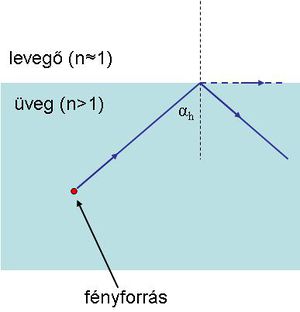
Gond akkor adódna, ha az ábrán látható eset áll elő:
| 1.7.2 ábra |
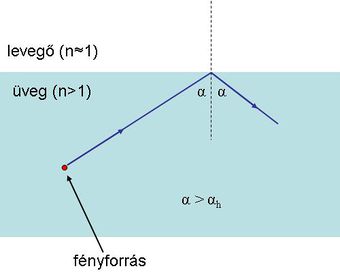
Ha az üveg felől érkező fényhullám iránya a közeghatár síkjának normálisával azt az 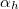 határszöget (1.7.2 ábra) zárja be, amelynél
határszöget (1.7.2 ábra) zárja be, amelynél 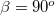 lenne, elérkeztünk a Schnellius-Descartes törvény alkalmazhatóságának határához. A törési törvény használatával a határszöget könnyen kiszámíthatjuk a következő formula segítségével:
lenne, elérkeztünk a Schnellius-Descartes törvény alkalmazhatóságának határához. A törési törvény használatával a határszöget könnyen kiszámíthatjuk a következő formula segítségével:
![\[ \frac {sin 90^o}{sin \alpha_h} = n \]](/images/math/c/8/2/c826a403853842bd174914051e90e897.png) |
(1.7.1) |
Az üveg felületén azonban a fény nem tud terjedni; a fény tehát teljes visszaverődést szenved az 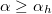 esetben (1.7.3 ábra).
esetben (1.7.3 ábra).
| 1.7.3 ábra |
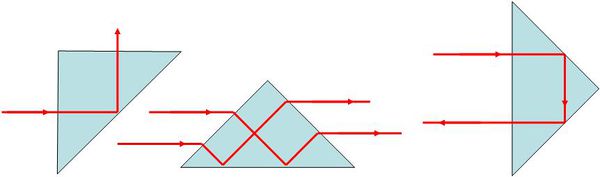
Ezt az effektust - a totálreflexiót - felhasználhatjuk a fény irányának megváltoztatására is például egy üvegprizma alkalmazásával (1.7.4.a ábra):
| 1.7.4.a ábra | 1.7.4.b ábra |
A macskaszem "működését" is teljes reflexióval magyarázhatjuk. A földmérők által használt reflexiós prizma is valójában egy macskaszem (1.7.4.b ábra).