Elektron fajlagos töltésének (e/m) mérése. Franck-Hertz kísérlet.

Szerkesztés alatt!

Elektron fajlagos töltésének (e/M) mérése

A mérés célja:

• elektromos- és mágneses térben mozgó töltött részecske viselkedésének megismerése
• az elektron fajlagos töltésének meghatározása.

Ennek érdekében :

• összefoglaljuk az elektromos- és mágneses térben mozgó töltött részecskére ható erők alaptörvényeit és az alkalmazott e/m mérési módszerek elvi alapjait,
• két független mérési módszerrel megmérjük az elektron fajlagos töltését.

Elméleti összefoglaló

Az általunk ismert anyag egyik alapvető építőköve az elektron, ezért legfontosabb adatainak ismerete az anyag tulajdonságainak mélyebb megértéséhez nélkülözhetetlen. Az elektron töltése (e) viszonylag egyszerű módszerrel meghatározható (először Millikan mérte meg ), tömegét (m) azonban közvetlenül nem tudjuk meghatározni. Megmérhető azonban töltésének és tömegének hányadosa (e/m), az úgynevezett fajlagos töltés, amelyből a töltés ismeretében a tömeg meghatározható.

A fajlagos töltés mérésének általunk használt módszerei azon alapulnak, hogy mágneses térben mozgó töltésre erő hat, amely eltéríti azt eredeti pályájától, és az eltérítés mértéke a fajlagos töltéstől függ. A mérés során speciális eltérítést valósítunk meg: a mágneses térben mozgó töltések a rájuk ható mágneses eltérítő erő hatására körpályán mozognak. A fajlagos töltés meghatározása lényegében a létrejött körpálya sugarának közvetlen vagy közvetett úton történő mérése alapján történik.

Egy $\setbox0\hbox{$E$}% \message{//depth:\the\dp0//}% \box0%$ térerősségű elektromos- és $\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$ mágneses indukciójú mágneses térben sebességgel mozgó e töltésre ható úgynevezett Lorentz-erő:

 

$\[ F_L = e(E+v\times B) \]$

(1)

A mozgó töltés a pályáján az elektromos tér hatására a térerősséggel párhuzamos egyenes mentén térül el, míg a mágneses tér a sebességre és a mágneses térre merőleges eltérülést okoz. Könnyen belátható, hogy ha csak mágneses tér van jelen és a töltés a mágneses térre merőlegesen mozog, akkor az eltérítő erő, – amely mindig merőleges a sebességre – a részecskét körpályára kényszeríti. (1. ábra)

Ábrát még pótolom

Mivel a részecskét körpályán tartó centripetális erő nagysága ekkor az

 

$\[ F_m = evB \]$

(2)

mágneses erő, a részecske mozfásegyenlete:

 

$\[ evB = m\frac{v^{2} }{r}. \]$

(3)

Ebből (a körpálya sugara helyett annak átmérőjét, d-t használva) a fajlagos töltésre az alábbi kifejezést kapjuk:

 

$\[ \frac{e}{m} =\frac{2v}{Bd} \]$

(4)

Ha tehát az elektron sebességét, a pálya átmérőjét és a mágneses indukcióvektor nagyságát ismerjük, akkor a fenti egyenletből a fajlagos töltés kiszámítható. A számításhoz szükséges adatokat az alábbi módon határozhatjuk meg.

Az elektronokat homogén elektromos térrel gyorsítjuk fel, így sebességük a munkatételből kiszámítható. (Az elektronok kezdősebessége elhanyagolható a gyorsítással megszerzett sebességhez képest.)

 

$\[ eU_gy = \frac{1}{2}mv^{2} \]$

(5)

 

$\[ v = \sqrt{\frac{2eU_gy}{m} } \]$

(6)

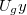Itt $\setbox0\hbox{$U_gy$}% \message{//depth:\the\dp0//}% \box0%$ az elektronokat gyorsító feszültség, melyet a mérés során magunk állíthatunk be és mérhetünk meg.

A mágneses teret az egyik mérési elrendezésnél két rövid tekerccsel (sokmenetű hurokkal) állítjuk elő, amelyeket közös tengely mentén úgy helyezünk el, hogy meneteik egymással párhuzamosan állnak és a tekercsek sugara megegyezik a távolságukkal.

2.ábra
3.ábra

Kimutatható (lásd Simonyi: Elméleti villamosságtan, Tankönyvkiadó), hogy ez az úgynevezett Helmoltz-féle elrendezés (Helmholtz-tekercs) a tekercsek közötti térrészben homogén mágneses teret hoz létre, melyben a mágneses indukcióvektor nagysága:

 

$\[ B=\frac{\mu_0 I_m N}{\left(\frac{5}{4}\right)^{\frac{3}{2} } a} , \]$

(7)

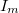ahol $\setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0%$ a tekercsek menetszáma, a azok egymástól mért távolsága, $\setbox0\hbox{$I_m$}% \message{//depth:\the\dp0//}% \box0%$ a mágneses teret létrehozó áram erőssége, 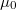$\setbox0\hbox{$\mu_0$}% \message{//depth:\the\dp0//}% \box0%$ pedig a vákuum permeabilitása: 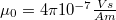$\setbox0\hbox{$\mu_0 = 4\pi10^{-7}\frac{Vs}{Am}$}% \message{//depth:\the\dp0//}% \box0%$. A második mérési módszernél a mágneses teret hosszú egyenes tekerccsel állítjuk elő, ekkor a mágneses indukcióvektor nagysága az ismert

 

$\[ B=\frac{\mu_0 I_m N}{l} \]$

(8)

összefüggésből kapható, amelyben $\setbox0\hbox{$N$}% \message{//depth:\the\dp0//}% \box0%$ a tekercs menetszáma, $\setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%$ a hossza és $I_m a mágnesező áram erőssége.

Az e/m arány mérése

e-m mérés a körpálya közvetlen megfigyelése alapján

Az elektron fajlagos töltésének meghatározására szolgáló egyik eljárás a körpályán mozgó elektronok - és a körpálya – közvetlen megfigyelésén alapul. Az ehhez használt berendezésben az eltérítő mágneses teret Helmholtz-tekerccsel hozzuk létre és egy speciális gáztöltésű üvegedényben láthatóvá válik a pálya, amelyen az elektronok mozognak. Ebben az esetben tehát a körpálya d átmérője közvetlenül megmérhető és az e/m értéke (4), (6), és (7) alapján további mérhető vagy ismert értékek segítségével kiszámítható:

 

$\[ \frac{e}{m} = \frac{8 \left(\frac{5}{4}\right)^{3} a^{2} U_{gy} }{(\mu_0 NdI_m)^{2} } \]$

(9)

Annak érdekében, hogy a fajlagos töltés értékét elegendő pontossággal kapjuk meg, több mérést célszerű végezni. (9) jobb oldalán álló kifejezés két paraméterét tudjuk változtatni. A pálya átmérője adott mágnesező áram mellett az alábbi szerint függ a gyorsító feszültségtől:

 

$\[ d=\frac{8^{\frac{1}{2} } \left(\frac{5}{4}\right)^{\frac{3}{2} } a }{\mu_0N\left(\frac{e}{m}\right)^{\frac{1}{2} } I_m } \sqrt{U_{gy} } \]$

(10)

Ha tehát megmérjük a pálya átmérőjét néhány gyorsító feszültség értéknél és megrajzoljuk a 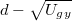$\setbox0\hbox{$d-\sqrt{U_{gy} }$}% \message{//depth:\the\dp0//}% \box0%$ grafikont, akkor a kapott egyenes meredeksége (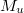$\setbox0\hbox{$M_u$}% \message{//depth:\the\dp0//}% \box0%$) többek között az e/m hányadossal arányos, vagyis:

 

$\[ \frac{e}{m} = \frac{8 \left(\frac{5}{4}\right)^{3} a^{2} }{\mu_0^{2}N^{2}I_m^{2}M_U^{2} } \]$

(11)

Állandó gyorsító feszültség mellett az elektronok pályasugara a mágnesező áramtól az alábbi szerint változik:

 

$\[ d= \frac{8^{\frac{1}{2} } \left(\frac{5}{4}\right)^{\frac{3}{2} } aU_{gy}^{\frac{1}{2} } }{\mu_0N\left(\frac{e}{m}\right)^{\frac{1}{2} } } \frac{1}{I_m} \]$

(12)

Most a különböző mágnesező áramok mellett kapott pályaátmérőket az 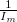$\setbox0\hbox{$\frac{1}{I_m}$}% \message{//depth:\the\dp0//}% \box0%$függvényében ábrázolva a grafikon 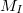$\setbox0\hbox{$M_I$}% \message{//depth:\the\dp0//}% \box0%$ meredekségével fejezhető ki az $\frac{e}{m} hányados:

 

$\[ \frac{e}{m} = \frac{8\left(\frac{5}{4}\right)^{3}a^{2}U_{gy} }{\mu_0^{2}N^{2}M_I^{2} } \]$

(13)

e/m mérése a körpálya közvetett vizsgálata alapján

Az itt használt második mérőberendezésben a mágneses térben mozgó elektronok pályájáról közvetett úton szerzünk információt. Ehhez egy olyan elektroncsövet használunk, amelyben az elektronokat kibocsátó katódot egy hengeres anódlemez veszi körül és a katóddal valamint a henger tengelyével párhuzamos mágneses térbe helyezzük. (9. ábra) Az anódra adott pozitív feszültség hatására a fűtött katódról az elektronok az anód felé mozognak, ezért az elektroncsövön áram (úgynevezett anódáram) folyik. Ha mágneses teret hozunk létre, akkor az elektronok eltérülnek a katódból (K) kiinduló sugárirányú pályájuktól és kis mágneses tér esetén az anódot (A) görbült pályán érik el. (2.a ábra)

A mágneses teret növelve elérünk egy olyan kritikus értéket, amelynél az elektronok zárt pályán mozognak és nem érik el az anódot (2.b ábra) Ekkor az elektroncsőben folyó áram megszűnik.

ábra 4

Ha ismerjük a kritikus mágneses teret, az elektronokat gyorsító feszültséget (ezáltal azok sebességét is) és a katód-anód távolságot (ami itt az elektronpálya átmérője lesz), akkor a fajlagos töltés – hasonlóan az előző módszerhez – a (4) alapján számítható.

Most tehát a mérés során állandó elektronpálya –átmérővel dolgozunk, és az elektroncsövön átfolyó áramot mérve megkeressük azt a mágnesező áramot (mágneses teret), amelynél a pályasugár éppen a cső szerkezetéből adódó érték.

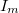A mágneses teret ebben az elrendezésben egy hosszú egyenes tekerccsel állítjuk elő , így a mágneses indukcióvektor nagysága ($\setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0%$) a tekercsben folyó $\setbox0\hbox{$I_m$}% \message{//depth:\the\dp0//}% \box0%$ mágnesező áram ismeretében a (8) egyenletből kapható meg.

Az elektronok sebességének meghatározása az előző méréshez képest most egy kicsit bonyolultabb. A probléma az, hogy az elektronok gyorsítása most az anód és katód közötti térben zajlik, ahol a potenciál értéke az izzó katódtól az anód felé haladva fokozatosan nő, tehát az elektronok sugárirányú sebessége csak fokozatosan éri el a (6) egyenletnek megfelelő értéket. Ennek következtében a mágneses térben mozgó elektronok sebessége a mozgás folyamán változik, így egyrészt az elektronok valódi pályája nem lesz pontosan kör alakú, másrészt az anódáram nem hirtelen, egy jól meghatározott mágneses indukciónál tűnik el, hanem a térerősség növelése során fokozatosan csökken. (2.c ábra)

Részletes számítások szerint a „körpálya” modell megtartható, ha a valódi 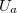$\setbox0\hbox{$U_a$}% \message{//depth:\the\dp0//}% \box0%$ anódfeszültség helyett egy „effektív” feszültséget definiálunk az alábbi egyenlettel:

 

$\[ U_{eff} = \frac{3}{2}U_a \]$

(14)

A jelenség elemzése azt is megmutatja, hogy a fokozatosan csökkenő anódáramból hogyan lehet a kritikus mágneses teret meghatározni: eszerint a kritikus mágneses tér az anódáram csökkenésének kezdetéhez rendelhető hozzá. Ennek megfelelően az anódáram-mágnesező áram grafikon alapján a 2.c ábrán látható módon meghatározzuk a kritikus mágnesező áramot (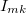$\setbox0\hbox{$I_{mk}$}% \message{//depth:\the\dp0//}% \box0%$), majd ebből (8) segítségével a kritikus mágneses indukciót.

Az effektív feszültség felhasználásával az elektronok „effektív” sebessége a (6) és (14) egyenletekkel így alakul.

 

$\[ v=\sqrt{\frac{3eU_a}{m} } \]$

(15)

A kritikus mágneses térnek megfelelő mágnesező áram (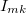$\setbox0\hbox{$I_{mk}$}% \message{//depth:\the\dp0//}% \box0%$) esetén az effektív körpálya sugara:

 

$\[ r=\frac{d}{2} \]$

(16)

ahol a katód-anód távolság. (2.b ábra) A fentiek alapján a (4), (15), (8) és (16) összefüggések segítségével az elektron fajlagos töltésére az alábbi kifejezést kapjuk:

 

$\[ \frac{e}{m} = \frac{12l^{2}U_a}{\mu_0^{2}N^{2}i_{mk}^{2}d^{2} } \]$

(17)

Ismernünk kell tehát a mágneses teret előállító tekercs adatait (hosszát, menetszámát), az elektroncső anód-katód távolságát, az anódfeszültséget és a kritikus mágnesező áramot.

A mérőberendezések és használatuk

e/m mérés a körpálya közverlen megfigyelése alapján

Az ehhez a méréshez használt speciális mérőberendezés vázlata a 3. és 4. ábrán található.

ÁÁBRAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

Az elektronok pályáját egy kisnyomású héliummal töltött üvegedényben figyeljük meg, ami lényegében egy speciális katódsugárcső. A csőben a nagysebességű elektronokat egy elektronágyú hozza létre, amelyben egy izzó katód elektronokat kelt majd ezeket egy kívülről szabályozható gyorsító feszültség felgyorsítja.

A felgyorsított elektronok egy része útja során a He atomokat gerjeszti, amelyek az alapállapotba való visszatérésük során látható tartományú fényt bocsátanak ki, és így kirajzolják az elektronok pályáját. A mágneses teret a katódsugárcsövet közrefogó Helmholtz-tekercsek hozzák létre, amelynek a méréséhez szükséges elektronikát tartalmazó dobozra vannak felszerelve. Maga a cső szintén ezen a dobozon helyezkedik el, de foglalata függőleges tengely körül forgatható, így az elektronok körpályájának síkja a tekercsekkel párhuzamosan , vagyis a mágneses térre merőlegesen beállítható.

A méréshez hozzátartozik egy sötétítő sapka, amelynek alkalmazásával a mérés nappali fénynél is elvégezhető. Az elektronpálya átmérőjének meghatározásához egy tükröző, megvilágított skála szolgál. A tükör azért szükséges, hogy a körpálya szélső pontjának helyét úgy tudjuk leolvasni, hogy a szemünket a pálya szélső pontjával összekötő egyenes merőleges legyen a skálára. (Így elkerülhető a parallaxis-hiba.)

Az elektronikát tartalmazó doboz (továbbiakban mérőegység) előlapján találjuk az elektromos csatlakozó hüvelyeket és a kezelőszerveket. (5. ábra)

ÁBRAAAAAAAAAAAAAAAAAAAAAAAAAAAAA