Kvantumpöttyök
Szerkesztés alatt!
Q.
Hát erről lesz szó, csak kicsit bővebben.
Tartalomjegyzék |
Kvantum pöttyök, energia skálák
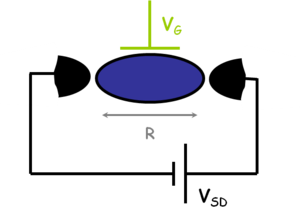
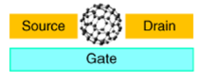
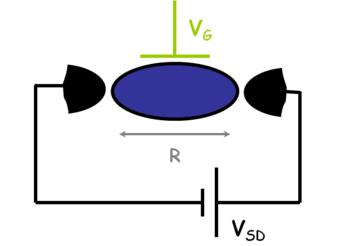
Korábban láttunk páldákat olyan nanoszerkezetekre, ahol az elektronok mozgása csak két illetve egy dimenzióban megengedett (GaAs/AlGaAs határfelületen létrejövő 2 dimenziós elektrongázok ill. pontkontaktusok). Ezen alacsony dimenziós szerkezetek olyan érdekes jelenségek megfigyelését teszik lehetővé, mint a kvantált Hall-effektus vagy a vezetőképesség kvantálás (linkek). Ebben a fejezetben egy további alacsony dimenziós nanoszerkezet családdal fogunk foglalkozni, az un. kvantum pöttyökkel (kvantum dotokkal), ahol az elektronok mozgását mind a három dimenzió mentén megszorítjuk. Ezen nulla dimenziós szerkezetek egy mesterséges szigetet jelentenek az elektronok számára, amik tipikus sugara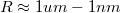 
(lásd 1. ábra). Kvantum pöttyöket gyakran a térvezérelt tranzisztorokhoz hasonló áramkörökbe építik (link): két elektródát kapcsolnak a szigethez (forrás/source és nyelő/drain), amikből elektronok juthatnak a szigetre és távozhatnak onnet. Ezt egy harmadik, un. kapu/gate elektróda egészíti ki, ami a sziget elektromos potenciájának változtatását teszi lehetővé.
 |
1. ábra Kvantum pötty/dot áramkörbe építve. Egy  sugarú sziget, forrás/source és nyelő/drain elektródág között (fekete) illetve egy kapu/gate elektródához csatolva (zöld).
|
 |
 |
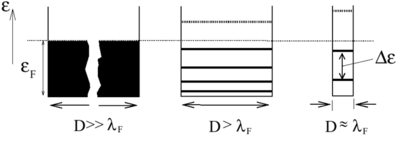
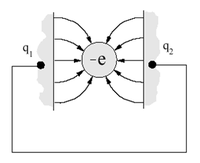
| 2a. ábra Kvantum bezártságból adódó energia szintek | 2b. ábra Kvatum pöttyre helyezett elektron elektrosztatikus energiája |
Kvantum pöttyöket különböző módszerekkel lehet létrehozni. Ezekre lássunk néhány példát:
- Egy kétdimenziós elektron gázra kapuelektródákat téve, az elektródákra adott negatív feszültséggel a kapu elektródák alól az elektronok kiszorulnak. A kapukat megfelelően elrendezve létre lehet hozni szigeteket az elektron gázból, amik kvantum pöttyként viselkednek (lásd. 3a ábra). A kapukra adott feszültség változtatásával
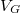a pötty potenciálja hangolható.
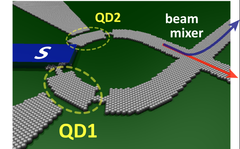
- Kvantum pöttyök készíthetőek változatos nanoszerkezetekből: szén nanocsövekből, félvezető nanopálcákból, grafénból. 3b. ábra mutat egy példát grafén kvantum pöttyre. Plazma marással egy szigetet vágunk ki a szén síkból, ami elvékonyított részekkel kapcsolódhat az elektródákhoz.
- Elektródák közé juttatott nagyobb molekula (pl. fullerén) is mutathat kvantum pötty viselkedést (lásd. 3.c ábra). A molekulák kis méretéből adódóan (
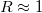nm)a három elektróda elhelyezése problémás.
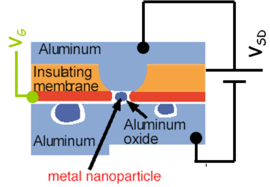
- Kvantum pöttyként működnek kis fémes szemcsék is. Ha ezeket szigetelő rétegbe ágyazzuk és fém elekródákot hozunk létre mellettük a szokásos forrást, nyelőt és kapu elektródát tartalmazó geometria létrehozható (lásd. 3.d ábra).
 |
 |
 |
 |
| 3a. ábra 2DEG-ban kapuelektródákkal létrehozott kvantum pötty Elektronok a sárga tartományban vannak. | 3b. ábra Grafénből kimart szerkezet két kvantum pöttyel (QD1 és QD2) | 3c. ábra Molekulán alapuló kvantum pötty | 3d. ábra Oxidba ágyazott fém nanoszemcsén alapuló kvantum pötty |
 |
 |
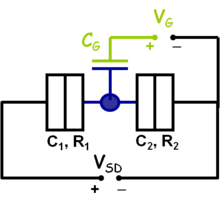
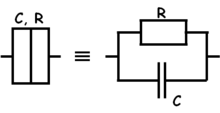
| 4a. ábra Kvantum pötty elektrosztatikus helyettestő képe | 4b. ábra Az elektródákat elválasztó alagútátmenetek helyettesítő képe |
 |
 |
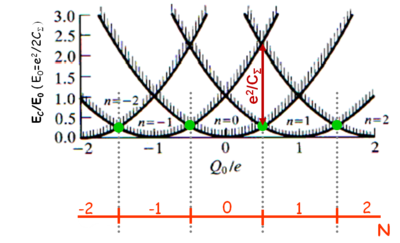
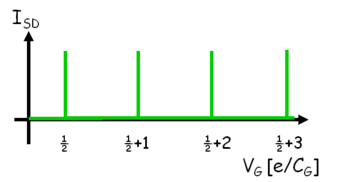
| 5a. ábra Kvantum pötty elektrosztatikus energiája különböző elektronszámnál (n) | 5b. ábra Coulomb blokád jelensége |
 |
 |
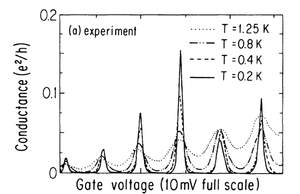
6a. ábra Kvantum pöttyök Coulomb-csúcsai kísérletben,
Y. Meir et al., Phys. Rev. Lett. 66, 3048 (1991). |
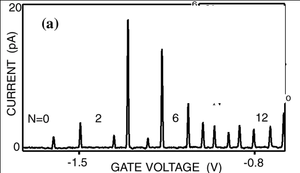
6b. ábra Coulomb-csúcsok nem ekvidisztans poziciókban,
S. Tarucha et al., Phys. Rev. Lett. 77, 3613 (1996). |
S. Tarucha et al., Phys. Rev. Lett. 77, 3613 (1996).
az va. Az teszi érdekessé, hogy kontaktálható... Mesterséges atomok,
![\[<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,\]](/images/math/5/b/a/5bab70164556df83b81d56389eb1de9a.png)
tárgyalt két dimenziós elektrongázok illetve láttunk páldákat, olyan 2 illetve nanoszerkezetek előállitásáról szóló
Elektrosztatikus energia kvantum pöttyökben
Coulomb gyémántok
Mesterséges atomok és kvantum bezártság
Pauli spin blokád
Cotunneling és Kondo effektus
Kvantum pöttyök felhasználása
Egy elektron pumpa, spin kvantum bit
| |
| 1. ábra |
Az MBE olyan termikus forrásfűtésű, 0.001
| |
|
| 3a. ábra | 3b. ábra |
abban a zaj fogalmát.
A korábbiakban láttuk, hogy egy egycsatornás kvantumvezeték vezetőképessége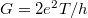 
, ahol 
a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. A fotonokkal végzett kétrés kísérlethez hasonlóan ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. vezetőképesség) abból adódik, hogy az elektronok -ed része teljesen transzmittálódik,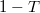 
-ed része pedig reflektálódik. Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.
 |
| 1. ábra |
Egy elektronra vonatkoztatva az áthaladt töltés $T$ valószínűséggel $e$, $1-T$ valószínűséggel pedig $0$, így várhatóértékben $$<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,$$ azaz a Landauer formulának megfelelően az áram $T$-vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét: $$<(\Delta Q)^2>=<Q^2>-<Q>^2=T\cdot e^2 - (T\cdot e)^2=T(1-T)e^2,$$ azaz az áram szórásnégyzete $T(1-T)$-vel arányos, ami $T=0$ és $T=1$ kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges zajt mutat.
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
</wlatex>
Az áram időbeli fluktuációja
A korábbiakban l
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
