Mágnesség és mágneses adattárolás
Tartalomjegyzék |
Mágnesség
Mágneses tulajdonságaik szerint az anyagokat általában három nagy csoportba osztjuk. Vannak paramágneses, diamágneses és ferromágneses (ill. antiferromágneses) anyagok. A para ill. diamágneses hatás általában igen gyenge, ezért kimutatásuk sem egyszerű. A mágneses tulajdonságok leírása tulajdonképpen csak a modern szilárdtestfizika (kvantummechanika) módszereinek segítségével adható meg. Most nem ezt az utat követjük, hanem néhány egyszerűsítő, szemléletes képpel próbálunk magyarázatot adni a jelenségekre.
A paramágnesség
A paramágneses anyagokban a mágneses dipólmomentummal rendelkező atomok külső tér hiányában a hőmérsékleti rendezetlenség miatt nem orientálódnak; ilyenkor az anyag nem mutat mágneses tulajdonságot (1.1.1 ábra). A külső mágneses tér hatására azonban az - atomi köráramokból adódó - elemi dipólmomentumok igyekeznek a tér irányába beállni, így a paramágneses mintának makroszkópikus dipólmomentuma lesz 1.1.2 ábra. Ha például egy ilyen anyaghoz egy rúdmágnessel közelítünk, akkor az anyagdarabra ható erők eredője vonzó jellegű kölcsönhatást eredményez. Általánosságban elmondható, hogy egy paramágnes a nagyobb térerősségű hely felé igyekszik elmozdulni.
| 1.1.1 ábra | 1.1.2 ábra |
A diamágnesség
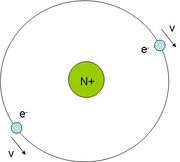
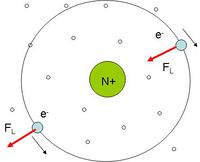
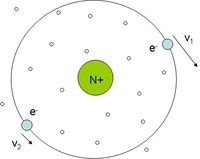
A diamágneses anyagok éppen fordítva viselkednek; ezeket az anyagdarabokat a permanens mágnesek taszítják. A diamágneses anyagok atomjainak nincs eredő mágneses momentumuk. A klasszikus atommodell szerint az atommag körül keringenek az elektronok. Egy körpályán keringő elektron – melyet az elektrosztatikus vonzóerő tart körpályán – úgy viselkedik, mint egy köráram, azaz mágneses momentuma van. Most tételezzük fel, hogy egy körpályán két elektron kering egymással ellentétes irányban azonos sebességgel, de közöttük nincs kölcsönhatás; ekkor az atom eredő momentuma zérus (1.2.1. ábra). Ha azonban külső mágneses indukciós térbe helyezzük az atomot, akkor a Lorentz erő az egyik elektron esetében erősíti, míg a másik irányban keringő elektron esetén gyengíti a centripetális erőt. A körpálya sugara nem változhat, ezért az egyik elektron sebessége nagyobb lesz, míg a másiké kisebb. Ez a különbség természetesen a két "köráramhoz" tartozó, ellentétes irányba mutató dipólmomentum nagyságának különbségében is megjelenik, ezáltal lesz az atomnak mágneses dipólmomentuma (1.2.2.a és b ábra, ahol a kis körök a kép síkjából kifelé mutató B indukciós teret jelölik). Az előzőekben elmondottak alapján könnyű belátni, hogy az atomnak az eredeti indukciós térrel ellentétes irányú mágneses momentuma alakul ki, azaz egy makroszkópikus diamágnes a kisebb térerősségű hely felé igyekszik elmozdulni. Vannak anygok, amelyek egyszerre para és diamágneses tulajdonsággal is rendelkeznek.
| 1.2.1 ábra | 1.2.2.a ábra | 1.2.2.b ábra |
Igen intenzív mágneses térben csaknem minden anyag mutat diamágneses tulajdonságot.
A ferromágnesség
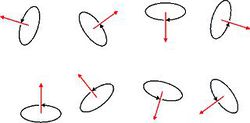
A ferromágneses effektus nagyságrendekkel erősebb, mint a para vagy diamágneses hatás. Ennek oka az, hogy az egyes atomok közötti kvantummechanikai kölcsönhatás miatt a ferromágnesen belül egy-egy nagyobb tartományban az ún. doménben az elemi dipólmomentumok mind egy irányba állnak. A doméneket doménfalak választják el egymástól. Természetesen előfordulhat, hogy külső tér hiányában egy makroszkópikus ferromágnes nem mutat mágneses jelleget, mert a domének orientációja véletlenszerű és lerontják egymás hatását (1.3.1. ábra). Erős külső indukciós térben azonban a tér irányába eső domének "bekebelezik" a szomszédos doméneket, vagyis azokat is átrendezik az eredő tér irányába. Igen erős térben csaknem minden domén orientációja beáll a külső tér irányába (1.3.2 ábra). A külső tér hatásának megszűntével azonban nem áll vissza a véletlenszerű orientáció. Ez ad lehetőséget arra, hogy erős permanens mágnes készülhessen a ferromágneses anyagokból. Ferromágneses tulajdonsággal kevés fém rendelkezik; mindössze a Fe, Co, Ni, Gd, Dy ill. azok ötvözetei. A Curie-hőmérséklet felett az anyag ferromágnessége megszűnik, ekkor már a doménen belüli orientációt is véletlenszerűvé teszi a hőmérsékleti rendezetlenség; ilyenkor az anyag paramágnesként vagy diamágnesként viselkedik.
| 1.3.1 ábra | 1.3.2 ábra |
Mágneses tér és mágnesezettség
Méréssel könnyű igazolni, hogy a szolenoid belsejébe helyezett vasmag megnöveli az indukciós tér nagyságát. A mérésekből az is kiderül, hogy egy adott anyag esetében a növekedés mértéke mindig ugyanakkora. Ahhoz, hogy ezt jobban megértsük, nézzük meg, hogy miként is alakul egy szolenoid indukciós tere, ha vasmagot helyezünk a belsejébe. Tanultuk, hogy vasmag nélkül az indukciós tér nagysága:
![\[ B = \frac {\mu_0 NI}{\ell} \]](/images/math/e/d/1/ed1fec37091a11f5b374ab75350fdf01.png) |
(1.4.1) |
A vasmagot betolva a szolenoid beljesébe azt kapjuk, hogy:
![\[ B = \frac {\mu_0 NI}{\ell} \mu_r \]](/images/math/1/9/b/19bb453986fc5b989de4d979fb65a30e.png) |
(1.4.2) |
ahol 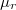 az anyagra jellemző relatív mágneses permeabilitás (vas esetében ez kb. 5000).
Az 1.4.2 formula átírható a következő alakba:
az anyagra jellemző relatív mágneses permeabilitás (vas esetében ez kb. 5000).
Az 1.4.2 formula átírható a következő alakba:
![\[ B = \frac {\mu_0 NI}{\ell} + (\mu_r -1)\frac {\mu_0 NI}{\ell}= \mu_0 (1 + \chi )\frac {NI}{\ell} \]](/images/math/5/7/6/576dca203b19fdcc1a11534959584542.png) |
(1.4.3) |
Itt 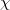 az anyag mágneses szuszceptibilitása. Ez utóbbi formula speciális formája az ennél általánosabb kifejezésnek, amely a
az anyag mágneses szuszceptibilitása. Ez utóbbi formula speciális formája az ennél általánosabb kifejezésnek, amely a  indukciós tér és a
indukciós tér és a  mágneses tér (mértékegysége:
mágneses tér (mértékegysége: 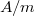 ) közötti kapcsolatot adja meg:
) közötti kapcsolatot adja meg:
![\[ B = \mu_0 \mu_r H \]](/images/math/3/e/3/3e301312d99efadcce6e688cea0ec56b.png) |
(1.4.4) |
ahol a mágneses tér erőssége a szolenoidon belül:
![\[ H = \frac {NI}{\ell} \]](/images/math/d/f/9/df92b56804c0194bf32b53050d24e661.png) |
(1.4.5) |
Az 1.4.3 formula megadható más formában is:
![\[ B = \mu_0 (H+M) \]](/images/math/e/3/b/e3b3e7615d517bbdc1bd4dc1210c7350.png) |
(1.4.6) |
Ez a fontos összefüggés megadható az általánosabb vektoriális formában is:
![\[ \vec B = \mu_0 (\vec H + \vec M) \]](/images/math/c/f/c/cfc6ab7ed580ffdffec58bd522f905fb.png) |
(1.4.7) |
Az M mágnesezettség az anyag válasza a mágneses térre; szemléletes jelentése: mágneses dipólmomentumsűrűség. Mint azt már említettük, a külső mágneses tér hatásának megszűnte után sem szűnik meg az anyag mágneses tulajdonsága, azaz permanens mágnesként viselkedhet, mert az anyag mágnesezettsége nagyrészt megmarad. Az 1.4.6 egyenlet analógiája az elektrosztatikában a következő egyenlet:
![\[ D = \varepsilon_0 E + P \]](/images/math/f/0/3/f036f82cdb798ba5d1608d78fc62313e.png) |
(1.4.8) |
ahol  az ún. eltolási vektor,
az ún. eltolási vektor,  az elektromos térerősség és
az elektromos térerősség és  a polarizáció. Az eltolási vektort Maxwell vezette be az Ampère-törvény általános alakjának felírásával, hiszen vákuumban az
a polarizáció. Az eltolási vektort Maxwell vezette be az Ampère-törvény általános alakjának felírásával, hiszen vákuumban az 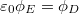 , ahol
, ahol 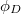 természetesen az eltolási vektor fluxusa.
természetesen az eltolási vektor fluxusa.
A  és a
és a  (vagy a
(vagy a  és az
és az  ) közötti lineáris kapcsolat nem mindig teljesül. Ennek egyik oka lehet az, hogy az anyag telítődik, azaz a növekvő mágneses tér már nem tudja a mágnesezettséget növelni, hiszen az orientáció teljes. Másrészt az anyag "emlékszik" a mágneses előéletére. Az elmondottakat demonstrálja a következő ábrán a
) közötti lineáris kapcsolat nem mindig teljesül. Ennek egyik oka lehet az, hogy az anyag telítődik, azaz a növekvő mágneses tér már nem tudja a mágnesezettséget növelni, hiszen az orientáció teljes. Másrészt az anyag "emlékszik" a mágneses előéletére. Az elmondottakat demonstrálja a következő ábrán a  és
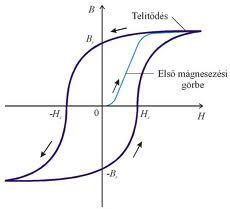
és  kapcsolatát bemutató hiszterézis görbe.
kapcsolatát bemutató hiszterézis görbe.
| 1.4.1 ábra |
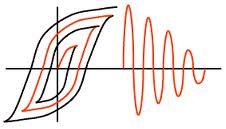
Az egyszer már felmágneseződött ferromágneses anyag permanens mágnességét meg is lehet szüntetni; ezt lemágnesezésnek vagy demagnetizálásnak nevezik. Az eljárás lényege a következő: a felmágnesezett anyagot olyan térrészbe kell helyezni, ahol az egyre kisebb amplitúdójú, de váltakozó mágneses tér megszünteti az anyag mágnesezettségét, ezt mutatja a 1.4.2 ábra (a vízszintes és a függőleges tengely természetesen a  és a
és a  tengelyek).
tengelyek).
| 1.4.2 ábra |
Mágneses adathordozók
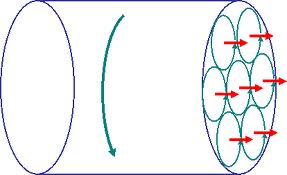
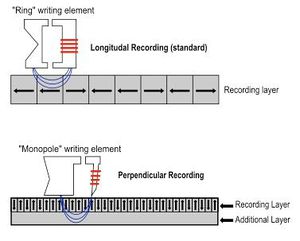
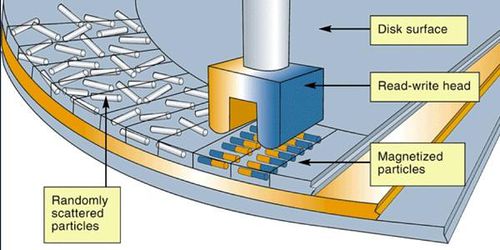
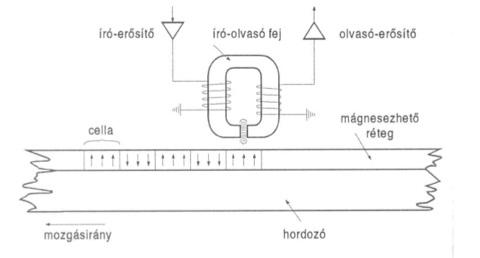
A mágneses adatrögzítésnek, az adattárolásnak és az adat kiolvasásának van egy viszonylag egyszerű módja. Azt már láttuk, hogy ferromágneses anyagot külső mágneses térrel fel lehet mágnesezni és az sokáig megtartja mágneses momentumát. Ezt a hatást felhasználva lehet például a mágneslemez apró tartományait egymástól függetlenül felmágnesezni, vagy mágneses momentumának irányát megváltoztatni. Mint azt a következő két ábra mutatja, a mágnesező fej (író fej) a lemez (vagy szalag) felületével párhuzamos ill. arra merőleges mágnesezettséget is be tud állítani; az utóbbinál nagyobb az adatsűrűség.
| 2.1.1 ábra | 2.1.2 ábra |
Az adatok kiolvasása pedig a következőképpen történhet: a forgó felület felett álló olvasófej vasmagjának légrésében változik a mágneses tér, ez a vasmagban fluxusváltozáshoz vezet, amely feszültséget indukál a kiolvasó áramkör tekercsében és ezt az elektromos jelet erősíti és dolgozza fel a kiolvasó áramkör (2.1.3 ábra). Feszültség ennél az elrendezésnél csak akkor indukálódik, ha változik a lemezen rögzített mágnesezettség. Ez azt jelenti, hogy az adatokat a mágnesezettség változása kódolja. A kombinált író-olvasó fej mindkét funkciót ellátja.
| 2.1.3 ábra |
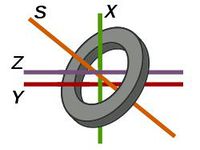
Az adattároló mágneslemez kis tartományainak mágneses állapotát kiolvashatjuk az ún. óriás mágneses ellenállás effektus felhasználásával is. Az effektust felhasználó magnetorezisztív fej olvasó részének ellenállása függ a mágneses tér nagyságától és irányától, ez lehetőséget ad a fej áramának mérésével az adatok kiolvasására. 2003 óta minden winchestert ilyen olvasófejjel gyártanak. A mágneses adattárolásnak vannak más módszerei is, azonban ezeket ebben a fejezetben nem részletezzük. Most csak megemlítjük az egyik, a 70-es évek elejéig használt technikát. Ez a ferritgyűrűs memória, amely a mágnesezhető ferritgyűrűk mátrixba kötött (huzalozott) rendszerét használta. A gyűrű közepén átmenő vezetékek segítségével oldották meg az írást és a bit kiolvasását (2.1.4 ábra).
| 2.1.4 ábra |