Tehetetlenségi nyomaték vizsgálata
A mérés célja:
- elmélyíteni a tehetetlenségi nyomatékkal kapcsolatos ismereteket,
- megismertetni a hallgatókat egy a tehetetlenségi nyomaték mérésére alkalmas módszerrel.
Ennek érdekében:
- összefoglaljuk a tehetetlenségi nyomatékkal kapcsolatos ismereteket, majd megvizsgáljuk egy olyan rendszer viselkedését, amelynek segítségével tehetetlenségi nyomatékot tudunk mérni,
- a mérések során meghatározzuk a méréséhez használandó rendszer paramétereit, majd a megismert rendszer segítségével tehetetlenségi nyomatékot mérünk, és kísérletileg igazoljuk a Steiner-tételt.
Elméleti ismeretek
A tehetetlenségi nyomaték
A tömegpontokból álló rendszer z-tengelyre vonatkozó tehetetlenségi nyomatékát az alábbi kifejezés adja meg:
![\[\theta=\sum_{i=1}^n m_i\cdot l_i^2=\sum_{i=1}^n m_i\cdot (x_i^2+y_i^2),\]](/images/math/9/f/2/9f23e35952dd7e86ca6770f89af2ee91.png)
ahol 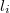 az
az  sorszámú,
sorszámú, 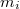 tömegű pont
tömegű pont  -tengelytől való távolsága,
-tengelytől való távolsága, 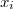 és
és 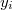 ugyanennek a pontnak az
ugyanennek a pontnak az  , illetve
, illetve  koordinátája.
Folytonos tömegeloszlású testek esetén a tehetetlenségi nyomaték:
koordinátája.
Folytonos tömegeloszlású testek esetén a tehetetlenségi nyomaték:
![\[\theta=\int_V \rho\cdot l^2 \,\mathrm{d}V=\int_V \rho\cdot (x^2+y^2)\,\mathrm{d}V,\]](/images/math/f/3/7/f375903662754b68d34de03b9ed28dfb.png)
ahol  a test sűrűsége. A tehetetlenségi nyomaték értéke egyszerűbb esetekben számítással határozható meg, egyébként mérésekkel állapítható meg.
Ha ismerjük egy test tehetetlenségi nyomatékát a súlypontján átmenő tengelyre vonatkozóan (
a test sűrűsége. A tehetetlenségi nyomaték értéke egyszerűbb esetekben számítással határozható meg, egyébként mérésekkel állapítható meg.
Ha ismerjük egy test tehetetlenségi nyomatékát a súlypontján átmenő tengelyre vonatkozóan (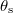 ), akkor egy ezzel a tengellyel párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka (
), akkor egy ezzel a tengellyel párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka ( ) a Steiner-tétel segítségével adható meg:
) a Steiner-tétel segítségével adható meg:
![\[\theta=\theta_\mathrm{s}+m\cdot r^2.\]](/images/math/b/5/9/b590a7e3a69045b18bf5e4d45130d81b.png)
Itt  a test tömege,
a test tömege,  a két tengely egymástól mért távolsága.
a két tengely egymástól mért távolsága.
Forgási rezgések
A tehetetlenségi nyomatékkal kapcsolatos vizsgálatainkat egy forgási rezgéseket végző torziós asztal (2. ábra) segítségével hajtjuk végre, ezért az alábbiakban egy ilyen rendszer viselkedését vizsgáljuk.
A rendszer egyensúlyi helyzetét egyik végén a tengelyhez, a másik végén a kerethez rögzített spirálrugó biztosítja. A rendszer egyensúlyi helyzetéhez képest, a tengely körül  (rad) szöggel való elforgatásához szükséges forgatónyomaték, nem nagy szögek esetén:
(rad) szöggel való elforgatásához szükséges forgatónyomaték, nem nagy szögek esetén:
![\[M=-D^*\cdot\varphi,\]](/images/math/d/0/0/d0084dcdef36a4cc88ba91a7ab3bdf85.png)
ahol 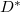 (Nm/rad) a rugó direkciós nyomatéka.
(Nm/rad) a rugó direkciós nyomatéka.
Csillapítatlan forgási rezgések
Ha a torziós asztal tárcsájának a tengelyre vonatkozó tehetetlenségi nyomatéka  és emellett a rendszer többi elemének tehetetlenségi nyomatéka, valamint a súrlódási veszteségek figyelmen kívül hagyhatók, akkor a rendszer mozgásegyenlete:
és emellett a rendszer többi elemének tehetetlenségi nyomatéka, valamint a súrlódási veszteségek figyelmen kívül hagyhatók, akkor a rendszer mozgásegyenlete:
![\[\theta\cdot\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}=-D^*\cdot\varphi.\]](/images/math/a/1/8/a182805b713fd6c53807f43201d0833a.png)
Ezen mozgásegyenlet megoldása a
![\[\varphi=\phi\cdot\sin(\omega\cdot t+\alpha)\]](/images/math/d/4/5/d450777e0ed950a751ef18d2111689ca.png)
egyenlettel leírható harmonikus forgási rezgés, ahol 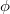 és
és  értékét a kezdeti feltételek határozzák meg és a megoldás során adódik, hogy a körfrekvencia:
értékét a kezdeti feltételek határozzák meg és a megoldás során adódik, hogy a körfrekvencia:
![\[\omega=\sqrt{\frac{D^*}{\theta} }\]](/images/math/6/0/7/6078f796895fc8aff0856337e9dd93ab.png)
amiből a rezgés periódusideje:
![\[T=2\pi\sqrt{\frac{\theta}{D^*} }.\]](/images/math/d/1/d/d1d768736d1a0f81cfa567a12f3d25e1.png)
Csillapodó forgási rezgések
A fentiekben szereplő csillapítatlan forgási rezgés 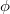 amplitúdója állandó. A gyakorlatban megvalósítható rezgéseknél a mindig jelen lévő súrlódás miatt az amplitúdó folyamatosan csökken. Az ilyen mozgásoknál a rugó által létrehozott nyomatékon kívül megjelenő súrlódási erő hatását a szögsebességgel arányosnak feltételezve, (az arányosságot a
amplitúdója állandó. A gyakorlatban megvalósítható rezgéseknél a mindig jelen lévő súrlódás miatt az amplitúdó folyamatosan csökken. Az ilyen mozgásoknál a rugó által létrehozott nyomatékon kívül megjelenő súrlódási erő hatását a szögsebességgel arányosnak feltételezve, (az arányosságot a  állandóval véve figyelembe) a rezgés mozgásegyenlete:
állandóval véve figyelembe) a rezgés mozgásegyenlete:
![\[\theta\cdot\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}=-D^*\cdot\varphi-k\cdot\frac{\mathrm{d}\varphi}{\mathrm{d}t}.\]](/images/math/6/4/a/64ac5f14be2b463b806aa82ce3932a9f.png)
A (4) egyenlet megoldása az 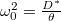 és
és 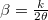 jelölésekkel
jelölésekkel
![\[\varphi=\phi_0\cdot e^{-\beta\cdot t}\cdot\sin(\omega\cdot t+\alpha),\]](/images/math/8/6/c/86cbae218e901097c3188001531dc78a.png)
ahol  a csillapítási tényező,
a csillapítási tényező, 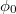 és
és  a kezdeti feltételektől függő állandók. A
a kezdeti feltételektől függő állandók. A 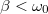 esetben:
esetben:
![\[\omega^2=\omega_0^2-\beta^2.\]](/images/math/5/2/f/52f9ea27b8cb2c87c70891bd8cf65de3.png)
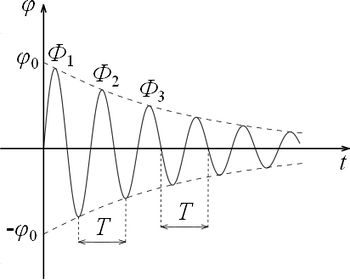
A (5) egyenlettel leírt mozgás 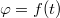 függvénye a 1. ábrán látható. A rezgés amplitúdója exponenciálisan csökken:
függvénye a 1. ábrán látható. A rezgés amplitúdója exponenciálisan csökken: 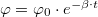 . A rendszer az egyensúlyi helyzeten a
. A rendszer az egyensúlyi helyzeten a 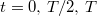 időpontokban halad át, a szélső
időpontokban halad át, a szélső 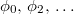 helyzeteket azonban nem a
helyzeteket azonban nem a 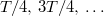 időpontokban éri el, de a szélső helyzetek között eltelt idő
időpontokban éri el, de a szélső helyzetek között eltelt idő 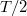 .
.
A torziós asztal és jellemzőinek meghatározása
Ahhoz, hogy egy rezgőmozgást végző rendszert felhasználhassunk ismeretlen minta tehetetlenségi nyomatékának meghatározásához, vagy a Steiner-tétel igazolásához, ismernünk kell rendszerünket és annak fizikai jellemzőit. Az alábbiakban a további vizsgálatokhoz felhasználandó eszközt, a torziós asztalt mutatjuk be, és ismertetünk néhány módszert, amely alkalmas a rendszer jellemzőinek meghatározására.
A torziós asztal
A további vizsgálatokhoz használt eszköz, a forgási rezgéseket végző torziós asztal fényképe a 2. ábrán látható.
A torziós asztalban alkalmazott spirálrúgó direkciós nyomatékának (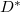 ) meghatározása
) meghatározása
A direkciós nyomaték meghatározásánál a (2) egyenletből indulhatunk ki. Megmérve a rugóra ható nyomatékot és a nyomaték által létrehozott szögelfordulást, a direkciós nyomaték:
![\[D^*=\frac{M}{\varphi}.\]](/images/math/1/1/c/11c438805c5d8651c493105d89ff5135.png)
A mérés pontosságának növelése érdekében célszerű meghatározni a 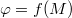 függvényt. A mérési pontokra egyenest illesztve az meredekségéből megkapható a rugó jellemzője.
függvényt. A mérési pontokra egyenest illesztve az meredekségéből megkapható a rugó jellemzője.
A csillapítási tényező ( ) meghatározása
) meghatározása
A csillapítási tényező meghatározása a (5) egyenlet felhasználásával lehetséges. A lengő torziós asztal kitérése egy tetszőleges 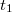 időpontban, illetve ez után
időpontban, illetve ez után  egészszámú periódusidővel később a
egészszámú periódusidővel később a 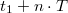 időpontban:
időpontban:
![\[\varphi_1=\phi_0\cdot e^{-\beta\cdot t_1}\cdot\sin(\omega\cdot t_1+\alpha),\]](/images/math/d/3/e/d3e42bf4ca38d6d9f572d074c6ba98e0.png)
![\[\varphi_{n+1}=\phi_0\cdot e^{-\beta(t_1+n\cdot T)}\cdot\sin[\omega(t_1+n\cdot T)+\alpha].\]](/images/math/6/7/8/67878ae241b5cd544299a9cf8e339a9b.png)
Mivel a két kifejezésben a szinuszos tagok értéke megegyezik, a szögkitérések hányadosának természetes alapú logaritmusa:
![\[\ln\frac{\varphi_1}{\varphi_{n+1}}=n\cdot T\cdot\beta,\]](/images/math/5/8/f/58fd5d8c195444d6614e9aa54db874d6.png)
ahonnan
![\[\beta=\frac{1}{n\cdot T}\cdot\ln\frac{\varphi_1}{\varphi_{n+1} }.\]](/images/math/e/7/4/e74a1f5577a8509614ae20c990a6a328.png)
A csillapítási tényező gyakorlati meghatározásánál célszerű a szélső helyzetek figyelembevétele, a 1. ábra jelöléseihez igazodva:
![\[\frac{\varphi_1}{\varphi_{n+1} }{{=}}\frac{\phi_i}{\phi_{n+i} },\]](/images/math/4/5/b/45bc6278858485d832191583bb784dc9.png)
ahol 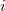 és
és  pozitív egész szám.
A csillapítási tényező ismeretében dönthető el, hogy a rendszer csillapítatlan vagy csillapított mozgást végzőnek tekinthető-e. Ha
pozitív egész szám.
A csillapítási tényező ismeretében dönthető el, hogy a rendszer csillapítatlan vagy csillapított mozgást végzőnek tekinthető-e. Ha 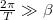 , akkor a (6) összefüggés alapján a torziós asztal mozgása csillapítatlan mozgásnak tekinthető. (A
, akkor a (6) összefüggés alapján a torziós asztal mozgása csillapítatlan mozgásnak tekinthető. (A  periódusidő mérhető.)
periódusidő mérhető.)
A torziós asztal tehetetlenségi nyomatékának meghatározása
Az asztal tehetetlenségi nyomatékának meghatározása tömegének és sugarának ismeretében
Az (1) egyenletből levezethetően  sugarú és
sugarú és  tömegű homogén korong tehetetlenségi nyomatéka forgástengelyére vonatkozóan:
tömegű homogén korong tehetetlenségi nyomatéka forgástengelyére vonatkozóan:
![\[\theta=\frac{1}{2}mR^2.\]](/images/math/5/e/2/5e274e9eb379047de030c1ed32e3da75.png)
Így az asztal tömegének és sugarának megmérése után tehetetlenségi nyomatéka számolható.
Az asztal tehetetlenségi nyomatékának meghatározása a rugó direkciós nyomatékának, a lengésidőnek és a csillapítási tényezőnek az ismeretében
A (6) egyenletből kiindulva felírható, hogy:
![\[\omega^2=\left(\frac{2\pi}{T} \right )^2=\frac{D^*}{\theta}-\beta^2,\]](/images/math/b/2/5/b2573991a0065522b664544d1ebd5029.png)
ahonnan
![\[\theta=\frac{D^*}{\left(\frac{2\pi}{T} \right )^2+\beta^2}.\]](/images/math/d/0/9/d095f108606511fe1b4cef255470c517.png)
Ha a mozgás csillapítatlannak tekinthető
![\[\theta=\left(\frac{T}{2\pi} \right )^2\cdot D^*.\]](/images/math/c/3/a/c3ab08118eed9739810b4a12bd9be8e8.png)
Az asztal tehetetlenségi nyomatékának meghatározása ismert tehetetlenségi nyomatékú tárcsa felhasználásával
Ha a torziós asztal önmagában végez lengéseket (6) alapján
![\[\omega^2=\left(\frac{2\pi}{T} \right )^2=\frac{D^*}{\theta}-\beta^2.\]](/images/math/7/e/0/7e02d223b7e76662258a9011eaaca9a8.png)
Ha a torziós asztal közepére ismert (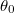 ) tehetetlenségi nyomatékú korongot szerelünk (a korong tengelye egybeesik az asztal tengelyével) a rendszer tehetetlenségi nyomatéka:
) tehetetlenségi nyomatékú korongot szerelünk (a korong tengelye egybeesik az asztal tengelyével) a rendszer tehetetlenségi nyomatéka: 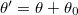 -ra módosul és a lengés körfrekvenciája:
-ra módosul és a lengés körfrekvenciája:
![\[\omega'^2=\left(\frac{2\pi}{T'} \right )^2=\frac{D^*}{\theta+\theta_0}-\beta^2.\]](/images/math/0/2/1/0217dc87939749b0f7d239dd162bb9c5.png)
Feltételeztük, hogy a csillapítás nem változott. (10) és (11) hányadosából az asztal tehetetlenségi nyomatéka kiszámítható:
![\[\left(\frac{4\pi^2}{T^2}+\beta^2\right )\left/\left(\frac{4\pi^2}{T'^2}+\beta^2\right )\right.=\frac{\theta+\theta_0}{\theta},\]](/images/math/a/2/d/a2d80a78e3ae548c1dc7fd760537299f.png)
ahonnan
![\[\theta=\theta_0\frac{T^2\cdot T'^2}{T'^2-T^2}\cdot\left(\frac{1}{T'^2}+\frac{\beta^2}{4\pi^2}\right).\]](/images/math/f/3/9/f3995674ec42cfc9e80ebb17ff3e9c25.png)
Ha a zárójelben lévő kifejezés második tagja nem éri el az első tag 0,01-ad részét, úgy az elhanyagolható és a lengés csillapítatlannak tekinthető. A  értéke csillapítatlan lengés esetén
értéke csillapítatlan lengés esetén
![\[\theta=\theta_0\frac{T^2}{T'^2-T^2}.\]](/images/math/9/3/6/936c4c76d944c8a46942a222907d0c6b.png)
Mintadarab súlypontján átmenő tengelyre vonatkozó tehetetlenségi nyomatékának meghatározása
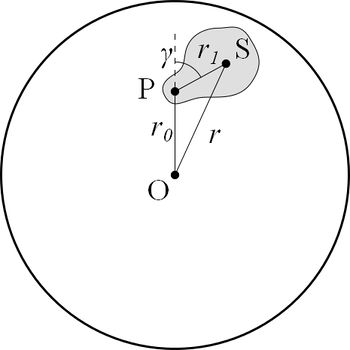
Ha a torziós asztal mozgása csillapítatlan rezgésnek tekinthető, a mozgás periódusidejét a (3) összefüggés adja meg. Helyezzünk a torziós asztalra a 3. ábra szerint egy mintát, mely az asztal egy pontja körül (P) körbe forgatható. Az ábrán látható jelölésekkel a Steiner-tétel és a koszinusz tétel alkalmazásával a minta tehetetlenségi nyomatéka az O ponton átmenő tengelyre vonatkozóan.
![\[\theta_x+mr^2=\theta_x+m(r_0^2+r_1^2+2r_0r_1\cos\gamma),\]](/images/math/3/6/f/36f09c35b60794e9ba88bfafe620f849.png)
ahol 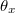 a minta súlypontján (S) átmenő, a rendszer forgástengelyével párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka,
a minta súlypontján (S) átmenő, a rendszer forgástengelyével párhuzamos tengelyre vonatkozó tehetetlenségi nyomatéka,  a tömege és
a tömege és 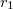 a minta súlypontjának távolsága a P ponttól. Ha a torziós asztal tehetetlenségi nyomatéka
a minta súlypontjának távolsága a P ponttól. Ha a torziós asztal tehetetlenségi nyomatéka  , a rendszer periódusideje (8)-ból:
, a rendszer periódusideje (8)-ból:
![\[T'^2=\frac{4\pi^2}{D^*}\left[\theta+\theta_x+m(r_0^2+r_1^2)\right]+\frac{4\pi^2}{D^*}2mr_0r_1\cos\gamma,\]](/images/math/d/9/a/d9ad9e1d918946fd54112e14fa012364.png)
vagyis a periódusidő négyzete 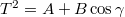 függvény szerint változik.
Ha a mintát körbeforgatva mérjük a rezgésidőket (14) alakú függvényt kapunk. A mérési pontokra görbét illesztve
függvény szerint változik.
Ha a mintát körbeforgatva mérjük a rezgésidőket (14) alakú függvényt kapunk. A mérési pontokra görbét illesztve  és
és  értéke meghatározható, melyek ismeretében a (14)-ben szereplő két ismeretlen (
értéke meghatározható, melyek ismeretében a (14)-ben szereplő két ismeretlen (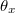 és
és 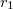 ) is kiértékelhető. Belátható, hogy a minta forgatása közben a legnagyobb lengésidőt akkor kapjuk, amikor a súlypont a legmesszebb van az O forgástengelytől és a lengésidő akkor a legkisebb mikor a minta súlypontja a legközelebb van O-hoz. Ebben a két esetben a lengésidőket a
) is kiértékelhető. Belátható, hogy a minta forgatása közben a legnagyobb lengésidőt akkor kapjuk, amikor a súlypont a legmesszebb van az O forgástengelytől és a lengésidő akkor a legkisebb mikor a minta súlypontja a legközelebb van O-hoz. Ebben a két esetben a lengésidőket a
![\[{T'}^2_\mathrm{max}=\frac{4\pi^2}{D^*}\left[\theta+\theta_x+m(r_0+r_1)^2) \right ],\]](/images/math/0/5/f/05f16bb107f138a36912f0c28d28bb99.png)
illetve
![\[{T'}^2_\mathrm{min}=\frac{4\pi^2}{D^*}\left[\theta+\theta_x+m(r_0-r_1)^2) \right ],\]](/images/math/c/7/7/c777042805d0b88630a60d0e64af3a08.png)
összefüggések adják meg, melyekből 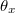 és
és 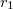 szintén meghatározhatóak. (A
szintén meghatározhatóak. (A 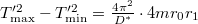 egyenletből megkaphatjuk
egyenletből megkaphatjuk 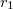 -et, majd ezen eredmény felhasználásával (15)-ből vagy (16)-ból számítható
-et, majd ezen eredmény felhasználásával (15)-ből vagy (16)-ból számítható 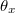 ).
A fenti eljárást a minta egy másik pontja körüli forgatásra megismételve, meghatározható a súlypont távolsága ettől a ponttól is. A súlypont két ismert ponttól való
távolsága egyértelműen megadja a súlypont helyét.
).
A fenti eljárást a minta egy másik pontja körüli forgatásra megismételve, meghatározható a súlypont távolsága ettől a ponttól is. A súlypont két ismert ponttól való
távolsága egyértelműen megadja a súlypont helyét.
A Steiner-tétel igazolása
Ha az ismert 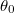 tehetetlenségi nyomatékú tárcsát úgy helyezünk el torziós asztalon, hogy súlypontja az asztal forgástengelyétől ismert
tehetetlenségi nyomatékú tárcsát úgy helyezünk el torziós asztalon, hogy súlypontja az asztal forgástengelyétől ismert  távolságra legyen, a rendszer tehetetlenségi nyomatéka a Steiner-tétel szerint
távolságra legyen, a rendszer tehetetlenségi nyomatéka a Steiner-tétel szerint
![\[\theta'=\theta+mr^2.\]](/images/math/0/d/a/0daaeff33b1b53622a39eb445825f596.png)
Csillapítatlan rezgéseket feltételezve (3) szerint a mozgás periódusidejének négyzete
![\[T^2=\frac{4\pi^2}{D^*}(\theta_0+\theta)+\frac{4\pi^2}{D^*}m\cdot r^2,\]](/images/math/9/3/d/93da80b26515a536117bcea4b6fd5638.png)
azaz a 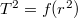 függvény egyenest ad.
Ha mérjük a rendszer lengésidejét (
függvény egyenest ad.
Ha mérjük a rendszer lengésidejét ( ) a tárcsa súlypontjának az asztal forgástengelyétől való távolságának (
) a tárcsa súlypontjának az asztal forgástengelyétől való távolságának ( ) függvényében, és ábrázoljuk a periódusidő négyzetét az
) függvényében, és ábrázoljuk a periódusidő négyzetét az 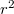 függvényében, a mérési pontokra egyenes illeszthető.
Megjegyezzük, hogy a most kapott egyenes meredekségének és tengelymetszetének meghatározása az adott tehetetlenségi nyomatékú tárcsa tömegének ismeretében újabb lehetőséget ad a rendszer
függvényében, a mérési pontokra egyenes illeszthető.
Megjegyezzük, hogy a most kapott egyenes meredekségének és tengelymetszetének meghatározása az adott tehetetlenségi nyomatékú tárcsa tömegének ismeretében újabb lehetőséget ad a rendszer 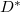 direkciós nyomatékának és
direkciós nyomatékának és  tehetetlenségi nyomatékának meghatározására.
tehetetlenségi nyomatékának meghatározására.
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
- A mérések megkezdése előtt a torziós asztal talpán található csavarok és a mérőhelyen található libella segítségével az asztal síkját állítsa vízszintesre!
1. Határozza meg a spirálrugó D* direkciós nyomatékát!
A feladatot a (2) összefüggés felhasználásával oldja meg! Az elfordulást létrehozó forgatónyomatékot csigán átvetett fonál végén lévő edénykébe helyezett csapágygolyók segítségével hozza létre!
- A fonal befűzéséhez használjon tűbefűzőt!
- Adatok:
- golyók tömege: 4,07 g
- mérlegedény tömege: 4,6 g
- A tárcsa sugarát mérje meg!
A szögelfordulás az asztalon található fokbeosztás segítségével határozható meg. A mérés közben fellépő súrlódás hatásának csökkentése érdekében minden egyes nyomaték alkalmazásánál mérje meg a nyomatékhoz tartozó maximális és minimális szögkitérés értékét és a kettő számtani közepét vegye figyelembe.
- A minimális és maximális szögkitérést a tárcsa kocogtatásával keresheti meg.
10-12 mérési pontot vegyen fel, ábrázolja a 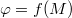 függvényt, mérési pontjaira illesszen egyenest, majd a kapott egyenes meredekségéből határozza meg a direkciós nyomatékot!
függvényt, mérési pontjaira illesszen egyenest, majd a kapott egyenes meredekségéből határozza meg a direkciós nyomatékot!
2. Határozza meg a rendszer csillapítási tényezőjét!
Határozza meg a csillapítási tényező értékét a (7) összefüggés segítségével! A lengésidőt – itt, és a továbbiakban is – legalább 5-5 lengés idejét mérve maximum 180°-os amplitúdóval indulva legalább ötször mérje meg! Az így kapott lengésidők átlagát használja a továbbiakban! A lengési amplitúdó csökkenésének vizsgálatánál 90°-os kitérésből induljon és 20 lengés után mérje meg a lecsökkent amplitúdót! A kapott eredmények ismeretében hasonlítsa össze a körfrekvencia és a csillapítási állandó értékét!
- Csillapítatlan rezgésnek tekintheti-e a torziós asztal mozgását?
3. Határozza meg a torziós asztal tehetetlenségi nyomatékát!
a) A 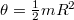 összefüggés alapján. Számítsa ki a tárcsa tehetetlenségi nyomatékát! A tárcsa anyaga alumínium (
összefüggés alapján. Számítsa ki a tárcsa tehetetlenségi nyomatékát! A tárcsa anyaga alumínium ( = 2700 kgm−3). Méreteit méréssel határozza meg!
= 2700 kgm−3). Méreteit méréssel határozza meg!
b) A rúgó direkciós nyomatékának, a rendszer lengésidejének és csillapítási tényezőjének ismeretében. A korábbi mérési eredményei felhasználásával a (8) vagy (9) összefüggés alapján számítsa ki a torziós asztal tehetetlenségi nyomatékát!
- Végezzen gyors számítást, és ellenőrizze, hogy a két módszerrel kiszámított eredmények nagyságrendileg egyeznek-e!
c) Ismert tehetetlenségi nyomatékú minta felhasználásával. Az ismert tehetetlenségi nyomatékú minta egy középen kis furattal ellátott korong. A korong tömege ismert (rá van írva), sugarát mérje meg és számítsa ki 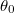 tehetetlenségi nyomatékát! Az ismert tehetetlenségi nyomatékú mintát a közepén lévő furat és egy csavar segítségével rögzítse az asztal közepére! A torziós asztal lengésidejét és csillapítási tényezőjét korábbról ismeri. Most mérje meg a megnövelt tehetetlenségi nyomatékú rendszer lengésidejét (
tehetetlenségi nyomatékát! Az ismert tehetetlenségi nyomatékú mintát a közepén lévő furat és egy csavar segítségével rögzítse az asztal közepére! A torziós asztal lengésidejét és csillapítási tényezőjét korábbról ismeri. Most mérje meg a megnövelt tehetetlenségi nyomatékú rendszer lengésidejét (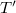 ) és a (12) vagy (13) összefüggés alkalmazásával határozza meg a torziós asztal tehetetlenségi nyomatékát!
) és a (12) vagy (13) összefüggés alkalmazásával határozza meg a torziós asztal tehetetlenségi nyomatékát!
- A számítás során két egymáshoz közeli mennyiséget fog egymásból kivonni, ami nagyon megnöveli a hibát. Ezért mérje a periódusidőt minél gondosabban és pontosabban!
4. Határozza meg egy inhomogén tömegeloszlású lemezből készült minta tehetetlenségi nyomatékát a súlypontján átmenő és a lemez síkjára merőleges tengelyre vonatkozóan!
A mérőhelyen található mintát - amelynek tömegét ismeri (rá van írva) - rögzítse a torziós asztalra a mintán található furat és egy csavar segítségével! Az asztalon található rögzítési pontok közül ismeretei alapján válassza ki az optimálisnak tűnő rögzítési pontot!
- Melyik rögzítési pontot választja? Indokolja választását!
Mérje meg a rendszer lengésidejét a mintának a rögzítési pont körüli elforgatása és 30°-onkénti rögzítése mellett. (Ilyen módon 12 különböző lengésidőt mérhet. Minden lehetséges rögzítési pont körül 30°-os szögbeosztás található.) Ábrázolja a mért lengési idők négyzetét az elforgatási szög függvényében! Illesszen a mért adatokra megfelelő függvényt, és az illesztett függvény adataiból határozza meg 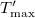 és
és 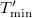 vagy
vagy  és
és  értékét, majd határozza meg a minta
értékét, majd határozza meg a minta 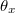 tehetetlenségi nyomatékát és a minta súlypontjának
tehetetlenségi nyomatékát és a minta súlypontjának 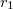 távolságát a mintán található furattól! (
távolságát a mintán található furattól! (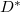 -ot,
-ot,  -t és
-t és  -et ismeri.)
-et ismeri.)
Ismételje meg a feladat első részét a mintán található másik furat felhasználásával! Ennek a mérésnek az elvégzése után megadhatja a súlypont helyét a mintán található furatoktól mérhető távolsága segítségével. Rajzolja le a mintát, jelölje be a furatokat és a tömegközéppont helyét!
- Adatok:
- Sárgaréz csap tömege: 2,2 g
- Piros fejű csap tömege: 2,08 g
5. Igazolja a Steiner-tételt!
Fakultatív feladat! (Ennek a feladatnak a megoldása nem kötelező, csak akkor foglalkozzon vele, ha marad elég idő rá.)
Az ismert tehetetlenségi nyomatékú kis korongot rögzítse a torziós asztal tengelyétől különböző távolságban lévő rögzítési pontokhoz, és mérje meg a rögzítési pontokhoz tartozó lengési időket! Mérési eredményei alapján ábrázolja a 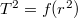 függvényt! Mérési pontjaira illesszen egyenest! Az egyenes paramétereiből határozza meg a rendszer
függvényt! Mérési pontjaira illesszen egyenest! Az egyenes paramétereiből határozza meg a rendszer 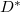 direkciós nyomatékát és
direkciós nyomatékát és  tehetetlenségi nyomatékát! Hasonlítsa össze eredményeit a korábban kapott értékekkel!
tehetetlenségi nyomatékát! Hasonlítsa össze eredményeit a korábban kapott értékekkel!