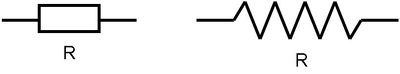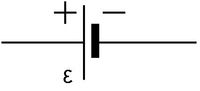Az elektromos áram
Tartalomjegyzék |
Az elektromos áram (egyenáram)
Az elektrosztatika fejezetben láttuk, hogy az elektromos töltéseknek elektromos tere van és az elektromos térben a töltésekre erő hat, valamint azt is, hogy egy töltés (vagy töltések) terében elmozdított másik elektromos töltésen a tér mekkora munkát végez. Az ott megtanult fogalmakat és jelöléseket használjuk ebben és a későbbi fejezetekben is. Töltések áramlását, mozgását – kissé pontatlanul – elektromos áramnak nevezzük. Közvetlen környezetünkben számos elektromos berendezés van, némelyik váltóárammal, más típusok egyenárammal működnek. Egyenáramot használ pl. a kalkulátor, a hátmasszírozó gép, a táskarádió, a mobiltelefon, a laptop, stb. Ebben a fejezetben főként az egyenáram és a legegyszerűbb egyenáramú körök leírásával foglalkozunk.
Egy adott felületen egységnyi idő alatt áthaladt töltésmennyiséget nevezzük elektromos áramerősségnek:
![\[I = \frac{\Delta Q}{\Delta t} \qquad {\rm pontosabban} \qquad I = \frac{d Q}{d t}\]](/images/math/7/7/1/77111a3df6d018d14cdfa842b03f0b50.png) |
(1.1) |
Az elektromos áramerősség mértékegysége – definícióból adódóan – Coulomb/másodperc, azaz Amper, jele: 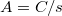 . Tipikus értékek: néhány műszerben μA-os áram folyik, míg egy villámban a kisülés következtében fellépő áramerősség néhányszor
. Tipikus értékek: néhány műszerben μA-os áram folyik, míg egy villámban a kisülés következtében fellépő áramerősség néhányszor 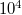 A is lehet.
Amennyiben az áramerősséget elosztjuk az adott felülettel, amelyen az áram átfolyik, akkor kapjuk az elektromos áramsűrűség nagyságát:
A is lehet.
Amennyiben az áramerősséget elosztjuk az adott felülettel, amelyen az áram átfolyik, akkor kapjuk az elektromos áramsűrűség nagyságát:
![\[J = \frac{\Delta I}{\Delta A} \qquad {\rm vagy} \qquad J = \frac{d I}{d A}\]](/images/math/e/b/5/eb509eaf66238b3c5b8096a7d63c9c15.png) |
(1.2) |
amelynek mértékegysége: 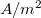 .
Gyakori eset, hogy a töltött részecskék nem egy irányba mozognak. Ebben az esetben az áramlási tér leírása pontosabb az áramsűrűség vektor alkalmazásával, amelynek iránya a tér egy adott pontjában a töltött részecskék sebességével párhuzamos, vagy ellentétes irányú a részecskék előjelétől függően. Az áramsűrűség vagy az áram irányát a pozitív töltések mozgásának iránya adja, azaz a negatív töltések – leggyakrabban az elektronok – sebességvektorával ellentétes az áramirány; ezt technikai áramiránynak is nevezik.
Valamely áramlási térben egy adott felületen áthaladó áramot a következőképpen számíthatjuk ki:
.
Gyakori eset, hogy a töltött részecskék nem egy irányba mozognak. Ebben az esetben az áramlási tér leírása pontosabb az áramsűrűség vektor alkalmazásával, amelynek iránya a tér egy adott pontjában a töltött részecskék sebességével párhuzamos, vagy ellentétes irányú a részecskék előjelétől függően. Az áramsűrűség vagy az áram irányát a pozitív töltések mozgásának iránya adja, azaz a negatív töltések – leggyakrabban az elektronok – sebességvektorával ellentétes az áramirány; ezt technikai áramiránynak is nevezik.
Valamely áramlási térben egy adott felületen áthaladó áramot a következőképpen számíthatjuk ki:
![\[I = \int\limits_{A} \vec J d \vec A \]](/images/math/2/8/c/28c035bba135aa442bd26ffd41d38541.png) |
(1.3) |
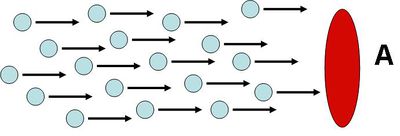
tehát az áramsűrűség és a felületelem skalárszorzatát kell az adott felületre integrálni. Az elektromos vezetés pontos leírása fémes vezetőkben illetve félvezetőkben vagy akár gázokban a modern fizika (kvantumfizika) módszereit használva adható meg. A kvantummechanikai módszerek tárgyalása helyett most vegyünk egy igen egyszerű modellt: az áramlási térben a részecskék sűrűsége valamint sebessége és töltése állandó (1.1 ábra).
| 1.1 ábra |
Könnyen belátható, hogy ha minden részecske az állandó 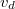 (drift vagy sodródási) sebességgel halad, akkor az
(drift vagy sodródási) sebességgel halad, akkor az  felületen
felületen 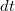 idő alatt áthaladó töltés:
idő alatt áthaladó töltés:
![\[dQ = nq v_d A dt \]](/images/math/1/f/9/1f92dcadcf108a870e5ea63d8990eaef.png) |
(1.4) |
Ahol  a részecskesűrűség és
a részecskesűrűség és  a részecskék töltése. Ezután az (1.1) segítségével már könnyen megadható az elektromos áramerősség:
a részecskék töltése. Ezután az (1.1) segítségével már könnyen megadható az elektromos áramerősség:
![\[I = \frac {dQ}{dt} = nq v_d A \]](/images/math/0/e/5/0e51b5a4562923b93da6bf8d09c230f1.png) |
(1.5) |
és az áramsűrűség nagysága is:
![\[J = \frac {I}{A} = nq v_d \]](/images/math/e/d/3/ed358c66462677ca0408047a381f7e30.png) |
(1.6) |
Vizsgáljuk a fémes vezetést, hogy meghatározhassuk a drift-sebesség értékét. Tegyük fel, hogy a fémes vezető kristályrácsát alkotó ionok közötti térben az elektronok csaknem szabadon mozoghatnak. Ebben az esetben az  elektromos térben az elektronok gyorsulása:
elektromos térben az elektronok gyorsulása:
![\[a = \frac {qE}{m} \]](/images/math/0/e/d/0ed08ccdbdec1df2119ecd936ed3a8a1.png) |
(1.7) |
ahol is  az elektron töltése és
az elektron töltése és  a tömege. Az elektronok azonban mozgási energiájukat ütközés során leadhatják a kristályrács rezgési módusainak. Tételezzük fel, hogy átlagosan
a tömege. Az elektronok azonban mozgási energiájukat ütközés során leadhatják a kristályrács rezgési módusainak. Tételezzük fel, hogy átlagosan  időnként történik ütközés, amelyben az elektron az összes energiáját elveszíti, azonban két ütközés között
időnként történik ütközés, amelyben az elektron az összes energiáját elveszíti, azonban két ütközés között  gyorsulással mozog. Így most már az átlagos sodródási sebesség könnyen számítható:
gyorsulással mozog. Így most már az átlagos sodródási sebesség könnyen számítható:
![\[v_d = a \tau = \frac {qE}{m}\tau \]](/images/math/a/8/0/a80e8c2e2533d78827fdb6977112ae7d.png) |
(1.8) |
Ohm törvénye
Tekintsünk most egy 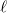 hosszúságú vezetékdarabot. A vezetékdarab két vége között az elektromos potenciálkülönbség:
hosszúságú vezetékdarabot. A vezetékdarab két vége között az elektromos potenciálkülönbség: 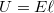 . Ebből az
. Ebből az  térerősség nagyságát kifejezhetjük és behelyettesíthetjük a drift-sebességet megadó (1.8) formulába, amelyet beírva az áramerősséget meghatározó (1.5) képletbe, kapjuk:
térerősség nagyságát kifejezhetjük és behelyettesíthetjük a drift-sebességet megadó (1.8) formulába, amelyet beírva az áramerősséget meghatározó (1.5) képletbe, kapjuk:
![\[I = \frac {nq^2\tau A}{m\ell}U \]](/images/math/8/8/d/88d34927374e2b7f5c78fd55d9342193.png) |
(2.1) |
Az áramerősség tehát arányos a vezető két végére kapcsolt feszültséggel. A (2.1) formulát kissé átrendezve kapjuk az Ohm törvényt:
![\[R = \frac {U}{I} \]](/images/math/1/2/b/12bf9f07e8486e62884a05dac851007c.png) |
(2.2) |
A feszültség és az áramerősség hányadosát ellenállásnak nevezzük. Az ellenállás mértékegysége az Ohm, jele: 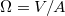 . Az ellenállást egyen- és váltóáramú körökben általában a 2.1 ábrán látható szimbólumokkal jelöljük.
. Az ellenállást egyen- és váltóáramú körökben általában a 2.1 ábrán látható szimbólumokkal jelöljük.
| 2.1 ábra |
A piacon beszerezhető ellenállások ellenállás-értékének megjelölésére négy ill. ötsávos színkódot használnak (ezek ellenállása a néhány  - tól a több
- tól a több 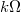 - ig változhat):
- ig változhat):
| 2.2 ábra |
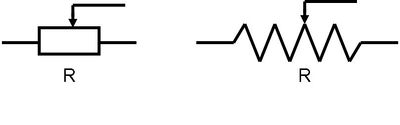
A változtatható ellenállás, más néven potenciométer vagy becenevén potméter áramköri jelölése:
| 2.3 ábra |
Egy ilyen eszközzel állíthatjuk be pl. a laptop fülhallgatójának hangintenzitását is.
Az 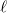 hosszúságú,
hosszúságú,  keresztmetszetű vezetékdarab
keresztmetszetű vezetékdarab  ellenállását kifejezhetjük tehát (2.1) és (2.2) felhasználásával:
ellenállását kifejezhetjük tehát (2.1) és (2.2) felhasználásával:
![\[R = \frac {m}{nq^2\tau} \frac {\ell}{A}=\rho \frac{\ell}{A} \]](/images/math/3/a/e/3ae8ad53f8338d82962e140d922b6fff.png) |
(2.3) |
ahol  a vezeték anyagának fajlagos ellenállása, mértékegysége:
a vezeték anyagának fajlagos ellenállása, mértékegysége: 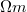 . Jól látszik, hogy ez csak az anyagi minőségtől függ. Szokás még megadni az anyag vezetőképességét is:
. Jól látszik, hogy ez csak az anyagi minőségtől függ. Szokás még megadni az anyag vezetőképességét is: 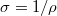 . A fémes vezetők fajlagos ellenállása – és természetesen a vezetőképessége is – hőmérsékletfüggő. A
. A fémes vezetők fajlagos ellenállása – és természetesen a vezetőképessége is – hőmérsékletfüggő. A 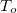 szobahőmérsékleten ( 20°C ) mért
szobahőmérsékleten ( 20°C ) mért 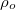 értékkel
értékkel 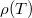 kifejezhető a következő alakban:
kifejezhető a következő alakban:
![\[\rho (T) = \rho_o[1+\alpha(T-T_o)+\beta(T-T_o)^2 + ...] \]](/images/math/9/c/c/9cc39b1cf05b9fb7aad34b6499bcab0c.png) |
(2.4) |
A legtöbb esetben elegendő az elsőrendű közelítés. A vezetőképesség hőmérsékletfüggésén alapul az ellenálláshőmérők működése (néhány típus látható az 2.4 ábrán).
| 2.4 ábra |
Természetesen nem csak hőmérsékletet, hanem más fizikai paramétert, illetve annak változását is meg lehet határozni ellenállásmérés segítségével, amennyiben az ellenállás egyértelmű függést mutat az adott paraméterrel. Az ellenállás ill. az ellenállás változásának mérésére használható egyszerű áramkör a Wheatstone-híd.
Néhány fémes vezető ellenállása az adott fémre jellemző küszöbhőmérséklet alatt zérussá válik. Ezt a jelenséget szupravezetésnek nevezzük. Az effektust felhasználva építenek szupravezető mágneseket. A szupravezetők tulajdonságainak leírása a modern szilárdtestfizika módszereivel lehetséges. Ez meghaladná a jegyzet kereteit. Annyit egyelőre elég tudni a szupravezetésről, hogy az áramvezetés elektronpárokkal – az un. Cooper párokkal – valósul meg és a Cooper párok képesek úgy mozogni a kristályrácsban, hogy amint a elektronpár egyik tagja impulzust veszítene, ugyanakkor a pár másik elektronja visszakapja azt és így az elektronpár akadálytalanul képes haladni. A Cooper párok kötési energiája általában olyan kicsi, hogy néhány K (Kelvin) felett a hőmérsékleti rendezetlenségből adódó gerjesztések, perturbációk megakadályozzák elektron-párok kialakulását. Ez az oka annak, hogy szupravezetés általában igen alacsony hőmérsékleten valósul meg.
A (2.1) formulát átalakíthatjuk az áramsűrűség és a vezetőképesség definíciójának felhasználásával és nyerjük a
![\[J = \sigma E \]](/images/math/9/0/2/902eae0a4515eb02f43327cc757e6021.png) |
(2.5) |
összefüggést. Előfordulhat, hogy a vezető nem minden irányban vezeti ugyanolyan jól az áramot, ilyenkor a vezetőképesség nem egy állandó, hanem egy tenzor (ekkor fontossá válik, hogy az áramsűrűség és az elektromos térerősség is egy-egy három komponensű vektor).
Amennyiben egy gyakorlatban előforduló vezetőre – mondjuk rézre – számítanánk ki a drift-sebesség értékét, akkor 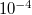 m/s körüli érték jönne ki. Termodinamikai tanulmányainkból már tudjuk, hogyan lehet egy ideális gáz molekuláinak átlagsebességét meghatározni. Ha most a fémben lévő – vezetési elektronokból álló – elektrongázt ideális gáznak tekintjük, akkor az elektronok átlagsebességére szobahőmérsékleten nagyságrendileg
m/s körüli érték jönne ki. Termodinamikai tanulmányainkból már tudjuk, hogyan lehet egy ideális gáz molekuláinak átlagsebességét meghatározni. Ha most a fémben lévő – vezetési elektronokból álló – elektrongázt ideális gáznak tekintjük, akkor az elektronok átlagsebességére szobahőmérsékleten nagyságrendileg 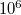 m/s – os értéket kapunk és az elektronok sebességének iránya egyenletesen véletlenszerű a
m/s – os értéket kapunk és az elektronok sebességének iránya egyenletesen véletlenszerű a 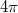 térszögben külső erőtér hiányában. A driftsebesség nagysága tehát több nagyságrenddel kisebb, mint az elektronok átlagsebessége. A fémben lévő elektrongáz elektromos vezetését a klasszikus fizikában tehát úgy foghatjuk fel, mintha az egy
térszögben külső erőtér hiányában. A driftsebesség nagysága tehát több nagyságrenddel kisebb, mint az elektronok átlagsebessége. A fémben lévő elektrongáz elektromos vezetését a klasszikus fizikában tehát úgy foghatjuk fel, mintha az egy 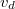 sebességgel sodródó ideális gázként viselkedne. Az áram hatása természetesen nem
sebességgel sodródó ideális gázként viselkedne. Az áram hatása természetesen nem 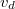 sebességgel halad, hanem az elektromos tér terjedésére jellemző fénysebességgel. Ezért van az, hogy a villanykapcsolótól általában jó néhány méternyire lévő villanykörte a felkapcsolás után szinte azonnal felizzik.
sebességgel halad, hanem az elektromos tér terjedésére jellemző fénysebességgel. Ezért van az, hogy a villanykapcsolótól általában jó néhány méternyire lévő villanykörte a felkapcsolás után szinte azonnal felizzik.
Joule törvény
Az előző szakaszban bemutatott egyszerű példában azt láttuk, hogy az elektrongáz az említett ütközések miatt egy átlagos 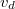 sebességgel halad az
sebességgel halad az  elektromos térben. Ez úgy lehetséges, hogy az ütközések során az elektronok – folyamatosan – átadják mozgási energiájukat a fém ionrácsának, azaz felmelegítik a vezetőt. Most kiszámítjuk, hogy mekkora teljesítményt ad le egy
elektromos térben. Ez úgy lehetséges, hogy az ütközések során az elektronok – folyamatosan – átadják mozgási energiájukat a fém ionrácsának, azaz felmelegítik a vezetőt. Most kiszámítjuk, hogy mekkora teljesítményt ad le egy  ellenálláson az
ellenálláson az  áram.
Tegyük fel, hogy
áram.
Tegyük fel, hogy 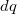 töltésmennyiség áthalad egy tartományon miközben a feszültségesés
töltésmennyiség áthalad egy tartományon miközben a feszültségesés  . Az elektrosztatikában tanultuk, hogy ekkor a tér által a részecskén végzett munka
. Az elektrosztatikában tanultuk, hogy ekkor a tér által a részecskén végzett munka 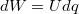 .
A teljesítmény azonnal adódik:
.
A teljesítmény azonnal adódik:
![\[P =\frac{dW}{dt}=U \frac {dq}{dt} \]](/images/math/b/5/9/b599a754ca72cb8528707d9284b2b08a.png) |
(3.1) |
Az áram definícióját és az Ohm törvényt felhasználva az  ellenálláson disszipált teljesítmény könnyen kiszámítható:
ellenálláson disszipált teljesítmény könnyen kiszámítható:
![\[P = UI = RI^2 = \frac{U^2}{R} \]](/images/math/9/b/5/9b5c17166d705e20884c9e6d4c2c9c87.png) |
(3.2) |
Ez Joule törvénye, amelynek alapján könnyű megérteni és számítással ellenőrizni pl. egy merülőforraló működését.
Egyenáramú körök
A legegyszerűbb egyenáramú áramkörök ellenállásokat, kapcsolókat és feszültségforrásokat (áramforrásokat) tartalmaznak. A feszültségforrás egy olyan telep, melynek kapcsain terheletlen állapotban (amikor nincs rákötve fogyasztó)  feszültség mérhető. Jele:
feszültség mérhető. Jele:
| 4.1 ábra |
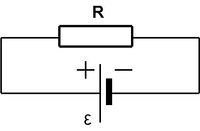
Ezután tekintsük a lehető legegyszerűbb áramkört!
| 4.2 ábra |
A vezetékek ellenállását zérusnak tekintjük. Ez természetesen azt is jelenti, hogy egy – egy vezetékdarabon (rajtuk ill. bennük) a feszültségérték állandó. Ekkor az  ellenálláson átfolyó áramerősség:
ellenálláson átfolyó áramerősség: 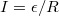 és a telep által leadott teljesítmény
és a telep által leadott teljesítmény 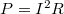 .
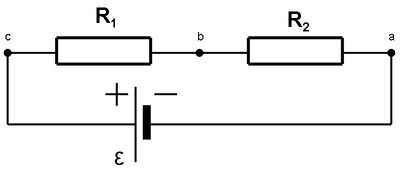
Ezután tekintsük az 4.3 ábrán látható elrendezést, azaz vizsgáljuk meg, hogy mi történik, ha két különböző ellenállást kapcsolunk sorba (egymás után).
.
Ezután tekintsük az 4.3 ábrán látható elrendezést, azaz vizsgáljuk meg, hogy mi történik, ha két különböző ellenállást kapcsolunk sorba (egymás után).
| 4.3 ábra |
Legyen az elektromos potenciál értéke zérus az a pontban (gondolhatjuk azt is, hogy az a pontot tartalmazó vezetékág a földhöz van kötve, azaz le van földelve). Jelöljük a b pontbeli potenciálértéket 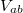 -vel, valamint a b és c pont közötti feszültséget
-vel, valamint a b és c pont közötti feszültséget 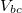 –vel. Minthogy két pont között az elektromos feszültség nem függhet attól, hogy milyen úton jutok el egyik pontból a másikba, ezért
–vel. Minthogy két pont között az elektromos feszültség nem függhet attól, hogy milyen úton jutok el egyik pontból a másikba, ezért
![\[\varepsilon = V_{ab} + V_{bc} \]](/images/math/8/b/f/8bf39f3f354c0e3d13d77e5178d23130.png) |
(4.1) |
Most a két ellenállást egyetlen 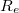 eredő ellenállással szeretnénk helyettesíteni, amely ugyanúgy viselkedik, mint a sorba kötött
eredő ellenállással szeretnénk helyettesíteni, amely ugyanúgy viselkedik, mint a sorba kötött  és
és  ellenállás, azaz ugyanakkora áram folyik át rajta, mintha helyette a két ellenállás lenne bekötve. Ohm törvényét használva erre az egyszerű kapcsolásra:
ellenállás, azaz ugyanakkora áram folyik át rajta, mintha helyette a két ellenállás lenne bekötve. Ohm törvényét használva erre az egyszerű kapcsolásra:
![\[IR_e = IR_1 + IR_2 \]](/images/math/1/d/f/1df1a72f7fcd9aca09314f96d787f9e2.png) |
(4.2) |
Itt felhasználtuk, hogy mindkét ellenálláson ugyanakkora áram folyik át, azaz töltések nem tűnnek el, nem keletkeznek ill. nem csapdázódnak sehol. Egyszerűsítés után:
![\[R_e = R_1 + R_2 \]](/images/math/a/d/9/ad93298f7c551f5c28089642fd69a930.png) |
(4.3) |
Hasonló gondolatmenettel megadhatjuk a több tagból álló, sorba kötött ellenállások eredő ellenállását is:
![\[ R_e = \sum_{i=1}^{N} R_i \]](/images/math/b/2/0/b209a7bb74fde61d54fdbb84165efe73.png) |
(4.4) |
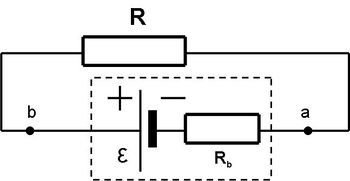
A tanultak alkalmazására nézzünk egy igen egyszerű példát! Ehhez tekintsük a 4.4 ábrán lévő egyszerű áramkört, azonban a telepről feltételezzük, hogy van saját 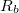 belső ellenállása is:
belső ellenállása is:
| 4.4 ábra |
A szaggatott vonallal bezárt téglalap szimbolizálja a telepet az elektromotoros erejével és a belső ellenállásával együtt. A terhelés, azaz az  ellenállás és a telep
ellenállás és a telep 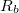 belső ellenállása sorba vannak kapcsolva (mint az a 4.4 ábrán jól látszik). Az áramkörben kialakuló áramerősség tehát:
belső ellenállása sorba vannak kapcsolva (mint az a 4.4 ábrán jól látszik). Az áramkörben kialakuló áramerősség tehát:
![\[ I = \frac{\varepsilon}{R+R_b} \]](/images/math/c/d/d/cdd7ac6364ed54bca870f1d65d286653.png) |
(4.5) |
Kérdés, hogy most mekkora feszültség jut a terhelésre. A válasz kézenfekvő; az  és
és  pontok között mérhető kapocsfeszültség:
pontok között mérhető kapocsfeszültség: 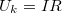 , azaz
, azaz
![\[ U_k = \frac{R}{R+R_b}\varepsilon \]](/images/math/f/3/d/f3dbc871baefca1b1cee5dae63e8d5d4.png) |
(4.6) |
Az eredmény jól mutatja, hogy a terhelésre jutó feszültség, a rajta átfolyó áram illetve a leadott teljesítmény függ az  és az
és az 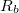 viszonyától. A telep belső ellenállásának figyelmen kívül hagyása csak azért nem szokott általában gondot okozni, mert a terhelés mértéke többnyire nagyságrendekkel nagyobb a belső ellenállásnál.
viszonyától. A telep belső ellenállásának figyelmen kívül hagyása csak azért nem szokott általában gondot okozni, mert a terhelés mértéke többnyire nagyságrendekkel nagyobb a belső ellenállásnál.
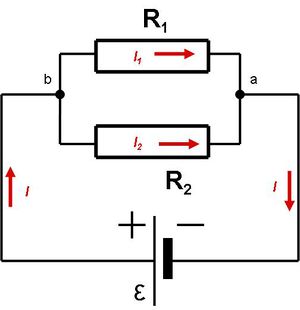
Ezután vizsgáljuk meg, hogyan viselkedik két párhuzamosan kapcsolt ellenállás. Tekintsük a 4.5 ábrán látható egyszerű elrendezést!
| 4.5 ábra |
Az ábrán látható  és
és  pontok között a feszültség
pontok között a feszültség  . Az
. Az  és
és  pontoknál bemenő illetve kimenő áramok összege megegyezik (töltésmegmaradás), azaz:
pontoknál bemenő illetve kimenő áramok összege megegyezik (töltésmegmaradás), azaz:
![\[ I = I_1 + I_2 \]](/images/math/a/d/0/ad0f1fcaee77b7e836e3a7d851bebfa8.png) |
(4.7) |
Ohm törvényének alkalmazásával:
![\[ \frac{\varepsilon}{R_e} = \frac{\varepsilon}{R_1} + \frac{\varepsilon}{R_2} \]](/images/math/b/0/2/b02cc5813ccfb3ccd7d94d5f54cf5099.png) |
(4.8) |
Egyszerűsítés után könnyű belátni, hogy a két párhuzamosan kapcsolt ellenállást helyettesítő eredő ellenállás:
![\[ R_e = \frac{R_1R_2}{R_1+R_2} \]](/images/math/e/5/7/e57f06900818fa87c5f26ec6f2be11e9.png) |
(4.9) |
Az eredő ellenállás értékét megadó (4.9) kifejezést replusz – nak hívják, amelyet (4.8)-ból nyertünk:
![\[ \frac{1}{R_e} = \frac{1}{R_1} + \frac{1}{R_2} \]](/images/math/3/e/9/3e9c74c5f90c4f529988947ab7dd44c8.png) |
(4.10) |
Hasonló gondolatmenet segítségével meghatározhatjuk több tagból álló, párhuzamosan kötött ellenállások eredő ellenállását is:
![\[ \frac{1}{R_e} = \sum_{i=1}^{N} \frac{1}{R_i} \]](/images/math/f/8/5/f853c031a4357f0e12cc66af38f2a92d.png) |
(4.11) |
Összetettebb egyenáramú kapcsolások eredő ellenállásának meghatározásához gyakran elegendő a bemutatott módszerek alkalmazása. Néhány - bonyolultabb - áramkör esetében (mint pl. a csillag-delta) helyettesítő képpel lehet élni, melyek mögött általában egy-egy fizikai megfontolás húzódik.
Kirchhoff törvények
Több hurokból álló és több feszültségforrást tartalmazó, bonyolultabb kapcsolások esetében is lehetne az előbbiekben tanultak alapján eljárni. Ezt oly módon tehetnénk meg, hogy minden egyes telepre, a többi forrás figyelmen kívül hagyásával (rövidzárral helyettesítjük őket) kiszámítanánk az egyes ágakban folyó áramokat, majd végül az egyes feszültségforrások által generált áramokat előjelhelyesen összeadnánk az adott ágban. (A módszer természetesen csak abban az esetben használható, ha az áramköri elemek lineárisak, azaz az Ohm törvény érvényes rájuk, vagyis az áram arányos az egyes tagokon eső feszültséggel.) Ez a módszer nehézkes és igencsak számolásigényes. Ehelyett használjuk a Kirchhoff törvényeket.
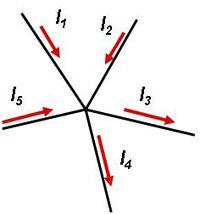
Kirchhoff I. törvénye az un. csomóponti törvény azt mondja ki, hogy az egy csomópontba befolyó áramok előjeles összege megegyezik a kimenő áramok összegével, azaz 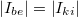 .
.
| 5.1 ábra |
Az 5.1 ábrán, amely egy csomópontot ábrázol, mindez könnyen demonstrálható: 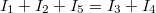 .
.
Kirchhoff II. törvénye az ún. hurok-törvény: amennyiben egy áramkör egyik hurkán egy irányban körbejárva az áramköri elemeken mérhető (számítható) feszültségértékeket előjelhelyesen összesítjük, akkor ennek az összegnek zérusnak kell lennie, azaz:
![\[ \oint\limits_\ell \vec E \vec s = 0 \]](/images/math/b/4/f/b4fa29afb5de7c1de07fe6fbb5745830.png) |
(5.1) |
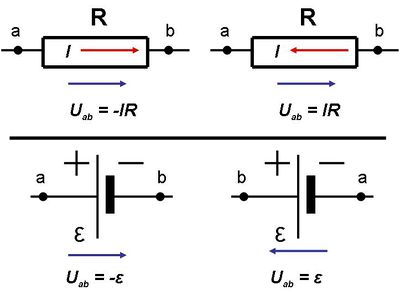
(Ha nem így lenne, akkor ez a hurok örökmozgóként működhetne.) Az ellenállás és feszültségforrás esetében számításba veendő feszültségértékek – az áramirány (piros) ill. a haladási irány (kék) figyelembe vételével – láthatók az 5.2 ábrán.
| 5.2 ábra |
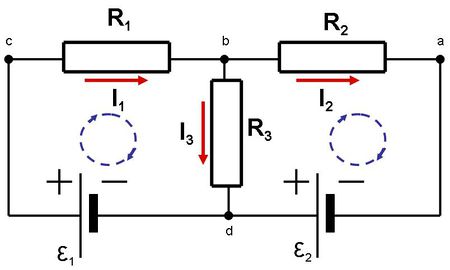
Nézzünk Kirchhoff törvényének alkalmazására egy konkrét példát! Határozzuk meg a 5.3 ábrán látható áramkörben létrejövő áramerősségeket!
| 5.3 ábra |
A csomóponti törvény felhasználásával felírhatjuk az első egyenletet:
![\[ I. \qquad I_1 = I_2 + I_3 \]](/images/math/e/2/f/e2fb9c7cf782835d65b8839d1dd05bd8.png) |
(5.2) |
A huroktétel alkalmazásával még két egyenletet nyerünk az adott áramirányok illetve körüljárási irány figyelembe vételével:
![\[ II. \qquad \varepsilon_1 - I_1 R_1 - I_3 R_3 = 0 \]](/images/math/5/b/8/5b8bd3f48cd45262c20013f5da62ac3a.png) |
(5.3) |
![\[ III. \qquad \varepsilon_2 - I_2 R_2 - I_3 R_3 = 0 \]](/images/math/c/b/6/cb602f2caa962c1d282eaa90bc3a7959.png) |
(5.4) |
Az elsőfokú három ismeretlenes egyenletrendszert megoldva kapjuk a megfelelő áramerősségeket. Amennyiben valamelyik áramerősség értékére negatív számot kaptunk, akkor az csak azt jelenti, hogy a technikai áramirány az eredetileg felvett (feltételezett) áramirányhoz képest ellentétes irányú.
Az áramerősség és a feszültség mérése
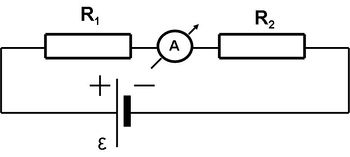
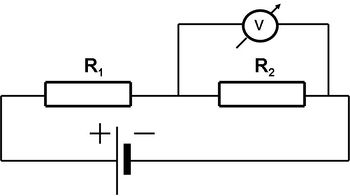
Egy egyenáramú áramkör egyes ágaiban az áramerősség és az adott áramköri elemeken a feszültség mérését olyan eszközzel kell végrehajtani, amely nem ”rontja el” a mérést, azaz nem változtatja meg jelentősen a mérendő értéket. Ennek érdekében az igen kis ellenállású áramerősség-mérőt az áramköri elemekkel (terheléssel, ellenállással) sorba kötjük be. Ez látszik a 6.1 ábrán:
| 6.1 ábra |
Az áramerősség-mérő (ampermérő) méréshatárát  - szeresére növelhetjük, ha vele párhuzamosan kötünk egy, a saját belső ellenállásánál
- szeresére növelhetjük, ha vele párhuzamosan kötünk egy, a saját belső ellenállásánál  - szer kisebb ellenállást (az un. shunt-öt).
- szer kisebb ellenállást (az un. shunt-öt).
Az egyes ellenállásokon eső feszültség mérésére a mérendő ellenállásnál jóval nagyobb ellenállású feszültség-mérőt (voltmérőt) az adott terheléssel párhuzamosan kötjük be:
| 6.2 ábra |
A voltméter méréshatárát pedig olyan módon növelhetjük meg  – szeresére, hogy a feszültségmérő elé, azzal sorosan egy, a műszer belső ellenállásánál
– szeresére, hogy a feszültségmérő elé, azzal sorosan egy, a műszer belső ellenállásánál  – szer nagyobb ellenállást (az un. előtét-ellenállást) kötünk.
– szer nagyobb ellenállást (az un. előtét-ellenállást) kötünk.
Az RC-kör
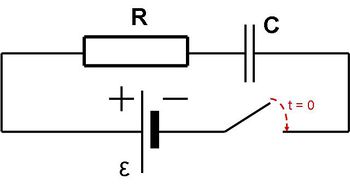
Amennyiben egy egyenáramú áramkör valamelyik ágában egy kondenzátort is elhelyeznek (sorosan bekötnek), akkor azon az ágon elvileg áram nem folyhat, hiszen a kondenzátor szakadásnak, azaz 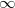 ellenállásnak felel meg. (Természetesen a sérült kondenzátor terhelésnek vehető, mert a dielektrikumon áram folyik át; ekkor az eszköz ellenállása véges.) A kondenzátort áramköri elemként tartalmazó egyenáramú áramkörökben az áram – még a kondenzátort tartalmazó ágakban is – a tranziens jelenségek miatt lehet zérustól különböző. Ennek a jelenségnek a modellezésére vizsgáljuk meg a 7.1 ábrán látható kapcsolást!
ellenállásnak felel meg. (Természetesen a sérült kondenzátor terhelésnek vehető, mert a dielektrikumon áram folyik át; ekkor az eszköz ellenállása véges.) A kondenzátort áramköri elemként tartalmazó egyenáramú áramkörökben az áram – még a kondenzátort tartalmazó ágakban is – a tranziens jelenségek miatt lehet zérustól különböző. Ennek a jelenségnek a modellezésére vizsgáljuk meg a 7.1 ábrán látható kapcsolást!
| 7.1 ábra |
A kapcsolót a t = 0 időpontban kapcsoljuk be, azaz ekkor záródik az áramkör. A kondenzátor eredetileg, a kapcsoló nyitott állásánál nem volt feltöltve. Az áramkörben a bekapcsolás után ( t > 0 ) töltések fognak áramolni a feszültségforrástól a kondenzátor fegyverzetei felé, hogy feltöltsék azokat. A töltések mozgása természetesen azt eredményezi, hogy az áramkörben 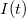 áram alakul ki. Határozzuk meg az áram időfüggését! Ehhez felhasználhatjuk Kirchhoff II. törvényét:
áram alakul ki. Határozzuk meg az áram időfüggését! Ehhez felhasználhatjuk Kirchhoff II. törvényét:
![\[ \varepsilon - IR - \frac{Q}{C} = 0 \]](/images/math/1/2/f/12faf84bd684316a47ece546bea0ea7f.png) |
(7.1) |
Ez átírható más alakba is. Az áramkörben kialakuló 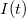 áramerősség és a kondenzátor fegyverzetein megjelenő, időben változó
áramerősség és a kondenzátor fegyverzetein megjelenő, időben változó 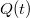 töltés közötti jól ismert összefüggés (1.1) segítségével
töltés közötti jól ismert összefüggés (1.1) segítségével  kifejezhető és behelyettesítve az előző egyenletbe:
kifejezhető és behelyettesítve az előző egyenletbe:
![\[ \varepsilon - \frac{dQ}{dt} R - \frac{Q}{C} = 0 \]](/images/math/5/9/e/59ed191c27c889e22cedb504a5338c3f.png) |
(7.2) |
Átrendezve:
![\[ \frac{dQ}{dt} = - \frac{1}{RC}Q + \frac{\varepsilon}{R} \]](/images/math/a/7/4/a74dba00b883fd2335a8678d86806892.png) |
(7.3) |
Behelyettesítéssel könnyen meggyőződhetünk róla, hogy ennek a differenciálegyenletnek a megoldása:
![\[ Q(t)= C\varepsilon \left[1-e^{-\frac{1}{RC}t}\right] \]](/images/math/6/2/9/629cad93fb5b99dee63e32c16d0843bc.png) |
(7.4) |
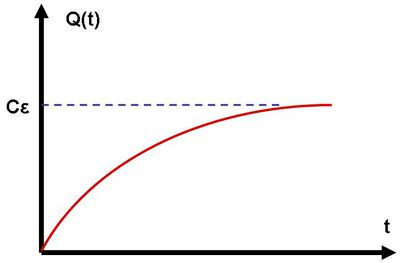
Mindezt grafikonon ábrázolva:
| 7.2 ábra |
Itt természetesen az látszik, ahogy a kondenzátor feltöltődik. A töltés időfüggésének ismeretében az áramerősség is meghatározható:
![\[ I(t)= \frac{\varepsilon}{R} e^{-\frac{1}{RC}t} \]](/images/math/f/5/c/f5c741b0d7abeb443611bf1dc157073b.png) |
(7.5) |
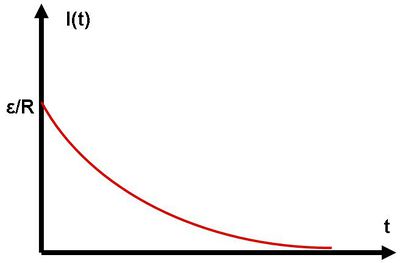
Tehát az áramerősség az idővel exponenciálisan csökken annak megfelelően, ahogy a kondenzátor egyre jobban feltöltődik. Ez látható a 7.3 ábrán.
| 7.3 ábra |