Electron transport in nanowires: Landauer formula, conductance quantization
Tartalomjegyzék |
Characteristic length scales
The conduction properties of a nanoscale object differ from the familiar features on the macroscopic scale.
The resistance of a macroscopic wire is well described using Ohm’s law: the current density (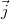 ) equals to the conductivity (
) equals to the conductivity ( ) multiplied by the electric field (
) multiplied by the electric field (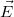 ); the conductance (
); the conductance (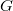 ) is proportional to the cross-section of the wire (
) is proportional to the cross-section of the wire ( ) and inversely proportional to its length (
) and inversely proportional to its length ( ):
):
![\[\vec{j}=\sigma \cdot \vec{E}, \ \ \ G=R^{-1}=\frac{A\cdot \sigma}{L}\]](/images/math/7/b/c/7bc09554c31016e9d495c03164518ac1.png)
Ohm’s law is easily explained by the Drude model of electric conduction: the electrons travel in the crystal lattice gaining 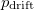 momentum and then losing it by scattering into a random direction. The time elapsed between two scattering events is called the momentum relaxation time and is denoted by
momentum and then losing it by scattering into a random direction. The time elapsed between two scattering events is called the momentum relaxation time and is denoted by 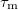 . The momentum gained by the electrons in time
. The momentum gained by the electrons in time 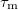 is:
is:
![\[p_\mathrm{drift}=m\cdot v_\mathrm{drift}=eE\tau_\text{m}.\]](/images/math/d/e/a/dea37f6b81839d7d09148a38ae1948f4.png)
According to this, the current density and the conductivity in case of electron density  :
:
![\[\vec{j}=n\cdot e\cdot v_\mathrm{drift}\ \ \ \rightarrow \ \ \ \sigma=\frac{ne^2\tau_\text{m}}{m}.\]](/images/math/a/7/c/a7cf74f960f47af7c9ac7fc6ae2c818b.png)
Between two scattering events -- in time 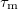 -- electrons travel a distance
-- electrons travel a distance 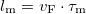 , where
, where 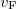 is the Fermi velocity. This distance is called the momentum relaxation length. The Drude model loses its meaning if the characteristic size (
is the Fermi velocity. This distance is called the momentum relaxation length. The Drude model loses its meaning if the characteristic size ( ) of the wire in question is less than the momentum relaxation length characterizing the scale of the scatterings. Based on this we can differentiate between diffusive and ballistic wires. In the diffusive case (
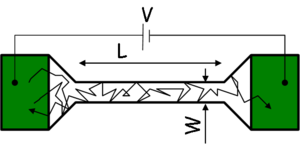
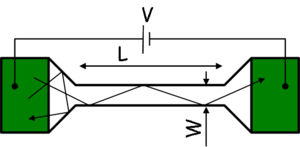
) of the wire in question is less than the momentum relaxation length characterizing the scale of the scatterings. Based on this we can differentiate between diffusive and ballistic wires. In the diffusive case (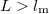 ) the electrons scatter many times before they get from one electrode into the other (figure 1/a), while in the ballistic case (
) the electrons scatter many times before they get from one electrode into the other (figure 1/a), while in the ballistic case (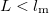 ) the electrons scatter don't scatter inside the wire, only on its walls (figure 1/b).
) the electrons scatter don't scatter inside the wire, only on its walls (figure 1/b).
| Figure 1/a. Diffusive wire | Figure 1/b. Ballistic wire |
The length dependence of the resistance clearly demonstrates the difference between the two limiting cases: while the resistance of a diffusive wire increases by lengthening the wire, the electrons that get in a ballistic wire can travel through it without scattering back, i.e. that the resistance does not depend on the length of the wire.
Taking into account the wave nature of electrons it is worth to investigate whether the phase information of electrons is conserved or not on the size-scale of the examined system. If the size of the sample is smaller than the 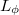 phase-relaxation length, then the conduction properties show interesting interference phenomena that can’t be seen on the macroscopic scale. We cover these phenomena in chapter interference and decoherence in nanostructures.
phase-relaxation length, then the conduction properties show interesting interference phenomena that can’t be seen on the macroscopic scale. We cover these phenomena in chapter interference and decoherence in nanostructures.
Another interesting question is whether the spin information of electrons is conserved in the nanostructure under investigation. In nanostructures that are smaller than the so-called spin diffusion length (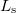 ) and contain magnetically ordered regions interesting spintronic phenomena can be observed.
) and contain magnetically ordered regions interesting spintronic phenomena can be observed.
Further interesting phenomena occur if the cross-section of the wire becomes comparable to the Fermi wavelength of electrons: 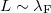 . We explain this below.
. We explain this below.
Resistance of quantum wires
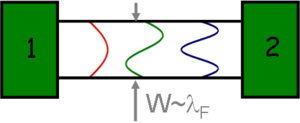
Let’s consider the properties of nanowires comparable with the wavelength of electrons using a simple model: we connect two electron reservoirs with a 2-dimensional ideal quantum wire with parallel walls, in which the electrons travel without scattering (figure 2.).
| Figure 2. Ideal quantum wire |
Using hard wall boundary condition (i.e. the enclosing potential is zero inside and infinite outside of the wire) the wavefunction of the electrons:
![\[\Psi_{n,k}(x,y)=e^{ikx}\cdot \sin\left(\frac{n \pi y}{W} \right),\]](/images/math/c/b/b/cbb631029abef03f779de5d448cf7b17.png)
that is, in the longitudinal direction we get plane wave propagation, while in the transversal direction standing waves. According to this the energy of the electrons:
![\[\varepsilon_n(k)=\frac{\hbar^2k^2}{2 m} + \frac{\pi^2 \hbar^2}{2 m W^2}\cdot n^2,\]](/images/math/c/7/7/c772508502b24caf1faa4c68c5109a51.png)
where  is the wavenumber belonging to the plane wave propagation along the
is the wavenumber belonging to the plane wave propagation along the  -direction and
-direction and  describes the quantised transverse modes (standing waves along the
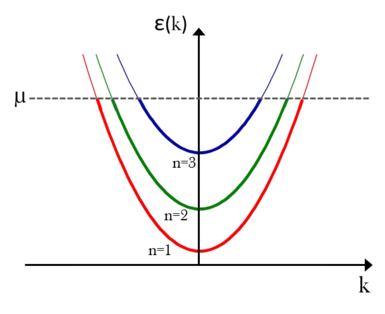
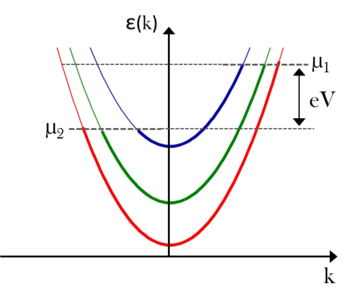
describes the quantised transverse modes (standing waves along the  -direction). This expression for the energy corresponds to the one-dimensional energy dispersion relation offset by the transverse mode energies as depicted in the figure. Reasonably, current can only flow through those modes (the so-called conduction channels) that have transverse mode energies smaller than the Fermi energy of the electrodes that is, the dispersion relation intersects with the Fermi level. The modes that satisfy this criterion, are called open conduction channels and the number of open conduction channel is denoted by
-direction). This expression for the energy corresponds to the one-dimensional energy dispersion relation offset by the transverse mode energies as depicted in the figure. Reasonably, current can only flow through those modes (the so-called conduction channels) that have transverse mode energies smaller than the Fermi energy of the electrodes that is, the dispersion relation intersects with the Fermi level. The modes that satisfy this criterion, are called open conduction channels and the number of open conduction channel is denoted by  .
.
| 3/a. ábra. Dispersion relation in an ideal quantum wire | 3/b. ábra. Dispersion relation when a bias is applied to the sample |
If we turn on  bias between the two electron reservoirs, the electron states of the nanowire will be filled as represented in figure 3/b. The states with positive
bias between the two electron reservoirs, the electron states of the nanowire will be filled as represented in figure 3/b. The states with positive  values originate from the left electrode, so these are filled to energies
values originate from the left electrode, so these are filled to energies 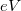 higher than the states coming from the right electrode with negative
higher than the states coming from the right electrode with negative  values. Only the states with positive
values. Only the states with positive  and in the region between chemical potentials
and in the region between chemical potentials 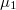 and
and 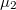 contribute to the current transport, as below the
contribute to the current transport, as below the 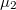 chemical potential both the positive and negative propagating states are filled, so the total current becomes zero.
chemical potential both the positive and negative propagating states are filled, so the total current becomes zero.
For a given conduction channel the velocity of the electrons and the density of states are as follows:
![\[v_n=\frac{1}{\hbar}\frac{\partial \varepsilon_n(k)}{\partial k},\ \ \ \ g_n=\frac{L}{2\pi}\left(\frac{\partial \varepsilon_n(k)}{\partial k}\right)^{-1}.\]](/images/math/f/4/f/f4f7ceadc88e3403d53b0023da1ad7c4.png)
The electron density in the 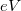 range is calculated as:
range is calculated as: 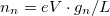 . To calculate the total current flowing through the wire we multiply the electron charge, the velocity and the electron density then sum these up for the individual conduction channels:
. To calculate the total current flowing through the wire we multiply the electron charge, the velocity and the electron density then sum these up for the individual conduction channels:
![\[I=2\sum_{n=1}^{M}e v_n n_n =\frac{2e^2}{h}MV,\]](/images/math/6/1/c/61ce1c2052a80ff9f33efa0b2b800ba5.png)
where the multiplier 2 corresponds to the spin degeneracy. Since the derivative of the energy dispersion in the product of the velocity and the electron density cancels, the conductance of the quantum wire is simply the integer multiple of the conductance quantum 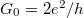 . It’s worth to note that momentum is conserved in the
. It’s worth to note that momentum is conserved in the  -direction due to the longitudinal translation invariance, which prohibits the scattering between conduction channels, as it would change the wavenumber
-direction due to the longitudinal translation invariance, which prohibits the scattering between conduction channels, as it would change the wavenumber  so we really can treat the current contribution of the individual conduction channels independently.
so we really can treat the current contribution of the individual conduction channels independently.
The above calculation was derived from the assumption that occupied states are only to be found below the chemical potential  of the electrodes that is, the temperature is zero. At finite temperature, we can find both occupied and unoccupied states in the
of the electrodes that is, the temperature is zero. At finite temperature, we can find both occupied and unoccupied states in the 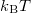 wide range around the chemical potential. The possibility of a state being occupied is described by the Fermi function:
wide range around the chemical potential. The possibility of a state being occupied is described by the Fermi function:
![\[f(\varepsilon)=\frac{1}{e^{\frac{\varepsilon -\mu}{k_{\text{B}}T}}+1}.\]](/images/math/6/c/3/6c3faca094e66816c7e7afcf3d3a8f79.png)
Inside the quantum wire the electron states originating from the left electrode (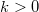 ) are occupied according to
) are occupied according to 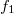 , the occupation number function of electrode 1, while the electron states from the right electrode (
, the occupation number function of electrode 1, while the electron states from the right electrode (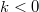 ) according to
) according to 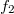 the occupation number function of electrode 2. Here
the occupation number function of electrode 2. Here 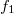 and
and 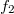 are Fermi functions offset with energy
are Fermi functions offset with energy 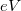 relative to each other. This description also presumes the electron reservoirs to be perfect: the electrons that enter the electrode from the quantum wire can scatter back into the quantum wire only after thermalisation, so the electrons leaving the electrode truly follow the energy distribution that corresponds to the Fermi function of the given electrode.
As a consequence of the arguments above, the current flowing in the wire at finite temperature into the positive and the negative direction respectively:
relative to each other. This description also presumes the electron reservoirs to be perfect: the electrons that enter the electrode from the quantum wire can scatter back into the quantum wire only after thermalisation, so the electrons leaving the electrode truly follow the energy distribution that corresponds to the Fermi function of the given electrode.
As a consequence of the arguments above, the current flowing in the wire at finite temperature into the positive and the negative direction respectively:
![\[I^+=\frac{2 e}{L} \sum \limits_{k>0} v_k f_1(\varepsilon_k) = 2e \int \frac{\mathrm{d}k}{2 \pi}\frac{\partial \varepsilon_k}{\hbar \partial k} f_1(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_1(\varepsilon),\]](/images/math/3/1/c/31c4678e29410e7fa637f9687cb858a1.png)
![\[I^-=\frac{2 e}{L} \sum \limits_{k<0} v_k f_2(\varepsilon_k) = \frac{2 e}{h}\int \mathrm{d} \varepsilon f_2(\varepsilon),\]](/images/math/e/2/f/e2f6fb8f6d0d0eadf5b25d606c80db97.png)
i.e. the total current is:
![\[I=I^+-I^-=\frac{2 e}{h} \int \mathrm{d} \varepsilon (f_1(\varepsilon)-f_2(\varepsilon))=\frac{2 e}{h}e V.\]](/images/math/e/8/0/e80de55ed30db22f813dd9ffdbc36397.png)
The integral 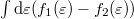 equals eV at any finite temperature, which infers the conductance of a single-channel ideal quantum wire to be the conductance quantum,
equals eV at any finite temperature, which infers the conductance of a single-channel ideal quantum wire to be the conductance quantum, 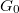 at arbitrary temperature, which corresponds to a resistance of
at arbitrary temperature, which corresponds to a resistance of 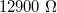 .
.
Landauer formalism
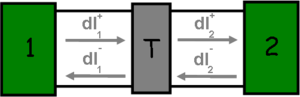
Let’s examine the simple model of a single-channel ideal quantum wire with a scattering centre in the middle, which transmits electrons with probability  . In this case, the states travelling from the electrodes in the direction of the scattering region still originate from the corresponding electrode and adhere to its distribution function (see current contributions
. In this case, the states travelling from the electrodes in the direction of the scattering region still originate from the corresponding electrode and adhere to its distribution function (see current contributions 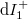 and
and 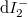 in figure 4). On the other hand, the states travelling from the scattering region towards the electrodes are mixed, e.g. in case of the
in figure 4). On the other hand, the states travelling from the scattering region towards the electrodes are mixed, e.g. in case of the 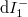 current contribution both the states backscattered from the scattering region originating from electrode 1 and the states coming from electrode 2 then transmitted by the scattering region.
current contribution both the states backscattered from the scattering region originating from electrode 1 and the states coming from electrode 2 then transmitted by the scattering region.
4. ábra. Single-channel quantum wire with scattering centre with transmission probability 
|
At zero temperature only the states below the 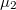 chemical potential can come from both of the electrodes, but the total current of the states with
chemical potential can come from both of the electrodes, but the total current of the states with 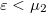 equals to zero because it corresponds to the case where the bias applied to the system is zero. Thus the states with energy
equals to zero because it corresponds to the case where the bias applied to the system is zero. Thus the states with energy 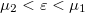 account for the finite current, which can originate only from electrode 1. So the total current can easily be calculated in the lead section between the scattering centre and electrode 2. Here the electrons in the energy band
account for the finite current, which can originate only from electrode 1. So the total current can easily be calculated in the lead section between the scattering centre and electrode 2. Here the electrons in the energy band 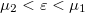 would give
would give 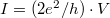 current for
current for 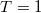 , which would scale with the number of the transmitted electrons for
, which would scale with the number of the transmitted electrons for 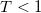 :
: 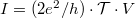 . So the conductance of a single-channel nanowire with a scattering centre in the middle which has transmission probability
. So the conductance of a single-channel nanowire with a scattering centre in the middle which has transmission probability  :
:
![\[G=\frac{2e^2}{h}\mathcal{T}.\]](/images/math/1/7/e/17ef448d62d7bc359f42df27cdb8b65d.png)
Let’s check whether this solution is valid for finite temperatures. The current components 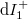 and
and 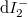 originate solely from electrode 1 or 2, thus their current contributions in the energy range
originate solely from electrode 1 or 2, thus their current contributions in the energy range 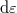 :
:
![\[\mathrm{d}I_1^+(\varepsilon)=\frac{2 e}{h}\cdot f_1(\varepsilon)\mathrm{d}\varepsilon,\;\; \mathrm{d}I_2^-(\varepsilon)=\frac{2 e}{h}\cdot f_2(\varepsilon)\mathrm{d}\varepsilon.\]](/images/math/e/9/8/e983f21ad16c4ed34dc48057d58842ce.png)
If we want to calculate the current in the lead section between the scattering centre and lead 1, then we also need the current component 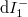 , which originates with probability
, which originates with probability  from the transmission of the mode coming from electrode 2, or with probability
from the transmission of the mode coming from electrode 2, or with probability 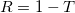 from the reflection of the mode coming from electrode 1:
from the reflection of the mode coming from electrode 1:
![\[\mathrm{d}I_1^-(\varepsilon)=\mathrm{d}I_1^+(\varepsilon)\cdot (1-\mathcal{T}) + \mathrm{d}I_2^-(\varepsilon)\cdot \mathcal{T},\]](/images/math/1/c/a/1ca0063385d01527198c7d015ff1c0a9.png)
so the combined contributions of the currents flowing into the negative and positive directions:
![\[\mathrm{d}I_1=\mathrm{d}I_1^+ - \mathrm{d}I_1^- = \frac{2 e}{h} \cdot \mathcal{T} \cdot [f_1(\varepsilon)-f_2(\varepsilon)]\mathrm{d}\epsilon.\]](/images/math/f/3/9/f39db877ac18b4c6636656330ee65181.png)
We obtain the total current by integration:
![\[I=\frac{2 e}{h} \cdot \int \mathcal{T}\cdot [f_1(\varepsilon)-f_2(\varepsilon)]\mathrm{d}\varepsilon.\]](/images/math/f/c/b/fcb985a47ca9ef664771724359b3c658.png)
The difference of the two Fermi functions differs from zero only in the energy range between the chemical potentials 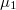 and
and 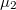 and the
and the 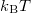 wide vicinity of the chemical potentials. Assuming that the transmission probability
wide vicinity of the chemical potentials. Assuming that the transmission probability  is energy independent, and utilizing the equation
is energy independent, and utilizing the equation 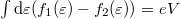 , we get
, we get
![\[G=\frac{2 e^2}{h}\cdot \mathcal{T}\]](/images/math/3/9/c/39c19c41cf54b36e17aafebf82ee4a19.png)
for the conductance even for finite temperatures. If the transmission probability cannot be treated energy independently, then  has to be considered as the average transmission probability in the relevant energy range.
has to be considered as the average transmission probability in the relevant energy range.
5. ábra. Description of a multi-channel quantum wire with transmission matrix 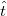
|
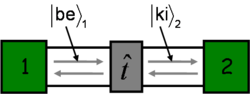
In case of more conduction channels the effect of the scattering centre can be described by the complex transmission matrix (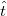 ) (see figure 5) which connects the incoming modes into the individual channels on the left side propagating from the electrode towards the scattering centre (in figure 5 denoted by
) (see figure 5) which connects the incoming modes into the individual channels on the left side propagating from the electrode towards the scattering centre (in figure 5 denoted by 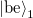 ) and the outgoing modes on the right side propagating from the scattering region in the direction of the electrode (
) and the outgoing modes on the right side propagating from the scattering region in the direction of the electrode (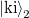 in the figure):
in the figure):
![\[\left| \mathrm{out} \right>_2=\hat{t} \left| \mathrm{in} \right>_1.\]](/images/math/4/1/2/412af4551bc707620180107fc587f2c8.png)
One can show that the conductance then is written as:
![\[G = \frac{2 e^2}{h} \mathrm{Tr}(\hat{t}^\dagger \hat{t}).\]](/images/math/5/b/2/5b2aaf381d945f89746eb144dcd28942.png)
One can rewrite 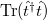 as
as 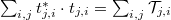 , where
, where 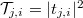 gives the probability of scattering from channel
gives the probability of scattering from channel 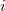 on the left side into channel
on the left side into channel  on the right side. Thus the conductance:
on the right side. Thus the conductance:
![\[G = \frac{2 e^2}{h} \sum \limits_{i,j} \mathcal{T}_{j,i}.\]](/images/math/0/0/b/00b521e061d3967022701dfad93d6678.png)
Choosing a proper basis one can diagonalise the problem, this way restricting electrons to scatter from channel 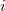 on the left side solely into channel
on the left side solely into channel 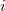 on the right side. One can then consider the system to consist of N – corresponding to the number of open conduction channels – independent one-dimensional wire and simply sum up their conductance contribution:
on the right side. One can then consider the system to consist of N – corresponding to the number of open conduction channels – independent one-dimensional wire and simply sum up their conductance contribution:
![\[G = \frac{2 e^2}{h} \sum \limits_{i=1..N} \mathcal{T}_i.\]](/images/math/b/5/d/b5ddacc209168c8bfd3c40d09bd11038.png)
The 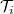 transmission coefficients corresponding to the eigenvalues of the operator
transmission coefficients corresponding to the eigenvalues of the operator 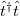 give us the transmission probability of the
give us the transmission probability of the 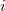 th eigenchannel.
th eigenchannel.
Vezetőképesség-kvantálás kvantum-pontkontaktusban
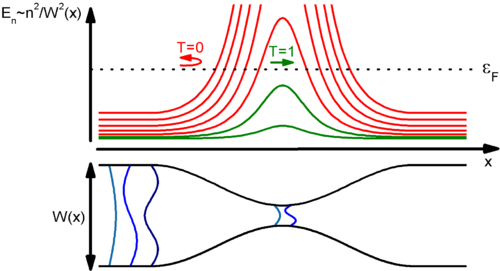
Vegyünk egy olyan kétdimenziós kvantumvezetéket, melyben nincsenek szórócentrumok, a vezeték 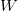 szélessége pedig lassan (adiabatikusan) változik a hossztengely mentén (6. ábra alsó panel). A lassan változó szélességnek köszönhetően a vezeték lokálisan mindenütt jól közelíthető egy párhuzamos falú vezetékdarabbal, és a hullámfüggvények leírhatók az adott szélességhez tartozó keresztirányú állóhullámokkal, illetve hosszirányú síkhullám terjedéssel. A 6. ábra felső panele a keresztirányú állóhullámokhoz tartozó energiát ábrázolja a vezeték mentén különböző vezetési csatornákra. Egyértelmű, hogy azon vezetési csatornák tudnak csak átjutni a vezetéken (ú.n. kvantum-pontkontaktuson), melyek keresztirányú energiája a vezeték legkisebb keresztmetszeténél is a Fermi-energia alatt van.
szélessége pedig lassan (adiabatikusan) változik a hossztengely mentén (6. ábra alsó panel). A lassan változó szélességnek köszönhetően a vezeték lokálisan mindenütt jól közelíthető egy párhuzamos falú vezetékdarabbal, és a hullámfüggvények leírhatók az adott szélességhez tartozó keresztirányú állóhullámokkal, illetve hosszirányú síkhullám terjedéssel. A 6. ábra felső panele a keresztirányú állóhullámokhoz tartozó energiát ábrázolja a vezeték mentén különböző vezetési csatornákra. Egyértelmű, hogy azon vezetési csatornák tudnak csak átjutni a vezetéken (ú.n. kvantum-pontkontaktuson), melyek keresztirányú energiája a vezeték legkisebb keresztmetszeténél is a Fermi-energia alatt van.
| 6. ábra. Keresztirányú energiák egy adiabatikus kvantum-pontkontaktusban |
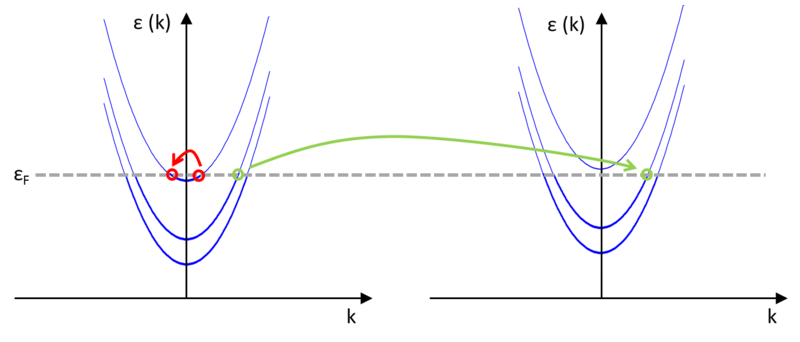
A 7. ábra a vezetékben kialakuló diszperziós relációkat mutatja a vezeték két közeli tartományában. A jobb oldali panel egy kicsit keskenyebb vezetékszakaszhoz tartozik mint a bal oldali, így a nagyobb keresztirányú energia miatt a parabolikus diszperziók felfele tolódnak. Mivel a vezeték lokálisan közel transzlációinvariáns, így a hosszirányú impulzus és a  hullámszám csak keveset változhat miközben az elektron egy adott tartományból eljut egy másik, közeli tartományba. Egy adott vezetési csatornában
hullámszám csak keveset változhat miközben az elektron egy adott tartományból eljut egy másik, közeli tartományba. Egy adott vezetési csatornában  hullámszámmal rendelkező állapot a vezeték keskenyedése során csak úgy tud mindig kis impulzusváltozással előre haladni, ha ugyanabban a vezetési csatornában marad (lásd zöld nyíl). Más csatornába történő átszóródás, illetve visszaszóródás esetén
hullámszámmal rendelkező állapot a vezeték keskenyedése során csak úgy tud mindig kis impulzusváltozással előre haladni, ha ugyanabban a vezetési csatornában marad (lásd zöld nyíl). Más csatornába történő átszóródás, illetve visszaszóródás esetén  jelentősen változna. Kicsit más a helyzet, ha az előrehaladás után az adott csatorna diszperziós relációjának alja a Fermi-energia fölé kerül, azaz az elektron nem tud továbbhaladni. Ebben az esetben az a legkisebb impulzusváltozással járó folyamat, ha nullához közeli de pozitív bejövő
jelentősen változna. Kicsit más a helyzet, ha az előrehaladás után az adott csatorna diszperziós relációjának alja a Fermi-energia fölé kerül, azaz az elektron nem tud továbbhaladni. Ebben az esetben az a legkisebb impulzusváltozással járó folyamat, ha nullához közeli de pozitív bejövő  -val rendelkező elektron ugyanazon csatorna
-val rendelkező elektron ugyanazon csatorna 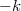 állapotába szóródik vissza (piros nyíl).
állapotába szóródik vissza (piros nyíl).
| 7. ábra. Adiabatikus kvantumvezetékben az elektronok a saját vezetési csatornájukban haladnak előre, illetve ha a csatorna bezáródik, akkor visszaszóródnak |
A fenti érvek alapján elmondható, hogy egy lassan változó szélességű kvantum-pontkontaktusban az összes olyan csatorna, melyhez tartozó keresztirányú energia a legkisebb keresztmetszetben is a Fermi-energia alatt van, 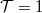 valószínűséggel transzmittálódik (lásd zöld görbék a 6. ábrán), az összes többi csatorna pedig
valószínűséggel transzmittálódik (lásd zöld görbék a 6. ábrán), az összes többi csatorna pedig 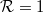 valószínűséggel reflektálódik (piros görbék a 6. ábrán), azaz a vezetőképesség a vezetőképesség-kvantum egész számú többszöröse:
valószínűséggel reflektálódik (piros görbék a 6. ábrán), azaz a vezetőképesség a vezetőképesség-kvantum egész számú többszöröse:
![\[G=\frac{2e^2}{h}M,\]](/images/math/a/5/a/a5af2626ce765f8c594e3b30ae49e615.png)
ahol  a legkisebb keresztmetszetben elférő keresztirányú módusok száma.
a legkisebb keresztmetszetben elférő keresztirányú módusok száma.
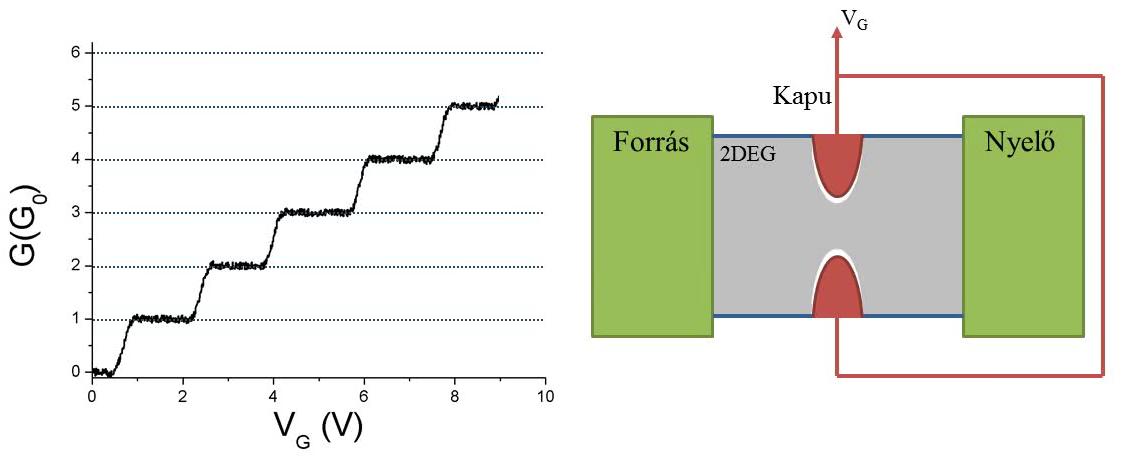
Ez a jelenség kísérletekben is megfigyelhető, elsőként van Wees és szerzőtársai,1 illetve Wharam és szerzőtársai2 demonstrálták a vezetőképesség-kvantálást kétdimenziós elektrongáz-rendszerből kialakított kvantum-pontkontaktusban. A kísérletet sematikusan a 8. ábra szemlélteti. A kétdimenziós elektrongázban két felső kapuelektróda segítségével egy keskeny csatornát alakítunk ki, a csatorna szélessége a kapuelektródákra adott feszültséggel hangolható. Először a kapuelektródák alatt teljesen kiürítjük a kétdimenziós elektrongázt, majd a kapufeszültség változtatásával folyamatosan kinyitjuk a csatornát, és egyre szélesebb pontkontaktust alakítunk ki a két elektróda között. A vezetőképesség eközben lépcsőszerűen változik, először zérusról 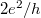 -ra nő, majd a vezetési csatornák egyenkénti kinyílásával a vezetőképesség-kvantum egész számú töbszöröseinél látunk platókat.
-ra nő, majd a vezetési csatornák egyenkénti kinyílásával a vezetőképesség-kvantum egész számú töbszöröseinél látunk platókat.
| 8. ábra. Vezetőképesség-kvantálás kvantum-pontkontaktusban |
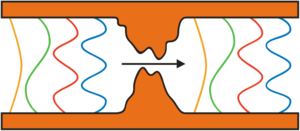
Fontos megjegyezni, hogy egy félvezetőben - így a 8. ábrán szemléltetett kvantum-pontkontaktusban - az elektronok Fermi-hullámhossza párszor tíz nanométer nagyságrendű, így az elektronok nem látják az anyag atomi felépítéséből adódó, tized nanométer nagyságrendű egyenetlenséget, hanem egy sima, közel adiabatikus csatornát látnak. Ezzel szemben fémekben a Fermi-hullámhossz a szomszédos atomok távolságával összemérhető, így egyetlen vagy pár nyitott vezetési csatornával rendelkező pontkontaktust úgy kaphatunk, ha két elektródát mondjuk egyetlen atom köt össze. Ebben az esetben az elektronok a hullámhosszukkal azonos skálán változó, az anyag atomi felépítését tükröző potenciálban mozognak (lásd 9. ábra), melyről nem várjuk hogy adiabatikus legyen, azaz vezetőképesség-kvantálást sem várunk. A kísérletek ezt alá is támasztják,3 a legtöbb fémből készült atomi méretű kontaktusban ugyan csak pár nyitott vezetési csatorna áll rendelkezésre, de az azokhoz tartozó 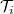 transzmissziós sajátértékek általában tökéletlen transzmissziónak felelnek meg. Atomi mérető kontaktusok viselkedéséről röviden a Nanoszerkezetek előállítási és vizsgálati technikái fejezetben számolunk be.
transzmissziós sajátértékek általában tökéletlen transzmissziónak felelnek meg. Atomi mérető kontaktusok viselkedéséről röviden a Nanoszerkezetek előállítási és vizsgálati technikái fejezetben számolunk be.
| 9. ábra. A hullámhossz skáláján változó potenciálban nem várunk vezetőképesség-kvantálást |
Bibliography
Articles referenced above
Recommended books and review articles
- S. Datta: Electronic Transport in Mesoscopic Systems, Cambridge University Press (1997)
- Thomas Ihn: Semiconducting nanosctructures, OUP Oxford (2010)
- Yuli V. Nazarov, Yaroslav M. Blanter: Quantum Transport: Introduction to Nanoscience, Cambridge University Press (2009)
Recommended courses
- Új kísérletek a nanofizikában, Halbritter András és Csonka Szabolcs, BME Fizika Tanszék
- Transzport komplex nanoszerkezetekben, Halbritter András, Csonka Szabolcs, Csontos Miklós, Makk Péter, BME Fizika Tanszék
- Alkalmazott szilárdtestfizika, Mihály György, BME Fizika Tanszék
- Fizika 3, Mihály György, BME Fizika Tanszék (mérnök hallgatóknak)
- Mezoszkopikus rendszerek fizikája, Zaránd Gergely, BME Elméleti Fizika Tanszék
- Mezoszkopikus rendszerek fizikája, Cserti József, ELTE Komplex Rendszerek Fizikája Tanszék