Fénytörés és visszaverődés vizsgálata
Szerkesztés alatt!
A mérés célja:
- elmélyíteni a hallgatók geometriai optikai ismereteit.
Ennek érdekében:
- áttekintjük a fénytörés és visszaverődés elméletét,
- geometriai optikai méréseket végzünk,
- vizsgáljuk a polarizált fény visszaverődését.
Tartalomjegyzék |
Elméleti összefoglaló
Törésmutató meghatározása a reflexió vizsgálatával
A testeket érő elektromágneses sugárzás részben visszaverődik a felületről, részben elnyelődik, egy része pedig áthalad rajta. Ezen három rész intenzitás-aránya anyagonként más és más, és függ a hullámhossztól is.
Méréstechnikai szempontból legegyszerűbben a visszaverődő és az áthaladó hányad mérhető meg, míg az elnyelt részt az energia-megmaradás törvénye alapján határozhatjuk meg. Minthogy az elektromágneses sugárzás transzverzális, így nem lényegtelen megvizsgálnunk, hogy milyenek a polarizációs viszonyok a visszaverődéskor. Ezért tanulmányozzuk a lineárisan poláros fény visszaverődését is.
Essen két közeg határfelületére lineárisan poláros, 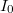 intenzitású fény. Legyen az első közeg levegő, míg a másodiknak a levegőre vonatkozó törésmutatója
intenzitású fény. Legyen az első közeg levegő, míg a másodiknak a levegőre vonatkozó törésmutatója  . A beeső, a visszaverődő és a megtört sugárzás intenzitásait jelölje
. A beeső, a visszaverődő és a megtört sugárzás intenzitásait jelölje 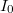 ,
,  , és
, és 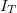 . Az egyszerűség kedvéért itt eltekintünk az elnyelődéstől.
. Az egyszerűség kedvéért itt eltekintünk az elnyelődéstől.
Tudjuk, hogy merőleges beesésnél a visszavert és a megtört sugár egyaránt merőlegesek a felületre és az intenzitásokra az energia-megmaradás értelmében:
![\[ I_0 = I_R + I_T \]](/images/math/6/6/e/66e5071e95175dfa38414adba00e98bc.png)
avagy kifejezve az áthaladó fény intenzitását a közeg törésmutatójával:
![\[ I_0 = I_R + I_0\frac{4n}{(n+1)^2} \]](/images/math/3/4/6/346ef3a1d526c01a8eed48a9f8dc036d.png)
A visszaverődő fény intenzitását kifejezve az
![\[ I_R = \left( \frac{n-1}{n+1}\right) ^2 I_0 \]](/images/math/f/6/3/f63cdec0a810209eb6d17bf3fb043f8c.png)
összefüggés adódik. Jól látható, hogy még merőleges beesésnél is a sugárzás egy jelentős hányada visszaverődik (pl. 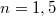 törésmutatójú üveget véve alapul, a beeső fény intenzitásának 4 %-a verődik vissza). Ha a veszteségektől eltekintünk, az áthaladó intenzitás a leírt összefüggések alapján meghatározható.
törésmutatójú üveget véve alapul, a beeső fény intenzitásának 4 %-a verődik vissza). Ha a veszteségektől eltekintünk, az áthaladó intenzitás a leírt összefüggések alapján meghatározható.
Most vizsgáljuk meg azon eseteket, amikor lineárisan poláros fény esik a felületre (a) úgy, hogy a fény rezgési síkja merőleges a beesési síkra, ill. (b) a rezgési sík párhuzamos a beesési síkkal. Emlékeztetőül: a beesési sík a beeső, a visszavert és a megtört sugarak által meghatározott sík. A fenti két esetnek megfelelő viszonyokat az 1. ábrán vázoltuk, ahol körrel jelöltük a síkra merőleges, és sugárra merőleges kétirányú nyíllal a párhuzamos rezgést.
A számolások részletezése nélkül (ez bármelyik optikával foglalkozó kézikönyvben megtalálható) megadjuk az ún. Fresnel-formulákat, melyek a fenti eseteknek megfelelő amplitúdó (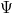 ) viszonyokat írják le. Az (a) esetre
) viszonyokat írják le. Az (a) esetre
![\[ \frac{\Psi_{T\perp}}{\Psi_{0\perp}} = \frac{2}{1+n\frac{cos \beta}{cos\alpha}} \]](/images/math/7/1/b/71be1fcb82e85ae4d9e97b47734b23d0.png)
![\[ \frac{\Psi_{R\perp}}{\Psi_{0\perp}} = \frac{-1+n\frac{cos \beta}{cos\alpha}}{1+n\frac{cos \beta}{cos\alpha}}, \]](/images/math/8/c/b/8cbf4eca305a35692d862900398b5592.png)
ahol 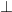 a síkra merőleges komponenseket jelöli. A (b) esetre pedig
a síkra merőleges komponenseket jelöli. A (b) esetre pedig
![\[ \frac{\Psi_{T\parallel}}{\Psi_{0\parallel}} = \frac{2}{n+\frac{cos \beta}{cos\alpha}} \]](/images/math/b/3/5/b35b909d9dacf6b396523963c03f48bb.png)
![\[ \frac{\Psi_{R\parallel}}{\Psi_{0\parallel}} = \frac{n-\frac{cos \beta}{cos\alpha}}{n+\frac{cos \beta}{cos\alpha}}, \]](/images/math/2/2/7/2272ea6e5342fba81d1bfedd311f281e.png)
ahol 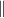 a síkkal párhuzamos komponenseket jelöli.
a síkkal párhuzamos komponenseket jelöli.
Az fenti összefüggések alapján tetszőleges beesési szögű és polarizációjú fény visszavert és megtört (áthaladó) amplitúdóit kiszámíthatjuk, vagy ezek négyzetét képezve az intenzitások is meghatározhatók. Ugyanakkor tetszőleges beeső fény esetén is következtetni lehet a visszavert ill. megtört sugárzás polarizációs viszonyaira is. Hogy ezt igazoljuk, vizsgáljuk meg a Brewster-törvényt, mely szerint bizonyos 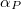 beesési szög esetén a visszavert és a megtört sugarak merőlegesek egymásra, és a visszavert sugár lineárisan poláros (teljesen). A 2. ábra jelölései szerint ekkor
beesési szög esetén a visszavert és a megtört sugarak merőlegesek egymásra, és a visszavert sugár lineárisan poláros (teljesen). A 2. ábra jelölései szerint ekkor 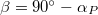 , és így a törési törvény szerint
, és így a törési törvény szerint
![\[ \frac{\sin \alpha_P}{\sin \beta} = \frac{\sin \alpha_P}{\sin 90^\circ -\alpha_P} = \frac{\sin \alpha_P}{\cos \alpha_P}, \]](/images/math/1/6/2/162821ec1a8aca9144d9dd8c00e3e89f.png)
tehát
![\[ \mathrm{tg} \alpha_P = n. \]](/images/math/e/d/f/edffa9e2199362229a18240780b5abf3.png)
Ez az ún. Brewster-törvény. Vizsgáljuk meg az 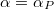 szögben beeső fény esetét a Fresnel-formulák alapján!
szögben beeső fény esetét a Fresnel-formulák alapján!
Ha a rezgési sík párhuzamos a beesési síkkal, akkor
![\[ \frac{cos \beta}{cos \alpha_P} = tan \alpha_P = n, \]](/images/math/e/b/3/eb34d3f34a35f9275cc698b94d3282bf.png)
és így (4) alapján
![\[ \Psi_{R\parallel} = 0 \]](/images/math/7/d/6/7d6953dc5f05bd76006ecaec53fbc29a.png)
tehát a teljes fényintenzitás visszaverődő része zérus. Merőleges rezgési síkú beeső fény esetén viszont a fény egy része képes behatolni, hiszen
![\[ \Psi_{T\perp} = \frac{2}{1+n^2}\Psi_{0\perp} \neq 0. \]](/images/math/d/3/6/d368cf1a32ee8d104159cd050df33334.png)
A fentiek szemléletessé tétele érdekében a 3. ábrán egy 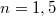 törésmutatójú üveg reflexióképességét ábrázoltuk, mint a beesési szög függvényét, ahol a reflexióképességet az
törésmutatójú üveg reflexióképességét ábrázoltuk, mint a beesési szög függvényét, ahol a reflexióképességet az 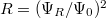 összefüggéssel definiáltuk. Az ábrán látható
összefüggéssel definiáltuk. Az ábrán látható 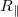 a beesési síkkal párhuzamosan, az
a beesési síkkal párhuzamosan, az 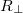 az azzal merőlegesen poláros fényre vonatkozó görbe, míg
az azzal merőlegesen poláros fényre vonatkozó görbe, míg 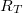 a természetes fényre vonatkozik, ahol
a természetes fényre vonatkozik, ahol
![\[ R_T = \frac{R_\parallel+R_\perp}{2}. \]](/images/math/e/b/c/ebc6070c9d41007ec49208e5bae0bd49.png)
A mérési módszer
A gyakorlaton egy ismeretlen törésmutatójú üveglemez visszaverő képességét fogjuk vizsgálni a beesési szög függvényében a 4. ábrán vázolt elrendezéssel.
A fényforrás (F) lencse (L) segítségével párhuzamosított fénye a vizsgálandó üveglemezre esik, melyről visszaverődve (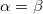 ) egy fényérzékelőre (FÉ) kerül. Az egyszerűség kedvéért olyan érzékelőt használunk, amely a megvilágítást méri, és lux egységekben mutatja azt. Az ábrán látható eszköz "kar"-jai szögosztású körasztal mentén mozgathatók.
) egy fényérzékelőre (FÉ) kerül. Az egyszerűség kedvéért olyan érzékelőt használunk, amely a megvilágítást méri, és lux egységekben mutatja azt. Az ábrán látható eszköz "kar"-jai szögosztású körasztal mentén mozgathatók.
A polarizációs viszonyok vizsgálata ugyanezen eszköz segítségével történhet. Ekkor a fényforrás után egy polarizátort helyezünk el; így annak csak valamely síkban lineárisan poláros fénye esik a vizsgálandó üveglemezre. A polarizációs sík tetszőlegesen változtatható.
A mérés során ellenőrizzük, hogy nem jut-e be a teremvilágítás fénye a dobozba. Ha igen, úgy ezt a "háttér megvilágítást" a mérési adatainkból le kell vonni. Vigyázzunk arra is, hogy a reflexió képesség nem közvetlenül a műszerről leolvasott érték, hanem a mért érték és a beeső (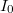 ) megvilágítás hányadosa.
) megvilágítás hányadosa.
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
Két közeg sík határfelületén a fény a
![\[ \sin \alpha = n_{12}\sin \beta \]](/images/math/f/0/3/f03eb5697d3a9c19ee18f025825d8b38.png)
törési törvény szerint megtörik. Az összefüggésben  és
és  a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét,
a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét, 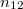 pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
![\[ n_{12} = \frac{n_{2}}{n_{1}}. \]](/images/math/f/c/c/fcc73de627160897a6c60cb60a485d7d.png)
Ha a határfelületre az optikailag sűrűbb (s) közegből érkezik a fény, akkor a relatív törésmutató 1-nél kisebb. Ekkor a törési törvény alapján a fény csak akkor léphet be az optikailag ritkább (r) közegbe, ha
![\[ \alpha < \alpha_h \]](/images/math/e/a/a/eaaa8e53353bf8b8c17303905d610b89.png)
ahol 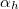 a teljes visszaverődés határszöge. A törési törvény alapján
a teljes visszaverődés határszöge. A törési törvény alapján
![\[ \sin \alpha_h = n_{sr} = \frac{1}{n_{rs}}. \]](/images/math/4/d/f/4df51c882b13ab7180cc1c838505c983.png)
Ha a beesési szög a határszögnél nagyobb, akkor a beeső fény teljesen visszaverődik. Az előző összefüggés alapján a határszög mérésével a relatív törésmutató meghatározható.
A mérési módszer
Az 5/a ábrán látható, forgatható asztalra tett 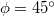 törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép.
törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép.
Az asztal (és a prizma) megfelelő szöggel való elforgatásával elérhető, hogy a fénysugár már nem verődik vissza teljesen, hanem 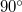 -os törési szöggel, a felületet súrolva, kilép az üvegből.
-os törési szöggel, a felületet súrolva, kilép az üvegből.
Ekkor a következő összefüggéseket írhatjuk fel:
![\[ \sin \delta = n_u \sin \varepsilon, \]](/images/math/f/d/c/fdc23f8338b8a35adf2aecdf2cacc860.png)
![\[ \alpha_h + \varepsilon = \phi = 45^\circ, \]](/images/math/4/d/9/4d968daa3a43bab36ca151cf858e0167.png)
![\[ \sin \alpha_h = \frac{1}{n_u}. \]](/images/math/2/4/a/24a54c91407c10daf5cf29ea9d89c3fb.png)
A három összefüggés alapján 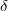 mérésével az üveg levegőre vonatkoztatott
mérésével az üveg levegőre vonatkoztatott 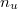 törésmutatója (valamint az
törésmutatója (valamint az  szög és az
szög és az 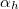 határszög) meghatározható.
határszög) meghatározható.
A 6. ábrán látható elrendezés két ugyanilyen prizmából van összeállítva. A két prizma közé folyadék önthető. A fénysugár most is először merőlegesen, törés nélkül lép be az üvegbe (6. a) ábra), majd megtörve belép a folyadékba, ismét megtörve átlép a másik prizmába, végül (törés nélkül) kilép a levegőbe.
Az asztal (és a prizma) megfelelő szöggel való elforgatásával ekkor is elérhető, hogy a fénysugár éppen 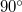 -os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
-os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
![\[ \sin \delta^\prime = n_u sin \varepsilon^\prime, \]](/images/math/a/2/a/a2a8c944bd6a0ad408e7d21dabf60d4b.png)
![\[ \alpha_h^\prime - \varepsilon^\prime = \phi = 45^\circ, \]](/images/math/0/3/f/03fa1cf35251b26b628d283b5fc08c06.png)
![\[ \sin \alpha_h^\prime = \frac{n_f}{n_u}. \]](/images/math/7/1/4/714c6c29288cfa49a93e48f812a51558.png)
Az előző mérésből 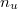 ismert, így a három összefüggés segítségével
ismert, így a három összefüggés segítségével 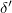 mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az
mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az  szög és az
szög és az 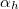 határszög) meghatározható.
határszög) meghatározható.
Leképzés optikai lencsékkel
Görbült felületek esetében a fénytörés szintén a törési törvény alapján számítható, de ekkor a beesési merőleges helyről helyre változik.
A törési törvény alapján levezethető, hogy egy 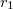 és
és 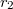 görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha
görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha 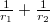 . (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 7. ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az
. (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 7. ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az 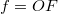 fókusztávolság, a lencse anyagának
fókusztávolság, a lencse anyagának  törésmutatója és a görbületi sugarak között az
törésmutatója és a görbületi sugarak között az
![\[ \frac{1}{f} = (n-1)\left(\frac{1}{r_1}+\frac{1}{r_2} \right) \]](/images/math/8/4/a/84a0e9228d0b072744ebe46bedec6cf1.png)
összefüggés áll fent.
Ha 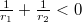 , akkor
, akkor 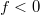 , és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (8. ábra).
, és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (8. ábra).
A gyűjtőlencse egy, a fókuszpontnál távolabbi pontból kiinduló fénysugarakat egy másik pontban gyűjti össze (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, 9.ábra), és így létrejön a  tárgy valódi (ernyőn megjeleníthető)
tárgy valódi (ernyőn megjeleníthető)  képe. A
képe. A 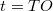 tárgytávolság, a
tárgytávolság, a 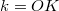 képtávolság és az
képtávolság és az  fókusztávolság között az
fókusztávolság között az
![\[ \frac{1}{t} + \frac{1}{k} = \frac{1}{f} \]](/images/math/0/e/7/0e73cce9cbf37f16a8c5467cd34538fc.png)
leképezési törvény teremt kapcsolatot.
A képlet akkor is használható, ha vagy ha  negatív. Ekkor
negatív. Ekkor  -ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (10. ábra).
-ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (10. ábra).
Több lencséből álló leképzésnél az első lencse képe a második lencse tárgya lesz. Ilyenkor, ha az első lencse által létrehozott valódi kép a második lencse mögött keletkezne, akkor 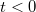 is előfordulhat ("látszólagos tárgy").
is előfordulhat ("látszólagos tárgy").
A mérési módszer
Gyűjtőlencse fókusztávolságának mérése
Ha a 9. ábrának megfelelő elrendezésben egy tárgyról valódi képet hozunk létre, megmérjük a  tárgytávolságot, és a
tárgytávolságot, és a  képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
Ezt a nehézséget küszöböli ki a következő mérési eljárás: Állítsuk a tárgyat és az ernyőt egymástól  távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha
távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha 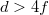 , akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje
, akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje 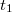 ,
, 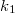 ill.
ill. 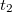 ,
, 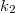 . A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig
. A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig 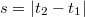 . Felhasználva, hogy a szimmetria miatt
. Felhasználva, hogy a szimmetria miatt 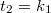 (és
(és 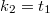 ):
):
![\[ \frac{1}{t_1} + \frac{1}{k_1} = \frac{1}{f}, \]](/images/math/4/b/9/4b9d59ca70cd713830a03cfacdb5d7a6.png)
![\[ t_1 + k_1 = d, \]](/images/math/a/7/e/a7e3335c77a51ab42b3045073e1ccd87.png)
![\[ |t_1 - k_1| = s. \]](/images/math/3/b/0/3b0499ef281b72fda0118dfe576b7c0c.png)
Az egyenletekből 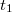 -et és
-et és 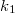 -et kiküszöbölve:
-et kiküszöbölve:
![\[ f = \frac{d^2-s^2}{4d}, \]](/images/math/0/d/f/0df5c748777c483d967c242cf30ec45d.png)
tehát a fókusztávolság  és
és  ismeretében kiszámítható.
ismeretében kiszámítható.
Szórólencse fókusztávolságának mérése
Szórólencsével nem lehet ernyőn megjeleníthető valódi képet létrehozni, így a képtávolságot nem tudjuk mérni. Egy gyűjtő- és egy szórólencséből azonban összeállítható olyan lencserendszer, amely valódi képet ad (11. ábra). A 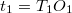 , a
, a 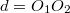 és a
és a 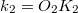 távolság mérhető.
távolság mérhető.
Felhasználva, hogy
![\[ t_2 = d - k_1 < 0 \]](/images/math/9/5/0/950b3f9ee4e4968e9e4aad051354337f.png)
és felírva a két lencse leképzési törvényét 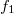 ,
, 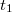 ,
,  és
és 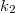 segítségével a szórólencse fókusztávolsága kifejezhető.
segítségével a szórólencse fókusztávolsága kifejezhető.
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
Törésmutató meghatározása a reflexió vizsgálatával
1. Természetes fény segítségével mérje meg a kapott üveglemez reflexióképességét a beesési szög függvényében!
2. Ábrázolja a kapott eredményt grafikusan! Extrapolálással állapítsuk meg a 0 és a 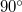 beesési szögekhez tartozó értékeket!
beesési szögekhez tartozó értékeket!
3. Az 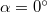 esetét véve alapul, számolja ki az üveg törésmutatóját!
esetét véve alapul, számolja ki az üveg törésmutatóját!
4. Helyezze a polarizátort a fényforrásra! A polarizációs síkot úgy állítsa be, hogy merőleges legyen a beesési síkra! Mérje meg a visszaverőképességet a szög függvényében!
- A polarizátor le- ill. felhelyezésénél ügyeljen arra, hogy a műanyag foglalat menetes része ne sérüljön!
5. Ismételje meg a mérést a polarizátor 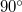 -kal való elforgatása után!
-kal való elforgatása után!
6. Ábrázolja az eredményeket és a számolt 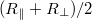 értékeket! Hasonlítsa ezt össze az 1. feladatban kapott eredménnyel!
értékeket! Hasonlítsa ezt össze az 1. feladatban kapott eredménnyel!
7. A Brewster-szög meghatározásával (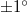 pontossággal) is számítsa ki az üveg törésmutatóját! Hasonlítsa össze a 3. feladatban kapott eredménnyel!
pontossággal) is számítsa ki az üveg törésmutatóját! Hasonlítsa össze a 3. feladatban kapott eredménnyel!
- Ennél a feladatnál a luxmérőt a legkisebb méréshatárban és a kisebb érzékelővel használja!
- Hogy az érzékelő a megfelelő magasságba kerüljön, a tartóba először a mellékelt hasábot helyezze be! Ezután a mérőfejet "fejjel lefelé" rakja a tartóba!
- A műszert csak akkor kapcsolja a legkisebb méréshatárba, ha a doboz fedelét már lezárta!
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
8. Tegye fel a forgatható asztalra a prizmát! Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a prizma anyagának levegőre vonatkoztatott törésmutatóját!
9. Cserélje ki a prizmát a két prizmából összeállított rendszerre! Öntsön a prizmák közé desztillált vizet. Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a víz levegőre vonatkoztatott törésmutatóját!
Leképzés optikai lencsékkel
10. Helyezze a fényforrást és az ernyőt az optikai sín két végére! A tárgyat (diát) a fényforrás elé kb. 5 cm távolságba helyezze! Mérje meg a tárgy és az ernyő  távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti
távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti  távolságot, és határozza meg a lencse fókusztávolságát!
távolságot, és határozza meg a lencse fókusztávolságát!
11. Helyezze az (1) jelű gyűjtőlencse és az ernyő közé a (2) jelű szórólencsét! Elméleti megfontolások után az ernyő és/vagy a lencsék megfelelő mozgatásával állítson elő éles képet! Mérje meg a tárgy, a lencsék és az ernyő közti távolságokat, és határozza meg a szórólencse fókusztávolságát!
12. A kis fókusztávolságú lencse segítségével állítson össze minél nagyobb nagyítású leképzést! A tárgytartóba most a hajszálat tegye (diakeretben, az Optika 2. méréssel közös eszköz). A vonalzó képének megmérésével állapítsa meg a nagyítást és határozza meg a hajszál vastagságát!