Fotoeffektus vizsgálata
A mérés célja:
- Megismerkedni a fényelektromos jelenségekkel, a fénykibocsátó diódákkal és egyéb félvezető átmenetekkel,
- megismerkedni a diffrakció jelenségével,
- igazolni, hogy a fotoelektronok kinetikus energiája, illetőleg a vele arányos lezáró feszültség független a fény intenzitásától,
- az
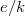 és a
és a 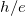 arány meghatározása méréssel.
arány meghatározása méréssel.
Ennek érdekében:
- Megmérjük egy tranzisztor p-n átmenetének karakterisztikáját
- Meghatározzuk különböző színű fénykibocsátó diódák hullámhosszát egy mobiltelefon és egy CD darab segítségével
- Megmérjük a fénykibocsájtó diódák áram-feszültség karakterisztikáját
- Megmérjük egy vákuumfotodióda lezárási feszültségét különböző intenzitású fénynél és különböző hullámhosszú fénynél
Tartalomjegyzék |
Elméleti összefoglaló
A fotoeffektus
A külső fényelektromos hatás alapjelensége: ha egy fémlemezre fény esik, a lemezből elektronok lépnek ki. E jelenség vizsgálata néhány olyan eredményre vezetett, melyeket a fény folytonos hullámelméletével nem lehet megmagyarázni. Ezek a következők:
- Az elektronok csak akkor lépnek ki, ha a fény frekvenciája nagyobb egy, az illető fémre jellemző határfrekvenciánál. A klasszikus szemlélet szerint azonban a
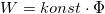 feltételnek megfelelő sugárzási intenzitás minden frekvencián biztosítható.
feltételnek megfelelő sugárzási intenzitás minden frekvencián biztosítható.
- Megfelelő fényfrekvencia esetén az elektronok kilépése akármilyen gyenge fény hatására azonnal (10-9 s-on belül) bekövetkezik. (A kísérletek során használt fémeknél a kilépési munka 10-19 J nagyságrendű, az elektron által „lefedett” terület, ahonnan energiát gyűjthet ~
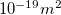 , egy átlagos megvilágítást feltételezve, ami
, egy átlagos megvilágítást feltételezve, ami 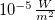 , a
, a 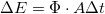 alapján
alapján 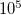 s , ~ 28 óra lenne a folyamathoz szükséges idő.)
s , ~ 28 óra lenne a folyamathoz szükséges idő.)
- A kilépő elektronok száma arányos a megvilágítás erősségével, de energia eloszlásuk független attól. A maximális mozgási energia a fény frekvenciájának lineáris függvénye, a klasszikus számítások szerint ez nem lineáris.
E kvalitatív tapasztalatok kvantitatív magyarázatát Albert Einstein adta meg azzal, hogy Planck kvantumhipotézisét a fényjelenségekre is kiterjesztette. Feltételezte, hogy a Planck-féle 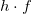 energiacsomag nem csak a sugárzó oszcillátor diszkrét energiaváltozásait adja meg, hanem a sugárzási térben is
energiacsomag nem csak a sugárzó oszcillátor diszkrét energiaváltozásait adja meg, hanem a sugárzási térben is 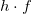 adagokban van jelen az energia. A fényenergia diszkrét energiaadagokban terjed. Ezek a fotonok.
Tehát egy foton energiája:
adagokban van jelen az energia. A fényenergia diszkrét energiaadagokban terjed. Ezek a fotonok.
Tehát egy foton energiája:
![\[E = h \cdot f \]](/images/math/5/c/0/5c07bee9bace405835bbce9a8dd08e00.png)
ahol  a Planck-féle állandó,
a Planck-féle állandó,  pedig a sugárzás– esetünkben a fény – frekvenciája. Az elektronok kilépése csak akkor indulhat meg, ha a beeső fotonok energiája legalább az elektronok kötési energiájával egyenlő. A kilépés feltétele tehát:
pedig a sugárzás– esetünkben a fény – frekvenciája. Az elektronok kilépése csak akkor indulhat meg, ha a beeső fotonok energiája legalább az elektronok kötési energiájával egyenlő. A kilépés feltétele tehát:
![\[ h \cdot f \geq W = h \cdot f_{0} \]](/images/math/1/a/4/1a46565ae3f9a2d869c6e6f813b4772b.png)
ahol 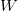 az elektron kötési energiája, az úgynevezett kilépési munka,
az elektron kötési energiája, az úgynevezett kilépési munka,  pedig a fémre jellemző küszöbfrekvencia. Általános esetben:
pedig a fémre jellemző küszöbfrekvencia. Általános esetben:
![\[ h \cdot f = W + \frac{1}{2} m v^2 \]](/images/math/3/4/b/34b779e4ab9bda9585f2c8e861050c97.png)
vagyis a foton energiatöbblete a kilépő elektron kinetikus energiájaként jelenik meg. Nagyobb fényintenzitás több fotont, tehát több kilépő elektront jelent. Ilyen módon magyarázatot nyert a külső fényelektromos jelenség valamennyi felsorolt sajátsága.
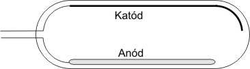
A fényelektromos jelenség egyik legelterjedtebb gyakorlati alkalmazása a fotocella, ami egy légritkított üvegcső, mely egyik oldalán a belső felületére felvitt fémréteg képezi a katódot, a vele szemben elhelyezett dróthurok pedig az anód (1.ábra). Mint a (3) egyenletből látható, a határfrekvencia esetétől eltekintve a kilépő elektronok kinetikus energiával is rendelkeznek, ami feszültségmentes tér esetén elegendő ahhoz, hogy az anódig repüljenek, ezért 0 anódfeszültség esetén is mérhető bizonyos – igen kicsi – áram.
Ahhoz, hogy a fotocella tetszőleges megvilágítás ellenére teljesen árammentes legyen, akkora ellenteret kell az anód és a katód között létesíteni, mely a legnagyobb energiájú elektronokat is meggátolja az anód elérésében. Az árammentesség feltétele tehát:
![\[ e U_{0} = \frac{1}{2} m v^2_{max} \]](/images/math/b/1/6/b167bd4a9a4b50f7679105d3418c2382.png)
ahol  az elektron töltése,
az elektron töltése,  pedig a lezáró feszültség. A fotocella anódja és a katódja tekinthető egy kapacitásnak, mely a fotoáram hatására elektromosan feltöltődik (ha a kimenetei "lebegnek", azaz nem zárjuk rövidre egy véges ellenállással) mindaddig, amíg potenciálja el nem éri az
pedig a lezáró feszültség. A fotocella anódja és a katódja tekinthető egy kapacitásnak, mely a fotoáram hatására elektromosan feltöltődik (ha a kimenetei "lebegnek", azaz nem zárjuk rövidre egy véges ellenállással) mindaddig, amíg potenciálja el nem éri az  lezáró feszültséget. Erre az
lezáró feszültséget. Erre az  feszültségre a (3) és (4) egyenletekb a következő kifejezést kapjuk:
feszültségre a (3) és (4) egyenletekb a következő kifejezést kapjuk:
![\[ U_{0} = \frac{h}{e} f - \frac{W}{e} \]](/images/math/f/c/7/fc712ba7b78513272126457b561a81b9.png)
A fotocellát különböző, jól meghatározott frekvenciájú fénnyel megvilágítva a  -
- 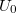 grafikonon egy egyenest kapunk, melynek meredeksége a Planck-állandó (
grafikonon egy egyenest kapunk, melynek meredeksége a Planck-állandó ( ) és az elektron töltésének (
) és az elektron töltésének ( ) hányadosa.
) hányadosa.
Fénykibocsátó dióda (LED)
A fotoeffektus tulajdonságaiból adódik, hogy a fenti méréshez olyan fényt kell juttatni a fotocellára, mely monokromatikus. Ez a fénykibocsátó diódákra, azaz a LED-ekre jó közelítéssel teljesül. A LED-ek, ahogy a nevük is mutatja olyan félvezető p-n átmenetek (dióák), melyek fotonokat képesek kibocsájtani, tehát egy, a fotoeffektussal ellentétes folyamat megy bennük végre, amiben a p-n átmeneten áthaladó, majd rekombinálódó elektronok energiát adnak le egy foton kibocsátása formájában.
Félvezető p-n átmenet tulajdonságai - e/k állandó meghatározása
Félvezetőkben az elektromos áramot elektronok és lyukak (elektronhiányok) mozgása eredményezi. Bizonyos adalék anyagok (foszfor, arzén) hatására a félvezetőkben az elektronok annyira túlsúlyba kerülnek a lyukakhoz képest, hogy gyakorlatilag csak elektronvezetés alakul ki: az ilyen félvezetőt n típusúnak nevezik. Más adalékok (bór, gallium, alumínium) viszont a félvezetőben lyukvezetést hoznak létre: az ilyen félvezetők a p típusú félvezetők.
Ha egy p típusú és egy n típusú félvezetőt érintkezésbe hozunk (ez az ún. p–n átmenet), akkor az érintkezési helyen kontaktpotenciál jön létre, mert energetikai okok miatt az n típusú részből elektronok mennek át a p típusú részbe (így az negatív többlettöltésre tesz szert), a p típusú részből viszont lyukak mennek át az n típusú részbe (így abban pozitív többlettöltés jön létre). A kontaktus létrejöttének pillanatában tehát egy, a p rétegből az n rétegbe irányuló kezdeti áram folyik. Az áram hatására a potenciálkülönbség nő, ami egyre jobban akadályozza a további töltésátmenetet, ezért egy bizonyos feszültség elérése után a p→n irányú áram megszűnik, és kialakul egy állandósult kontaktpotenciál. Ezzel egyidejűleg a kontaktus két oldalán létrejön egy olyan tartomány, amelyben nincsenek mozgásképes töltéshordozók. A töltéshordozók áthaladását (a p→n irányú áramot) ezen a kiürített tartományon át a létrejött 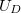 magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.
magasságú potenciálgát akadályozza, ezért külső feszültség nélkül a töltéshordozók csak a termikus mozgás segítségével, véletlenszerűen jutnak át.
Eléggé általánosan igaz, hogy a termikusan aktivált folyamat gyakorisága az 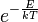 faktorral arányos, ahol
faktorral arányos, ahol  a továbbhaladáshoz szükséges energia,
a továbbhaladáshoz szükséges energia,  a Boltzmann-állandó,
a Boltzmann-állandó,  pedig az abszolút hőmérséklet. Ennek megfelelően annak gyakorisága, hogy egy lyuk p→n irányban vagy egy elektron n→p irányban az
pedig az abszolút hőmérséklet. Ennek megfelelően annak gyakorisága, hogy egy lyuk p→n irányban vagy egy elektron n→p irányban az 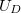 magasságú potenciálgáton átugrik, az
magasságú potenciálgáton átugrik, az 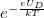 faktorral arányos (
faktorral arányos ( az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy p→n irányú, ún. injektált áram folyik:
az elektron töltésének nagysága). Ez egyben azt is jelenti, hogy a termikus aktiváció segítségével a potenciálgáton át egy p→n irányú, ún. injektált áram folyik:
![\[ I_I = C e^{-\frac{e U_D}{kT} } \]](/images/math/d/5/e/d5ef6635b7ee6ed2836b080edd6ef241.png)
A kiürített tartományon át ugyanakkor létrjön egy ellenkező irányú áram is, ami annak következménye, hogy a termikus mozgás (termikus aktiváció) révén, ha kis számban is, de mindig keletkeznek töltéshordozók, így – többek között – a kiürített réteg n oldalán lyukak, p oldalán pedig elektronok jelennek meg. Mivel a kontaktpotenciál ezeknek a mozgását a kontaktuson át éppen elősegíti, ily módon egy n→p irányú, ún. telítési (szaturációs) áram, 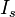 jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor
jön létre. Ez az áram nem függ a kontaktuson kialakult feszültségtől, csak a termikusan keltett töltéshordozók mennyiségétől. Külső feszültség nélküli (egyensúlyi) állapotban a két áram egymást kiegyenlíti, vagyis ekkor 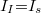 .
.
Ha a p–n átmenetre  külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most
külső feszültséget kapcsolunk, akkor ez módosítja a potenciálgát magasságát, ezért megváltoztatja az injektált áramot, amely most
![\[ I_I = C e^{-\frac{e\left( U_D - U \right)}{kT} } \]](/images/math/8/d/5/8d52f071d230da35dd0220e54f80dabc.png)
Itt  állandó, az
állandó, az  feszültség pedig negatív, ha a feszültség a kontaktpotenciállal egyirányú, és pozitív, ha azzal ellentétes. Mivel
feszültség pedig negatív, ha a feszültség a kontaktpotenciállal egyirányú, és pozitív, ha azzal ellentétes. Mivel 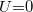 esetén
esetén 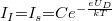 ,
,
![\[ C=I_se^{\frac{eU_D}{kT} }, \]](/images/math/1/3/4/1348ca7c3a4c1bbff6ab1dbb2f69fa94.png)
amivel az injektált áramra azt kapjuk, hogy
![\[ I_I=I_se^{\frac{eU}{kT} }. \]](/images/math/8/2/5/825146574af2ec40b07a5921788d49ac.png)
A kontaktuson átfolyó  eredő áram a feszültségfüggő
eredő áram a feszültségfüggő 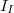 injektált áram és a feszültségtől független
injektált áram és a feszültségtől független 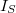 telítési áram különbsége:
telítési áram különbsége:
![\[ I=I_s\left(e^{\frac{eU}{kt} }-1 \right). \]](/images/math/2/0/3/20373aab9f22485f5557b92b75afa4df.png)
Ez az összefüggés azt az ismert tapasztalatot tükrözi, hogy egy ilyen kontaktus különböző irányban előfeszítve különböző nagyságú áramot bocsát át, más szóval egyenirányít. Az ilyen egyenirányító p–n átmenetet félvezető diódának nevezik.
Ha megvizsgáljuk az (5) egyenlettel leírható áram-feszültség összefüggést (ún. áram–feszültség karakterisztikát), látható, hogy az exponensben megjelenik az elektron töltésének ( ) és a Boltzmann-állandónak (
) és a Boltzmann-állandónak ( ) a hányadosa.
) a hányadosa.
Így a (5) alakú karakterisztikából az 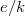 hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy
hányados elvileg meghatározható, de az összefüggés egyszerűsítésével a feladat is egyszerűsíthető. Mivel méréseinket szobahőmérséklethez közeli hőmérsékleteken végezzük, érvényes, hogy 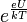 , így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége
, így az egyenletben az exponenciális tag mellett az „1” elhanyagolható, mivel a félvezetők jellemző tiltott sávszélessége 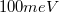 nagyságrendű. Ezért jó közelítéssel érvényes, hogy
nagyságrendű. Ezért jó közelítéssel érvényes, hogy
![\[ I=I_se^{\frac{eU}{kt} }. \]](/images/math/a/7/3/a738095ed4541519d1a47bcf258ead0d.png)
Ha az egyenlet mindkét oldalának a természetes alapú logaritmusát vesszük, akkor az 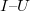 összefüggés linearizálható, hiszen
összefüggés linearizálható, hiszen
![\[ln I =ln I_s+\frac{e}{kT}U. \]](/images/math/8/8/8/88814faa90c3b80efa94343955c051fb.png)
Ez azt jelenti, hogy ha a hőmérsékletet állandó értéken tartva megmérjük az áram-feszültség karakterisztikát, majd az áramértékek természetes logaritmusát ábrázoljuk a feszültség függvényében, akkor a pontok egy egyenest adnak. Jelölje a mérési pontokhoz illesztett egyenes meredekségét 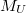 .
.
![\[ M_U=\frac{e}{kT} \]](/images/math/d/b/e/dbe303f83138bf5e451e17680d13b539.png)
összefüggés, amiből az 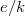 hányadosra azt kapjuk, hogy
hányadosra azt kapjuk, hogy
![\[ \frac{e}{k} =M_UT \]](/images/math/7/1/8/718657f25de1d93f7cf2bced52b351ac.png)
Ezzel a hőmérséklet ismeretében meghatározható az 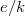 arány.
arány.
Planck-állandó és elektron töltés arányának meghatározása LED-ekkel
Ahogy már említettük, a LED-ek gyakorlatilag p-n átmenetek, melyek kontaktpotenciálja az 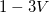 -os tartományba esik. Ha a LED-re „nyitóirányban” feszültséget kapcsolunk, az a kialakult kontaktpotenciált csökkenti és egy diódára jellemző értéknél (ún. nyitófeszültség) kiegyenlíti, ekkor az elektronok/lyukak áramlása jelentősen megnő, ezáltal a diódán áram folyik. Ennek következtében a p-n átmenet határára folyamatosan töltéshordozók érkeznek és ott rekombinálódnak, mely során a félvezető tiltott sávnak megfelelő enegriát adnak le fotonok formájában, így a LED fényt bocsát ki. Ezzel gyakorlatilag a fotoeffektus ellentétes folyamata játszódik le és mivel a LED nyitófeszültsége jó közelítéssel (idealizált esetben) arányos a tiltott sáv szélességével, különböző színű LED-ek nyitófeszültségének és a kibocsájtott fényük frekvenciájának vizsgálatával szintén meghatározható a
-os tartományba esik. Ha a LED-re „nyitóirányban” feszültséget kapcsolunk, az a kialakult kontaktpotenciált csökkenti és egy diódára jellemző értéknél (ún. nyitófeszültség) kiegyenlíti, ekkor az elektronok/lyukak áramlása jelentősen megnő, ezáltal a diódán áram folyik. Ennek következtében a p-n átmenet határára folyamatosan töltéshordozók érkeznek és ott rekombinálódnak, mely során a félvezető tiltott sávnak megfelelő enegriát adnak le fotonok formájában, így a LED fényt bocsát ki. Ezzel gyakorlatilag a fotoeffektus ellentétes folyamata játszódik le és mivel a LED nyitófeszültsége jó közelítéssel (idealizált esetben) arányos a tiltott sáv szélességével, különböző színű LED-ek nyitófeszültségének és a kibocsájtott fényük frekvenciájának vizsgálatával szintén meghatározható a 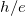 arány.
arány.
Hullámhossz meghatározása diffrakció segítségével
A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens-Fresnel-elv" segítségével lehet meg-magyarázni: a Huygens-Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást.
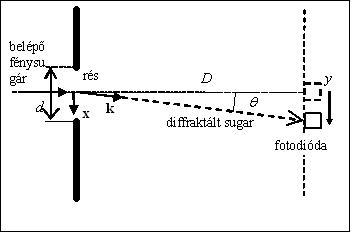
Egyszerű példaképp vizsgáljuk meg az optikai rés esetét. A rés egy átlátszatlan felületen kialakított keskeny, a fény hullámhosszával összemérhető szélességű, hosszú nyílás. Világítsuk meg a rést egy koherens, párhuzamos fénynyalábbal (legegyszerűbben egy lézer fényével). A fény a résen áthaladva elhajlik. A réstől távol elhelyezett ernyőn a résből kiinduló elemi hullámok interferenciája alakítja ki a diffrakciós képet. A diffrakciós képet – az intenzitást a hely függvényében - egy fotodióda mozgatásával könnyen meg lehet mérni (2. ábra).
A k hullámszámvektor irányában a relatív intenzitást a Fourier-integrál segítségével lehet kiszámítani. Az intenzitás arányos az integrál abszolút értékének négyzetével:
![\[ I(\pmb{k}) = \left \lvert \int_{-\infty}^{\infty} e^{\pmb{kx}i}f(\pmb{x})d\pmb{x} \right \rvert^2. \]](/images/math/9/6/6/9663788744b887e93547c4b60e644842.png)
A kifejezésben
![\[|\pmb{k}| = k = \frac{2\pi}{\lambda},\]](/images/math/e/e/d/eede5e35ac948ed5edd2f2c0e0f933f8.png)
![\[\pmb{kx} = kx \sin \theta \approx kx\theta \; (\theta\ll1), \]](/images/math/1/6/3/16352f870f8061cacbb3124b500b23b9.png)
![\[ f(x) = \begin{cases} \frac{1}{d} \; \mathrm{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; \mathrm{ha} \; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} \]](/images/math/8/0/f/80fc88f0461a627382a9bb9ce5f935cc.png)
Felhasználva, hogy
![\[ y = D \mathrm{tg} \theta \approx D\theta \; (\theta<<1), \]](/images/math/f/2/2/f22288c877cdce402826e2269aca0b3b.png)
és elvégezve az integrálást
![\[ I(y) = \left( \frac{\lambda D}{\pi yd} \right)^2\sin^2\left( \frac{\pi yd}{\lambda D} \right).\]](/images/math/0/a/6/0a6a92de54041fb3e92b33500738749a.png)
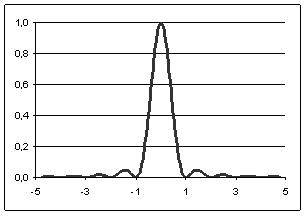
A diffrakciós kép az 3. ábrán látható. A vízszintes tengely 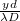 egységekben van skálázva. Az intenzitás az
egységekben van skálázva. Az intenzitás az 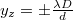 helyen válik először zérussá. Az két zérushely közti távolság (
helyen válik először zérussá. Az két zérushely közti távolság (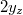 ) és a
) és a  távolság mérésével a
távolság mérésével a  hullámhossz ismeretében a
hullámhossz ismeretében a  résszélesség,
résszélesség,  ismeretében pedig a
ismeretében pedig a  hullámhossz meghatározható.
hullámhossz meghatározható.
Bonyolultabb optikai struktúrák (például egy optikai rács) esetén a diffrakciós kép hasonlóan kiszámítható, csak 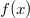 kifejezését kell ennek megfelelően módosítani. A részletes számítást elvégezve megállapítható, hogy egy optikai rács esetén a maximumok távolsága szintén arányos a hullámhosszal, illetve a geometriai paraméterekkel. Így egy ismert hullámhosszú fényforrás diffrakciós képe alapján egy fixált geometriájú elrendezés kalibrálható és segítségével meghatározható ismeretlen fényforrások hullámhossza.
kifejezését kell ennek megfelelően módosítani. A részletes számítást elvégezve megállapítható, hogy egy optikai rács esetén a maximumok távolsága szintén arányos a hullámhosszal, illetve a geometriai paraméterekkel. Így egy ismert hullámhosszú fényforrás diffrakciós képe alapján egy fixált geometriájú elrendezés kalibrálható és segítségével meghatározható ismeretlen fényforrások hullámhossza.
Mérési feladatok
Aktualizálás alatt!