Granulált anyagok vizsgálata
A mérés célja:
- megismerkedni a granulált anyagok viselkedésével.
Ennek érdekében:
- röviden ismertetjük a granulált anyagokkal foglalkozó szakirodalmat,
- mérjük különböző anyagok rézsűszögét,
- vizsgáljuk a különböző anyagok rázásakor kialakuló mintázatokat.
Tartalomjegyzék |
Elméleti összefoglaló
Granulált anyagok
A granulált (szemcsés, granuláris) anyagok nagyszámú, szilárd szemcséből állnak. A természetben és az ipari gyakorlatban nagyon sok egymástól különböző anyag tartozik ebbe a csoportba. A szemcsék mérete tág határok között változik a néhány mikrométeres festékporoktól a kőomlások méteres nagyságú szikladarabjaiig. Még nagyobb a változatosság a szemcsék alakjában a szabályos kis golyóktól a teljesen szabálytalan, szögletes formákig. Jelentősen befolyásolja a granulált anyagok viselkedését a szemcsék közti teret kitöltő anyag (levegő, víz vagy más folyadék). A száraz és a nedves homok közti különbséget mindenki ismeri gyerekkorából: a száraz homok szinte folyadékként önthető, a nedves homokból viszont – a szemcsék közti kohéziónak köszönhetően – várat lehet építeni. A továbbiakban csak száraz granulált anyagokkal foglalkozunk, ahol a szemcsék közti kohézió elhanyagolható.
A granulált anyagok sztatikája
Ha a kohézió elhanyagolható, akkor a granulált anyag egyensúlyát a gravitáción kívül kizárólag a szemcsék közti és a külső határolófelületek által kifejtett nyomó és súrlódási erők határozzák meg. A probléma azonban ennek ellenére nagyon bonyolult: nemcsak a szemcsék nagy száma és általában szabálytalan alakja, hanem a tapadási súrlódási erők következtében létrejövő befeszülések, beékelődések miatt is. A nyugalomban lévő granulált anyag termodinamikai szempontból tipikus nemegyensúlyi rendszer. A lehetséges minimális értéknél jóval nagyobb potenciális energiájú elrendeződések is "befagyhatnak", hiszen az atomi méreteknél jóval nagyobb szemcsék aktiválásához szobahőmérsékleten a termikus gerjesztés nagyon kevés, a külső mechanikai hatások megszűnése után a szemcsék rugalmatlan ütközései pedig hamar felemésztik a rendszer kinetikus energiáját.
A granulált anyagok sztatikájának legegyszerűbb kísérleti vizsgálata a rézsűszög mérése. Játszótéri tapasztalatból mindenki ismeri, hogy bár a száraz granulált anyag folyadékként önthető, ha egy nyíláson (például tölcséren) át kiöntjük az anyagot egy sík felületre, akkor – a folyadékokkal ellentétben – nem folyik szét teljesen, hanem egy többé-kevésbé szabályos kúpot alkot. A kúp alkotójának vízszintessel bezárt  szöge a rézsűszög. A szemcsék méretétől, alakjától, anyagi minőségétől, nedvességétől függő rézsűszöggel jól jellemezhető egy granulált anyag – bár a kialakuló szög függ a lejtő létrehozásának módjától is. Erről és további granulált anyagokkal való érdekességekről lásd [1] -et. A rézsűszög fontos gyakorlati szempontból is: például annak meghatározásához, hogy egy adott mennyiségű szemcsés anyagot mekkora területen lehet ömlesztve tárolni.
szöge a rézsűszög. A szemcsék méretétől, alakjától, anyagi minőségétől, nedvességétől függő rézsűszöggel jól jellemezhető egy granulált anyag – bár a kialakuló szög függ a lejtő létrehozásának módjától is. Erről és további granulált anyagokkal való érdekességekről lásd [1] -et. A rézsűszög fontos gyakorlati szempontból is: például annak meghatározásához, hogy egy adott mennyiségű szemcsés anyagot mekkora területen lehet ömlesztve tárolni.
A szemcsék közti bonyolult kölcsönhatás kifejezésére szokás bevezetni a 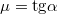 makroszkopikus súrlódási együtthatót, ahol
makroszkopikus súrlódási együtthatót, ahol  a rézsűszög. (A definíció alapja, hogy egy szemcse akkor lehet egyensúlyban egy hajlásszögű lejtőn, ha a szemcse és a lejtő közt legalább
a rézsűszög. (A definíció alapja, hogy egy szemcse akkor lehet egyensúlyban egy hajlásszögű lejtőn, ha a szemcse és a lejtő közt legalább  a súrlódási együttható.) A szemcsék egymás közötti és a határolófelületekkel való súrlódásának egyik érdekes, a gyakorlati életben szintén fontos következménye, hogy egy tartályba töltött granulált anyag a folyadékoktól eltérően terheli a tartály alaplapját és oldalfalát. Példaképp vizsgáljunk egy
a súrlódási együttható.) A szemcsék egymás közötti és a határolófelületekkel való súrlódásának egyik érdekes, a gyakorlati életben szintén fontos következménye, hogy egy tartályba töltött granulált anyag a folyadékoktól eltérően terheli a tartály alaplapját és oldalfalát. Példaképp vizsgáljunk egy  sugarú,
sugarú,  magasságú hengeres tartályt, ahol
magasságú hengeres tartályt, ahol 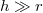 . Ha a tartályba granulált anyagot töltünk, a tartály aljára ható nyomás kezdetben a folyadékok hidrosztatikai nyomásához hasonlóan növekszik. A beöntött anyag mennyiségével azonban nő az oldalfalra és a szemcsék között ható nyomás, és ezzel együtt az oldalfalon és a szemcsék közt fellépő súrlódás is növekszik. Ha egy
. Ha a tartályba granulált anyagot töltünk, a tartály aljára ható nyomás kezdetben a folyadékok hidrosztatikai nyomásához hasonlóan növekszik. A beöntött anyag mennyiségével azonban nő az oldalfalra és a szemcsék között ható nyomás, és ezzel együtt az oldalfalon és a szemcsék közt fellépő súrlódás is növekszik. Ha egy 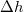 vastagságú szemcserétegre a fal nagyobb súrlódási erőt fejt ki, mint a réteg súlya, akkor a nyomás nem növekszik tovább:
vastagságú szemcserétegre a fal nagyobb súrlódási erőt fejt ki, mint a réteg súlya, akkor a nyomás nem növekszik tovább:
![\[p_{\text{max} }2r\pi\Delta h\mu^*=r^2\pi\Delta h\rho g,\]](/images/math/e/f/c/efcfa299b79cb196523785fd38fdcc99.png)
ahol 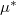 a korábban definiált szemcsék közti makroszkopikus súrlódási együttható és a szemcsék és a fal közti súrlódási együttható közül a kisebbik. (Attól függően, hogy melyik együttható kisebb, vagy a szemcsék egymáson, vagy pedig a szemcsék a tartály falán csúsznak meg.) Ebből a maximális nyomás és a tartály aljára ható maximális erő
a korábban definiált szemcsék közti makroszkopikus súrlódási együttható és a szemcsék és a fal közti súrlódási együttható közül a kisebbik. (Attól függően, hogy melyik együttható kisebb, vagy a szemcsék egymáson, vagy pedig a szemcsék a tartály falán csúsznak meg.) Ebből a maximális nyomás és a tartály aljára ható maximális erő
![\[p_{max}=\frac{r\rho g}{2\mu^*}\quad\text{és}\quad F_{max}=p_{max}r^2\pi=\frac{r^3\pi\rho g}{2\mu^*}\]](/images/math/1/c/e/1ce7c35e9875a693602ddae008d7e10d.png)
A beöntött anyag súlyának egy részét az oldalfal fogja megtartani, amelyre a folyadékoktól eltérően nemcsak vízszintes, hanem függőleges erők is hatnak. A problémát tovább bonyolítja, hogy ha a granulált anyagot beöntés közben, vagy utólag (pl. rázással) tömörítjük, a részecskék közti és az edény falára ható nyomás ennél nagyobb is lehet, a tapadási súrlódási erők pedig nem csak tarthatják, hanem akár lefelé is nyomhatják az anyagot – tovább növelve a nyomást. Az ilyen jellegű befeszülések granulált anyagok tárolására szolgáló hatalmas épületek (pl. cement- vagy gabonatároló silók) "érthetetlen" összeomlását is okozhatják.
A granulált anyagok dinamikája
A granulált anyag folyamatosan mozgásban tartható, ha a szemcsék rugalmatlan ütközése során elvesző (elsősorban hővé alakuló) energiát külső mechanikai gerjesztéssel (rázással, keveréssel, öntögetéssel, stb.) folyamatosan pótoljuk. A granulált anyagok dinamikai leírása a sztatikai leíráshoz hasonlóan bonyolult. A jelenségek nagy részének egyelőre hiányos az elméleti magyarázata, a számítógépes szimulációk pedig a részecskék nagy száma és bonyolult kölcsönhatása miatt szintén csak komoly egyszerűsítésekkel készülnek. A következőkben csak a mérésen is vizsgált két fontos jelenséget tárgyalunk.
Szegregáció
Az egyik legmeglepőbb jelenség a különböző részecskékből álló granulált anyagok mozgatásakor a szinte törvényszerűen fellépő szegregáció, azaz a különböző anyagú, sűrűségű, méretű, alakú, felületű részecskék spontán szétválása. Rázás, forgódobos keverés, átöntés hatására a különböző szemcsék a várakozással ellentétben nem összekeverednek, hanem térben szétválnak. Különböző rézsűszögű szemcsékből álló keverékek öntésekor a szegregáció következtében spontán rétegződés jöhet létre. Ha a keverék összetevői különböző színűek, és az anyag két átlátszó és párhuzamos lemez közé ömlik, akkor a rétegek jól megfigyelhetőek. (Ez a mérés első része.) A jelenség részleteiről szintén [1] -ben lehet olvasni.
Mintázatképződés
A mérés második részében granulált anyag rázásakor kialakuló mintázatok vizsgálata a feladat. A rázás hatására, ha a maximális gyorsulás nagyobb, mint 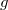 , a szemcsék egymáshoz képest is mozogni kezdenek, egymással és az edény falával ütköznek, az ütközések között pedig a gravitáció és a közegellenállás által meghatározott pályán repülnek.
, a szemcsék egymáshoz képest is mozogni kezdenek, egymással és az edény falával ütköznek, az ütközések között pedig a gravitáció és a közegellenállás által meghatározott pályán repülnek.
Egyetlen szabadeséssel függőlegesen mozgó és egy harmonikusan rezgő vízszintes lemezzel ütköző golyó mozgásának leírása se könnyű, hiszen a kialakuló mozgás nem periodikus. Nagyon nagy számú szemcse háromdimenziós mozgása (amit kis szemcseméret esetén a közegellenállás is jelentősen befolyásol) és (az általában szabálytalan alak miatt különösen) bonyolult ütközései teljesen kiszámíthatatlan mozgást sejtet.
Ezzel szemben a tapasztalat szerint a szemcsék rezgetésekor gyakran többé-kevésbé szabályos mintázatok keletkeznek. Miközben az egyes szemcsék mozgása hosszútávon valóban teljesen megjósolhatatlan, a sokaság kollektív mozgása mégis rendezettnek tűnik. A szemcsék tulajdonságainak, a rázott granulált anyag mennyiségének, valamint a rázási frekvenciának és amplitúdónak a függvényében nagyon változatos formák jelenhetnek meg: állóhullámok, négyszöges és hatszöges mintázatok, örvénylés, "fortyogás", dombképződés, stb.
Egy adott tulajdonságú és rétegvastagságú granulált anyag rezgetésekor kialakuló mintázatok a gyorsulás- frekvencia 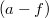 fázistérben szemléltethetőek. A mérés során használt szemcseméret esetén a 10-30 Hz-es frekvenciatartományban és a néhányszor
fázistérben szemléltethetőek. A mérés során használt szemcseméret esetén a 10-30 Hz-es frekvenciatartományban és a néhányszor 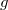 nagyságú gyorsulástartományban figyelhetőek meg mintázatok. (A rezgetés maximális gyorsulását
nagyságú gyorsulástartományban figyelhetőek meg mintázatok. (A rezgetés maximális gyorsulását 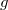 egységekben szokás mérni.) A vizsgálatot nehezíti, hogy egy adott frekvencia és gyorsulásérték esetén kialakuló mintázat függ a rendszer „előéletétől” is, azaz nem mindegy, hogy
egységekben szokás mérni.) A vizsgálatot nehezíti, hogy egy adott frekvencia és gyorsulásérték esetén kialakuló mintázat függ a rendszer „előéletétől” is, azaz nem mindegy, hogy  vagy
vagy  értéke növekszik-e vagy csökken.
értéke növekszik-e vagy csökken.
A granulált anyag rázásakor megfigyelhető egyik legérdekesebb jelenség az oszcillon. Az oszcillon egy hosszabb ideig stabilan megmaradó, az edény frekvenciájának felével rezgő lokalizált gerjesztés. Az oszcillon a rezgetés egy teljes periódusa alatt kúpszerű kiemelkedés, majd egy teljes perióduson keresztül kúpszerű bemélyedés. A leggyakrabban hivatkozott publikáció.[2] . A híres oszcillon kép megtalálható [1] -ben is.
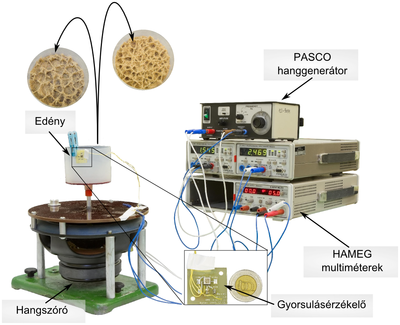
A mintázatképződés vizsgálatához használt eszközök
A rázógép függőleges tengelyű hengeres műanyag edényét egy hangszórómembrán hozza függőleges irányú rezgőmozgásba. A rezgés frekvenciája és amplitúdója a hangszórómembránra kapcsolt szinuszos jel frekvenciájától és nagyságától függ. A frekvencia 0 és 100 Hz között változtatható. Az amplitúdó maximum 7 mm lehet, és nagysága a rákapcsolt feszültség nagyságán kívül a frekvenciától és a terheléstől is függ. A rázógép meghajtására egy más mérésekből már ismert PASCO gyártmányú hanggenerátor szolgál. A hanggenerátor frekvenciáját egy erre a célra szolgáló kimeneten megjelenő, a frekvenciával arányos egyenfeszültség segítségével lehet mérni. A rázógép maximális gyorsulása a frekvenciából és az amplitúdóból meghatározható:
![\[a_{\text{max} }=A\omega^2=A(2\pi f)^2.\]](/images/math/2/6/8/26875de147e586e17d70b20f702a65e9.png)
Az amplitúdó azonban nehezen mérhető, ezért előnyös az edény gyorsulását egy gyorsulásérzékelő csippel közvetlenül mérni. Az ANALOG DEVICES által gyártott ADXL78 gyorsulásmérő csip a gyorsulás hatására elmozduló miniatürizált alkatrész elmozdulását – és ezen keresztül a gyorsulást – egy visszacsatolt kapacitásmérő híd segítségével méri. Az eszköz működéséhez 5 V tápfeszültség szükséges, amit egyenfeszültségű tápegység biztosít. A felépítés és a működés részletei megtalálhatóak az eszközismertetőben[3] . A teljes mechanika és elektronika egyetlen 5 mm x 5 mm x 2 mm-es IC-ben található. Az IC kimenetén 2,5 V 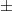 a gyorsulással arányos feszültség jelenik meg. (Az érzékelő természetesen nem tudja megkülönböztetni a tényleges gyorsulást és a Föld gravitációs terét, ezért a nullapont
a gyorsulással arányos feszültség jelenik meg. (Az érzékelő természetesen nem tudja megkülönböztetni a tényleges gyorsulást és a Föld gravitációs terét, ezért a nullapont 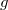 -nek megfelelő értékkel eltolódik.) A rázógépre egy
-nek megfelelő értékkel eltolódik.) A rázógépre egy 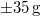 tartományban mérő eszköz (AD22279) van szerelve, ennek érzékenysége körülbelül
tartományban mérő eszköz (AD22279) van szerelve, ennek érzékenysége körülbelül 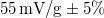 . Az eszköz pontos paramétereit kalibrálással meg kell határozni.
. Az eszköz pontos paramétereit kalibrálással meg kell határozni.
A gyorsulással lineárisan változó feszültséget oszcilloszkóp segítségével is lehet vizsgálni. Az oszcilloszkópról nem csak a maximális gyorsulás olvasható le, hanem a rezgés harmonikus jellege (és a frekvenciája) is ellenőrizhető.
Irodalom (ajánlott olvasmányok)
- Jánosi Imre: A homok titkai, Természet Világa 129 pp19-22 (1998. január), http://www.termeszetvilaga.hu/tv98/tv9801/sand.html
- P.B. Umbanhowar, F. Melo, H.L. Swinney: Localized excitations in a vertically vibrated granular leyer. Nature 382 p793 (1996)
- ANALOG DEVICES ADXL78, http://www.analog.com/static/imported-files/data_sheets/ADXL78.pdf
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
1. Rézsűszög és szegregáció vizsgálata.
Öntse bele először a három különböző homogén granulált anyag egyikét a párhuzamos falú edénybe, és mérje meg a rézsűszögét! Ismételje meg a kísérletet egészen lassú beöntéssel is! Öntse vissza az anyagot a dobozába, és tisztítsa ki az edényt! Végezze el a mérést a másik két homogén anyaggal is!
Az edény kitisztítása után töltse bele az egyik (mák-homok) keveréket! Mérje meg a rézsűszöget és a kialakuló rétegek vastagságát! Ismételje meg a kísérletet egészen lassú beöntéssel is! A mérés után öntse vissza a keveréket a dobozába és tisztítsa ki az edényt! Ismételje meg a mérést a másik keverékkel (sárga üveggyöngy - piros díszhomok) is!
- Gyors öntésnél a tölcsér áteresztőképessége szab határt. Lassú öntésnél az edény finom kocogtatásával lehet egyenletesen önteni az anyagot.
- A keverékek rázás hatására inkább szegregálódnak. A keveréshez használja a kiskanalat.
- A rézsüszög megállapításánál „illesszen egyenest” a vonalzóval a rézsűre, és olvassa le a vízszintes és függőleges tengelymetszeteket. A szög (és hibája) ebből számolható.
- A rétegvastagságról készítsen statisztikát!
- Ha van fényképezőgépe (mobiltelefonja), fényképezze le a rézsűket és a rétegződéseket.
2. Mintázatképződés vizsgálata.
Az állvány alján lévő csavarok segítségével vízszintezze be a rázóedényt!
- Az alja nem teljesen sík, így nem lehet „tökéletes” eredményt elérni.
Kapcsolja a hangszórót a hanggenerátorra. A hanggenerátor frekvenciáját az Állóhullámok megfeszített, rugalmas húrban mérésben megismert módon DC feszültségmérővel mérje.
Kalibrálja a gyorsulásmérőt!
- Kapcsoljon a gyorsulásmérő fekete és piros bemenetére 5 V tápfeszültséget.
- Figyeljen a polaritásra! A piros csatlakozót kell a pozitív feszültségre kapcsolni.
- Mérje a feszültséget a fekete és a kék kivezetés között egyenáramú (DC) feszültségmérővel.
- Az érzékelő lassú forgatásával keresse meg a gravitáció által okozott minimális és maximális „gyorsulásértéket”. (Az egyik
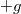 , a másik
, a másik 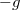 értékhez tartozik.) Ez alapján kalibrája a gyorsulásmérőt.
értékhez tartozik.) Ez alapján kalibrája a gyorsulásmérőt.
- Ezután csipesszel rögzítse a gyorsulásmérőt az edény falán.
- Figyeljen arra, hogy a gyorsulásmérő mérési iránya függőleges legyen!
- Ha a hanggenerátorral megrezgeti az edényt, akkor a gyorsulásmérő 10-30 Hz frekvenciával változó feszültségjelét a DC műszer nem tudja követni. Állítsa át a műszert AC üzemmódra. Ilyenkor a műszer a gyorsulásmérő által kiadott feszültségjel váltakozó komponensének effektív értékét méri.
- Hogyan határozható meg ezek alapján az edény maximális gyorsulása (gyorsulásamplitúdója)?
Öntsön kb. 1 mm vastagon homokot a rázógép edényébe! Vizsgálja az anyag viselkedését a 10-30 Hz frekvencia- és a 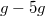 gyorsulástartományban. Állapítsa meg, hogy az egyes jellegzetes mintázatok milyen frekvencia- és gyorsulásértékeknél fordulnak elő.
gyorsulástartományban. Állapítsa meg, hogy az egyes jellegzetes mintázatok milyen frekvencia- és gyorsulásértékeknél fordulnak elő.
- A rezgés amplitúdóját semmiképp ne növelje annyira, hogy a rázóedény hozzáütődjön az alapzathoz!
- A jellegzetes mintázatokról készítsen fényképet!
Ábrázolja a mintázatok kialakulását az 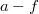 fázistérben!
fázistérben!
- A méréshez korábban 0,15 mm átmérőjű üveggyöngyöt használtunk, amivel sokkal szebb mintázatok alakultak ki. Sajnos a készlet néhány év alatt „elpattogott”, és egyelőre nem sikerült hasonló anyagot szerezni.
Vissza a Fizika laboratórium 1. tárgyoldalára.