Kinematika - 1.4.7
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Bacsi (vitalap | szerkesztései) 2013. szeptember 25., 14:41-kor történt szerkesztése után volt.
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika gyakorlat 1. |
| Gyakorlatok listája: |
| Mechanika - Mozgástan |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- (1.4.7) Egy síkban mozgó pontszerűnek tekinthető test sebességvektorát az alábbi összefüggés írja le:
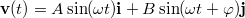 .
.
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
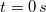 időpontban a test az
időpontban a test az 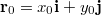 koordinátájú pontban tartózkodott!
koordinátájú pontban tartózkodott!
- b) Határozza meg a test gyorsulásvektorát az idő függvényében!
- c) Milyen pályán mozog a test, ha
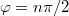 valamilyen
valamilyen  egész számmal?
egész számmal?
- a) Írja fel a tömegpont helyvektorát mint az idő függvényét, ha a
Megoldás
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.
![\[\mathbf{r}(t)=\mathbf{r}_{0}+\int_{0}^{t}\mathbf{v}(t')dt'=\left(x_{0}+\frac{A}{\omega}-\frac{A}{\omega}\cos(\omega t)\right)\mathbf{i} +\left( y_{0}+\frac{B}{\omega}\cos\varphi- \frac{B}{\omega}\cos(\omega t+\varphi)\right)\mathbf{j}\]](/images/math/f/6/2/f62220f95be66aa4732794d4b5e8a0a2.png)
- b) A gyorsulásvektor
![\[\mathbf{a}(t)=\frac{d\mathbf{v}}{dt}=A\omega\cos(\omega t)\mathbf{i} + B\omega\cos(\omega t+\varphi)\mathbf{j}\,.\]](/images/math/2/d/c/2dca3b96182c5367983d7b411e106adf.png)
- c) Vezessük be az
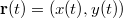 helyvektor komponensei helyett az változókat a rövidebb jelölés érdekében! Ez a transzformáció egy eltolás és egy nyújtás kombinációjának felel meg. A helyvektor komponenseinek időfüggése alapján
helyvektor komponensei helyett az változókat a rövidebb jelölés érdekében! Ez a transzformáció egy eltolás és egy nyújtás kombinációjának felel meg. A helyvektor komponenseinek időfüggése alapján![\[X(t)=\frac{\omega}{A}\left(x(t)-x_{0}-\frac{A}{\omega}\right)\qquad \mbox{és}\qquad Y(t)=\frac{\omega}{B}\left(y(t)-y_{0}-\frac{B}{\omega}\cos\varphi\right)\]](/images/math/d/3/1/d31b01ef48662a94fb9e74541ef84848.png) Az egyenletek átrendezhetők olyan formába, amelyben az időfüggést már csak
Az egyenletek átrendezhetők olyan formába, amelyben az időfüggést már csak![\[X(t)=-\cos(\omega t) \qquad \mbox{és} \qquad Y(t)=-\cos(\omega t)\cos\varphi + \sin(\omega t)\sin\varphi\,.\]](/images/math/7/b/e/7be0929b7f29b13d808553e3f9be8083.png)
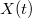 és
és 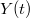 hordozzák. Ez az egyenlet határozza meg a test pályáját. Hogy pontosabban lássuk, hogy milyen pályáról van szó, vezesük be az
hordozzák. Ez az egyenlet határozza meg a test pályáját. Hogy pontosabban lássuk, hogy milyen pályáról van szó, vezesük be az![\[X(t)^2-2X(t)Y(t)\cos\varphi+Y(t)^{2}=\sin^{2}\varphi\]](/images/math/1/2/b/12b0e8c919c80307d50f6e572f359edf.png) változókat! Ez a transzformáció egy 45 fokos forgatásnak felel meg. Az új változókkal az
változókat! Ez a transzformáció egy 45 fokos forgatásnak felel meg. Az új változókkal az![\[U(t)=\frac{X(t)+Y(t)}{\sqrt{2}} \qquad \mbox{és} \qquad V(t)=\frac{X(t)-Y(t)}{\sqrt{2}}\]](/images/math/4/6/1/4616ed890868820441677907fcaa2572.png) egyenletre jutunk. Érdemes megvizsgálni az egyenletet különböző
egyenletre jutunk. Érdemes megvizsgálni az egyenletet különböző![\[U(t)^2(1-\cos\varphi)+V(t)^{2}(1+\cos\varphi)=\sin^{2}\varphi\]](/images/math/5/8/5/585b72effa956f3247e901e7980549a8.png)
 értékek esetén. Ha
értékek esetén. Ha 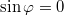 (ez lehetséges
(ez lehetséges 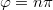 esetén, ahol
esetén, ahol  tetszőleges egész szám), akkor a pálya egyenlete egy egyenes menti harmonikus rezgőmozgást ír le. Ha
tetszőleges egész szám), akkor a pálya egyenlete egy egyenes menti harmonikus rezgőmozgást ír le. Ha 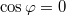 (ez lehetséges
(ez lehetséges 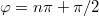 esetén), akkor a pálya egyenlete egy körmozgást ír le. A visszatranszformálás során azonban a valódi térbeli mozgásra csak akkor kapunk körmozgást, ha
esetén), akkor a pálya egyenlete egy körmozgást ír le. A visszatranszformálás során azonban a valódi térbeli mozgásra csak akkor kapunk körmozgást, ha 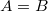 . Minden egyéb esetben a test pályája egy ellipszis.
. Minden egyéb esetben a test pályája egy ellipszis.
- a) A tömegpont helyvektora az alábbiak szerint határozható meg.