Mechanika - Függvényalak átalakítása
A Fizipedia wikiből
A lap korábbi változatát látod, amilyen Gombkoto (vitalap | szerkesztései) 2012. december 2., 15:41-kor történt szerkesztése után volt.
Feladat
- (*6.19.) Határozzuk meg az
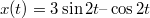 törvény szerint harmonikus rezgőmozgást végző tömegpont mozgásának amplitúdóját és periódusidejét!
törvény szerint harmonikus rezgőmozgást végző tömegpont mozgásának amplitúdóját és periódusidejét!
Megoldás
SI egységekben gondolkodva leolvasható, hogy a körfrekvencia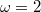 , így a periódusidő
, így a periódusidő 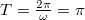 . Az amplitúdót akkor kaphatjuk meg, ha összevetjük a megadott függvényalakot egy
. Az amplitúdót akkor kaphatjuk meg, ha összevetjük a megadott függvényalakot egy ![\[x(t)=A\sin(2t+\phi)=A\sin(2t)cos{\phi}+A\cos(2t)sin{\phi}\]](/images/math/5/a/4/5a41e73b334e6e00587888fbbf4af0b8.png)
 -ra és
-ra és 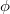 -re két egyenlet kapható:
-re két egyenlet kapható: ![\[A\cos{\phi}=3\]](/images/math/b/7/6/b76bb45605edc2248ecdd6e21cf2ef3c.png)
![\[A\sin{\phi}=-1\]](/images/math/d/8/f/d8f5b736e5e9c91d94fb05e9d266d4af.png)
![\[A^2=9+1=10,\]](/images/math/c/7/5/c754ad3f40fb4a1f985c9ca3cb62ae08.png)
Érdemes megjegyezni, hogy a szinusz és koszinusz függvény két lineárisan független alapmegoldás, azaz bázist alkotnak a megoldások kétdimenziós lineáris terében. Bizonyos értelemben még ortogonálisak is, így a (3,-1) együtthatókat derékszögü koordináták vektoraként is értelmezhetjük, melynek hossznégyzete pitagoraszi öszzegzéssel kapható, ezt láttuk fentebb.