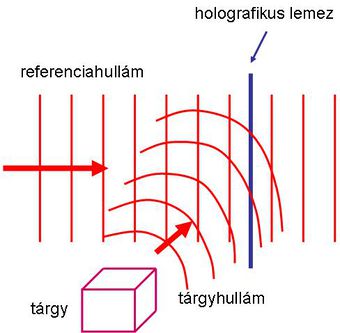
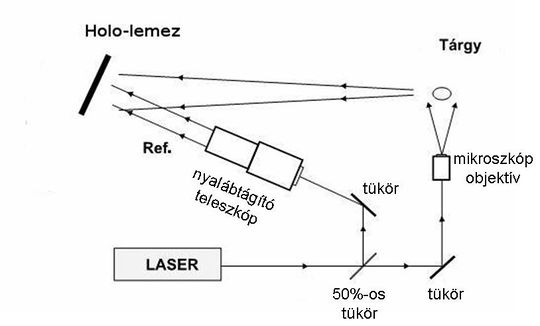
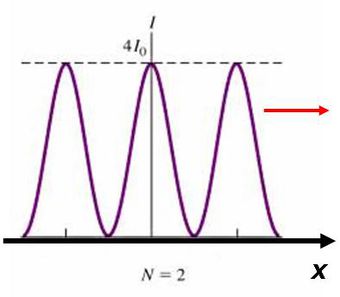
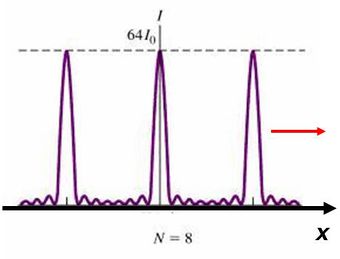
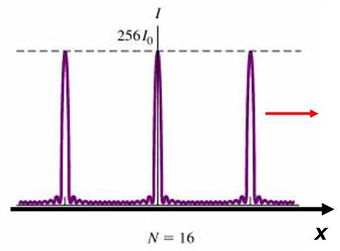
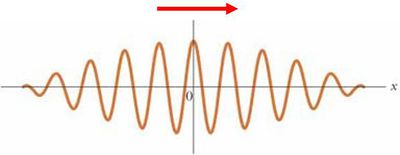
Optika és információ
Tartalomjegyzék
|
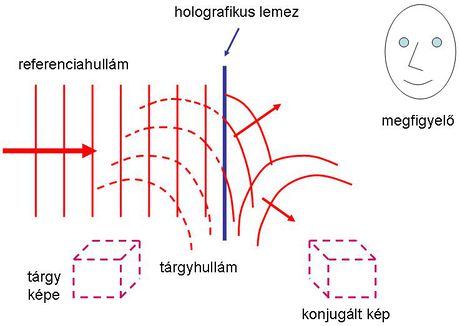
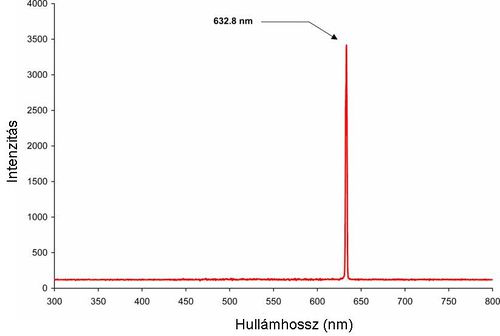
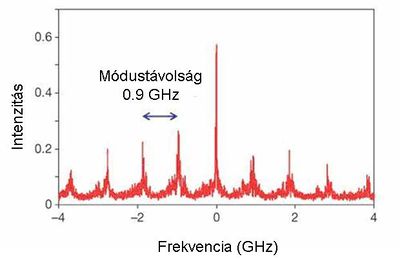
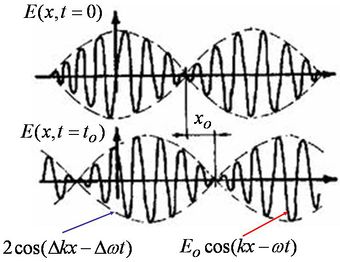
A fény szerepe a földi élet kialakulásában és az azt követő biológiai evolúcióban alapvető jelentőségű volt. Az emberi agy számára a "látás" közvetíti a legtöbb információt a világról. Gondoljunk arra, hogy csupán egy pillantást vetve a környezetünkre utólag milyen sok mindent fel tudunk idézni a látottakból. Az ember már igen korán megpróbálta a vizuális élményeit rögzíteni. A sziklarajzoktól a 3D moziig terjed a sikeres technikák vonulata. Tapasztalatból tudjuk, hogy egy fénykép információtartalma korlátozott, ugyanakkor holografikus módon sokkal több információt tudunk rögzíteni. Vajon mi akadályoz minket abban, hogy az oly sikeres litográfiás technikával a mainál sokkal nagyobb alkatrészsűrűséget érjünk el? Mitől függ egy digitális kamera felbontása?
Az informatikában igen fontos a gyors és nagymennyiségű adatforgalom. Az optikai szálak használata ugrásszerűen megnövelte az átviteli csatornák kapacitását. Az optika megjelent az adatrögzítés területén is. Vajon miként növelhető (egyáltalán növelhető-e tovább) a DVD lemezek adatsűrűsége? Ebben a fejezetben választ kapunk olyan érdekes kérdésekre is, mint például: hogyan lehet az, hogy egy távcsővel figyelve egy távoli tárgyat mégsem látjuk élesen annak részeit, annak ellenére, hogy a nagyítás megfelelő, vagy miért nem lehet egy optikai mikroszkóppal lefényképezni az atomokat?
Geometriai optika
A geometriai optika elvei
Az optika az elektromágneses hullámok elméletéhez tartozik, hiszen a látható tartomány (400 nm <  < 750 nm) az elektromágneses spektrum része. Különleges fontossággal bír ez a tudományterület, mert számos optikai mérést illetve berendezést fejlesztettek ki, amelyek segítségével információt kaphatunk – eredetileg esetleg szemmel nem, vagy nem jól látható – tárgyakról illetve folyamatokról, amelyek a minket körülvevő világ pontosabb leírását adhatják.
< 750 nm) az elektromágneses spektrum része. Különleges fontossággal bír ez a tudományterület, mert számos optikai mérést illetve berendezést fejlesztettek ki, amelyek segítségével információt kaphatunk – eredetileg esetleg szemmel nem, vagy nem jól látható – tárgyakról illetve folyamatokról, amelyek a minket körülvevő világ pontosabb leírását adhatják.
Az elektromágneses hullámok tárgyalása során tett megállapítások, valamint bizonyítások az optikában is jól használhatók. Ismételjük át ezeket:
| 1. | A síkhullám egy olyan transzverzális hullám, amelyben az elektromos és mágneses térerősség-komponensek merőlegesek egymásra és a hullám terjedési irányára. |
| 2. | A síkhullám szabad térben (vákuumban vagy levegőben, akadálymentes tartományban) egyenes vonalban terjed  fénysebességgel. fénysebességgel.
|
| 3. | Sík felületről úgy verődik vissza, hogy a beesési és a visszaverődési szög megegyezik. |
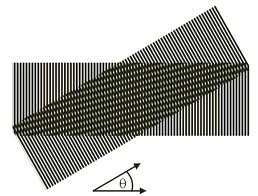
Az egyenes vonalú terjedésről, valamint a beesési és visszaverődési szög megegyezéséről csaknem mindenkinek vannak tapasztalatai; elég csak arra gondolni, hogy milyennek is látjuk a lézer-mutató nyalábját, amint egy sima felületről pl. egy sima asztallapról, üvegről, vagy egy tükörről verődik vissza (1.1.1.a és b ábra).
| 1.1.1.a ábra | 1.1.1.b ábra |
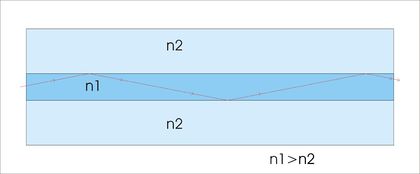
Idáig nem beszéltünk arról, hogy az EMH miként terjed különböző közegekben. Ezen jegyzet kereteibe nem fér be jó néhány igen érdekes és fontos eset, mint például az EMH és plazma kölcsönhatása, stb. Ezért most korlátozzuk vizsgálatainkat – ha "közegről" vagy "anyagról" van szó – dielektrikumokra. Mérések segítségével kimutatták, hogy a fény a dielektrikumokban (pl. a vízben) lassabban halad a vákuumbeli  fénysebességnél. Az anyagot jellemezhetjük a két sebességérték hányadosával, ez az anyagra jellemző törésmutató (egy adott hullámhosszon):
fénysebességnél. Az anyagot jellemezhetjük a két sebességérték hányadosával, ez az anyagra jellemző törésmutató (egy adott hullámhosszon):
![\[ n = \frac {c}{v} \]](/images/math/9/8/7/987ee51ae0a9f610f6c53bdce94eb008.png) |
(1.1.1) |
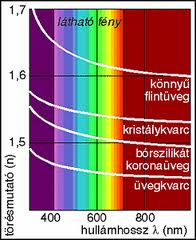
Igen sok mérés alapján megállapítható, hogy a legtöbb anyag törésmutatója függ a hullámhossztól; mint az az 1.1.2. ábrán is látható.
| 1.1.2 ábra |
Az előzőekből következik, hogy a vákuumban eredetileg  hullámhosszúságú síkhullám hullámhossza – minthogy a fény frekvenciája nem változik – a dielektrikumban:
hullámhosszúságú síkhullám hullámhossza – minthogy a fény frekvenciája nem változik – a dielektrikumban:
![\[ \lambda' = v T = \frac {c}{n}T = \frac{\lambda}{n} \]](/images/math/f/3/3/f33b6d89baba3240ec8a0c08b6b9a7f3.png) |
(1.1.2) |
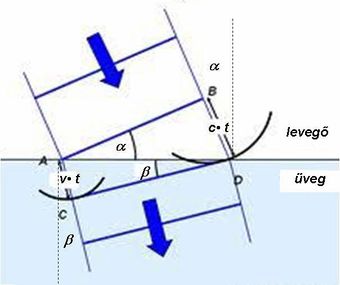
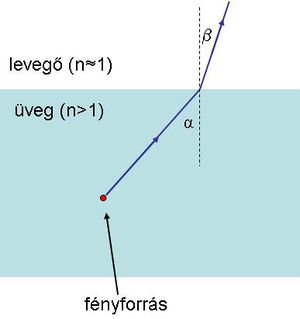
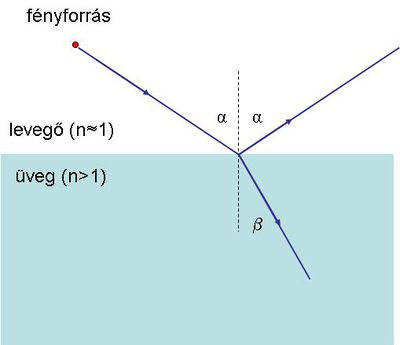
Ezután megvizsgáljuk, hogy miként is törik meg a fény, ha vákuumból (vagy levegőből) valamely dielektrikumba lép be. Tekintsük a következő ábrát, amelynek alapján megmagyarázhatjuk a fénytörés jelenségét a Huygens-elv felhasználásával.
| 1.1.3 ábra |
Az 1.1.3 ábrán látható, hogy a felső, levegőt tartalmazó tartományból érkező síkhullám 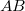 hullámfrontja miként változtatja meg terjedési irányát. A beeső síkhullám terjedési iránya
hullámfrontja miként változtatja meg terjedési irányát. A beeső síkhullám terjedési iránya  szöget zár be a felületi normálissal. Amint a síkhullám
szöget zár be a felületi normálissal. Amint a síkhullám  pontot tartalmazó része eléri a dielektrikumot, akkor ez a rész (az egyszerűség kedvéért az
pontot tartalmazó része eléri a dielektrikumot, akkor ez a rész (az egyszerűség kedvéért az  pont) Huygens-elvéből következően a dielektrikumban maga is egy hullámforrás lesz, azaz egy gömbhullám kiindulópontja. Amíg
pont) Huygens-elvéből következően a dielektrikumban maga is egy hullámforrás lesz, azaz egy gömbhullám kiindulópontja. Amíg  időtartam alatt a levegőben a hullámfront a
időtartam alatt a levegőben a hullámfront a  pontból eléri a közeghatárt, ugyanazon
pontból eléri a közeghatárt, ugyanazon  idő alatt az
idő alatt az  pontból kiinduló gömbhullám sugara
pontból kiinduló gömbhullám sugara 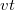 értékre növekszik. Ekkor a gömbhullámok alkotta hullámfront – az ábrán a
értékre növekszik. Ekkor a gömbhullámok alkotta hullámfront – az ábrán a 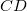 szakasz – meghatározza a síkhullám terjedési irányát a dielektrikumban; ez azt jelenti, hogy a hullámterjedés iránya
szakasz – meghatározza a síkhullám terjedési irányát a dielektrikumban; ez azt jelenti, hogy a hullámterjedés iránya  szöget zár be a felületi normálissal. Az ábráról leolvasható:
szöget zár be a felületi normálissal. Az ábráról leolvasható:
![\[ vt = AD sin(\beta) \qquad {\rm \acute{e}s} \qquad ct = AD sin(\alpha) \]](/images/math/6/f/f/6ffef834d66b9a5d6e25c2b655f1b1a9.png) |
(1.1.3) |
Ebből következik – a 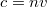 felhasználásával – a Schnellius-Descartes törvény:
felhasználásával – a Schnellius-Descartes törvény:
![\[ n = \frac {sin \alpha}{sin \beta} \]](/images/math/f/5/6/f5609b66e75262b49e8afd78d8b4e0ad.png) |
(1.1.4) |
Könnyű belátni, hogy amennyiben a fény nem levegőből vagy vákuumból érkezik a határfelülethez, hanem egy másik dielektrikumból, akkor a Schnellius-Descartes törvény általános alakja:
![\[ n_1 sin \alpha_1 = n_2 sin \alpha_2 \]](/images/math/1/7/8/1788f09980eb8528aba6c23de801894a.png) |
(1.1.5) |
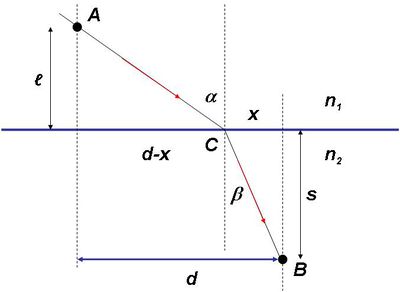
A most bemutatott – és többek által már a középiskolában tanult – törvénynek van egy fontos következménye. Ennek szemléltetésére tekintsük a következő ábrát!
| 1.1.4 ábra |
A fény az  pontból indulva a
pontból indulva a  ponton keresztül (ott megtörve) halad a
ponton keresztül (ott megtörve) halad a  pontba. A felső régióban
pontba. A felső régióban 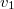 , míg az alsóban
, míg az alsóban 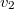 sebességgel halad. Most egy kis időre felejtsük el a törési törvényt! Kérdés, hogy
sebességgel halad. Most egy kis időre felejtsük el a törési törvényt! Kérdés, hogy  milyen értékénél ér a fénysugár a legrövidebb idő alatt az
milyen értékénél ér a fénysugár a legrövidebb idő alatt az  pontból a
pontból a  -be? A fény az
-be? A fény az 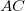 távolságot
távolságot 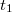 , míg a
, míg a 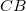 távolságot
távolságot 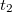 időtartam alatt teszi meg, azaz:
időtartam alatt teszi meg, azaz:
![\[ t_1 = \frac {AC}{v_1} \qquad {\rm \acute{e}s} \qquad t_2 = \frac {CB}{v_2} \]](/images/math/9/3/1/9317921b0a523a76d29e04bfa2d5c3bc.png) |
(1.1.6) |
vagyis:
![\[ t_1 = \frac {\sqrt{\ell^2 + (d-x)^2}}{v_1} \qquad {\rm \acute{e}s} \qquad t_2 = \frac {\sqrt{s^2 + x^2}}{v_2} \]](/images/math/9/a/6/9a68199c8b9b3f6c8912522142656107.png) |
(1.1.7) |
A teljes  időtartam tehát ezek szerint
időtartam tehát ezek szerint  -től függ:
-től függ:
![\[ t = \frac {\sqrt{\ell^2 + (d-x)^2}}{v_1} + \frac {\sqrt{s^2 + x^2}}{v_2} \]](/images/math/a/1/e/a1e45fa558da8792355b92c17781df47.png) |
(1.1.8) |
Azt, hogy mely  érték mellett lesz a
érték mellett lesz a  minimális, megkaphatjuk az
minimális, megkaphatjuk az  szerinti deriválással:
szerinti deriválással:
![\[ \frac {dt}{dx} = \frac {x-d}{v_1 \sqrt{\ell^2 + (d-x)^2}} + \frac {x}{v_2 \sqrt{s^2 + x^2}}= 0 \]](/images/math/0/d/a/0dafaba367670faf180f5c3b7d084d48.png) |
(1.1.9) |
Az 1.1.4 ábráról leolvasható, hogy:
![\[ sin \alpha = \frac {d-x}{\sqrt{\ell^2 + (d-x)^2}} \qquad {\rm \acute{e}s} \qquad sin \beta = \frac {x}{\sqrt{s^2 + x^2}} \]](/images/math/d/9/3/d93d1d87993bb709696b23c47d6a20ef.png) |
(1.1.10) |
Ez utóbbi két összefüggés felhasználásával 1.1.9 a következő alakba írható:
![\[ \frac {sin\alpha}{v_1} = \frac {sin\beta}{v_2} \]](/images/math/9/f/0/9f0fb78773c5ed37bddaf1016f459b33.png) |
(1.1.11) |
Amennyiben a terjedési sebességeket a törésmutatókkal adjuk meg, azaz 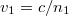 és
és 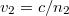 , akkor az 1.1.11 formulát megkaphatjuk a következő alakban:
, akkor az 1.1.11 formulát megkaphatjuk a következő alakban:
![\[ n_1 sin \alpha = n_2 sin \beta \]](/images/math/d/f/7/df725de16bb15e12c2e37e731a690e04.png) |
(1.1.12) |
Ez pedig éppen a most megismert Schnellius-Descartes törvény általános alakja. Megállapíthatjuk tehát, hogy a fény olyan pályán terjed az egyik pontból a másikba, amelyre az jellemző, hogy a hullámterjedéshez szükséges időtartam a legrövidebb. Ez az elv természetesen általános esetben is megfogalmazható. Amennyiben a közeg törésmutatója helyfüggő, azaz 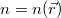 , akkor az előbb szóban megfogalmazott elv matematikai alakban is megadható:
, akkor az előbb szóban megfogalmazott elv matematikai alakban is megadható:
![\[ \int\limits_a^b dt = \int\limits_a^b \frac{1}{v} ds = \int\limits_a^b \frac{n(\vec r)}{c} ds = min. \]](/images/math/6/e/8/6e8956bfe80747a07f841426b0157da5.png) |
(1.1.13) |
Mivel a fénysebesség állandó, így elhagyható és kapjuk a Fermat-elvet:
![\[ \int\limits_a^b n(\vec r) ds = min. \]](/images/math/5/c/e/5ce696ca495142ac0d2a034343073701.png) |
(1.1.14) |
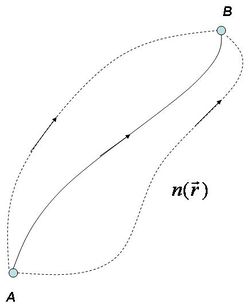
Ennek a formulának a következő az olvasata: az összes olyan pálya közül, amelyen a fénynyaláb az  pontból a
pontból a  pontba juthat, az 1.1.14 feltétel által kiválasztott útvonalon fog a fény terjedni. (A fizikailag megvalósuló, az 1.1.14-ből meghatározható fényutat folytonos vonallal, míg a virtuális pályákat szaggatott vonallal jelöltük a következő ábrán.) Itt csak megjegyezzük, hogy a mechanika és az elektrodinamika törvényei is megfogalmazhatók variációs elv segítségével.
pontba juthat, az 1.1.14 feltétel által kiválasztott útvonalon fog a fény terjedni. (A fizikailag megvalósuló, az 1.1.14-ből meghatározható fényutat folytonos vonallal, míg a virtuális pályákat szaggatott vonallal jelöltük a következő ábrán.) Itt csak megjegyezzük, hogy a mechanika és az elektrodinamika törvényei is megfogalmazhatók variációs elv segítségével.
| 1.1.5 ábra |
Az említett elv segítségével, az elemi geometria alkalmazásával könnyen bizonyítható például, hogy reflexiónál a beesési szög megegyezik a visszaverődési szöggel.
A Fermat-elv alkalmazásával meghatározhatjuk például egy fénynyaláb pályáját olyan esetekben is, amikor például a törésmutató folytonosan változik.
A geometriai optika törvényei fénysugarakra és azok terjedésére vonatkoznak. Az elektromágneses hullámokról tanultak a  határátmenetben visszaadják a geometriai optika szabályait. Az előzőekben bemutatott példák alapján a geometriai optika törvényeit a következőkben foglalhatjuk össze:
határátmenetben visszaadják a geometriai optika szabályait. Az előzőekben bemutatott példák alapján a geometriai optika törvényeit a következőkben foglalhatjuk össze:
| 1. | A fény(sugár) egyenes vonalban terjed. |
| 2. | Különböző közegek határfelületein a fénysugár egy része reflektálódik, más része fénytörést szenvedve behatol a másik közegbe. |
| 3. | A szuperpozíció elvéből következően két vagy több fénynyaláb áthaladhat a tér egy pontján (tartományán) anélkül, hogy zavarnák egymást. |
| 4. | Ha a fénysugár az egyik pontból a másikba egy meghatározott pályán halad, akkor visszafelé a második pontból az eredetibe ugyanazon az úton terjed a fény. |
A geometriai optika törvényeinek alkalmazásával tárgyalhatjuk gömbtükrök és lencsék, illetve lencserendszerek, stb. leképezési tulajdonságait.
Képalkotás gömbtükörrel
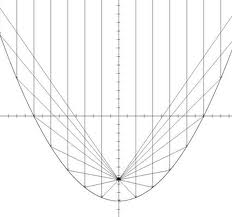
A parabolatükörre az optikai tengellyel párhuzamosan érkező fénysugarak - mint az az elemi geometriából ismert – a parabola fókuszpontján mennek át (1.2.1 ábra).
| 1.2.1 ábra |
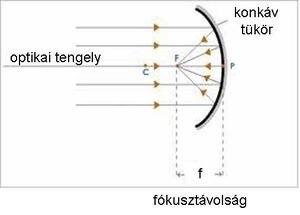
Hasonló jelenséget észlelhetünk, ha egy tükröző, homorú gömbfelülettel szeretnénk a párhuzamosan érkező fénysugarakat összegyűjteni, fókuszálni (1.2.2 ábra).
| 1.2.2 ábra |
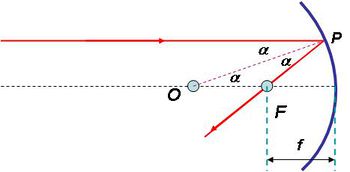
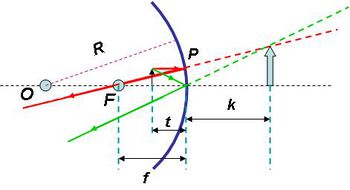
Vizsgáljuk meg ezt a fókuszálási jelenséget kissé részletesebben! Ehhez tekintsük a következő ábrát!
| 1.2.3 ábra |
Az optikai tengellyel (szaggatott vonal) párhuzamosan érkező fénysugár az  görbületi sugarú gömbtükörről a
görbületi sugarú gömbtükörről a  pontban reflektálódik, majd az
pontban reflektálódik, majd az  fókuszponton megy át. A beesési és a visszaverődési szög megegyezik. Ez azt jelenti, hogy a fénysugár az
fókuszponton megy át. A beesési és a visszaverődési szög megegyezik. Ez azt jelenti, hogy a fénysugár az 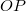 szakasszal ugyanakkora szöget zár be, mint az
szakasszal ugyanakkora szöget zár be, mint az 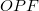 szög, ez viszont megegyezik a
szög, ez viszont megegyezik a 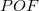 szöggel, tehát az
szöggel, tehát az 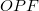 egy egyenlő szárú háromszög, vagyis
egy egyenlő szárú háromszög, vagyis 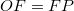 . Az ábráról leolvasható, hogy
. Az ábráról leolvasható, hogy 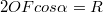 . Amennyiben
. Amennyiben 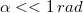 és ennek következtében
és ennek következtében 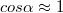 , akkor ebből már következik, hogy
, akkor ebből már következik, hogy 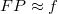 , azaz a gömbtükör fókusztávolsága:
, azaz a gömbtükör fókusztávolsága:
![\[ f \approx \frac {R}{2} \]](/images/math/6/3/e/63ea5791977f39a4a185ef6791319e5a.png) |
(1.2.1) |
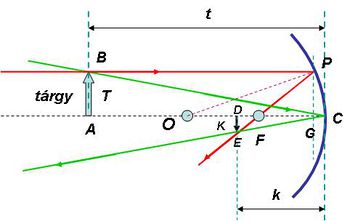
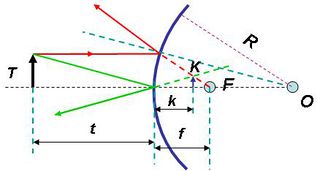
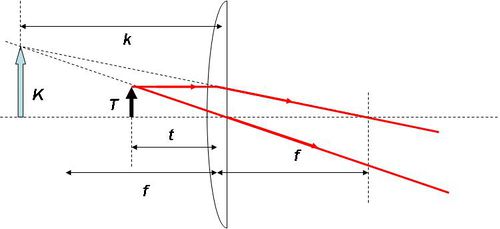
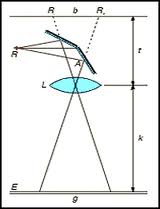
Egy gömbtükörrel azonban nem csak a végtelenből (gyakorlatilag a tükör görbületi sugaránál sokkal nagyobb távolságból) érkező fénysugarak fókuszálása oldható meg, hanem egy tárgy leképezése is. A képalkotás folyamatának megértésében segíthet a következő ábra.
| 1.2.4 ábra |
A tükörtől  távolságban lévő,
távolságban lévő,  magasságú
magasságú 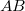 tárgy
tárgy  pontjából kiinduló két jellegzetes fénysugár közül az egyik (pirossal jelölt) az optikai tengellyel párhuzamosan halad, majd a tükörről visszaverődve áthalad a fókuszponton. A másik (zöld vonallal jelölt) fénysugár a tükör közepén, a
pontjából kiinduló két jellegzetes fénysugár közül az egyik (pirossal jelölt) az optikai tengellyel párhuzamosan halad, majd a tükörről visszaverődve áthalad a fókuszponton. A másik (zöld vonallal jelölt) fénysugár a tükör közepén, a  pontban reflektálódik. A két fénysugár az
pontban reflektálódik. A két fénysugár az  pontban metszi egymást, azaz a tárgy
pontban metszi egymást, azaz a tárgy  pontját a tükör az
pontját a tükör az  pontba képezi le. Minthogy a tárgy méretére – azon kívül, hogy az
pontba képezi le. Minthogy a tárgy méretére – azon kívül, hogy az 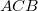 szög legyen kicsi ( << 1 rad) – semmilyen megkötést nem tettünk, így nyugodtan mondhatjuk, hogy az
szög legyen kicsi ( << 1 rad) – semmilyen megkötést nem tettünk, így nyugodtan mondhatjuk, hogy az  pontban lévő tárgyat a tükör az attól
pontban lévő tárgyat a tükör az attól  távolságban lévő,
távolságban lévő,  méretű
méretű 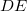 -be képezi le. A leképezés azt jelenti, hogy a tükörtől
-be képezi le. A leképezés azt jelenti, hogy a tükörtől  távolságban lévő ernyőn a tárgy – leképező optika, vagy lencse nélkül is látható - valódi képe jelenik meg, azaz a tárgy egy pontjának képe ideális esetben egy képpont lesz, nem pedig egy fényfolt (ekkor homályos képet kapunk). A leképezés törvényét a geometria módszereinek alkalmazásával adhatjuk meg. Az
távolságban lévő ernyőn a tárgy – leképező optika, vagy lencse nélkül is látható - valódi képe jelenik meg, azaz a tárgy egy pontjának képe ideális esetben egy képpont lesz, nem pedig egy fényfolt (ekkor homályos képet kapunk). A leképezés törvényét a geometria módszereinek alkalmazásával adhatjuk meg. Az 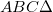 hasonló a
hasonló a 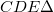 -höz, vagyis:
-höz, vagyis:
![\[ \frac {K}{T} = \frac {k}{t} \]](/images/math/3/d/1/3d191e49d7b46f0439a01ea85541b5f5.png) |
(1.2.2) |
Hasonlóképpen felhasználhatjuk azt is, hogy az 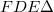 hasonló a
hasonló a 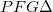 -höz (A
-höz (A 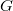 pont az optikai tengely és a
pont az optikai tengely és a  pontban a tengelyre állított merőleges egyenes metszéspontja. Kis szögeket feltételezve a
pontban a tengelyre állított merőleges egyenes metszéspontja. Kis szögeket feltételezve a 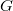 és a
és a  pont csaknem egybeesik.) Ebből következik, hogy:
pont csaknem egybeesik.) Ebből következik, hogy:
![\[ \frac {K}{T} = \frac {k-f}{f} \]](/images/math/a/2/f/a2f1e4f823123b947292f321c3a643ba.png) |
(1.2.3) |
Az 1.2.2 és 1.2.3 jobb oldalát egyenlővé téve és a kapott egyenletet átrendezve kapjuk az 1/f szabályt:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f} \]](/images/math/5/d/8/5d859b74de084110d14edc1fb0a417a9.png) |
(1.2.4) |
Az 1.2.4 – ből adódik (és az 1.2.4 ábrán is látszik), hogy ha a 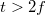 , akkor a kép a tükörtől mérve a fókuszpont és a gömb középpontja közé esik:
, akkor a kép a tükörtől mérve a fókuszpont és a gömb középpontja közé esik: 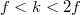 . Ebben az esetben a tárgynak egy valódi, fordított állású, kicsinyített képe jelenik meg. A nagyítás mértékét a kép és a tárgy méretének arányával, vagy a képtávolság és a tárgytávolság hányadosával adhatjuk meg:
. Ebben az esetben a tárgynak egy valódi, fordított állású, kicsinyített képe jelenik meg. A nagyítás mértékét a kép és a tárgy méretének arányával, vagy a képtávolság és a tárgytávolság hányadosával adhatjuk meg:
![\[ N = \frac {K}{T} = \frac {k}{t} \]](/images/math/a/6/2/a62d7060d483ee3e83ebd1b925708cc2.png) |
(1.2.5) |
A gömbtükör előzőekben tárgyalt leképezései esetében a nagyítást egyértelműen meghatározza a tárgytávolság; az 1.2.4 - ből kifejezve  – t és behelyettesítve 1.2.5 - be kapjuk:
– t és behelyettesítve 1.2.5 - be kapjuk:
![\[ N = \frac {f}{t-f} \]](/images/math/8/c/9/8c95d9239b4375535b3ccd02355000f0.png) |
(1.2.6) |
A fénysugarak megfordíthatóságának elvéből következik, hogy ha 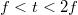 , akkor
, akkor 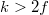 , és a tárgy valódi, fordított állású, nagyított képe jelenik meg. Amennyiben
, és a tárgy valódi, fordított állású, nagyított képe jelenik meg. Amennyiben 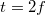 , akkor természetesen
, akkor természetesen 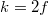 , és
, és 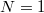 . Már csak azt az esetet nem néztük meg, hogy miként valósul meg a képalkotás, ha
. Már csak azt az esetet nem néztük meg, hogy miként valósul meg a képalkotás, ha 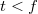 . Ehhez tekintsük a következő ábrát:
. Ehhez tekintsük a következő ábrát:
| 1.2.5 ábra |
A háromszögek hasonlóságát felhasználva, az előzőekben bemutatott módon, könnyen megkaphatjuk a leképezési törvényt a borotválkozó tükör esetén is:
![\[ \frac {1}{t} - \frac {1}{k} = \frac {1}{f} \]](/images/math/f/8/7/f8773ab926afaebe97041f0dd7b4ed13.png) |
(1.2.7) |
Az 1.2.5 ábrán látható, hogy miként lehet megszerkeszteni a tárgy (fekete nyíl) képét (kék nyíl) a tárgy egy pontjából kiinduló két jellegzetes sugárral. Ebben az esetben a tárgy egyenes állású virtuális képe (ernyőn fel nem fogható) áll elő, hiszen a tárgy egy pontjából kiinduló fénysugarak a tükörről visszaverődve széttartók (divergensek) lesznek. Borotválkozás (vagy szépítkezés) közben a képet csak azért látjuk, mert a szemünk lencséje a képet, mint egy másodlagos tárgyat, leképezi a retinánkra.
| 1.2.6.a ábra | 1.2.6.b ábra |
A nagyítás az 1.2.7 felhasználásával:
![\[ N = \frac {f}{f-t} \]](/images/math/3/7/2/372466c35d2c6bdd9a0e56b7421eb587.png) |
(1.2.8) |
Egy gömbtükörnek természetesen a domború oldala is használható tükörként; lásd a következő két képet.
| 1.2.7.a ábra | 1.2.7.b ábra |
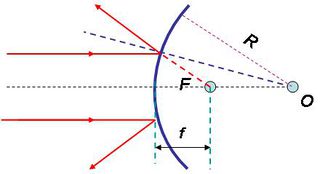
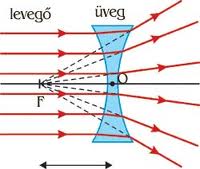
A következő ábra alapján könnyen belátható, hogy a domború gömbtükörre érkező, az optikai tengellyel párhuzamos fénysugarak a reflexió után széttartóvá válnak, és úgy terjednek, mintha az  fókuszpontból indultak volna.
fókuszpontból indultak volna.
| 1.2.8 ábra |
Kis szögek esetén itt is használhatjuk az 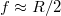 közelítést. A leképezést megszerkeszthetjük az 1.2.9 ábrán látható módon:
közelítést. A leképezést megszerkeszthetjük az 1.2.9 ábrán látható módon:
| 1.2.9 ábra |
Az előzőekben már bemutatott hasonló háromszögek módszerével kapjuk az 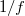 szabály domború gömbtükörre alkalmazható alakját:
szabály domború gömbtükörre alkalmazható alakját:
![\[ \frac {1}{t} - \frac {1}{k} = -\frac {1}{f} \]](/images/math/d/2/c/d2cc3e3c3f3a6462f07a9f36e7aa2e51.png) |
(1.2.9) |
Az 1.2.9 segítségével bizonyítható és az 1.2.9 ábráról is leolvasható, hogy domború (konvex) gömbtükör használatával egyenes állású, virtuális képet kapunk. A legtöbb esetben egy ilyen tükör erősen torzított képet ad, mégis széleskörűen alkalmazzák a közlekedési eszközökön visszapillantó tükörként, illetve a közlekedést segítendő útkereszteződésekben, mert bár a kép torz, viszont nagy látószögű.
| 1.2.10.a ábra | 1.2.10.b ábra |
A most bemutatott, gömbtükörrel megvalósítható leképezések esetében felállíthatunk egy gyakorlati szabályt: amennyiben a kép vagy (és) a fókuszpont a tükör "másik oldalán" van, akkor  vagy (és)
vagy (és)  helyett
helyett 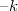 -t vagy (és)
-t vagy (és) 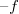 –t kell behelyettesíteni az
–t kell behelyettesíteni az 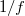 formulába.
formulába.
Lencse és lencserendszer képalkotása
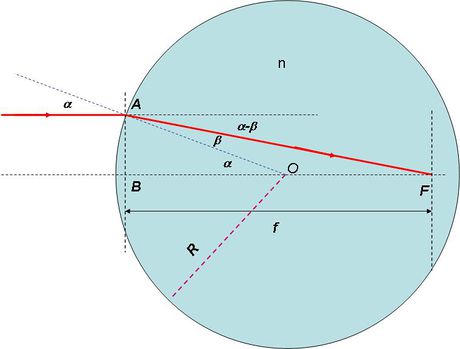
Mielőtt lencsékkel és lencsékből összerakható leképező eszközökkel foglalkoznánk, először tekintsünk egy egyszerű modellt. Vizsgáljuk meg, hogy mi történik, ha egy  törésmutatójú,
törésmutatójú,  sugarú, átlátszó dielektrikum gömbre síkhullám esik. A síkhullám terjedését egy fénysugár nyomon követésével modellezzük:
sugarú, átlátszó dielektrikum gömbre síkhullám esik. A síkhullám terjedését egy fénysugár nyomon követésével modellezzük:
| 1.3.1 ábra |
A beeső fénysugár az  pontban éri el a gömbfelszínt, majd ott megtörik, és az optikai tengelyt az
pontban éri el a gömbfelszínt, majd ott megtörik, és az optikai tengelyt az  fókuszpontban metszi. Próbáljuk most megadni a fókusztávolságot a sugárral és a törésmutatóval! Vizsgálatainkat kis szögekre korlátozzuk, vagyis
fókuszpontban metszi. Próbáljuk most megadni a fókusztávolságot a sugárral és a törésmutatóval! Vizsgálatainkat kis szögekre korlátozzuk, vagyis 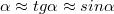 és
és 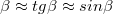 . Az
. Az  fókusztávolság meghatározásához induljunk ki a következő összefüggésből:
fókusztávolság meghatározásához induljunk ki a következő összefüggésből:
![\[ \frac {AB}{f}= tg(\alpha - \beta) \approx \alpha - \beta \]](/images/math/6/1/3/6132b4ea96f201039ef8bd22172820ed.png) |
(1.3.1) |
A fénytörési törvény megadja  és
és  hányadosát:
hányadosát:
![\[ \frac {sin \alpha}{sin \beta}= n \approx \frac{\alpha}{\beta} \]](/images/math/8/9/5/895f15911c23082c45967a1d04e6794f.png) |
(1.3.2) |
Az 1.3.1 és 1.3.2 formulákból kapjuk az 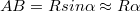 közelítés (az 1.3.1 ábráról leolvasható) felhasználásával a fókusztávolságot:
közelítés (az 1.3.1 ábráról leolvasható) felhasználásával a fókusztávolságot:
![\[ f= \frac{Rn}{n-1} \]](/images/math/8/6/8/8688532528bca10a59494e0ebd925568.png) |
(1.3.3) |
Az  sugarú,
sugarú,  törésmutatójú dielektrikum gömb, mint a legegyszerűbb leképező eszköz a természetben is megtalálható. A híradásokban néha hallani, hogy az erdőtüzet esetleg a napfényt fókuszáló vízcsepp okozhatta. Az 1.3.2 ábrán jól látszik egyrészt, hogy a vízcsepp, ha nem is egy pontba (nem tökéletes gömb), de egy kisebb területre fókuszálja a fényt; másrészt pedig mint egy nagyító (lencse) "működik".
törésmutatójú dielektrikum gömb, mint a legegyszerűbb leképező eszköz a természetben is megtalálható. A híradásokban néha hallani, hogy az erdőtüzet esetleg a napfényt fókuszáló vízcsepp okozhatta. Az 1.3.2 ábrán jól látszik egyrészt, hogy a vízcsepp, ha nem is egy pontba (nem tökéletes gömb), de egy kisebb területre fókuszálja a fényt; másrészt pedig mint egy nagyító (lencse) "működik".
| 1.3.2 ábra |
(Az evolúció ellenzői - Darwin elméletének tarthatatlanságát bizonyítandó - a szem összetett szerkezetét (is) felemlegették. Érvelésük lényege az volt, hogy a fajok folyamatos változása során nem alakulhatott ki egy ilyen bonyolult optikai eszköz lépésről lépésre. Az előzőekben bemutatott modell jól mutatja, hogy egy - a környezetétől eltérő törésmutatójú - dielektrikum gömb is alkalmas optikai leképezésre, csakúgy, mint a fényképezőgép őse, a camera obscura. Mindkét optikai jelenség részét képezi a szem evolúcióját bizonyító magyarázatoknak.)
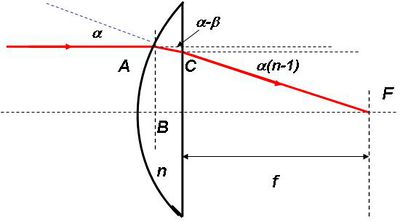
Ezután képzeljük el, hogy lencsét készítünk a gömb alakú dielektrikumból úgy, hogy annak nagy részét leválasztjuk róla (1.3.3 ábra).
| 1.3.3 ábra |
Most határozzuk meg a lencse fókusztávolságát! Az előző modell vizsgálatából már tudjuk, hogy a dielektrikumon belül a fénysugár az optikai tengellyel 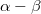 szöget zár be, de ugyanekkora szöget zár be a lencsét határoló sík felületi normálisával is. A lencséből kilépve a fénysugár ismét törést szenved (a
szöget zár be, de ugyanekkora szöget zár be a lencsét határoló sík felületi normálisával is. A lencséből kilépve a fénysugár ismét törést szenved (a  pontban); ekkor újra felírhatjuk a Schnellius-Descartes törési törvényt:
pontban); ekkor újra felírhatjuk a Schnellius-Descartes törési törvényt:
![\[ \frac {sin\gamma}{sin(\alpha - \beta)} \approx \frac {\gamma}{\alpha - \beta} \approx n \quad \Longrightarrow \quad \gamma \approx n (\alpha - \beta) \approx n(\alpha - \frac {\alpha}{n})\approx \alpha (n-1) \]](/images/math/a/8/b/a8b871d19ce500f0d88648bc471eb282.png) |
(1.3.4) |
ahol a kilépő nyaláb  szöget (ezt külön nem jelöltük az ábrán) zár be az optikai tengellyel. A lencséről feltesszük, hogy annyira vékony, hogy a vastagságából adódó eltolással nem kell foglalkozni. Ekkor a fókusztávolság így számítható:
szöget (ezt külön nem jelöltük az ábrán) zár be az optikai tengellyel. A lencséről feltesszük, hogy annyira vékony, hogy a vastagságából adódó eltolással nem kell foglalkozni. Ekkor a fókusztávolság így számítható:
![\[ f \approx \frac {AB}{\alpha (n-1)} \approx \frac {R\alpha}{\alpha (n-1)} \approx \frac {R}{n-1} \]](/images/math/0/9/4/0942a89d796eca5b9ae12034c88312dd.png) |
(1.3.5) |
Ebből már meghatározhatjuk, hogy hány dioptriás egy vékony sík-domború lencse; a dioptria-szám a fókusztávolság reciproka:
![\[ D = \frac {1}{f}=(n-1)\frac {1}{R} \]](/images/math/c/4/0/c40cc8938279f6a01e437f608fdfe9f1.png) |
(1.3.6) |
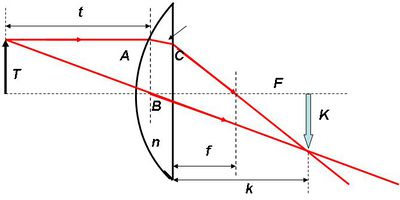
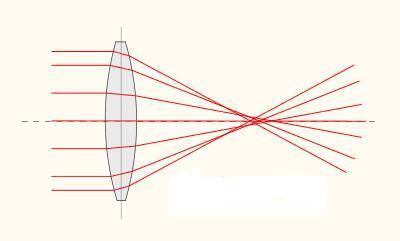
A jellegzetes fénysugarak által megszerkeszthető leképezés segítségével felírható a lencse leképezési törvénye. A tárgy egy pontjából kiinduló, az optikai tengellyel párhuzamosan haladó fénynyaláb a lencse másik oldalán átmegy a fókuszponton. A lencse közepén átmenő fénysugár pedig nem szenved törést (úgy tekinthetjük, mintha egy vékony plánparalell lemezen menne át).
| 1.3.4 ábra |
A lencse vastagságával nem törődve felírhatók a hasonló háromszögek közötti arányok. Könnyű belátni, hogy egy ilyen lencse esetén is leírható a leképezés az 1/f szabály alkalmazásával:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f} \]](/images/math/5/d/8/5d859b74de084110d14edc1fb0a417a9.png) |
(1.3.7) |
Itt most nem diszkutáljuk a különböző eseteket, de kitérünk a nagyító (lupe) esetére. Amennyiben a tárgytávolság kisebb a fókusztávolságnál, akkor is megszerkeszthetjük az említett módszerek segítségével a képet:
| 1.3.5 ábra |
A megfelelő háromszögek hasonlóságát felhasználva nem nehéz bizonyítani, hogy:
![\[ \frac {1}{t} - \frac {1}{k} = \frac {1}{f} \]](/images/math/f/8/7/f8773ab926afaebe97041f0dd7b4ed13.png) |
(1.3.8) |
Ennek segítségével a nagyítás is megadható:
![\[ N = \frac {f}{f-t} \]](/images/math/3/7/2/372466c35d2c6bdd9a0e56b7421eb587.png) |
(1.3.9) |
Vagyis a nagyítás – természetesen – függ a tárgytávolságtól. A lencsék nagyítását mégis valahogyan jellemezni kell. Megállapodás szerint a tisztánlátás távolsága 0.25m; ezt képtávolságnak választva a 1.3.9 segítségével belátható, hogy:
![\[ N = \frac {f+0.25}{f} \]](/images/math/4/9/f/49fc33a34296598914c4529cb6a26b24.png) |
(1.3.10) |
amennyiben a fókusztávolságot méterben számítják. Ha bemegyünk egy optikai szaküzletbe, láthatjuk, hogy a lupék nagyítása egy számmal van megadva; ez az 1.3.10-nek megfelelően lett meghatározva. Egy ilyen gyűjtőlencse nagyítása jellemzően 2 és 8 közötti érték.
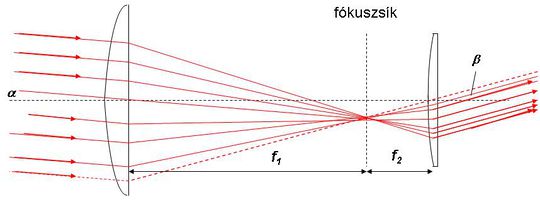
Ezután vizsgáljuk meg, hogy mi történik, ha az 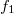 fókusztávolságú lencse után közvetlenül odahelyezünk még egy másik
fókusztávolságú lencse után közvetlenül odahelyezünk még egy másik 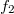 fókusztávolságút. Számítsuk ki a két lencséből álló "lencserendszer" fókuszának hosszát. Tegyük fel, hogy mindkét lencse követi az 1/f szabályt. Ekkor az első lencse által a kép a lencse mögött
fókusztávolságút. Számítsuk ki a két lencséből álló "lencserendszer" fókuszának hosszát. Tegyük fel, hogy mindkét lencse követi az 1/f szabályt. Ekkor az első lencse által a kép a lencse mögött  képtávolságban képeződne le, amelyre:
képtávolságban képeződne le, amelyre:
![\[ \frac {1}{t} + \frac {1}{k} = \frac {1}{f_1} \quad \Longrightarrow \quad \frac {1}{k} = \frac {1}{f_1} - \frac {1}{t} \]](/images/math/1/0/7/1072b96e032fe6b72431f211855fd120.png) |
(1.3.11) |
Viszont a második lencsénél ennek a képtávolságnak a 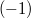 - szerese lesz a tárgytávolság. Most megint alkalmazható a leképezési szabály:
- szerese lesz a tárgytávolság. Most megint alkalmazható a leképezési szabály:
![\[ \frac {1}{t} - \frac {1}{f_1} + \frac {1}{k'} = \frac {1}{f_2} \quad \Longrightarrow \quad \frac {1}{t} + \frac {1}{k'} = \frac {1}{f_1} + \frac {1}{f_2} = D_1 + D_2 = D_e \]](/images/math/1/f/a/1fa608d68f04af20dc9dda54fdda7d4e.png) |
(1.3.12) |
ahol 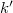 a második lencse után kialakult képtávolság. Az eredő fókusztávolság tehát:
a második lencse után kialakult képtávolság. Az eredő fókusztávolság tehát:
![\[ f = \frac {1}{D_e} \quad \Longrightarrow \quad f = \frac {f_1 f_2}{f_1 + f_2} \]](/images/math/0/c/b/0cb4891155438f09d7f70daab3b67dde.png) |
(1.3.13) |
Az 1.3.12 összefüggés ( 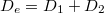 ), a "dioptriák törvénye" csak vékony lencsékre alkalmazható; vékonynak tekinthetünk egy lencsét, ha a vastagsága (középen) jóval kisebb az átmérőjénél.
), a "dioptriák törvénye" csak vékony lencsékre alkalmazható; vékonynak tekinthetünk egy lencsét, ha a vastagsága (középen) jóval kisebb az átmérőjénél.
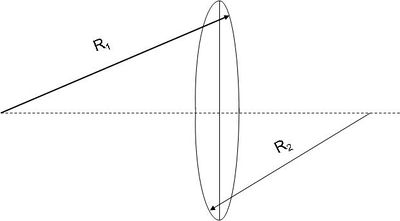
A sík-domború lencsére kapott 1.3.6 eredményt és a dioptriák összeadásának szabályát felhasználhatjuk arra, hogy meghatározzuk egy olyan lencse fókusztávolságát, amelyet két  és
és  görbületi sugarú felület határol. Úgy is tekinthetünk egy ilyen lencsére, mintha két sík-domború lencséből lenne összeragasztva.
görbületi sugarú felület határol. Úgy is tekinthetünk egy ilyen lencsére, mintha két sík-domború lencséből lenne összeragasztva.
| 1.3.6 ábra |
A dioptriákat összeadva adódik az eredő fókusztávolság az 1.3.6 segítségével:
![\[ \frac {1}{f_1}=(n-1)\frac {1}{R_1} \qquad {\rm \acute{e}s} \qquad \frac {1}{f_2}=(n-1)\frac {1}{R_2} \]](/images/math/4/6/d/46daf77088afa9569044d97dee4df89c.png) |
(1.3.14) |
tehát:
![\[ \frac {1}{f}= \frac {1}{f_1} + \frac {1}{f_2} = (n-1) \left( \frac {1}{R_1} + \frac {1}{R_2} \right) \]](/images/math/a/c/5/ac564374abc9cb16f015c2d8e7a0e9b5.png) |
(1.3.15) |
Ez a formula megadja nemcsak a gyűjtőlencse (a közepe vastagabb a szélénél), hanem a szórólencse (a közepe vékonyabb a szélénél) fókusztávolságának képletét is. Azonban vegyük észre, hogy egy szórólencse fókusztávolsága negatív érték (a homorú oldalhoz tartozó görbületi sugár 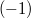 -szeresét kell venni). Ez érthető is, hiszen a szórólencsén az optikai tengellyel párhuzamosan érkező fénysugarak úgy szóródnak, mintha a belépő oldalon lévő fókuszpontból mint forrásból lépnének ki:
-szeresét kell venni). Ez érthető is, hiszen a szórólencsén az optikai tengellyel párhuzamosan érkező fénysugarak úgy szóródnak, mintha a belépő oldalon lévő fókuszpontból mint forrásból lépnének ki:
| 1.3.7 ábra |
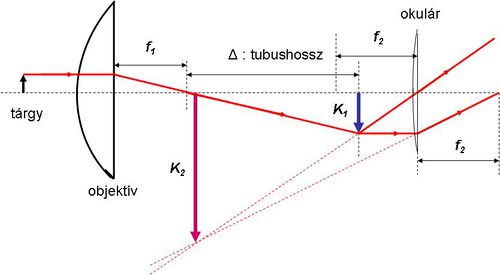
A távcső
A távoli tárgyak minél pontosabb megfigyelése iránti igény már évszázadokkal ezelőtt felvetődött. A távcső megjelenése a csillagászatban forradalmi változásokat hozott. Ugyanígy a tengeri navigációban is. A legegyszerűbb optikai távcsövet fogjuk elemezni. A Kepler-féle távcső két – eltérő fókusztávolságú – lencséből áll. A lencsék egy optikai tengelyre vannak "felfűzve", és közös fókuszsíkkal rendelkeznek, azaz a két lencse közötti távolság a fókusztávolságok összege. A nagy távolságban lévő tárgy egy pontjából kiinduló fénysugarak gyakorlatilag párhuzamosnak tekinthetők, ezért a fókuszsík egy pontján mennek át.
| 1.4.1 ábra |
A távcső nagyítását az első lencsére (objektív) beeső és a második lencsét (okulár) elhagyó párhuzamos sugárnyalábok optikai tengellyel bezárt szögeinek arányával adjuk meg:
![\[ N = \frac {\beta}{\alpha} \approx \frac {tg(\beta)}{tg(\alpha)} = \frac {f_1}{f_2} \]](/images/math/4/c/5/4c55e03a6098333dff98afa3671203c4.png) |
(1.4.1) |
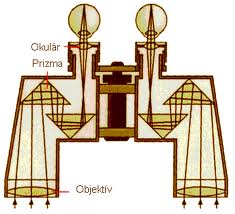
A Kepler-féle távcső fordított állású képet ad, ezért a földi megfigyelésre használatos távcsövek a képet két prizma segítségével "visszafordítják" (az objektív és okulár lencséket egy-egy összetett lencserendszer helyettesíti a jobb képminőség érdekében).
| 1.4.2.a ábra | 1.4.2.b ábra | 1.4.2.c ábra |
A Newton-féle távcsőben az objektívet egy konkáv tükörrel helyettesítik (a 0.5 m-nél nagyobb átmérőjű távcsövek szinte kivétel nélkül Newton rendszerűek):
| 1.4.3.a ábra | 1.4.3.b ábra |
Egy ilyen távcső vázlatos képe látható az 1.4.3.a ábrán; a gömbtükörről visszavert nyalábot általában egy síktükörrel oldalra kivezetik az okulárhoz a könnyebb kezelhetőség érdekében. Ma már gyakran nem szemmel néznek a távcsőbe, hanem egy megfelelően átalakított CCD kamerát használnak az okulároldalon, majd csatlakoztatják számítógéphez és a monitoron láthatók a megfigyelni kívánt objektumok. Az itt felsorolt távcső típusokon kívül még számos egyéb elrendezésű "messzelátó" berendezést építettek.
A mikroszkóp
A mikroszkóp használatával a szabad szemmel nem látható tárgyakat, élőlényeket tudjuk láthatóvá tenni. A mikroszkóp fejlődése az egyre nagyobb felbontású optikai mikroszkópok fejlesztésével kezdődött. A mikroszkóp segítségével a biológusok egy új, addig nem látott világba nyertek bepillantást. A botanikus Brown mikroszkópjával felfedezte a virágpollen darabkák véletlenszerű mozgását, amelyet azóta Brow-mozgásnak neveznek. Ezt az effektust végül Albert Einstein tudta megmagyarázni; ez volt az első komoly bizonyíték az atomok létezésére.
A legegyszerűbb mikroszkóp szintén két lencséből áll, az objektívből és az okulárból.
| 1.5.1 ábra |
A mikroszkóp működésének megértéséhez tekintsük a következő ábrát:
| 1.5.2 ábra |
A tárgyat az objektívlencse leképezi a 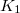 közbenső képbe. Az ábráról leolvasható, hogy az első leképezés nagyítása a tubushossz és az
közbenső képbe. Az ábráról leolvasható, hogy az első leképezés nagyítása a tubushossz és az 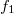 fókusz hányadosa:
fókusz hányadosa:
![\[ N_{obj.} = \frac {\Delta}{f_1} \]](/images/math/a/c/5/ac5aa9c19ea6d0379c7013874d058ffc.png) |
(1.5.1) |
Az okulár nagyítását megadhatjuk 1.3.10 formula segítségével, kihasználva, hogy 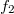 általában jóval kisebb
általában jóval kisebb 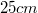 -nél (fókusztávolság méterben számítandó):
-nél (fókusztávolság méterben számítandó):
![\[ N_{ok.} = \frac {f_2 + 0.25}{f_2} \approx \frac {0.25}{f_2} \]](/images/math/f/5/7/f573b6f9803dee6baaa635fe0a74fd2c.png) |
(1.5.2) |
A mikroszkóp nagyítása az objektív és az okulár nagyításának szorzata:
![\[ N_{obj.} N_{ok.} = \frac {0.25 \Delta}{f_1 f_2} \]](/images/math/c/d/6/cd6ae38540754097e5f7bb5b2d7ec769.png) |
(1.5.3) |
A fénymikroszkópok nagyítása jellemzően 50 és 3000 közé esik. Arról majd a későbbiekben lesz szó, hogy a mikroszkóp nagyítását miért nem lehet egy bizonyos határ fölé növelni. Ezt akkor sem lehetne megtenni, ha a lencsékkel illetve lencserendszerekkel torzításmentes leképezést lehetne megvalósítani.
Lencsehibák
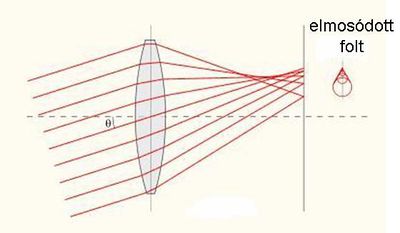
A lencsével történő képalkotás általában nem tökéletes. Ennek például az az oka, hogy a tárgy egy pontjából kiinduló fénysugarak az ernyőn, vagy a szemünkben nem egy pontban találkoznak, hanem egy foltot hoznak létre; ezáltal lesz a kép homályos. Más típusú lencsehibák is előfordulhatnak. A szférikus felületekkel határolt lencsék hibái közül itt csak néhányat említünk meg.
A szférikus aberráció abból fakad, hogy az optikai tengellyel párhuzamosan futó, de attól kissé távolabbi sugarak az optikai tengelyt más-más pontban érik el (1.6.1 ábra). A szférikus aberráció kiküszöbölésére aszférikus felülettel határolt lencséket használnak.
| 1.6.1 ábra |
A lencsével történő képalkotás esetében fellépő kóma (vagy üstököshiba) azért jön létre, mert a ferde sugarak nem találkoznak a fókuszsíkon illetve a leképezés síkjában (1.6.2 ábra). Ez a típusú hiba általában a kép szélén okoz problémát; főként nagy látószögű objektívek alkalmazásánál lehet jelentős a hatása.
| 1.6.2 ábra |
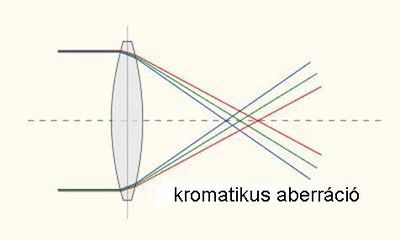
Idáig nem foglalkoztunk azzal, hogy milyen hullámhosszú fénnyel is dolgozunk. A tükrökkel megvalósítható leképezésnél ez nem is lényeges. A lencsék esetében azonban a színes tárgyak képalkotásánál kromatikus aberráció léphet fel a törésmutató hullámhosszfüggése miatt. Láttuk, hogy a fókusztávolság függ a törésmutatótól; ez azt eredményezi, hogy a különböző színű fénysugarakra más fókusztávolság adódik (1.6.3 ábra).
| 1.6.3 ábra |
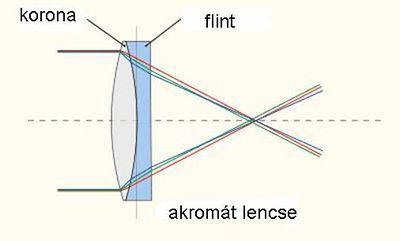
A kromatikus aberráció (színhiba) csökkentését általában két, különböző törésmutatójú üvegből (pl. korona és flint üveg) készült lencse együttes alkalmazásával érik el (1.6.4 ábra). Az apokromát lencsével pedig még jobb korrekció érhető el.
| 1.6.4 ábra |
Joggal kérdezhetné valaki, hogy ha ennyi fajta lencsehiba léphet fel, miért alkalmazunk üveglencséket. Erre az lehetne a válasz, hogy ugyan ma már széleskörűen használnak fröccsöntéssel készült műanyag lencséket, amelyeket aszférikus felületek határolnak kiküszöbölendő a lencsehibák egy része, azonban a szférikus felületekkel határolt lencséket még mindig sokkal pontosabban lehet megmunkálni. A lencsehibákat pedig lencserendszerek alkalmazásával korrigálni lehet, ezért például egy "tökéletes", azaz lencsehibáktól csaknem mentes (diffrakciólimitált) objektív általában jó néhány lencséből áll (1.6.5 ábra). Egy-egy ilyen lencserendszer tervezése többnyire igen bonyolult számítógépes feladat.
| 1.6.5 ábra |
Teljes visszaverődés (totálreflexió)
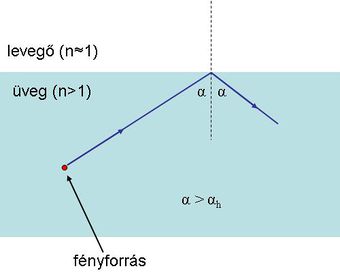
Idáig részletesebben nem foglalkoztunk azzal az esettel, hogy mi történik akkor, ha egy fénysugár a nagyobb törésmutatójú közegből az optikailag ritkább felé halad. Egy ilyen fénysugár fénytörését szintén a Schnellius-Descartes törvénnyel tudjuk leírni (1.7.1 ábra).
| 1.7.1 ábra |
Gond akkor adódna, ha az ábrán látható eset áll elő:
| 1.7.2 ábra |
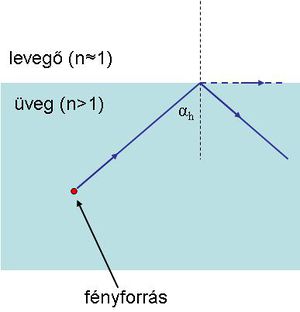
Ha az üveg felől érkező fényhullám iránya a közeghatár síkjának normálisával azt az 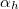 határszöget (1.7.2 ábra) zárja be, amelynél
határszöget (1.7.2 ábra) zárja be, amelynél 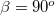 lenne, elérkeztünk a Schnellius-Descartes törvény alkalmazhatóságának határához. A törési törvény használatával a határszöget könnyen kiszámíthatjuk a következő formula segítségével:
lenne, elérkeztünk a Schnellius-Descartes törvény alkalmazhatóságának határához. A törési törvény használatával a határszöget könnyen kiszámíthatjuk a következő formula segítségével:
![\[ \frac {sin 90^o}{sin \alpha_h} = n \quad \Longrightarrow \quad sin \alpha_h = \frac{1}{n} \]](/images/math/3/b/0/3b09dc01cf992f2bee340042cc66aca8.png) |
(1.7.1) |
Az üveg felületén azonban a fény nem tud terjedni; a fény tehát teljes visszaverődést szenved az 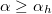 esetben (1.7.3 ábra).
esetben (1.7.3 ábra).
| 1.7.3 ábra |
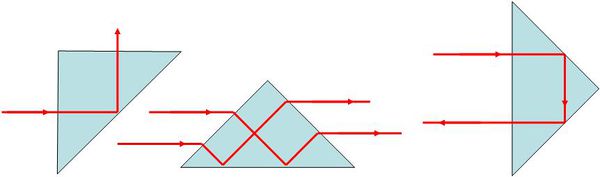
Ezt az effektust - a totálreflexiót - felhasználhatjuk a fény irányának megváltoztatására is például egy üvegprizma alkalmazásával (1.7.4.a ábra):
| 1.7.4.a ábra | 1.7.4.b ábra |
A macskaszem "működését" is teljes reflexióval magyarázhatjuk. A földmérők által használt reflexiós prizma is valójában egy macskaszem (1.7.4.b ábra).
Fizikai optika
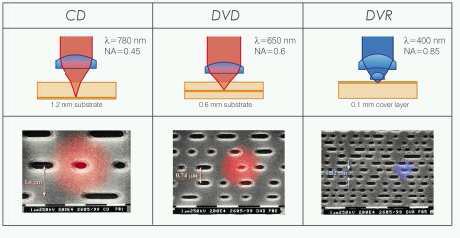
A geometriai optika leképezési törvényeit úgy tudtuk felírni, hogy nem vettük figyelembe a fény hullámtermészetét. A mikroszkóp és a távcső felbontását – mint azt korábban említettük – nem lehet minden határon túl növelni. Hasonló okokból kifolyólag nem lehetséges jelentősen növelni a DVD írás-sűrűségét sem. A fényterjedés leírásában a fény hullámtermészetét is felhasználó leírás a hullámoptika.
Interferencia
Az elektromágneses hullámok terjedésének illetve energiaviszonyainak tanulmányozása során láttuk, hogy polarizált EMH-k interferálhatnak. A legegyszerűbb eset látható a következő ábrán; a felső sorban az eredő hullámkép, míg a két alsó kép az összeadódó (rész)hullámokat mutatja:
| 2.1.1 ábra |
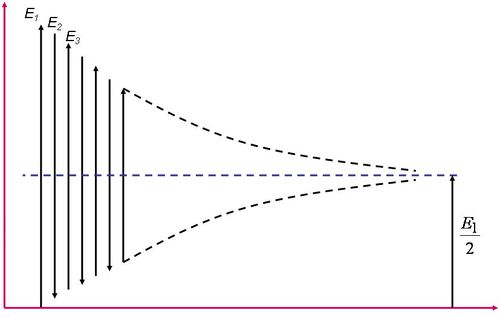
A baloldali ábrán a konstruktív interferenciára látunk példát. Amennyiben a két, lineárisan polarizált hullám - azonos polarizációs iránnyal - fázisban találkozik és erősítik egymást; akkor az eredő hullám amplitúdója éppen duplája lesz az összetevő, megegyező amplitúdójú hullámokénak. A jobb oldali ábrán a két hullám között 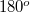 -os fáziskülönbség van, ezért kioltják egymást.
-os fáziskülönbség van, ezért kioltják egymást.
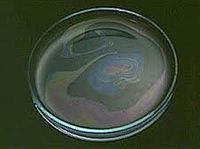
Az interferencia jelenségére számos példa van a természetben; nyáron szinte mindenki látott már eső után "színes olajfoltot" az utcán. A következő két képen az üvegcsészében lévő vízfelszínen elterülő olajfoltot illetve annak felnagyított képét láthatjuk.
| 2.1.2.a ábra | 2.1.2.b ábra |
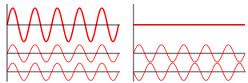
Felmerül a kérdés, hogy milyen feltételek mellett látható interferencia jelenség, mert hiszen a megvilágított tárgyak felszínén általában nem jelenik meg interferencia mintázat. Erre a következő válasz adható: az EMH-k szinte mindig interferálnak, azonban ezt nem észleljük. Amennyiben detektálható, szemmel is látható interferenciaképet szeretnénk kapni, akkor a - tárgyat vagy ernyőt megvilágító - hullámok közötti fáziskülönbségnek időben állandónak kell lennie. Ezt koherens hullámokkal lehet elérni. Ez azt jelenti, hogy a fény hullámhossza és fázisa időben nem változik. A folytonos lézerek által kibocsátott fény koherensnek tekinthető. Az egyéb fényforrások, például villanykörte vagy fénycső fénye nemkoherens hullám. Ennek az az oka, hogy a bennük található atomok egymástól függetlenül bocsátják ki fényüket. Az általuk megvilágított tárgy egy pontjába így véletlenszerű fázissal érkeznek a különböző atomokból kisugárzott hullámok, ezért a lineáris szuperpozíció következtében előálló interferenciakép a megfigyelési idő törtrésze alatt megváltozik, így a "remegő" interferencia mintázat elmosódik. Nemkoherens nyalábok fázis és hullámhosszviszonyait ábrázolja az 2.1.3 ábrán látható két alsó rajz. Különböző hullámhosszú és véletlen fázisú hullámokat (legalsó rajz) bocsát ki például egy villanykörte, egy takarékos izzó, vagy egy fénycső, de a nap fénye is ilyen. A középső ábrán látható hullámok hullámhossza megegyező ugyan, de fázisuk véletlenszerűen változik, ezért ez sem tekinthető koherens hullámnak; ilyen fényt sugároz egy interferencia-lámpa (ez általában egy fémgőz-lámpa, pl. Hg-gőz lámpa). A fölső rajzon látható egy koherens hullám vázlatos képe.
| 2.1.3 ábra |
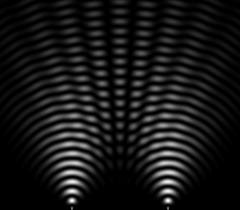
A legegyszerűbb interferencia kísérletek során két síkhullám (2.1.4.a ábra, szimuláció), vagy egy síkhullám és egy gömbhullám (2.1.4.b ábra, interferenciakép) esetleg két gömbhullám (2.1.4.c ábra, hullámkádas demonstráció) interferál egymással, jellemző interferencia mintázatot hozva létre egy ernyőn.
| 2.1.4.a ábra | 2.1.4.b ábra | 2.1.4.c ábra |
Természetesen a hullámok interferenciájára tett általános megállapítások, melyeket az elektromágneses hullámok tárgyalásánál láttunk, most is alkalmazhatók. Az interferenciakép intenzitásviszonyait leíró formula az optikában is hasznos:
![\[ I = I_1 + I_2 + 2\sqrt{I_1 I_2}\,cos(\Delta \varphi) \]](/images/math/5/1/c/51c7cae0aad0cc22f648460c40a441d8.png) |
(2.1.1) |
ahol a fáziskülönbséget az úthosszakkal is kifejezhetjük:
![\[ I = I_1 + I_2 + 2\sqrt{I_1 I_2}\,cos(k s_2 - k s_1 ) \]](/images/math/3/b/6/3b6d026ef92d0df74f94cc930a92c921.png) |
(2.1.2) |
A 2.1.1-ből következik, hogy ha (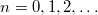 ):
):
![\[ k( s_2 - s_1) = \frac{2\pi}{\lambda}\Delta s = n(2\pi) \]](/images/math/3/2/2/3228f496f57521fa0a4dc29aedd5a62c.png) |
(2.1.3) |
akkor a két hullám erősíti egymást (konstruktív interferencia), azaz világos foltot kapunk; ekkor a két hullám 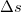 úthosszkülönbsége a hullámhossz egész számú többszöröse. Ha azonban:
úthosszkülönbsége a hullámhossz egész számú többszöröse. Ha azonban:
![\[ k (s_2 - s_1) = \frac{2\pi}{\lambda}\Delta s = (2n+1)\pi \]](/images/math/b/8/7/b87274b92cb8a0ceeee965f042f00352.png) |
(2.1.4) |
akkor destruktív interferencia lép fel, azaz kioltás következik be, vagyis sötét foltot látunk (pl. 2.1.5 ábra); ekkor a két hullám 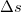 úthosszkülönbsége a hullámhossz felének páratlan számú többszöröse.
úthosszkülönbsége a hullámhossz felének páratlan számú többszöröse.
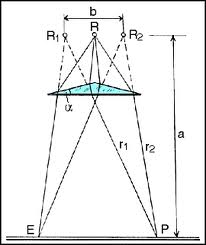
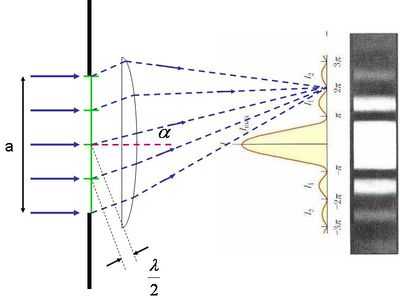
Az egyik leggyakrabban bemutatott és legkönnyebben megérthető demonstráció a Young-féle kétréses interferencia kísérlet.
| 2.1.5 ábra |
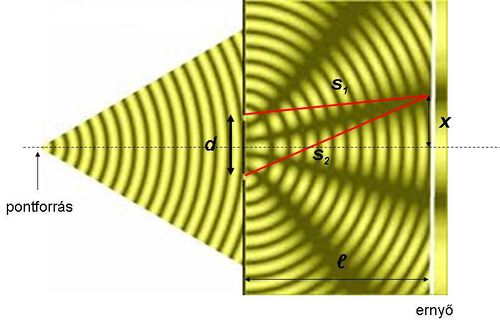
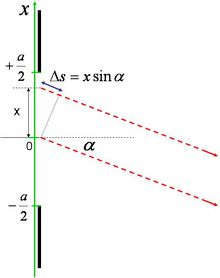
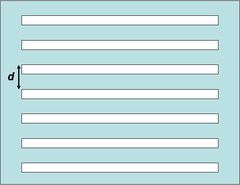
A kísérleti elrendezés oldalnézeti képe látható a 2.1.5 ábrán. Az egymástól  távolságban lévő, két keskeny résre a fény azonos fázisban esik. Feltesszük, hogy az ábra síkjára merőleges irányban az elrendezésnek transzlációs szimmetriája van, ezzel két dimenziósra egyszerűsödik a leírás. Sok interferencia kísérlet által létrehozott interferencia mintázat magyarázható két (koherens) pontforrás gömbhullámainak interferenciájával, így a következő számítás - kis módosítással - azokra is használható. A 2.1.5 ábra jelöléseit használva meghatározzuk a legsötétebb (
távolságban lévő, két keskeny résre a fény azonos fázisban esik. Feltesszük, hogy az ábra síkjára merőleges irányban az elrendezésnek transzlációs szimmetriája van, ezzel két dimenziósra egyszerűsödik a leírás. Sok interferencia kísérlet által létrehozott interferencia mintázat magyarázható két (koherens) pontforrás gömbhullámainak interferenciájával, így a következő számítás - kis módosítással - azokra is használható. A 2.1.5 ábra jelöléseit használva meghatározzuk a legsötétebb (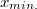 ) és a legvilágosabb (
) és a legvilágosabb (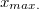 ) pontok helyét. Az
) pontok helyét. Az 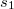 és
és 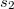 optikai úthosszak a két pontforrásnak minősülő nyílás és az ernyő egy, az origótól (az ernyő közepétől) mért
optikai úthosszak a két pontforrásnak minősülő nyílás és az ernyő egy, az origótól (az ernyő közepétől) mért  távolságban lévő pontja között:
távolságban lévő pontja között:
![\[ s_1 = \sqrt{\ell^{\,2} + \left(x - \frac{d}{2}\right)^2} \qquad {\rm \acute{e}s} \qquad s_2 = \sqrt{\ell^{\,2} + \left(x + \frac{d}{2}\right)^2} \]](/images/math/f/6/0/f601d179cb7cf8b50310c3141cabb990.png) |
(2.1.5) |
Az úthosszkülönbség tehát:
![\[ \Delta s = \sqrt{\ell^{\,2} + \left(x + \frac{d}{2}\right)^2} - \sqrt{\ell^{\,2} + \left(x - \frac{d}{2}\right)^2} \]](/images/math/0/6/c/06c10a86b9805606bba6f2d8434814de.png) |
(2.1.6) |
Maximális intenzitást ott lehet mérni 2.1.2 alapján, ahol 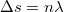 , azaz:
, azaz:
![\[ n\lambda = \sqrt{\ell^{\,2} + \left(x + \frac{d}{2}\right)^2} - \sqrt{\ell^{\,2} + \left(x - \frac{d}{2}\right)^2} \]](/images/math/d/0/5/d051bb7fef3cf3037487630b07d6fcba.png) |
(2.1.7) |
Az interferencia kísérletekben az ernyő és a nyílásokat tartalmazó fal távolsága általában jóval nagyobb, mint a két rés távolsága, illetve az ernyő közepétől mért távolság, vagyis 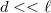 és
és 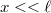 . Ezt a tényt felhasználhatjuk arra, hogy közelítést használjunk:
. Ezt a tényt felhasználhatjuk arra, hogy közelítést használjunk:
![\[ s_1 = \sqrt{\ell^{\,2} + \left(x - \frac{d}{2}\right)^2} \approx \ell \left(1 + \frac{1}{2} \frac{\left(x-d/2 \right)^2}{\ell^{\,2}}\right) \]](/images/math/3/6/1/361d155db7f676d1e72339665dff49ab.png) |
(2.1.8) |
és
![\[ s_2 = \sqrt{\ell^{\,2} + \left(x + \frac{d}{2}\right)^2} \approx \ell \left(1 + \frac{1}{2} \frac{\left(x+d/2 \right)^2}{\ell^{\,2}}\right) \]](/images/math/4/9/1/491443f06757bf7f3ef3550cd8b28b9f.png) |
(2.1.9) |
Az úthosszkülönbség tehát megadható a következő egyszerű formában:
![\[ \Delta s \approx \frac{xd}{\ell} \]](/images/math/0/7/a/07a968ea53810d9f4f8b1400887cb520.png) |
(2.1.10) |
A 2.1.10 és a 2.1.7 segítségével meghatározhatjuk a legvilágosabb pontok (sávok) távolságát az ernyő középpontjától:
![\[ x_{max.} \approx n\frac{\ell \lambda}{d} \]](/images/math/c/7/d/c7dbb6e88ca37a7bd15f9eded56a9faf.png) |
(2.1.11) |
A legsötétebb pontok, viszont az origótól – a 2.1.4 és az 2.1.10 felhasználásával:
![\[ x_{min.} \approx (2n+1)\frac{\ell \lambda}{2d} \]](/images/math/8/8/3/883f4ac509dd93c45491687559f9de71.png) |
(2.1.12) |
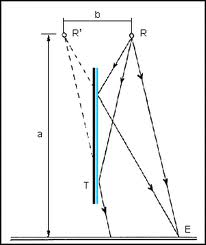
A Young-féle kétréses interferencia kísérleten kívül hasonló számítással adhatjuk meg a Fresnel-féle tükörkísérlet (2.1.6.a ábra) esetén vagy a Fresnel-féle biprizmás kísérletben (2.1.6.b ábra) és a Lloyd-féle kísérletben (2.1.6.c ábra) is a fényes csíkok helyzetét, illetve a szomszédos csíkok közötti távolságot.
| 2.1.6.a ábra | 2.1.6.b ábra | 2.1.6.c ábra |
Arról még nem volt szó, hogy a reflexiónál történik-e fázisugrás vagy sem. A mechanikai hullámok tanulmányozásánál láttuk, hogy egy hullám reflexiónál 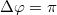 fázistolást szenved, ha ritkább közegből érkezik sűrűbb közeghez; viszont nincs fázisváltozás, amennyiben a sűrűbb közegből érkezik a közeghatárhoz. Ezek a megállapítások érvényesek az elektromágneses hullámokra, azaz a fényre is.
fázistolást szenved, ha ritkább közegből érkezik sűrűbb közeghez; viszont nincs fázisváltozás, amennyiben a sűrűbb közegből érkezik a közeghatárhoz. Ezek a megállapítások érvényesek az elektromágneses hullámokra, azaz a fényre is.
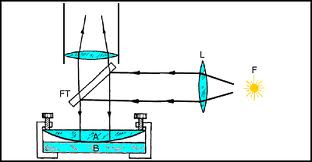
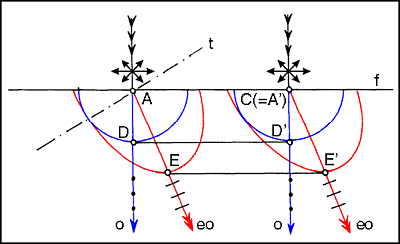
Interferenciagyűrűket kaphatunk, ha egy síkdomború lencsét a domború felével lefelé egy sík, tükröző felületre helyezünk, majd felülről megvilágítjuk, és szintén felülről megfigyeljük. A berendezés elvi rajza a 2.1.7.a, az interferenciagyűrűk a 2.1.7.b ábrán láthatók.
| 2.1.7.a ábra | 2.1.7.b ábra |
Középen sötét foltnak kell lennie, mert a lencse belső felületéről visszavert nyaláb nem szenved fázistolást, míg a plánparalell lemezről visszavert igen, azaz a két reflektált hullám között 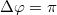 fáziskülönbség van, tehát kioltják egymást. A gyűrűk sugarát a lencse és a sík üvegfelület közötti távolság határozza meg; tehát a lencse görbületi sugarából számíthatjuk ki.
fáziskülönbség van, tehát kioltják egymást. A gyűrűk sugarát a lencse és a sík üvegfelület közötti távolság határozza meg; tehát a lencse görbületi sugarából számíthatjuk ki.
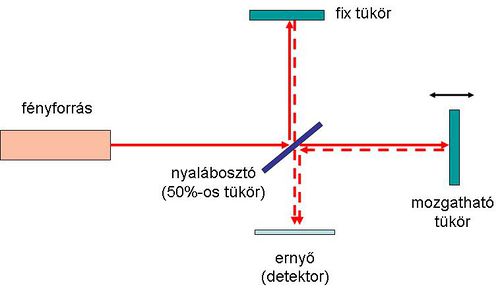
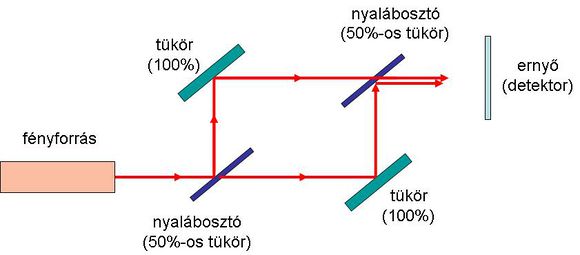
A hullámok interferenciájára épülő berendezések az interferométerek. Az egyik ilyen optikai elrendezés a Michelson-interferométer (2.1.8 ábra).
| 2.1.8 ábra |
Az előző ábrán jól látszik az interferométer felépítése. A fényforrás (általában) kollimált nyalábját a féligáteresztő tükör (50 % -os tükör) osztja két nyalábra, melyek aztán a fényútra merőleges tükrökről (R=100%) visszaverődnek, majd a féligáteresztő tükörről a detektor vagy az ernyő felé haladnak. Amennyiben az interferométer egyik karjának hossza megnő vagy csökken a hullámhossz negyedével, akkor a két hullám közötti fáziskülönbség éppen 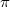 – vel változik meg, ami az ernyőn igen jelentős intenzitásváltozást eredményez, azaz világos helyett sötét, vagy sötét helyett világos folt jelenik meg az ernyő közepén. Ezt könnyű detektálni vagy akár szabad szemmel megfigyelni; vagyis egy ilyen interferométer mérési pontossága a fényforrás hullámhosszának negyede, vagy annál valamivel jobb (jó esetben ez akár
– vel változik meg, ami az ernyőn igen jelentős intenzitásváltozást eredményez, azaz világos helyett sötét, vagy sötét helyett világos folt jelenik meg az ernyő közepén. Ezt könnyű detektálni vagy akár szabad szemmel megfigyelni; vagyis egy ilyen interferométer mérési pontossága a fényforrás hullámhosszának negyede, vagy annál valamivel jobb (jó esetben ez akár 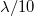 is lehet). Az elrendezés kis felületi egyenetlenségek kimutatására is alkalmas, hiszen amennyivel kidudorodik (vagy éppen bemélyed) a felület, annak a távolságnak a kétszeresével változik meg a fényút, ezt pedig az említett mérési pontossággal mérni lehet.
is lehet). Az elrendezés kis felületi egyenetlenségek kimutatására is alkalmas, hiszen amennyivel kidudorodik (vagy éppen bemélyed) a felület, annak a távolságnak a kétszeresével változik meg a fényút, ezt pedig az említett mérési pontossággal mérni lehet.
A másik gyakran alkalmazott interferométer típus a Mach-Zhender interferométer (2.1.9 ábra):
| 2.1.9 ábra |
Az interferométer két tükörből és két féligáteresztő tükörből áll. Egy ilyen berendezéssel a tesztágba helyezett átlátszó anyag (például üveg, folyadék, stb.)  törésmutatóját lehet pontosan megmérni, hiszen – mint az könnyen belátható – a tesztág optikai úthosszának megváltozása:
törésmutatóját lehet pontosan megmérni, hiszen – mint az könnyen belátható – a tesztág optikai úthosszának megváltozása:
![\[ \Delta s = (n-1)d \]](/images/math/1/6/3/1638cd813efa88d917e8ac969e32f42c.png) |
(2.1.13) |
ahol  a vizsgált anyagdarab vastagsága.
a vizsgált anyagdarab vastagsága.
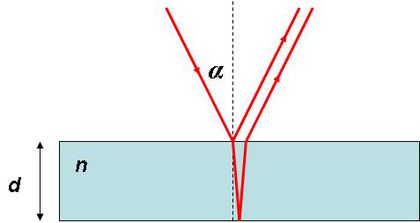
Ezek után már könnyen találunk magyarázatot a színes olajfoltok "rejtélyére". Ehhez tekintsük a következő ábrát, amely azt mutatja, hogy a  vastagságú és
vastagságú és  törésmutatójú dielektrikum két felületéről reflektálódó fénynyalábok miképpen interferálhatnak.
törésmutatójú dielektrikum két felületéről reflektálódó fénynyalábok miképpen interferálhatnak.
| 2.1.10 ábra |
A dielektrikumra a felületi normálissal  szöget bezáró
szöget bezáró  hullámhosszúságú beeső fénysugár egy része a felső felületről reflektálódik. (A megtört nyaláb
hullámhosszúságú beeső fénysugár egy része a felső felületről reflektálódik. (A megtört nyaláb  szöget zár be a normálissal, azonban azt az ábrán nem jelöltük.) A megtört nyaláb az alsó felületről visszaverődve a felső felületnél újra megtörve lép ki a felső térrészbe és halad a normálissal
szöget zár be a normálissal, azonban azt az ábrán nem jelöltük.) A megtört nyaláb az alsó felületről visszaverődve a felső felületnél újra megtörve lép ki a felső térrészbe és halad a normálissal  szöget bezáró irányba, azaz párhuzamosan a felső felületről reflektált nyalábbal; ez a két hullám pedig interferálhat. A két reflektált hullám közötti fáziskülönbség:
szöget bezáró irányba, azaz párhuzamosan a felső felületről reflektált nyalábbal; ez a két hullám pedig interferálhat. A két reflektált hullám közötti fáziskülönbség:
![\[ \Delta \varphi = \pi + 2n \frac{2\pi}{\lambda}\frac{d}{cos\beta} \]](/images/math/6/f/d/6fd5310791775e6c4e6751cc1d0422bf.png) |
(2.1.14) |
A jobboldal első tagja a felső felületen történő reflexiónál fellépő 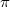 fázistolás miatt jelenik meg. Az alsó felületről tükröződve nem szenved a hullám fázistolást, hiszen optikailag sűrűbb közegből terjed a felület felé. Figyelembe vettük, hogy a dielektrikumban terjedő fény hullámhossza a vákuumbeli
fázistolás miatt jelenik meg. Az alsó felületről tükröződve nem szenved a hullám fázistolást, hiszen optikailag sűrűbb közegből terjed a felület felé. Figyelembe vettük, hogy a dielektrikumban terjedő fény hullámhossza a vákuumbeli  hullámhossz
hullámhossz  -ed része. (Vagy akár azt is mondhatjuk, hogy az optikai úthossz a geometriai úthossz
-ed része. (Vagy akár azt is mondhatjuk, hogy az optikai úthossz a geometriai úthossz  -szerese.)
Kis beesési szöget feltételezve a továbbiakban élhetünk a
-szerese.)
Kis beesési szöget feltételezve a továbbiakban élhetünk a 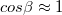 közelítéssel.
közelítéssel.
A két reflektált hullám erősíti egymást, ha 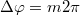 (ahol m =1, 2, 3,…); ebben az esetben a dielektrikum vastagsága:
(ahol m =1, 2, 3,…); ebben az esetben a dielektrikum vastagsága:
![\[ d = \frac{1}{2n}\left(m - \frac{1}{2} \right)\lambda \]](/images/math/6/3/1/631ca072214b2889cc24c519ad9201e5.png) |
(2.1.15) |
Ez az eredmény jól mutatja, hogy a dielektrikum (akár a vízen úszó olajfolt) vastagsága meghatározza a visszavert fény színét. (Amennyiben a beesési szög nem elhanyagolható, akkor is hasonló eredmény adódik, de kissé több számítást igényel a levezetés.)
A két hullám ki is olthatja egymást, amennyiben a réteg vastagsága:
![\[ d = m\frac{\lambda}{n}\frac{1}{2} \]](/images/math/1/c/c/1cc971123648275d066176e34ef6f395.png) |
(2.1.16) |
Egy ilyen vékonyréteg a legegyszerűbb antireflexiós réteg. Vékonyréteg struktúra alkalmazásával szélessávú – vagyis nem csak néhány hullámhosszra, hanem egy hullámhossztartományra is használható – antireflexiós rétegrendszer is kialakítható.
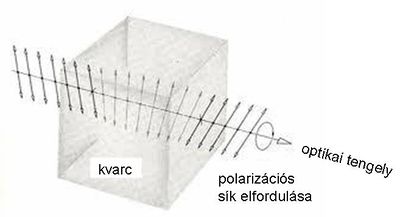
A fény polarizációja
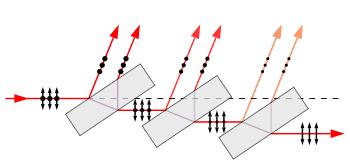
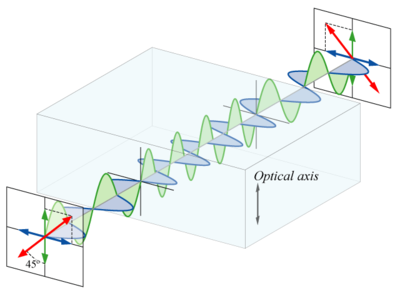
Idáig nem említettük a fényhullámok polarizációs tulajdonságait; ezekre az EMH fejezetben elmondottak érvényesek, vagyis egy síkhullám lehet lineárisan poláros és cirkulárisan poláros (2.2.1 a és b ábra).
| 2.2.1.a ábra | 2.2.1.b ábra |
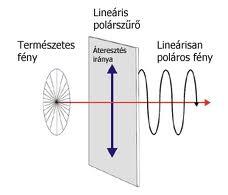
A cirkulárisan polarizált fény természetesen lehet jobbra vagy balra cirkulárisan poláros annak megfelelően, hogy az elektromos tér a terjedés során merre forog (az óramutató járásával megegyező vagy ellentétes irányban). A fény polarizációs síkját – csakúgy mint az elektromágneses hullámnak – egy polárszűrővel be lehet "állítani" (ilyenkor néha azt mondják, hogy preparálják a fényt). A polárszűrő általában hosszú makromolekulák rendezett szerkezete; a molekula hosszirányban könnyen polarizálható, szimmetriatengelyére merőleges irányban viszont nehezen, így a rá merőleges elektromos térerősség a molekulát rezgésbe hozza, vagyis az energia nagy részét elnyeli. A polárszűrő tehát a rá eső fény egyik komponensét engedi csak át; ennek a komponensnek az iránya a polarizációs irány. Amennyiben lineárisan polarizált fény esik be rá merőlegesen, de annak polarizációs síkja (vagyis az  térerősség síkja)
térerősség síkja)  szöget zár be a polarizációs iránnyal, akkor a polárszűrő másik oldalán megjelenő fény térerősségének maximuma az eredeti (beeső) hullám amplitúdójának
szöget zár be a polarizációs iránnyal, akkor a polárszűrő másik oldalán megjelenő fény térerősségének maximuma az eredeti (beeső) hullám amplitúdójának 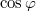 - szerese:
- szerese: 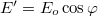 . A fény intenzitása viszont a térerősség négyzetével arányos, vagyis a polarizátorra beeső
. A fény intenzitása viszont a térerősség négyzetével arányos, vagyis a polarizátorra beeső 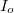 intenzitású fény a kilépő oldalon "gyengébb" (általában kisebb intenzitású) lesz; ezt írja le a Mahlus-törvény:
intenzitású fény a kilépő oldalon "gyengébb" (általában kisebb intenzitású) lesz; ezt írja le a Mahlus-törvény:
![\[ I = I_{\circ}\cos^{\,2}\varphi \]](/images/math/d/b/9/db942341f7a29d25b2e2e0405e459c36.png) |
(2.2.1) |
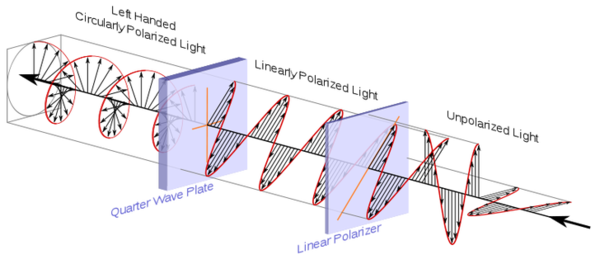
Amennyiben viszont a polarizátorra eső fény cirkulárisan poláros, akkor a polárszűrő után (minthogy az csak az egyik komponensét engedi át) már lineárisan polarizált lesz. Hasonlóan, ha nem polarizált - azaz véletlen polarizációjú, vagy természetes - fény (napfény, termikus fényforrás fénye, stb.) esik a polarizátorra, akkor annak másik oldalán szintén lineárisan polarizált nyaláb lép ki.
| 2.2.2 ábra |
A polárszűrő működésére részletesebb magyarázatot majd a modern fizika fejezetben adunk.
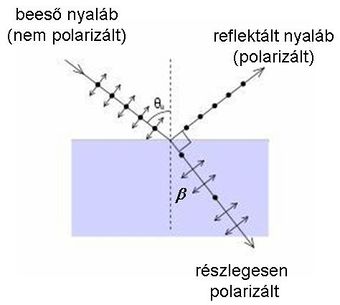
A Schnellius-Descartes törvény bemutatásánál nem foglalkoztunk a beeső fény polarizációs tulajdonságaival. Általános esetben a közeghatárhoz érkező fénynyaláb egy része megtörik, míg a másik része reflektálódik a beeső fény polarizációs tulajdonságaitól függetlenül (2.2.3 ábra); a veszteségektől eltekintünk.
| 2.2.3 ábra |
A gyakorlati alkalmazások szempontjából az egy igen fontos kérdés, hogy a felülettel párhuzamos és a rá merőleges polarizációs iránnyal jellemzett fénysugár hányadrésze reflektálódik, illetve törik meg. Az energiamegmaradás és a határfeltételek felhasználásával a válasz természetesen megadható az előbbi kérdésre.
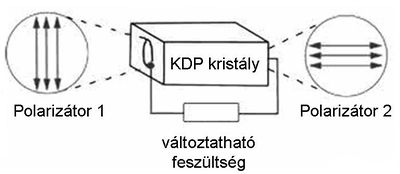
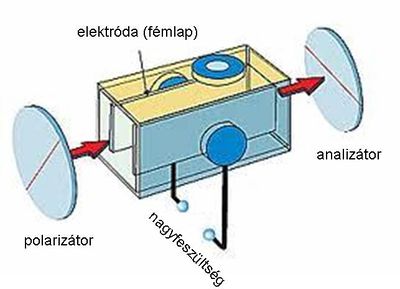
Amennyiben a beeső fénysugár a felületi normálissal Brewster szöget zár be, azaz a reflektált és a megtört nyaláb egymással 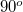 -os szöget zár be, akkor a reflektált nyalábban nem jelenik meg a felületre merőleges síkban polarizált komponens (2.2.4 ábra).
-os szöget zár be, akkor a reflektált nyalábban nem jelenik meg a felületre merőleges síkban polarizált komponens (2.2.4 ábra).
| 2.2.4 ábra |
A 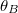 Brewster szög értéke egyszerűen meghatározható (2.2.2); mindössze a reflektált és a dielektrikumban haladó nyalábok merőlegességét kell felhasználni:
Brewster szög értéke egyszerűen meghatározható (2.2.2); mindössze a reflektált és a dielektrikumban haladó nyalábok merőlegességét kell felhasználni:
![\[ \frac{sin\theta_B}{sin\beta} = \frac{sin\theta_B}{sin(90^{\circ}-\theta_B)} = tg\theta_B =n \]](/images/math/c/a/4/ca4403c4dcb911df0b528dd343d9b898.png) |
(2.2.2) |
Ennek az érdekes - és gyakorlati szempontból is igen fontos - jelenségnek a magyarázata az elektromágneses hullámok keletkezésével kapcsolatos. Az EMH-ok tulajdonságait bemutató fejezetben láttuk, hogy a rezgő elektromos dipól sugárzásának van iránykarakterisztikája. Ennek az az egyik jellegzetessége, hogy a dipól a rezgés irányában nem sugároz. A dielektrikumnak a beeső fény időben változó elektromos terének hatására polarizálódó molekulái szintén rezgő elektromos dipólmomentumként viselkednek. Az EMH transzverzális hullám, és a molekulák elemi dipólmomentumainak irányát az elektromos tér határozza meg. Így tehát a polarizálódó molekulák nem sugároznak a hullám terjedési irányára merőlegesen. Ebből már következik, hogy ha a reflektált nyaláb merőleges a dielektrikumban haladó megtört nyalábra, akkor a reflektált nyaláb - a 2.2.4 ábrának megfelelően - polarizált lesz. Ezt a jelenséget felhasználhatjuk polarizált nyaláb előállításához is (2.2.5 ábra).
| 2.2.5 ábra |
Diffrakció
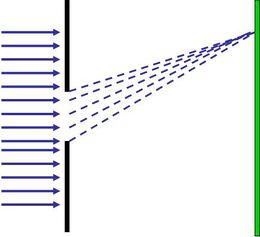
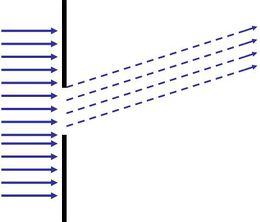
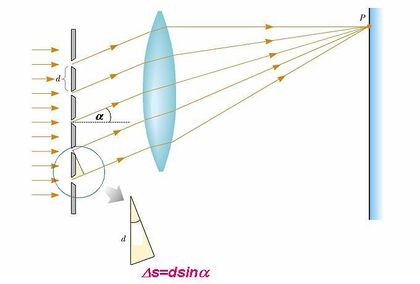
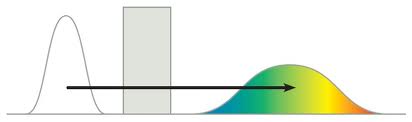
Miért építünk egyre nagyobb távcsöveket? Optikai mikroszkóppal miért nem látjuk a fény hullámhosszánál kisebb (jóval kisebb) részleteket a vizsgált objektumon? Mindezekre a geometriai optikában tanultak nem adnak választ, mert a sugároptika módszerei nem veszik figyelembe a fény hullámtermészetét. Tegyük fel, hogy egy átlátszatlan falba nyílást vágunk, majd ezt a nyílást megvilágítjuk az egyik oldaláról és a fal másik oldalára helyezett ernyőn megfigyeljük a nyílás "képét". Mit látunk? Amennyiben a nap fényét vagy egy lámpát használunk a megvilágításhoz, akkor általában nem csodálkozunk azon, hogy az ernyőn kapott fényes folt széle – az árnyékhatár – nem éles, hiszen egy kiterjedt fényforrást használtunk. Ha azonban monokromatikus síkhullámot (kollimált lézernyalábot) használunk, akkor a geometriai optika alapján azt várnánk, hogy az ernyőn a nyílás éles képe jelenjen meg. A kísérleti tapasztalat azonban ezzel ellentétben az, hogy az árnyékhatár nemcsak hogy nem éles, hanem furcsa intenzitás mintázatok is megjelennek, ráadásul a fény egy része az árnyéktérbe is behatol (négyzet alakú rés képe: 2.3.1 ábra).
| 2.3.1 ábra |
A kísérletet megismételhetjük egy borotvával is (2.3.2.a ábra); látható, hogy az ernyőn a borotva éle sem azonosítható be könnyen (2.3.2.b ábra).
| 2.3.2.a ábra | 2.3.2.b ábra |
Ezt a jelenséget – azaz, hogy a fény behatol az árnyéktérbe és gyakran intenzitás mintázato(ka)t is létre hoz – fényelhajlásnak vagy más néven diffrakciónak nevezzük. Az effektus egyszerű magyarázatához Huygens-elvét használhatjuk. Eszerint a hullámtér, azaz a fénytér minden egyes pontja egy gömbhullám kiindulópontja, az árnyéktérbe pedig ezek a hullámok behatolhatnak. Ha ezen gömbhullámok elektromos térerősség komponenseit fázishelyesen összeadjuk, akkor megkaphatjuk az intenzitás-eloszlást az ernyőn illetve a falba vágott nyílás vagy rés mögötti térrészben. A fény diffrakciójának részletes tárgyalása egyrészt meghaladja a jegyzet kereteit, másrészt a hallgatóktól felsőbb fokú matematikai jártasságot igényelne. Ezért a fényelhajlás jelenségének bemutatásához a legegyszerűbb modellek vizsgálatára szorítkozunk és a diffrakciós integrált kvalitatív meggondolások alapján vezetjük be.
Tekintsünk egy egyszerű elrendezést! Tegyük fel, hogy egy átlátszatlan, vékony sík falhoz az egyik oldalról monokromatikus, lineárisan polarizált síkhullám (fény) érkezik a falra merőleges irányból, így a falba vágott rés síkjában a hullám fázisa állandó (2.3.3 ábra).
| 2.3.3 ábra |
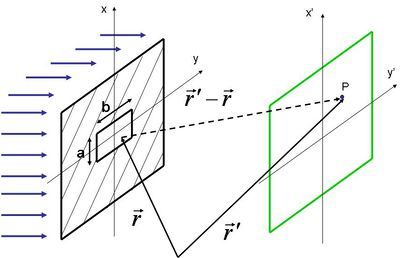
A réssel ellátott fal másik oldalán lévő – a fallal párhuzamos – ernyő 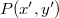 pontjában szeretnénk az elektromos térerősséget meghatározni. Az elektromágneses hullámok interferenciáját tárgyaló fejezetben láttuk, hogy hogyan lehet két koherens hullámot "összeadni". Most mindössze annyi a különbség, hogy a rés minden egyes pontjából kiinduló gömbhullámok terét kell fázishelyesen összeadni; az összegzés természetesen integrálást jelent. Figyelembe kell még azt is vennünk, hogy a gömbhullám intenzitása a távolság négyzetével fordítva arányos. Egy gömbhullám elektromos terének nagyságát a forrástól
pontjában szeretnénk az elektromos térerősséget meghatározni. Az elektromágneses hullámok interferenciáját tárgyaló fejezetben láttuk, hogy hogyan lehet két koherens hullámot "összeadni". Most mindössze annyi a különbség, hogy a rés minden egyes pontjából kiinduló gömbhullámok terét kell fázishelyesen összeadni; az összegzés természetesen integrálást jelent. Figyelembe kell még azt is vennünk, hogy a gömbhullám intenzitása a távolság négyzetével fordítva arányos. Egy gömbhullám elektromos terének nagyságát a forrástól  távolságban a következő formulával adhatjuk meg:
távolságban a következő formulával adhatjuk meg:
![\[ E(r,t) = \frac{E_{\circ}}{r}exp\left[i(kr-\omega t)\right] \]](/images/math/2/4/9/2492ec6e55b02ec3673292fbdf6874f9.png) |
(2.3.1) |
Az előző ábra jelöléseivel (most még csak egy pontforrást feltételezve):
![\[ E(\vec r\,',t) = \frac{E_{\circ}}{\left| \vec r\,'- \vec r\, \right| }exp\left[i(k\left| \vec r\,'- \vec r\, \right|-\omega t)\right] \]](/images/math/b/e/b/beb833a901a32cf551f1a84bdc9962d3.png) |
(2.3.2) |
Amennyiben a gömbhullám elektromos terét szeretnénk megkapni az ernyő síkjában, akkor ez utóbbi tagot meg kell még szorozni a térerősségvektor és az ernyő síkja közötti szög koszinuszával.
![\[ E'(\vec r\,',t) = \frac{E_{\circ}}{\left| \vec r\,'- \vec r\, \right| }exp\left[i(k\left| \vec r\,'- \vec r\, \right|-\omega t)\right]\cos\theta \]](/images/math/b/e/2/be2018b45525c10865849217f387b233.png) |
(2.3.3) |
A  szög függ a pontforrás és az ernyőn vizsgálandó pont helyzetétől is:
szög függ a pontforrás és az ernyőn vizsgálandó pont helyzetétől is: 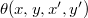 .
Most jön az összegzés a rés összes pontforrására:
.
Most jön az összegzés a rés összes pontforrására:
![\[ E'(\vec r\,',t) = \int\limits_A \frac{E_{\circ}}{\left| \vec r\,'- \vec r\, \right| }exp\left[i(k\left| \vec r\,'- \vec r\, \right|-\omega t)\right]\cos\theta dxdy \]](/images/math/6/6/b/66b4f3c669f5b5df08b0d0e28d8e661d.png) |
(2.3.4) |
Az integrált a rés felületére kell elvégezni. /Síkhullám esetében természetesen 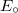 állandó, de általános esetben ez egy komplex
állandó, de általános esetben ez egy komplex 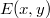 lehet./ Ez a formula mindössze egy konstans szorzóban különbözik a résen történő elhajlást leíró Fresnel-féle diffrakciós formulától. Némi programozói tudással felvértezve érdemes "kipróbálni" a 2.3.4-es formulát és numerikus szimulációval kiszámítani téglalap és kör alakú nyílás elhajlási képét.
lehet./ Ez a formula mindössze egy konstans szorzóban különbözik a résen történő elhajlást leíró Fresnel-féle diffrakciós formulától. Némi programozói tudással felvértezve érdemes "kipróbálni" a 2.3.4-es formulát és numerikus szimulációval kiszámítani téglalap és kör alakú nyílás elhajlási képét.
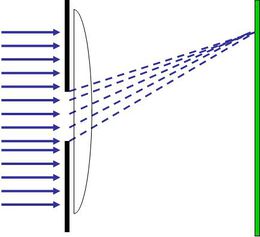
Különböző alakú rések elhajlási képének, vagy tárgyakon történő fényelhajlás kiszámításánál általában a gyakorlati alkalmazások szempontjából két esetet különböztetünk meg. Az egyik esetben az ernyő nincs túl nagy távolságra a rés mögött (2.3.4.a ábra), ezt nevezzük Fresnel-diffrakciónak (általános esetben a rést megvilágító fényforrás is véges távolságban van a réstől). A másik tipikus elrendezésben az ernyő nagyon távol (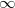 távol) van a réstől; ez a Fraunhofer-diffrakció (2.3.4. b ábra), amely határesete a Fresnel-diffrakciónak. A laboratóriumi vizsgálatokban nem szükséges nagyon messzire tenni az ernyőt a rés síkjától. Mindössze egy, közvetlenül a rés mögé helyezett gyűjtőlencse fókusztávolságában elhelyezett ernyőn (2.3.4. c ábra) kell a diffrakciós képet megfigyelni. (A gyűjtőlencse a végtelen távoli pontforrás képét a fókuszsíkra képezi le.)
távol) van a réstől; ez a Fraunhofer-diffrakció (2.3.4. b ábra), amely határesete a Fresnel-diffrakciónak. A laboratóriumi vizsgálatokban nem szükséges nagyon messzire tenni az ernyőt a rés síkjától. Mindössze egy, közvetlenül a rés mögé helyezett gyűjtőlencse fókusztávolságában elhelyezett ernyőn (2.3.4. c ábra) kell a diffrakciós képet megfigyelni. (A gyűjtőlencse a végtelen távoli pontforrás képét a fókuszsíkra képezi le.)
| 2.3.4.a ábra | 2.3.4.b ábra | 2.3.4.c ábra |
Néhány egyszerű elrendezés esetén analitikusan is meg lehet kapni az elhajlási képet. Először a Fraunhofer-diffrakció alkalmazásárára látunk néhány alkalmazást.
Fraunhofer-diffrakció
Elhajlás résen
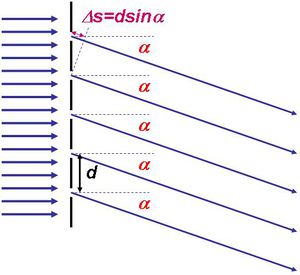
Tekintsünk egy  szélességű, hosszú rést (
szélességű, hosszú rést (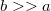 ). Modellünket még tovább egyszerűsíthetjük. Tegyük fel, hogy a résnek a hosszabbik szimmetriatengelye (
). Modellünket még tovább egyszerűsíthetjük. Tegyük fel, hogy a résnek a hosszabbik szimmetriatengelye ( ) mentén transzlációs szimmetriája van, így vizsgálatainkat leegyszerűsíthetjük egy kétdimenziós problémára, ráadásul korlátozzuk magunkat a kis szögű elhajlásra (
) mentén transzlációs szimmetriája van, így vizsgálatainkat leegyszerűsíthetjük egy kétdimenziós problémára, ráadásul korlátozzuk magunkat a kis szögű elhajlásra ( 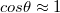 ). Ezt a két egyszerűsítést elfogadva a 2.3.4 összefüggést a következő alakban írhatjuk fel (az időfüggést szeparáltuk):
). Ezt a két egyszerűsítést elfogadva a 2.3.4 összefüggést a következő alakban írhatjuk fel (az időfüggést szeparáltuk):
![\[ E'(\vec r\,',t) = exp(-i\omega t)\int\limits_{-a/2}^{a/2} \frac{E_{\circ}}{\left| \vec r\,'- \vec r\, \right| }exp\left[ik\left| \vec r\,'- \vec r\, \right|\right] dxdy \]](/images/math/c/7/4/c74107e59c0c3245802d8e50c4710f52.png) |
(2.4.1.1) |
Minthogy az elhajlási kép a végtelen távoli ernyőn jelenik meg, ezért:
![\[ \frac{1}{\left| \vec r\,'- \vec r\, \right| } \approx \frac{1}{R} \]](/images/math/d/1/9/d19bf69d4bcd7c9e05a21c5f485b2720.png) |
(2.4.1.2) |
ahol  a rés közepe és a nagyon távoli pont közötti távolság.
a rés közepe és a nagyon távoli pont közötti távolság.
Az átlátszatlan falon lévő rés valamely pontjának fázistényezőjére a következő ábra
| 2.4.1.1 ábra |
jelöléseit felhasználva kapjuk, hogy:
![\[ exp\left[i(k(R+\Delta s))\right] = exp\left[i(k(R+xsin\alpha))\right] \]](/images/math/1/5/b/15ba9cd223db5f848a91e379d1e2f48b.png) |
(2.4.1.3) |
Ezt az eredményt alkalmazva és az időfüggést elhagyva, majd az összes konstanst egy tagba összegyűjtve a 2.4.1.1 összefüggést a következő alakra egyszerűsíthetjük:
![\[ E'(\alpha) = K \int\limits_{-a/2}^{a/2} exp\left[ikxsin\alpha \right] dx \]](/images/math/6/6/e/66eb818d4a6243fe30ca0146377cef1a.png) |
(2.4.1.4) |
Az integrált kiszámíthatjuk:
![\[ E'(\alpha) = \frac{-iK}{ksin\alpha}\left[exp(ikxsin\alpha )\right]^{+a/2}_{-a/2} \]](/images/math/3/5/6/35670c51dacc8a1cee07960d24599506.png) |
(2.4.1.5) |
Ezt most részletesebben is kiírhatjuk:
![\[ E'(\alpha) = -iK \frac{1}{ \frac{k}{2}sin(\alpha) } \frac{exp\left(i \frac{kasin( \alpha )}{2} \right) - exp\left(-i \frac{kasin( \alpha )}{2} \right)}{2} \]](/images/math/5/6/e/56e312e6622e291e621cd49582d02cc5.png) |
(2.4.1.6) |
Ugyanez egyszerűbb alakban:
![\[ E'(\alpha) = Ka \frac{sin\left(\frac{kasin( \alpha )}{2} \right) }{ \frac{k}{2}asin(\alpha)} \]](/images/math/7/2/e/72eb88943865713530aab84f8bcd5a54.png) |
(2.4.1.7) |
Minthogy az intenzitás arányos az 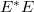 -vel, így a diffrakciós kép intenzitásfüggése:
-vel, így a diffrakciós kép intenzitásfüggése:
![\[ I(\alpha) = I_o \left( \frac{sin\beta}{\beta} \right)^2 \]](/images/math/7/1/5/715ca0e7791419edfcbaec2368f21f8c.png) |
(2.4.1.8) |
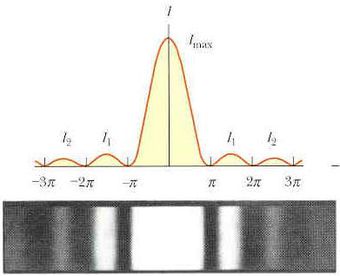
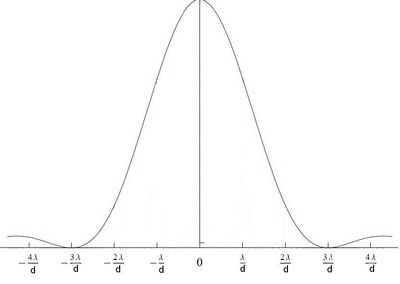
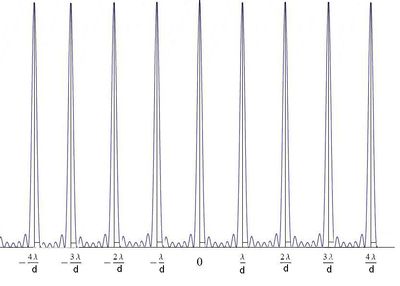
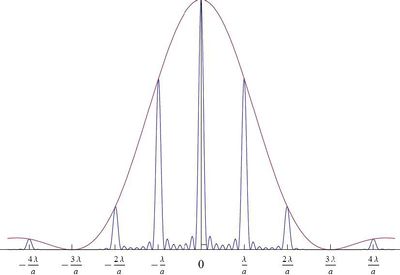
ahol 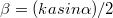 . A mérések is igen jó egyezést mutatnak az elért eredménnyel; jól demonstrálja ezt a következő ábrán látható grafikon és elhajlási kép:
. A mérések is igen jó egyezést mutatnak az elért eredménnyel; jól demonstrálja ezt a következő ábrán látható grafikon és elhajlási kép:
| 2.4.1.2 ábra |
A 2.4.1.8 összefüggés alapján nyilvánvaló, hogy sötét csík, azaz kioltás, vagyis minimális intenzitású hely ott található, ahol 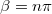 , vagyis:
, vagyis:
![\[ \frac{kasin( \alpha )}{2} = n\pi \qquad {\rm azaz } \qquad \frac{2\pi}{\lambda} \frac{asin( \alpha )}{2} = n\pi \]](/images/math/d/4/a/d4a576ca4665c62a7689cefdbb5b8b05.png) |
(2.4.1.9) |
Tehát a minimumhelyek:
![\[ sin \alpha_{min} = n\frac{\lambda}{a} \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/9/1/d/91d55e42ca9804c7f930e6c2a356e8b6.png) |
(2.4.1.10) |
Az  jelentése: az
jelentése: az  szögben szóródott nulladrend (a legintenzívebb folt) megjelenése.
szögben szóródott nulladrend (a legintenzívebb folt) megjelenése.
A minimális intenzitású helyek között körülbelül középen (a két szomszédos minimum helyétől számítva) találhatók a maximális intenzitás csúcsai.
A minimális intenzitású (sötét) foltok helyzetét megkaphatjuk sokkal egyszerűbb módon is.
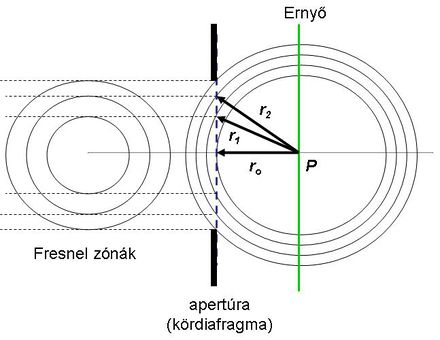
Osszuk fel a rést egyenközű, úgynevezett Fresnel zónákra. Amennyiben két szomszédos zóna aljáról - az  szöggel jellemezhető irányba - induló fénysugarak közötti úthosszkülönbség éppen fél hullámhossznyi (2.4.1.3 ábra), akkor a két szomszédos zóna sugarai éppen kioltják egymást.
szöggel jellemezhető irányba - induló fénysugarak közötti úthosszkülönbség éppen fél hullámhossznyi (2.4.1.3 ábra), akkor a két szomszédos zóna sugarai éppen kioltják egymást.
| 2.4.1.3 ábra |
Ezt könnyű belátni, hiszen nem csak a két zóna két legalsó pontját lehet így párba állítani, hanem mindegyik olyan pontpárra fennáll a 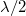 úthosszkülönbség, amelyek ugyanakkora távolságban vannak a saját zónájuk aljától. Ha tehát páros számú zónára lehet felosztani a rést, és az előbb említett feltétel kielégül, akkor a szomszédos zónák páronként kioltják egymást. Ugyanez matematikai alakban:
úthosszkülönbség, amelyek ugyanakkora távolságban vannak a saját zónájuk aljától. Ha tehát páros számú zónára lehet felosztani a rést, és az előbb említett feltétel kielégül, akkor a szomszédos zónák páronként kioltják egymást. Ugyanez matematikai alakban:
![\[ \frac{a}{2n}sin\alpha_{min} = \frac{\lambda}{2} \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/3/a/5/3a587e7405b5b778c90d816940e180e9.png) |
(2.4.1.11) |
azaz:
![\[ sin\alpha_{min} = n\frac{\lambda}{a} \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/7/a/a/7aa42c746e2bd8201b9267c0ebe0480a.png) |
(2.4.1.12) |
Ez pedig pontosan ugyanaz az eredmény, mint amit a diffrakciós formula alkalmazásával kaptunk (2.4.1.10).
Diffrakció kör alakú nyíláson (diafragmán)
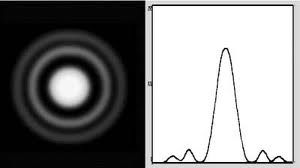
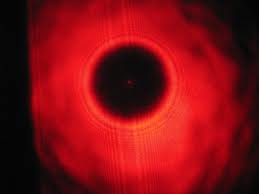
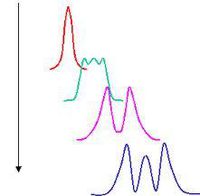
Kör alakú nyílás elhajlási képe egy interferencia gyűrűrendszer (2.4.2.1 ábra).
| 2.4.2.1 ábra |
Megfigyelhetjük, hogy középen megjelenik egy nulladrendű maximum, a legintenzívebb kör alakú folt, majd ezt veszi körbe a világos és sötét gyűrűk rendszere. Ennek a gyűrűrendszernek az intenzitás-eloszlása természetesen mérhető (2.4.2.2 ábra), viszont a matematikai leírás jóval bonyolultabb, mint a hosszú, keskeny, téglalap alakú rés esetében.
| 2.4.2.2 ábra |
A minimumhelyek helyzetét, azaz, hogy az első, a második és a többi sötét gyűrű mekkora szögben látszik (a 2.4.1.3 ábrához hasonlót kell elképzelni) azonban egy, a 2.4.1.12 – hoz hasonló formula segítségével adhatjuk meg:
![\[ Dsin\alpha_{min} = p_n \lambda \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/f/d/c/fdc21604b7e112b626ab5e7f08ada9f3.png) |
(2.4.2.1) |
Itt  a diafragma átmérője, a
a diafragma átmérője, a 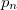 együtthatókat Sir George Airy határozta meg (
együtthatókat Sir George Airy határozta meg (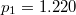 ,
, 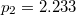 ,
, 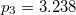 ,
, 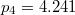 …).
…).
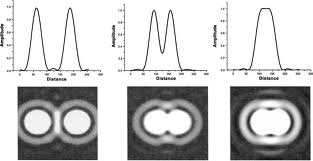
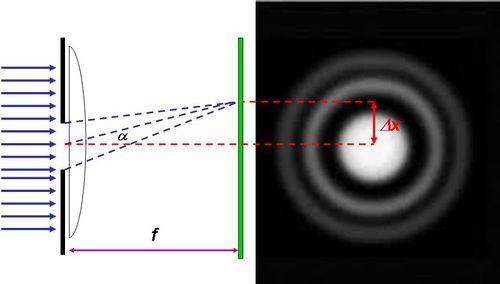
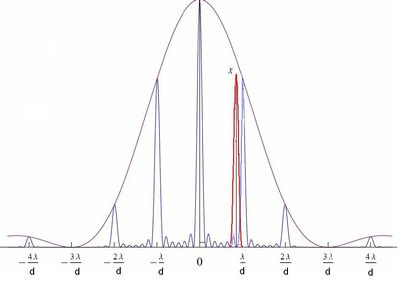
Most képzeljük el, hogy a diafragmától, annak átmérőjéhez képest sokkal nagyobb távolságra az optikai tengely (a kör alakú nyílás közepén átmenő, annak síkjára merőleges egyenes) közelében van két pontszerű fényforrás. Ezen két pontforrás Fraunhofer elhajlási képe – azaz a kör alakú nyílás mögé helyezett lencsével annak fókuszsíkjába helyezett ernyőn látható képe – két egymásra rakódott gyűrűrendszer (2.4.2.3 ábra).
| 2.4.2.3 ábra |
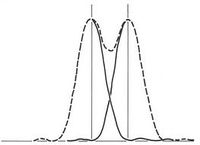
Itt látható, hogy még viszonylag könnyedén megkülönböztető a két forrás képe. Ha azonban a két pontforrás kisebb szögben látszik (vagyis közelebb vannak egymáshoz azonos távolságot feltételezve), akkor már nehezebb a két pont képét egymástól elkülöníteni (2.4.2.4 és 2.4.2.5 ábra).
| 2.4.2.4 ábra |
| 2.4.2.5 ábra |
Felvetődik a kérdés, hogy például egy D átmérőjű távcsőnek mekkora a felbontása, azaz mekkora szögben látszik két pont, hogy még éppen megkülönböztethessük őket. Annak érdekében, hogy kvantitatív megállapítást tehessünk, azaz hogy egy optikai eszköz – egy távcső vagy mikroszkóp – felbontását egy számmal jellemezhessünk, egy megállapodáson alapuló kritériumot érdemes elfogadni. Megállapodás szerint akkor tudjuk még két, azonos intenzitású pontforrás képét felbontani, ha az egyiknek a főmaximuma (az elhajlási kép középső csúcsa) a másik elsőrendű minimumát adó sötét gyűrűre esik (2.4.2.6 ábra). Ez a Rayleigh-feltétel.
| 2.4.2.6 ábra |
Tehát kör alakú apertúránál a maximális felbontást a 2.4.2.1 felhasználásával a következőképpen adhatjuk meg:
![\[ sin\alpha_{min} = 1.22 \frac{\lambda}{D} \]](/images/math/d/a/c/dac1a485858e23e82387fde62b065994.png) |
(2.4.2.2) |
Amennyiben kis szögekről van szó (a gyakorlatban általában ez megvalósul), élhetünk a közelítéssel, vagyis:
![\[ \alpha_{min} = 1.22 \frac{\lambda}{D} \]](/images/math/4/2/e/42e3595443c2b008d28f6d499f925358.png) |
(2.4.2.3) |
Itt az 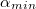 természetesen radiánban értendő.
természetesen radiánban értendő.
A fókuszsíkra történő leképezés esetében az elsőrendű minimumot jelentő gyűrű sugarát jelöljük  -el, amely a Raileigh-kritérium szerint két, még éppen felbontható képpont távolságát jelenti.
-el, amely a Raileigh-kritérium szerint két, még éppen felbontható képpont távolságát jelenti.
| 2.4.2.7 ábra |
Az ábráról leolvasható, hogy 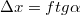 . Kis szögek esetében
. Kis szögek esetében 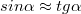 . A felbontást megadó 2.4.2.2 formula felhasználásával kapjuk:
. A felbontást megadó 2.4.2.2 formula felhasználásával kapjuk:
![\[ \Delta x = 1.22 \frac{\lambda}{D}f \]](/images/math/e/7/3/e73e954e6fadaccd70b26d50c06351ae.png) |
(2.4.2.4) |
Könnyű leolvasni ezen legutóbbi eredmény jelentését; minél kisebb a fény hullámhossza illetve minél nagyobb átmérőjű a távcső objektíve, annál kisebb 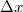 , azaz annál nagyobb az eszköz felbontása. (Ezért építenek ma már akár 10 méternél nagyobb átmérőjű Newton-rendszerű távcsöveket.) Hasonló megfontolások érvényesek a mikroszkóp felbontására is. Az előzőekben bemutatott jelenség magyarázata teszi érthetővé azt a sok felhasználó által is ismert tényt, miszerint az egyre kisebb hullámhossz és az egyre nagyobb numerikus apertúra alkalmazása a CD illetve a DVD olvasó fej esetében egyre nagyobb írássűrűséget (adatsűrűséget) jelent.
, azaz annál nagyobb az eszköz felbontása. (Ezért építenek ma már akár 10 méternél nagyobb átmérőjű Newton-rendszerű távcsöveket.) Hasonló megfontolások érvényesek a mikroszkóp felbontására is. Az előzőekben bemutatott jelenség magyarázata teszi érthetővé azt a sok felhasználó által is ismert tényt, miszerint az egyre kisebb hullámhossz és az egyre nagyobb numerikus apertúra alkalmazása a CD illetve a DVD olvasó fej esetében egyre nagyobb írássűrűséget (adatsűrűséget) jelent.
| 2.4.2.8 ábra |
Elhajlás optikai rácson
Egy hosszú, vékony rés elhajlási képében – mint azt az előző fejezetben láttuk – a maximális és a minimális intenzitású foltok illetve vonalak helyzete nem csak az elhajlás szögétől, hanem a fény hullámhosszától is függ (2.4.1.8 és 2.4.1.10). Amennyiben a rést nem monokromatikus fénnyel világítjuk meg, hanem például egy higanygőz lámpa kollimált fényével, akkor azt várhatnánk, hogy a különböző hullámhosszú nyalábok más-más irányba diffraktálódnak. Ez többé-kevésbé igaz is, azonban a viszonylag széles maximumok általában átfedik egymást és így szinte lehetetlen különválasztani a különböző színű (különböző hullámhosszúságú) komponenseit. Létrehozhatunk azonban egyetlen rés helyett egy olyan eszközt (2.4.3.1 ábra), amely egymással párhuzamos, azonos síkban, egymástól azonos  távolságban kialakított rések sorozatából áll, ez egy optikai rács.
távolságban kialakított rések sorozatából áll, ez egy optikai rács.
| 2.4.3.1 ábra |
Azt várjuk, hogy egy ilyen eszköz alkalmas lehet különböző hullámhosszkomponensek szétválasztására. Az optikai rácsra eső fehér fény felbontása látható a következő ábrán.
| 2.4.3.2 ábra |
Ahhoz, hogy az optikai rács működését megértsük, tekintsük a legegyszerűbb elrendezést (2.4.3.3 ábra).
| 2.4.3.3 ábra |
A rács normálisának irányából érkező monokromatikus síkhullám azokba az irányokba diffraktálódik, amelyekre teljesül a következő (az interferenciajelenségeket tárgyaló fejezetben már említett) feltétel: a két szomszédos, ugyanabba az irányba induló nyaláb közötti 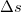 úthosszkülönbség a
úthosszkülönbség a  hullámhossz egész számú többszöröse (2.4.3.1).
hullámhossz egész számú többszöröse (2.4.3.1).
![\[ dsin\alpha_{n} = n \lambda \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/e/4/7/e477fd8eeae371658a733a2f8ac6d9a2.png) |
(2.4.3.1) |
Az optikai rács Fraunhofer elhajlási képét egy gyűjtőlencse alkalmazásával az attól fókusztávolságban felállított ernyőn kapjuk. (2.4.3.4 ábra).
| 2.4.3.4 ábra |
A 2.4.3.1 által leírt feltétel megadja ugyan, hogy mely irányokba diffraktálódik a fény, azonban az elhajlási kép intenzitás-eloszlásáról még semmit nem tudunk mondani. A szomszédos nyalábok közötti úthosszkülönbség 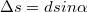 . Az ehhez tartozó fáziskülönbség:
. Az ehhez tartozó fáziskülönbség:
![\[ \Delta \varphi = \frac{2\pi}{\lambda}\Delta s = \frac{2\pi}{\lambda}dsin\alpha \]](/images/math/8/6/d/86dfe68b3ca29980ceea6e57f4029968.png) |
(2.4.3.2) |
Az ernyő egy adott  pontjában – melyet meghatároz az
pontjában – melyet meghatároz az  szög – kiszámíthatjuk az eredő térerősség nagyságát, ha fázishelyesen összegezzük az összes, az optikai rácsot alkotó
szög – kiszámíthatjuk az eredő térerősség nagyságát, ha fázishelyesen összegezzük az összes, az optikai rácsot alkotó  számú rés által diffraktált hullámot, azaz:
számú rés által diffraktált hullámot, azaz:
![\[ E(\alpha) = Ka\frac{sin \left(\frac{k}{2} asin\alpha \right)}{\left(\frac{k}{2} asin\alpha \right)} \left[1 + e^{i\varphi} + e^{i2\varphi} + ... + e^{i(N-1)\varphi} \right] \]](/images/math/e/e/8/ee8965fcc3b37ccdf986841c3decdb49.png) |
(2.4.3.3) |
Itt azt vettük figyelembe, hogy az első rés hullámához képest a második 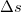 -el, a harmadik
-el, a harmadik 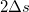 -el, stb. hosszabb utat tesz meg. Ez természetesen azt jelenti, hogy a fáziskülönbség az első és a második között
-el, stb. hosszabb utat tesz meg. Ez természetesen azt jelenti, hogy a fáziskülönbség az első és a második között 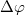 , az első és a harmadik között
, az első és a harmadik között 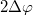 , valamint az első és az
, valamint az első és az  -edik között
-edik között 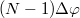 . (Az előző formula jobb oldalán a kapcsos zárójel előtti tag pedig az első rés által diffraktált hullám elektormos térerősségének nagysága (2.4.1.7).) Könnyű észrevenni, hogy a kapcsos zárójelben lévő tag egy mértani sor, így:
. (Az előző formula jobb oldalán a kapcsos zárójel előtti tag pedig az első rés által diffraktált hullám elektormos térerősségének nagysága (2.4.1.7).) Könnyű észrevenni, hogy a kapcsos zárójelben lévő tag egy mértani sor, így:
![\[ 1 + e^{i\varphi} + e^{i2\varphi} + ... + e^{i(N-1)\varphi} = \frac{1-e^{iN\varphi}}{1-e^{i\varphi}} \]](/images/math/1/1/2/112a8f5db88f0e851d87b219050f649c.png) |
(2.4.3.4) |
Ezt még tovább alakíthatjuk azért, hogy végül az intenzitásra egyszerűbb alakot kaphassunk:
![\[ 1 + e^{i\varphi} + e^{i2\varphi} + ... + e^{i(N-1)\varphi} = \frac{e^{i\frac{N}{2}\varphi}-e^{-i\frac{N}{2}\varphi}}{e^{i\frac{\varphi}{2}}-e^{-i\frac{\varphi}{2}}} e^{i\left(\frac{N}{2} - 1 \right)\varphi} \]](/images/math/d/6/c/d6c02f5367eebdc6e6af74ce743c82fa.png) |
(2.4.3.5) |
Az Euler-formula alkalmazásával további átalakításra nyílik lehetőség, így:
![\[ E(\alpha)=Ka\frac{sin\left(\frac{kasin( \alpha )}{2} \right) }{ \frac{k}{2}asin(\alpha)}\frac{sin\left(N\frac{\pi}{\lambda}dsin( \alpha )\right) }{ \left(N\frac{\pi}{\lambda}dsin( \alpha )\right)}e^{i\left(\frac{N}{2} - 1 \right)\varphi} \]](/images/math/7/8/0/780d3105fdd5f568c682a3a8521f6cec.png) |
(2.4.3.6) |
Az intenzitás-eloszlást pedig a 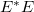 szorzat kiszámításával kaphatjuk meg:
szorzat kiszámításával kaphatjuk meg:
![\[ I(\alpha)=I_o f(\alpha)g(\alpha) =I_o \frac{sin^2 \left(\frac{kasin( \alpha )}{2} \right) }{ \left(\frac{k}{2}asin(\alpha)\right)^2}\frac{sin^2 \left(N\frac{\pi}{\lambda}dsin( \alpha )\right) }{ \left(N\frac{\pi}{\lambda}dsin( \alpha )\right)^2} \]](/images/math/e/8/0/e808da8db4bb3eee7a12adb8c874558a.png) |
(2.4.3.7) |
Azért, hogy szemléletesebbé tegyük ezt az eredményt, tekintsük egy hét résből álló rács diffraktált nyalábjának intenzitás-eloszlását az ernyőn. Először nézzük meg, hogy milyen is az 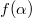 függvény grafikonja (2.4.3.5 ábra)! Az egyszerűbb áttekinthetőség miatt a vízszintes tengely
függvény grafikonja (2.4.3.5 ábra)! Az egyszerűbb áttekinthetőség miatt a vízszintes tengely 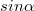 -val skálázódik.
-val skálázódik.
| 2.4.3.5 ábra |
Most ábrázoljuk külön a 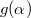 -t:
-t:
| 2.4.3.6 ábra |
A két függvény szorzata (a konstans együtthatók elhagyásával):
| 2.4.3.7 ábra |
A 2.4.3.7 összefüggés felhasználásával nem nehéz megmutatni, hogy két főmaximum között 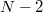 mellékmaximum van.
mellékmaximum van.
Az előbbiekben leírt rácshatásra a hétköznapi életben is találunk példákat. Ha egy igen sűrű szövésű függöny kis részére esik csak napfény, akkor odapillantva színes foltokat láthatunk. Gyakrabban megfigyelhető jelenség a fehér fénnyel megvilágított CD "színjátéka":
| 2.4.3.8 ábra |
Most lássunk egy gyakorlati alkalmazást! Valamely felhevített gáz – legyen ez most H-gáz – által kisugárzott fény egy részéből kollimált nyalábot formálunk. Ezzel megvilágítjuk a 2.4.3.4 ábrán látható eszközt (spekrtoszkópot), majd az ernyőt egy fotólemezzel, vagy egy kamerával helyettesítjük, akkor felvehetjük a H emissziós spektrumát (2.4.3.9 ábra).
| 2.4.3.9 ábra |
Ezen a spektrumon megfigyelhetjük, hogy a különböző hullámhosszak jól elkülönülnek, de azt is láthatjuk, hogy 400 nm körül a spektrumvonalak már egyre közelebb vannak egymáshoz. Egy rácsos spektroszkóp vagy spektrográf (amellyel a felvétel rögzíthető) "lelke" maga az optikai rács. A 2.4.3.9 ábrán látható spektrumra tekintve felvetődik a kérdés, hogy mekkora egy ilyen eszköz felbontása, azaz milyen közel lehet egymáshoz két spektrumvonal (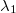 és
és 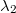 ), hogy még éppen megkülönböztethessük azokat. Az optikai rács felbontását - minthogy ez általában egynél jóval nagyobb érték - egy arányszámmal jellemezzük:
), hogy még éppen megkülönböztethessük azokat. Az optikai rács felbontását - minthogy ez általában egynél jóval nagyobb érték - egy arányszámmal jellemezzük:
![\[ R = \frac{\lambda}{\Delta \lambda} \]](/images/math/b/b/5/bb5f84a01c878f3aa5c3394d0eb67829.png) |
(2.4.3.8) |
ahol 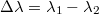 és minthogy
és minthogy 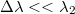 , így
, így 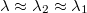 .
.
Két különböző hullámhosszhoz azonos rendben tartozó főmaximum megkülönböztethetősét a Rayleigh-feltétel alkalmazásával vizsgálhatjuk. Ha tehát az egyik főmaximuma a másik főmaximum melletti minimumhelyére esik, akkor még éppen azonosíthatók a spektrumvonalak és nem olvadnak egybe (a 2.4.3.10 ábrán az egyszerűbb ábrázolhatóság miatt az elsőrendben ábrázoltuk a feltételt kielégítő megoldást).
| 2.4.3.10 ábra |
A rács elhajlási képének intenzitáseloszlását megadó 2.4.3.7 formula vizsgálatából megállapítható, hogy a főmaximum és a mellette található minimum helyének különbsége fázisban éppen 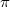 (természetesen radiánban). Tehát a Rayleigh-kritérium a két spektrumvonal felbontására akkor teljesül, ha:
(természetesen radiánban). Tehát a Rayleigh-kritérium a két spektrumvonal felbontására akkor teljesül, ha:
![\[ N\frac{\pi}{\lambda_1}dsin\alpha_{max}= N\frac{\pi}{\lambda_2}dsin\alpha_{max}-\pi \]](/images/math/c/5/0/c500e2d3be0f1a69a2aa9ad77edca36d.png) |
(2.4.3.9) |
Ezután felhasználhatjuk a maximumok irányát megadó 2.4.3.1 feltételt:
![\[ dsin\alpha_{max} = m\lambda_1 \quad \Longrightarrow \quad sin\alpha_{max} = m\frac{\lambda_1}{d} \]](/images/math/f/4/1/f41fee011d1e98422ec49c95390edcad.png) |
(2.4.3.10) |
A 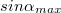 - ra adódott eredményt behelyettesíthetjük 2.4.3.9-be, majd az egyszerűsítéseket elvégezve kapjuk:
- ra adódott eredményt behelyettesíthetjük 2.4.3.9-be, majd az egyszerűsítéseket elvégezve kapjuk:
![\[ Nm = Nm \frac{\lambda_1}{\lambda_2}-1 \]](/images/math/7/7/3/7730d87f81089df3c9bb01a97d92e3b9.png) |
(2.4.3.11) |
A 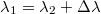 összefüggést felhasználva már csak elemi átalakításokat kell elvégezni, hogy kifejezhessük az optikai rács felbontóképességét:
összefüggést felhasználva már csak elemi átalakításokat kell elvégezni, hogy kifejezhessük az optikai rács felbontóképességét:
![\[ R = Nm \]](/images/math/b/4/f/b4f3715b105d04c92082940f9a810672.png) |
(2.4.3.12) |
A rács felbontása tehát annál jobb (nagyobb), minél magasabb rendben végezzük a mérést és a rácsot alkotó rések száma minél több.
A nagyfelbontású optikai spektroszkópia fontos eszköz az atomok és a molekulák szerkezetének tanulmányozásában. A Doppler-effektus figyelembe vételével spektroszkópiai vizsgálatok segítségével sikerült Hubble-nak igazolnia az univerzum tágulását. A Nap fényének spektroszkópiai analízise mutatott rá egy új elem, az akkor a Földön még nem azonosított hélium létezésére is.
A törésmutató hullámhosszfüggésén alapul a prizmás spektroszkóp működése (2.4.3.11 ábra).
| 2.4.3.11 ábra |
A precízebb vizsgálatokhoz általában rácsos spektrométert alkalmaznak, mert annak nagyobb a felbontása. A felbontóképességen kívül jellemezhetjük még mindkét eszközt egy másik paraméter definiálásával is; ez a diszperzió (vagy szögdiszperzió):
![\[ D = \frac{d\alpha}{d\lambda} \]](/images/math/e/a/a/eaa452e6b556ec62dfd8c3d798800801.png) |
(2.4.3.13) |
Egy optikai rács diszperziója általában már első-rendben is nagyobb, mint egy üvegprizmáé.
A röntgen-diffrakció
Az optikai rács diffrakciójának tárgyalása után könnyen megérthetjük monokromatikus röntgennyalábok egykristályokon megfigyelhető Laue szóródását is. Egy "szabályos" kristályban (egykristályban) az atomok vagy a molekulák a térben periodikus rendeződést mutatnak. A 2.4.4.1 ábrán a grafitkristály szerkezeti ábrája látható; a kis körök egy-egy atomot reprezentálnak.
| 2.4.4.1 ábra |
Jól látszik, hogy a szomszédos kristálysíkok azonos távolságban vannak egymástól; a jellemző távolságot rácsállandónak hívják.
Az atomok elektronjain szóródnak a kristályra eső röntgenhullámok. Az atomok másodlagos pontforrásnak minősülnek. Amennyiben ezen pontforrások röntgen-hullámait koherens módon összegezzük, akkor megkapjuk a kristályon bizonyos irányokban diffraktálódott nyalábokat. A kísérleti vizsgálatokhoz használt elrendezés elvi vázlata látható a következő ábrán. (A vákuumcsőben felgyorsított elektronok az anódba becsapódnak, azaz igen kis távolságon lefékeződnek; közben az energiájuk egy jelentős részét röntgensugárzás formájában adják le.)
| 2.4.4.2 ábra |
A "megvilágítás" (vagy besugárzás) után a fotólemezen a képet fotokémiai eljárással hívják elő; ilyenkor a következő ábrához hasonlóan egy szimmetrikus mintázat szokott előállni.
| 2.4.4.3 ábra |
A jelenségre a magyarázatot Sir William Bragg adta meg. A röntgennyaláb hullámhossza (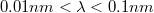 ) összemérhető a kristály rácsállandójával. Most tekintsük a következő ábrán látható szóródás mechanizmusát!
) összemérhető a kristály rácsállandójával. Most tekintsük a következő ábrán látható szóródás mechanizmusát!
| 2.4.4.4 ábra |
Jól látható, hogy a második és a harmadik kristálysík egymás alatti atomjairól szóródó nyalábok közötti úthossz-különbség 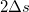 , ahol
, ahol 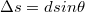 . A két nyaláb "fázisban van", ha az úthossz-különbség a hullámhossz egész számú többszöröse, vagyis:
. A két nyaláb "fázisban van", ha az úthossz-különbség a hullámhossz egész számú többszöröse, vagyis:
![\[ 2dsin\theta = n \lambda \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/4/1/c/41c9bad313e1f4c42c3917e76aa295e5.png) |
(2.4.4.1) |
Ez a Bragg-feltétel; ez határozza meg, hogy mely irányokban szóródik egy egykristályon a röntgennyaláb.
Könnyű belátni, hogy a porrá őrölt kristályokon (vagyis sok, kis, rendezetlen egykristályon) szóródó nyaláb esetén a Bragg-feltétel azt jelenti, hogy a kritérium alapján meghatározható  szögben diffraktálódó nyalábok a nulladrenddel, azaz a megvilágító nyalábbal (középső fényes folt)
szögben diffraktálódó nyalábok a nulladrenddel, azaz a megvilágító nyalábbal (középső fényes folt)  szöget zárnak be. A kristálydarabok véletlen orientációja miatt az előhívott fotólemezen koncentrikus gyűrűk láthatók (2.4.4.5 ábra).
szöget zárnak be. A kristálydarabok véletlen orientációja miatt az előhívott fotólemezen koncentrikus gyűrűk láthatók (2.4.4.5 ábra).
| 2.4.4.5 ábra |
A röntgendiffrakciós vizsgálati módszer az anyagvizsgálat nélkülözhetetlen eszköze. A DNS alakjának megfejtésében is kulcsfontosságú szerepet játszott. A 2.4.4.6.a ábrán a DNS röntgenelhajlási képe, míg a 2.4.4.6.b ábrán az ebből kiszámított, mindenki által ismert kettős spirál szimulált képe látható.
| 2.4.4.6.a ábra | 2.4.4.6.b ábra |
Fresnel-diffrakció
Amennyiben a megvilágított rés (vagy valamilyen tárgy) mögé nem teszünk egy gyűjtőlencsét és az ernyő nincs nagyon nagy távolságban a rés jellemző méreteihez képest, akkor a 2.3.4 integrál kiszámításával kaphatjuk meg az ernyőn az elektromos tér komponensét; ebből már adódik az intenzitás-eloszlás. Általános esetben numerikus módszerek alkalmazásával szimulálhatjuk az elhajlást. A Fresnel diffrakciós formula különböző közelítő módszerei segítségével általában jelentősen egyszerűsödik a számítás menete, de ezekkel a technikákkal nem foglalkozunk. Mindössze a kördiafragmán (kör alakú nyíláson) történő elhajlás speciális esetét tárgyaljuk. Tegyük fel, hogy a kördiafragmát (és az azt tartalmazó átlátszatlan falat) monokromatikus síkhullám világítja meg a normálisának irányából, vagyis a rés síkjában a hullám amplitúdója és fázisa mindenütt ugyanaz az érték. Ahhoz, hogy egy szemléletes modell segítségével kvalitatív állítást tehessünk, osszuk fel a 2.5.1 ábrán látható módon a kört koncentrikus körgyűrűkre.
| 2.5.1 ábra |
A  pontból a kör alakú nyílás közepéhez húzott sugár hosszát jelöljük
pontból a kör alakú nyílás közepéhez húzott sugár hosszát jelöljük  -val. Most vegyünk fel
-val. Most vegyünk fel 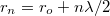 sugarú
sugarú 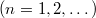 ,
,  középpontú gömböket, majd képezzük a kördiafragma síkjával vett metszetüket. Ezek – az ábra bal oldalán látható –
középpontú gömböket, majd képezzük a kördiafragma síkjával vett metszetüket. Ezek – az ábra bal oldalán látható – 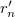 sugarú koncentrikus körök melyek a Fresnel-zónák határait jelölik ki. Elemi számítással megadhatjuk az
sugarú koncentrikus körök melyek a Fresnel-zónák határait jelölik ki. Elemi számítással megadhatjuk az 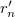 közelítő értékét felhasználva, hogy
közelítő értékét felhasználva, hogy
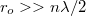 :
:
![\[ r'_n = \sqrt{\left(r_{\circ}+ n \frac{\lambda}{2} \right) ^2 - r^2_{\circ}} = \sqrt{n\lambda r_{\circ}+ n^2 \frac{\lambda^2}{4}} \approx \sqrt{n\lambda r_{\circ}} \qquad {\rm ahol } \qquad n=1,2,3,... \]](/images/math/c/5/f/c5fa7c214e216d1dd0a82ce16c6dcec4.png) |
(2.5.1) |
Szintén elemi számítással adódik, hogy az 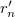 és
és 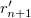 sugarú körök által meghatározott körgyűrű területe első közelítésben
sugarú körök által meghatározott körgyűrű területe első közelítésben 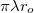 , vagyis független
, vagyis független  – től, azaz a körcikkek területe megegyezik. Minthogy
– től, azaz a körcikkek területe megegyezik. Minthogy 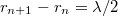 , tehát két, szomszédos körgyűrűből a
, tehát két, szomszédos körgyűrűből a  pontba érkező hullámok fáziskülönbsége
pontba érkező hullámok fáziskülönbsége 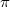 (a kördiafragma síkjában a fázisuk és az amplitúdójuk megegyezik), ezért a
(a kördiafragma síkjában a fázisuk és az amplitúdójuk megegyezik), ezért a  pontban éppen kioltják egymást. Ezt az első pillanatban talán kissé hihetetlen eredményt kísérletileg viszonylag könnyű igazolni az ernyő mozgatásával. Ha az ernyőt az optikai tengelyre merőlegesen mozgatjuk, azaz
pontban éppen kioltják egymást. Ezt az első pillanatban talán kissé hihetetlen eredményt kísérletileg viszonylag könnyű igazolni az ernyő mozgatásával. Ha az ernyőt az optikai tengelyre merőlegesen mozgatjuk, azaz 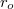 változtatásával elérjük, hogy kördiafragma páratlan vagy páros számú körgyűrűvel, Fresnel-zónával fedhető le, akkor az ernyő
változtatásával elérjük, hogy kördiafragma páratlan vagy páros számú körgyűrűvel, Fresnel-zónával fedhető le, akkor az ernyő  pontja körüli centrális folt fényes vagy sötét lesz; összhangban az előzőekkel. Mindez jól bizonyítja a fény hullámtulajdonságát.
Rögtön felvetődik a kérdés, hogy az azonos területű körcikkekkel meg lehet-e magyarázni egy kör alakú akadály (körlap vagy gömb) mögött kialakuló hullámtér optikai tengelyen mérhető intenzitáseloszlását. A körlap síkjában vegyük fel az
pontja körüli centrális folt fényes vagy sötét lesz; összhangban az előzőekkel. Mindez jól bizonyítja a fény hullámtulajdonságát.
Rögtön felvetődik a kérdés, hogy az azonos területű körcikkekkel meg lehet-e magyarázni egy kör alakú akadály (körlap vagy gömb) mögött kialakuló hullámtér optikai tengelyen mérhető intenzitáseloszlását. A körlap síkjában vegyük fel az 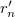 sugarú koncentrikus köröket. Az azonos területű körcikkek közül az első, amelyiknek a külső széle a körlapon kívül esik, fogja meghatározni a szimmetriatengelyen a fény intenzitását, hiszen az összes többi egymás után következők páronként éppen kiejtik egymást. Ennek az a következménye, hogy a körlap (vagy gömb) mögött a fénytér közepén mindig világos folt, az úgynevezett Poisson-féle folt (2.5.2 ábra) látható.
sugarú koncentrikus köröket. Az azonos területű körcikkek közül az első, amelyiknek a külső széle a körlapon kívül esik, fogja meghatározni a szimmetriatengelyen a fény intenzitását, hiszen az összes többi egymás után következők páronként éppen kiejtik egymást. Ennek az a következménye, hogy a körlap (vagy gömb) mögött a fénytér közepén mindig világos folt, az úgynevezett Poisson-féle folt (2.5.2 ábra) látható.
| 2.5.2 ábra |
Ha egy meghatározott távolságra és hullámhosszra kiszámított 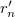 sugarú koncentrikus körök által meghatározott azonos területű körcikkek közül minden másodikat átlátszatlanná tesszük, akkor kapjuk a Fresnel-féle zónalemezt (2.5.3 ábra).
sugarú koncentrikus körök által meghatározott azonos területű körcikkek közül minden másodikat átlátszatlanná tesszük, akkor kapjuk a Fresnel-féle zónalemezt (2.5.3 ábra).
| 2.5.3 ábra |
Az előzőek alapján nyilvánvaló, hogy sokkal fényesebb foltot láthatunk az optikai tengely  pontjában (a zónalemez fókuszában), mintha nem lennének átlátszatlanok a páros sorszámú körcikkek (hiszen ilyenkor az elsőt leszámítva a többiek párban éppen kiejtenék egymást); ez szintén "fényes" bizonyítéka a fény hullámtermészetének.
pontjában (a zónalemez fókuszában), mintha nem lennének átlátszatlanok a páros sorszámú körcikkek (hiszen ilyenkor az elsőt leszámítva a többiek párban éppen kiejtenék egymást); ez szintén "fényes" bizonyítéka a fény hullámtermészetének.
A bemutatott közelítő módszer természetesen csak korlátozottan alkalmazható. Amikor például igen nagy számú zónalemezt veszünk figyelembe, akkor – mint az a következő ábrán is látható – az eredő térerősség, vagyis 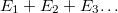 az
az 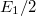 - höz tart (ez egy "hamis" kép, vagyis az első, a második, stb. körgyűrű által az
- höz tart (ez egy "hamis" kép, vagyis az első, a második, stb. körgyűrű által az  pontban létrehozott elektromos térerősség
pontban létrehozott elektromos térerősség 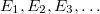 egymáshoz képest egy kicsit el vannak tolva).
egymáshoz képest egy kicsit el vannak tolva).
| 2.5.4 ábra |
Holográfia
A holografikus képrögzítés és a tárgy képének 3 dimenziós megjelenítése az interferencia és a diffrakció jelenségének alkalmazásán alapul. Az első hologramot Gábor Dénes készítette.
A legegyszerűbb hologram készítési elrendezés elvi vázlata látható a következő ábrán.
| 2.6.1 ábra |
A hologramlemezt (nagyfelbontású fotólemezt) a tárgyról szóródott fényen kívül még egy, a tárgyhullámmal koherens referenciahullám (a tárgyhullámmal interferenciára képes hullám) is megvilágítja. Ez a gyakorlatban általában azt jelenti, hogy egy lézer nyalábját egy féligáteresztő tükör segítségével két részre osztják, majd az egyikből lesz a referenciahullám, míg a másikkal megvilágítják a tárgyat (2.6.2 ábra).
| 2.6.2 ábra |
Azt, hogy a tárgyhullám és a referenciahullám koherens legyen a holografikus lemez síkjában azzal érik el, hogy a kettéválasztott lézernyaláb két fényútjának (referencia és tárgyhullám) hossza közötti különbséget a koherenciahossznál kisebbre állítják be. A két koherens hullám interferál, azaz a tárgyhullám 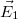 és a referenciahullám
és a referenciahullám 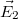 térerősségvektorai összeadódnak;
térerősségvektorai összeadódnak; 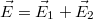 . Ezután a fotólemezt érő fényintenzitást is meghatározhatjuk, vagyis
. Ezután a fotólemezt érő fényintenzitást is meghatározhatjuk, vagyis 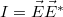 ; részletesebben:
; részletesebben:
![\[ I = (\vec E_1 + \vec E_2)(\vec E^*_1 + \vec E^*_2)= \vec E_1 \vec E^*_1 + \vec E_2 \vec E^*_2 + \vec E_1 \vec E^*_2 + \vec E_2 \vec E^*_1 \]](/images/math/c/7/3/c73044b2818cba88821e6b99b966a05c.png) |
(2.6.1) |
A jobboldalon álló első két tag a tárgy illetve a referenciahullám intenzitása, így:
![\[ I = I_1 + I_2 + \vec E_1 \vec E^*_2 + \vec E_2 \vec E^*_1 \]](/images/math/e/d/b/edb7b79ceff973e0dc416036cba2c16f.png) |
(2.6.2) |
A fotografikus lemezt az expozíció (megvilágítás) után fotokémiai eljárásokat alkalmazva előhívják. Elérhető, hogy az előhívott fotólemez transzmissziója arányos legyen a zselatinrétegben található, a fény hullámhosszánál is jóval kisebb ezüst-halogenid részecskék által elnyelt energiával. Ez azt jelenti, hogy a lemez transzmissziója egy meghatározott helyen arányos lesz az megvilágítás intenzitásával: 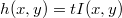 , tehát lefényképeztük a referencia és a tárgyhullám által létrehozott interferenciamintázatot, vagyis előállítottuk a hologramot. (A holografikus lemez természetesen oly módon is használható, és a gyakorlatban inkább ez valósul meg, hogy a lemez abszorpciója arányos az expozíciónál alkalmazott intenzitással és akkor a lemez transzmissziója
, tehát lefényképeztük a referencia és a tárgyhullám által létrehozott interferenciamintázatot, vagyis előállítottuk a hologramot. (A holografikus lemez természetesen oly módon is használható, és a gyakorlatban inkább ez valósul meg, hogy a lemez abszorpciója arányos az expozíciónál alkalmazott intenzitással és akkor a lemez transzmissziója 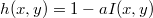 ; így is lineáris marad a kapcsolat.) Az interferenciamintázat általában nagyon sűrű. Szabad szemmel nem látható. A következő képen egy hologram kis részletének felnagyított képe látható. Természetes, hogy a képen (2.6.3 ábra) nem lehet felismerni a tárgyat, hiszen nem történt leképezés (ezért is hívják a holográfiát néha "lencse nélküli fényképezés"-nek).
; így is lineáris marad a kapcsolat.) Az interferenciamintázat általában nagyon sűrű. Szabad szemmel nem látható. A következő képen egy hologram kis részletének felnagyított képe látható. Természetes, hogy a képen (2.6.3 ábra) nem lehet felismerni a tárgyat, hiszen nem történt leképezés (ezért is hívják a holográfiát néha "lencse nélküli fényképezés"-nek).
| 2.6.3 ábra |
Ha már van egy kész hologram, akkor abból rekonstruálni lehet a tárgy képét. Ehhez csak annyit kell tenni, hogy a hologramot újra meg kell világítani a referenciahullámmal (2.6.4 ábra).
| 2.6.4 ábra |
A referenciahullámmal megvilágított hologramlemez mögötti térrészben a hullámtér a következőképpen számítható:
![\[ h \vec E_2 = t \vec E_2(I_1 + I_2) + t \vec E_1 \vec E^*_2 \vec E_2 + t\vec E_2 \vec E_2 \vec E^*_1 \]](/images/math/a/f/9/af90870631e8c3c2c8187a598f37768b.png) |
(2.6.3) |
A jobboldali első tag az úgynevezett nulladrend, vagyis ez a nyaláb halad tovább az eredeti referencianyaláb irányában. A harmadik tag az eredeti tárgynyaláb hullámával egy konstans szorzótól eltekintve megegyezik a hologram másik oldalán. Ez a nyaláb a referencianyalábnak a rögzített interferenciaképen, tehát egy igen sűrű optikai rácson történő diffrakciójaként áll elő. Ez ugyanolyan, mint az eredeti tárgyhullám, azaz a tárgy valódi 3D-s képe rekonstruálódott. A (2.6.3) utolsó tagja az úgynevezett konjugált kép megjelenésére ad magyarázatot.
Ha egy fényképet kettétépünk és csak az egyik felét tartjuk meg, akkor az eredeti információ fele elvész. Mi történik, ha egy hologramot kettévágunk és csak az egyik felét használjuk rekonstrukcióra? A válasz egyszerű; mivel az expozíció folyamán nem történt leképezés, ezért a fotólemez minden pontjába érkezett fény (információ) a tárgy minden pontjából, így a fél hologramból is rekonstruálható az egész tárgy. Információvesztés azonban mégis fellép; ez a visszaállított kép felbontásának gyengülését eredményezi. A holografikus mérési módszerek ipari alkalmazásaira számos példa van. Minthogy a tárgy 3D képének visszaállítása lehetséges, így tárgyak (szobrok, alkatrészek, stb.) 3D-s alakmérése is igen nagy pontossággal megoldható, ráadásul a vizsgált tárgyak igen kis deformációja illetve elmozdulása is mérhetővé válik. A számítógépes holográfia hologramlemez helyett általában CCD kamerát használ; a kamerával rögzített képet aztán számítógéppel rekonstruálják. Ennek nagy előnye a hagyományos hologramkészítési technikákkal szemben a gyors képrögzítés, ugyanis kihagyható az általában igencsak hosszadalmas kémiai hívási folyamat. A komputer-holográfia segítségével interferometrikus pontossággal összehasonlítható akár két, egymástól nagy távolságban létező tárgy is. A hologramról az információ csak a megfelelő referenciahullámmal olvasható ki. A holografikus memória létrehozásánál ezt használnák fel egyrészt az adatok titkosítására, másrészt, pedig ha a memória egy része megsérül, akkor még mindig van lehetőség az információ visszaállítására.
Csoport és fázissebesség
Az optikában mindezidáig nem foglalkoztunk azzal, hogy a fényforrások általában nem monokromatikus hullámokat bocsátanak ki. Hologram készítésénél – az előző fejezetben leírtak miatt és kényelmi okok miatt is – általában olyan lézernyalábot használnak, amelynek nagy a koherencia-hossza, azaz csaknem monokromatikus. A következő ábrán egy He-Ne lézer spektruma látható; ez kielégíti az előző mondatban megfogalmazott feltételt, hiszen – mint majd látni fogjuk – a keskeny spektrum feltétele a nagy koherencia-hossznak (ez akár több méter is lehet).
| 2.7.1 ábra |
Az optikai adatátvitel és a lézeres anyagvizsgálati módszerek azonban rövid (impultushossz:  ) fényimpulzusokat használnak. A természetben lezajló fény-anyag kölcsönhatások is általában véges időtartam alatt mennek végbe; az atomi gerjesztések élettartama jellemzően
) fényimpulzusokat használnak. A természetben lezajló fény-anyag kölcsönhatások is általában véges időtartam alatt mennek végbe; az atomi gerjesztések élettartama jellemzően  s vagy akár ennél jóval kisebb is lehet.
s vagy akár ennél jóval kisebb is lehet.
A lézerek jelentős része nem egy hullámhosszon működik; egy ilyen lézer tipikus spektruma látható a 2.7.2 ábrán (a középső, legintenzívebb nyalábtól való eltérést mutatja az ábra különböző módusokra).
| 2.7.2 ábra |
Azért, hogy megérthessük mi is történik ebben az esetben, először tekintsünk egy egyszerű modellt. Vegyünk egy olyan lézert, amely mindössze két hullámhosszon sugároz azonos intenzitással. Az  tengely mentén haladó síkhullámot feltételezve felírható az eredő elektromos tér, vagyis a két síkhullám összege:
tengely mentén haladó síkhullámot feltételezve felírható az eredő elektromos tér, vagyis a két síkhullám összege:
![\[ E = E_{\circ}cos(k_1 x - \omega_1 t) + E_{\circ}cos(k_2 x - \omega_2 t) \]](/images/math/a/6/0/a60b0b1a89f9ac70d1ca9cb1639ea7a4.png) |
(2.7.1) |
Legyen a két hullámhossz közötti különbség kicsi, így egyszerű algebrai módszerekkel az előző összefüggés átalakítható:
![\[ E = 2E_{\circ}cos(kx - \omega t) cos(\Delta k x - \Delta \omega t) \]](/images/math/6/6/5/6656acb857e31611ae890bb21f01a475.png) |
(2.7.2) |
ahol  , így
, így 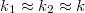 .
.
| 2.7.3 ábra |
A 2.7.3 ábra felső része mutatja az 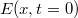 függvényt. Jól látható, hogy van egy vivőhullám:
függvényt. Jól látható, hogy van egy vivőhullám: 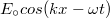 és ezt modulálja a
és ezt modulálja a 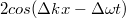 burkolófüggvény. A vivőhullám terjedési sebessége - ezt már láttuk az EMH fejezetben - a fázissebesség:
burkolófüggvény. A vivőhullám terjedési sebessége - ezt már láttuk az EMH fejezetben - a fázissebesség:
![\[ v_f = \frac{\omega}{k} \]](/images/math/5/9/1/591c84118a822cc0617eab32702c8627.png) |
(2.7.3) |
A burkoló ettől természetesen eltérő sebességgel haladhat. Amennyiben a burkoló 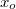 távolságot mozdult arrébb
távolságot mozdult arrébb 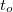 idő alatt, akkor az ábrán jelölt zérushely fázisa nem változhatott (2.7.3 ábra alsó része), azaz:
idő alatt, akkor az ábrán jelölt zérushely fázisa nem változhatott (2.7.3 ábra alsó része), azaz:
![\[ \Delta k x = \Delta k (x+x_{\circ})- \Delta \omega t_{\circ} \]](/images/math/0/8/f/08fe31b1c101e94caf058d89a954fcda.png) |
(2.7.4) |
Innen egyszerűsítés után:
![\[ 0= \Delta k x_{\circ}- \Delta \omega t_{\circ} \]](/images/math/c/6/7/c67d735372a0e4b021628c492905cd3c.png) |
(2.7.5) |
Ebből már könnyen kiszámítható a burkolóhullám terjedési sebessége, ez az úgynevezett csoportsebesség:
![\[ v_{cs} = \frac{x_{\circ}}{t_{\circ}} = \frac{\Delta \omega}{\Delta k} \]](/images/math/c/3/c/c3c29a73ace2bf7da41da7231f34f59f.png) |
(2.7.6) |
Ha az optikai tengely mentén az intenzitás-eloszlást egy adott pillanatban meg tudnánk mérni, akkor a következő ábrán látható periodikus mintázatot figyelhetnénk meg (2.7.4 ábra). Az 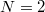 arra utal, hogy két, különböző hullámhosszúságú, de azonos amplitúdójú síkhullámot adtunk össze; a vivőhullám gyors változását nem ábrázoltuk.
arra utal, hogy két, különböző hullámhosszúságú, de azonos amplitúdójú síkhullámot adtunk össze; a vivőhullám gyors változását nem ábrázoltuk.
| 2.7.4 ábra |
Ha most nem 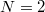 , hanem
, hanem 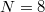 , vagy
, vagy 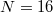 azonos amplitúdójú, de különböző hullámhosszúságú hullámot összegeznénk (ezek spektrumára általában jellemző:
azonos amplitúdójú, de különböző hullámhosszúságú hullámot összegeznénk (ezek spektrumára általában jellemző: 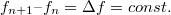 ), akkor a 2.7.5.a és 2.7.5.b ábrához hasonló pillanatszerű intenzitás-eloszlást kapnánk. (A számítás menete hasonló az optikai rács diffrakciójának leírására alkalmazott technikához.)
), akkor a 2.7.5.a és 2.7.5.b ábrához hasonló pillanatszerű intenzitás-eloszlást kapnánk. (A számítás menete hasonló az optikai rács diffrakciójának leírására alkalmazott technikához.)
| 2.7.5.a ábra | 2.7.5.b ábra |
Vagyis minél több hullámból építkezünk, azaz minél szélesebb a spektrum, az így kialakult impulzus annál rövidebb. Folytonos spektrum esetén elérhető, hogy mindössze egyetlen, rövid lézerimpulzust kapjunk (2.7.6 ábra).
| 2.7.6 ábra |
A spektrum kiszélesítésével el lehet érni, hogy mindössze néhány femtoszekundumos fényimpulzus (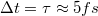 ) lépjen ki a lézerből; ez már a térben egy mindössze néhány hullámhossz hosszúságú impulzus (2.7.7 ábra). A
) lépjen ki a lézerből; ez már a térben egy mindössze néhány hullámhossz hosszúságú impulzus (2.7.7 ábra). A 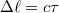 impulzushossz gyakorlatilag egyben a lézer koherenciahossza is.
impulzushossz gyakorlatilag egyben a lézer koherenciahossza is.
| 2.7.7 ábra |
A burkoló és a vivőhullám mozgásának vizsgálatára természetesen a magányos fényimpulzusok esetében is van lehetőség. Minthogy a spektrumvonalak közötti különbség rövid impulzusok esetében igen kicsi, ezért a 2.7.6 így általánosítható:
![\[ v_{cs} = \frac{d \omega}{d k} \]](/images/math/4/8/2/482b20a384b04c4e50fb39d5bc927a66.png) |
(2.7.7) |
Gauss-os impulzusnak a spektruma is Gaussos. Ezt a Fourier-transzformációs összefüggés alapján nem nehéz belátni, és azt is meg lehet mutatni, hogy 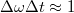 . Könnyű leolvasni ezen utolsó formula jelentését; minél szélesebb a spektrum, annál rövidebb a fényimpulzus és fordítva, azaz minél élesebb a spektrum, annál laposabb, a térben is annál elnyújtottabb az impulzus, vagyis annál nagyobb a koherencia-hossza. Ez az összefüggés már szerepelt az EMH-k fejezetben is.
. Könnyű leolvasni ezen utolsó formula jelentését; minél szélesebb a spektrum, annál rövidebb a fényimpulzus és fordítva, azaz minél élesebb a spektrum, annál laposabb, a térben is annál elnyújtottabb az impulzus, vagyis annál nagyobb a koherencia-hossza. Ez az összefüggés már szerepelt az EMH-k fejezetben is.
Amennyiben egy lézerimpulzus vákuumban, vagy levegőben terjed, akkor valamennyi, különböző hullámhosszúságú komponense ugyancsak  fénysebességgel halad; ez azt jelenti, hogy a hullámcsomag "egyben marad", tehát nem változtatja meg az alakját. Ha azonban egy fényimpulzus olyan közegben halad (vagy egy olyan dielektrikumrétegen transzmittálódik), amelynek a törésmutatója hullámhosszfüggő, akkor ez azt jelenti, hogy a különböző hullámhosszal rendelkező komponensek más-más sebességgel haladnak; ennek leggyakrabban az a következménye, hogy a jel ellaposodik, diszperziót szenved (2.7.8.a ábra). A diszperzió azonban gyakran nem csak azt eredményezi, hogy a jel kiszélesedik, hanem alakja is megváltozhat (2.7.8.b ábra) a terjedés során; a nyíl az időfejlődés irányát mutatja.
fénysebességgel halad; ez azt jelenti, hogy a hullámcsomag "egyben marad", tehát nem változtatja meg az alakját. Ha azonban egy fényimpulzus olyan közegben halad (vagy egy olyan dielektrikumrétegen transzmittálódik), amelynek a törésmutatója hullámhosszfüggő, akkor ez azt jelenti, hogy a különböző hullámhosszal rendelkező komponensek más-más sebességgel haladnak; ennek leggyakrabban az a következménye, hogy a jel ellaposodik, diszperziót szenved (2.7.8.a ábra). A diszperzió azonban gyakran nem csak azt eredményezi, hogy a jel kiszélesedik, hanem alakja is megváltozhat (2.7.8.b ábra) a terjedés során; a nyíl az időfejlődés irányát mutatja.
| 2.7.8.a ábra | 2.7.8.b ábra |
A diszperzió ellen bizonyos esetekben "lehet védekezni", azaz a hatását kiküszöbölni. A diszperzió jelensége a rövid impulzusokat előállító lézerekben, lézerrendszerekben is problémát okozhat; erre a "chirp-ölt tükrök" alkalmazása adhat megoldást.
Optikai kettőstörés
Homogén anyagok – például a víz, az üveg, vagy a levegő – optikai szempontból a törésmutatójukkal jellemezhetők; egy adott hullámhosszon ez egy egynél nagyobb szám. Ez egyben a törésmutató irányfüggetlenségét is mutatja, vagyis egy ilyen közegben nyugodtan használhatjuk a Huygens elvet, azaz a hullámtér minden egyes pontjából gömbhullám indul ki, és ezen gömbhullámok együtt képezik a hullámfrontot. Kristályok és aszimmetriával bíró molekulákat tartalmazó anyagok, sőt bizonyos esetekben oldatok viselkedése is eltérhet az előbbiekben leírtakról. Helyezzünk például egy kalcit kristályt egy írott szövegrészre (2.8.1 ábra)
| 2.8.1 ábra |
Jól látszik, hogy a szöveg "duplán jelenik meg". Ez az anyag úgynevezett optikai kettőstörő tulajdonságának következménye. Ennek oka az, hogy a kétféle (egymásra merőleges) polarizációs irányra más a törésmutató, ráadásul az egyiknek a törésmutatója még irányfüggést is mutat; ezt nevezzük extraordinárius sugárnak. A másik polarizációs iránnyal rendelkező nyalábot ordináriusnak hívják, erre a törésmutató irányfüggetlen; mindezt egy törésmutató-ellipszoid ábrával lehet szemléltetni (2.8.2 a és b ábra).
| 2.8.2.a ábra | 2.8.2.b ábra |
Ez természetesen azt is jelenti, hogy az ordinárius nyalábra igaz az, hogy a hullámtér miden pontja egy gömbhullám forrása (a megfelelő fázisban). Ha viszont az extraordinárius nyalábra alkalmazzuk a Huygens elvet, akkor azt annyiban kell módosítanunk, hogy a hullámtér pontjaiból egy olyan hullám indul, amelynek hullámfrontja egy ”felfúvódó” ellipszoid. Most már könnyen meg tudjuk magyarázni, hogy miért is látszik a 2.8.1 ábrán a szöveg megkettőzve. A magyarázathoz tekintsük a 2.8.3 ábrát. A rajz azt mutatja, hogy a kristály felületéhez a normális irányából érkező síkhullám két pontjából induló gömbhullámok alakjában induló gömbhullámok (ordinárius hullám, kékkel jelölve), valamint ugyanabból a két pontból induló és felfúvódó ellipszoid alakú hullámok (extraordinárius hullám, pirossal jelölve) hogyan alakítják ki a két nyaláb hullámfrontját. (A kristály tengelye, a  nem párhuzamos a beesési iránnyal.)
nem párhuzamos a beesési iránnyal.)
| 2.8.3 ábra |
Az optikai kettőstörés nem csak egy érdekes effektus; hasznos optikai elemek készíthetők kettőstörő kristályokból. Egy hullám 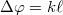 fázistolást szenved, amint egy
fázistolást szenved, amint egy 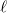 vastagságú rétegen halad át. Ennek törésmutató-függését is megadhatjuk felhasználva a
vastagságú rétegen halad át. Ennek törésmutató-függését is megadhatjuk felhasználva a 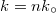 összefüggést:
összefüggést:
![\[ \Delta \varphi = n\frac{2 \pi}{\lambda_{\circ}}\ell \]](/images/math/5/7/d/57dd1f897c08178843317207944b9ab7.png) |
(2.8.1) |
Most legyen a beeső, lineárisan polarizált hullám úgy preparálva, hogy a polarizációs iránya 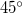 -os szöget zárjon be a kristály két főtengelyével, amelyekre a jellemző törésmutató különböző (no és ne), valamint a terjedés iránya merőleges az említett tengelyekre. Ekkor a hullám felbontható két, egymásra merőleges polarizációjú hullámra, hiszen maga az elektromos tér vektora is felbontható két egymásra merőleges komponensre, amelyek párhuzamosak a kristály két főtengelyére. A két hullám fázistolása viszont a törésmutatók különbözősége miatt eltérő, azaz:
-os szöget zárjon be a kristály két főtengelyével, amelyekre a jellemző törésmutató különböző (no és ne), valamint a terjedés iránya merőleges az említett tengelyekre. Ekkor a hullám felbontható két, egymásra merőleges polarizációjú hullámra, hiszen maga az elektromos tér vektora is felbontható két egymásra merőleges komponensre, amelyek párhuzamosak a kristály két főtengelyére. A két hullám fázistolása viszont a törésmutatók különbözősége miatt eltérő, azaz:
![\[ \Delta \varphi_1 = n_1\frac{2 \pi}{\lambda_{\circ}}\ell \qquad {\rm \acute{e}s} \qquad \Delta \varphi_2 = n_2\frac{2 \pi}{\lambda_{\circ}}\ell \]](/images/math/9/e/6/9e68d2f4ac1ec3f9f0cf9648a37cb4d9.png) |
(2.8.2) |
Ennek az a következménye, hogy a kristály kilépő oldalán megjelenő hullám polarizációs iránya a két fázistolás különbségétől függ.
Egy kristály vastagságát csiszolással beállíthatják úgy, hogy a 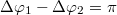 feltétel teljesüljön. Könnyű belátni, hogy ebben az esetben a kilépő nyaláb polarizációs iránya éppen merőleges a beesőére. Ezt az optikai elemet lambda-feles lemeznek hívják (2.8.4 ábra).
feltétel teljesüljön. Könnyű belátni, hogy ebben az esetben a kilépő nyaláb polarizációs iránya éppen merőleges a beesőére. Ezt az optikai elemet lambda-feles lemeznek hívják (2.8.4 ábra).
| 2.8.4 ábra |
Ha azonban a 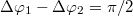 feltétel teljesül, akkor a kilépő oldalon egy cirkulárisan poláros hullám fog megjelenni. Ezt az eszközt lambda-negyedes lemeznek (és még negyedhullámú lemeznek is) nevezik (2.8.5 ábra).
feltétel teljesül, akkor a kilépő oldalon egy cirkulárisan poláros hullám fog megjelenni. Ezt az eszközt lambda-negyedes lemeznek (és még negyedhullámú lemeznek is) nevezik (2.8.5 ábra).
| 2.8.5 ábra |
Optikai aktivitás
Az EMH fejezetben megmutattuk, hogy ha a fény útjába helyezünk két egymásra merőleges polarizációs irányt kijelölő polarizátort, akkor a második polarizátoron már nem lép ki fény (gyakorlatilag a transzmittált nyaláb intenzitása több nagyságrenddel kisebb, mint a belépőé) (2.9.1 ábra).
| 2.9.1 ábra |
A polarizátorok közül az elsőt polarizátornak, a másodikat analizátornak szokták nevezni. Ha a keresztezett polarizátorok közé bizonyos kristályokat (például kvarc egykristályt) vagy például cukoroldatot helyezünk, akkor az analizátor mögött nem elhanyagolható intenzitású fénynyaláb lép ki. Ez csak egyféleképpen magyarázható: a két polárszűrő közötti minta valahogyan elforgatja a fény polarizációs síkját (2.9.2 ábra).
| 2.9.2 ábra |
Mielőtt rátérnénk a jelenség leírására, frissítsük fel az EMH polarizációs tulajdonságairól tanultakat. A  tengely mentén haladó jobbra cirkulárisan poláros síkhullám felírható a következő alakban:
tengely mentén haladó jobbra cirkulárisan poláros síkhullám felírható a következő alakban:
![\[ E_x (z,t)= E_{\circ}cos(\omega t - kz) \qquad {\rm \acute{e}s} \qquad E_y (z,t)= E_{\circ}sin(\omega t - kz) \]](/images/math/0/b/0/0b000af440d312dd2818162aae05abb1.png) |
(2.9.1) |
Vagyis:
![\[ \vec E_j (z,t)= E_{\circ}cos(\omega t - kz)\vec i + E_{\circ}sin(\omega t - kz)\vec j \]](/images/math/9/2/f/92fb33157c60f49971eaef29a8484380.png) |
(2.9.2) |
A balra cirkulárisan poláros síkhullám pedig:
![\[ \vec E_b (z,t)= -E_{\circ}cos(\omega t - kz)\vec i + E_{\circ}sin(\omega t - kz)\vec j \]](/images/math/3/d/d/3ddcd099d213fb69434c5b73e42179b3.png) |
(2.9.3) |
A 2.9.2 és a 2.9.3 által leírt két hullám összege egy, az  tengely irányú lineárisan polarizált hullám:
tengely irányú lineárisan polarizált hullám:
![\[ \vec E_{lin,y} (z,t)= \vec E_j (z,t) + \vec E_b (z,t) \]](/images/math/2/3/9/239109c37c02785d11820cbb0cefa7d0.png) |
(2.9.4) |
Ezt az egyenletet azonban visszafelé is olvashatjuk, azaz egy lineárisan polarizált síkhullám felbontható két, cirkulárisan polarizált hullámra. Vannak úgynevezett jobbra és balra forgató kristályok, attól függően, hogy bennük a jobbra és a balra cirkulárisan poláros fényre a két törésmutató (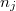 és
és 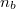 ) közül melyik a nagyobb. Ha tehát felbontjuk a lineárisan polarizált hullámot a két cirkulárisan poláros komponensére, és a két hullámra más a törésmutató, akkor már könnyű belátni, hogy a kilépő nyaláb polarizációs iránya más, mit a belépőé. Az elfordulás szöge arányos a minta
) közül melyik a nagyobb. Ha tehát felbontjuk a lineárisan polarizált hullámot a két cirkulárisan poláros komponensére, és a két hullámra más a törésmutató, akkor már könnyű belátni, hogy a kilépő nyaláb polarizációs iránya más, mit a belépőé. Az elfordulás szöge arányos a minta 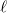 vastagságával:
vastagságával:
![\[ \Delta \varphi \sim (n_j - n_b)k_{\circ} \ell \]](/images/math/b/6/d/b6d1f839e63269b1e128b1d5d3bfbf4d.png) |
(2.9.5) |
Elektrooptikai effektus
Az optikai aktivitásra "rá is lehet segíteni". Vannak olyan kristályok (az optikai tengelyeknek megfelelően hasítottak), amelyekkel a polarizációs irány elforgatásának szöge a kristályra kapcsolt feszültséggel szabályozható. A Pockels-cella egy olyan eszköz, amelyben az elektromos tér az optikai tengellyel párhuzamos, és a polarizáció elfordulásának szöge arányos a kristályra (pl. KDP) kapcsolt feszültséggel ( 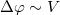 ); ez a jelenség az úgynevezett elsőrendű elektrooptikai effektus (2.10.1 ábra).
); ez a jelenség az úgynevezett elsőrendű elektrooptikai effektus (2.10.1 ábra).
| 2.10.1 ábra |
A másodrendű elektrooptikai jelenség esetén a polarizációs irány elfordulásának szöge a kristályra kapcsolt feszültség négyzetével arányos ( 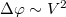 ). Ezt a fény-anyag kölcsönhatást feltalálója után Kerr effektusnak nevezik; az említett hatáson alapuló optikai eszköz a Kerr-cella (2.10.2 ábra).
). Ezt a fény-anyag kölcsönhatást feltalálója után Kerr effektusnak nevezik; az említett hatáson alapuló optikai eszköz a Kerr-cella (2.10.2 ábra).
| 2.10.2 ábra |
A Kerr-cella előnye a Pockels-cellával szemben az, hogy jóval kisebb feszültséggel (bizonyos előfeszítés mellett) lehet nagy modulációt (akár 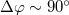 ) elérni.
) elérni.
Optikai adatátvitel
Jelátvitelhez a vonalas telefon, a fax vagy a televíziós műsorszórás (kábel-TV) esetén főként rézvezetéket, koaxiális kábelt, stb. használnak. A 60-as évek hidegháborús időszakában rájöttek, hogy egy légköri atombomba robbanás olyan intenzív elektromágneses viharokat kelt, amelyek hatására a "szokásos" távközlési és hírközlési rendszerek egy országban (vagy akár egy kontinensen) használhatatlanná válhatnak. Ez volt az egyik oka annak, hogy a 60-as években az elektromágneses zavarokra érzéketlen üvegszálas jelátviteli rendszerek fejlesztése elindult, ezt elősegítette, hogy az első lézerek éppen ebben az időszakban jelentek meg. A kezdeti próbálkozások során az optikai adattovábbítás azon az ötleten alapult, hogy a teljes visszaverődés a fényt az üvegszálban tartja. Az ötlet alkalmazhatóságát mutatja szemléletesen egy vízsugárban oda-vissza pattogó fénynyaláb (2.11.1..a és b ábra, rajz és kísérleti demonstráció).
| 2.11.1.a ábra | 2.11.1.b ábra |
A módszer tényleg működik, jól látható ez a következő képen; a nagyobbik fiú bevezeti a lézerfényt az optikai szálkötegbe, melynek a másik végén lép ki a lézernyaláb.
| 2.11.2 ábra |
A teljes visszaverődés feltétele az, hogy az optikailag sűrűbb közegből haladjon a fény az optikailag ritkább felé (és persze a normálissal bezárt szöge nagyobb legyen a határszögnél); tehát az üvegszálat körülvevő köpeny törésmutatója kisebb legyen, mint az üvegszál – más néven a szál magja – törésmutatója (2.11.3 ábra).
| 2.11.2 ábra |
A fényvezetést azonban nem lehet kielégítően megmagyarázni a teljes visszaverődés effektusával. Ennek oka az, hogy a geometriai optika módszereivel már nem tudjuk leírni a fényterjedést, ha az optikai szál magjának átmérője összemérhető a hullámhosszal. Ebben az esetben a hullámoptika elméletét kell használni. (A függelékben található egy egyszerű szendvicsszerkezet hullámvezetési tulajdonságainak leírása.) Egy optikai szál módusainak leírása messze túlmutat ezen jegyzet keretein. Az eljárás lényege a következő: a Maxwell-egyenletekből levezethető hullámegyenlet megoldásait kell megkeresni a határfeltételek figyelembevételével. A számítás eredménye azt mutatja, hogy az optikai szálban különböző sebességgel haladó módusok alakulnak ki. (Az EMH-okról szóló fejezetben bemutatott hullámvezetett módusokhoz hasonlóan). Ezek a módusok nem szorulnak teljes egészében a magba, hanem a teljesítmény egy része a köpenyben halad, hiszen az elektromos és mágneses térerősség a köpenyben sem zérus, viszont általában exponenciálisan lecseng a szál optikai tengelyétől mért távolság függvényében. A pontos számításokból az is kiderül, hogy annál kevesebb módus jelenik meg, minél kisebb a szál magjának átmérője. Ennek egyik fontos következménye az, hogy megfelelően megválasztott magátmérő esetén már csak egy módus alakul ki az optikai szálban. Ezt nevezik egymódusú szálnak és ebben az esetben a módusdiszperzió nem torzítja az üvegszálon továbbított jelet. A többmódusú szálakban mind kromatikus, mind módusdiszperzió fellép (meghatározott hullámhosszakon ezek éppen kiejthetik egymást). Az optikai adatátviteli rendszerek jeladója áltatában egy félvezető lézer, míg a vevőoldalon félvezető detektorokat alkalmaznak.
Detektorok
Szemünkkel látjuk a fényt, és annak intenzitásváltozásairól is szinte mindenkinek van valami tapasztalata. Ez a tapasztalat azonban általában igencsak szubjektív. (Elég csak arra gondolni, hogy gyakran vita tárgya még "jól látók" között is például egy ruha színének megítélése; leggyakrabban kék és zöld színt "keverik".) Jogosan merül fel tehát az igény a fény intenzitásának mérésére. Ezt nem túl kis intenzitások esetén félvezető detektorokkal oldják meg (2.12.1 ábra).
| 2.12.1 ábra |
A detektor érzékelő lapjára érkező fény az eszközben mérhető elektromos áramot kelt. A jelenséget vázlatosan – a legegyszerűbb elrendezést tekintve – szemlélteti a következő ábra.
| 2.12.2 ábra |
A p-n átmenetre beeső fotonok elektron lyuk párokat "felszabadítva" elektromos áramot generálnak. Ez a "foto-áram" azonban energiaforrásként is felhasználható. A napelemek nem csak épületek energiaellátására alkalmazhatók, hanem például az űrállomásokon gyakran ez az egyedüli energiaforrás (2.12.3 ábra).
| 2.12.3 ábra |
Miniatürizált félvezető lapkák (pixelek) alkalmazásával állítják össze a CCD kamerát, amelynek segítségével a tér egy tartományában a fény intenzitás-eloszlása mérhető; leképező optika segítségével képalkotásra is alkalmazható (2.12.4 ábra).
| 2.12.4 ábra |
A félvezető eszközök működéséről és a CCD kameráról bővebben lesz szó a szilárdtestfizika fejezetben.
Az igen kis fényintenzitások mérése fotoelektron sokszorozóval oldható meg. Az eszköz működését alapvetően két effektus biztosítja. Az egyik a fotoeffektus. Ahhoz, hogy egy fémes vezetőből eltávolítsunk egy elektront, valamennyi munkát kell végeznünk; ezt hívják kilépési munkának. A fémek vezetési elektronjai ugyan csaknem szabadon mozognak a fémen belül, azonban a fémből nem tudnak kilépni, hacsak valahogyan nem tesznek szert a (minden fémre különböző) kilépési munkához szükséges energiára. Amennyiben egy vezetőre fény esik, akkor annak egy része elnyelődik. Most higgyük el, amit a modern fizika részben részletesebben tárgyalunk majd, hogy a fény fotonokból, fényrészecskékből áll, amelyeknek energiájuk, impulzusuk, sőt még perdületük (impulzusmomentumuk) is van. Ha a bejövő fény fotonjainak elegendően nagy az energiája, vagyis nagyobb, mint a kilépési munka, akkor egy elektronnak egy elnyelt foton energiájával megnövelt mozgási energiája már elég ahhoz, hogy az elektron (a fotoelekton) kilépjen a fémből (2.12.5 ábra).
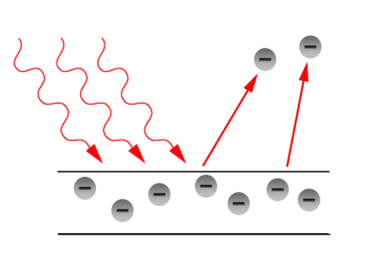
|
| 2.12.5 ábra |
A foto-effektushoz hasonló a következő jelenség is; ha foton helyett egy olyan elektron ütközik fémbe, amelynek mozgási energiája a fém kilépési energiájának többszöröse, akkor akár több elektron is kiléphet a fémből (2.12.6 ábra).
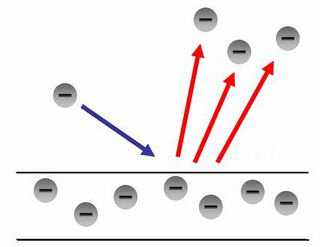
|
| 2.12.6 ábra |
Mindkét effektus alkalmazásával egy igen érzékeny detektort lehet építeni; ezt gyakran az angol photomultiplier névvel illetjük. A fotoelektron sokszorozó működésének vázlatos ismertetéséhez tekintsük az 2.12.7 ábrán látható rajzot.
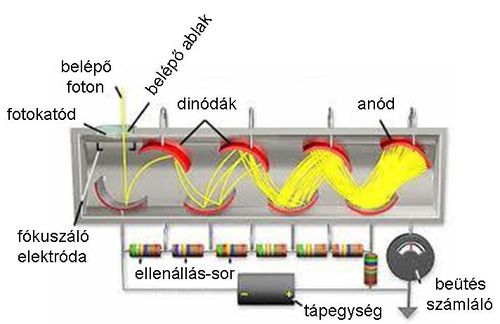
|
| 2.12.7 ábra |
A beérkező foton a katódból kivált egy elektront, amely az első dinódáig – a közöttük lévő több 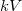 gyorsítófeszültség hatására – igen nagy sebességre gyorsul. A dinódába becsapódó nagyenergiájú elektron abból még több elektront vált ki, melyek aztán a második dinódáig gyorsulnak, ahonnan az ütközés után még annál is több elektron lép ki. (Az ábrán jól látszik, hogy a feszültségosztó ellenállás-sor biztosítja a gyorsítófeszültséget a dinódák között, valamint az utolsó dinóda és az anód között is.) Mindegyik dinóda után erősödik a elektronáram, amely aztán az anódba csapódva már egy mérhető áramlökést eredményez. A "magányos" fotonok beütését is detektálni képes elrendezés erősítési tényezője akár
gyorsítófeszültség hatására – igen nagy sebességre gyorsul. A dinódába becsapódó nagyenergiájú elektron abból még több elektront vált ki, melyek aztán a második dinódáig gyorsulnak, ahonnan az ütközés után még annál is több elektron lép ki. (Az ábrán jól látszik, hogy a feszültségosztó ellenállás-sor biztosítja a gyorsítófeszültséget a dinódák között, valamint az utolsó dinóda és az anód között is.) Mindegyik dinóda után erősödik a elektronáram, amely aztán az anódba csapódva már egy mérhető áramlökést eredményez. A "magányos" fotonok beütését is detektálni képes elrendezés erősítési tényezője akár 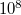 is lehet. A fotoelektron sokszorozók hatásfoka általában jóval kisebb, mint 100%; azaz egy 10% kvantumhatásfokú eszköz átlagosan mindössze egyet jelez 10 fotonbecsapódásból. A photomultiplier kiváltható az avalanche fotodiódával; ez egy olyan félvezető eszköz, amely egyrészt igen jó hatásfokkal (
is lehet. A fotoelektron sokszorozók hatásfoka általában jóval kisebb, mint 100%; azaz egy 10% kvantumhatásfokú eszköz átlagosan mindössze egyet jelez 10 fotonbecsapódásból. A photomultiplier kiváltható az avalanche fotodiódával; ez egy olyan félvezető eszköz, amely egyrészt igen jó hatásfokkal ( 50%) képes detektálni a fotonokat, másrészt pedig igen egyszerű az alkalmazása.
50%) képes detektálni a fotonokat, másrészt pedig igen egyszerű az alkalmazása.
Melléklet
Fényvezetés dielektrikumrétegekben (szendvicsszerkezetű dielektrikumban)
Az Optikai adatátvitel című fejezetben már történt arra utalás, hogy a fényvezetést nem lehet jól leírni a teljes visszaverődés effektusával. Egy valódi optikai szál hullámvezetési tulajdonságainak leírására ebben a jegyzetben nem vállalkozhatunk. Egy igen egyszerű dielektrikum-rétegrendszer (3.1.1 ábra) fényvezetési tulajdonságainak jellemzőit viszont könnyen meghatározhatjuk, így kvalitatív képet kaphatunk a fénytávközlés alapját képező optikai szál hullámvezetési sajátosságairól is.

|
| 3.1.1 ábra |
Az előző ábrán látható rétegrendszerben az alsó és a felső dielektrikumréteg törésmutatója kisebb, mint a középső rétegé, azaz 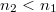 . (Mint az a későbbiekben ki fog derülni; erre nem azért van szükség, hogy a teljes visszaverődés feltételének eleget tegyünk, hanem sokkal inkább azért, hogy a vezetett módus többé-kevésbé a középső rétegbe szoruljon.) A dielektrikumban terjedő fény sebessége megadható az anyagi állandókkal:
. (Mint az a későbbiekben ki fog derülni; erre nem azért van szükség, hogy a teljes visszaverődés feltételének eleget tegyünk, hanem sokkal inkább azért, hogy a vezetett módus többé-kevésbé a középső rétegbe szoruljon.) A dielektrikumban terjedő fény sebessége megadható az anyagi állandókkal:
![\[ {c}'=\frac{c}{n}=v=\frac{1}{\sqrt{\varepsilon \mu }} \]](/images/math/6/4/4/6444b497bea84c9d22c7a6d602f1e360.png) |
(3.1.1) |
A rétegekről feltételezhetjük, hogy mágneses tulajdonságaik figyelmen kívül hagyhatók, így azonnal adódik egy igen fontos összefüggés:
![\[ n=\sqrt{\varepsilon _r} \]](/images/math/6/6/a/66a20770b563114ffe7a119d5cc9ce45.png) |
(3.1.2) |
A rétegek törésmutatóira tett megállapodásunk következménye tehát: 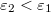 . A 3.1.1 ábrán látszik az is, hogy a rendszernek az
. A 3.1.1 ábrán látszik az is, hogy a rendszernek az  tengely mentén transzlációs szimmetriája van. (A gyakorlatban ez azt jelenti, hogy a rétegek szélessége több nagyságrenddel nagyobb, mint a középső réteg vastagsága.)
tengely mentén transzlációs szimmetriája van. (A gyakorlatban ez azt jelenti, hogy a rétegek szélessége több nagyságrenddel nagyobb, mint a középső réteg vastagsága.)
Most tételezzük fel, hogy elektromágneses síkhullám terjed a  tengely irányában; ennek haladását a
tengely irányában; ennek haladását a ![\setbox0\hbox{$exp[i(\omega t-\beta z)]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/b/a/b/bab4f8482a3c8aaf020ff41874287d33.png) komplex hullámalak segítségével szeretnénk leírni, ahol
komplex hullámalak segítségével szeretnénk leírni, ahol  a vezetett hullám körfrekvenciája és
a vezetett hullám körfrekvenciája és  a hullámszáma. Az EMH elektromos és mágneses térerősség-komponensei természetesen még függnek az
a hullámszáma. Az EMH elektromos és mágneses térerősség-komponensei természetesen még függnek az  -tól is, azonban a
-tól is, azonban a  és
és  függését az előbbi exponenciális taggal adjuk meg. A hullámterjedés tulajdonságainak meghatározásához a Maxwell-egyenletekből indulunk ki. Az Ampere-törvényt és a Faraday-törvényt megadó egyenleteket felírhatjuk mindhárom komponensre, azonban most azt is figyelembe vesszük, hogy az
függését az előbbi exponenciális taggal adjuk meg. A hullámterjedés tulajdonságainak meghatározásához a Maxwell-egyenletekből indulunk ki. Az Ampere-törvényt és a Faraday-törvényt megadó egyenleteket felírhatjuk mindhárom komponensre, azonban most azt is figyelembe vesszük, hogy az  tengely menti transzlációs szimmetria következtében az
tengely menti transzlációs szimmetria következtében az  szerinti deriváltak elhagyhatók:
szerinti deriváltak elhagyhatók:
![\[ \frac{\partial H_z}{\partial y}+i\beta H_y=i\omega \varepsilon_{\circ} \varepsilon_j E_x \]](/images/math/d/8/7/d87c4650dea5e2b9515de7dad06d4a78.png) |
(3.1.3) |
![\[ -i\beta H_x = i\omega \varepsilon_{\circ} \varepsilon_j E_y \]](/images/math/b/c/6/bc63526350b91ebd1accad6bf32990e0.png) |
(3.1.4) |
![\[ -\frac{\partial H_x}{\partial y}=i\omega \varepsilon_{\circ} \varepsilon_j E_z \]](/images/math/a/4/9/a497125779a80aeea19975bfdf037eda.png) |
(3.1.5) |
![\[ \frac{\partial E_z}{\partial y}+i\beta E_y=-i\omega \mu_{\circ} H_x \]](/images/math/f/3/8/f38700d8abdada5b6a60465000e13a2e.png) |
(3.1.6) |
![\[ -i\beta E_x = -i\omega \mu_{\circ} H_y \]](/images/math/4/6/0/460367dc3b7ff7f579738b5d8eb7cc67.png) |
(3.1.7) |
![\[ -\frac{\partial E_x}{\partial y}=-i\omega \mu_{\circ} H_z \]](/images/math/9/b/5/9b56e8ff430e845f0e33bb1a6ea77ed3.png) |
(3.1.8) |
ahol  az
az  és
és  értékeket veheti fel (attól függően, hogy melyik rétegben vizsgáljuk a hullámterjedést).
értékeket veheti fel (attól függően, hogy melyik rétegben vizsgáljuk a hullámterjedést).
Könnyű észrevenni, hogy a 3.1.3, a 3.1.7 és a 3.1.8 egyenletek "összetartoznak" és egy – a másik háromtól független – egyenletrendszert határoznak meg, hiszen az 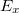 , a
, a 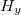 és a
és a 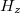 csak ezekben szerepel. Minthogy az elektromos térerősségnek az említett egyenletrendszerben nincs
csak ezekben szerepel. Minthogy az elektromos térerősségnek az említett egyenletrendszerben nincs  komponense, ezért az egyenletrendszer megoldásával kapott hullám transzverzális elektromos, de nem transzverzális mágneses hullám, hiszen
komponense, ezért az egyenletrendszer megoldásával kapott hullám transzverzális elektromos, de nem transzverzális mágneses hullám, hiszen 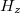 komponense nem zérus. Az ilyen síkhullámot nevezzük transzverzális elektromos módusnak; jelölése: TE. A másik három egyenlet megoldásaként egy TM módus adódik. A 3.1.7-ből
komponense nem zérus. Az ilyen síkhullámot nevezzük transzverzális elektromos módusnak; jelölése: TE. A másik három egyenlet megoldásaként egy TM módus adódik. A 3.1.7-ből 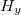 -t és a 3.1.8-ból
-t és a 3.1.8-ból  -t kifejezve, majd behelyettesítve a 3.1.3-ba kapjuk a következő hullámegyenletet:
-t kifejezve, majd behelyettesítve a 3.1.3-ba kapjuk a következő hullámegyenletet:
![\[ \frac{\partial^{2} E_x}{\partial y^{2}}+\left ( k_{\circ}^{2}-\beta^{2} \right )E_x=0 \qquad {\rm ahol} \qquad k_{\circ}= \omega \sqrt{\varepsilon_{\circ} \mu_{\circ} } \]](/images/math/0/1/6/0166d7250d9b274ae797caac94570a33.png) |
(3.1.9) |
Ez a hullámegyenlet felírható a középső és a két másik (az alsó és a felső) rétegre is, így feltételezhetjük, hogy a megoldásként kapott hullámvezetett módus, amely a réteghatárokon a térerősségekre a határfeltételeket kielégíti, mind a középső, mind a két szélső rétegben egyidejűleg terjed. Egyszerű fizikai megfontolás alapján feltételezhetjük, hogy fennáll a következő reláció:
![\[ k_{\circ}^{2} \varepsilon_{2} < \beta^{2} < k_{\circ}^{2} \varepsilon_{1} \]](/images/math/a/2/7/a2750f2dc823eb3c1e5f80cd9fe17257.png) |
(3.1.10) |
Ez az egyenlőtlenség azt jelenti, hogy a síkhullám gyorsabban halad, mintha csak a középső rétegben terjedne, de lassabban, mintha csak valamelyik szélső (alsó vagy felső) rétegben létezne. (Az értelmezéshez felhasználhatjuk a hullám fázissebességére már megismert összefüggést: 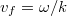 .) Most vezessünk be két új változót (változót, hiszen a
.) Most vezessünk be két új változót (változót, hiszen a  értékét nem ismerjük):
értékét nem ismerjük):
![\[ k_{1}^{2} = k_{\circ}^{2} \varepsilon_{1} - \beta^{2} \]](/images/math/2/2/0/2203e5688df43213b84a98b60cb97c1e.png) |
(3.1.11) |
![\[ \kappa _{2}^{2} = \beta^{2}- k_{\circ}^{2} \varepsilon_{2} \]](/images/math/e/c/6/ec618839a2b6c6d3fbda520cac88d7c8.png) |
(3.1.12) |
A 3.1.9 hullámegyenlet most már egyszerűbb alakban is megadható. Írjuk fel 3.1.9 módosított alakját a középső, 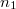 törésmutatójú közegre:
törésmutatójú közegre:
![\[ \frac{d^{2}E_x}{dy^{2}}+k_{1}^{2}E_x = 0 \]](/images/math/6/4/a/64acbaa5a7ed21a18a4629cf9994affd.png) |
(3.1.13) |
Ennek az egyenletnek az általános megoldása: 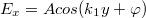 . Az egyszerűbb írásmód kedvéért maradjunk a szimmetrikus módust leíró páros függvénynél, azaz:
. Az egyszerűbb írásmód kedvéért maradjunk a szimmetrikus módust leíró páros függvénynél, azaz:
![\[ E_x = A cos (k_1 y ) \]](/images/math/b/4/4/b44564fb4ed8390f9bb393ed3683f005.png) |
(3.1.14) |
A 3.1.7 és 3.1.8 segítségével megkaphatjuk a 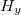 -t és
-t és 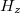 -t:
-t:
![\[ H_y = A\frac{\beta }{\omega \mu _{\circ}}cos\left ( k_{1}y \right ) \qquad {\rm \acute{e}s} \qquad H_z = -A\frac{k_{1} }{i\omega \mu _{\circ}}sin\left ( k_{1}y \right ) \]](/images/math/1/8/c/18ccbfc654d923da498231ca074ae0ed.png) |
(3.1.15) |
Most az előzőekhez hasonlóan írjuk fel a hullámegyenletet a két 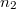 törésmutatójú dielektrikumrétegben is:
törésmutatójú dielektrikumrétegben is:
![\[ \frac{d^{2}E_x}{dy^{2}}-\kappa_{2}^{2}E_x = 0 \]](/images/math/c/2/1/c21848a017f29513a9152dadac6fe1ff.png) |
(3.1.16) |
Ennek az egyenletnek a megoldása:
![\[ E_x = Be^{-\kappa \left | y \right |} \]](/images/math/2/4/1/241acf27a492662e28e2e43b07c02c3d.png) |
(3.1.17) |
(Természetesen megoldása az 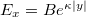 is, de egy divergáló megoldást egyszerű fizikai megfontolások alapján nem fogadhatunk el.)
is, de egy divergáló megoldást egyszerű fizikai megfontolások alapján nem fogadhatunk el.)
A 3.1.7 és 3.1.8 felhasználásával meghatározhatjuk a 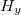 -t és a
-t és a 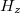 -t is:
-t is:
![\[ H_y = B\frac{\beta }{\omega \mu _{\circ}}e^{-\kappa \left | y \right |} \qquad {\rm \acute{e}s} \qquad H_z = \mp B\frac{\kappa _ 2}{i\omega \mu _{\circ}}e^{-\kappa \left | y \right |} \]](/images/math/4/a/0/4a0696700ee7968d2505e995f8ce6b75.png) |
(3.1.18) |
A réteghatárokon teljesülnie kell a határfeltételeknek, vagyis az 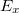 és a
és a 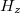 folytonos az
folytonos az 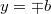 helyen, tehát az
helyen, tehát az 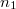 és
és 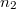 törésmutatójú közegre kapott megoldásokat illeszteni kell:
törésmutatójú közegre kapott megoldásokat illeszteni kell:
![\[ Acos\left ( k_{1}b \right )=Be^{-\kappa b} \qquad {\rm \acute{e}s} \qquad A\frac{k_{1}}{i\omega \mu _{\circ}}sin\left ( k_{1}b \right )=B\frac{\kappa _{2}}{i\omega \mu _{\circ}}e^{-\kappa b} \]](/images/math/9/6/5/9658a2ba4a09bfbba240e1bc8e804a2f.png) |
(3.1.19) |
Könnyen belátható, hogy mindkét egyenlet csak akkor teljesülhet egyidejűleg, ha:
![\[ tg\left ( k_{1}b \right )=\frac{\kappa _2}{k_1} \]](/images/math/8/f/3/8f319d64a49f09d648a5d803e8f33a4f.png) |
(3.1.20) |
Ez egy transzcendens egyenlet  -ra (ne feledjük, hogy
-ra (ne feledjük, hogy 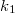 és
és 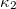 a
a  függvénye, lásd 3.1.11 és 3.1.12). Az egyenletnek numerikus megoldásai ismertek, azaz számítógéppel csaknem tetszőleges pontossággal kiszámítható
függvénye, lásd 3.1.11 és 3.1.12). Az egyenletnek numerikus megoldásai ismertek, azaz számítógéppel csaknem tetszőleges pontossággal kiszámítható  értéke adott
értéke adott  esetében, a
esetében, a  értékéből pedig kapjuk a
értékéből pedig kapjuk a 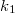 -t és
-t és 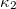 -t. Az elektromos tér transzverzális komponense, az
-t. Az elektromos tér transzverzális komponense, az 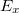 (ebből pedig a
(ebből pedig a 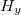 és a
és a 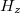 is) pedig egy konstans együttható (mely megadja a tér amplitúdóját) erejéig meghatározható.
A numerikus szimuláció helyett a kevésbé pontos, de szemléletes grafikus módszerrel is próbálkozhatunk a megoldás keresésében. Ennek érdekében először vezessünk be két új változót:
is) pedig egy konstans együttható (mely megadja a tér amplitúdóját) erejéig meghatározható.
A numerikus szimuláció helyett a kevésbé pontos, de szemléletes grafikus módszerrel is próbálkozhatunk a megoldás keresésében. Ennek érdekében először vezessünk be két új változót:
![\[ u=k_1 b \qquad {\rm \acute{e}s} \qquad w=\kappa_2 b \]](/images/math/4/a/3/4a3f371d5a951b183958830ed670f287.png) |
(3.1.21) |
Érdemes még az anyagi állandóktól függő és a középső réteg vastagságával arányos  úgynevezett normalizációs frekvenciát is alkalmazni:
úgynevezett normalizációs frekvenciát is alkalmazni:
![\[ V=bk_{\circ} \sqrt{\varepsilon_1 -\varepsilon _2} \]](/images/math/a/3/6/a365e2c1f5700418504f516d5eea4521.png) |
(3.1.22) |
A 3.1.11 és 3.1.12 összegéből kifejezhetjük 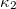 -t:
-t:
![\[ \kappa_2 = \sqrt{k_{\circ}^{2}(\varepsilon_1 -\varepsilon _2)- k_{1}^{2} } \]](/images/math/e/4/3/e434a6efe07ce2818110591ffd33de4c.png) |
(3.1.23) |
A bevezetett új változókkal kaphatunk egy könnyen levethető összefüggést:
![\[ u^2 + w^2 = V^2 \]](/images/math/5/c/e/5ce5fdf933b5d6a4f851314f8a060d02.png) |
(3.1.24) |
A 3.1.20 egyenlet is átírható egyszerűbb alakra:
![\[ utg(u) = \sqrt{V^2 - u^2 }\]](/images/math/1/b/f/1bfff5542a302f4eb8e2ce33031a8a42.png) |
(3.1.25) |
Ezen két utolsó egyenlet segítségével használhatjuk a – már említett – grafikus módszert. Az 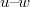 síkon a 3.1.24 egy kör egyenletét adja. A 3.1.25 egyenlet megoldását ezek után az
síkon a 3.1.24 egy kör egyenletét adja. A 3.1.25 egyenlet megoldását ezek után az 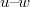 síkon a
síkon a  sugarú kör és az
sugarú kör és az 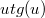 függvény metszete adja (3.1.2 ábra).
függvény metszete adja (3.1.2 ábra).
|
| 3.1.2 ábra |
Az ábrán jól látszik, hogy mindössze két metszéspont adódik a  esetén, azaz két TE módus valósulhat meg. A metszéspontok
esetén, azaz két TE módus valósulhat meg. A metszéspontok  koordinátája leolvasható; ebből megkapjuk
koordinátája leolvasható; ebből megkapjuk 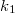 -t, amelyből viszont meghatározhatjuk
-t, amelyből viszont meghatározhatjuk  közelítő értékét. A becsatolt fény frekvenciája általában ismert, vagyis az
közelítő értékét. A becsatolt fény frekvenciája általában ismert, vagyis az 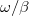 hányados kiszámításával megkapjuk a módus fázissebességét. Minden metszésponthoz (megoldáshoz) más
hányados kiszámításával megkapjuk a módus fázissebességét. Minden metszésponthoz (megoldáshoz) más 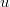 érték tartozik, ebből már következik, hogy egy adott
érték tartozik, ebből már következik, hogy egy adott 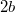 rétegvastagság (az
rétegvastagság (az 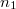 törésmutatójú középső réteg vastagsága) esetén minden módus sebessége más. Az is leolvasható a 3.1.2 ábráról, hogy mindössze egyetlen vezetett módus haladhat a rétegrendszerben, ha
törésmutatójú középső réteg vastagsága) esetén minden módus sebessége más. Az is leolvasható a 3.1.2 ábráról, hogy mindössze egyetlen vezetett módus haladhat a rétegrendszerben, ha  értéke
értéke 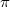 -nél kisebb. A normalizációs frekvencia arányos a középső lemez vastagságával (
-nél kisebb. A normalizációs frekvencia arányos a középső lemez vastagságával (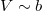 ). Az előző ábra alapján az is nyilvánvaló, hogy minél vastagabb a középső dielektrikumréteg, annál több módus terjedhet más-más sebességgel; ez okozza a módusdiszperziót. A módusdiszperzió ellen a megfelelően kialakított elrendezéssel (
). Az előző ábra alapján az is nyilvánvaló, hogy minél vastagabb a középső dielektrikumréteg, annál több módus terjedhet más-más sebességgel; ez okozza a módusdiszperziót. A módusdiszperzió ellen a megfelelően kialakított elrendezéssel (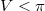 ) védekezhetünk. A 3.1.25 egyik következménye, hogy az
) védekezhetünk. A 3.1.25 egyik következménye, hogy az 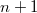 -edik módus is megjelenik, amint
-edik módus is megjelenik, amint 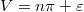 teljesül. Igen kis
teljesül. Igen kis  mellett a
mellett a  értéke is kicsi, ebből következik, hogy
értéke is kicsi, ebből következik, hogy 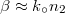 . Ez azt jelenti, hogy a nyaláb terjedésére az
. Ez azt jelenti, hogy a nyaláb terjedésére az 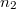 törésmutatójú közegben haladó fény sebessége jellemző. Mi lehet ennek a fizikai magyarázata? Amennyiben
törésmutatójú közegben haladó fény sebessége jellemző. Mi lehet ennek a fizikai magyarázata? Amennyiben 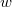 értéke alig nagyobb zérusnál, akkor az exponenciális lecsengést biztosító
értéke alig nagyobb zérusnál, akkor az exponenciális lecsengést biztosító 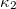 érték is kicsi. Ennek az a következménye, hogy a jel erőssége a középső rétegtől távolodva lassan csökken, vagyis a fényteljesítmény jelentős része a két szélső
érték is kicsi. Ennek az a következménye, hogy a jel erőssége a középső rétegtől távolodva lassan csökken, vagyis a fényteljesítmény jelentős része a két szélső 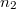 törésmutatójú közegben halad, így érthető, hogy miért éppen ezen dielektrikumok törésmutatója határozza meg a terjedési sebességet. A vázolt gondolatmenet fordítva is működik. Nagyobb
törésmutatójú közegben halad, így érthető, hogy miért éppen ezen dielektrikumok törésmutatója határozza meg a terjedési sebességet. A vázolt gondolatmenet fordítva is működik. Nagyobb 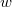 számérték esetén az exponenciális levágást biztosító
számérték esetén az exponenciális levágást biztosító 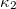 hatása is jelentősebb, tehát a fényteljesítménynek kis hányada terjed csak a két
hatása is jelentősebb, tehát a fényteljesítménynek kis hányada terjed csak a két 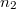 törésmutatójú dielektrikumban. Ennek következtében a hullám "beszorul" a középső rétegbe, így annak
törésmutatójú dielektrikumban. Ennek következtében a hullám "beszorul" a középső rétegbe, így annak 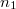 törésmutatója határozza meg döntő mértékben a jel fázissebességét. Mindezt jól példázza a következő ábra. Itt egyrészt azt láthatjuk, hogy egyre nagyobb rétegvastagság (
törésmutatója határozza meg döntő mértékben a jel fázissebességét. Mindezt jól példázza a következő ábra. Itt egyrészt azt láthatjuk, hogy egyre nagyobb rétegvastagság ( ) mellett egyre több módus jelenik meg. Másrészt pedig mindig, amikor egy új módus "belép" (vagyis a
) mellett egyre több módus jelenik meg. Másrészt pedig mindig, amikor egy új módus "belép" (vagyis a  értéke éppen csak meghaladja
értéke éppen csak meghaladja  egész számú többszörösét), akkor annak haladási sebességét az
egész számú többszörösét), akkor annak haladási sebességét az  törésmutató határozza meg.
törésmutató határozza meg.
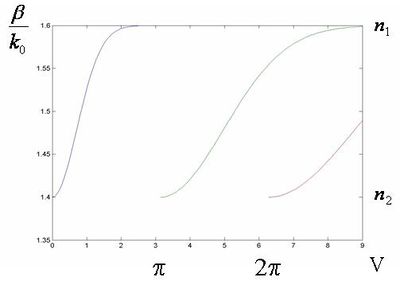
|
| 3.1.3 ábra |
Azt is leolvashatjuk a grafikonról, hogy nagy  esetén a módusok terjedésére a középső közeg
esetén a módusok terjedésére a középső közeg  törésmutatója jellemző. Mint azt már az előzőekben említettük, ennek oka az, hogy a jel egyre jobban beszorul a középső dielektrikumrétegbe. Az elmondottakat demonstrálja a következő két grafikon.
törésmutatója jellemző. Mint azt már az előzőekben említettük, ennek oka az, hogy a jel egyre jobban beszorul a középső dielektrikumrétegbe. Az elmondottakat demonstrálja a következő két grafikon.
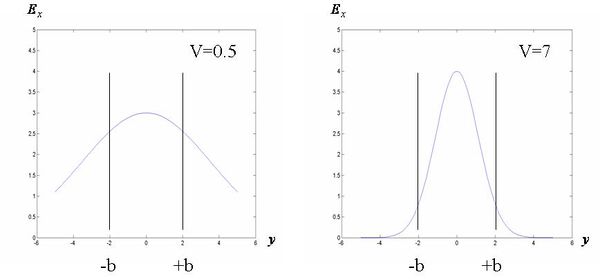
|
| 3.1.4 ábra |
A dielektrikum-rétegrendszerben terjedő síkhullám (csak a fázisa állandó, a térerősség amplitúdója nem) leírásával kvalitatív képet kaptunk a – többnyire hengerszimmetrikus – optikai szálban terjedő jel tulajdonságairól. Hasonló megfontolások érvényesek mindkét geometriára. Amennyiben az optikai szál magja, vagyis a középső, néhány  átmérőjű és
átmérőjű és  törésmutatójú (a magot koaxiálisan körülvevő köpenyé pedig
törésmutatójú (a magot koaxiálisan körülvevő köpenyé pedig 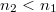 ) henger ármérője elegendően kicsi, akkor mindössze egyetlen módus létezhet a szálban. Az ilyen optikai kábelt nevezik egymódusú optikai szálnak. Vastagabb magátmérő esetén több módus is haladhat a szálban; ezek a többmódusú optikai szálak. A többmódusú szálakban terjedő jel az anyagi diszperzión kívül általában módusdiszperziót is szenved. Bizonyos esetekben a kétfajta diszperzió ki is ejtheti egymást. A zérus-diszperzió egymódusú szálakban általában egy hullámhosszon valósul meg; a gyakorlatban természetesen ez egy keskeny hullámhossztartományt jelent, hiszen az optikai jelátvitel nem egy tökéletesen monokromatikus hullámmal, hanem fényimpulzusokkal valósítható meg.
) henger ármérője elegendően kicsi, akkor mindössze egyetlen módus létezhet a szálban. Az ilyen optikai kábelt nevezik egymódusú optikai szálnak. Vastagabb magátmérő esetén több módus is haladhat a szálban; ezek a többmódusú optikai szálak. A többmódusú szálakban terjedő jel az anyagi diszperzión kívül általában módusdiszperziót is szenved. Bizonyos esetekben a kétfajta diszperzió ki is ejtheti egymást. A zérus-diszperzió egymódusú szálakban általában egy hullámhosszon valósul meg; a gyakorlatban természetesen ez egy keskeny hullámhossztartományt jelent, hiszen az optikai jelátvitel nem egy tökéletesen monokromatikus hullámmal, hanem fényimpulzusokkal valósítható meg.
"Különleges" optikai elemek
Az optikai kettőstörés jelenségének bemutatásánál láttuk, hogy bizonyos kristályokban a két, egymásra merőleges polarizációjú nyalábhoz különböző törésmutatók tartoznak ( és
és  ). A különböző törésmutatókhoz pedig más-más határszöget kapunk a teljes visszaverődésre. Ez lehetőséget ad olyan optikai elemek létrehozására, melyekkel a különböző polarizációjú komponensek szétválaszthatók például egy nem ismert, vagy véletlen polarizációjú nyalábban. Itt most ezen eszközök közül néhányat sorolunk fel a részletes optikai leírás nélkül.
). A különböző törésmutatókhoz pedig más-más határszöget kapunk a teljes visszaverődésre. Ez lehetőséget ad olyan optikai elemek létrehozására, melyekkel a különböző polarizációjú komponensek szétválaszthatók például egy nem ismert, vagy véletlen polarizációjú nyalábban. Itt most ezen eszközök közül néhányat sorolunk fel a részletes optikai leírás nélkül.
Az első ilyen eszköz a már régóta használatos optikai elem a Nicol-prizma (3.2.1 ábra).
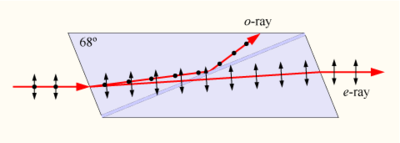
|
| 3.2.1 ábra |
A következő három osztóprizma is hasonló elven működik.
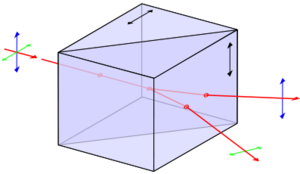
|
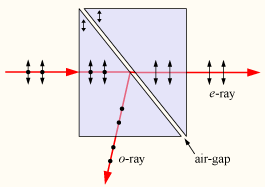
|
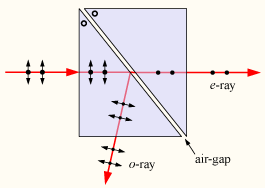
|
| Wollaston-prizma | Glan-Taylor-prizma | Glan-Foucault-prizma |
| 3.2.2.a ábra | 3.2.2.b ábra | 3.2.2.c ábra |
Némely optikai méréshez szükség van 50%-os osztótükörre is. Ezt gyakran egy, a Glan-Foucault-prizmához kinézetre hasonló nyalábosztó prizmával (3.2.3.a ábra) oldják meg, de légrés helyett vékonyréteg-rendszer segítségével érik el az 50%-os nyalábosztást (a 3.2.3.b ábrán látható egy ilyen prizma transzmissziós görbéje a két polarizációs irányra 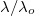 függvényében).
függvényében).

|
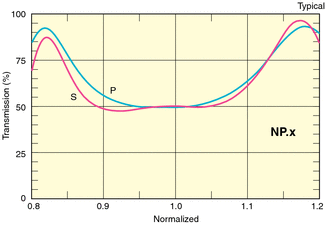
|
| 3.2.3.a ábra | 3.2.3.b ábra |
Az ilyen prizmákkal szemben gyakran támasztanak még egy követelményt, mégpedig azt, hogy a reflektált nyaláb fázistolása 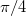 legyen a transzmittáltéhoz képest; a vékonyréteg-rendszerrel ez a feltétel is kielégíthető. Az előbb bemutatott nem-polarizációs nyalábosztó mellett igen gyakran használnak még polarizációs nyalábosztót is (3.2.4 ábra).
legyen a transzmittáltéhoz képest; a vékonyréteg-rendszerrel ez a feltétel is kielégíthető. Az előbb bemutatott nem-polarizációs nyalábosztó mellett igen gyakran használnak még polarizációs nyalábosztót is (3.2.4 ábra).
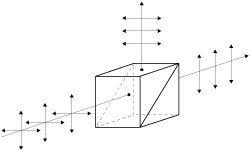
|
| 3.2.4 ábra |
Egy ilyen polarizációs nyalábosztó természetesen a cirkulárisan polarizált hullámot felbontja két lineárisan polarizált nyalábra.
A jobbra és a balra forgató kristályok alkalmazásával Fresnel készített egy olyan nyalábosztót, amely a jobbra és a balra cirkulárisan polarizált nyalábokat választja szét (3.2.5 ábra).
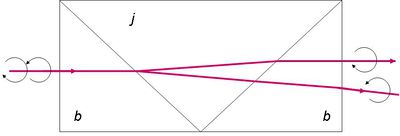
|
| 3.2.5 ábra |
Ez az optikai elem pedig egy lineárisan polarizált nyalábot választ szét két cirkulárisan poláros komponensére.
Fotonikus kristályok
A fotonikus kristály egy olyan nanotechnológiai eljárással készült eszköz, amelyben az anyag törésmutatója (dielektromos állandója) periodikus struktúrával rendelkezik. Ez a periódus általában kisebb, mint a vezetett, vagy eltérített, esetleg visszavert fény hullámhossza. Az elektrodinamika és a fizikai optika egyenleteinek felhasználásával numerikus szimuláció segítségével meghatározhatók egy fotonikus kristály jellemző optikai tulajdonságai. A fotonikus kristály szerkezetű optikai szálat általában speciális mérésekben alkalmazzák főként kis vesztesége és megfelelő (akár negatív) diszperziója miatt. A következő ábrán egy ilyen szál keresztmetszetének elektronmikroszkópos képe látható.

|
| 3.3.1 ábra |
Nanostruktúrájú fotonikus eszközök használhatók optikai csatolóként, illetve nyalábosztóként is. Két ilyen eszköz szimulációs technikával demonstrálható fényvezetése látható a 3.3.2.a és 3.3.2.b ábrákon.
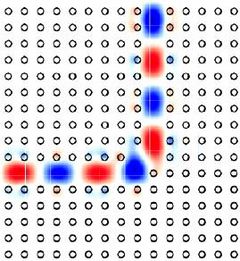
|
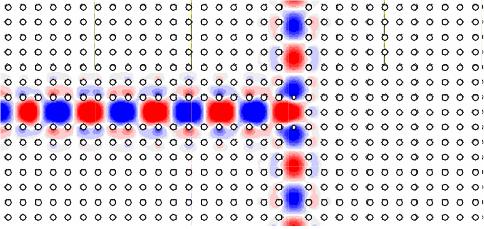
|
| 3.3.2.a ábra | 3.3.2.b ábra |
A kék-morpho lepke szárnyának színét sem festékmolekulák határozzák meg, hanem a szárnyfelszín nanostruktúrája miatt látjuk kékes árnyalatúnak (3.3.3 ábra).

|
| 3.3.3 ábra |
A szárnyfelszín nanoszerkezetének egy kis részlete látható a következő ábrán:

|
| 3.3.4 ábra |
Közelítő módszerek a geometriai optikában (Paraxiális mátrixoptika)
Egy összetett optikai rendszer (távcső, fényképezőgép objektív, stb.) képalkotása gyakran a geometriai optika sugárkövetési módszerével megfelelő pontossággal leírható. Ennek általában az az oka, hogy az alkalmazott optikai elemek jellemző mérete több nagyságrenddel nagyobb, mint a fény hullámhossza, vagyis fényelhajlás jelenségét nem szükséges figyelembe venni. Amennyiben a fénysugarak az optikai tengellyel kis szöget zárnak be ( 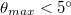 ), akkor elfogadható pontossággal használhatók a következő közelítések:
), akkor elfogadható pontossággal használhatók a következő közelítések:
![\[ sin \theta \approx tg \theta \approx \theta \qquad {\rm \acute{e}s} \qquad cos\theta =\sqrt{1-sin^{2}\theta }\approx\sqrt{1-\theta ^{2}}\approx 1-\frac{\theta ^{2}}{2} \]](/images/math/5/b/9/5b99546872ebf993eec010c6016062c8.png) |
(3.4.1) |
A következő két, könnyen érthető példán mutatjuk be a közelítő módszer alkalmazhatóságát.
Tekintsük először a szabadtéri sugárkövetést. Legyen a  tengely az optikai tengely. A nyalábot egy adott
tengely az optikai tengely. A nyalábot egy adott  helyen jellemezzük a tengelytől mért
helyen jellemezzük a tengelytől mért  távolsággal, valamint a tengellyel bezárt
távolsággal, valamint a tengellyel bezárt  szöggel (megállapodás szerint ez akkor pozitív, amikor a nyaláb "felfelé" halad). A következő ábrán látható, amint egy fénysugár az optikai tengelytő
szöggel (megállapodás szerint ez akkor pozitív, amikor a nyaláb "felfelé" halad). A következő ábrán látható, amint egy fénysugár az optikai tengelytő 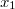 távolságban lévő
távolságban lévő  pontból a
pontból a  pontba jut, miközben a
pontba jut, miközben a  tengely mentén
tengely mentén  utat tesz meg.
utat tesz meg.
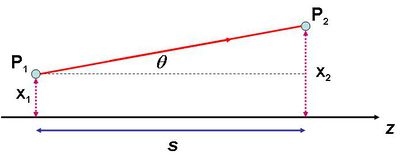
|
| 3.4.1 ábra |
A  pont
pont 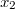 távolsága az optikai tengelytől könnyen kiszámítható:
távolsága az optikai tengelytől könnyen kiszámítható:
![\[ x_{2}=x_{1}+s\cdot tg\theta \]](/images/math/8/2/1/8219e199597957ac65b339339cb4eec7.png) |
(3.4.2) |
A 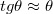 közelítéssel ez egyszerűbb alakba is írható:
közelítéssel ez egyszerűbb alakba is írható:
![\[ x_{2}=x_{1}+s\cdot \theta \]](/images/math/a/5/7/a57af1cc31f559688def59e58be3652f.png) |
(3.4.3) |
A nyalábot a 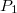 pontban az
pontban az 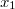 és
és 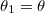 koordinátákkal jellemzzük. A nyaláb iránya a
koordinátákkal jellemzzük. A nyaláb iránya a 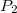 pontban ugyanaz (
pontban ugyanaz ( 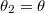 ), így a koordináták transzformációja egyszerűen megadható:
), így a koordináták transzformációja egyszerűen megadható:
![\[ \begin{bmatrix} x_2 \\ \theta_2 \end{bmatrix}= \begin{pmatrix} 1 & s \\ 0 & 1 \end{pmatrix} \begin{bmatrix} x_1 \\ \theta _1 \end{bmatrix} \]](/images/math/b/a/2/ba2f9a40fa1e55cd775bf639133f93ca.png) |
(3.4.4) |
Második modellünk a vékony gyűjtőlencsével történő leképezés. Tekintsük ehhez a következő ábrát:
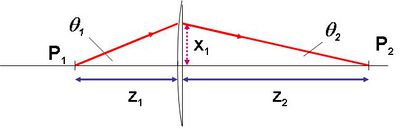
|
| 3.4.2 ábra |
Az ábráról leolvashatók a nyalábok irányát megadó szögek a közelítés felhasználásával:
![\[ \frac{x_1}{z_1}=\theta _1 \qquad {\rm \acute{e}s} \qquad \frac{x_1}{z_2}=\theta _2 \]](/images/math/f/2/8/f286a6072f7a3d950a50f8d8e9e1af2a.png) |
(3.4.5) |
Az 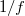 szabályt felírhatjuk a leképezésre:
szabályt felírhatjuk a leképezésre:
![\[ \frac{1}{f}=\frac{1}{z_1}+\frac{1}{z_2} \]](/images/math/1/d/5/1d5f214c30848b98606b163ebeefaf5a.png) |
(3.4.6) |
A 3.4.6 mindkét oldalát beszorozhatjuk 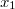 - el:
- el:
![\[ \frac{x_1}{f}=\frac{x_1}{z_1}+\frac{x_1}{z_2} \]](/images/math/3/8/0/3801e880f7871829263f2b36981c9373.png) |
(3.4.7) |
Ezt az egyenletet 3.4.5 - öt felhasználva átírhatjuk:
![\[ \frac{x_1}{f}=\theta_1+\theta_2 \]](/images/math/7/9/0/7904377fca6c08e972eb6f43ad6ce994.png) |
(3.4.8) |
A vékony lencse hatása most már egyszerűen megadható:
![\[ \theta_2=\theta_1-\frac{x_1}{f} \]](/images/math/4/b/4/4b4eee190d10bb881d39e61014e6da7a.png) |
(3.4.9) |
A lencse transzformációját tehát a következő formában írhatjuk fel ( 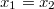 ):
):
![\[ \begin{bmatrix} x_2 \\ \theta_2 \end{bmatrix}= \begin{pmatrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{pmatrix} \begin{bmatrix} x_1 \\ \theta _1 \end{bmatrix} \]](/images/math/0/4/e/04e1cbbd73b6772400fdf04d9c4e34f0.png) |
(3.4.10) |
Az előbbiekben bemutatott technika segítségével egyszerűen meghatározható a szórólencse, a síktükör, a gömbtükör, stb. átmeneti mátrixa, így lineáris transzformációk egymás utáni alkalmazásával egy összetett, nem túl sok optikai elemből álló rendszer modellezése is megoldható. Ha a maximális szög kisebb, mint 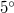 , akkor egy transzformációra a relatív hiba nem nagyobb 0.12 %-nál (
, akkor egy transzformációra a relatív hiba nem nagyobb 0.12 %-nál (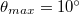 esetén a relatív hiba körülbelül 0.5%). Az optikai elemszám növelésével viszont a hiba exponenciálisan növekszik; ez a lineáris transzformáción alapuló szimulációt erősen korlátozza.
Az említett közelítéseket sugárkövetésre felhasználó analitikus módszer a paraxiális mátrixoptika. Az előbbiekben bemutatott technika alkalmazására jól használható számítógépes programok használatosak. Ezek némelyike szabad felhasználású, és az internetről is letölthetők Optical design software néven.
esetén a relatív hiba körülbelül 0.5%). Az optikai elemszám növelésével viszont a hiba exponenciálisan növekszik; ez a lineáris transzformáción alapuló szimulációt erősen korlátozza.
Az említett közelítéseket sugárkövetésre felhasználó analitikus módszer a paraxiális mátrixoptika. Az előbbiekben bemutatott technika alkalmazására jól használható számítógépes programok használatosak. Ezek némelyike szabad felhasználású, és az internetről is letölthetők Optical design software néven.