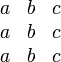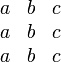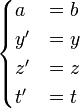|
|
| 1. sor: |
1. sor: |
| − | <wlatex>
| |
| − |
| |
| − | <!--[[Kategória:Mechanika]]-->
| |
| − | [[Kategória:Elektromosságtan]]
| |
| − | [[Kategória:Hőtan]]
| |
| − | <!--[[Kategória:Kvantummechanika]]-->
| |
| − | <!--[[Kategória:Statisztikus fizika]]-->
| |
| − | <!--[[Kategória:Nanofizika]]-->
| |
| − | <!--[[Kategória:Optika]]-->
| |
| − | <!--[[Kategória:Szilárdtestfizika]]-->
| |
| − | <!--[[Kategória:Mag és részecskefizika]]-->
| |
| − | <!--[[Kategória:Informatika]]-->
| |
| − | [[Kategória:Laborgyakorlat]]
| |
| − | <!--[[Kategória:Fizika laboratórium 1.]]-->
| |
| − | [[Kategória:Fizika laboratórium 2.]]
| |
| − | <!--[[Kategória:Fizika laboratórium 3.]]-->
| |
| − | <!--[[Kategória:Fizika laboratórium 4.]]-->
| |
| − | [[Kategória:Szerkesztő:Vankó]]
| |
| − |
| |
| − | ''A mérés célja:''
| |
| − | * elmélyíteni a hallgatók termoelektromos effektusokkal kapcsolatos ismereteit,
| |
| − | * megismertetni a hallgatókat a félvezető termoelemmel és a Peltier-elemmel (termoelektromos hűtő elemmel).
| |
| − |
| |
| − | ''Ennek érdekében:''
| |
| − | * összefoglaljuk a félvezető termoelemmel és a Peltier-elemmel kapcsolatos elméleti tudnivalókat,
| |
| − | * mérések segítségével meghatározzuk a félvezető termoelem és a Peltier-elem fontosabb jellemzőit,
| |
| − | * a mért Seebeck és Peltier együttható hányadosából meghatározzuk az abszolút hőmérsékletet.
| |
| − |
| |
| − | __TOC__
| |
| − |
| |
| − | ==Elméleti összefoglaló==
| |
| − |
| |
| − | A [[Hőmérsékletérzékelők hitelesítése]] című mérés elméleti részében részletesebben foglalkoztunk a két vezetőből készült termoelemek működésével és alkalmazásával. Most az ott elmondottakra is támaszkodunk.
| |
| − |
| |
| − | ===Termoelektromos jelenségek===
| |
| − |
| |
| − | A félvezető termoelem és a Peltier-elem működését termoelektromos és hőtani folyamatok határozzák meg. A termoelektromos jelenségek elektromos és hőtani folyamatok közötti kapcsolatokat adnak meg. Összefoglalónkat ezen effektusok (a Seebeck-, a Peltier-, a Thomson-effektus) és a Joule-hő ismertetésével kezdjük, majd a tisztán hőtani folyamatok leírásával folytatjuk, míg végül megvizsgáljuk ezek együttes hatását a termoelem és a Peltier-elem viselkedésére.
| |
| − |
| |
| − | A termoelektromos jelenségek fémek esetében is fellépnek, de az effektusok sokkal erősebbek félvezetők alkalmazásakor: például egy félvezető termoelem hőfoktényezője egy nagyságrenddel nagyobb, mint egy fém termoelemé. Ezért a gyakorlatban használt Peltier-elemek (termoelektromos hűtőelemek) is félvezetőkből készülnek és a mérésen is ilyet használunk.
| |
| − |
| |
| − | Egy n- és p-típusú félvezetőből kialakított termoelemet mutat az 1/b ábra. Ha az '''A''' és '''B''' pont <math>T_0</math> hőmérsékleten van és '''C''' pont hőmérséklete <math>T</math>, (<math>T\neq T_0</math>) az '''A''' és '''B''' pont között <math>U</math> feszültséget mérhetünk. Ez a Seebeck-effektus. Az effektusra jellemző az anyagtól és hőmérséklettől függő <math>\alpha</math> állandót az <math>\alpha = \left( \frac{{\rm d}U}{{\rm d}T}\right)_{T_0}$</math> egyenlettel definiáljuk.
| |
| − |
| |
| − | Ha a fenti összeállításon áram folyik, az áram irányától függően a '''C''' pontban hő szabadul fel, vagy hő nyelődik el. Ez a Peltier-effektus.
| |
| − | Az egységnyi idő alatt felszabaduló vagy elnyelt hőnek megfelelő hőteljesítmény (<math>P_P</math>) arányos az <math>I</math> árammal: <math>P_P=\frac{{\rm d}Q}{{\rm d}t}=\pi I=\alpha TI$</math> ahol <math>Q</math> a hő, <math>\pi</math> a Peltier-együttható, <math>T</math> az abszolút hőmérséklet, míg <math>\alpha</math> a Seebeck-együttható.
| |
| − |
| |
| − | Amikor <math>I</math> áram folyik olyan homogén vezetőben, amelyben az áram irányába eső <math>{\rm d}T/{\rm d}x</math> gradiens van, az áram és a hőmérséklet gradiens irányától, valamint a vezető anyagától függően hő szabadul fel, vagy nyelődik el. Ez a Thomson-effektus. Az időegység alatt a vezető egységnyi hosszúságú részében fejlődő Thomson-hő arányos az áramerősséggel és a hőmérséklet gradienssel: <math>P_T=\tau \frac{{\rm d}T}{{\rm d}x} I$</math> ahol <math>\tau</math> a vezető anyagától és a hőmérséklettől függő előjeles mennyiség, a Thomson-állandó. A Thomson-hő pozitív előjelű – azaz hő szabadul fel – ha <math>\tau</math> pozitív előjelű és az áram a magasabb hőmérsékletű hely felől az alacsonyabb hőmérsékletű hely felé folyik.
| |
| − |
| |
| − | Az árammal átjárt vezetőben hő szabadul fel: az úgynevezett Joule-hő. A Joule-törvény értelmében a teljesítmény, ha <math>R</math> ellenállású vezetőn <math>I</math> áram folyik: <math>P_J=I^2 R$$
| |
| − |
| |
| − | Az eszköz működésével kapcsolatos "tisztán" hőtani folyamatok közül egyedül az elem belsejében lejátszódó hővezetés hatását vesszük figyelembe. Ha a meleg oldal <math>T_1</math> és a hideg oldal <math>T_0</math> hőmérsékletű (<math>T_1 > T_0</math>), akkor a meleg oldalról a hideg oldal felé lejátszódó hővezetés teljesítménye: <math>P_v=\lambda \frac{A}{d}\left(T_1-T_0\right)$</math> ahol <math>\lambda</math> a hővezető-képesség, <math>A</math> az elem keresztmetszetének területe és <math>d</math> a vastagság. A termoelemként és Peltier-elemként is használható eszköz vázlata a 1/d ábrán látható.
| |
| − |
| |
| − | {| cellpadding="5" cellspacing="0" align="center"
| |
| − | |-
| |
| − | | [[Fájl:termoelempeltier_1_abra.jpg|közép|600px|]]
| |
| − | |-
| |
| − | | align="center"|1. ábra
| |
| − | |}
| |
| − |
| |
| − |
| |
| − | ===Félvezető termoelem===
| |
| − |
| |
| − | Ha két fémből ('''1''' és '''2''') termoelemet hozunk létre (1/a ábra), az '''A''' és '''B''' pontok között mérhető feszültség a '''C''' pont <math>T</math> hőmérséklete és az '''A''' és '''B''' pont közös <math>T_0</math> hőmérsékletének különbségétől (<math>T-T_0</math>), valamint a két fém anyagi minőségétől függ. A kapott feszültség nem függ a két fém '''C''' pontban történ összeforrasztására használt harmadik fém anyagi minőségétől. A fém termoelemhez hasonlóan, két különböző módon szennyezett félvezetőből is létrehozhatunk termoelemet. Ezek érzékenysége kb. egy nagyságrenddel nagyobb, mint a fémből készült termoelemeké. A félvezető termoelem vázlata az 1/b ábrán, perspektivikus rajza pedig az 1/c ábrán látható.
| |
| − |
| |
| − | A termoelem egyik jellemzője az 1.1 részben bevezetett Seebeck-együttható, ami az l°C hőmérséklet-különbség hatására kialakuló termofeszültséget adja meg.
| |
| − | Az első közelítésben a termoelem üresjárási feszültségének hőmérsékletfüggése az <math>U_0=\alpha_{12}\left(T-T_0\right)$</math> összefüggéssel adható meg.
| |
| − |
| |
| − | A vizsgálat tárgyát képező félvezető termoelem <math>k</math> darab p-n átmenetet tartalmaz, amelyek elektromosan sorba kapcsolódnak (1/d ábra), így feszültségük összeadódik: <math>U=kU_0$$
| |
| − |
| |
| − | Az átmenetek két alumínium lemezhez csatlakoznak, jó hővezető, de elektromosan szigetelő réteggel (1/d ábra). Az alumínium lemezek közül az egyik (a meleg oldal) <math>T_1</math> hőmérsékleten, míg a másik (a hideg oldal) <math>T_0</math> hőmérsékleten van. Ilyen módon az elemek hőtani szempontból párhuzamosan kapcsolódnak.
| |
| − |
| |
| − | Vizsgálatainkhoz a termoelemet két hőcserélő közé helyezzük (3/a ábra). A hideg oldalhoz csatlakozó hőcserélőn (alumínium tömb) csapvizet vezetünk keresztül és ennek az oldalnak a hőmérsékletét állandó (<math>T_0</math>) értéken tartjuk. A meleg oldalhoz csatlakozó alumínium tömbben ellenállás fűtőtest van, amit alacsony feszültségű külső áramforrás segítségével működtetünk. Így a meleg oldal hőmérsékletét változtatni tudjuk.
| |
| − |
| |
| − | Ha különböző <math>T_1</math> hőmérsékletek mellett megmérjük a termoelem <math>U_0</math> üresjárási feszültségét, az <math>U_0</math> – <math>\left(T_1-T_0\right)</math> összefüggést ábrázolva egyenest kapunk. Az egyenes meredeksége a Seebeck-együttható.
| |
| − |
| |
| − | A termoelem fontos jellemzője a belső ellenállása. A belső ellenállást a [[Hőmérsékletérzékelők hitelesítése]] című jegyzetben leírtak (6. feladat) szerint mérhető.
| |
| − |
| |
| − | Termoelemünk termikus energia hatására termel villamos energiát. Mekkora hatásfokkal teszi ezt?
| |
| − | Erre a kérdésre a következő módon kaphatunk feleletet:
| |
| − | A termoelemet belső ellenállásával azonos nagyságú ellenállással terheljük. Ekkor tudjuk kivenni a maximális elektromos teljesítményt. Ehhez a melegoldali alumínium tömböt kb. 20 W villamos teljesítménnyel felfűtjük, majd a fűtést kikapcsolva mérjük az időben csökkenő hőmérsékletet és a terhelő ellenálláson jelentkező villamos teljesítményt. Ha feltételezzük, hogy rendszerünk a környezettől jól szigetelt, akkor azt mondhatjuk, hogy a fűtött alumínium tömb által leadott hő hatására nyerünk elektromos teljesítményt. A leadott hőteljesítmény: <math>P_h=\frac{{\rm d}Q}{{\rm d}t}=cm\frac{{\rm d}T}{{\rm d}t}$</math> ahol <math>c</math> és <math>m</math> az alumínium fajhője ill. a tömb tömege.
| |
| − |
| |
| − | A fentiek alapján termoelem hatásfoka úgy állapítható meg, hogy a <math>T(t)</math> hűlési görbe vizsgált pontján meghatározzuk <math>{\rm d}T/{\rm d}t</math> értékét és az előzőképlet alapján számítjuk a hőteljesítményt (<math>P_h$-t), miközben mérjük az ugyanezen időponthoz tartozó villamos teljesítményt: <math>P_v=\frac{U^2}{R}$$
| |
| − |
| |
| − | Az átalakítás hatásfoka ezek után: <math>\eta=\frac{P_h}{P_v}$$
| |
| − |
| |
| − | A fentiekből a hatásfok hőmérséklet-különbség függése [az <math>\eta(\Delta T)</math> kapcsolat] is meghatározható.
| |
| − |
| |
| − | ===Peltier-elem===
| |
| − |
| |
| − | Az 1.1 részben áttekintett effektusok eredményeként röviden összefoglalva a vizsgált Peltier-elem belsejében a következő folyamatok játszódnak le:
| |
| − |
| |
| − | * Az áram irányától függően a Peltier-effektus miatt az egyik oldalon az átmenetnél hő nyelődik el (hideg oldal, <math>T_0</math> hőmérsékleten), másik oldalon hő szabadul fel (meleg oldal, <math>T_1</math> hőmérsékleten).
| |
| − |
| |
| − | * A Thomson-effektus következtében a félvezető elemek anyagától függően az elem belsejében hő szabadul fel vagy nyelődik el.
| |
| − |
| |
| − | * A Joule-hő következtében az elem belsejében hő fejlődik. Ezt egyszerűség kedvéért úgy tekintjük, hogy egyenlő arányban jut a két felületre.
| |
| − |
| |
| − | * A hővezetés eredménye egy a meleg oldalról a hideg oldal felé történő hőáramlás.
| |
| − |
| |
| − | Az elmondottak alapján a Peltier-elem hideg oldalán a hűtőteljesítmény: <math>P_H=\alpha T_0 I - \tau \frac{T_1-T_0}{2} I - \frac{I^2 R}{2} - \lambda \frac{A}{d}\left(T_1-T_0\right)$$
| |
| − |
| |
| − | A meleg oldal fűtő teljesítménye: <math>P_H=\alpha T_1 I + \tau \frac{T_1-T_0}{2} I + \frac{I^2 R}{2} - \lambda \frac{A}{d}\left(T_1-T_0\right)$$
| |
| − |
| |
| − | Az elektromos teljesítmény: <math>P_E=\alpha \left(T_1-T_0\right) I + \tau \left(T_1-T_0\right) I + I^2 R=U_p I_p$$
| |
| − |
| |
| − | A Peltier-elem energetikai folyamatait a 2. ábra szemlélteti. A hőerőgépek és a hűtőgépek működése az ideális Carnot-körfolyamat segítségével közelíthető. Hőerőgépként a Carnot-gép <math>W</math> munkát végez, miközben a rendszer a magasabb <math>T_1</math> hőmérsékletű hőtartályból <math>Q_1</math> hőmennyiséget vesz fel, míg a kisebb <math>T_0</math> hőmérsékletű hőtartálynak <math>Q_0</math> hőt ad le. Az így nyert munka <math>W=Q_1-Q_0</math>. A gép hatásfoka illetve maximális hatásfoka pedig rendre <math>\eta=W/Q_1</math> ill. <math>\eta_{max}=\left(T_1-T_0\right)/T_1</math>. (Így működik a termoelem.) Hűtőgépként (hőszivattyúként) a Peltier-elem fordított Carnot-gépnek tekinthető. Külső <math>W</math> munka befektetése árán a hidegebb <math>T_0</math> oldalról <math>Q_0</math> hőt von ki, míg a melegebb oldalon <math>Q_1=W+Q_0</math> hőt ad le. A folyamat teljesítménytényezője <math>\varepsilon=Q_0/W</math> ill. <math>\varepsilon_{max}=T_0/\left(T_1-T_0\right)</math>. Vegyük észre, hogy <math>\varepsilon > 1</math> is lehet. A hatásfok ill. teljesítménytényező a megfelelő teljesítmények segítségével is kifejezhető.
| |
| − |
| |
| − | {| cellpadding="5" cellspacing="0" align="center"
| |
| − | |-
| |
| − | | [[Fájl:termoelempeltier_2_abra.jpg|közép|300px|]]
| |
| − | |-
| |
| − | | align="center"|2. ábra
| |
| − | |}
| |
| − |
| |
| − | A Peltier-elem vizsgálatához használt eszköz a félvezető elemből és a két oldalára szerelt fémtömbökből áll (3/b ábra). Az egyik tömb vízzel hűthető (így <math>T_0</math> hőmérséklete közel állandó), míg a másik oldal hőszigetelt és fűthető. Ennek megfelelően, a változó hőmérsékletű oldal hőháztartását az alábbi egyenlet írja le: <math>cm\frac{{\rm d}T}{{\rm d}t}=-P_h+P_f-\lambda\frac{A}{d}\left(T-T_0\right)$</math> ahol <math>c</math> és <math>m</math> a tömb tömege ill. fajhője, <math>P_h</math> a hőszivattyúként működtetett Peltier-elem által kivont hőteljesítmény, <math>P_f</math> a fűtőteljesítmény, míg a harmadik tag a Peltier-elemen keresztül hővezetéssel átjutó ismeretlen hőteljesítmény. Termikus egyensúlyban a baloldal 0, vagyis a jobboldali tagok kiejtik egymást.
| |
| − |
| |
| − | Legyen kezdetben <math>T=T_0</math>. Ha a Peltier-elemet a fűtés bekapcsolása nélkül <math>P_p=U_p I_p</math> elektromos teljesítmény befektetése mellett működtetjük, <math>T</math> olyan értékre áll be, melynél <math>P_h=\lambda (A/d)\left(T_0-T\right)</math>. <math>P_p</math> növelésével <math>P_h</math>, és ezzel a hőmérséklet-különbség is nő. Mivel azonban <math>\lambda (A/d)</math> ismeretlen, a teljesítménytényező így nem határozható meg.
| |
| − |
| |
| − | Az <math>\varepsilon</math> teljesítménytényező meghatározásához állandó teljesítménnyel működtetjük a Peltier-elemet, miközben változó <math>P_f</math> fűtőteljesítmény mellett vizsgáljuk a kialakuló <math>T_0-T</math> egyensúlyi hőmérséklet-különbségeket. Alkalmasan választott fűtőteljesítmény esetén a két oldal közti hőmérséklet-különbség eltűnik. Ekkor a <math>P_f=U_f I_f</math> fűtőteljesítmény éppen megegyezik a Peltier-elem által a vízhűtött oldalra átszivattyúzott <math>P_h</math> hőteljesítménnyel (<math>P_h=P_f</math>), vagyis a teljesítménytényező az <math>\varepsilon=P_f/P_p</math> összefüggés alapján számítható.
| |
| − |
| |
| − | Akkor, amikor a hőmérséklet-különbség eltűnik, meghatározható a Peltier-elem belső ellenállása és a Peltier-együttható értéke is.
| |
| − |
| |
| − | $\Delta T=0</math> estében nem keletkezik termofeszültség, így a Peltier-elem belső ellenállása az <math>R=\frac{U_p}{I_p}$</math> képlettel meghatározható.
| |
| − |
| |
| − | $\Delta T=0</math> estében nincsen hővezetés (és Thomson-hő) se, így a Peltier-együttható a definiáló képlet alapján könnyen kifejezhető: <math>\pi=\frac{P_P}{I}=\frac{P_f+\frac{1}{2}P_p}{I_p}=\frac{P_f}{I_p}+\frac{U_p}{2}$</math> (A Peltier-elemnek a fűtőellenállás által leadott teljesítményt és a Peltier-elemre kapcsolt, Joule-hőként felszabaduló elektromos teljesítmény felét kell átszivattyúznia.)
| |
| − |
| |
| − |
| |
| − | ==Mérési elrendezés==
| |
| − |
| |
| − | A termoelem és a Peltier-elem vizsgálatához – kicsit különböző elrendezésben – ugyanazt az eszközt használjuk (3/a és 3/b ábra). A mérőeszköz két 50 g-os alumínium tömbből ill. közöttük elhelyezkedő 98 db sorba kötött p-n átmenetből áll. Az eszköznek a külső környezettel történő hőcseréjét többrétegű szigetelés akadályozza. Az egyik tömb hőmérsékletét vízhűtés rögzíti, míg a másik oldal egy tápegységgel (max. 25 V, 5 A) fűthető. A fűtőteljesítményt áram- és feszültségmérés alapján, az alumínium tömbök hőmérsékletét a Pt-hőmérők ellenállásából a <math>t(^{\circ} C)=\frac{1}{0,0039}\left(\frac{R(\Omega)}{100}-1\right)$</math> összefüggés alapján számítjuk.
| |
| − |
| |
| − | A termoelem kimenetén mérhető a termofeszültség és a terhelő áram (3/a. ábra).
| |
| − |
| |
| − | A Peltier-elem működtetéséhez egy másik tápegységet (max. 40 V, 10 A) használunk (3/b ábra). A Peltier-teljesítményt áram- és feszültségmérés alapján számítjuk.
| |
| − |
| |
| − | {| cellpadding="5" cellspacing="0" align="center"
| |
| − | |-
| |
| − | | [[Fájl:termoelempeltier_3a_abra.jpg|közép|300px|]]
| |
| − | | [[Fájl:termoelempeltier_3b_abra.jpg|közép|300px|]]
| |
| − | |-
| |
| − | | align="center"|3/a ábra
| |
| − | | align="center"|3/b ábra
| |
| − | |}
| |
| − |
| |
| − |
| |
| − | ==Mérési feladatok==
| |
| − |
| |
| − | *''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
| |
| − |
| |
| − | '''1.''' Határozza meg a félvezető termoelem elektromotoros erejét a hőmérséklet függvényében! Ábrázolja az elektromotoros erő – hőmérséklet-különbség összefüggést és határozza meg a Seebeck-állandót.
| |
| − | A fűtőellenállásra kezdetben kb. 2 V, majd egyre nagyobb (max. 20 V) feszültséget kapcsolva folyamatosan fűtse a meleg oldalt, és néhány percenként olvassa le a hőmérséklet (ellenállás) és üresjárati feszültség értékeket.
| |
| − | * ''Az ellenállás alapján számított hőmérséklet:'' <math>t(^{\circ} C)=\frac{1}{0,0039}\left(\frac{R(\Omega)}{100}-1\right)$$
| |
| − |
| |
| − | '''2/a''' Határozza meg a termoelem belső ellenállását!
| |
| − | Az első feladat utolsó fűtőteljesítményének beállított értékén folytassa a fűtést a véghőmérséklet eléréséig, és ott határozza meg a termoelem belső ellenállását.
| |
| − | * ''Ilyen mérést végzett már a [[Hőmérsékletérzékelők hitelesítése]] közben is!
| |
| − | * Emlékeztetőül: A termoelem belső ellenállásához mérni kell
| |
| − | ** a termoelem üresjárati feszültségét (<math>U_0</math>),
| |
| − | ** a termoelem áramát egy ismert ellenálláson keresztül (<math>I</math>). Ez az ismert ellenállás maga az árammérő is lehet, pl. 20 mA vagy 200 mA méréshatáron.
| |
| − | ** Az árammérő ellenállását (<math>R_A</math>, ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. Az ellenállásmérőt egyszerűen rákötjük a – '''más áramkörbe ezalatt be nem kötött!''' –, megfelelő méréshatárra beállított árammérőre.
| |
| − | ** <math>U_0</math>, <math>I</math> és <math>R_A</math> ismeretében az <math>R_b</math> belső ellenállás számolható.
| |
| − | * Milyen méréshatárra állított árammérővel terheli a termoelemet? Miért?
| |
| − | * Mekkora az árammérő belső ellenállása ezen a méréshatáron?
| |
| − | * Hogyan fejezhető ki <math>R_b</math> a mért mennyiségek segítségével?''
| |
| − |
| |
| − | '''2/b''' Határozza meg a termoelem hatásfokát!
| |
| − |
| |
| − | A belső ellenállás meghatározása után kapcsoljon a belső ellenállással kb. megegyező ellenállást a termoelem kivezetéseire. Ehhez használjon ellenállásdekádot.
| |
| − |
| |
| − | A terhelés hatására csökkenni fog a kialakult hőmérséklet-különbség. Várja meg, amíg a hőmérséklet-különbség egy új értéken állandósul. Mérje meg ekkor a termoelem kimenetén (a terhelő ellenálláson) a kapocsfeszültséget. Számítsa ki a terhelő ellenálláson leadott teljesítményt (a hasznos teljesítményt) és – a fűtőteljesítmény ismeretében – a termoelem hatásfokát.
| |
| − |
| |
| − | '''3.''' Mérje meg 5 W Peltier-teljesítmény esetén (a fűtőtest kiiktatásával) a kialakuló hőmérséklet-különbséget! Mérje a hőmérsékletet 10 percig és a függelékben megadott összefüggések illesztésével határozza meg a kialakuló max. (állandósult) hőmérséklet-különbséget!
| |
| − | * ''A változó hőmérsékletű (a Peltier-elemmel hűtött) oldal hőmérsékletét számítógépes adatgyűjtő segítségével mérje az idő függvényében.''
| |
| − |
| |
| − | '''4.''' Mérje rögzített Peltier-teljesítmény és különböző fűtőteljesítmények mellett a kialakuló hőmérséklet-különbségeket és ábrázolja ezeket!
| |
| − | Peltier-teljesítmény 5 W, fűtőteljesítmények: 3-11 W között 3-4 értéken mérve. A Peltier-elemet működtető tápegységet állandó feszültségen használja, és minden esetben írja fel az áramértékeket is! Mérje a hőmérsékletet esetenként 10 percig és a függelékben megadott összefüggések illesztésével határozza meg a fenti teljesítményeknél kialakuló max. hőmérséklet-különbségeket!
| |
| − | * ''A változó hőmérsékletű (a Peltier-elemmel hűtött, a fűtőellenállással viszont fűtött) oldal hőmérsékletét számítógépes adatgyűjtő segítségével mérje az idő függvényében.''
| |
| − |
| |
| − | '''5.''' Az állandósult hőmérséklet-különbség – fűtőteljesítmény kapcsolat alapján számítsa ki a Peltier-elem teljesítmény-tényezőjét és belső ellenállását!
| |
| − | * ''Ehhez ábrázolja az állandósult hőmérséklet-különbséget a fűtőteljesítmény függvényében, és egyenesillesztéssel határozza meg, milyen fűtőteljesítménynél lenne nulla a hőmérséklet-különbség.
| |
| − | * A nulla hőmérséklet-különbséghez tartozó Peltier-áramot interpolálással határozza meg.
| |
| − | * A Peltier-elem belső ellenállására kapott eredményét hasonlítsa össze a termoelem belső ellenállásával.''
| |
| − |
| |
| − | '''6.''' Határozza meg a Peltier-együtthatót! A Seebeck-együttható és a Peltier-együttható ismeretében számítsa ki a <math>T_0</math> abszolút hőmérsékletet!
| |
| − |
| |
| − |
| |
| − | ''Függelék
| |
| − | * A termikus egyensúly beállása viszonylag hosszú időt igényel. Ezért a <math>T_\infty</math> véghőmérséklet meghatározásánál kihasználjuk, hogy a fűthető oldal hőmérsékletének (<math>T</math>) időbeli változása jó közelítéssel exponenciális jellegű: <math>T(t)=T_\infty+\left(T_0-T_\infty\right)\exp(-t/\tau)$</math> ahol <math>T_0</math> a hőmérséklet kezdeti értéke, míg <math>\tau</math> a hőmérséklet-változás karakterisztikus ideje.''
| |
| − |
| |
| − |
| |
| − |
| |
| − | </wlatex>
| |
| | | | |
| | ===Teszt (1)=== | | ===Teszt (1)=== |
![\[\frac{1}{2}\cdot\sqrt[3]{125}\]](/images/math/3/9/9/399ea5af56346c4048610159a571cddb.png)
körte 
![\[(a+b)^2=a^2+2a\cdot b+b^2\]](/images/math/3/f/4/3f4a35f429e205b8fed4be39c628b552.png)
![\displaystyle \sqrt[3]{125}](/images/math/0/8/a/08ac613bc387f90315c6f344e7547e03.png)
![\[\begin{matrix} a & b & c \\ a & b & c \\ a & b & c_1 \end{matrix} \]](/images/math/2/5/f/25f6f6f72aaa05807c211eb906511360.png)
![\[\begin{array}{ccc} a & b & c \\ a & b & c \\ a & b & c \end{array} \]](/images/math/9/f/d/9fdcb879f74bd6a793369e25577b0f4d.png)
![\[\begin{bmatrix} a_{11}&a_{12}&a_{13}&\dots&a_{1n}\\ a_{21}&a_{22}&a_{23}& &a_{2n}\\ a_{31}&a_{32}&a_{33}&\dots&a_{3n}\\ \vdots& &\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&a_{m3}&\dots&a_{mn} \end{bmatrix}\]](/images/math/5/7/9/579a63bd84dbc4b50edbd01d8ebed185.png)
![\[\begin{cases} a &= b \\ y' &= y \\ z' &= z \\ t' &= t \end{cases}\]](/images/math/8/b/e/8be2c53c1098c6d101e06f1964875f71.png)
![\[ \begin{split} 100 &= 1+8+27+64 = {}\\ &= 1+3+5+7+9+{}\\ &\quad+11+13+15+17+19 \end{split} \]](/images/math/7/9/e/79e2036d77ae7b8249b1aa1071bfc03d.png)
![\[\begin{split} H_c&=\frac{1}{2n} \sum^n_{l=0}(-1)^{l}(n-{l})^{p-2} \sum_{l _1+\dots+ l _p=l}\prod^p_{i=1} \binom{n_i}{l _i}\\ &\quad\cdot[(n-l )-(n_i-l _i)]^{n_i-l _i}\\ &\quad\cdot \Bigl[(n-l )^3-\sum^p_{j=1}(n_i-l _i)^2\Bigr]. \end{split}\]](/images/math/c/8/0/c80c1745d394823af65ae46a8af06330.png)
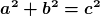
![\[ D^{a+2}_1 \qquad \sum_{i=1}^5 \qquad \textstyle \sum_{i=1}^5 \qquad \sum_{\substack{ a \le 5 \\ b < 3}} \qquad \displaystyle\sum_{\substack{ a \le 5 \\ b < 3}} \qquad \sideset{_a^b}{_c^d}\prod \qquad \displaystyle\sideset{_a^{b+1}}{_{c-1}^d}\sum_{i=n}^{x+y} \]](/images/math/7/d/1/7d12e4227da1c670eff8de330e202b4e.png)
![\[\left(\frac34\right) \qquad \left\{\frac5{15}\right\} \qquad \left<\frac14\right| \qquad \left.\frac{11}{14}\right) \qquad \left[\frac68\right. \qquad \]](/images/math/a/a/c/aac2b4e52f4a26d5def17c08429f4d7c.png)
![\[ \binom12 \qquad \binom{x}{y} \qquad \]](/images/math/e/f/0/ef0b7e2a8963cfd7d00a26b2905145bb.png)
![\[ f(x)=\begin{cases} 1 & \text{ha $x>0$} \\ 0 & \text{ha $x=0$} \\ -1 & \text{egyéb esetekben} \end{cases} \]](/images/math/0/4/1/0417b7ff4a8c29a581ffcddea753be19.png)
![\[ a \overset{\mathrm{def}}{=} b + c \qquad a \overset{?}{<} b \qquad x = y \underset{\cdot}{+} z \qquad \]](/images/math/d/d/0/dd02b90c672332dcb4475fa9f5ae30af.png)
![\[ \int \qquad \int_a^b \qquad \int\limits_a^b \qquad \iint \qquad \iiint \qquad \idotsint \qquad \underbrace{\idotsint}_n \qquad \]](/images/math/d/3/f/d3faf8fd4c9eddf9c1773b820d226800.png)
![\[ \begin{array}{c||c|c|c|c|c|} {\bf +} & 0x & 1 & 2 & 3 & 4 \\ \hline\hline 0 & 0 & 1 & 2 & 3 & 4 \\ \hline 1 & 1 & 2 & 3 & 4 & 0 \\ \hline 2 & 2 & 3 & 4 & 0 & 1 \\ \hline 3 & 3 & 4 & 0 & 1 & 2 \\ \hline 4 & 4 & 0 & 1 & 2 & 3 \\ \hline \end{array} \qquad \text{és} \qquad \begin {array}{c||c|c|c|c|c|} {\bf *} & 0 & 1 & 2 & 3 & 4 \\ \hline\hline 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 1 & 0 & 1 & 2 & 3 & 4 \\ \hline 2 & 0 & 2 & 4 & 1 & 3 \\ \hline 3 & 0 & 3 & 1 & 4 & 2 \\ \hline 4 & 0 & 4 & 3 & 2 & 1 \\ \hline \end{array} \]](/images/math/1/7/1/1712985aa62e3e475b79fc2ad8b704d5.png)
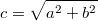
![\[c=\sqrt{a^2+b^2}\]](/images/math/8/0/4/804cc8338c427c581dbe860d66bbe2d6.png)
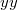és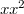 
mellet 
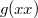értéke 
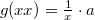lesz.
![\[x=x^3\cdot y\]](/images/math/f/4/d/f4d2427d80e918cfc467ce70315c65ab.png)
