„RLC körök mérése” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „Szerkesztés alatt!”)
 
1. sor: 1. sor:
 
Szerkesztés alatt!
 
Szerkesztés alatt!
 +
 +
<wlatex>
 +
__TOC__
 +
 +
''A mérés célja:''
 +
 +
-megismerkedni a leggyakrabban használt frekvenciafüggő áramköri elemekkel és az ezekből felépülő szelektív áramkörökkel.
 +
 +
''Ennek érdekében:''
 +
 +
-áttekintjük a váltakozó áramú hálózatok reaktáns elemeinek tulajdonságait és néhány egyszerű szűrő és egy rezgőkör frekvenciafüggő viselkedését;
 +
-méréseket végzünk a fent említett hálózatokon.
 +
 +
==Elméleti összefoglaló==
 +
 +
===Tekercs===
 +
 +
A tekercsben indukálódó feszültséget az
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ u(t) = L \frac{\textrm{d} i(t)}{\textrm{d} t} \]</latex></div>
 +
| align = "right" | <span id="eq1"> (1) </span>
 +
|}
 +
 +
egyenlet írja le. Szinuszos gerjesztés [ $ i(t)=I_0 \textrm{sin}\omega t $ ]  esetén
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ u(t) = L \omega I_0 \textrm{cos}\omega t,  \]</latex></div>
 +
| align = "right" | <span id="eq2"> (2) </span>
 +
|}
 +
 +
ami a következő alakba is írható:
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ u(t) = L \omega I_0 \textrm{sin}( \omega t + 90^\circ ),  \]</latex></div>
 +
| align = "right" | <span id="eq3"> (3) </span>
 +
|}
 +
 +
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest. A jelenség magyarázata a Lenz-törvényen alapul.
 +
 +
===Kondenzátor===
 +
 +
A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ i(t) = C \frac{\textrm{d} u(t)}{\textrm{d} t}.  \]</latex></div>
 +
| align = "right" | <span id="eq4"> (4) </span>
 +
|}
 +
 +
Szinuszos gerjesztés [ $ u(t)=U_0 \textrm{sin}\omega t $ ] esetén:
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ i(t) = C \omega U_0 \textrm{cos}\omega t,  \]</latex></div>
 +
| align = "right" | <span id="eq5"> (5) </span>
 +
|}
 +
 +
ami a fentiekhez hasonlóan a következő alakba írható:
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ i(t) = C \omega U_0 \textrm{sin}( \omega t + 90^\circ ),  \]</latex></div>
 +
| align = "right" | <span id="eq6"> (6) </span>
 +
|}
 +
 +
azaz a kondenzátor árama 90°-ot siet a feszültségéhez képest. Magyarázata az, hogy először áram folyik, így töltések kerülnek a lemezekre, és ezek hozzák létre a feszültséget.
 +
Gyakran szükséges a kondenzátor feszültségének ismerete, ami (4) alapján az alábbiak szerint számítható:
 +
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ u(t) = \frac{1}{C} \int i(t)\textrm{d}t .  \]</latex></div>
 +
| align = "right" | <span id="eq7"> (7) </span>
 +
|}
 +
 +
===Aluláteresztő szűrők===
 +
 +
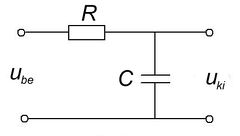
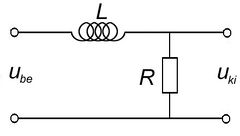
Írjuk fel az 1.a és 1.b ábrákon látható kapcsolások kimenő feszültségeit! (A vastag betűs mennyiségek komplex változók.)
 +
 +
{| cellpadding="2" style="border: 1px solid darkgray;" align="center"
 +
|- border="0"
 +
|- align="center"
 +
| [[Fájl:LowpassA.jpg|bélyegkép|240px]]
 +
| [[Fájl:LowpassB.jpg|bélyegkép|240px]]
 +
|- align="center"
 +
| <div class="texdisplay"><latex display >\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1}{1 + j\omega RC} \end{array}  \]</latex></div> || <div class="texdisplay"><latex display >\[  \begin{array}{rcl}  \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{R}{R + j\omega L} \\ \\ \mathbf{U}_{ki}  & = &  \mathbf{U}_{be} \frac{1}{1 + j\omega L/R}  \end{array}  \]</latex></div>
 +
|}

A lap 2012. február 10., 15:33-kori változata

Szerkesztés alatt!


Tartalomjegyzék


A mérés célja:

-megismerkedni a leggyakrabban használt frekvenciafüggő áramköri elemekkel és az ezekből felépülő szelektív áramkörökkel.

Ennek érdekében:

-áttekintjük a váltakozó áramú hálózatok reaktáns elemeinek tulajdonságait és néhány egyszerű szűrő és egy rezgőkör frekvenciafüggő viselkedését; -méréseket végzünk a fent említett hálózatokon.

Elméleti összefoglaló

Tekercs

A tekercsben indukálódó feszültséget az

\[ u(t) = L \frac{\textrm{d} i(t)}{\textrm{d} t} \]
 (1)

egyenlet írja le. Szinuszos gerjesztés [ 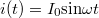\setbox0\hbox{$ i(t)=I_0 \textrm{sin}\omega t $}% \message{//depth:\the\dp0//}% \box0% ] esetén

\[ u(t) = L \omega I_0 \textrm{cos}\omega t, \]
 (2)

ami a következő alakba is írható:

\[ u(t) = L \omega I_0 \textrm{sin}( \omega t + 90^\circ ), \]
 (3)

tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest. A jelenség magyarázata a Lenz-törvényen alapul.

Kondenzátor

A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:

\[ i(t) = C \frac{\textrm{d} u(t)}{\textrm{d} t}. \]
 (4)

Szinuszos gerjesztés [ 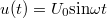\setbox0\hbox{$ u(t)=U_0 \textrm{sin}\omega t $}% \message{//depth:\the\dp0//}% \box0% ] esetén:

\[ i(t) = C \omega U_0 \textrm{cos}\omega t, \]
 (5)

ami a fentiekhez hasonlóan a következő alakba írható:

\[ i(t) = C \omega U_0 \textrm{sin}( \omega t + 90^\circ ), \]
 (6)

azaz a kondenzátor árama 90°-ot siet a feszültségéhez képest. Magyarázata az, hogy először áram folyik, így töltések kerülnek a lemezekre, és ezek hozzák létre a feszültséget. Gyakran szükséges a kondenzátor feszültségének ismerete, ami (4) alapján az alábbiak szerint számítható:

\[ u(t) = \frac{1}{C} \int i(t)\textrm{d}t . \]
 (7)

Aluláteresztő szűrők

Írjuk fel az 1.a és 1.b ábrákon látható kapcsolások kimenő feszültségeit! (A vastag betűs mennyiségek komplex változók.)

LowpassA.jpg
LowpassB.jpg
\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1}{1 + j\omega RC} \end{array} \]
\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{R}{R + j\omega L} \\ \\ \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1}{1 + j\omega L/R} \end{array} \]
A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=RLC_körök_mérése&oldid=2808”