„Spektrumanalízis szerkesztőlap” változatai közötti eltérés
(Új oldal, tartalma: „===Spektrumanalízis===”) |
(→Spektrumanalízis) |
||
| 1. sor: | 1. sor: | ||
===Spektrumanalízis=== | ===Spektrumanalízis=== | ||
| + | <wlatex> | ||
| + | Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg. | ||
| + | $$f(\omega)=\int_{-\infty}^{\infty}F(t)e^{-i\omega t}dt.$$ | ||
| + | Azonban mivel a mérést véges időintervallumban végezzük a spektrum felbontása nem tökéletes. A véges ideig mért jel spektrumára gyakorlatilag úgy tekinthetünk, mintha az a T ideig mért jel periodikus kiterjesztésének a spektruma lenne. Ha a mért jelünk a T időablakban nem periodikus, akkor a periodikusan kiterjesztett jel az időablak határain ugrásokat mutathat, melyek miatt fals nagyfrekvenciás komponensek jelennek meg a spektrumban. Ezen probléma kiküszöbölésére olyan ablakfüggvények használatára van szükség, amelyek a mérési intervallum szélén eltűnnek. A Fourier-transzformációt tehát a vizsgált jel és az ablakfüggvény szorzatán végezzük | ||
| + | |||
| + | $$f_W(\omega)=\int_{-\infty}^{\infty}W(t)F(t)e^{-i\omega t}dt,$$ | ||
| + | |||
| + | ahol $W(t)$ súlyfüggvény egy T időablakon kívül zérus. | ||
| + | |||
| + | Két függvény szorzata a Fourier-térben a függvények Fourier-transzfor-máltjának konvolúciójával egyezik meg: | ||
| + | |||
| + | $$f_W(\omega)=\int_{-\infty}^{\infty}f(\omega')w(\omega-\omega')\frac{d\omega'}{2\pi},$$ | ||
| + | |||
| + | azaz a spektrum $\omega$ frekvenciájához az ablakfüggvény bekever jelet az $\omega'$ frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük. | ||
| + | |||
| + | A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük. | ||
| + | Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük: | ||
| + | |||
| + | $$f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,$$ | ||
| + | ahol $\Delta t$ a két diszkrét mintavételezés között eltelt idő (a mérési idő $T=N\Delta t$). | ||
| + | A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg. | ||
| + | |||
| + | A Nyquist-Shannon mintavételezési törvény értelmében $\Delta t$ mintavételezési idővel legfeljebb $\omega_{max}=\frac{2\pi}{2\Delta t}$ maximális frekvenciáig lehetséges a jel rekonstrukciója. | ||
| + | |||
| + | Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét $\omega_k$ értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén $\mathcal{O}(N^2)$ műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye $\mathcal{O}(NlogN)$ nagyságrendű. Az FFT algoritmus az $N=2^n$ adatpontból álló jel Fourier-spektrumát $\omega_k=\frac{2\pi k}{N\Delta t}, k=0,1,..N/2$ diszkrét körfrekvenciapontokon adja meg. | ||
| + | |||
| + | Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű $\omega_0$ jelet vizsgálunk. Könnyen belátható, hogy ha $\omega_0=\omega_k$ $k$ bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az $f_W(\omega)$ jelünk $\omega_0$ környékén. | ||
A lap 2018. május 16., 19:31-kori változata
Spektrumanalízis
Egy időben változó jel spektrumát a Fourier-transzformáció segítségével ismerhetjük meg.
![\[f(\omega)=\int_{-\infty}^{\infty}F(t)e^{-i\omega t}dt.\]](/images/math/8/5/e/85ef324eb4aa203303778f249b1a850f.png)
Azonban mivel a mérést véges időintervallumban végezzük a spektrum felbontása nem tökéletes. A véges ideig mért jel spektrumára gyakorlatilag úgy tekinthetünk, mintha az a T ideig mért jel periodikus kiterjesztésének a spektruma lenne. Ha a mért jelünk a T időablakban nem periodikus, akkor a periodikusan kiterjesztett jel az időablak határain ugrásokat mutathat, melyek miatt fals nagyfrekvenciás komponensek jelennek meg a spektrumban. Ezen probléma kiküszöbölésére olyan ablakfüggvények használatára van szükség, amelyek a mérési intervallum szélén eltűnnek. A Fourier-transzformációt tehát a vizsgált jel és az ablakfüggvény szorzatán végezzük
![\[f_W(\omega)=\int_{-\infty}^{\infty}W(t)F(t)e^{-i\omega t}dt,\]](/images/math/3/5/8/358e08414d5fd63a56b0bd3f383c0404.png)
ahol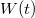 
súlyfüggvény egy T időablakon kívül zérus.
Két függvény szorzata a Fourier-térben a függvények Fourier-transzfor-máltjának konvolúciójával egyezik meg:
![\[f_W(\omega)=\int_{-\infty}^{\infty}f(\omega')w(\omega-\omega')\frac{d\omega'}{2\pi},\]](/images/math/3/b/b/3bbabc3324c3fcc7a2837a36d2369ce3.png)
azaz a spektrum 
frekvenciájához az ablakfüggvény bekever jelet az 
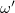frekvenciából is. Ezt a jelenséget spektrális szivárgásnak nevezzük.
A gyakorlati spektrumanalizáláshoz nem csak a véges időintervallumban végzett mérést kell figyelembe venni, hanem azt is, hogy a mért jelet nem folytonosan, hanem diszkrét pontokon mintavételezzük. Az ablakfüggvénnyel szorzott jel integrálját ennek megfelelően egy diszkrét összeggel közelítjük:
![\[f_W(\omega)=\sum_{n=0}^{N-1}F(n\Delta t)W(n\Delta t)e^{-i\omega n\Delta t}\Delta t,\]](/images/math/8/1/e/81e072541760e95c8c13a9926ef052ec.png)
ahol 
a két diszkrét mintavételezés között eltelt idő (a mérési idő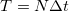 
).
A diszkrét Fourier-transzformáció (DFT) tehát a diszkrét pontokon felvett függvény spektrumát adja meg.
A Nyquist-Shannon mintavételezési törvény értelmében mintavételezési idővel legfeljebb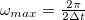 
maximális frekvenciáig lehetséges a jel rekonstrukciója.
Nem csak a mintavételezés történik diszkrét időnként, hanem a DFT kiszámítása is diszkrét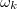 
értéken valósul meg. A diszkrét Fourier-transzformáció műveletigénye egyszerű "brute force" eljárással N frekvencia pont esetén 
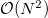műveletet igényel. Ez rendkívül időigényes, ezért egy más számítási algoritmust használnak a szoftverek a jel feldolgozásához. Ez a gyors Fourier-transzformáció (FFT), amelynek működési alapelve, hogy a mintát kettéválasztja páros és páratlan pontokra, így az N pontos DFT két N/2 pontos DFT-re bomlik. Ezt követően ezeket tovább felezi, és azokat is tovább, stb. Ehhez természetesen szükséges, hogy a mérési pontok száma kettő hatványa legyen. Könnyen belátható, hogy ennek az algoritmusnak a műveletigénye 
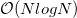nagyságrendű. Az FFT algoritmus az 
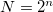adatpontból álló jel Fourier-spektrumát 
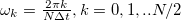diszkrét körfrekvenciapontokon adja meg.
Most a DFT definiálását követően megvizsgálhatjuk az ablakfüggvények különböző tulajdonságát. Tételezzük fel, hogy egy egykomponensű 
jelet vizsgálunk. Könnyen belátható, hogy ha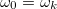 
bármelyik értékére, akkor a spektrális szivárgás nulla lesz. Ez pontosan annak felel meg, amikor a jelünk a T időablakban periodikus. Azonban az esetek többségében értelemszerűen ez nem teljesül. Ekkor a spektrális szivárgáson kívül romlik a jel frekvenciafelbontása és amplitúdópontossága is. Ez előbbi a centrális csúcs keskenységével jellemezhető, míg az utóbbinál éppen ellenkezőleg arra van szükség, hogy megfelelően lapos legyen az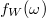 
jelünk környékén.
