Spintronika
Tartalomjegyzék |
Spindiffúziós hossz
Egy makroszkopikus vezetőben az elektronok számtalanszor szóródnak miközben eljutnak eaz egyik elektródából a másikba. Ahogy a nanovezetékek tárgyalásának bevezetésekor láttuk a szennyezőkön és rácshibákon történő rugalmas szórás az elektronok elektromos tértől nyert impulzusának elvesztéséhez vezet. Ennek a folyamatnak a karakterisztikus skáláját az átlagos momentumrelaxációs szabadúthossz,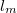 
jellemzi. Rugalmatlan szórások esetén (pl. kölcsönhatás rácsrezgésekkel) az elektronok energiája megváltozik, és így elveszik a a fázisinformáció, azaz megszűnik az interferenciaképesség. Ennek a folyamatnak a karakterisztikus skálája az ún. fázisdiffúziós szabadúthossz, 
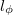. Megfelelő távolságon belül az elektronok a mágneses momentumuk, azaz a spinjükhöz tartozó információt is elvesztik, amit a spindiffúziós hosszal, 
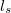jellemezhetünk.
Egy spindiffúziós hossznál kisebb, mágnesesen rendezett építőelemeket tartalmazó nanoszerkezetben azonban számos érdekes, az elektronok spin szerinti polarizáltságához kötődő jelenséggel találkozhatunk.
Spinpolarizáció ideális nanovezetékekben
A korábbiakban láttuk, hogy ha két elektróda közé egy ideális, szórásmentes nanovezetéket helyezünk, akkor abban keresztirányban állóhullámok, hosszirányban pedig síkhullám terjedés alakul ki, a vezetőképesség pedig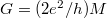 
, ahol M a nyitott vezetési csatornák száma, azaz azon különböző keresztmódusokhoz tartozó egydimenziós parabolikus diszperziók száma, melyek metszik a Fermi-energiát. A kettes szorzó a spin szerinti degenerációból adódott.
Egy ferromágneses nanovezetékben azonban különbséget kell tenni a fel és a le spinű elektronok között.
A vezeték mágnesezettségét legegyszerűbben Stoner-képben vehetjük figyelembe, azaz az energidiszperziókhoz hozzáadjuk a kicserőlédési energiát, mely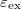 
-el különbözik a fel illetve le spinű (
) elektronokra:
![\[\varepsilon_n^{\sigma}(k)=\varepsilon(k)+\varepsilon_n-\sigma\varepsilon_{\mathrm{ex}}.\]](/images/math/1/e/c/1ec90d32189d7f827dd5dcf27b159654.png)
Emlékeztetőül: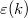 
a hosszirányú terjedést, 
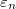pedig a keresztirányú állóhullámok energiáját írja le. Fontos megjegyezni, hogy 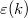lehet tetszőleges Bloch-állapot diszperziója, nem kell feltétlenül szabad elektronoknak megfelelő parabolikus diszperziót feltételezni.
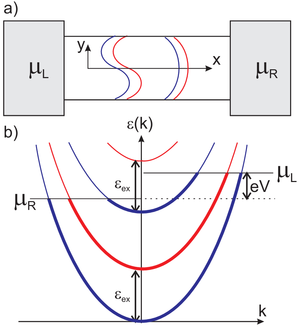
Az 1. ábra parabolikus szabad elektron diszperzió esetén szemlélteti az energiaviszonyokat. A kék görbék a fel, a piros görbék pedig a le spinű elektronokhoz tartoznak, azaz a piros parabolák minig 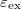energiával a megfelelő kék parabola felett helyezkednek el. A korábbiaknak megfelelően a 
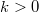állapotok a bal oldali eletródából származnak, így annak a 
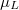kémiai potenciákjáig vannak betöltve, míg a 
állapotok a jobb oldali,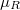 
kémiai potenciálú eletródából származnak.
 |
| 1. ábra |
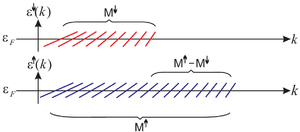
Értelemszerűen egy ferromágneses nanovezetékben a nyitott csatornák száma különbözhet a különböző spinű elektronokra (2. ábra), így az áram
![\[ I=\sum_{\sigma =\frac{1}{2},-\frac{1}{2}} \frac{e^2}{h}M^{\sigma}V \]](/images/math/2/b/7/2b7d2e5ba1e46a9261434fa189e97c4c.png)
Alakban írható, ahol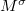 
(illetve máshogy jelölve 
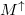és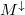 
) a fel és le spinű elektronokhoz tartozó nyitott csatornák száma.
 |
| 2. ábra. Diszperziós görbék ferromágneses nanovezetékben a Fermi-energia körül. Fel spinű elektronoknak (kék) több nyitott vezetési csatorna áll rendelkezésre mint le spinű elektronoknak (piros). |
Fontos megjegyezni, hogy itt figyelembe vettük, hogy a nanovezetéken belül az elektronok spinállapota nem változik, ennek köszönhető hogy a fel és le spinű elektronokat egymástól független csatornaként kezelhetjük az áram felírásakor.
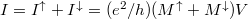. Látjuk, hogy ferromágneses ideális nanovezetékben a vezetőképesség 
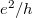szerint kvantált.
Az elektronok spin szerinti polarizáltságának fokát
![\[ P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}} \]](/images/math/0/e/5/0e5488e876f0c988e1bdb1710aabad98.png)
képlettel definiálhatjuk, ami ideális nanovezetékben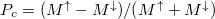 
formában is írható. Ez a spinpolarizáció 
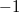és 
közötti értékeket vehet föl, tökéletes spinpolarizáció (
) félfémben érhető el, amikor csak fel spinű elektronok találhatók a Fermi-energia környékén. Fontos megjegyezni, hogy mindig a fel spint vesszük többségi spinorientációnak, mely a ferromágneses tartomány mágnesezettség-irányának felel meg. Később látni fogjuk, hogy a spinpolarizáció lehet a mágnesezettséggel ellentétes előjelű.
Landauer formula spinpolarizált esetben
Egy mágneses nanovezeték valósághűbb leírását kapjuk, ha szórást is megengedünk a vezetéken belül. Ezt a legegyszerűbben a korábban megismert Landauer formalizmus keretében tehetjük meg. A Landauer képben az elektrontranszportot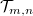 
transzmisszós valószínűségekkel írjuk le, melyek a bal oldali 
-edik vezetési csatornából a jobb oldali 
-edik csatornába történő szóródás valószínűségét adják meg. Míg 
a fent tárgyalt ideális kvantumvezetéknek felel meg. Ha a vezetéken belül az elektronok rácshibákon, illetve szennyezőkön szóródnak, akkor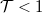 
transzmissziós valószínűségeket kapunk. Fontos megjegyezni, hogy a Landauer-kép inelasztikus szórásokat (pl. elektron-fonon kölcsönhatás) és spinszórásokat nem tud figyelembe venni.
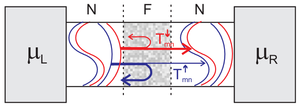
Vizsgáljuk meg a 3. ábrán szemléltetett rendszer vezetési tulajdonságait: a nanovezeték két nemmágneses ideális kvantumvezeték között egy ferromágneses tartományt tartalmaz, melyben szóródhatnak az elektronok.
 |
| 3. ábra |
Mivel spinszórás nem történik, az áramot továbbra is egymástól függetlenül számolhatjuk a két spincsatornára a transzmissziós valószínűségek figyelembe vételével:
![\[ I^\sigma=\frac{e^2}{h}\sum_{n,m=1}^{M^\sigma}T_{m,n}^\sigma V. \]](/images/math/b/2/9/b2946c7ec106adeeaa500e7cdca002d2.png)
A 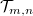értékek függnek az elektronok Fermi-hullámhosszától, ami egy adott -edik csatorna esetén jelentősen eltérhet a két spin-orientációra a kicserélődési felhasadás miatt. Ez alapján spinszórás (pl. spin-pálya kölcsönhatás) nélkül is a transzmisszós valószínűségek különböznek a két spincsatornára, ezt vesszük figyelembe a 
indexszel.
A spinfüggő áramot átírhatjuk
![\[ I^\sigma=\frac{e^2}{h}M^\sigma \bar{T}^\sigma V \]](/images/math/d/2/d/d2d35eeca080566f9f4c66f8bf6956c4.png)
formába, ahol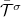 
az átlagos transzmissziós valószínűség a spin-orientációhoz tartozó összes nyitott vezetési csatornára. Ezzel a jelöléssel az áram spin szerinti polarizáltságát
![\[ P_c=\frac{I^{\uparrow}-I^{\downarrow}}{I^{\uparrow}+I^{\downarrow}}=\frac{M^{\uparrow}\bar{T}^\uparrow-M^{\downarrow}\bar{T}^\downarrow}{M^{\uparrow}\bar{T}^\uparrow+M^{\downarrow}\bar{T}^\downarrow}. \]](/images/math/e/e/f/eef78545d0cb4c40985d9947b3b4657e.png)
formában írhatjuk. Spinpolarizált áramot a két spincsatorna között a nyitott vezetési csatornák számában illetve az az átlagos transzmissziós valószínűségben fellépő különbség egyaránt eredményezhet.
Kevés vezetési csatorna (pl. egyatomos kontaktus) esetén a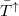 
és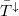 
jelentős spinpolaizációt okozhat akkor is, ha a vezetési csatornák száma megegyezik a két spinirányra. Sok csatornás struktúrákban viszont 
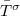sok, különböző Fermi-hullámszámú csatornára vett átlag, így a spindiffúziós hossznál kisebb struktúrákban, ahol csak a rugalmas szórásokat vesszük figyelembe, azt átlagos transzmisszós valószínűséget közel azonosnak várjuk a két spinirányra. Ennek megfelelően
az áram spinpolarizációjához az elsődleges járulékot a vezetési csatornák számának különbsége adja:
![\[ P_c\approx \frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}, \]](/images/math/6/1/1/611330a8e456659423f82d2fa3ef19bc.png)
akkor is ha nem ideális a vezeték, azaz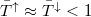 
.
Korábbi megfontolások alapján a vezetési csatornák számát formálisan:
![\[ M^\sigma=\frac{2\pi\hbar}{L}\sum_{n=1}^{M^\sigma}v_n^{\sigma}g_n^{\sigma}. \]](/images/math/1/4/4/144e6325977480a78786c18fdfefa79f.png)
alakban írhatjuk. Vezessünk be egy átlagos Fermi-sebességet, mely a különböző csatornák Fermi sebességeinek átlaga a csatornák állapotsűrűségével súlyozva,
![\[ \bar{v}_F^\sigma=\frac{\sum_{n} g_n^\sigma v_n^\sigma}{\sum_{n} g_n^\sigma}. \]](/images/math/7/f/d/7fdffe40d2405e6b6303c04984afd354.png)
Figyelembe véve, hogy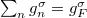 
a Fermi szint teljes állapotsűrűsége, az áram spinpolarizációjára vonatkozó formulánkat átírhatjuk
![\[ P_c\approx\frac{M^{\uparrow}-M^{\downarrow}}{M^{\uparrow}+M^{\downarrow}}=\frac{g_F^{\uparrow}\bar{v}_F^{\uparrow}-g_F^{\downarrow}\bar{v}_F^{\downarrow}}{g_F^{\uparrow}\bar{v}_F^{\uparrow}+g_F^{\downarrow}\bar{v}_F^{\downarrow}}. \]](/images/math/7/f/8/7f84d7e5b0af9c5d7c274bf6cad4e433.png)
alakba. Ez a formula lehetőséget ad arra, hogy a spinpolarizációt sávszerkezet-parameterek (Fermi-felület állapotsűrűsége és Fermi-sebesség) alapján értelmezzük.
Ferromágneses anyag sávmodelljét szemlélteti a 4. ábra. Mindkét panelen az energiatengelytől jobbra a fel, míg balra a le spinű elektronok állapotsűrűsége létszik. Az 
-elektronokhoz tartozó parabolikus energiafüggésű állapotsűrűség mellett a keskeny 
(vagy 
) sávokhoz tartozó állapotűrűség-csúcsokat láthatjuk, az utóbbi energiában felhasad a kicserélődési kölcsönhatás miatt.
Az anyag mágnesezettsége a betöltött (Fermi-energia alatti) fel és le spinű elektronok számának különbségéből adódik. Mindkét panelen a fel spinű elektronok vannak nagyobb számban, azaz a fel spint tekintjük többségi spinorientációnak. Ezzel szemben a transzport tulajdonságokhoz, így az áram spinpolarizációjához csak a Fermi-felületen közelében levő elektronok adnak járulékot. Az a) panelen a fel spinű elektronok vannak jelen nagyobb számmal a Fermi-szintnél, így pozitív a spinpolarizáció. Ezzel szemben a b) panelen a Fermi-energia máshol helyezkedik el a -sávokhoz képest, így végül a le spinű elektronok állnak rendelkezésre nagyobb számban a Fermi-energiánál, azaz a pozitív mágnesezettség ellenére negatív spinpolarizációt kapunk. Negatív spinpolarizációt valós anyagokban is tapasztalhatunk, pl. Co és Ni esetében.
Spinpolarizált transzport alkalmazása: spin szelep
A spin szabadsági fok kihasználásával számos érdekes eszközt építhetünk. A továbbiakban a gyakorlati felhasználás szempontjából legelterjedtebb, merevlemezek olvasófejében alkalmazott eszközt, a spin-szelepet mutatjuk be.
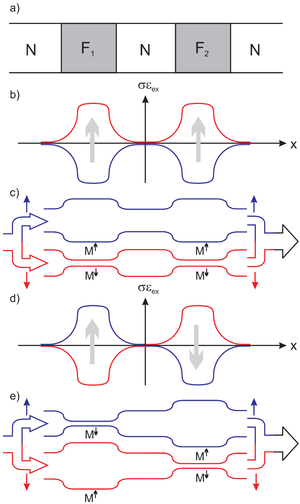
Az alap ötlet, az óriás mágneses ellenállást mutató nanoszerkezet felfedezése Albert Fert \cite{PhysRevLett.61.2472} és Peter Grünberg nevéhez kötődik, akik 2007-ben Nobel-díjat kaptak felfedezésükért. Az szerkezet két ferromágneses rétegből áll, melyeket egy, a spindiffúziós hossznál vékonyabb paramágneses réteg köt össze (lásd 5/a. ábra). A tapasztalatok alapján ennek a nanostruktúrának az ellenállása lényegesen nagyobb akkor, ha a két mágneses réteg mágnesezettsége azonos irányba mutat, mint ha ellentétes irányba mutatnak. Ezt a jelenséget lehet kihasználni mágnesesen tárolt információ kiolvasására, ha a felső réteg mágnesezettségét rögzítjük, az alsó réteg mágnesezettsége pedig az alatta mozgatott adattároló lemez mágnesezettségének megfelelően áll be, így az információ egyszerű ellenállás-méréssel kiolvasható. Ezzel a módszerrel a merevlemezek tárolókapacitásának jelentős növekedését lehetett elérni az eredeti induktív, illetve a későbbi anizotróp mágneses ellenállás mérésen alapuló módszerekhez képest.
 |
| 5. ábra |
Először tegyük fel, hogy mindkét ferromágneses réteg mágnesezettsége felfelé mutat. Az 5/b. ábra szemlélteti a fenti Stoner-modell keretében a kicsrélődési energia alakulását a fel spinű elektronokra (kék görbe) illetve a le spinű elektronokra (piros görbe). A kicserélődési felhasadás hatását legegyszerűbben úgy szemléltethetjük, hogy mind a normál mind a ferromágneses tartományokat ideális nanovezetéknek tekintjük. Ebben az esetben a pozitív kicserélődési energia ekvivalens azzal, mint ha egy nemmágneses tartományban keresztirányú 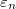energia megnőne, azaz a vezeték összeszűkülne, míg a negatív kicserélődési energiát úgy tekinthetjük, mint ha 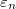csökkenne, azaz a vezeték szélessége megnőne. Ezt az ekvivalens képet szemlélteti az 5/c. ábra az 5/b. ábrának megfelelő mágnesezettség-irányok mellett, illetve az 5/e ábra abban az esetben, ha a két mágneses réteg mágnesezettsége ellentétes irányba mutat.
Ebben az ekvivalens képben a fel és a le spinű elektronok is egy adiabatikus nanovezetéket látnak, így a legkisebb keresztmetszetben elférő nyitott csatornák száma fogja meghatározni a vezetőképességet.
Jelöljük a nyitott csatornák számát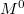 
-al a normál vezetékdarabban, 
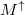-el ha az elektronok spinje a többségi spinorientációnak felel meg (azaz 
spinű elektronok mennek mágnesezettésű tartományban vagy 
elektronok mennek tartományban), illetve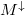 
-vel, ha egy adott mágnesezettségű tartományban ellentétes spinű (kisebbségi spinorientációjú) elektronok haladnak. A mágneses rétegek azonos irányú (parallel, 
) beállása esetén a fel spinű elektronokra 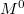, míg a le spinű elektronokra 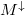a csatornák száma a legkisebb keresztmetszetben, azaz a
a vezetőképesség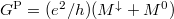 
. Ellentétes mágnesezettségű rétegek esetén (antiparallel, 
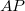) mindkét spinirányra 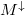számú csatorna fér el a legkisebb keresztmetszetben, azaz a vezetőképesség 
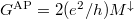. Így a relatív vezetőképességváltozás a két beállás között:
\[
\frac{\Delta G}{G^\mathrm{P}}=\frac{G^\mathrm{P}-G^\mathrm{AP}}{G^\mathrm{P}}=\frac{M^\0-M^\downarrow}{M^\0+M^\downarrow},
\]
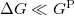), és feltételezve hogy LaTex syntax error\setbox0\hbox{$M^\0-M^\downarrow \approx M^\uparrow-M^\0$}%
\message{//depth:\the\dp0//}%
\box0%
![\[ \frac{\Delta G}{G^\mathrm{P}}\approx=\frac{1}{2}\frac{M^\uparrow-M^\downarrow}{M^\uparrow+M^\downarrow} \approx P_c \]](/images/math/e/0/0/e00dd2fc65a8bf1e77eb2ebb1bdc8659.png)
adódik. Ez az egyszerűsített, ideális kvantumvezetékeken alapuló kép természetesen nem írja le valósághűen a merevlemezben használt spinszelepek vezetési tulajdonságait.
Valósághűbb képet kapunk, ha a különböző tartományokban szórási folyamatokat is megengedünk.
Ha a spin-szelep struktúra kisebb a fázisdiffúziós hossznál (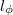
), akkor a két réteg közötti oda-visza szórásokat koherensen kell összeadni, így a teljes vezetőképesség interferencia-jelenségek finom részleteitől függ.
A fázisdiffúziós hossznál nagyobb (de a spindiffúziós hossznál kisebb) spin-szelep esetén viszont könnyen számolhatunk, mert elvész a koherencia, és így a sorosan kötött ellenállások egyszerűen összeadódnak. Hogy eredményeinket összehasonlíthassuk az ideális kvantumvezetékek modelljével, a számolást vezetőképességekkel végezzük: többségi spinorientáció esetén a vezetőképesség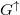 
, kisebbségi spinorientáció esetén pedig 
.
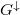A rétegek beállása esetén a teljes vezetőképessé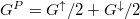g 
, míg 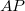beállás esetén 
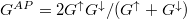, azaz a relatív vezetőképesség-változás:
![\[ \frac{\Delta G}{G^\mathrm{P}}=\left(\frac{G^\uparrow-G^\downarrow}{G^\uparrow+G^\downarrow}\right)^2=P_c^2. \]](/images/math/5/5/2/552457b3bed91e57b9929964490c5f4d.png)
Látszik, hogy mindkét modellben a relatív vezetőképesség-változás a spinpolarizációval skálázódik, és tökéletes spinpolarizáció esetén $Mfollows. Note, that this model is equivalent with the common resistor model of the GMR phenomenon.\cite{0022-3727-35-18-201}
 |
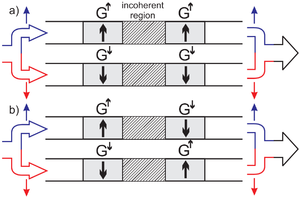
| 6. ábra |
\begin{figure} [!h]
\centering
\includegraphics[width=\columnwidth]{fig10.eps}
\caption{\it Resistive model of the GMR effect. The two magnetic layers are
separated by an incoherent nonmagnetic region. The top panel demonstrates the
parallel alignment of the magnetic layers (both layers have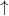
magnetization direction), whereas the bottom panel demonstrates the
antiparallel alignment (the left layer has 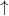and the right layer has
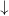magnetization direction). 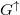and 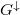denote
the conductance of a layer for electrons with majority and minority spin
direction, respectively.}
\label{GMR2}
\end{figure}
For even larger junctions, where phase coherence between the two magnetic layers
is already lost (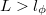
), but the spin information is still preserved
(
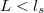), the two scattering regions are connected \emph{incoherently}
(Fig.~\ref{GMR2}), and accordingly their resistances are simply summed to get
the total resistance.\cite{note1} In this limit the magnetoresistance of the
spin valve structure is also easily calculated. To compare with the previous
ballistic model we calculate with conductances: the conductance for majority
spin states is 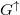, whereas for minority spins it is .
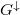For antiparallel oriented magnetic layers the total conductance is
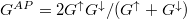, whereas for
parallel oriented layers it is 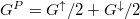. From these
![\[ \frac{\Delta G}{G^\mathrm{P}}=\left(\frac{G^\uparrow-G^\downarrow}{G^\uparrow+G^\downarrow}\right)^2=P_c^2 \]](/images/math/1/9/3/193c43bfdda2554c0ee0f1ba2ac691a3.png)
follows. Note, that this model is equivalent with the common resistor model of the GMR phenomenon.\cite{0022-3727-35-18-201}
Both of the above simple models show that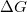 
is positive, i.e. the
parallel orientation has higher conductance than the antiparallel one. Depending
on the model, the relative conductance change ranges between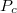 
and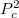 
which indicates that a more complicated model based on the coherent
superposition of two scattering regions would also give a result between the
above two extreme limits. These considerations show that for typical values of
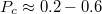, the relative amplitude of the GMR effect is expected to be
significant regardless of the details of the model. Note, however, that this
is only valid if the spin information is fully preserved in the spacer layer. As
the separation of the magnetic layers becomes larger than the spin diffusion length the GMR
effect exponentially decays.\cite{PhysRevB.48.7099,0953-8984-19-18-183201}
The magnetic layers of a spin valve are decoupled by paramagnetic spacer, and this allows switching between parallel and antiparallel alignments. As the relative alignment depends on the external magnetic field, the GMR effect can be used for magnetic sensing. For this purpose the orientation of one layer is pinned by growing it on top of an antiferromagnet, while the unpinned free layer can rotate even under the influence of a weak magnetic field. Spin valves are extensively applied as the read head of hard disks, which utilizes the fast and reliable reading of the magnetic information by an electric signal.
The spin valve structure can also be used to store magnetic information. This type of non-volatile memory consists of a large number of spin valves, each of them being addressed separately in a crossbar wire architecture. The orientation of the free layer defines bit ``0 and bit ``1, which can be changed by the stray field of the nearby crossing wires. The information written in this way is red out by the GMR effect. However, the areal density of this type of magnetoresistive random access memories (MRAM) is limited by the length scale of the slowly decreasing stray fields.
In the most advanced novel MRAMs no external field (and extra wiring) is required to write information in a spin valve memory element. In these devices the orientation of the free layer is manipulated by high density spin polarized currents, while the magnetic information is obtained by low current GMR measurements. The writing is based on the spin-flip electron scattering processes occurring in the free layer, which exert a torque on the magnetization. Even though such spin-flips are rare events (the spin diffusion length is much larger than the characteristic size of the nanodomain), at current densities of about \(10^9 -10^{10}\, \textrm{A/cm}^2\), the induced torque becomes large enough to reverse the magnetization. The details of the spin transfer torque phenomenon are reviewed in Ref.~\cite{Ralph20081190}. Here we just point out the importance of the strongly non-equilibrium state of this nanoscale device: while the above current densities would lead to melting in any macroscopic metal, in this device the length scales which determine its transparency (i.e. its resistance) are well below the inelastic mean free path, and as a consequence the Joule heat is produced outside the device, in a much larger volume. In spite of the huge current densities, the nanoscale electronics defines appropriate signal levels for practical applications (below \(100\,\mu\)A, and around \(1\,\)V). Finally it is to be noted that the spin transfer torque magnetoresistive random access memory (STT-MRAM) is one of the most promising candidate for future spintronic applications.
\section{Conclusions}
Nanoscale phenomena of spin related transport were discussed both theoretically and experimentally. Based on the spin dependent band structure of a magnetic metal, we discussed the propagation of electrons in the ballistic and diffusive limits, and by applying the Landauer formalism, we supplied a \emph{nanoscopic} background for the conventional expression of the current spin polarization. As the most direct experimental method for spin polarization measurements, the Andreev reflection spectroscopy was introduced, and experimental results on Fe and Co were shown. The analysis demonstrated the reliability of measurements carried out in the ballistic limit. The method was also extended for the determination of the spin diffusion length, one of the most important parameters of metals in spintronic applications. The operation of spin valves was described in terms of the Landauer formalism and the magnitude of the GMR effect was determined in the coherent ballistic and the incoherent diffusive limits. Finally a short overview on spin valve applications was given.
