TLS noise
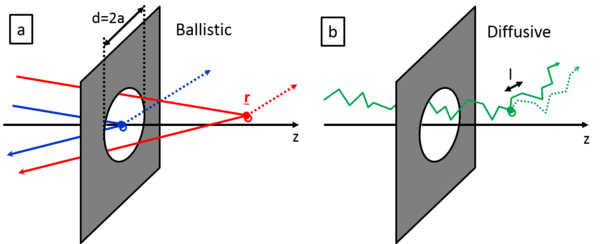
Next, we model the temporal fluctuations of the conductance based on the scattering on dynamical defects in a point contact geometry following the theoretical models summarized in a previous review paper of one of the authors, [Fredicikk]. We consider both the ballistic and the diffusive limit, i.e. junctions with diameter smaller or larger than the mean free path of the electrons, 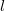 (see Fig.?a and b respectively).
(see Fig.?a and b respectively).
In the ballistic limit the conductance of an orifice-like point-contact is given by the Sharvin formula, 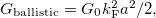
 being the contact radius,
being the contact radius, 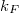 the Fermi wavenumber and
the Fermi wavenumber and 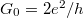 the conductance quantum. Once an electron scatters on a dynamical defect (or two level system, TLS) close to the junction, this conductance is perturbed, and having different perturbation in the different states of the defect, a conductance noise is introduced. We model this conductance noise as
the conductance quantum. Once an electron scatters on a dynamical defect (or two level system, TLS) close to the junction, this conductance is perturbed, and having different perturbation in the different states of the defect, a conductance noise is introduced. We model this conductance noise as 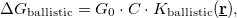 where C defines the amplitude of the temporal conductance fluctuation within the bandwidth of the measurement for a TLS positioned in the center of the ballistic contact, whereas
where C defines the amplitude of the temporal conductance fluctuation within the bandwidth of the measurement for a TLS positioned in the center of the ballistic contact, whereas 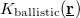 accounts for the variation of this conductance noise with the position of the TLS. In our simplified model we take a constant
accounts for the variation of this conductance noise with the position of the TLS. In our simplified model we take a constant 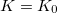 close to the contact (
close to the contact (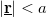 ), and
), and  if
if 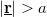 . The latter is the asymptotic dependence of
. The latter is the asymptotic dependence of  along the contact axis scaling with the square of the solid angle at which the contact is seen from the TLS position (see eq. 99 in Ref. Fredicikk), whereas
along the contact axis scaling with the square of the solid angle at which the contact is seen from the TLS position (see eq. 99 in Ref. Fredicikk), whereas  approximates the small distance limit of the same equation. The effect of multiple TLSs is modeled with a constant TLS density,
approximates the small distance limit of the same equation. The effect of multiple TLSs is modeled with a constant TLS density,  using uniform
using uniform 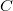 for all TLSs. Considering the contribution of the different TLSs being independent of each other
for all TLSs. Considering the contribution of the different TLSs being independent of each other 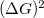 is additive, and is easily integrated for the entire space yielding a normalized conductance noise of
is additive, and is easily integrated for the entire space yielding a normalized conductance noise of
![\[\left(\frac{\Delta G}{G} \right)_\textrm{ballistic}=\left(\frac{\Delta I}{I} \right)_\textrm{ballistic}=\tilde{C}_\textrm{ballistic} \sqrt{\frac{\rho_\textrm{TLS}}{k^3_\textrm{F}}}\left(R_\textrm{M}G_0 \right)^\frac{1}{4}.\]](/images/math/c/d/5/cd555362072ce51dfa571ab32ecd1ebf.png)
The corresponding power law 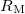 dependence with an exponent of
dependence with an exponent of 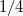 is demonstrated by the blue dashed line in Fig.4b. Here the
is demonstrated by the blue dashed line in Fig.4b. Here the 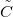 prefactor is
prefactor is 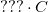 for the orifice-like junction geometry of our model, whereas for a more realistice Ag nanowire junction with
for the orifice-like junction geometry of our model, whereas for a more realistice Ag nanowire junction with 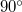 opening angle (see ref [Ruiti condfluct PRB]) we estimate
opening angle (see ref [Ruiti condfluct PRB]) we estimate 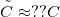 .
.
In a diffusive junction the Sharvin formula is replaced by the Maxwell conductance, 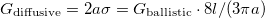 [see eq. 36 in Fredicikk],
[see eq. 36 in Fredicikk], 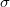 being the conductivity. On the other hand according to eq. 167 in [Fredicikk] the diffusive environment of the TLS yields a
being the conductivity. On the other hand according to eq. 167 in [Fredicikk] the diffusive environment of the TLS yields a  reduction of the geometrical factor. From these
reduction of the geometrical factor. From these
![\[\left(\frac{\Delta G}{G} \right)_\textrm{diffusive}=\tilde{C}_\textrm{diffusive} k_\textrm{F} l^\frac{5}{2} \sqrt{\rho_\textrm{TLS}}\left(R_\textrm{M}G_0 \right)^\frac{3}{2}\]](/images/math/d/f/8/df8dce8e808cc614683b2ca35c6c119a.png)
follows, giving a power law exponent of 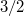 in the diffusice limit, as demonstrated by the red dashed line in Fig.4b.
Here the
in the diffusice limit, as demonstrated by the red dashed line in Fig.4b.
Here the 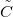 is
is 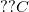 using our orifice geometry, and we estimate
using our orifice geometry, and we estimate 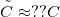 in a junction with
in a junction with 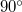 opening angle.
opening angle.
The 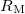 dependence of the CNR predicted by this simple model calculation clearly follows the experimentally observed trends both in the ballistic and in the diffusive limit. Here we emphasize, that in both limits
dependence of the CNR predicted by this simple model calculation clearly follows the experimentally observed trends both in the ballistic and in the diffusive limit. Here we emphasize, that in both limits 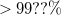 of the CNR stems from the
of the CNR stems from the 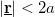 region, i.e. the small junction acts as a magnifier for the processes happening in the junction neighborhood, and suppressing the further processes. This is in sharp contrast to the original nanobridge geometry of the electromigrated Ag wires, where all the TLSs within the nanobrige give relevant contribution to the noise.
region, i.e. the small junction acts as a magnifier for the processes happening in the junction neighborhood, and suppressing the further processes. This is in sharp contrast to the original nanobridge geometry of the electromigrated Ag wires, where all the TLSs within the nanobrige give relevant contribution to the noise.
Whereas our model includes numerous simplifications yielding uncertain prefactors, still as a validation we use this model as a fitting curve such that the experimental data are fitted with the diffusive/ballistic limit bellow/above the crossing point of the ballistic and diffusiv power law lines on the log-log plot. Using 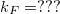 [hivatkozás] and the
[hivatkozás] and the  opening angle geometry the least square fitting of our data yields
opening angle geometry the least square fitting of our data yields  and
and 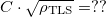 . Ezt majd az eredményeket látva diszkutáljuk.
. Ezt majd az eredményeket látva diszkutáljuk.
, i.e. all the scattering processes happening in the vicinity of the junction have highly enhanced influance on the conductance, and therefore it is even possible to observe the temporal conductance fluctuations due to a single two level system [Ralph, Caro, Kaijsers]. On the other hand the processes happening far away from the junction have highly suppressed contribution to the conductance. For the sake of simplicity we model an orifice like point contact, i.e. an orifice with diameter d in an infinite isolating plane between two conducting electrodes (see Figure). Without any scattering in the junction region, this orifice like \emph{ballistic} point contact has a conductance of [Fredicikk]
![\[G_\textrm{ballistic}=\frac{2e^2}{h}M,\ M=\left(\frac{k_\textrm{F}a}{2}\right)^2,\]](/images/math/c/9/a/c9a2f7766c9f70a9691b01f14c11e40f.png)
where M is the number of open conductance channels in the contact,  is the radius of the contact,
is the radius of the contact, 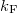 is the Fermi wavenumber, and
is the Fermi wavenumber, and 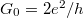 is the quantum conductance unit. If a TLS is placed to the center of the orifice, i.e. an atom or a group of atoms can fluctuate between two or more metastable positions, the electrons will scatter on the TLS modifying the above ballistic conductance formula (see Fig.? a, red lines). If we consider the scattering on a single atom-sized structural defect, the correction of the conductance to the above formula is on the order of the quantum conductance unit, or smaller. This conductance correction may differ in the various states of the TLS (see the solid and the dotted line after the scatterring on the TLS in Fig.?), introducing a temporal conductance variation,
is the quantum conductance unit. If a TLS is placed to the center of the orifice, i.e. an atom or a group of atoms can fluctuate between two or more metastable positions, the electrons will scatter on the TLS modifying the above ballistic conductance formula (see Fig.? a, red lines). If we consider the scattering on a single atom-sized structural defect, the correction of the conductance to the above formula is on the order of the quantum conductance unit, or smaller. This conductance correction may differ in the various states of the TLS (see the solid and the dotted line after the scatterring on the TLS in Fig.?), introducing a temporal conductance variation, 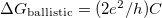 . Here C defines the amplitude the temporal conductance variation in the units of
. Here C defines the amplitude the temporal conductance variation in the units of 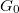 for a single TLS positioned in the center of a ballistic point contact within the bandwidth of the measurement. Based on earlier studies, the reasonable values of C are at the range of the fractions of
for a single TLS positioned in the center of a ballistic point contact within the bandwidth of the measurement. Based on earlier studies, the reasonable values of C are at the range of the fractions of 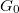 , like
, like 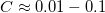 [????]. If the TLS is placed further away from the contact, the fluctuation of the conductance decreases with a geometrical factor
[????]. If the TLS is placed further away from the contact, the fluctuation of the conductance decreases with a geometrical factor 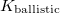 ,
, 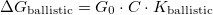 . According to the detailed calculations in Ref. [Fredicikk] this geometrical factor scales with the square of the solid angle,
. According to the detailed calculations in Ref. [Fredicikk] this geometrical factor scales with the square of the solid angle, 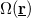 at witch the orifice is seen from the position of the TLS,
at witch the orifice is seen from the position of the TLS, 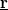 . Simply speaking, the scattering on the TLS only modifies the conductance, if the electron passing through the contact arrives to the TLS, and after that it is scattered back through the contact (see figure), where both the arrival to the TLS and the scattering back through the contact scales with
. Simply speaking, the scattering on the TLS only modifies the conductance, if the electron passing through the contact arrives to the TLS, and after that it is scattered back through the contact (see figure), where both the arrival to the TLS and the scattering back through the contact scales with 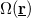 . Following these considerations we use a simplified approximation for
. Following these considerations we use a simplified approximation for 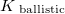 taking it unity, if the distance of the TLS from the contact center is smaller than the contact radius,
taking it unity, if the distance of the TLS from the contact center is smaller than the contact radius, 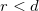 , and taking the large distance asymptotic value of
, and taking the large distance asymptotic value of 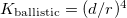 if
if 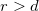 . Having separated the strength of the electron scattering on the various states of the TLS (C) and the geometrical factor (K) we apply a simple model considering the same
. Having separated the strength of the electron scattering on the various states of the TLS (C) and the geometrical factor (K) we apply a simple model considering the same 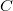 for all the TLSs, and introducing a TLS density,
for all the TLSs, and introducing a TLS density,  . Considering the scattering on the TLSs independent of each other the mean squared conductance fluctiations of the various TLSs are additive, and therefore the summed mean squared deviation of the conductance can be calculated as
. Considering the scattering on the TLSs independent of each other the mean squared conductance fluctiations of the various TLSs are additive, and therefore the summed mean squared deviation of the conductance can be calculated as
![\[\Delta G^2_\textrm{ballistic}=G_0^2C^2 \int_0^\infty 4\pi r^2 K^2_\textrm{ballistic}(r)\rho_\textrm{TLS}\textrm{d}r=G_0^2C^2\rho_\textrm{TLS}\frac{32}{15}\pi a^3.\]](/images/math/3/0/d/30db3d0496be909e01ac1e54e57dd8bd.png)
(Note that the solid angle, at wich the orifice is seen from position r on the contact axis is \Omega_r~(d/r)^2.) (pontosítani, mert ez 4pi-re normált). In a diffusive contact there are several further scattering centers with an averge distance of the mean free path, l, so if d>>l the electrons follow diffusive trajectories even inside the junction (see fig. ...). In this case the conductance of the junction can also be calculated yielding the so-called Maxwell conductance, G_diff=\sigma *d, where \sigma=ne^2\tau/m, where \tau=l/v_F is the momentum relaxation time, v_F being the absolute vaue of the Fermi velocity. Expressing the electron density by k_F, one gets: G_diff=G_ball* (16/3\pi)*(l/d). If a single TLS is placed in a diffusive point contcact, the temporal fluctuation of the conductance is \Delta G_diff=2e^2/h * C*K_diff, where C still tells us the conductance fluctuation, if the TLS would be inside a ballistic junction, whereas K_diff is a geometrical factor characteristic for diffusive junctions.