Életünk és az elektromágneses hullámok
Már több mint 100 éve (1989) ismerjük az elektromágneses hullámokat (EMH). A XX. század elején felfedezték azt is, hogy elektromágneses hullámokkal jeleket (információt) továbbíthatunk. A szikratávírót mára felváltotta a távközlési műholdak és a mobiltelefon-hálózatok bonyolult rendszere. A kábel TV szolgáltatásnál és az internetes hálózatoknál is jelen van az EMH. De a háztartási eszközeinkben (mikrohullámú sütő), vagy a "radarkontroll" felirat mögött is az EMH léte húzódik meg.
A klímaváltozásban szerepet játszó üvegházhatás is az infravörös sugárzás (EMH) tulajdonságainak következtében lép fel.
Az elektromágneses síkhullám
Az elektrosztatika tárgyalása során láttuk, hogy az elektromos töltések elektromos teret hoznak létre maguk körül. A Biot-Savart illetve az Ampére-törvény segítségével pedig mozgó töltések (áramok) mágneses terét tudjuk meghatározni. Mindkét esetben töltött – anyagi – részecskék által létrehozott térről beszélhetünk. Mind az elektromos, mind a mágneses tér az azokat létrehozó töltött részecské(ke)t tartalmazó tartományon kívül is általában igen nagy térrészben mérhető. Ezután felvetődik a kérdés, hogy létezhet-e  vagy
vagy  vagy együttesen
vagy együttesen  és
és  az anyagi részecskéktől függetlenül. (Ennek a kérdésnek a részletes elméleti tárgyalása messze túlmutat a jegyzet keretein, ezért most egy olyan vizsgálati módszert követünk, amely a Maxwell-egyenletek ismeretén kívül mást nem tételez fel; ez a megközelítés a klasszikus fizika területén a XIX. század végének tudományos szintjét jelenti.)
A mágneses tér illetve a mágneses fluxus változása – mint az ismeretes – elektromos teret indukálhat; ezt a jelenséget írja le a Faraday törvény:
az anyagi részecskéktől függetlenül. (Ennek a kérdésnek a részletes elméleti tárgyalása messze túlmutat a jegyzet keretein, ezért most egy olyan vizsgálati módszert követünk, amely a Maxwell-egyenletek ismeretén kívül mást nem tételez fel; ez a megközelítés a klasszikus fizika területén a XIX. század végének tudományos szintjét jelenti.)
A mágneses tér illetve a mágneses fluxus változása – mint az ismeretes – elektromos teret indukálhat; ezt a jelenséget írja le a Faraday törvény:
![\[ \oint\vec E d\vec s = - \frac {d\Phi_B}{dt} \]](/images/math/f/7/c/f7ce90b02164c90e3f1e34cef6690814.png) |
(1.1) |
Az elektromos tér változása pedig mágneses teret hozhat létre, amint azt az általánosított Ampére-törvény leírja:
![\[ \oint\vec B d\vec s = \mu_0 I + \mu_0 \varepsilon_0 \frac {d\Phi_E}{dt} \]](/images/math/f/5/d/f5d122cd41cf84bc466694344bd3fddc.png) |
(1.2) |
Az egyenlet egyszerűsödik, ha anyagi részecskék nincsenek a vizsgált térrészben:
![\[ \oint\vec B d\vec s = \mu_0 \varepsilon_0 \frac {d\Phi_E}{dt} \]](/images/math/4/0/1/40161e5e299a9a57eef10f0232c31ea3.png) |
(1.3) |
Az (1.1) és az (1.3) egyenlet segítségével megpróbálhatjuk megadni a vákuumban (minden anyagi ill. töltött részecskétől távol) időben változó elektromos és mágneses tér dinamikáját. Ennek leírásához egy igen egyszerű modellt fogunk használni: az általunk választott Descartes koordináta-rendszerben az elektromos és mágneses térnek legyen csak  illetve
illetve  komponense:
komponense:
![\[ \vec E = (E_x (t),0,0) \qquad {\rm \acute{e}s} \qquad \vec B = (0,B_y (t),0) \]](/images/math/9/9/d/99dcea6bd450024a2b4266923ea6b69f.png) |
(1.4) |
Feltételezhetjük, hogy a komponensek helyfüggését is számításba kell venni. Az egyszerűség végett legyen a rendszernek az  és
és  tengely menti transzlációs szimmetriája; ez azt jelenti, hogy egy, a
tengely menti transzlációs szimmetriája; ez azt jelenti, hogy egy, a  tengelyre merőleges síkban egyidejűleg az
tengelyre merőleges síkban egyidejűleg az  is és a
is és a  is mindenhol ugyanazt az értéket veszi fel, azaz:
is mindenhol ugyanazt az értéket veszi fel, azaz: 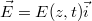 és
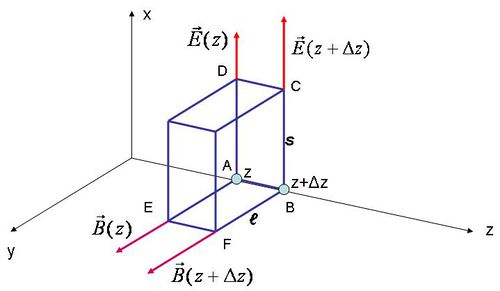
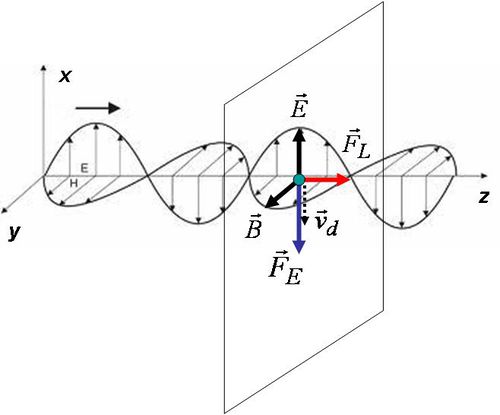
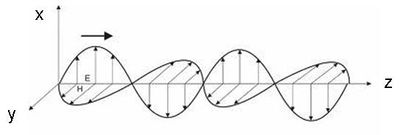
és 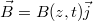 . Ezt szemlélteti az 1.1 ábra:
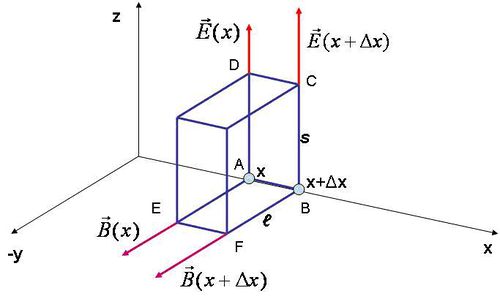
. Ezt szemlélteti az 1.1 ábra:
| 1.1 ábra |
Az ábra jelöléseit használva az (1.1) egyenletet a következő alakban adhatjuk meg:
![\[ \left[ E_x (z + \Delta z)- E_x (z) \right]s = - s \Delta z \frac{\Delta B_y}{\Delta t} \]](/images/math/9/3/d/93d947d55ebd6b3f1331fee96f42f000.png) |
(1.5) |
ahol az  térerősségre kiszámítandó körintegrált és a mágneses indukciós tér fluxusát az
térerősségre kiszámítandó körintegrált és a mágneses indukciós tér fluxusát az 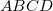 zárt hurokra (a körbejárási irány is fontos!) írtuk fel. Egyszerűsítés után kapjuk:
zárt hurokra (a körbejárási irány is fontos!) írtuk fel. Egyszerűsítés után kapjuk:
![\[ \frac {\left[ E_x (z + \Delta z)- E_x (z) \right]}{\Delta z} = - \frac{\Delta B_y}{\Delta t} \]](/images/math/4/0/5/4055d0a6b05273893a2b7e312f9b1ba1.png) |
(1.6) |
Ehhez hasonlóan átírhatjuk az (1.3) formulát is az 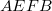 hurokra:
hurokra:
![\[ \left[ - B_y (z + \Delta z)+ B_y (z) \right]\ell = \mu_0 \varepsilon_0 \ell \Delta z \frac{\Delta E_x}{\Delta t} \]](/images/math/f/c/8/fc8dd856382322281f4696390cb2230b.png) |
(1.7) |
Most is érdemes egyszerűsíteni:
![\[ \frac {\left[ B_y (z + \Delta z)- B_y (z) \right]}{\Delta z} = - \mu_0 \varepsilon_0 \frac{\Delta E_x}{\Delta t} \]](/images/math/9/6/a/96ab9834b8162873f26befbe136da075.png) |
(1.8) |
Az (1.6) és (1.8) egyenletek a 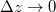 határeset figyelembe vételével átalakíthatók:
határeset figyelembe vételével átalakíthatók:
![\[ \frac {\partial E_x}{\partial z} = - \frac{\partial B_y}{\partial t} \]](/images/math/6/a/d/6ad17830de2ae808c1ad1e7604ae81cc.png) |
(1.9) |
és
![\[ \frac {\partial B_y}{\partial z} = - \mu_0 \varepsilon_0 \frac{\partial E_x}{\partial t} \]](/images/math/9/6/1/9612e8d61d75ea35aa76a894c3c98ab4.png) |
(1.10) |
Ha most az (1.9) mindkét oldalát deriváljuk  szerint, majd az (1.10) egyenletben lévő tagokat
szerint, majd az (1.10) egyenletben lévő tagokat  szerint és a megegyező tagokat kiejtjük, akkor kapjuk a következő egyenletet:
szerint és a megegyező tagokat kiejtjük, akkor kapjuk a következő egyenletet:
![\[ \frac {\partial ^2 E_x}{\partial z^2} = \mu_0 \varepsilon_0 \frac{\partial ^2 E_x}{\partial t^2} \]](/images/math/5/6/a/56aa94ac1cd56ddca124138e0d6eae32.png) |
(1.11) |
Ennek a differenciálegyenletnek – az ún. hullámegyenletnek – a megoldása egy síkhullám:
![\[ E_x (z,t) = E_o e^{i(\omega t \pm kz)} \]](/images/math/5/7/7/5776ed7ada056230d1800a49bb782bd9.png) |
(1.12) |
ahol is 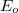 az amplitúdó (maximális elektromos térerősség),
az amplitúdó (maximális elektromos térerősség),  a rezgés körfrekvenciája, míg
a rezgés körfrekvenciája, míg  a hullám hullámszám-vektorának abszolút értéke.
a hullám hullámszám-vektorának abszolút értéke.
Emlékeztetőül: a hullám körfrekvenciája és hullámszáma – mint az ismert – megadható a frekvencia (vagy a T periódusidő) és a hullámhossz segítségével:
![\[ \omega = \frac{2\pi}{T}=2\pi f \qquad {\rm \acute{e}s} \qquad k = \frac {2\pi}{\lambda} \]](/images/math/4/d/0/4d0526832d4cc1a53b8a6323fb599ae3.png) |
(1.13) |
Az (1.11) megoldása megadható természetesen valós kifejezéssel is:
![\[ E_x (z,t) = E_o cos(\omega t \pm kz) \]](/images/math/0/a/7/0a7649716df404a935188567ee4caa5b.png) |
(1.14) |
Az (1.12)-t vagy (1.14)-t visszahelyettesítve az (1.11)-be adódik, hogy:
![\[ c = \frac {\omega}{k} \]](/images/math/8/f/3/8f385e461d06b0f0e27cec4fe7fa54b2.png) |
(1.15) |
ahol  a hullám terjedési sebessége, vagyis a fénysebesség:
a hullám terjedési sebessége, vagyis a fénysebesség:
![\[ c = \frac {1}{\sqrt {\mu_0 \varepsilon_0}} \]](/images/math/5/a/1/5a12051ebe7d48eeb5071886437eef8c.png) |
(1.16) |
A kapott összefüggés rámutat arra, hogy a fénysebesség a 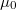 és az
és az 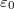 fizikai állandókból is meghatározható. Néhány évvel ezelőtt még bonyolult mérési összeállításokkal próbálták a fénysebesség értékét a fény terjedési sebességének mérésével egyre pontosabban meghatározni, azonban erre az SI egységrendszerben nincs szükség, mert a fénysebességet
fizikai állandókból is meghatározható. Néhány évvel ezelőtt még bonyolult mérési összeállításokkal próbálták a fénysebesség értékét a fény terjedési sebességének mérésével egyre pontosabban meghatározni, azonban erre az SI egységrendszerben nincs szükség, mert a fénysebességet 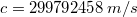 – nak definiáljuk. (Gyakorlatban használhatjuk a
– nak definiáljuk. (Gyakorlatban használhatjuk a 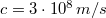 közelítő értéket is.)
Ha most (1.9)-et deriváljuk az idő szerint és (1.10)-et
közelítő értéket is.)
Ha most (1.9)-et deriváljuk az idő szerint és (1.10)-et  szerint, akkor a
szerint, akkor a  -re kaphatunk az (1.11)-hez hasonló hullámegyenletet:
-re kaphatunk az (1.11)-hez hasonló hullámegyenletet:
![\[ \frac {\partial ^2 B_y}{\partial z^2} = \mu_0 \varepsilon_0 \frac{\partial ^2 B_y}{\partial t^2} \]](/images/math/a/4/3/a43d59d1a4c27af3c94053afd38d0bbf.png) |
(1.17) |
amelynek a megoldása:
![\[ B_y (z,t) = B_o cos(\omega t \pm kz) \]](/images/math/b/7/e/b7e5f6857ae90ac24397ee7c9b841d44.png) |
(1.18) |
Ha most az elektromos térre kapott (1.14) és az indukciós térre kapott (1.18) megoldást behelyettesítsük az (1.9) vagy az (1.10) egyenletbe, akkor a szükséges műveletek elvégzése után kapjuk a következő igen fontos összefüggéseket:
![\[ \frac {1}{c} E_x (z,t)= B_y (z,t) \qquad {\rm vagy} \qquad \frac {1}{c} E_o = B_o \]](/images/math/0/c/c/0cc41035b0c12e0d0f45a93a03f798d9.png) |
(1.19) |
Az (1.18) és az (1.14) együtt egy elektromágneses síkhullám leírását adják; tehát egy, a 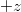 tengely mentén terjedő elektromágneses síkhullám térerősség komponensei:
tengely mentén terjedő elektromágneses síkhullám térerősség komponensei: 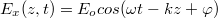 és
és 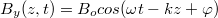 , ahol
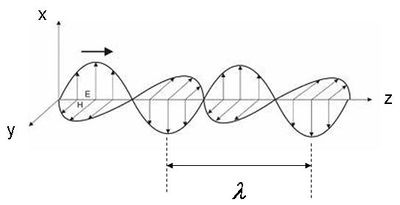
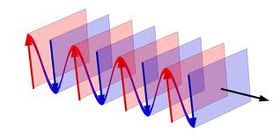
, ahol  értéke a kezdeti feltételektől függ (1.2 ábra):
értéke a kezdeti feltételektől függ (1.2 ábra):
| 1.2 ábra |
A Maxwell-egyenletek segítségével tehát megmutattuk, hogy létezhet a vákuumban terjedő elektromágneses hullám, amelyben az elektromos és a mágneses térerősség "egymásba alakul át", hiszen az időben változó elektromos tér hozza létre a mágneses indukciós teret, míg a változó indukciós tér generálja az elektromos teret. Mindezt – a fentiektől kissé eltérő módon – maga Maxwell bizonyította elméleti számításaival, vélhetően 1865-ben.
Az EMH-k létének elméleti levezetése után a kísérleti bizonyíték sem sokat váratott magára. Heinrich Hertz 1887-ben a saját építésű kísérleti berendezésével demonstrálta az EMH-k létezését. Furcsa, de Hertz maga nem tulajdonított gyakorlati jelentőséget kutatási eredményeinek; ennek ellenére jó néhány évvel később beköszöntött a "wireless korszak".
Az elektromágneses hullámot jellemezhetjük a frekvenciájával ( ) vagy a hullámhosszával (
) vagy a hullámhosszával ( ) is, közöttük a jól ismert összefüggés áll fenn:
) is, közöttük a jól ismert összefüggés áll fenn:
![\[ f= \frac {c}{\lambda} \]](/images/math/d/d/4/dd4a94c7c6f44823b9254b89b07b8e7e.png) |
(1.20) |
Az elektromágneses hullámok spektruma
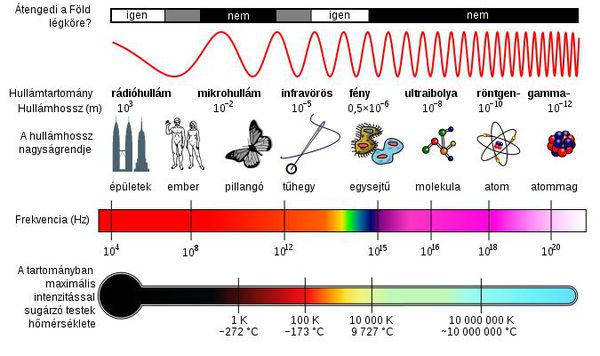
Az elektromágneses spektrum különböző tartományait – leggyakrabban a hullámhosszal megadva – más-más névvel illetik (2.1 ábra).
| 2.1 ábra |
Ugyanez kissé részletesebben, táblázatos formában is megtalálható itt: elektromágneses spektrum és itt: elektromágneses hullám. A látható tartományt színek szerint is osztályozhatjuk:
| Elnevezés | Hullámhossz (nm) |
|---|---|
| vörös | 640 – 780 |
| narancs | 600 – 640 |
| sárga | 570 – 600 |
| zöld | 490 – 570 |
| kék | 430 – 490 |
| ibolya | 380 – 430 |
Néhány érdekesség: Az emberi szem legérzékenyebb a zöld fényre. A CD és a DVD vörös lézerfénnyel dolgozik, míg a blue-ray disc ibolya nyalábbal írható és olvasható (a kisebb hullámhossz természetesen nagyobb adatsűrűséget jelent). Az ultraibolya tartományú (200 nm <  < 380 nm) lámpákat például orvosi rendelők vagy műtők fertőtlenítésére használják, de alkalmazzák élelmiszerek baktériummentesítésére is. A 200 nm-nél rövidebb hullámhosszúságú kemény UV fényforrás a processzorgyártásban nélkülözhetetlen litográfia eszköze.
< 380 nm) lámpákat például orvosi rendelők vagy műtők fertőtlenítésére használják, de alkalmazzák élelmiszerek baktériummentesítésére is. A 200 nm-nél rövidebb hullámhosszúságú kemény UV fényforrás a processzorgyártásban nélkülözhetetlen litográfia eszköze.
Az EMH energiasűrűsége, intenzitása és a Poynting-vektor
Az általunk vizsgált egyszerű modellben az 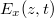 és
és 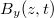 komponensek egy olyan elektromágneses síkhullám megoldását adták, amely a
komponensek egy olyan elektromágneses síkhullám megoldását adták, amely a  tengely mentén terjed. Az 1.1 és az 1.2 ábra alapján is megállapíthatjuk, hogy az
tengely mentén terjed. Az 1.1 és az 1.2 ábra alapján is megállapíthatjuk, hogy az 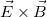 párhuzamos a
párhuzamos a  tengellyel, vagyis a síkhullám terjedési irányával. Néhány speciális esettől eltekintve mondható, hogy az EMH terjedési iránya valamint a hullám által szállított energia terjedésének iránya megegyezik; ezt az irányt a Poynting-vektor segítségével adhatjuk meg:
tengellyel, vagyis a síkhullám terjedési irányával. Néhány speciális esettől eltekintve mondható, hogy az EMH terjedési iránya valamint a hullám által szállított energia terjedésének iránya megegyezik; ezt az irányt a Poynting-vektor segítségével adhatjuk meg:
![\[ \vec S = \vec E \times \vec H \]](/images/math/c/a/d/cad3ba6a7a4a1c7c7664ce267915b668.png) |
(3.1) |
ahol  a mágneses tér vektora (vákuumban:
a mágneses tér vektora (vákuumban: 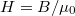 ).
).
Most meghatározzuk a Poynting-vektor abszolút értékét (ehhez felhasználhatjuk, hogy az  és a
és a  merőlegesek egymásra):
merőlegesek egymásra):
![\[ \left| \vec S \right| = EH = E\frac{B}{\mu_0} = \frac {1}{\mu_0} E_o B_o cos^2 (\omega t - kz)\]](/images/math/4/2/0/420b5140f088c45caa8ef667b53f0d40.png) |
(3.2) |
Az (1.16) és az (1.19) eredmények alkalmazásával ez a formula még tovább egyszerűsíthető:
![\[ \left| \vec S \right| = S = \sqrt{\frac {\varepsilon_o}{\mu_0}} E_o^2 cos^2 (\omega t - kz)\]](/images/math/7/9/3/793fdec7b56ffdbb7231236e44141a41.png) |
(3.3) |
Az átlagteljesítmény kiszámításánál használt módszert alkalmazva meghatározhatjuk a Poynting-vektor nagyságának átlagos értékét is:
![\[ \left< S \right> = \frac {1}{2}\sqrt{\frac {\varepsilon_o}{\mu_0}} E_o^2 \]](/images/math/7/f/e/7fe8b91a79c4372a9d155abdec23b195.png) |
(3.4) |
Ezután megvizsgáljuk azt a kérdést, hogy mennyi energiát szállít az elektromágneses hullám.
Azt már megmutattuk, hogy az elektromos és a mágneses tér energiasűrűsége:
![\[ \varepsilon_E = \frac{1}{2} \varepsilon_o E^2 \qquad {\rm \acute{e}s} \qquad \varepsilon_B = \frac{1}{2} \frac{1}{\mu_o} B^2 \]](/images/math/2/1/c/21cdefd25a2ac36e7e7f7c37c85693f3.png) |
(3.5) |
Az (1.16) és az (1.19) segítségével könnyen bizonyítható, hogy az elektromos és a mágneses tér energiasűrűsége megegyezik, vagyis 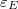 =
= 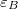 . Az elektromágneses síkhullám teljes energiasűrűsége tehát:
. Az elektromágneses síkhullám teljes energiasűrűsége tehát:
![\[ u = \varepsilon_E + \varepsilon_B = \varepsilon_o E^2 = \frac{1}{\mu_o} B^2 = \varepsilon_o E_o^2 cos^2 (\omega t - kz) \]](/images/math/3/8/2/3821eb4834346784eb7f98c65185cba6.png) |
(3.6) |
A cos-os időfüggés – mint azt az előzőekben láttuk – átlagolásnál egy 0.5 - s szorzófaktort jelent:
![\[ \left< u \right > = \left< \varepsilon_E + \varepsilon_B \right > = \frac{1}{2} \varepsilon_o E_o^2 = \frac{1}{2} \frac{1}{\mu_o} B_o^2 \]](/images/math/c/9/4/c9460d60fca5ff68f3c129ad8c1b9b91.png) |
(3.7) |
Ez viszont arányos a Poynting-vektor átlagértékével:
![\[ \left< S \right > = c \left< u \right > \]](/images/math/0/8/3/0839d0d5bcb520f553f775d977aa2787.png) |
(3.8) |
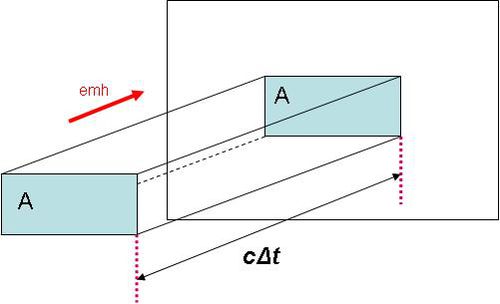
Ezután kiszámítjuk, hogy egy síklap (vagy akár egy képzeletbeli sík)  felületére (3.1 ábra) mennyi energiát szállít egy
felületére (3.1 ábra) mennyi energiát szállít egy 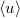 átlagos energiasűrűségű síkhullám
átlagos energiasűrűségű síkhullám  idő alatt a felületre (vagy a síkra) merőlegesen haladva:
idő alatt a felületre (vagy a síkra) merőlegesen haladva:
![\[ \Delta W = \left< u \right >Ac\Delta t \]](/images/math/a/2/f/a2f7e918e0d7301989d50d2001893797.png) |
(3.9) |
| 3.1 ábra |
Amennyiben az előző kifejezést elosztjuk  -vel, akkor kapjuk a felületre eső teljesítményt, és ha ezt még elosztjuk a felület nagyságával is, akkor adódik az EMH intenzitása:
-vel, akkor kapjuk a felületre eső teljesítményt, és ha ezt még elosztjuk a felület nagyságával is, akkor adódik az EMH intenzitása:
![\[ {\rm intenzit\acute{a}s} = I = \frac{\Delta W}{A\Delta t}=\left< u \right >c \]](/images/math/b/4/6/b46a391247372b8ed2e428d84d53184b.png) |
(3.10) |
A hullám intenzitása tehát, mint az a (3.8)-ból következik, megegyezik a Poynting-vektor átlagos nagyságával: intenzitás = 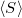 .
.
Az EMH impulzusa és a fénynyomás
Az előzőekben láttuk tehát, hogy az EMH-nak van energiája (illetve energiasűrűsége). Értelemszerűen adódik a kérdés, hogy van-e impulzusa, és ha van, akkor mi lehet ennek a következménye? A választ erre a kérdésre az 1.1 és az 1.2 ábrán is látható egyszerű esetben (azaz 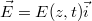 és
és 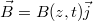 ) keressük (4.1 ábra).
) keressük (4.1 ábra).
| 4.1 ábra |
Az ábrán látható – téglalap alakú – fémlapra, amely párhuzamos az 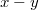 síkkal, beesik a
síkkal, beesik a  tengely mentén terjedő EMH. A térerősség hatására a jó vezetőképességű anyagban lévő elektron(ok)ra ható erő nagysága (mint azt már ismert):
tengely mentén terjedő EMH. A térerősség hatására a jó vezetőképességű anyagban lévő elektron(ok)ra ható erő nagysága (mint azt már ismert):
![\[ F_E = qE = bv_d \]](/images/math/f/7/7/f77b4301c8107e62906d9c33547681e5.png) |
(4.1) |
ahol  az elektron töltése,
az elektron töltése,  egy állandó és
egy állandó és 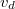 a driftsebesség:
a driftsebesség:
![\[ v_d = \frac {qE}{b} \]](/images/math/c/a/9/ca9597e17cd0fede67fb164e5849baa0.png) |
(4.2) |
Mivel az elektron töltése negatív, ezért a rá ható erő az elektromos térrel ellentétes irányú (ez látszik az 4.1 ábrán is), ezért az elektron drift-sebességének iránya is ellentétes lesz az elektromos térhez képest. A mozgó elektromos töltésre viszont az indukciós térben Lorentz-erő hat, amely párhuzamos a  tengellyel, és amelynek nagysága:
tengellyel, és amelynek nagysága:
![\[ F_L = qv_d b = \frac {q^2 E}{b}B = \frac {q^2 E^2}{bc} \]](/images/math/2/f/1/2f1e127f69d89c56494ac3964b7e5bd8.png) |
(4.3) |
Az átlagosan drift-sebességgel mozgó elektronra 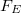 erő hat, így az általa "elnyelt" teljesítmény:
erő hat, így az általa "elnyelt" teljesítmény:
![\[\frac {dW}{dt} = F_E v_d = qE\frac {q E}{b} = \frac {q^2 E^2}{b} \]](/images/math/4/4/e/44e23f2bcfb3e368573b0bca85726ac6.png) |
(4.4) |
A (4.3)-ból és a (4.4)-ből következik, hogy:
![\[\frac {dW}{dt} = cF_L \]](/images/math/3/3/8/3384414ff0b072475e9e056ee6ed0698.png) |
(4.5) |
Newton 2. törvényét alkalmazva (4.5) felírható a következő alakban:
![\[\frac {dW}{dt} = c\frac {dp}{dt} \]](/images/math/f/a/9/fa92293c483dfdcec2b6c8b311167645.png) |
(4.6) |
ahol  az elektronnak átadott
az elektronnak átadott  irányú impulzus. Ebből a formulából két figyelemre méltó eredmény is származtatható.
irányú impulzus. Ebből a formulából két figyelemre méltó eredmény is származtatható.
Az egyik – igen fontos – összefüggés azonnal következik, ha (4.6) mindkét oldalát integráljuk az idő szerint; ekkor:
![\[ W = cp \]](/images/math/0/0/3/003f00e9e8bb6b744d0770eb317b41e2.png) |
(4.7) |
Minthogy az elektron az elektromágneses térből nyeri az impulzust és az energiát is, így ebből következik, hogy az elektromágneses síkhullám energiája és impulzusa közötti összefüggést a (4.7) adja.
A másik fontos következményt úgy kapjuk, hogy az erőt a nyomás és a felület szorzataként írjuk fel, azaz 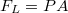 , így (4.5) vagy (4.6) kissé más alakban:
, így (4.5) vagy (4.6) kissé más alakban:
![\[\frac {dW}{dt} = cPA \]](/images/math/a/7/9/a791b7970dcd250242f60cc87120a068.png) |
(4.8) |
Ebből a  nyomást kifejezve kapjuk a lemezre ható fénynyomást:
nyomást kifejezve kapjuk a lemezre ható fénynyomást:
![\[\frac {dW}{cAdt} = P \]](/images/math/9/9/b/99b7143c440685bceba826c1fa938905.png) |
(4.9) |
A (3.10) alapján nyilvánvaló, hogy a (4.9) bal oldala az intenzitás osztva a fénysebességgel, amely viszont megegyezik az átlagos energiasűrűséggel:
![\[P = \frac{1}{c}I_{(int.)} = \frac{1}{c} \left< S \right> = \left< u \right > \]](/images/math/b/f/b/bfb15fd3f80559682fd9f5a645309b7f.png) |
(4.10) |
Ebben a modellben hallgatólagosan feltettük, hogy a fém elektronjai elnyelik az EMH energiáját. Ha azonban feltesszük, hogy egy tökéletesen reflektáló felületről a hullám visszaverődik, akkor a hullám impulzusváltozásának nagysága éppen duplája lesz annak az előbb vizsgált esetnek, amikor is a hullám elnyelődött az anyagban. Tehát egy 100%-os tükörről visszaverődő EMH fénynyomása a tükör felületén:
![\[P = 2\frac{1}{c}I_{(int.)} = 2\frac{1}{c} \left< S \right> = 2\left< u \right > \]](/images/math/e/6/0/e60f5363c854bcac99d0b18bdf37e023.png) |
(4.11) |
Az EMH polarizációja
Az általunk idáig vizsgált speciális esetben (1.2 ábra) egy olyan, a  tengely mentén haladó elektromágneses síkhullámot vizsgáltunk, amelynek az elektromos térerősség komponense
tengely mentén haladó elektromágneses síkhullámot vizsgáltunk, amelynek az elektromos térerősség komponense  irányú volt (
irányú volt (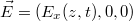 ). Az ilyen síkhullámot – amelyben tehát az elektromos (és természetesen a mágneses) térerősség komponens egy síkban rezeg – lineárisan polarizált hullámnak nevezzük. Lineárisan polarizált az a
). Az ilyen síkhullámot – amelyben tehát az elektromos (és természetesen a mágneses) térerősség komponens egy síkban rezeg – lineárisan polarizált hullámnak nevezzük. Lineárisan polarizált az a  tengely mentén terjedő síkhullám is, amelyben a térerősség x és y komponense fázisban van, azaz:
tengely mentén terjedő síkhullám is, amelyben a térerősség x és y komponense fázisban van, azaz:
![\[ E_{x} (z,t) = E_{0x} cos(\omega t - kz) \qquad {\rm \acute{e}s} \qquad E_{y} (z,t) = E_{0y}cos(\omega t - kz) \]](/images/math/f/f/6/ff63e959d16f4b7f4aca569eb9e28c3a.png) |
(5.1) |
Könnyen belátható, hogy ez is egy síkhullám, hiszen az elektromos térerősség egy olyan síkban rezeg, amely az  síkkal
síkkal 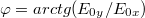 szöget zár be. Ha azonban
szöget zár be. Ha azonban 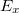 és
és 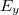 között (a frekvenciájuk és a hullámhosszuk természetesen azonos)
között (a frekvenciájuk és a hullámhosszuk természetesen azonos) 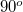 - os fáziskülönbség van, akkor
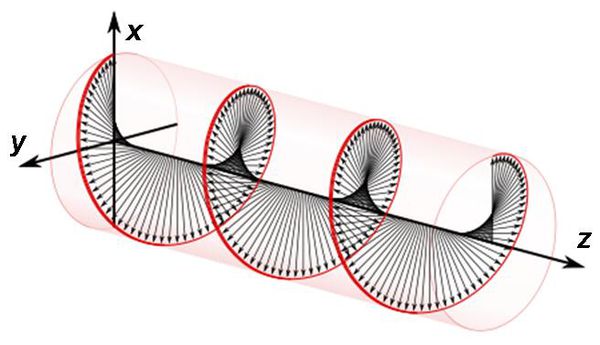
- os fáziskülönbség van, akkor 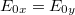 esetén egy cirkulárisan polarizált nyaláb-ot kapunk, amelynek az elektromos térerősség komponense
esetén egy cirkulárisan polarizált nyaláb-ot kapunk, amelynek az elektromos térerősség komponense  szögsebességgel forog a
szögsebességgel forog a  tengely körül (5.1 ábra).
tengely körül (5.1 ábra).
| 5.1 ábra |
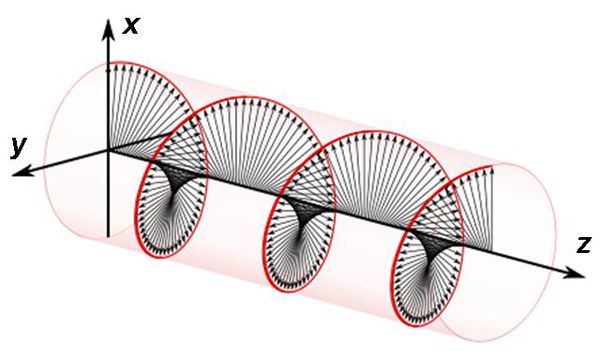
Természetesen az elektromos térerősség vektora foroghat az ellenkező irányba is:
| 5.2 ábra |
Az előző két ábra alapján nyilvánvaló, hogy a forgásirányokat tekintve megkülönböztethető jobbra (5.1 ábra) illetve balra (5.2 ábra) cirkulárisan polarizált hullám.
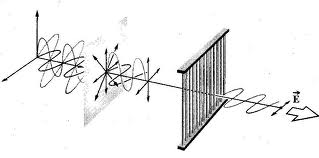
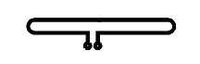
Az EMH polarizációs tulajdonságait viszonylag egyszerűen lehet vizsgálni egy olyan "polarizációs szűrővel", amely egy szigetelő keretből és az arra rögzített egymással párhuzamos egyenközű hosszú, egyenes vezetődarabokból áll (5.3 ábra).
| 5.3 ábra |
Az ábrán szemléltetett polarizációs hatás, tehát hogy a vezetődarabokkal párhuzamos polarizációjú hullám elnyelődik, könnyen magyarázható: a függőleges polarizációjú hullám a hosszú, vékony vezetőkben az elektronokra hat és azok a vezető mentén elmozdulhatnak, tehát az elektromos tér áramokat kelt és ez (ohmikus) veszteséget okoz. A vízszintes polarizációjú hullám nem képes az elektronokat jelentős mértékben megmozgatni, így az energia disszipációja sem jelentős. A Hertz által használt eszköz látható a következő fényképen:
| 5.4 ábra |
(A keret a kép bal oldalán látható; a vezetékek nem láthatók a kis felbontású felvételen, mert azok sűrűn helyezkednek el.)
EMH-k keltése
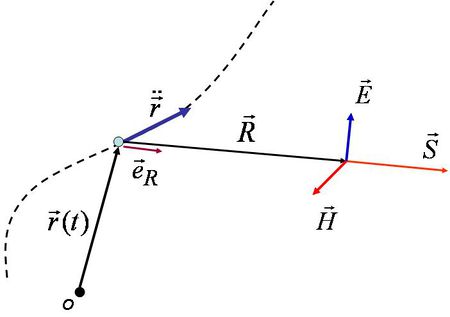
Az EMH-k legfőbb jellemzőivel már megismerkedtünk, azonban azok keletkezéséről még nem beszéltünk. A Maxwell-egyenletekből levezethető, hogy egy gyorsuló, töltött részecske elektromos és mágneses tere távoltérben (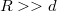 , ahol
, ahol  az EMH forrásának jellemző mérete) a 6.1 ábra jelöléseivel:
az EMH forrásának jellemző mérete) a 6.1 ábra jelöléseivel:
![\[ \vec H \sim \frac{q}{R}\ddot{\vec r} \times \vec e_R \]](/images/math/f/f/7/ff7fbd99be06a7334d2ab6f3cfb688d3.png) |
(6.1) |
![\[ \vec E \sim \frac{q}{R} \left( \ddot{\vec r} \times \vec e_R \right )\times \vec e_R \]](/images/math/e/0/d/e0deb323d6d410c212cb7c934bf28ff1.png) |
(6.2) |
| 6.1 ábra |
A Poynting-vektor 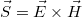 alakban írható; ebből következik a 6.1 és 6.2 következményeképpen, hogy a gyorsuló részecske által keltett EMH hullám intenzitása arányos egyrészt a gyorsulás négyzetével:
alakban írható; ebből következik a 6.1 és 6.2 következményeképpen, hogy a gyorsuló részecske által keltett EMH hullám intenzitása arányos egyrészt a gyorsulás négyzetével:
![\[ \left| \vec S \right| \sim \left( \ddot{\vec r} \right )^2 \]](/images/math/4/e/d/4edd260e8d7e0038ee2a1c7358785cc2.png) |
(6.3) |
másrészt pedig arányos a távolság négyzetének reciprokával:
![\[ \left| \vec S \right| \sim \frac {1}{R^2} \]](/images/math/6/f/5/6f584c826d961b5310cacf2068b7db83.png) |
(6.4) |
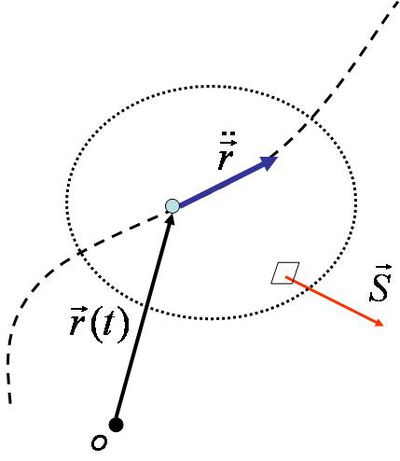
A 6.2 ábrán látható gyorsulva mozgó részecske sugárzási teljesítménye úgy adható meg, hogy az intenzitást integráljuk a forrást körülvevő zárt felületre (szaggatott vonallal jelölve):
![\[ P_{sug} = \oint\limits_A \vec S d\vec A \]](/images/math/b/f/a/bfa159dacb702596ebe3e15f3420389e.png) |
(6.5) |
| 6.2 ábra |
Megállapíthatjuk tehát, hogy egy gyorsuló töltött részecske sugárzási teljesítménye arányos a gyorsulás négyzetével:
![\[ P_{sug} \sim \left( \ddot{\vec r} \right )^2 \]](/images/math/f/2/c/f2cb4210fbca9f0d781fe5b15a44e36a.png) |
(6.6) |
(A zárt felületre számított integrálásnál természetesen az intenzitás irányfüggését is figyelembe kell venni, azonban ez mindössze egy állandó szorzófaktort jelent a sugárzási teljesítmény meghatározásánál; valamint a távolságfüggés természetesen kiesik.)
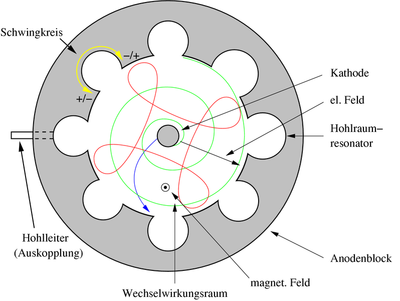
Töltött részecskét kétféleképpen lehet viszonylag egyszerűen gyorsítani. Az egyik módszer szinte kézenfekvő; a töltött részecské(ke)t valahogyan körmozgásra kell kényszeríteni, és – mint azt már láttuk – a köríven vagy görbe vonalú pályán mozgó részecskének centripetális gyorsulása van. Az egyik olyan eszköz, amelynek segítségével köríven mozgathatunk részecskéket a – már tanult – részecskegyorsító a ciklotron (betatron), azonban ez igencsak költséges berendezés. A másik alkalmas eszköz a magnetron; működését megérthetjük a 6.3 ábra alapján.
| 6.3 ábra |
Az ábrán egy tipikus magnetron keresztmetszeti képe látszik. A középen elhelyezkedő forró katódból kilépő elektronok a keresztmetszeti síkra merőleges mágneses térben a kezdősebességtől függően különböző görbe vonalú pályákon mozoghatnak (kékkel, zölddel, pirossal jelölt pályák). A magnetron a részecskegyorsítónál jóval olcsóbb berendezés. Egy mikrohullámú sütőben hullámforrásként alkalmazott magnetron látható a következő képen.
| 6.4 ábra |
A radar-jeladóban is leggyakrabban magnetront használnak. Egy tipikus radar-jeladót láthatunk a 6.5 ábrán:
| 6.5 ábra |
Ma már számos példa van a radar hétköznapi alkalmazására; például a légi irányítás nélkülözhetetlen eszköze. A radar működéséhez természetesen szükség van még egy effektusra is, nevezetesen arra, hogy a hullám visszaverődjön a tárgyak felületéről.
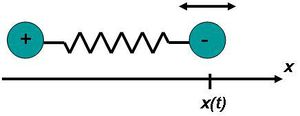
Láttuk az előzőekben, hogy EMH-t kelt egy gyorsulva mozgó elektromosan töltött részecske. Ennek segítségével érthető meg az is, hogy miért sugároz egy rezgő dipól (6.6 ábra).
| 6.6 ábra |
Az ábrán a két tömegpontot rugó köti össze; ez a rugó szimbolizálja azt, hogy a két részecske közötti kölcsönhatás jellegéből következően mindkettő harmonikus rezgést végezhet az egyensúlyi hely körül. Az egyszerűség kedvéért tegyük fel, hogy az ábrán látható elrendezésben a pozitív töltésű részecske tömege több nagyságrenddel nagyobb, mint az  tengely mentén mozgó negatív töltésűé. Ekkor elegendő a negatív töltésű részecske mozgását figyelembe venni. A rendszer elektromos dipólmomentuma:
tengely mentén mozgó negatív töltésűé. Ekkor elegendő a negatív töltésű részecske mozgását figyelembe venni. A rendszer elektromos dipólmomentuma: 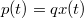 . A 6.1 és 6.2 egyenletekben tehát
. A 6.1 és 6.2 egyenletekben tehát 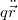 helyett
helyett 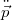 - t írhatunk. Mindkét említett formula jobb oldalán szerepel az
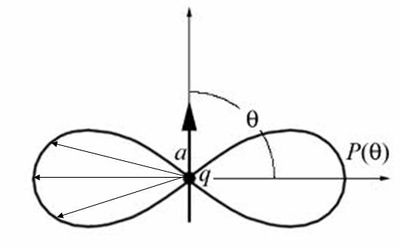
- t írhatunk. Mindkét említett formula jobb oldalán szerepel az 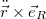 kifejezés, amely a sugárzás irányfüggéséért felelős; mindezt jól mutatja a rezgő dipól sugárzási iránykarakterisztikája (6.7 ábra).
kifejezés, amely a sugárzás irányfüggéséért felelős; mindezt jól mutatja a rezgő dipól sugárzási iránykarakterisztikája (6.7 ábra).
| 6.7 ábra |
Az ábráról leolvasható, hogy a sugárzási teljesítmény maximális a rezgés irányára merőlegesen, míg a rezgés irányában (vagyis a gyorsulás irányában) a dipól nem sugároz. A 6.1 és 6.2 formulák és az intenzitás definíciójának alkalmazásával az is könnyen belátható, hogy a kisugárzott EMH intenzitása távoltérben 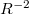 – al arányos.
– al arányos.
Hertz kísérlete
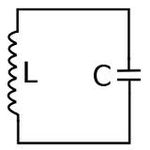
Az RLC-kör tulajdonságait megadó – már ismertetett – módszert felhasználhatjuk egy LC-kör leírására is. Az ideális, veszteségmentes LC-körben (7.1 ábra) harmonikus oszcilláció alakulhat ki 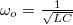 körfrekvenciával.
körfrekvenciával.
| 7.1 ábra |
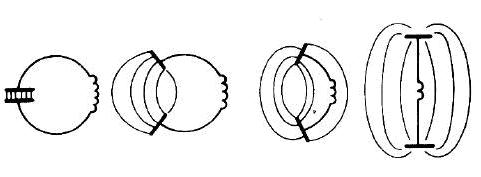
Ez az oszcilláció azt jelenti, hogy az energia a kondenzátor és a tekercs között hasonlóan oszlik meg, mint a potenciális és a mozgási energia a rugó végére kötött harmonikus rezgőmozgást végző test esetében. A rezgés természetesen azt is jelenti, hogy a kondenzátor lemezein felváltva jelenik meg a pozitív és a negatív töltés a 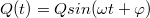 - nek megfelelően, és a lemezek közötti elektromos tér nagysága és iránya is hasonlóan változik. Abban az esetben, ha a kondenzátor lemezeit "kihajtjuk" (7.2 a és b ábra), akkor az elektromos térerősség-vonalak kívül a térben "jutnak el" az egyik töltéssel rendelkező kondenzátor lemeztől a másikig (a pozitívtól a negatívig); így kaptunk egy nyitott LC-kört.
- nek megfelelően, és a lemezek közötti elektromos tér nagysága és iránya is hasonlóan változik. Abban az esetben, ha a kondenzátor lemezeit "kihajtjuk" (7.2 a és b ábra), akkor az elektromos térerősség-vonalak kívül a térben "jutnak el" az egyik töltéssel rendelkező kondenzátor lemeztől a másikig (a pozitívtól a negatívig); így kaptunk egy nyitott LC-kört.
| 7.2.a ábra | 7.2.b ábra |
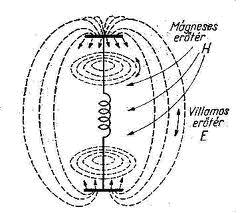
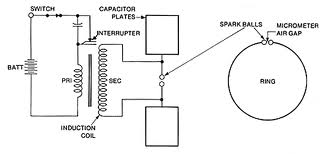
Minthogy a kondenzátor lemezei felváltva lesznek pozitív és negatív töltésűek, így az általuk keltett elektromos tér iránya is ennek megfelelően fog változni. De mi történt az előző fél-periódusban létrehozott elektromos térrel? A válasz egyszerű; azok a térerősség-vonalak leváltak és távolodnak az őket létrehozó dipól-antennától (rezgő dipóltól). Az antennáról leváló hullámok létezéséről először Heinrich Hertz adott kísérleti bizonyítékot 1887-ben. Hertz kísérleti berendezésének vázlata látható a 7.3 ábrán.
| 7.3 ábra |
Az ábra bal oldali részén látható szikra-induktor segítségével lehet pótolni az LC-kör energiaveszteségeit, vagyis a nyílt LC-kört "meghajtani". A kísérletben a vevő egy – az ábra jobb oldalán látható – kis légréssel megszakított körvezető. A körvezető légrésében szikra jelenik meg demonstrálva a leváló és terjedő elektromos (és mágneses) tér, azaz az EMH által szállított energiát. A következő ábrán a Hertz-féle kísérletnek egy egyszerűbb, de szintén megvalósítható elrendezése látható.
| 7.4 ábra |
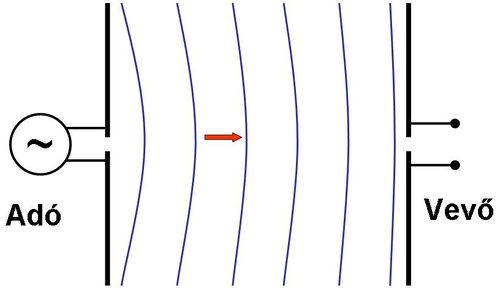
Az adó oldali, EMH kibocsátására alkalmas antenna két hosszú egyenes vezetékdarabból áll; a vevő oldali antenna is hasonló szerkezetű. Azért lehetséges a 7.2 ábrán látható nyitott LC kört helyettesíteni két egyenes vezetővel, mert ennek az egyszerű elrendezésnek is van kapacitása és induktivitása is. Az ilyen szerkezetű adó és vevő antenna az ún. dipólantenna (7.5 ábra).
| 7.5 ábra |
Antennák
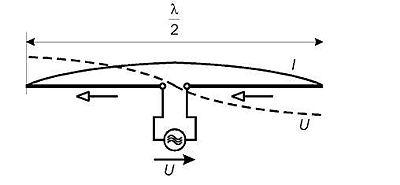
Az elektromágneses hullámok keltésére vagy kisugárzására, illetve vételére számos antennatípust dolgoztak ki. Ezek közül csak néhányat sorolunk fel. Az előzőekben már említett dipólantennát félhullámú dipólus antennának is nevezik, mert hossza a kisugárzott EMH hullámhosszának fele (8.1 ábra). Amennyiben vevőként használjuk, természetesen a hossz akkor is meghatározó a legjobb vételi frekvencia tekintetében.
| 8.1 ábra |
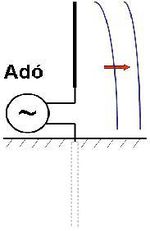
Az elektrosztatika fejezetben láttuk, hogy a vezető sík felett elhelyezett töltés hatására a vezető felületén indukált felületi töltéssűrűség és az általa létrehozott elektromos tér olyan, mintha egy tükörtöltés lenne a vezető másik oldalán. Ezt a tükörkép-hatást lehet felhasználni arra, hogy a sugárzó dipólantennának csak a felét kelljen megépíteni, hiszen a dipól egyik oldalának ellentétes töltésű tükörképe (a dipól másik fele) azért jelenik meg, mert a föld felszíne általában jó vezető (8.2 ábra). Ezért ezt az antennát negyedhullámú antennának is hívják.
| 8.2 ábra |
Több helyen lehet látni hajlított dipólus antennát (8.3 ábra), amely két, párhuzamosan kapcsolt dipólantennaként értelmezhető.
| 8.3 ábra |
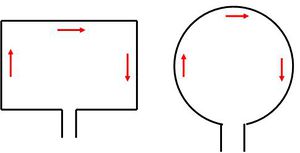
A rezonanciahullámnál jóval nagyobb hullámhosszú adások vételére szokták használni a keretantennákat, amelynek két legegyszerűbb típusa látható a következő ábrán.
| 8.4 ábra |
A piros nyilak egy pillanatnyi áramirányt mutatnak. Minthogy a keret mérte általában jóval kisebb, mint az EMH hullámhossza, ezért adóoldali antennaként általában nem használják, hiszen a szemközti oldalakon folyó ellentétes áramok ellenfázisban vannak, így a sugárzás gyenge hatásfokkal valósítható csak meg.
Az irányított antennarendszerek, vagy iránysugárzók általában egy kisebb térszögben sugároznak. Ezt különböző hullámhosszakon más-más technikával érik el.
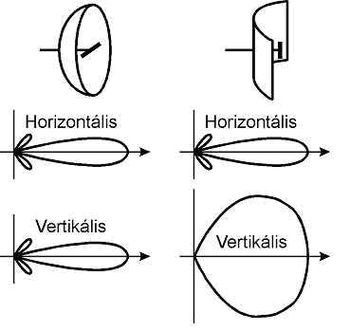
Iránysugárzó mikrohullámú adókhoz általában reflektort használnak (8.5 a és b ábra).
| 8.5.a ábra | 8.5.b ábra |
A 8.5.a ábrán a két adó sugárzási iránykarakterisztikája látható. Az irányított sugárzást nagyobb hullámhosszakon általában antennarendszerek segítségével oldják meg (8.6 ábra).
| 8.6 ábra |
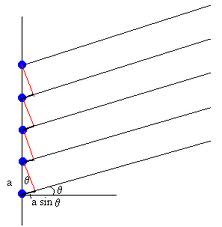
Az iránysugárzó antennarendszerek a hullámok szuperpozíciójának elvén működnek. Egy megadott irányban az egyes hullámok közötti fáziskülönbséget egyrészt a geometriai elrendezés (8.7 ábra), másrészt az egyes antennákat meghajtó jelek fázisa határozza meg; ezen fázisok kontrolljával érhető el az, hogy a kívánt irányba sugározzon az adó. (A jelenséget leíró elméleti módszert az optika fejezetben tárgyaljuk.)
| 8.7 ábra |
(Amennyiben az antennák azonos fázisban sugároznak, akkor az olyan 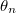 szöggel jellemzett irányban sugároz az antennarendszer, amely irányban a két szomszédos antennára az úthosszkülönbség éppen a hullámhossz egész számú többszöröse adódik, azaz
szöggel jellemzett irányban sugároz az antennarendszer, amely irányban a két szomszédos antennára az úthosszkülönbség éppen a hullámhossz egész számú többszöröse adódik, azaz 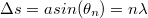 .)
.)
Kommunikáció
Elektromágneses hullámok segítségével információt lehet továbbítani. Ennek jelentőségére igen hamar rájöttek és létrejött a rádiózás (első rádióműsor: Lübeck 1914), valamint a morze-jeleket használó távíró (Marconi 1894., Popov 1896.).
Emberi hangot vagy zenét (és egyéb információt) különböző modulációs technikákat alkalmazva tudunk küldeni elektromágneses hullámok segítségével.
Az egyik, régebben használatos módszer az amplitúdó-moduláció. Mint nevéből is kitűnik, ez a technika a kisugárzott nagyfrekvenciás EMH amplitúdóját modulálja az átvinni kívánt hangfrekvenciás jellel (9.1 ábra).
| 9.1 ábra |
Ennek a módszernek azonban az a hátránya, hogy nem lehet nagyobb távolságon jó minőségű jelátvitelt elérni a környezeti hatások (reflexiók, abszorbció, stb. ) miatt.
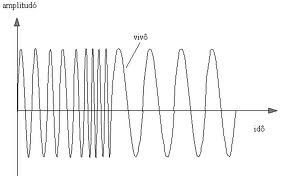
A környezeti tényezők zavaró hatásának csökkentésére fejlesztették ki a frekvenciamodulációs eljárást, amelynek alkalmazása során magával a jellel modulálják a rádiótorony által kisugárzott EMH frekvenciáját (9.2 ábra).
| 9.2 ábra |
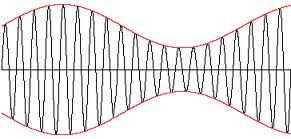
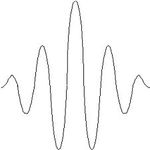
Elektromágneses impulzusok sorozatát is lehet információ továbbítására használni. Ebben az esetben az EMH-t "megszaggatják", vagy hullámcsomagot küldenek (9.3 a és b ábra).
| 9.3.a ábra | 9.3.b ábra |
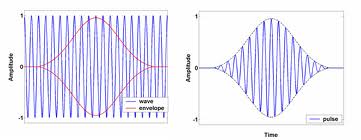
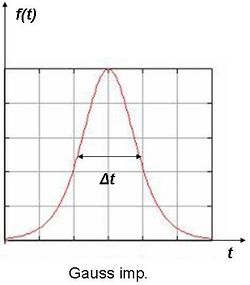
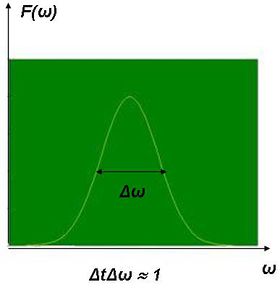
Az előző három ábra azt mutatja, hogy a szinuszos vivőhullám és az impulzusalak (a burkoló) hogyan formálják együttesen a hullámcsomagot. Az impulzus hossza vagy szélessége (időbeli) és spektrális kiszélesedése között fordított arány van. Gauss-os impulzus esetében: 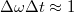 (9.4.a és b ábra). Tehát minél rövidebb az impulzus, a frekvenciatartománybeli kiszélesedése annál nagyobb.
(9.4.a és b ábra). Tehát minél rövidebb az impulzus, a frekvenciatartománybeli kiszélesedése annál nagyobb.
| 9.4.a ábra | 9.4.b ábra |
A rádióhullámok frekvencia kiosztása
A rádióhullámok tartományát frekvencia szerint is feloszthatjuk; frekvencia szerinti növekvő sorrendben beszélhetünk hosszú-, közép-, rövid- és ultrarövid hullámokról. A következő ábrán láthatók a különböző a rádiófrekvencia tartományok a Nemzetközi Rádiószabályzat alapján.
| 10.1 ábra |
Reflexió
Radarral akkor lehet bemérni egy repülőt, autót, vagy egy hajót, ha az azokra eső EMH-k egy része visszaverődik. A hajókra boltban is kapható radar reflektorokat (11.1 ábra) szerelnek azért, hogy ködben vagy éjszaka is lássák egymást.
| 11.1 ábra |
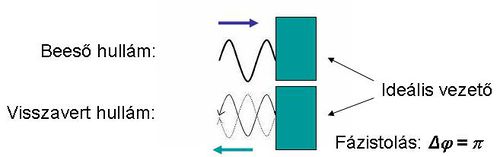
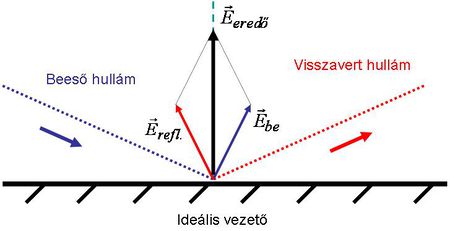
Először azt vizsgáljuk meg, hogy egy ideális vezető felületéről a rá merőlegesen beeső hullám hogyan verődik vissza. Minthogy az ideális vezető ellenállása zérus, azaz a vezetőképessége végtelen (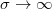 ), ez azt jelenti, hogy nincs ohmikus veszteség. Az elektrosztatika tárgyalásánál láttuk, hogy az ideális vezetőben az elektromos térerősség zérus. Azt is tanultuk, hogy az elektromos térerősség tangenciális komponense folytonosan megy át a határfelületen (Maxwell-egyenletek, határfeltételek). Az említett két feltétel egyszerre csak úgy teljesülhet, ha az EMH teljes egészében reflektálódik, mégpedig
), ez azt jelenti, hogy nincs ohmikus veszteség. Az elektrosztatika tárgyalásánál láttuk, hogy az ideális vezetőben az elektromos térerősség zérus. Azt is tanultuk, hogy az elektromos térerősség tangenciális komponense folytonosan megy át a határfelületen (Maxwell-egyenletek, határfeltételek). Az említett két feltétel egyszerre csak úgy teljesülhet, ha az EMH teljes egészében reflektálódik, mégpedig 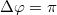 fázistolást szenvedve; ekkor ugyanis a vezető felületénél a beeső és a visszavert hullám éppen kioltják egymást. Az ideális vezető felületére beeső EMH síkhullám tehát
fázistolást szenvedve; ekkor ugyanis a vezető felületénél a beeső és a visszavert hullám éppen kioltják egymást. Az ideális vezető felületére beeső EMH síkhullám tehát 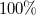 -ban reflektálódik (11.2 ábra).
-ban reflektálódik (11.2 ábra).
| 11.2 ábra |
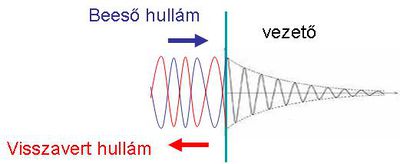
Ideális vezető a gyakorlatban természetesen nincs; a fémek viszont jó vezetők. Az ideális vezetőre a reflexióról az előbbiekben elmondottak csaknem igaznak bizonyulnak fémek esetében is. A különbség egyrészt abban áll, hogy a reflexióképesség nem 100%, bár igen jó (alumínium tükörre 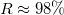 ), másrészt pedig a hullám behatol a vezetőbe, azonban ez a behatolás jellemzően mindössze néhány hullámhossznyi (11.3 ábra).
), másrészt pedig a hullám behatol a vezetőbe, azonban ez a behatolás jellemzően mindössze néhány hullámhossznyi (11.3 ábra).
| 11.3 ábra |
Amikor egy hullám nem merőlegesen esik az ideális vezetőre, akkor – mint az a 11.4 és 11.5 ábrán látható – az említett két feltétel úgy teljesül, hogy 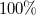 -os reflexió és
-os reflexió és 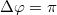 fázistolás mellett a beesési és a visszaverődési szög megegyezik, mert ekkor az elektromos térerősség tangenciális komponense a felület közelében zérus. Könnyű belátni, hogy ez a magyarázat abban az esetben is elfogadható, ha a polarizáció olyan, hogy az elektromos térerősség a felülettel párhuzamos.
fázistolás mellett a beesési és a visszaverődési szög megegyezik, mert ekkor az elektromos térerősség tangenciális komponense a felület közelében zérus. Könnyű belátni, hogy ez a magyarázat abban az esetben is elfogadható, ha a polarizáció olyan, hogy az elektromos térerősség a felülettel párhuzamos.
| 11.4 ábra |
| 11.5 ábra |
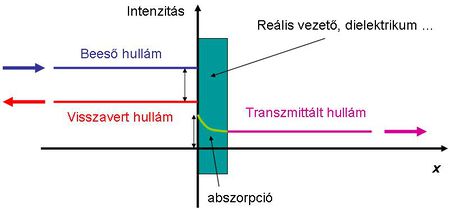
Egy reális vezető, vagy dielektrikum esetében egy nem túl vastag rétegre beeső hullám egy része reflektálódik, egy része elnyelődik (abszorbeálódik) az anyagban, míg a maradék rész megjelenik a réteg másik oldalán; ezt nevezzük transzmittált hullámnak. A beeső hullám intenzitása megegyezik a reflektált nyaláb, a transzmittált hullám és az elnyelt intenzitás összegével, azaz 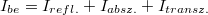 (11.6 ábra):
(11.6 ábra):
| 11.6 ábra |
Mint azt említettük, a fémek reflexióképessége általában igen jó. Ez az oka annak, hogy a parabola antenna tányérja, a radarok reflektora, a mikrohullámú rádiócsillagászatban használt antennák, stb. fémből készülnek (11.7.a, b, c ábrák).
| 11.7.a ábra | 11.7.b ábra | 11.7.c ábra |
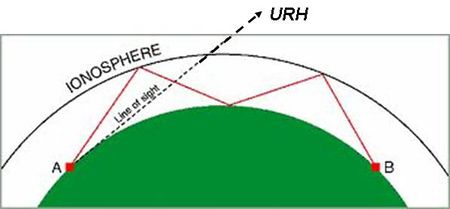
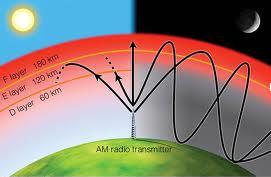
Fontos megemlíteni, hogy a rádiózásban igen nagy jelentősége van a Földet körülvevő ionoszférának. A plazmafrekvenciánál kisebb frekvenciájú rádióhullámok visszaverődnek az ionoszféráról; ezért volt lehetséges például, hogy az internet korszak előtti időkben a magyar adókat a tengerentúlon is hallgathatták (11.8 ábra).
| 11.8 ábra |
Természetesen a többszörös visszaverődések gyakran bizonytalan útvonalakat biztosítottak, ráadásul a nappali és az éjszakai ionoszféra szerkezete is eltérő egy kissé, úgyhogy a tengerentúli vétel minősége általában elég gyenge volt (11.9 ábra).
| 11.9 ábra |
Interferencia
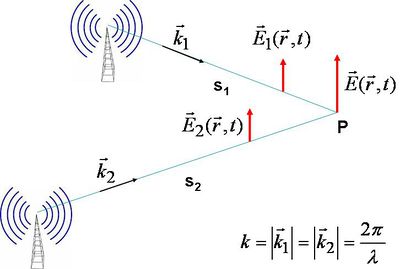
Az előző fejezetben volt arról szó, hogy az ionoszféráról visszaverődő rádióhullámok különböző utakon juthatnak el a vevőhöz és emiatt a vétel minősége gyenge, vagy változó. Minthogy a különböző utak különböző 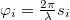 fázisokat jelentenek, valamint a különböző fázisokkal a tér egy megadott pontjába érkező hullámok erősíthetik vagy akár ki is olthatják egymást, ezért a térben kialakul egy (gyakran időben sem mindig állandó) intenzitás-eloszlás, vagy más néven interferenciamintázat. (Az optikában ezt interferenciaképnek hívják, mert jól látható mintázatok figyelhetők meg.) Ez a jelenség a mikrohullámú sütő belső terében is megjelenik. A magnetron által kibocsátott hullámok a falakról visszaverődnek és egy meghatározott intenzitás-eloszlást hoznak létre. A melegedni betett étel az interferenciamintázatnak megfelelően néhol – ahol az intenzitásnak maximuma van – melegedne, máshol pedig – ahol a hullámok kioltják egymást – hideg maradna, ha a tálca nem forogna. Az interferenciamintázat kialakulásának vizsgálatához tekintsünk egy egyszerű modellt; tegyük fel, hogy két rádióadó azonos – állandó – frekvencián sugároz (12.1 ábra). Az egyszerűség kedvéért a két adó sugárzása legyen azonos fázisban (a dipólok együtt "rezegnek").
fázisokat jelentenek, valamint a különböző fázisokkal a tér egy megadott pontjába érkező hullámok erősíthetik vagy akár ki is olthatják egymást, ezért a térben kialakul egy (gyakran időben sem mindig állandó) intenzitás-eloszlás, vagy más néven interferenciamintázat. (Az optikában ezt interferenciaképnek hívják, mert jól látható mintázatok figyelhetők meg.) Ez a jelenség a mikrohullámú sütő belső terében is megjelenik. A magnetron által kibocsátott hullámok a falakról visszaverődnek és egy meghatározott intenzitás-eloszlást hoznak létre. A melegedni betett étel az interferenciamintázatnak megfelelően néhol – ahol az intenzitásnak maximuma van – melegedne, máshol pedig – ahol a hullámok kioltják egymást – hideg maradna, ha a tálca nem forogna. Az interferenciamintázat kialakulásának vizsgálatához tekintsünk egy egyszerű modellt; tegyük fel, hogy két rádióadó azonos – állandó – frekvencián sugároz (12.1 ábra). Az egyszerűség kedvéért a két adó sugárzása legyen azonos fázisban (a dipólok együtt "rezegnek").
| 12.1 ábra |
A P pontban a két hullám eredőjeként kialakuló elektromos tér meghatározható a szuperpozíció elvének alkalmazásával: 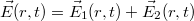 . Fontos megjegyezni, hogy az elektromos térerősség vektora függőleges (ez nyilvánvaló például a 7.2.b ábra alapján), vagyis az EMH függőleges polarizációjú. Láttuk, hogy a
. Fontos megjegyezni, hogy az elektromos térerősség vektora függőleges (ez nyilvánvaló például a 7.2.b ábra alapján), vagyis az EMH függőleges polarizációjú. Láttuk, hogy a  tengely mentén haladó síkhullám (12.2.a és b ábra) megadható a következő alakban:
tengely mentén haladó síkhullám (12.2.a és b ábra) megadható a következő alakban:
![\[ E_x (z,t) = E_o cos(\omega t - kz) \]](/images/math/d/a/6/da6aecf56d291d3b2d638dff918cf0c4.png) |
(12.1) |
| 12.2.a ábra | 12.2.b ábra |
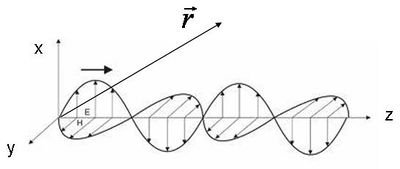
A síkhullámban az elektromos tér nagysága és iránya (és természetesen a fázisa) egy, a terjedési irányra merőleges síkban állandó. Az elektromos térerősség vektor  komponense megadható nemcsak a
komponense megadható nemcsak a  tengely mentén, hanem a tér egy tetszőleges pontjában is. A 12.3 ábra jelöléseit használva könnyű belátni, hogy
tengely mentén, hanem a tér egy tetszőleges pontjában is. A 12.3 ábra jelöléseit használva könnyű belátni, hogy 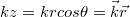 , így most már megadhatjuk a (12.1) általánosított alakját:
, így most már megadhatjuk a (12.1) általánosított alakját:
![\[ E_x (z,t) = E_o cos(\omega t - \vec k \vec r) \]](/images/math/a/b/8/ab87e2429f45df6b32e79d710de8f0dc.png) |
(12.2) |
| 12.3 ábra |
Ez utóbbi formula még tovább alakítható az egyszerűbb írásmód kedvéért (a továbbiakban nem jelöljük a komponenst):
![\[ E (z,t) = E_o e^{i(\omega t - \vec k \vec r)} \]](/images/math/e/6/5/e6570f4bdd32503f79fb6d7b37ba5225.png) |
(12.3) |
A (3.10) és (3.7) alapján belátható, hogy az intenzitás arányos a térerősség négyzetével, vagyis 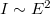 , vagy másképpen:
, vagy másképpen: 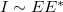 . A két EMH (12.1 ábra) eredő terének intenzitása tehát a következőképpen számítható:
. A két EMH (12.1 ábra) eredő terének intenzitása tehát a következőképpen számítható:
![\[ I \sim (E_1 + E_2) (E_1^* + E_2^* )=E_1 E_1^* + E_2 E_2^* + E_1 E_2^* + E_2 E_1^* \]](/images/math/6/3/a/63a940d9d99b917c8c92b7b81d07e5cb.png) |
(12.4) |
Ha most az 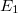 és
és 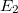 helyébe az (51) komplex kifejezésnek megfelelő alakot írjuk be, és figyelembe vesszük, hogy a két rádióadótól a
helyébe az (51) komplex kifejezésnek megfelelő alakot írjuk be, és figyelembe vesszük, hogy a két rádióadótól a  pontig a két hullám esetében
pontig a két hullám esetében 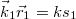 és
és 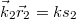 fázistolás lép fel, akkor az intenzitásra a következő alakot kapjuk:
fázistolás lép fel, akkor az intenzitásra a következő alakot kapjuk:
![\[ I = I_1 +I_2 + 2\sqrt{I_1 I_2}cos \left[k(s_2 - s_1 )\right] \]](/images/math/7/d/5/7d57c5979a9f72a64c88664842d9b100.png) |
(12.5) |
Ez utóbbi eredmény azt mutatja, hogy a két hullám interferenciájaként létrejövő intenzitás-eloszlás a két hullám fáziskülönbségétől függ (12.6).
![\[ I = I_1 +I_2 + 2\sqrt{I_1 I_2}cos (\Delta \varphi ) \]](/images/math/3/e/0/3e0851f7629917dedc42c96b2352c3dd.png) |
(12.6) |
Levonható tehát a következtetés, miszerint két hullám erősíti egymást, ha a fáziskülönbségük 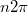 , vagyis az úthossz-különbség
, vagyis az úthossz-különbség 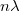 (ahol
(ahol  egész szám), mivel
egész szám), mivel 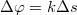 . Kioltás pedig ott van, ahol a fáziskülönbség
. Kioltás pedig ott van, ahol a fáziskülönbség 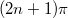 és ennek megfelelően az úthossz-különbség
és ennek megfelelően az úthossz-különbség 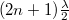 .
Fontos megemlíteni, hogy teljes kioltás, vagyis tökéletes interferencia abban az esetben lép fel, ha a két interferáló hullám elektromos térerősség-vektorai párhuzamosak, azaz
.
Fontos megemlíteni, hogy teljes kioltás, vagyis tökéletes interferencia abban az esetben lép fel, ha a két interferáló hullám elektromos térerősség-vektorai párhuzamosak, azaz 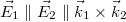 .
.
Hullámvezetők
Arra láttunk példát, hogy a feszültségforrástól vagy a teleptől vezető(k) használatával hogyan vihető át a teljesítmény a fogyasztó(k)hoz. Joggal vetődhet fel a kérdés, hogy az elektromágneses hullámok csak szabadtéri terjedéssel juthatnak-e a felhasználóhoz, vagy valamiképpen vezethetők is felhasználás helyére. A problémára, vagyis az EMH vezetésére, vagy irányítására megoldást jelenthetnek a már említett reflektorok. Ezeknél azonban léteznek általánosabb és jobban használható eszközök is, ezek az ún. hullámvezetők. Most csak a legegyszerűbb elrendezést fogjuk részletesebben megvizsgálni. Először is nézzük meg, hogy mi történik, ha egy elektromágneses síkhullám két nagyméretű, párhuzamos fémvezetővel határolt térrészben alakul ki. Amennyiben a hullám terjedési iránya merőleges a falakra, akkor az EMH a falakról visszaverődve állóhullámot képezhet. (Hasonló jelenség játszódik le hanghullámok esetében; például egy orgonasípban, vagy egy dobban – vagyis egy rezonátorban – is kialakulhat állóhullám). Ezt a folyamatot könnyen leírhatjuk a 13.1 ábra jelöléseit használva.
| 13.1 ábra |
Az  tengely mentén haladó hullámnak a tengelyre merőleges elektromos térerőssége felírható a következő formában:
tengely mentén haladó hullámnak a tengelyre merőleges elektromos térerőssége felírható a következő formában: 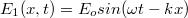 . A visszaverődő (az ellentétes irányban haladó) hullám pedig:
. A visszaverődő (az ellentétes irányban haladó) hullám pedig: 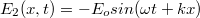 . A szuperpozíció elvét használva kapjuk, hogy:
. A szuperpozíció elvét használva kapjuk, hogy:
![\[ E (x,t) = E_1 (x,t)+E_2 (x,t)= E_o sin(\omega t - kx)-E_o sin(\omega t + kx)= -2E_o sin(kx)cos(\omega t)\]](/images/math/0/5/b/05b334ea713db0fea13fccb1e09e5e0d.png) |
(13.1) |
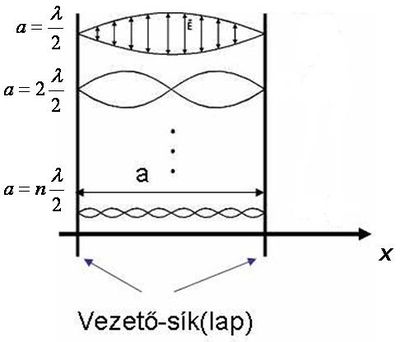
Jól látható, hogy ez éppen egy állóhullám, hiszen az eredő hullám helyfüggése azt mutatja, hogy egymástól azonos távolságra lesznek a csomópontok (és a duzzadóhelyek). A vezetőből készült falakban az elektromos tér értéke zérus (elektrosztatika). Az elektromos térerősség tangenciális komponense folytonosan megy át egyik közegből a másikba; ez az a határfeltétel, amelyet ki kell elégítenie a 13.1 állóhullámnak. Ha tehát a falban, vagyis a vezetőben zérus a térerősség, akkor a fal felületénél az elektromos térerősségnek el kell tűnnie; ez teljesül is, ha
![\[ k = n\frac {\pi}{a} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/d/e/5/de5dbcefc3f23aae17b00b056b127c3d.png) |
(13.2) |
Ezután tegyük fel, hogy két, egymástól  távolságban lévő vezető sík között terjedhet az elektromágneses hullám (13.2 ábra).
távolságban lévő vezető sík között terjedhet az elektromágneses hullám (13.2 ábra).
| 13.2 ábra |
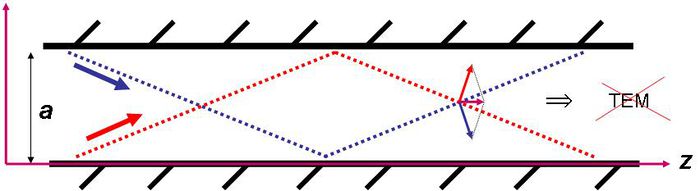
Az egyszerűség kedvéért tételezzük fel, hogy két síkhullám reflektálódik, "pattog" a két fal között, ahogyan az az előző ábrán látható. (A vastag piros és kék nyilak mutatják az egyes hullámok terjedési irányát.) A Maxwell egyenletek és a belőlük levezethető hullámegyenlet lineáris egyenletek, ami azt jelenti, hogy két megoldás összege is megoldás. Jelöltük a haladási irányra merőleges térerősség-vektorokat is (vékonyabb piros és kék vektorok); jól látszik, hogy ezek összege egy, a z tengely irányú térerősség 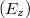 , vagyis a két "pattogó" hullám eredőjeként előálló vezetett módus már nem transzverzális elektromágneses (TEM) hullám. Részletesebb bizonyítás nélkül most csak fogadjuk el, hogy ennél a geometriai elrendezésnél vagy transzverzális elektromos (TE) vagy transzverzális mágneses (TM) módus alakulhat ki; ez a modellből egyébként kvalitatív megfontolásból is adódik. A határfeltétel kielégül az elektromos térerősség
, vagyis a két "pattogó" hullám eredőjeként előálló vezetett módus már nem transzverzális elektromágneses (TEM) hullám. Részletesebb bizonyítás nélkül most csak fogadjuk el, hogy ennél a geometriai elrendezésnél vagy transzverzális elektromos (TE) vagy transzverzális mágneses (TM) módus alakulhat ki; ez a modellből egyébként kvalitatív megfontolásból is adódik. A határfeltétel kielégül az elektromos térerősség  komponensére, ha az a falaknál zérus értéket vesz fel. Most még azt is figyelembe vehetjük, hogy a hullám halad a
komponensére, ha az a falaknál zérus értéket vesz fel. Most még azt is figyelembe vehetjük, hogy a hullám halad a  tengely mentén, vagyis:
tengely mentén, vagyis:
![\[ E_z (x,z,t) = E_o sin \left ( n\frac {\pi}{a}x\right ) e^{i(\omega t - \beta z)} \]](/images/math/a/4/4/a445e5d6d8826bc48df7f354af634f51.png) |
(13.3) |
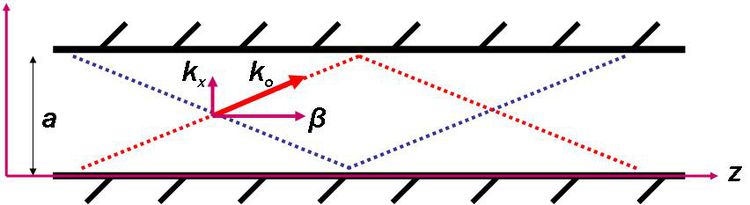
ahol  a két fémlap között haladó hullám hullámszáma. A 13.3 kifejezésben a trigonometrikus függvény argumentumában szereplő tag (amely egyébként megegyezik az 13.2 – vel) azt sugallja, hogy a vezetett módus a terjedési irányra merőlegesen olyan, mintha egy – a 13.1 ábrán látható – állóhullám lenne. Ez tehát azt jelenti, hogy az említett tag a hullámszám-vektor haladási irányra merőleges komponense:
a két fémlap között haladó hullám hullámszáma. A 13.3 kifejezésben a trigonometrikus függvény argumentumában szereplő tag (amely egyébként megegyezik az 13.2 – vel) azt sugallja, hogy a vezetett módus a terjedési irányra merőlegesen olyan, mintha egy – a 13.1 ábrán látható – állóhullám lenne. Ez tehát azt jelenti, hogy az említett tag a hullámszám-vektor haladási irányra merőleges komponense:
![\[ k_x = n\frac {\pi}{a} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/7/9/8/7986cde6418b29c402c7784e3998f5a6.png) |
(13.4) |
Ne feledkezzünk meg azonban arról, hogy két síkhullám szuperpozíciójával kaptuk a határfeltételeket is kielégítő megoldást, vagyis amennyiben 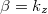 (13.3 ábra) , akkor:
(13.3 ábra) , akkor:
![\[ k_x^2 + \beta^2 = k_o^2 = \frac {\omega^2}{c^2} \]](/images/math/c/6/f/c6f7e69de988240cec5668aca5e46973.png) |
(13.5) |
ahol 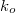 a vákuumban szabadon terjedő síkhullám hullámszáma, és
a vákuumban szabadon terjedő síkhullám hullámszáma, és  a fénysebesség.
a fénysebesség.
| 13.3 ábra |
Tehát a vezetett hullám hullámszáma:
![\[ \beta = \sqrt{\frac {\omega^2}{c^2}-k_x^2} = \frac{1}{c}\sqrt{\omega^2-\frac{c^2 n^2 \pi^2}{a^2}} \]](/images/math/8/9/d/89d422f7693923fbbd8f520249cbf05a.png) |
(13.6) |
A  hullámszám nem lehet képzetes, hiszen akkor az előjelétől függően egy exponenciálisan "elhaló" vagy egy önmagától erősödő hullámot írna le. A vezetett módus hullámszáma akkor valós, ha:
hullámszám nem lehet képzetes, hiszen akkor az előjelétől függően egy exponenciálisan "elhaló" vagy egy önmagától erősödő hullámot írna le. A vezetett módus hullámszáma akkor valós, ha:
![\[ \omega > n\frac {c\pi}{a} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/3/2/1/321bcb34a36c0f92bb37ae3df38042c3.png) |
(13.7) |
Ez azt jelenti, hogy az  -edik módusra adódó levágási frekvencia (körfrekvencia):
-edik módusra adódó levágási frekvencia (körfrekvencia):
![\[ \omega_n = n\frac {c\pi}{a} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/c/b/d/cbd591ef4240f98fba23e20a0aea0450.png) |
(13.8) |
Tehát 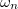 az a minimális körfrekvencia, amelyen az
az a minimális körfrekvencia, amelyen az  -edik módus létrejöhet.
-edik módus létrejöhet.
Tudjuk, hogy a hullám fázissebessége megadható a körfrekvencia és a hullámszám hányadosával, így most már könnyen megadhatjuk az  -edik módus fázissebességét:
-edik módus fázissebességét:
![\[ v_{n,f} = \frac{\omega}{\beta} = c\frac {\omega}{\sqrt{\omega^2-\frac{c^2 n^2 \pi^2}{a^2}}} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/3/0/f/30fc80cc2fe88c88c9db1ad88567ac7b.png) |
(13.9) |
A fázissebességre a vákuumbeli fénysebességnél nagyobb érték adódott, de ez nem jelenti azt, hogy információt lehetne fénysebességnél gyorsabban küldeni. Egy jel, egy elektromágneses hullámcsomag terjedésének sebességét a csoportsebességgel adhatjuk meg:
![\[ v_{n,cs} = \frac{d\omega}{d\beta} = c\frac {\sqrt{\omega^2-\frac{c^2 n^2 \pi^2}{a^2}}}{\omega} \qquad {\rm ahol} \qquad n=1,2,3... \]](/images/math/1/f/6/1f67fb859c4aab7eb5a0fed1063d6f94.png) |
(13.10) |
Ez már kisebb a fénysebességnél, vagyis az információtovábbítás sebessége nem lehet nagyobb, mint a vákuumbeli fénysebesség.
A 13.9 és a 13.10 segítségével könnyű belátni, hogy
![\[ v_{n,f} v_{n,cs} = c^2 \]](/images/math/e/7/5/e753954f0be2aa4154f41259183668bb.png) |
(13.11) |
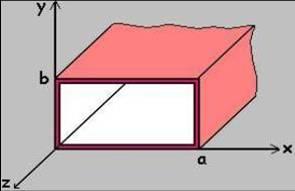
A két vezető síklap között haladó módus leírása természetesen nem életszerű, hiszen a hullámvezetők véges méretűek, azonban most már viszonylag könnyű megérteni, hogy egy négyszögletes hullámvezető esetében (13.4 ábra) is kiszámítható a levágási frekvencia és a térerősség a már tanult módon.
| 13.4 ábra |
A négyszögletes hullámvezetőben terjedő 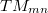 módus
módus 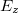 térerősségét az előzőekben látott megoldáshoz hasonló alakban adhatjuk meg:
térerősségét az előzőekben látott megoldáshoz hasonló alakban adhatjuk meg:
![\[ E_z (x,z,t) = E_o sin \left ( m\frac {\pi}{a}x\right ) sin \left ( n\frac {\pi}{b}y\right ) e^{i(\omega t - \beta z)} \qquad {\rm ahol} \qquad m,n=1,2,3... \]](/images/math/1/3/2/132344c4855036ddd990c6f84c528457.png) |
(13.12) |
A levágási frekvenciára pedig az adódik, hogy:
![\[ \omega_{mn} = \sqrt{\left(m\frac {c\pi}{a}\right )^2 + \left(n\frac {c\pi}{a}\right )^2 } \qquad {\rm ahol} \qquad m,n=1,2,3... \]](/images/math/8/2/3/823aefbf0d910231a309171137e8010e.png) |
(13.13) |
Négyszögletes hullámvezetők (egyenes és ívelt szakasz) és egy T-tag látható a következő képeken.
| 13.5.a ábra | 13.5.b ábra | 13.5.c ábra |
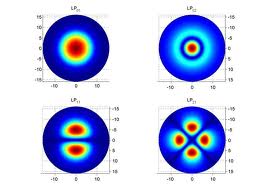
Hengerszimmetrikus geometriájú hullámvezető esetében a számítások menete a bemutatottnál jóval bonyolultabb, azonban a jelenség fizikája ugyanaz, vagyis a megoldásnak a határfeltételeket és természetesen a Maxwell-egyenleteket is ki kell elégítenie; a különböző módusok esetében a levágási frekvenciára általában különböző érték adódik. A következő ábrán látható egy hengeres hullámvezető néhány módusának módusképe. (A pirossal jelzett terület mutatja a legnagyobb térerősséget illetve intenzitást, míg a sötétkék a legkisebbet; természetesen az időfüggés nélkül.)
| 13.6 ábra |
A 11.8 és a 11.9 ábrán látható, hogy a Föld felszínéről és az ionoszféráról is visszaverődnek a középhullámú EMH-k. Valójában azt is mondhatnánk, hogy a földfelszín és az ionoszféra által kialakított hullámvezető "viszi el" a középhullámú rádióadó jelét igen nagy távolságokra.
A Lorentz-transzformáció
A mechanika tárgyalásánál láttuk, hogy egyik inercia-rendszerről a másikra a Galilei-transzformáció segítségével térhetünk át. Ezt könnyű belátni a következő – igen egyszerű – koordináta-rendszer választás esetén. Tekintsünk két  és
és 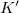 Descartes-rendszert, amelyek
Descartes-rendszert, amelyek  ,
,  és
és  tengelyei párhuzamosak. A továbbiakban a
tengelyei párhuzamosak. A továbbiakban a  rendszer tengelyeit
rendszer tengelyeit  ,
,  ,
,  – vel jelöljük, míg a
– vel jelöljük, míg a 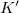 rendszer tengelyeit
rendszer tengelyeit 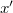 ,
, 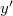 és
és 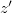 – vel. Az
– vel. Az  és
és 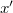 tengelyek origói az egyszerűség kedvéért essenek egybe a
tengelyek origói az egyszerűség kedvéért essenek egybe a 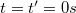 időpillanatban, valamint a
időpillanatban, valamint a 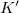 rendszer mozogjon
rendszer mozogjon 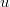 sebességgel az
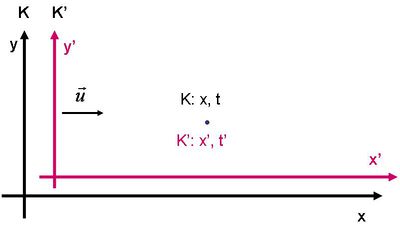
sebességgel az  tengely mentén, mint ahogyan az az alábbi ábrán látható.
tengely mentén, mint ahogyan az az alábbi ábrán látható.
| 14.1 ábra |
Egy eseményt (kék ponttal jelölve) tehát általános esetben az  és
és  hely és időkoordinátákkal adhatunk meg a
hely és időkoordinátákkal adhatunk meg a  rendszerben, míg
rendszerben, míg 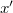 -vel és
-vel és 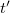 -vel a
-vel a 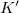 -ben. A Galilei-transzformáció szerint az áttérés egyik koordináta-rendszerről a másikra a következőképpen történhet:
-ben. A Galilei-transzformáció szerint az áttérés egyik koordináta-rendszerről a másikra a következőképpen történhet:
![\[ t = t' \qquad {\rm \acute{e}s} \qquad x=x'+ut \qquad {\rm valamint} \qquad y=y'\qquad {\rm \acute{e}s} \qquad z=z' \]](/images/math/2/5/9/25931a64eeb60341c35487960a9a190f.png) |
(14.1) |
Könnyű belátni, hogy ezen összefüggéseket alkalmazva ugyanaz adódik egy test gyorsulására mindkét koordináta-rendszerre, hiszen 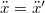 . Vagyis a mozgásegyenlet nem változik, megadva ezzel az erők transzformációs összefüggését is:
. Vagyis a mozgásegyenlet nem változik, megadva ezzel az erők transzformációs összefüggését is: 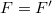 . A mechanika egyenletei tehát a Galilei-transzformációra invariánsak. Ez egyrészt azt jelenti, hogy mechanikai kísérletekkel nem tudunk különbséget tenni inercia-rendszerek között, másrészt pedig, hogy a világ leírása minden inercia-rendszerben hasonlóképpen történhet. Kérdés, hogy ez utóbbi állítás igaz-e a Maxwell-egyenletekre is. Gyakorlati tapasztalataink azt mutatják, hogy igen, azaz az elektromos és mágneses jelenségek hasonlóképpen zajlanak le egy laboratóriumban és egy gyorsan mozgó vonaton, vagy repülőgépen is. Azonban a Galilei-transzformációra a Maxwell-egyenletek nem invariánsak. Jogos elvárás például, hogy az egyik inercia-rendszerben észlelt EMH egy másik inercia-rendszerben is EMH legyen. Egyrészt ezzel ellenkező tapasztalatunk nincs, másrészt pedig ha a "fizika ugyanaz" minden inercia-rendszerben, akkor a Maxwell egyenleteknek és következményeinek – pl. az EMH-oknak és a fénysebességnek, stb. – ugyanolyan alakúnak kell lennie. H. A. Lorentz fedezte fel azt a transzformációs összefüggést, amely a Maxwell-egyenleteket egyik inerciarendszerről a másikba invariánsan viszi át. Ezt azóta is Lorentz-transzformációnak hívják. A Lorentz-transzformáció egyenletei a 14.1 ábra jelöléseit alkalmazva:
. A mechanika egyenletei tehát a Galilei-transzformációra invariánsak. Ez egyrészt azt jelenti, hogy mechanikai kísérletekkel nem tudunk különbséget tenni inercia-rendszerek között, másrészt pedig, hogy a világ leírása minden inercia-rendszerben hasonlóképpen történhet. Kérdés, hogy ez utóbbi állítás igaz-e a Maxwell-egyenletekre is. Gyakorlati tapasztalataink azt mutatják, hogy igen, azaz az elektromos és mágneses jelenségek hasonlóképpen zajlanak le egy laboratóriumban és egy gyorsan mozgó vonaton, vagy repülőgépen is. Azonban a Galilei-transzformációra a Maxwell-egyenletek nem invariánsak. Jogos elvárás például, hogy az egyik inercia-rendszerben észlelt EMH egy másik inercia-rendszerben is EMH legyen. Egyrészt ezzel ellenkező tapasztalatunk nincs, másrészt pedig ha a "fizika ugyanaz" minden inercia-rendszerben, akkor a Maxwell egyenleteknek és következményeinek – pl. az EMH-oknak és a fénysebességnek, stb. – ugyanolyan alakúnak kell lennie. H. A. Lorentz fedezte fel azt a transzformációs összefüggést, amely a Maxwell-egyenleteket egyik inerciarendszerről a másikba invariánsan viszi át. Ezt azóta is Lorentz-transzformációnak hívják. A Lorentz-transzformáció egyenletei a 14.1 ábra jelöléseit alkalmazva:
![\[ I.\quad x = \kappa (x'+ut') \qquad {\rm \acute{e}s} \qquad II.\quad t=\kappa \left( t'+ \frac{u}{c^2}x' \right) \]](/images/math/0/0/a/00aad4a53746e9f50c88792a91451df7.png) |
(14.2) |
![\[ III.\quad x' = \kappa (x-ut) \qquad {\rm \acute{e}s} \qquad IV.\quad t'=\kappa \left( t+ \frac{u}{c^2}x \right) \]](/images/math/d/4/1/d41001824d6c09452a9c871ef62de035.png) |
(14.3) |
![\[ y=y'\qquad {\rm \acute{e}s} \qquad z=z' \]](/images/math/6/9/7/69719c5254f841fb89d49db19f0d0fc5.png) |
(14.4) |
ahol  a fénysebesség értéke és
a fénysebesség értéke és
![\[ \kappa = \frac {1}{\sqrt{1-\frac{u^2}{c^2}}} \]](/images/math/c/1/f/c1f00448a2ea5a90a7279329223a5c2d.png) |
(14.5) |
Viszonylag egyszerűen bizonyítható általános esetben is, hogy a Maxwell-egyenletek invariánsak a fenti transzformációra, azonban mi most a fejezet elején bemutatott egyszerű modellt vizsgáljuk. Tekintsünk egy, az  tengely mentén terjedő EMH-t (14.2 ábra; ez hasonló az 14.1 ábrához, azonban a tengelyeket felcseréltük).
tengely mentén terjedő EMH-t (14.2 ábra; ez hasonló az 14.1 ábrához, azonban a tengelyeket felcseréltük).
| 14.2 ábra |
Az elektromos térnek most csak  , míg az indukciós térnek csak
, míg az indukciós térnek csak  komponense van. Az 1.9 egyenletet át kell alakítani a tengelyek cseréje miatt, így kapjuk a következő összefüggést.
komponense van. Az 1.9 egyenletet át kell alakítani a tengelyek cseréje miatt, így kapjuk a következő összefüggést.
![\[ \frac {\partial E_z}{\partial x} = \frac{\partial B_y}{\partial t} \]](/images/math/0/a/b/0abf7665759eefec8073465158702319.png) |
(14.6) |
Mindez természetesen a 14.2 ábra jelölései alapján a  rendszerbeli leírást adja. Most használjuk fel a Lorentz-transzformációt arra, hogy áttérjünk a
rendszerbeli leírást adja. Most használjuk fel a Lorentz-transzformációt arra, hogy áttérjünk a 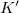 koordináta-rendszerre. Most ez azt jelenti, hogy nem
koordináta-rendszerre. Most ez azt jelenti, hogy nem  és
és  , hanem
, hanem 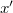 és
és 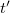 szerinti deriváltaknak kell megjelenni. Ez a következőképpen valósítható meg:
szerinti deriváltaknak kell megjelenni. Ez a következőképpen valósítható meg:
![\[ \frac {\partial E_z}{\partial x'} \frac {\partial x'}{\partial x} + \frac {\partial E_z}{\partial t'} \frac {\partial t'}{\partial x} = \frac{\partial B_y}{\partial x'} \frac {\partial x'}{\partial t} + \frac{\partial B_y}{\partial t'} \frac {\partial t'}{\partial t} \]](/images/math/b/b/9/bb90494b4f4f3d4381595a188f27cda3.png) |
(14.7) |
A 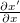 , a
, a 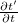 , stb. együtthatókat a 14.3 segítségével számíthatjuk ki, valamint a
, stb. együtthatókat a 14.3 segítségével számíthatjuk ki, valamint a 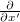 és
és 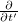 tagokat különválasztjuk:
tagokat különválasztjuk:
![\[ \frac {\partial }{\partial x'}\left[\kappa E_z + \kappa uB_y \right]= \frac {\partial }{\partial t'}\left[\kappa B_y + \kappa \frac{u}{c^2}E_z \right]\]](/images/math/2/3/1/23134ddca709d4a1793f326198bfe5be.png) |
(14.8) |
Könnyű észrevenni, hogy formailag ez éppen megegyezik a 14.6-al, de most 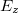 helyett
helyett
![\[ E'_{z'}= \kappa \left[E_z + uB_y\right]=\frac{E_z + uB_y}{\sqrt{1-\frac{u^2}{c^2}}} \]](/images/math/f/9/7/f978a49c5ca46a2dfb2198662e2235a3.png) |
(14.9) |
és 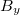 helyett
helyett
![\[ B'_{y'}= \kappa \left[B_y + \frac{u}{c^2}E_z\right]=\frac{B_y + \frac{u}{c^2}E_z}{\sqrt{1-\frac{u^2}{c^2}}} \]](/images/math/a/6/b/a6b8e5468d57849f6b0a94f606e34a47.png) |
(14.10) |
szerepel, ahol most már 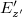 és
és 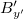 az elektromos és az indukciós térerősséget jelenti a
az elektromos és az indukciós térerősséget jelenti a 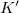 rendszerben. Foglaljuk össze az eredményeket: a
rendszerben. Foglaljuk össze az eredményeket: a  rendszerben felírt 14.6 egyenlet a 14.3 transzformációval egy
rendszerben felírt 14.6 egyenlet a 14.3 transzformációval egy 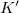 rendszerbeli egyenletbe megy át, vagyis
rendszerbeli egyenletbe megy át, vagyis
![\[ \frac {\partial E'_{z'}}{\partial x'} = \frac{\partial B'_{y'}}{\partial t'} \]](/images/math/5/8/7/58771ed15f93822067ef3b24d7ac87ea.png) |
(14.11) |
Ezennel beláttuk (igaz, hogy csak egy speciális esetre, de általánosan is így kell csinálni), hogy a Lorentz-transzformációra a Maxwell-egyenletek invariánsak.
Maga H. A. Lorentz az általa konstruált transzformáció mélyebb összefüggéseit és jelentőségét nem ismerte fel. Ezt valamivel később Albert Einstein tette meg; 1905-ben publikálta a speciális relativitás elméletének alapjait.
Doppler effektus
A hangtani Doppler effektus jelensége szinte mindennapi tapasztalataink közé tartozik. Csaknem mindenki észlelte már a szirénázó mentőautó hangjának hirtelen megváltozását, amint az autó éppen elhaladt mellette. Frekvencia-eltolódás vagy Doppler effektus az EMH-ok esetében is kimutatható, sőt számos berendezés működésének ez a fizikai effektus képezi az alapját. A jelenség bemutatásához felhasználjuk az előző fejezetben tanultakat.
Az előző fejezet jelöléseit megtartva tekintsünk egy, a  inerciarendszer
inerciarendszer  tengelye mentén haladó elektromágneses síkhullámot!
tengelye mentén haladó elektromágneses síkhullámot!
![\[ E_{z}\left ( x,t \right )=E_{o}cos\left ( \omega t-kx \right )=Acos\left ( 2\pi ft-\frac{2\pi }{\lambda }x \right ) \]](/images/math/c/1/5/c15d4b69f0593d0f83e81eb2c136e72c.png) |
(15.1) |
Ennek az EMH-nak az indukciós tere 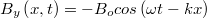 , vagyis a mágneses tér hely és időfüggése hasonló az elektromos térhez, mint ahogyan azt a fejezet elején már láttuk. Ez a tény, valamint a 14.9 és 14.10 következményei, azaz hogy a
, vagyis a mágneses tér hely és időfüggése hasonló az elektromos térhez, mint ahogyan azt a fejezet elején már láttuk. Ez a tény, valamint a 14.9 és 14.10 következményei, azaz hogy a 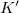 rendszerre történő áttérés esetén az
rendszerre történő áttérés esetén az 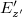 és a
és a 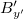 lineáris kombinációi az
lineáris kombinációi az 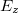 - nek és a
- nek és a 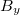 - nek, azt mutatja, hogy elegendő a trigonometrikus tag argumentumát vizsgálni. Ennek ellenére a szemléletesebb tárgyalás miatt kiírjuk a hullámfüggvényt, de az amplitúdó értékével a továbbiakban már nem foglalkozunk. Az EMH leírását a
- nek, azt mutatja, hogy elegendő a trigonometrikus tag argumentumát vizsgálni. Ennek ellenére a szemléletesebb tárgyalás miatt kiírjuk a hullámfüggvényt, de az amplitúdó értékével a továbbiakban már nem foglalkozunk. Az EMH leírását a 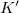 rendszerben a Lorentz-transzformáció alkalmazásával kaphatjuk, vagyis a 15.1-ben szereplő
rendszerben a Lorentz-transzformáció alkalmazásával kaphatjuk, vagyis a 15.1-ben szereplő  – t és
– t és  –t a 14.2 alkalmazásával kifejezzük
–t a 14.2 alkalmazásával kifejezzük 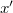 – vel és
– vel és 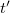 – vel, és visszahelyettesítjük.
– vel, és visszahelyettesítjük.
![\[ E'_{z'}\left ( x',t' \right )=A'cos\left [ 2\pi f\kappa \left ( t'+\frac{u}{c^2}x' \right ) - \frac{2\pi }{\lambda }\kappa \left ( x'+ut' \right )\right ] \]](/images/math/8/7/e/87ef8d8f0af4822c6a9b548a4440d2e0.png) |
(15.2) |
Az előbbi egyenletet átrendezzük és behelyettesítjük 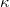 - t, hogy az átalakítás következményei könnyebben értelmezhetők legyenek:
- t, hogy az átalakítás következményei könnyebben értelmezhetők legyenek:
![\[ E'_{z'}\left ( x',t' \right )={A}'cos\left [ 2\pi f\frac{1-\frac{u}{c}}{\sqrt{1-\frac{u^2}{c^2}}} t'- \frac{2\pi }{\lambda }\frac{1-\frac{u}{c}}{\sqrt{1-\frac{u^2}{c^2}}}x'\right ] \]](/images/math/f/7/9/f79d8ef9518515fe6df41f53d24b5737.png) |
(15.3) |
, vagyis
![\[ E'_{z'}\left ( x',t' \right )= A'cos\left[ 2\pi f\sqrt{\frac{1-\frac{u}{c}}{1+\frac{u}{c}}} t'- 2\pi \frac{1 }{\lambda }\sqrt{\frac{1-\frac{u}{c}}{1+\frac{u}{c}}}x'\right ] \]](/images/math/5/4/f/54fdba8f46784c026efa9c41a7100dc6.png) |
(15.4) |
Most már csak le kell olvasni az eredményt. Annak az EMH-nak, amelynek  inercia-rendszerben eredetileg
inercia-rendszerben eredetileg  a frekvenciája és
a frekvenciája és  a hullámhossza, a hozzá képest
a hullámhossza, a hozzá képest 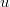 sebességgel mozgó
sebességgel mozgó 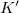 rendszerben a frekvenciája:
rendszerben a frekvenciája:
![\[ f' = f\sqrt{\frac{1-\frac{u}{c}}{1+\frac{u}{c}}} \]](/images/math/d/3/4/d343f8b3dc9aece1f9a601d2f010c575.png) |
(15.5) |
és a hullámhossza:
![\[ \lambda' = \lambda\sqrt{\frac{1+\frac{u}{c}}{1-\frac{u}{c}}} \]](/images/math/c/2/f/c2f7a2b78f3fa0f0b29f968a79e2513a.png) |
(15.6) |
alakban írható. Amennyiben a 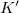 koordináta-rendszer vagy az EMH terjedési iránya az ellenkezőjére változna, akkor természetesen a 15.5-ben és a 15.6-ban az előjelek felcserélődnének. Fontos itt megjegyezni, hogy a Doppler-féle frekvencia-változás mindössze a két inercia-rendszer egymáshoz viszonyított relatív sebességétől függ. (Nincs külön formula annak megfelelően, hogy a forrás mozog, vagy a megfigyelő, mint a hangtani Doppler-effektus esetében.) A 15.5 és 15.6 formulák alapján levonható az a fontos következtetés, miszerint a frekvencia- és hullámhossz-megváltozás egyértékű függvénye az
koordináta-rendszer vagy az EMH terjedési iránya az ellenkezőjére változna, akkor természetesen a 15.5-ben és a 15.6-ban az előjelek felcserélődnének. Fontos itt megjegyezni, hogy a Doppler-féle frekvencia-változás mindössze a két inercia-rendszer egymáshoz viszonyított relatív sebességétől függ. (Nincs külön formula annak megfelelően, hogy a forrás mozog, vagy a megfigyelő, mint a hangtani Doppler-effektus esetében.) A 15.5 és 15.6 formulák alapján levonható az a fontos következtetés, miszerint a frekvencia- és hullámhossz-megváltozás egyértékű függvénye az 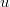 sebességnek.
A Doppler-féle frekvencia-eltolódás jól használható mozgó objektumok sebességének mérésére. Csaknem mindenki hallott már a lézeres traffipax-ról (esetleg kellemetlen élményei is lehettek azzal kapcsolatban); ennek a berendezések a működése is a Doppler-effektuson alapul.
sebességnek.
A Doppler-féle frekvencia-eltolódás jól használható mozgó objektumok sebességének mérésére. Csaknem mindenki hallott már a lézeres traffipax-ról (esetleg kellemetlen élményei is lehettek azzal kapcsolatban); ennek a berendezések a működése is a Doppler-effektuson alapul.
| 15.1 ábra |
Érdekes példát mutat a lézeres doppler-sebességmérésre a következő ábra. A sportoló körül áramló levegőnek nem csak az áramlási képét lehet egy szélcsatornában felvenni, hanem a "légáramok" sebességének mérési eredményeit felhasználva a sporteszközgyárak kisebb légellenállású sisakot, cipőt, motoros bakancsot, stb. is tudnak tervezni.
| 15.2 ábra |
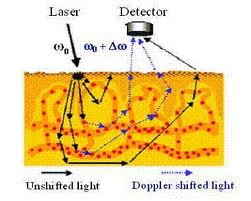
Az előbb említett mérési technika segítségével tanulmányozni lehet a bőrfelszín közelében húzódó erekben a vér áramlási sebességét is (15.3 ábra). Az érzékelő a lézerétől különböző frekvenciájú (ill. hullámhosszú) visszavert fénysugarakat detektálja, és ebből számítható a véráram sebessége. Újabban egyszerű detektor helyett különböző szűrőkkel ellátott kamerát használnak, így a számítógépes képfeldolgozás segítségével egy nagyobb területről is átfogó, szemléletesebb, informatívabb képet ("hamis" áramlási képet; amikor is a különböző sebességértékekhez különböző színeket rendelnek) készíthetnek.
| 15.3 ábra |
A Doppler-féle sebesség-meghatározás a csillagászat egyik legfontosabb mérési módszere. A távoli galaxisok fényének elemzésénél megfigyelték a különböző elemek, mint pl. a hidrogén spektrumvonalainak vöröseltolódását (15.4 ábra).
| 15.4 ábra |
Edwin Hubble a távoli galaxisok vöröseltolódását az univerzum tágulásával magyarázta. A mérések alapján levonta a következtetést: minél távolabb van tőlünk egy másik galaxis, annál nagyobb sebességgel távolodik tőlünk, valamint a távolság és a sebesség között lineáris kapcsolat áll fenn.
![\[ v = Hr \]](/images/math/f/d/c/fdc5ed4022dc68b1d2fc38bbd85d96fb.png) |
(15.7) |
Ez a híres Hubble-törvény;  az ún. Hubble állandó, értéke:
az ún. Hubble állandó, értéke: 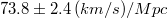 , ahol is
, ahol is 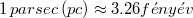 .
.
A mérési módszerek a XX. század második felében sokat javultak; ezek segítségével meghatározták néhány spirálgalaxis karjaiban a csillagok keringési sebességét, amelyek az elvártnál jóval nagyobbnak adódtak. Más jelenségekkel összhangban ez is okot adott az univerzum tömegének jelentős részét kitevő, de nem látható sötét anyag feltételezésére.
Bizonyos típusú szupernóvák (az ún. standard gyertyák) sebességének meghatározásából az szűrhető le, hogy az univerzum tágulása nem lassul. Ennek magyarázatára feltételezik az univerzum tágulását lassító tömegvonzást kompenzáló antigravitációs hatást, amelyért az egész univerzumot kitöltő sötét energia felelős.
Mobiltelefónia
A mobiltelefonok elterjedésének kezdeti időszakában még alkalmazták a már említett frekvencia-modulációs technikát, mára azonban a csomagkapcsolt adatátviteli technológia, a GPRS használatos. Ezen adatátviteli technika lényege, hogy az adatokat kisebb csomagokra, szimbólumokra bontva küldik el a szerverekből, átjátszókból, helyi reléállomásokból, stb álló igen összetett hálózaton. Ennek több előnye is van; egyrészt optimalizálni lehet az átvitelt az egyszerre működő csatornákon, ezzel jobb adatátviteli sebességet lehet elérni, másrészt nem az időtartamért, hanem az adatforgalomért kell csak fizetni, harmadrészt pedig az "okostelefon"-ok használhatják az internetet és a GPS-t is. Az antennákról szóló fejezetben említettük, hogy a félhullámú és a negyedhullámú antenna hossza a hullámhosszal arányos. Ahogyan a mobiltelefon technológiák fejlődését jellemzi az egyre nagyobb frekvenciák alkalmazása, ennek megfelelően a telefonok is egyre kisebbek lettek (16.1.a és b ábra). Ez főként az elektronika fejlődősének köszönhető, másrészt pedig az utóbbi időben inkább patch-antennát használnak dipól-antenna helyett.
| 16.1.a ábra | 16.1.b ábra |