Aktivációs analitikai gyakorlat
Tartalomjegyzék[elrejtés] |
Bevezetés
Az aktivációs analízis igen nagy érzékenységű, általában gyorsan elvégezhető analitikai módszer, minták elemi összetételének meghatározására. Az esetek jelentős részében roncsolás mentesen alkalmazható, azaz nem szükséges a minta előzetes kémiai feltárása. Több mint 60 féle elem esetében a kimutatási határ akár 0.05 μg alá szorítható, de mérési és besugárzási körülményektől függően bizonyos elemek esetén akár 10−6 μg is kimutatható.
A módszernek rengeteg alkalmazása van (geológiai, régészeti, környezetvédelmi, biológiai, kriminológiai, anyagtechnológiai, stb.). Például egy lőfegyvert elsütő kézen (puska használat) a lerakódott lőporból származó Ba és Sb mennyisége ezerszerese a rájuk vonatkozó kimutatási határnak.
A mérés célja az aktivációs analízis alapfogalmainak megismerése, és a módszer alapeljárásainak gyakorlása. A gyakorlat támaszkodik a gamma spektroszkópia gyakorlat során megszerzett ismeretekre, hiszen annak alkalmazásáról van szó.
Elméleti összefoglalás
Az aktivációs analízis lényege, hogy az elemzésre szánt mintát neutron, gamma, esetleg más, töltött részecske sugárzásnak tesszük ki. A sugárzás és a minta stabil atommagjai között lejátszódó kölcsönhatás(ok) eredményeképpen a mintában levő izotópok egy részéből radioaktív izotópok keletkeznek (aktiválás). A magreakciókat közvetlenül követheti, illetve a keletkezett radioaktív izotópok bomlását is kísérheti gamma fotonok kibocsátása, melyek a kibocsátó atommag megfelelő gerjesztési nívói közötti energia különbséget viszik magukkal, így a kibocsátó atommagra szinte egyedileg jellemzőek. Gamma-spektroszkópiai eszközökkel, azaz a gamma sugárzás energia szelektív méréséből származó gamma-spektrum feldolgozásával végzett radioaktív izotóp azonosítás alapján következtethetünk a minta eredeti elemösszetételére (kvalitatív analízis), valamint a megfelelő energiákon (a teljesenergia-csúcsoknál) mért gamma intenzitások alapján a már azonosított elemek mennyiségére (kvantitatív analízis). Az aktivációs analízis egyik leggyakrabban alkalmazott ága a Hevesy György által kidolgozott Neutron Aktivációs Analízis (NAA), melynek során a mintát neutronok hatására bekövetkező magreakciókkal aktiváljuk.
Az analízis céljára felhasználhatjuk a küszöb energia nélküli neutron befogást ( ,
,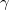 reakció), amikor is a töltéssel nem rendelkező neutronok elnyelődnek a target atommagokban, melynek következtében - a felszabaduló kötési energia miatt- a magok erősen gerjesztett állapotba jutnak. Ebben az esetben az analízis alapját képező gamma-spektroszkópiát alkalmazhatjuk a neutron befogáskor kilépő gamma fotonokra (neutronbefogásos prompt gamma aktivációs analitika), amely olyan speciális kísérleti berendezést igényel, ahol a besugárzás és a mérés egyidejűleg történhet, vagy a forrás impulzusszerűen üzemel (neutron-generátor), hiszen a gamma fotonok kilépése a neutron befogást azonnal követi (eltekintve az izomerektől).
reakció), amikor is a töltéssel nem rendelkező neutronok elnyelődnek a target atommagokban, melynek következtében - a felszabaduló kötési energia miatt- a magok erősen gerjesztett állapotba jutnak. Ebben az esetben az analízis alapját képező gamma-spektroszkópiát alkalmazhatjuk a neutron befogáskor kilépő gamma fotonokra (neutronbefogásos prompt gamma aktivációs analitika), amely olyan speciális kísérleti berendezést igényel, ahol a besugárzás és a mérés egyidejűleg történhet, vagy a forrás impulzusszerűen üzemel (neutron-generátor), hiszen a gamma fotonok kilépése a neutron befogást azonnal követi (eltekintve az izomerektől).
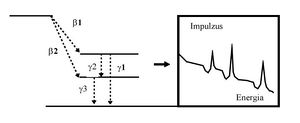
A másik lehetőség, hogy kihasználjuk a keletkezett leánymag béta instabilitását, ugyanis a neutron befogást követően az adott rendszámhoz tartozó stabilitást biztosító neutron-proton arány felborításával béta-bomló izotópokhoz juthatunk. Ha a béta bomlás a leánymag valamely gerjesztett nívójára történik, a nívó és az alapállapot közti energiának megfelelő gamma foton(ok) vonalas spektruma alapján elvégezhetünk elem azonosítást (késleltetett módszer). A gyakorlatban legtöbbször ezt a módszert alkalmazzák, ahogy a mostani laborgyakorlatnak is ez lesz a tárgya. A besugárzást többnyire nagy teljesítményű sugárforrással (reaktor zónája, ciklotron) végzik, de bizonyos elemekre akár a kisebb neutronfluxust biztosító zárt radioaktív neutronforrásos besugárzás is megfelelő lehet. A béta bomlás okozta késleltetés miatt a mérés megfelelően felszerelt laboratóriumban, szükség esetén alacsony hátterű kamrában, optimális körülmények között végezhető.
Felhasználhatók analízis céljára továbbá a neutron és atommag különböző küszöbenergiás reakciói (n, p), (n, 2n), rugalmatlan szórás, stb. Az előbbieknél a reakció béta instabilitást idézhet elő, melyet gamma fotonok kibocsátása követ, az utóbbinál az atommag az energiaközlés hatására gerjesztett állapotba kerül ahonnan gamma foton(ok) kibocsátásával térhet vissza alapállapotba. Az itt említett reakciók hatáskeresztmetszetei általában jóval kisebbek mint a termikus neutronokra vonatkozó befogásé. Ez a kimutathatóságot nagymértékben rontja.
Reaktorokban termikus és gyors neutronok jelenlétében például alumíniumban az alábbi fontosabb magreakciók játszódhatnak le különböző valószínűségekkel:
| Termikus neutronokra | 27Al(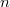 , ,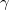 ) 28Al ) 28Al
|
| Gyors neutronokra | 27Al(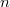 , ,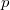 ) 27Mg ) 27Mg
|
27Al(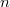 , ,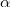 ) 24Na ) 24Na
| |
27Al(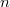 , ,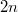 ) 26Al ) 26Al
| |
27Al(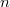 , ,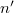 ) 27Al ) 27Al
|
A valószínűségek a neutron energiától (a reaktorbeli neutron spektrumnak megfelelően, lásd (Neutron fluxus mérés) és ezzel összefüggésben a megfelelő hatáskeresztmetszettől függenek. Hatáskeresztmetszet szempontjából általában a termikus neutronok abszorpciója a legkedvezőbb reakció típus (legtöbb elem esetében az abszorpciós hatáskeresztmetszet kisebb energiákon a neutronok sebességével fordított arányban növekedő tendenciát mutat). Összetett mintákban különböző elemek különböző magreakciói vezethetnek ugyanarra az eredményre (zavaró reakciók), ilyen esetben csak a végtermék alapján az izotópok elkülönítése nem lehetséges.
27Al(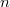 , ,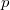 ) 27Mg ) 27Mg |
illetve | 26Mg(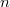 , ,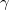 ) 27Mg ) 27Mg
|
28Si(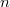 , ,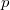 ) 28Al ) 28Al |
illetve | 27Al(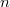 , ,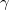 ) 28Al ) 28Al
|
Ilyenkor több minta különböző spektrumú besugárzásával (árnyékolás) a hatáskeresztmetszetek energiafüggésére alapozva lehet a komponenseket szétválasztani. Ha több elem együttes meghatározását végezzük, a gamma-spektrumon a teljesenergia-csúcsokhoz csatlakozó Compton-tartományok révén romolhat az elemek kimutathatósága, mivel a Compton-kontinuum mint háttér jelentkezik a kisebb energiájú teljesenergia-csúcsok számára. Ilyenkor a szeparációra kihasználhatjuk az eltérő felezési időket, vagy végső eszközként kémiai elválasztást alkalmazhatunk.
A mérés elve
Ahogy az elméleti összefoglalásban említettük, jelen gyakorlat keretében a reaktor zónájában végzett besugárzással aktivált minták minőségi és mennyiségi analízisét fogjuk elvégezni. Elsőként tekintsük át az aktiválás folyamatát.
A besugárzott minta aktivitása
A besugárzott mintában az aktív magok keletkezési sebessége egy adott reakció típusra az alábbi egyenlettel adható meg:
![\[ \frac{dN^*}{dt} = \Phi N \sigma - \lambda N^* \quad (reakci\acute{o} \ sebess\acute{e}g - boml\acute{a}si \ sebess\acute{e}g) \]](/images/math/4/2/0/42025a23579ab41db70a88bb507e8647.png) |
(1) |
ahol
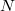 |
a target magok száma |
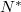 |
az adott reakcióval aktiválódott magok száma |
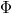 |
a neutron fluxus ekvivalens értéke a hatás keresztmetszet szempontjából fontos energia tartományra. |
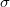 |
a reakcióra vonatkozó mikroszkopikus hatáskeresztmetszet (nem monoenergetikus neutronok esetén ekvivalens érték) |
Az aktivitás időben lineárisan növekedne a besugárzó neutron fluxus hatására, de az aktív magok számának növekedésével erősödő bomlás telítésbe viszi a növekedést. A besugárzás idejére ebből a minta aktivitásának időfüggése:
![\[ A(t) = A_\infty(1-exp(-\lambda t)) \]](/images/math/c/5/a/c5a8b9ea14f41d103adcd2f909992f0f.png) |
(2) |
ahol
![\[ A_\infty = \Phi N \sigma \]](/images/math/4/c/0/4c0ecde176b00470ab8a290b7a67e571.png) |
(3) |
A telítésbe futó exponenciális függvény felfutását a keletkező radioaktív izotóp felezési ideje határozza meg. Rövid felezési idejű izotóp gyorsabban aktiválható. A méréskor adott elem mintabeli aktivitását leíró összefüggés, melyben az aktivitás időbeli változását leíró függvény már kiegészül az aktiválás befejezését követő bomlást leíró taggal:
![\[ A (\tau) = \Phi \sigma \frac{mfN_A}{A_{rel}}(1-exp(-\lambda T))exp(-\lambda \tau) \]](/images/math/3/d/8/3d89a2a965b0c2a5eb6dcfaa23b96a65.png) |
(4) |
ahol
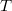 |
a teljes besugárzási idő |
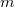 |
a besugárzott elem mennyisége |
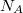 |
Avogadro szám |
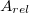 |
a besugárzott elem atomsúlya |
 |
hűtési idő |
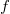 |
a kiindulási izotóp aránya a meghatározni kívánt elemre |
A gyakorlat keretében végrehajtható besugárzás behatárolja a lehetőségeket. A rövid besugárzási idő, és a kis vagy közepes teljesítmény miatt azon izotópokat lehet kimutatni, melyből keletkező leánymag felezési ideje elég rövid a gyors felaktiváláshoz, de nem annyira rövid, hogy néhány perces hűtési időt és mérési időt ne engedhetnénk meg. Magreakcióként szinte csak a termikus neutron befogás jöhet szóba, ott is elsősorban a nagy befogási hatáskeresztmetszettel rendelkező természetes elemek. Ezek szerint a fenti összefüggésekben a fluxus a termikus fluxus ekvivalens értéke, míg a hatáskeresztmetszet a neutron befogási hatáskeresztmetszet spektrumra átlagolt értéke. A felírt összefüggésekben elhanyagoltuk a minta önárnyékolását, melyet egy önárnyékolási tényezővel szoktak figyelembe venni.
Mennyiségi analízis
Mennyiségi analízis során adott izotóp mennyiségének meghatározása a minta aktivitásának mérésével történhet (abszolút módszer). Az aktivitás meghatározása a gamma-spektrum megfelelő teljesenergia-csúcsának nettó területe alapján történik.
![\[ \frac{I_{N}}{t_{m}}=Af_\gamma \varepsilon_\gamma \]](/images/math/6/6/5/6659f55a0c1021e3e9f2ac4dba5e1ac8.png) |
(5) |
ahol
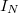 |
nettó teljesenergia-csúcsterület |
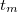 |
mérési idő |
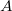 |
a minta aktivitása |
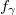 |
az adott energiájú gamma foton egy bomlásra eső gyakorisága |
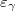 |
detektor hatásfok a mért gamma energián |
Ha a mérési idő összevethető a felezési idővel akkor a minta aktivitása nem tekinthető a mérés alatt állandónak. Ekkor:
![\[ I_{N}=\int\limits_{t_{0}}^{{t_{0}}+t} A_{0}f_\gamma \varepsilon_\gamma(exp(-\lambda t))dt \]](/images/math/e/f/8/ef8c7765f60dc74b2a486f44bc0533cb.png) |
(6) |
Az integrálás elvégzése után:
![\[ I_{N}=\varepsilon_{\gamma}f_{\gamma}A_{0} (1-exp (-\lambda{t}_{m}))/\lambda \]](/images/math/d/8/d/d8d98224a10917c6def7ec1cc4cdf1bc.png) |
(7) |
Az impulzus számlálási sebességből számított minta aktivitás alapján a kérdéses elem mennyisége becsülhető. A lehetséges hibaforrások (elsősorban a besugárzás körülményeinek bizonytalansága) és mérési bizonytalanságok egy része csökkenthető az u.n. relatív módszer alkalmazásával. Ennek lényege, hogy a meghatározni kívánt elemet ismert mennyiségben tartalmazó standardo(ka)t készítünk, melye(ke)t az elemzendő mintával teljesen azonos körülmények között besugárzunk. Ilyenkor az aktivitás meghatározása nélkül a megfelelő teljesenergia-csúcsok nettó impulzusszámainak segítségével fejezhető ki a meghatározni kívánt izotóp mennyiség.
![\[ m=\frac{m_{standard} N}{N_{standard}} \]](/images/math/c/c/5/cc5f0171cd9fe829756a1a24ac9ac58b.png) |
(8) |
A nettó impulzusszámokat természetesen korrigálni kell azonos mérési időre és azonos hűtési időre. Több standard alkalmazásával tömeg-impulzusszámlálási sebesség kalibrációs egyenes készíthető, mellyel a tömeg meghatározás pontossága javítható.
A mérés megtervezése
A mérés megkezdése előtt meg kell tervezni a besugárzás körülményeit és becsülni kell a mérendő minta tömeget, szem előtt tartva, hogy törekedni kell a lehetséges minimális aktivitás elérésére, hiszen a nagy aktivitású minta veszélyes, mellyel bizonyos szint felett már nem is dolgozhatunk. A megfelelő aktivitás elérése a mérés optimalizálás szempontjából is fontos (holtidő). Meg kell határozni a reaktor teljesítményt (ezzel összefüggésben a neutron fluxust), a besugárzás idejét, a hűtési időt, mérési geometriát (hatásfok), mérési időket, esetleg a komponensek elválasztásának módját.
A mérőlánc hatásfokának ismeretében adott izotópra - legyen példaként ez az arany - tervezzük meg a mérést, azaz próbáljuk megbecsülni mekkora tömegű minta szükséges adott impulzusszámlálási sebesség eléréséhez az adott mérési és besugárzási paraméterek mellett.
A természetes arany 100%-ban 197Au izotópból áll. Befogási hatáskeresztmetszete termikus neutronokra kb. 98.8 × 10−28 m2. Az (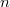 ,
,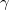 ) reakcióval keletkező béta-bomló 198Au felezési ideje t1/2 = 64.7 óra.
) reakcióval keletkező béta-bomló 198Au felezési ideje t1/2 = 64.7 óra.
| 99.0% | 0.412 MeV | |||
| A bomlást | 1.0% | gyakorisággal | 0.688 MeV | energiájú gamma-fotonok kisugárzása kíséri. |
| 0.2% | 1.090 MeV |
Természetesen a mennyiségi analízist a 0.412 MeV-es csúcsra kell alapozni. A detektor egyesített hatásfokát, melyet a mérési geometria (minta - detektor távolság), illetve a detektor típus együttesen határoz meg, vehetjük 0.2%-nak. Legyen az elérni kívánt számlálási sebesség 100 impulzus/sec. Ehhez az arany aktivitása:
![\[ A={\frac{10^{2}}{0.99\times0.002}}={5.05\times10^{4}}Bq \]](/images/math/3/e/1/3e1bb60ea769adca0e767443b8fb3a2a.png) |
(9) |
A reaktor termikus fluxusa 10 kW-on a G5-ös besugárzási pozícióban:
![\[ \Phi_{th}=2.4\times10^{15}m^{-2}s^{-1} \]](/images/math/0/9/f/09fea1fc6fde1c76880000eb46cb497d.png) |
(10) |
Ha a besugárzási időt 10 s-nak választjuk és a mérést a besugárzás után 45 perccel kezdjük el, akkor a minta besugárzás után közvetlenül mérhető aktivitása:
![\[ A_{0}=5.05\times10^{4}\times2^{0.75/64.7}=5.11\times10^{4}Bq \]](/images/math/5/a/4/5a45fa32b5f16745127a1ee5518d7fb6.png) |
(11) |
A minta szükséges tömege:
![\[ m=\frac{A_{0}\rho} {\displaystyle\sum_{akt}^{}\Phi_{th}(1-\exp (-\lambda{t}_{akt}))} \]](/images/math/e/e/8/ee85f842d31d70e608acd2b91889ac06.png) |
(12) |
Itt 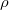 a sűrűséget,
a sűrűséget, 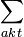 a 197Au termikus neutronokra vonatkozó makroszkópikus hatáskeresztmetszetét,
a 197Au termikus neutronokra vonatkozó makroszkópikus hatáskeresztmetszetét, 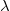 a 198Au bomlási állandóját,
a 198Au bomlási állandóját, 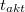 az aktiválás időtartamát jelenti.
az aktiválás időtartamát jelenti.
Mivel 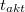 «
« 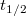 , a formula egyszerűsíthető:
, a formula egyszerűsíthető:
![\[ m=\frac{A_{0}\rho} {\displaystyle\sum_{akt}^{} \Phi_{akt} \lambda{t}_{akt}} \]](/images/math/5/0/0/5004abb953441bef936bc2d911c1a95a.png) |
(13) |
A 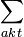 makroszkópikus hatáskeresztmetszetet írjuk fel a a mikroszkópikus hatáskeresztmetszet segítségével:
makroszkópikus hatáskeresztmetszetet írjuk fel a a mikroszkópikus hatáskeresztmetszet segítségével:
![\[ \sum_{akt}^{}=\sigma_{akt}N_{T}=\sigma_{akt}\frac{\rho{N_{a}}}{A_{au}} \]](/images/math/4/5/0/4509daf086d8c230cbbbb496a09af9b4.png) |
(14) |
Tehát:
![\[ m = \frac{A_{0}A_{Au}}{N_{A}\sigma_{akt}\Phi_{th}\lambda{t_{akt}}} = \frac{5.11\times10^{4}\times197}{6.023\times10^{23}\times98.8\times10^{-28}\times2.4\times10^{15}\times2.98\times10^{-6}\times10} = 2.28\times10^{-5}kg = 22.8mg \]](/images/math/f/7/2/f72955de5caabb9d2bfe115694da7234.png) |
(15) |
Mivel a besugárzási idő a mérési idő töredéke az exponenciális egyenessel helyettesíthető (sorfejtés 0 körül). Így például tized ekkora minta esetében 10-szer akkora besugárzási idővel, vagy 10-szer akkora fluxussal érhetnénk el hasonló mérési körülményeket.
Mérési feladat
- Kalibrálás
- A mérőlánc beállítása és energia kalibrálása.
- Minőségi analízis
- Egykomponensű ismeretlen (elemi) minta azonosítása az előzőleg hitelesített mérőlánc segítségével.
- Minőségi és mennyiségi analízis
- A besugárzott ismeretlen összetételű kétkomponensű minta-sorozat komponenseinek meghatározása,
- majd a komponensek ismeretében a sorozat egyik tagjának ismeretlen tömegét kell meghatározni relatív módszerrel.
- A meghatározandó kétkomponensű minta-sorozat keverék lehet vegyület, vagy ötvözet, ahol a komponensek aránya állandó.
Méréshez szükséges eszközök és anyagok
- Félvezető detektor (HPGE vagy GE(Li)),
- Nagyfeszültségű tápegység a detektorhoz,
- Spektroszkópiai erősítő,
- Sokcsatornás amplitúdó-analizátor,
- PC,
- 137Cs és 60Co etalon sugárforrások,
- Előzetesen aktivált "ismeretlen" fólia a minőségi analízishez,
- Előzetesen aktivált kétkomponensű minta-sorozat a minőségi és mennyiségi analízishez,
- Izotóp könyvtár (gamma-energia szerint és izotópok szerint rendezve),
- Sugárvédelmi felszerelés.
A mérőlánc használatát, működési elvét, beállításának módját a gyakorlatvezető ismerteti.
A mérés menete
- A reaktor pneumatikus csőpostája segítségével a megfelelő teljesítményen üzemelő reaktor zónába juttatjuk a besugárzandó mintákat, pontosan rögzítve a besugárzás körülményeit.
- A gyakorlat első lépéseként meghatározzuk az analizátorba belépő jel szükséges erősítését, oly módon hogy a 4096 csatorna kb. 3 MeV-es tartományt fogjon át. Ezt a 60Co izotóp spektrumának segítségével végezhetjük (teljesenergia-csúcsok 1173 és 1333 keV)
- Ha a holtidő miatt szükséges, a diszkriminátor szint megválasztásával vágjuk le a nagy zajjal terhelt kis energiás spektrum részt.
- Az etalon források 137Cs, 60Co spektrumának felvételével elvégezzük az energia kalibrációt. A csatorna(amplitúdó) - energia összefüggést közel lineárisnak tekinthető. A táblázatban megadott értékeket a megfelelő teljesenergia-csúcs maximumához rendeljük.
Ne feledjük, hogy a kalibrációra felhasznált intervallumon kívül az extrapoláció felerősíti az energia kalibrációnál elkövetett kis hibát. A 60Co izotóp kaszkád gamma-vonalak (közel azonos gyakoriság) nettó területének összevetésével a hatásfok csökkenés vizsgálható.
- A kalibráló spektrum teljesenergia-csúcsának vizsgálatával ellenőrizzük a rendszer stabilitását, energia felbontását. A teljesenergia-csúcsok Gauss-függvény alakjának torzulása erősítés elmászásra, vagy valamilyen zajra utal.
- Ha a 60Co csúcsok felett megtaláljuk (1460 keV) a természetes 40K izotóp csúcsát, ellenőrizzük az extrapolált energia kalibráció helyességét.
- A kalibrált mérőlánccal felvesszük az ismeretlen minta spektrumát és az energia szerint rendezett gamma-vonalak könyvtárából kikeressük azokat az izotópokat, melynek gamma vonalai a spektrumban azonosított csúcsok környezetébe esnek.
- Az izotópok szerint rendezett könyvtárban ellenőrizzük a kiválasztott izotópok gamma vonalait. Ha valamely izotóp esetén a spektrum valamennyi teljesenergia-csúcsa magyarázható az izotóp vonalaival, az elem azonosítás befejeződött. Kérdéses esetben új méréssel a felezési időt is becsülhetjük. A lehetséges izotópok kiválasztásánál vegyük figyelembe a felezési időket, valamint azt a tényt, hogy a keresett izotóp stabil izotópból jött létre - nagy valószínűséggel -, egyszeres neutron befogással.
- A gyakorlat fő feladata a kétkomponensű minta sorozat mennyiségi és minőségi analízise. Elsőként a minta-detektor távolságot kell úgy beállítani próbamérésekkel, hogy az mind a 4 minta mérésére megfeleljen (holtidő). A hatásfok meglehetősen bonyolultan függ a minta pozíciójától, tehát a relatív mérés során a minta pozíció nem változtatható. A próbamérés során a különböző teljesenergia-csúcsok impulzus számlálási sebességei segítségével, közelítőleg határozzuk meg a szükséges mérési időket.
- A felvett spektrumokon az analizátor kezelését végző szoftver segítségével jelöljük ki a teljesenergia-csúcsokat és határozzuk meg a csúcsok paramétereit. A spektrum felvételkor gondosan rögzítsük a mérés kezdetének időpontját.
Kiértékelés
Izotóp azonosítás
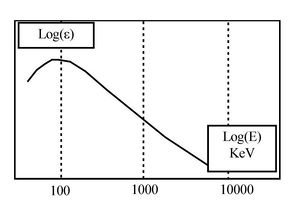
A gamma-spektrum kiértékelésre alkalmas objektumai a megfelelően lehatárolt teljesenergia-csúcsok. Az izotóp meghatározásra elsősorban a kalibrált spektrumról a csúcsok maximumánál leolvasható energia értékek szolgálnak. A jó felbontású (félértékszélesség 1-2 keV) félvezető detektorokkal felvett spektrumon ki kell választani mely izotópoknak van "észlelhető" gamma vonala az adott csúcs "közelében". Az észlelhetőségnél figyelembe kell venni az adott gamma átmenetre vonatkozó un. egy bomlásra jutó kibocsátási gyakoriságot (2. ábra), valamint azt a tényt, hogy a detektor hatásfoka a gamma energia növekedésével rohamosan csökken (ha eltekintünk a 200 keV alatti tartománytól ahol a detektor nem érzékeny külső részében történő elnyelődés megváltoztatja ezt a tendenciát).
A vizsgált csúcs körzetében valamekkora energia bizonytalansággal kell számolni a lehetséges gamma-vonalak kiválasztásánál. Az energia bizonytalanság a kalibráló izotópok vonalai által meghatározott intervallumon kívül növekszik. Az energia bizonytalanság még tökéletes linearitás mellett is törvényszerűen fellép a nukleáris jelek amplitúdóinak diszkretizálása miatt, további bizonytalansági forrás a mérőlánc nonlinearitása, illetve a csúcs alakja. Az intervallumon belül az energia bizonytalansága kb. a félérték szélesség nagyságának megfelelő, azon kívül az energia kalibrációs egyenes paramétereinek szórása által meghatározott módon növekszik, és szisztematikus jellegű.
A spektrumon megjelenhetnek olyan alakzatok, melyek teljesenergia-csúcsnak tűnnek, de nem tartozik hozzájuk gamma energia. Ilyenek a véletlen összegcsúcsok, melyek különösen nagyobb intenzitásoknál jelennek meg, vagy a párkeltés küszöbenergiáját jóval meghaladó gamma-vonalak esetén fellépő egyszeres és kétszeres kiszökési csúcsok, melyek a teljesenergia-csúcstól való távolság alapján azonosíthatók. A párkeltéssel kapcsolatban gyakran megjelenik 511 keV-nél egy csúcs ami a detektor környezetében keletkező és beszóródó annihilációs fotonoktól származik. Nem biztos, hogy a mintától származik a 40K 1460 keV-es csúcsa, mely bármilyen K tartalmú anyagtól (pl. a mérőpár másik tagjától) származhat. A reaktor körzetében felbukkanhat a radioaktív Ar 1290 keV-es csúcsa is. A visszaszórási csúcsok általában szélesebbek a teljesenergia-csúcsoknál, így ezeket kis gyakorlattal könnyű elkülöníteni. A fent felsoroltakon kívül a spektrumban megjelenő valamennyi csúcsot meg kell tudni magyarázni, illetve a kiválasztott izotópoknak nem lehet olyan jelentős gamma vonala amely nem látszik.
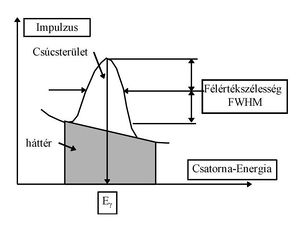
Csúcs terület és szórás meghatározás
A gamma spektroszkópiai gyakorlaton elvégzett módon el kell végezni a teljesenergia-csúcsok lehatárolását. A háttér becslése miatt kétoldalt megfelelő mennyiségű háttér csatornát kell kijelölni (3. ábra). A nettó csúcsterület meghatározásánál a hátteret trapézzal közelítsük. A nettó terület szórásának meghatározásakor vegyük figyelembe a háttér szórását is.
Ismeretlen minta tömegének meghatározása
Az ismeretlen tömeg meghatározásához készítsünk kalibráló egyenest az ismert tömegű minták segítségével. Ehhez válasszuk ki valamely mintabeli radioaktív izotóp egy markáns teljesenergia-csúcsát. Korrigáljuk a mért nettó - azonos mérési időtartamhoz tartozó - impulzusszámokat egy referencia időpontra (pl. a besugárzás végére) és az ismert tömegekre mint független változóra végezzünk lineáris regressziót. A regresszió számításakor az eltérésnégyzeteket súlyozzuk az (eredeti, nem korrigált) impulzus számok szórásnégyzetének reciprokával. A kalibrációs egyenes becsült paraméterei így:
![\[ a = \frac{\sum w_{i}y_{i}}{\sum w_{i}} \qquad b = \frac{\sum w_{i}(x_{i}-\bar{x})y_{i}}{\sum w_{i}(x_{i}-\bar{x})^2} \]](/images/math/1/4/c/14c0c01c31f1a91c06fb0dd167b965e0.png) |
(16) |
Ha az egyenes egyenlete 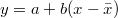 alakú. A
alakú. A 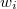 súlyok az
súlyok az 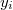 értékek szórásnégyzeteinek reciproka.
értékek szórásnégyzeteinek reciproka.
Mikor az ismeretlen minta tömegét akarjuk meghatározni, a fenti egyenest kell invertálnunk. Ekkor az ismeretlen  értéket 3 valószínűségi (
értéket 3 valószínűségi (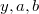 ) változó lineáris kombinációjával fejezzük ki. A meghatározandó
) változó lineáris kombinációjával fejezzük ki. A meghatározandó  érték az inverz forma várható értékeként áll elő. Szórásnégyzete felírható a három valószínűségi változó szórásnégyzetével.
érték az inverz forma várható értékeként áll elő. Szórásnégyzete felírható a három valószínűségi változó szórásnégyzetével.
Közelítő megoldás is lehetséges, ha feltüntetjük a regressziós egyenes szórását egy sáv formájában és ennek metszetét képezzük az 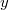 és szórásával kijelölhető sávval. A metszet pontok levetítése adja
és szórásával kijelölhető sávval. A metszet pontok levetítése adja  becsült értéke körül
becsült értéke körül  közelítő szórását.
közelítő szórását.
Felezési idő becslés
Az izotóp azonosításnál a jó energia-felbontású félvezető detektorok alkalmazásával már csak ritkán szükséges a felezési idő becslése vitás esetek eldöntésére. Ekkor időben egymásután, a feltételezett felezési idővel összevethető időkülönbséggel két spektrum mérést végzünk. Egy adott teljesenergia-csúcsot figyelve két különböző csúcsterületet kapunk azonos mérési idővel az aktivitás időbeli csökkenésének megfelelően (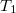 ,
, 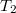 ).
).
![\[ T_{2} = \frac {T_{1}} {{2}^{{{\Delta}t}/t_{1/2}}} \]](/images/math/1/6/a/16a0bcb6d380eaa0ca229307fef96967.png) |
(17) |
ahol 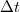 a két mérés között eltelt idő.
Innen a felezési idő már kifejezhető. Ha a két mérési idő különböző (
a két mérés között eltelt idő.
Innen a felezési idő már kifejezhető. Ha a két mérési idő különböző (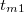 és
és 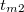 ), ami akár a holtidő különbségekből is származhat, akkor a két terület így fejezhető ki:
), ami akár a holtidő különbségekből is származhat, akkor a két terület így fejezhető ki:
![\[ T_{1}=\varepsilon\int\limits_{0}^{{t_{m1}}}A_{0}\exp(-\lambda\mathrm{t})dt={\frac{A_{0}}{\lambda}}\varepsilon(1-\exp(-\lambda{t_{m1}})) \]](/images/math/7/d/4/7d47a6b98de966d9cf4aae18208b8c1f.png) |
(18) |
![\[ T_{2}=\varepsilon\int\limits_{\Delta{t}}^{\Delta{t}+{t_{m2}} }A_{0}\exp(-\lambda{t})dt=\frac{A_{0}}{\mathit{\lambda}}\varepsilon\exp(-\lambda\Delta{t})(1-\exp(-\lambda{t_{m2}})) \]](/images/math/1/0/1/101034da6dbbb95048e7295415093a87.png) |
(19) |
Ahol 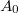 az aktivitás az első mérés megkezdésekor. A fenti két kifejezés hányadosaként
az aktivitás az első mérés megkezdésekor. A fenti két kifejezés hányadosaként 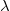 -ra transzcendens egyenletet kapunk.
-ra transzcendens egyenletet kapunk.
Ellenőrző kérdések
- Mi a neutron aktivációs analízis?
- Milyen sugárzás fajták detektálására alapozható az aktivált minták azonosítása?
- Mely tényezők határozzák meg adott elemre a mérhető legkisebb anyagmennyiséget?
- Hogyan mérhető az aktivált minták felezési ideje?
- Mi az abszolút és relatív mennyiségi analízis?
- Hogyan küszöbölhető ki a zavaró reakciók hatása?
- Milyen csúcsok jelenhetnek meg a gamma spektrumon, melyek nem
- köthetők közvetlenül a minta által kisugárzott gamma fotonokhoz?
- Milyen módon aktiválhatunk természetes izotópokat tartalmazó mintákat?
Irodalom
- Erdtmann, G., Solyka, W.: Die gamma-Linie der Radionuklide, JÜL-1003-AC (1974)
- Kiss D., Quittner P.: Neutronfizika, Akadémiai Kiadó, Budapest (1971)
- Lederer, G.M., Hollander, J.M.,Perlman,I.: Table of Isotopes, John Wiley, New York (1986)
- Lengyel T., Jász Á. : Izotóplaboratóriumi zsebkönyv, Műszaki Könyvkiadó, Budapest, (1966)
- Nagy L. Gy. : Radiokémia és izotóptechnika. Tankönyvkiadó, Budapest (1983)
- Szabó E., Simonits A. : Aktivációs analízis. Műszaki Könyvkiadó, Budapest, (1973)
Külső hivatkozások
A Neutron aktivációs analitika laborjegyzet forrása elérhető a [1] linken.