Bétasugárzás abszorpciójának és visszaszórásának vizsgálata, vastagságmérés
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A β-sugárzás
Előzetes tanulmányainkból ismeretes, hogy az atommagok pozitív elektromos töltésű protonokból és semleges neutronokból épülnek fel. A természetben általában olyan atommagok fordulnak elő, amelyek stabilak: bennük a protonok és neutronok számának aránya meghatározott értékű. Mesterségesen azonban létre lehet hozni olyan atommagokat, amelyekben a proton-neutron arány nem felel meg a természetben előforduló magoknak. Az így létrehozott atommagok jellemző tulajdonsága, hogy részecskéket bocsátanak ki, ezt a jelenséget nevezzük mesterséges radioaktivitásnak.
A felborult proton-neutron arány visszaállását csupán két módon lehet elképzelni. Az egyik legegyszerűbb elképzelés, hogy neutrontöbblet esetén neutronok távoznak a magból. A másik bonyolultabb elképzelés az, hogy a neutron átalakul protonná a magban, miközben, egy protonnal ellentétes töltésű részecske is keletkezik, hogy a töltésmegmaradás érvényesüljön. Hasonló folyamatok képzelhetők el protontöbblet esetén is. Vagy protonok távoznak a magból, vagy a protonból lesz neutron, és hogy a töltésmegmaradás elve teljesüljön, egy a proton töltésével azonos töltésű részecske is keletkezik. A két elképzelés közül az utóbbi bizonyult igaznak, ugyanis ezeknél a magoknál nem tapasztaltak neutron- vagy protonkilépést, hanem sokkal kisebb tömegű töltött részecskéket figyeltek meg. A mérésekből kiderült, hogy a távozó részecskék elektronok, illetve az elektronnal azonos tömegű, de ellentétes töltésű pozitronok. Érdekes jelenség, hogy a folyamatban keletkező elektronok illetve pozitronok energiája még az ugyanolyan típusú magok bomlásánál sem egy meghatározott értékű volt, hanem nullától egy bizonyos maximális energiáig terjedt. Ez látszólag ellentmondott az energia megmaradás törvényének, amelyet csak úgy lehetett megtartani, ha a folyamatban semleges részecskék is keletkeztek.
Fermi és Pauli együttes elképzeléseként mai ismereteink szerint a következő két folyamat mehet végbe az ilyen magokban:
![\[^1_0n\to^1_1p + e^- + \overline\nu\]](/images/math/8/c/7/8c77a6b612e58e2f4276e5f2e3aefdec.png)
![\[^1_0p\to^1_1n + e^+ + \nu\]](/images/math/f/8/c/f8cc790db4efdf37ff2b8da43e64e998.png)
ahol 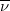 és
és  két semleges töltésű, nulla nyugalmi tömegű részecske, az antineutrínó és a neutrínó. A folyamatban keletkező
két semleges töltésű, nulla nyugalmi tömegű részecske, az antineutrínó és a neutrínó. A folyamatban keletkező 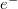 -t történeti okokból negatív
-t történeti okokból negatív 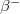 részecskének is nevezzük, míg az
részecskének is nevezzük, míg az 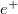 -t pozitív
-t pozitív 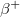 részecskének. A kilépő részecskék energiáját eV-ban szokás mérni: egy elektron 1 V potenciálkülönbségen áthaladva 1 eV energia többletre tesz szert. E definíció alapján 1 eV = 1,6∙10−19 Joule. A folyamatokban felszabaduló energiát a két részecske (
részecskének. A kilépő részecskék energiáját eV-ban szokás mérni: egy elektron 1 V potenciálkülönbségen áthaladva 1 eV energia többletre tesz szert. E definíció alapján 1 eV = 1,6∙10−19 Joule. A folyamatokban felszabaduló energiát a két részecske (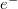 és
és 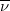 vagy
vagy 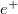 és
és  ) egymás között megosztja, így állhat elő az a helyzet, hogy azonos magokból kilépő elektronok illetve pozitronok energiája 0-tól egy maximális energiáig minden értéket felvehet.
) egymás között megosztja, így állhat elő az a helyzet, hogy azonos magokból kilépő elektronok illetve pozitronok energiája 0-tól egy maximális energiáig minden értéket felvehet.
β-részecskék kölcsönhatása az anyaggal
Az előző részben áttekintettük a  -sugárzás keletkezését és jellemzőit. Vizsgáljuk most meg röviden, mi történik a
-sugárzás keletkezését és jellemzőit. Vizsgáljuk most meg röviden, mi történik a  -sugárzással, ha anyagon halad át. A sugárzás különböző mechanizmusok révén energiát veszít, energiát ad át a környező anyagnak (abszorbensnek). Az energiaátadás és az ezzel fellépő jelenségek természetesen mind a sugárzás, mind az abszorbens tulajdonságaitól függenek. Amint a töltött részecskék semleges atomokon haladnak keresztül, a Coulomb erők révén kölcsönhatásba lépnek – ütköznek – az atomok elektronjaival. Jóllehet a részecske egyetlen kölcsönhatás során kinetikus energiájából csak néhány eV-nyit veszít, a nagyszámú ütközés miatt mégis jelentős lesz a részecske pályája mentén a hosszegységre eső (fajlagos) energiaveszteség dE/dx értéke. Az energia leadás eredményeképpen a részecskével ütközött atomok ionizálódnak vagy gerjesztődnek.
-sugárzással, ha anyagon halad át. A sugárzás különböző mechanizmusok révén energiát veszít, energiát ad át a környező anyagnak (abszorbensnek). Az energiaátadás és az ezzel fellépő jelenségek természetesen mind a sugárzás, mind az abszorbens tulajdonságaitól függenek. Amint a töltött részecskék semleges atomokon haladnak keresztül, a Coulomb erők révén kölcsönhatásba lépnek – ütköznek – az atomok elektronjaival. Jóllehet a részecske egyetlen kölcsönhatás során kinetikus energiájából csak néhány eV-nyit veszít, a nagyszámú ütközés miatt mégis jelentős lesz a részecske pályája mentén a hosszegységre eső (fajlagos) energiaveszteség dE/dx értéke. Az energia leadás eredményeképpen a részecskével ütközött atomok ionizálódnak vagy gerjesztődnek.
A fajlagos energiaveszteség (dE/dx) alapján definiáljuk azt az egyenesnek feltételezett átlagos távolságot, amelyen a részecske kinetikus energiáját teljesen elveszti. Ez az ún. hatótávolság, jele „R”, amely értelemszerűen azon dx távolságokból tevődik össze, ahol a részecske kezdeti E0 kinetikus energiája dE lépésekben nullára csökken:
![\[R = \int\limits_0^R dx = \int\limits_{E_0}^0{\frac{dx}{dE}\cdot dE} = -\int\limits_0^{E_0}{\left(\frac{dE}{dx}\right)}^{-1} \cdot dE\]](/images/math/f/b/3/fb3d7ef789119a472121decfca81d7a8.png)
Az elektronok és a nehéz töltött részecskék a fékező közegben gerjesztést és ionizációt váltanak ki. Lényeges eltérés, hogy egy elektron az ütközés során energiájának akár felét is elveszítheti, és erősen eltérhet eredeti haladási irányától, ugyanakkor egy nehéz részecske egy ütközésnél csak az energia m0/M ≈ 1/2000-ed részét veszítheti el, és pályája nagymértékben egyenes vonalú. (Az elektronok pályája az előbb elmondottakból adódóan értelemszerűen jellemzően nem egyenes vonal.) Egy határozott energiájú elektronnyaláb, miután keresztül haladt egy abszorbens rétegen, már jelentősen eltér a monoenergiától, ezért elektronok esetében a hatótávolság nem definiálható olyan egyszerűen, mint a nehéz részecskéknél. Az elektronok energiavesztesége sok ütközés után nulla és a teljes kezdeti energia közötti tetszőleges érték lehet. A nagy energiaszórás egyik következménye, hogy az elektronok által valóságosan megtett út nagyon erősen szór egy átlagérték körül.
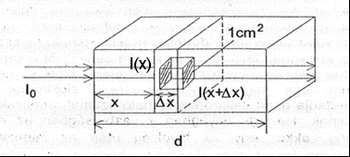
Ha egy „d” vastagságú anyagra kollimált (párhuzamos) elektronnyalábot ejtünk, akkor a „d” vastagság után az elektronnyalábban lévő elektronok száma lecsökken. Egy részecseknyaláb erősségét „I” intenzitásával szokták jellemezni, amely a nyalábra merőleges helyzetű egységnyi felületen (szokásosan 1 cm2 egységgel megadva) időegység alatt áthaladó részecskék számát jelenti. A detektorok által jelzett beütésszámok ezzel arányosak.
Vizsgáljuk meg, hogy az anyagon való áthaladás során hogyan változik meg ez az intenzitás. A változást két okra lehet visszavezetni: egyrészt arra, hogy az anyaggal való kölcsönhatás során az elektronnyalábban haladó részecskék egy része megváltoztatva haladási irányukat kiszóródik a nyalábból, míg mások a kölcsönhatások során ugyan haladási irányukat összességében nem (vagy nem nagyon) változtatják meg, de teljesen lelassulnak, és csak termikusan mozognak. Az anyagban lévő szóró és lassító centrumokat σ szórás és lassító tényezővel lehet jellemezni (más néven mikroszkopikus teljes hatáskeresztmetszet). Ez azt a felületet jelenti, amelyet megszorozva az időegység alatt egy négyzetcentiméterre eső elektronok számával (I intenzitás), megadja azon elektronok várható számát, amelyek kiszóródnak, illetve lelassulnak. Ha egy anyagban x mélységben az elektronnyaláb intenzitása I(x), akkor egy Δx távolság után az intenzitás annak következtében fog lecsökkenni I(x+Δx)-re, hogy a Δx vastagságú egységnyi alapterületű téglatestben lévő összes szóró és lassító centrumok kifejtik hatásukat (lásd 1. ábra). Ha „n” az egységnyi térfogatban lévő centrumok számát jelenti (azaz a centrumok sűrűségét), akkor az intenzitásváltozás:
![\[\Delta I = I(x) - I\left(x + \Delta x\right) = \Delta x \cdot n \cdot \sigma \cdot I\left(x\right)\]](/images/math/e/d/1/ed1f327333df42e3b3f1a9ef9819d953.png)
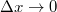 esetén a (4) differencia-egyenlet a következő differenciál-egyenletet szolgáltatja:
esetén a (4) differencia-egyenlet a következő differenciál-egyenletet szolgáltatja:
![\[\lim_{x\to0}\frac{I\left(x+\Delta x\right) - I\left(x\right)}{\Delta x} = -n\cdot \sigma \cdot I(x) \to \frac{dI}{dx} = -n \cdot \sigma \cdot I(x)\]](/images/math/3/6/d/36ddac51d675c717900304a69a07f000.png)
Az 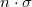 mennyiséget
mennyiséget  -vel szokás jelölni, neve lineáris abszorpciós együttható (vagy makroszkopikus „hatáskeresztmetszet”). Így az (5) egyenlet alakja:
-vel szokás jelölni, neve lineáris abszorpciós együttható (vagy makroszkopikus „hatáskeresztmetszet”). Így az (5) egyenlet alakja:
![\[\frac{dI}{dx} = -\mu \cdot I(x)\]](/images/math/6/1/b/61b1a2ea16ec6bb4655665a865ff9152.png)
Ha I0 a minta előtti intenzitás értéke, a fenti differenciál-egyenlet megoldása a következő lesz:
![\[I = I_0 e^{-\mu \cdot x}\]](/images/math/d/7/7/d777ad4116d3b61fa8d188548b50a0e3.png)
Tapasztalati tény, hogy  arányos a mindenkori abszorbens
arányos a mindenkori abszorbens  sűrűségével, vagyis a
sűrűségével, vagyis a 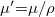 minden anyagra jó közelítéssel állandó. A
minden anyagra jó közelítéssel állandó. A 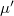 neve tömegabszorpciós állandó. Ennek bevezetésével (7) alakja a következő:
neve tömegabszorpciós állandó. Ennek bevezetésével (7) alakja a következő:
![\[I = I_0 e^{-\mu' \cdot \rho \cdot x}\]](/images/math/e/b/d/ebd1ec646fa53d902223ffa2e0a8f078.png)
A 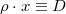 mennyiséget felületi sűrűségnek nevezzük, dimenziója: [D] = [ρ]∙[x] = g∙cm−3∙cm
= g∙cm−2, ezzel (8) alakja a következő lesz:
mennyiséget felületi sűrűségnek nevezzük, dimenziója: [D] = [ρ]∙[x] = g∙cm−3∙cm
= g∙cm−2, ezzel (8) alakja a következő lesz:
![\[I(d) = I_0 e^{-\mu' \cdot D}\]](/images/math/3/a/1/3a1bd661853262a9b549f9050d091ca2.png)
Mivel a detektorok által mért beütések arányosak I-vel, ezért a beütésszámokra is igaz az exponenciális összefüggés:
![\[N = N_0 e^{-\mu' \cdot D}\]](/images/math/5/7/9/579a269cd5ca2be20654dcb90d4bc3a2.png)
ahol N a tetszőleges hosszúságú rögzített idő alatt kapott beütésszámokat jelenti. A továbbiakban az anyagvastagságot „d” helyett D-vel jellemezzük.
Fontos fogalom az abszorpció mértékének jellemzésére a felezési vastagság 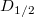 , amely azt a D értéket jelenti, amelynél a kezdeti N0 érték a felére csökken:
, amely azt a D értéket jelenti, amelynél a kezdeti N0 érték a felére csökken:
![\[\frac{N_0}{2} = N_0 e^{-\mu'\cdot D_{1/2} }\]](/images/math/b/c/e/bce69d01b4e35e36ede0f1f0265b93f5.png)
Ebből a definícióból a felezési vastagság és a μ' közötti kapcsolatot úgy kapjuk meg, ha N0 -al egyszerűsítünk és logaritmálunk:
![\[\frac{ln(2)}{\mu '} = D_{1/2}\]](/images/math/1/f/7/1f785dcf38f274c8f8f92d5a4ffc9871.png)
A másik fontos tényező a maximális hatótávolság „R”. Ennek értéke erősen függ a β-sugárzás maximális energiájától. R értékét is felületi sűrűségegységben szokás megadni (lásd 1. táblázat). Maximális hatótávolság alatt azt a rétegvastagságot értjük, melyen túlra a sugárzás részecskéi gyakorlatilag nem jutnak el. Méréstechnikailag azt a vastagságot tekintik hatótávolságnak, amelynél az intenzitás az eredeti értékének 104-ed részére csökken.
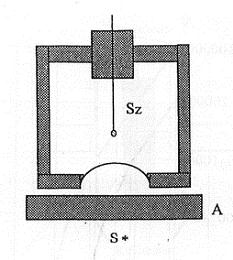
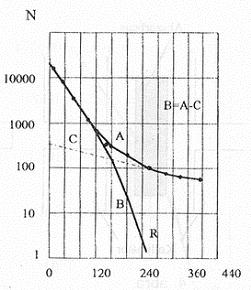
A 2. ábra egy elvi elrendezést mutat β-abszorpció kísérleti vizsgálatára. Az S* β-bomló radioaktív forrásból kilépő elektronok az „A” abszorbensen keresztül végablakos Geiger-Müller-detektorra (GM cső) esnek, melynek impulzusát regisztráljuk. A tapasztalt impulzusszám és az abszorbens réteg felületi sűrűsége között közelítőleg exponenciális kapcsolat van (a 3. ábrán log-lin ábrázolásban egyenes).
Nagy abszorbensvastagságoknál az abszorpciós görbe eltér az exponenciálistól (az ábrán az egyenestől). Ilyen görbék alapján közelítő értékeket lehet megállapítani a β-spektrum maximális energiájára vonatkozólag.
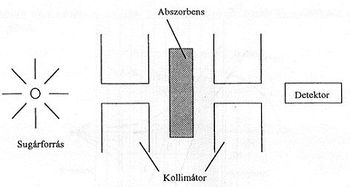
Az értékelhető abszorbens méréséhez megfelelő geometriai elrendezést kell alkalmazni, amely biztosítja, hogy a forrásból a tér minden irányába kilépő β-részecskékből csak szűk nyalábot tudjon érzékelni a detektor. Ilyen elrendezés látható a 4. ábrán
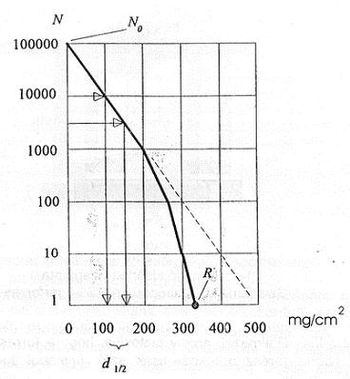
A 3. ábrán az abszorpciós görbén N0 jelenti a detektor által adott mérési idő alatt észlelt részecskék számát abszorbens nélkül, N pedig abszorbenssel. Az abszorbens vastagságát „D” jelöli felületi sűrűségegységben. A fél-logaritmikus koordináta-rendszerben ábrázolt görbéből látható, hogy a detektált részecskeszám kis abszorbens vastagságoknál (jelen esetben ha D < 200 mg/cm) közelítőleg exponenciálisan változik. Nagyobb vastagságoknál (D > 200 mg/cm) az abszorpciós görbe eltér a közelítőleg exponenciális változástól. Az R vastagság adja a maximális energiájú β-részecskék hatótávolságát, amely a β-spektrum maximális energiájától függ. E két mennyiség közötti összefüggés leírására tapasztalati úton több közelítő formulát szerkesztettek attól függően, hogy a maximális β-energia milyen energiaérték-tartományba esik. E formulák láthatók az alábbi 1. táblázatban:
| R[g/cm2] | Eβmax [MeV] |
|---|---|
| 0,150×Eβmax-0,0028 | 0,03-0,15 |
| 0,407×Eβmax1,38 | 0,15-0,8 |
| 0,542×Eβmax-0,133 | 0,8-1,0 |
| 0,571×Eβmax | 1,0- |
![\[1. t\acute{a}bl\acute{a}zat\ A\ hat\acute{o}t\acute{a}vols\acute{a}g\ energiaf\ddot{u}gg\acute{e}s\acute{e}t\ le\acute{i}r\acute{o}\ \ddot{o}sszef\ddot{u}gg\acute{e}sek\ (a\ hat\acute{o}t\acute{a}vols\acute{a}g\ fel\ddot{u}leti\ s\check{u}r\check{u}s\acute{e}gegys\acute{e}gben\ adott).\]](/images/math/7/2/1/721f7f881372d0a9f829ecf0c388d054.png)
A hatótávolság mérésével tehát meg lehet állapítani a β-sugárzás maximális energiáját. Az abszorpciós görbe exponenciális szakaszának meredekségéből is meg lehet állapítani Eβmax közelítő értékét tapasztalati tények alapján. Így pl. alumíniumban a μ' és Eβmax kapcsolatát az alábbi kifejezés írja le:
![\[ \mu ' \cong 17\cdot E_{ \beta_{max} }^{1,14} [cm^2/g] \]](/images/math/e/5/2/e524911638c8f2d94021fe441a9ff906.png)
A β-részecskék abszorpciójánál még egy effektust kell szemügyre vennünk annak érdekében, hogy a valóságban mért görbét értelmezni tudjuk: az ún. fékezési sugárzást. A kisugárzott nagy energiájú részecske (elektron vagy pozitron) és az abszorbensben levő elektronok Coulomb-kölcsönhatása következtében létrejövő gyorsulás (lehet negatív is) az oka az úgynevezett fékezési sugárzásnak. (Szokásos angol és német elnevezése Bremsstrahlung.) Miután a kibocsátott fotonok folytonos spektrumában az energiák nagyságrendileg a röntgensugárzás tartományába esnek, az effektust fékezési röntgensugárzásnak nevezzük. Az előzőekben csak az atomhéjban végbemenő kölcsönhatásokat, az ionizációt és gerjesztést vettük figyelembe, melynek következményei a nyalábból való kiszóródás és a részecske teljes lelassulása volt.
Elektrodinamikából tudjuk, hogy a töltések lassulását elektromágneses sugárzás kibocsátása kíséri, ahol a kisugárzott teljesítmény a gyorsulás négyzetétől függ. A gyorsulás Z∙e töltésű atommag (szórócentrum) és z∙e töltésű, „m” tömegű részecske esetén a z∙Z∙e2/m mennyiséggel arányos, így a kisugárzott teljesítmény:
![\[\frac{dE}{dt}\sim \frac{z^2Z^2}{m^2}\]](/images/math/3/3/8/338b82855453d5b211d39b96d6fd9ee2.png)
A sugárzás intenzitása fordítva arányos a tömeg négyzetével, ezért elektronok esetében jelentős, és viszonylag jelentéktelen nehéz ionizáló részecskék fékeződésénél. A fékezési sugárzásban elveszett energia eloszlása nulla és a maximális energia között lehet.
Az ionizációs és a sugárzási energiaveszteség aránya az elektron energiájától és az abszorbens rendszámától függ. A kétfajta energiaveszteség nagysága víz esetében (Z = 18) 100 MeV elektron energiánál egyezik meg, míg ólomnál (Z = 82) ez a kritikus energiaérték 10 MeV. A kritikus érték fölötti energiánál a fékeződésben a sugárzási veszteség dominál. A dE/dx fajlagos energiaveszteség sugárzási függése az elektron által megtett távolság függvényében közelítőleg exponenciális jellegű. Az a távolság, amelyen az elektron energiája e-ed részre csökken, az ún. „radiációs távolság”. Értéke vízben 36 g/cm2, alumíniumban 24 g/cm2, ólomban 6 g/cm2.
Az 5. ábrán látható görbének a D > 160 mg/cm2 feletti szakaszát a fékezési röntgensugárzás hozza létre, ugyanis a legtöbb  detektor a
detektor a  és röntgensugárzásra is érzékeny, így a röntgentartományba eső fékezési sugárzás is beütéseket okoz. Ezt a sugárzást az alumínium abszorbens növekvő vastagsága csak kis mértékben gyengíti, mivel az alumínium rendszáma kicsi. A fékezési sugárzást a nagy rendszámú anyagok abszorbeálják jól, mint pl. az ólom. A maximális hatótávolságot úgy tudjuk megállapítani, hogy a mérésből nyert „A” görbéből pontról pontra kivonjuk a (számunkra zajként tekintendő) fékezési röntgensugárzáshoz tartozó görbeszakasz d → 0 irányban extrapolált „C” részét.
és röntgensugárzásra is érzékeny, így a röntgentartományba eső fékezési sugárzás is beütéseket okoz. Ezt a sugárzást az alumínium abszorbens növekvő vastagsága csak kis mértékben gyengíti, mivel az alumínium rendszáma kicsi. A fékezési sugárzást a nagy rendszámú anyagok abszorbeálják jól, mint pl. az ólom. A maximális hatótávolságot úgy tudjuk megállapítani, hogy a mérésből nyert „A” görbéből pontról pontra kivonjuk a (számunkra zajként tekintendő) fékezési röntgensugárzáshoz tartozó görbeszakasz d → 0 irányban extrapolált „C” részét.
A mérésünkben használt 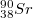 (stroncium) β-sugárzó izotóp energiaspektrumában a maximális energia értéke 2270 keV, tehát a fékezési röntgensugárzást figyelembe kell vennünk. A stroncium abszorpciós görbéje hasonló lesz az 5. ábrán látható görbéhez, ahol „A” a β sugárzásból származó „B” járulék és a fékezési sugárzásból adódó „C” járulék összege. A „C” egyenes szerkesztését úgy kell elvégezni, hogy a mért görbe azon szakaszára, amely a fékezési sugárzásból származik, illesztünk egy egyenest, ezt meghosszabbítjuk a kis vastagságok irányában, és az ennek megfelelő értékeket vonjuk le a mért „A” görbéből. A levonásnál ne felejtsük el, hogy az ábrázolás logaritmikus!
(stroncium) β-sugárzó izotóp energiaspektrumában a maximális energia értéke 2270 keV, tehát a fékezési röntgensugárzást figyelembe kell vennünk. A stroncium abszorpciós görbéje hasonló lesz az 5. ábrán látható görbéhez, ahol „A” a β sugárzásból származó „B” járulék és a fékezési sugárzásból adódó „C” járulék összege. A „C” egyenes szerkesztését úgy kell elvégezni, hogy a mért görbe azon szakaszára, amely a fékezési sugárzásból származik, illesztünk egy egyenest, ezt meghosszabbítjuk a kis vastagságok irányában, és az ennek megfelelő értékeket vonjuk le a mért „A” görbéből. A levonásnál ne felejtsük el, hogy az ábrázolás logaritmikus!
A β-sugárzás szóródása
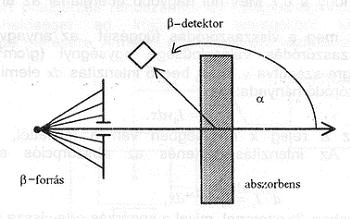
Ha kollimált β-sugárzás esik egy abszorbens felületére, akkor a sugárzásnak – mint láttuk – csak egy része halad a nyaláb eredeti irányában, a sugárzásban lévő többi részecske részben lelassul, részben különböző irányokba kiszóródik. A szórási kép mérésére szolgáló összeállítás látható a 6. ábrán
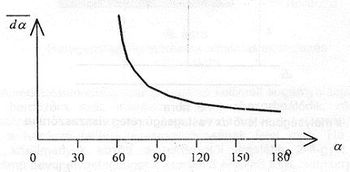
Alumíniumban a szóródó  -részecskék szögeloszlását mutatja példaként a 7. ábra. Külön ki kell emelni, hogy az ábra szerint vannak olyan részecskék is, amelyek a beérkezési irányokkal ellentétes irányban szóródnak (180°-os szórás, visszaszórás). A visszaszórás mértéke függ a részecskék energiájától, az anyag minőségétől és vastagságától. A visszaszórt sugárzás intenzitása az ún. telítési anyagvastagság eléréséig – változatlan anyagösszetétel mellett – változik az anyagvastagsággal. Ez a törvényszerűség a reflexiós vastagságmérés alapja. A telítési vastagságnál vastagabb anyag visszaszórása állandó, az anyagra jellemző, és annak rendszámától függ. Kísérleti tapasztalat, hogy az Ist telítési visszaszórt intenzitás, amely a detektor által szolgáltatott beütésszámmal arányos:
-részecskék szögeloszlását mutatja példaként a 7. ábra. Külön ki kell emelni, hogy az ábra szerint vannak olyan részecskék is, amelyek a beérkezési irányokkal ellentétes irányban szóródnak (180°-os szórás, visszaszórás). A visszaszórás mértéke függ a részecskék energiájától, az anyag minőségétől és vastagságától. A visszaszórt sugárzás intenzitása az ún. telítési anyagvastagság eléréséig – változatlan anyagösszetétel mellett – változik az anyagvastagsággal. Ez a törvényszerűség a reflexiós vastagságmérés alapja. A telítési vastagságnál vastagabb anyag visszaszórása állandó, az anyagra jellemző, és annak rendszámától függ. Kísérleti tapasztalat, hogy az Ist telítési visszaszórt intenzitás, amely a detektor által szolgáltatott beütésszámmal arányos:
![\[I_s^t = k\cdot I_0\cdot Z^{2/3}\]](/images/math/8/c/d/8cdbdf0f47182a175c1c879c1d402f13.png)
ahol I0 a beeső sugár intenzitása, „Z” pedig az anyag rendszáma. A „k” állandó a mérési elrendezéstől, valamint a β-sugárzás energiájától is függ. Megjegyezzük, hogy a 0,7 MeV-nél nagyobb energiánál az energiafüggés megszűnik.
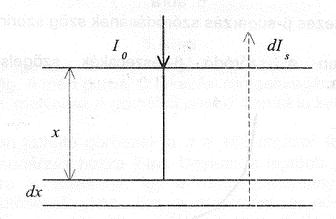
Vizsgáljuk meg, hogyan függ a visszaszóródás az anyagvastagságtól. Legyen a visszaszóródás valószínűsége egységnyi (g/cm2-ben mért) vastagságú rétegre számítva „v”. Az I0 beeső intenzitás dx elemi vastagságú rétegről visszaszóródó hányada:
![\[dI_s=I_0\cdot v\cdot dx\]](/images/math/4/0/9/4095b2f1ee2a1d3ba9f85c0af1ec75e1.png)
Ha azonban ez a réteg „x” mélységben van a felülettől, a sugárzás egy része odáig már abszorbeálódik. Az intenzitás csökkenése az abszorpciós együtthatóval kifejezhető:
![\[dI_s=I_0\cdot v\cdot e^{-2\cdot \mu \cdot x}\cdot dx\]](/images/math/2/7/9/279a1db818b14b55a233136670e14677.png)
ahol az exponensben 2x szerepel, mivel a sugárzás oda-vissza hatol át az x vastagságú rétegen, mire a detektorba jut. Ezt szemlélteti a 8. ábra.
A különböző mélységben található rétegekről visszaszórt teljes intenzitás (17) integrálásával adódik:
![\[I_s = \int\limits_0^xv\cdot I_0e^{-2\mu x}dx = I_s^t\cdot (1-e^{-2\mu x}) = I_s^t\cdot (1 - e^{-2\mu '\cdot D})\]](/images/math/6/5/f/65fb49c766540412cb01878cd2d0bdda.png)
ahol Ist = I0∙v/2μ, μ' a tömegabszorpciós együttható cm2/g-ban, D = ρ∙x, és ρ az anyag sűrűsége. Látható, hogy a visszaszórt intenzitás vékony rétegeknél a rétegvastagsággal nő, majd nagyobb rétegvastagságnál aszimptotikusan tart az Ist értékhez. Az Ist rendszámfüggése „v” és μ rendszámfüggéséből adódik.
Érdekes tapasztalat, hogy vegyületeknél, keverékeknél jó közelítéssel a súly szerinti átlagolással számított közepes rendszámnak megfelelő visszaszórást kapunk:
![\[Z = \sum_ig_iZ_i\]](/images/math/3/b/7/3b72eafc9547bc7bd781b464da24a56a.png)
ahol gi az i-edik atomfajta súlytörtje, Zi pedig a rendszáma. Kivétel ez alól a hidrogén, melynek visszaszórása rendellenesen kicsi.
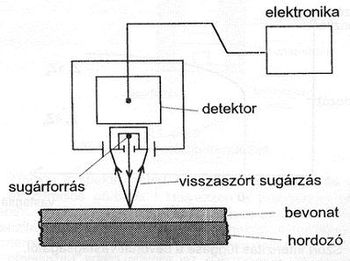
A β-reflexiós rétegvastagság mérés elve
A szórt  -sugárzás rendszámtól és rétegvastagságtól való egyidejű függése lehetőséget teremt különböző anyagokból készülő rétegek vastagságának mérésére. A mérési elrendezés elvi vázlatát a 9. ábra mutatja.
-sugárzás rendszámtól és rétegvastagságtól való egyidejű függése lehetőséget teremt különböző anyagokból készülő rétegek vastagságának mérésére. A mérési elrendezés elvi vázlatát a 9. ábra mutatja.
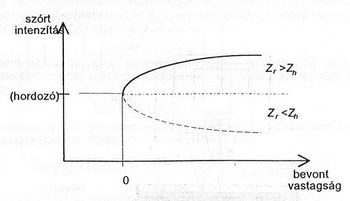
A védőtokban elhelyezett β-sugárzó kollimált sugárnyalábja bevonattal ellátott hordozóra esik, melyben részben abszorbeálódik, részben visszaszóródik róla. A szórt sugárzás intenzitása a bevonatvastagság x = 0 értéke mellett a hordozó telítési visszaszóródásának felel meg. Ha változatlan mérési körülmények között a hordozótól legalább 2-4-gyel különböző rendszámú anyagból készült bevonat vastagságát a kezdeti nulla értékről folyamatosan növeljük, a szórt sugárzás intenzitása megváltozik. Ha a bevonat (réteg) Zr rendszáma nagyobb, mint a hordozó anyag Zh rendszáma, a szórt intenzitás (15)-nek megfelelően nő, fordított esetben csökken. A két esetet a 10. ábra mutatja. A teljes visszaszórt intenzitás két részből adódik: egyrészt a hordozó telítési visszaszóródásából, amelyet a réteg (részben) abszorbeál: Isth∙e−2μx, másrészt a réteg visszaszóródásából Istr∙(1−e−2μx), amelyet a (18) összefüggés ír le. Így a visszaszórt intenzitás az alábbiak szerinti:
![\[I_s(x) = I_{s,h}^t e^{-2\mu \cdot x} + I_{s,r}^t (1 - e^{-2\mu \cdot x}) = I_{s,h}^t - (I_{s,h}^t - I_{s,r}^t) (1 - e^{-2\mu \cdot x})\]](/images/math/b/6/a/b6aa2b7bc7a1192977617e91335ff063.png)
ahol „x” a bevonat rétegvastagságát, Isth és Istr pedig a hordozó és a bevonat telítési visszaszórási intenzitását jelöli.
A fentiek alapján különböző energiájú sugárzást kibocsátó sugárforrások optimális megválasztásával lehetőség nyílik bevonatok rétegvastagságának mérésére a 0-50 μm közötti tartományban kb. 3-8% mérési pontossággal. Galván- és festékbevonatok vastagságának roncsolás mentes mérésére, folyamatos ellenőrzésére széleskörűen alkalmazhatók a β-reflexiós mérőberendezések, pl. a híradástechnikai és műszeriparban.
Mérési feladatok
β-abszorpciós mérési feladatok
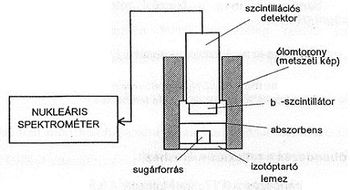
A mérési elrendezés a 11. ábrán látható. Detektorként szcintillációs mérőfejet, mérőműszerként NK-225 típusú nukleáris spektrométert használunk, melynek használati útmutatója megtalálható a függelékben.
- 1. Helyezze el a mérendő stroncium sugárforrást az ólomtorony aljára (11. ábra), majd a mérőhelyen lévő útmutató szerint végezze el az ellenőrző mérést! A sugárforrás tetején lévő β-sugárzást emittáló nyílásba nem szabad belenézni! Állítsa be az útmutató szerint előírt diszkriminátor feszültséget, a mérési időt, és az erősítést. A diszkriminátor ezen állása biztosítja, hogy a detektor zajimpulzusainak jelentős része ne okozzon beütést, csak valóban a
 -részecskéktől származzon a kapott beütésszám.
-részecskéktől származzon a kapott beütésszám.
- 2. Hagyja a spektrométert a beállított értéken és vegye fel a
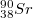 izotóp abszorpciós görbéjét. Helyezzen a β-sugárzás útjába egyre vastagabb abszorbenseket, és mérje meg az egyes abszorbenseken áthaladt intenzitásokkal arányos impulzusszámokat. A mellékelt alumínium lapkák szisztematikus cseréjével (a lapkák vastagsága ~0,05 mm-es lépésekben növekszik) addig növelje az abszorbens vastagságát, míg a beütésszám tovább már nem változik. Minden egyes abszorbenssel háromszor mérjen 20 sec-ig, és átlagolja az eredményeket. Ügyeljen arra, hogy az alumínium lapkákat mindig ugyanarra a polcra helyezze! Végezzen egy olyan mérést is, amikor nincs behelyezve abszorbens (ekkor csak a levegőréteg és a szcintillátor kristályát védő fényzáró réteg szerepel abszorbensként).
izotóp abszorpciós görbéjét. Helyezzen a β-sugárzás útjába egyre vastagabb abszorbenseket, és mérje meg az egyes abszorbenseken áthaladt intenzitásokkal arányos impulzusszámokat. A mellékelt alumínium lapkák szisztematikus cseréjével (a lapkák vastagsága ~0,05 mm-es lépésekben növekszik) addig növelje az abszorbens vastagságát, míg a beütésszám tovább már nem változik. Minden egyes abszorbenssel háromszor mérjen 20 sec-ig, és átlagolja az eredményeket. Ügyeljen arra, hogy az alumínium lapkákat mindig ugyanarra a polcra helyezze! Végezzen egy olyan mérést is, amikor nincs behelyezve abszorbens (ekkor csak a levegőréteg és a szcintillátor kristályát védő fényzáró réteg szerepel abszorbensként).
- 3. Mutassa ki a fékezési röntgensugárzást. Helyezzen el a legvastagabb alumínium abszorbens fölé egy kb. 2 mm vastagságú ólomkorongot! Esetenként 20 sec-ig mérve addig növelje a korongok számát (összvastagságát), amíg az impulzusszám a 20 sec-ra vonatkoztatott határsugárzás értékre nem csökken le. A mérést célszerű azzal kezdeni, hogy a forrás eltávolításával az ólomtoronyból 20 sec-ig hátteret kell mérni.
- 4. Ábrázolja az abszorpciós görbét számítógépen valamilyen erre alkalmas programmal. Ekkor az 5. ábrához hasonló görbét kapunk. A függőleges (logaritmikus) tengelyen a beütésszámot, a vízszintes tengelyen az alumínium lapkák vastagságát mg/cm2 vesszük fel. (A cm-ben mért vastagságot be kell szorozni az alumínium sűrűségével, ρAl = 2700 mg/cm3). Ügyeljen arra, hogy alumínium lapkák nélkül végrehajtott mérésnél sem zérus az abszorbens vastagság. A levegőréteg vastagságát a forrástól a szcintillátorig kell számítani. A levegő sűrűsége 1,273 mg/cm3, a levegőben megtett út kb. 4 cm, a szcintillátor kristály fényzáró rétegének vastagsága 1,2 mg/cm2.
- 5. Szerkessze meg a felezési rétegvastagságot (D½) és a hatótávolságot (R) a grafikonon!
- 6. Számítsa ki az 1. táblázat alapján Eβmax értékét!
- 7. Állapítsa meg, hány felezési rétegvastagságig érvényes az abszorpciós görbe közelítőleg exponenciális lefutása!
β-reflexiós mérési feladatok
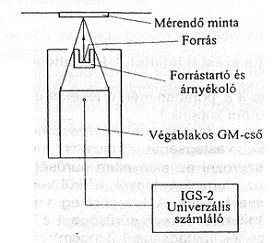
A mérési elrendezés a 12. ábrán látható. A forrás egy 2,5∙105 Bq aktivitású 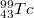 technécium izotóp, mely 290 keV energiájú β-sugárzást bocsát ki. A forrástartó úgy van kiképezve, hogy direkt
technécium izotóp, mely 290 keV energiájú β-sugárzást bocsát ki. A forrástartó úgy van kiképezve, hogy direkt  -sugárzást ne juthasson a GM csőre. A detektor jeleit egy univerzális számláló rögzíti.
-sugárzást ne juthasson a GM csőre. A detektor jeleit egy univerzális számláló rögzíti.
- 1. Telítési visszaszóródás rendszám függésének vizsgálata. A vizsgált anyagok rendszámai a 2. táblázatban találhatók.
Kapcsolja be a mérőberendezést. Tekerje le a védőkupakot, és mérje meg a mérőtartóból származó visszaszórt beütésszámot. Ezután a mérendő anyagokat egyenként helyezze a mérőtartóra, ügyelve arra, hogy lefedje a mérőfejen lévő lyukat, majd mérje meg a visszaszórt intenzitással arányos beütésszámot 1 perces mérési idővel.
Minden mérést háromszor kell megismételni. A három mérés átlagából a mérőtartóból származó beütésszámot le kell vonni. Ábrázolja a mért intenzitásokkal arányos beütésszámokat a rendszám függvényében logaritmikus skálákon! Határozza meg az egyenes iránytangensét a legkisebb négyzetek módszerével! Hasonlítsa össze a mérési eredményt a (13) összefüggés alapján várhatóval, és értelmezze az eredményt!
- 2. Vas hordozóra felvitt festékréteg relatív vastagságának meghatározása. A (20) összefüggés átalakításával a következő írható fel:
![\[2\mu x = ln\frac{I_{s,h}^t-I_{s,r}^t}{I_s^t(x)-I_{s,r}^t}\]](/images/math/1/4/f/14fbc2af6c8ba20db1dc3d9e746f5bef.png)
A mérésnél meg kell határozni a hordozó Isth telítési visszaszórását, a réteg Istr telítési visszaszórását a jelöletlen lemez mérésével, valamint a számozott minták Ist(x) visszaszórásait. Háttér visszaszórást nem kell mérni, mivel (21)-ben az intenzitások különbségei szerepelnek. A (21)-ben szereplő μ érték minden festékréteggel bevont lemezre azonos, ezért ha az 1-gyel jelölt lemez vastagságát egységnek választjuk, a mérés alapján a többi számozott lemez relatív vastagsága meghatározható. A mérési idő most is 1 perc, és minden mérést háromszor kell megismételni. A relatív vastagságok számításánál mindig a három mérés átlagával számoljon!
| alumínium | 13 |
| vas | 26 |
| réz | 29 |
| ezüst | 47 |
| wolfram | 74 |
| bizmut | 83 |
![\[2. t\acute{a}bl\acute{a}zat\ A\ vizsg\acute{a}lt\ anyagok\ rendsz\acute{a}mai\]](/images/math/e/5/0/e5028fd6daa1706b5fe842863a46d081.png)
Ellenőrző kérdések
- Milyen módon lépnek az anyaggal kölcsönhatásba a β-részecskék?
- Mi a hatótávolság meghatározása?
- Mennyiben térnek el egymástól a megtett út, az átlagos hatótávolság és a maximális hatótávolság fogalmak?
- Ismertesse az abszorpciós mérések geometriai elrendezését!
- Milyen az egyszerű abszorpciós görbe menete monoenergiás elektronokra?
- Ismertesse a β-sugárzás abszorpciós görbéjének menetét!
- Hogyan befolyásolja a fékezési sugárzás az abszorpciós görbét?
- Hogyan jön létre a fékezési röntgensugárzás?
- A β-reflexió mértéke minek a függvénye?
- Mit nevezünk telítési anyagvastagságnak?
- A telítési visszaszórt intenzitás hogyan függ a vizsgált anyag rendszámától?
- Írja fel a visszaszórt β-sugárintenzitás vastagság függését!
- Írja fel a β-sugárzás abszorpciós törvényét!
- Rajzolja fel a visszaszórt intenzitás rétegvastagság függését! Magyarázza meg a görbe viselkedést!
- Vegyületeknél, keverékeknél, hogyan függ az elemek rendszámától a visszaszórt intenzitás?
- Hogyan változik a visszaszórt intenzitás a bevonatvastagság függvényében Zr > Zh illetve Zr < Zh esetben?
- Rajzolja fel a reflexiós mérőberendezés elvi vázlatát!
PDF formátum