Elektromos alapmérés
A mérés célja:
- megismerkedni a legfontosabb elektromos jellemzők (az áram, a feszültség és az ellenállás) mérésének néhány egyszerű módszerével és a mérőeszközökkel
- egyszerű kapcsolások (például a feszültségosztó, alul/felüláteresztő szűrő, soros rezgőkör) összeállításának gyakorlása, majd mérések kivitelezése
Ennek érdekében:
- áttekintjük az egyen- és váltóáramú áramkörök törvényszerűségeit,
- ismertetjük a gyakorlat során alkalmazott mérési módszereket,
- egyszerű felépítésű áramkörök jellemzőit vizsgáljuk.
Tartalomjegyzék |
Elméleti összefoglaló
Az egyenáramú körökkel kapcsolatos alapfogalmak és törvények rövid összefoglalása
Áram, feszültség és ellenállás
A töltéshordozók áramlásának intenzitását jellemző mennyiség az áramerősség
![\[I=\frac{{\rm d}Q}{{\rm d}t}\]](/images/math/c/1/d/c1dc84d50abe61ab7ea9c23f7be10f5b.png)
ahol 
egy adott felületen átáramló töltést és 
az időt jelenti. Az áramerősség egysége az amper (A). Az egyenáram irányát – megállapodás alapján – a pozitív töltéshordozók mozgásának iránya adja meg. Egyenáramról beszélünk, ha az áram erőssége időben állandó.
Egy vezető két pontja között levő 
potenciálkülönbség (feszültség) áram kialakulásához vezet. A vezetőre kapcsolt feszültség és a benne folyó áram között sok esetben (pl. fémes vezetőkben) az
![\[U=RI\]](/images/math/d/a/7/da7dfc4aaac334c33bcb08664604f794.png)
összefüggés – az Ohm törvény – áll fenn. Itt 
a vezető ellenállása, amely a geometriai adatoktól (
hosszúság és 
keresztmetszet) valamint a vezető anyagától (
fajlagos ellenállás ) az alábbi módon függ:
![\[R=\rho\frac{l}{A}\]](/images/math/9/7/6/976cfd771443eee081282dffb56840c6.png)
A fajlagos ellenállás – sok más anyagi jellemzőhöz hasonlóan – hőmérsékletfüggő:
![\[\rho=\rho_0\left[1+\alpha(t-t_0)+\beta(t-t_0)^2+...\right]\]](/images/math/7/4/0/740ec02430313e290154d4d285124a6a.png)
ahol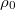 
a fajlagos ellenállás 
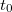hőmérsékleten, 
, 
, ... stb. anyagi állandók és a fajlagos ellenállás hőmérsékleten felvett értéke. A vizsgált hőmérsékleti tartomány nagysága és a kívánt pontosság meghatározza, hogy konkrét esetben a fajlagos ellenállás hőmérsékletfüggésének leírásánál milyen közelítést alkalmazunk, azaz a kifejezésben hányadrendű tagig megyünk el.
Kirchhoff-törvények
Egyenáramú áramkörökkel kapcsolatos számításokat a Kirchhoff-törvények segítségével végezhetünk. A töltésmegmaradás törvényének kifejezése az úgynevezett csomóponti törvény: egy csomópontba összefutó áramok előjeles összege nulla. Ha a ki- és befolyó áramokat ellentétes előjelűnek tekintjük:
![\[\sum_{i=1}^n I_i=0\]](/images/math/e/d/0/ed0ab427e26431a3a1a2d79e07330421.png)
Az energiamegmaradás törvényének következménye a huroktörvény, mely szerint egy zárt vezetőhurok feszültségeinek előjeles összege zérus:
![\[\sum_{i=1}^n U_i=0\]](/images/math/0/8/5/0851e4174ef34b149e0a18de582eb0fc.png)
A Kirchhoff-törvények alkalmazásának egy lehetséges módja az alábbi:
- Felrajzoljuk az áramkört és bejelöljük a telepek polaritását.
- Tetszőlegesen felvesszük az ág áramokat és bejelöljük az irányukat.
- Bejelöljük a hurkokban tetszőleges körüljárási irányokat.
- Felírjuk a csomóponti egyenleteket. (Például a csomópontba befolyó áramokat tekintjük pozitívnak, a kifolyókat pedig negatívnak.)
- Felírjuk a hurokegyenleteket. Ilyenkor pl. úgy járhatunk el, hogy a telepeken a pozitív pólustól a negatív pólus felé haladva a telep
üresjárati feszültségét pozitív előjellel vesszük figyelembe (fordított esetben pedig negatívval), az ellenállásokon eső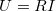 
feszültséget pedig akkor vesszük pozitív előjellel számításba, ha a körüljárási irány és a bejelölt ág áram iránya megegyezik (ellenkező esetben pedig negatívval).
- Megoldjuk az egyenletrendszert. Azok az áramok, amelyek pozitívnak adódnak ténylegesen az előzetesen felvett irányban folynak. Ha a számítások alapján az áramra negatív érték jön ki, a tényleges áramirány a felvettel éppen ellenkező.
Megmutatható, hogy egy áramkör esetében annyi egymástól független egyenlet írható fel, amennyi az ágak – vagyis az áramok – száma.
A Kirchhoff-törvények alkalmazásával könnyen megkapható, hogy 
darab sorba kapcsolt ellenállás eredője
![\[R_s=\sum_{k=i}^n R_i\]](/images/math/1/b/2/1b2531feef0ae8bd4cbee70c5ebb1371.png)
illetve a párhuzamosan kapcsolt ellenállások esetében az eredő reciproka:
![\[\frac{1}{R_p}=\sum_{i=1}^n \frac{1}{R_i}\]](/images/math/c/c/8/cc8c9f16cafd86b5d9071a4c8ed1dd4f.png)
Az áramkörbe be nem kötött, ún. nyitott telep sarkai között fellépő feszültség az üresjárati feszültség, melynek nagysága megegyezik a telep elektromotoros erejével. Az áramkörbe bekötött (árammal átjárt) telep sarkai között fennálló feszültség az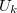 
kapocsfeszültség. Ennek értéke és előjele a telepen átfolyó áram irányától és nagyságától függően az üresjárási feszültségétől jelentősen eltérő lehet. Az eltérés az 
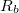belső ellenálláson eső feszültségből adódik:
![\[U_k=U_0-R_bI\]](/images/math/2/3/d/23d30fd9a10e698b33003e9eaca922de.png)
Áram és feszültség mérése
Egyenáram és egyenfeszültség mérése a kérdéses mennyiség nagyságának és irányának (polaritásának) meghatározását jelenti.
Az árammérőt (ampermérőt) mindig sorosan kell bekötni az áramkörbe, azaz úgy, hogy a mérni kívánt áram átmenjen a műszeren. Ebből következik, hogy ideális esetben az árammérő ellenállásának zérusnak kellene lennie. Ha a műszer ellenállása nem nulla, akkor az áramkör ellenállását és ezen keresztül az áram értékét is megváltoztatja, és így mérési hibát okoz. Az elkövetett hiba a vizsgált áramkör elemeinek és az alkalmazott műszer belső ellenállásának ismeretében meghatározható.
A feszültségmérő műszer (voltmérő) két bemeneti pontját mindig ahhoz a két ponthoz kell kötnünk, amelyek közötti feszültséget akarjuk megmérni. (Ha ez egy áramköri elem két végpontja, akkor ez azt jelenti, hogy a feszültségmérőt az áramköri elemmel párhuzamosan kell kapcsolni.) Ideális esetben a voltmérő belső ellenállásának végtelennek kellene lennie. Ellenkező esetben a műszer bekötése megváltoztatja a vizsgált két pont közötti ellenállást, és így egyúttal a mérni kívánt feszültséget is, vagyis mérési hibát okoz.
A digitális voltmérők ellenállása legalább 1 M
, ami a mérési gyakorlaton vizsgált ellenállásoknál 3-4 nagyságrenddel nagyobb. Ebben az esetben a voltmérő ideálisnak tekinthető.
A digitális ampermérő belső ellenállása méréshatár függő, érzékeny állásban akár 1 k is lehet, ami összemérhető a vizsgált ellenállások nagyságával. Így az árammérő nem tekinthető ideálisnak.
Ellenállásmérés Ohm-törvénye alapján
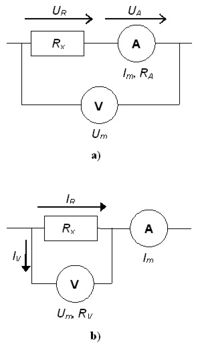
Ha ismerjük az ellenálláson átfolyó áram erősségét, valamint az ellenállás végei közötti feszültséget, akkor az ellenállás értéke az Ohm-törvény segítségével meghatározható. Ezen elv alkalmazásához az 1. ábrán látható, ellenállásmérésre alkalmas kapcsolásokat állíthatjuk össze.
Az ábra a) része alapján látható, hogy az ampermérő ténylegesen az ellenálláson át folyó áramot méri, de a voltmérő már az ellenálláson és az ampermérőn eső feszültségek összegét mutatja,
mivel az ampermérő ellenállása nem nulla. Így mérési eredményünk hibás lesz. Az ellenállás helyes értékének meghatározásához az ampermérőn eső feszültséget az ampermérő belső ellenállásának ismeretében lehet kiszámítani.
A mérendő 
ellenállás a mért értékek segítségével kifejezve:
![\[R_x=\frac{U_R}{I_m}=\frac{U_m-U_A}{I_m}=\frac{U_m-R_AI_m}{I_m}\]](/images/math/f/6/4/f6458cd478910579b0fc41d6bd19d794.png)
Mérési hibát követünk el akkor is, ha a kapcsolást az ábra b) része szerint állítjuk össze. Ekkor ugyan a voltmérő ténylegesen az ellenálláson eső feszültséget méri, az ampermérő viszont az ellenálláson és a voltmérőn átfolyó áramok összegét mutatja. Mivel a voltmérő ellenállása nem végtelen nagy, elvileg itt is a műszer ellenállásának ismeretében lehet csak meghatározni a mért ellenállást:
![\[R_x=\frac{U_m}{I_R}=\frac{U_m}{I_m-I_V}=\frac{U_m}{I_m-\frac{U_m}{R_V}}\]](/images/math/7/d/5/7d510c84917d441ce49e57451da9e850.png)
A mérési gyakorlaton előforduló esetekben azonban a voltmérő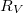 
ellenállása több nagyságrenddel nagyobb, mint a mérendő ellenállások, így a korrekcióra nincs szükség, az ellenállás egyszerűen az
![\[R_x=\frac{U_m}{I_m}\]](/images/math/0/5/f/05fa8eed70a50d17a18885ca563d74a4.png)
képlettel számolható. Éppen ezért a két lehetséges kapcsolás közül ezt érdemes választani a gyakorlaton.
A digitális multiméterekkel közvetlenül is lehet ellenállást mérni. Az ellenállásmérő is az Ohm-törvény alapján méri az ellenállás értékét: a műszer meghatározott nagyságú (kis) áramot bocsát át az ellenálláson, és méri az ellenálláson eső feszültséget. A műszer kijelzőjén közvetlenül az ellenállás értéke olvasható le.
FONTOS, hogy ellenállásmérővel csak áramkörbe be nem kötött (passzív) eszköz ellenállása mérhető. Ha a mérendő ellenállás egy áramkör része, akkor hibás lesz a mérési eredmény (hiszen az ellenálláson nem csak az ellenállásmérő által kibocsátott áram folyik), és ezen kívül a műszer is tönkremehet. Emiatt: TILOS az ellenállásmérőt feszültség alatt lévő áramkörre kapcsolni!
Az ellenállásmérővel megmérhető az ampermérő belső ellenállása is: Kapcsoljuk az egyik, ellenállásmérő üzemmódban lévő multimétert a másik, ampermérő üzemmódban lévő (számunkra érdekes méréshatárra állított) multiméterre. Az ellenállásmérő méri az ampermérő (méréshatárfüggő) belső ellenállását. (Eközben az ampermérő megméri az ellenállásmérő – szintén méréshatárfüggő – mérőáramát.)
Váltóáramú körökkel kapcsolatos alapvető tudnivalók
A fentiekben az áramot időben állandónak (vagy a méréshez képest nagyon lassan változónak) tekintettük, ami sok esetben teljesül, azonban fontos megemlíteni az időben változó áramok témakörét is. Ezen belül a periodikusan (szinuszosan) változó jelekhez kapcsolódó fontosabb információkat tekintjük át.
Komplex jelölés
Szinuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos 
körfrekvenciával változik, viszont a különböző áramköri elemeken eső feszültségek között fáziskülönbséget tapasztalhatunk.
A tekercsben indukálódó feszültséget az
![\[u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}\]](/images/math/7/0/d/70d81694316981734d9306478ac2b228.png)
egyenlet írja le. Szinuszos gerjesztés [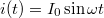
] alkalmazása esetén
![\[u(t) = L \omega I_0 \cos\omega t = L \omega I_0 \sin( \omega t + 90^\circ)\]](/images/math/c/2/7/c275e29b5fbcbfa7b60d84d561ea9873.png)
alakban írható fel. Míg a kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:
![\[i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}\]](/images/math/1/5/1/1514b1da65317e0322e95ce9e4387d82.png)
Szinuszos gerjesztés [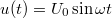
] esetén:
![\[i(t) = C\omega U_0\cos\omega t = C\omega U_0\sin(\omega t + 90^\circ)\]](/images/math/8/e/3/8e34b929a93dc659fb31b238e868ec52.png)
alakot kapjuk. A képletekből kiolvasható, hogy a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest, míg a kondenzátor árama 90°-ot siet a feszültségéhez képest.
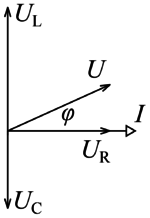
Az áramköri elemeken eső feszültség (vagy átfolyó áram) egymáshoz képesti fáziskülönbségeit ilyenkor fazorábrával szemléltethetjük. Az 2. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek. Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő fazor vektori eredője.
A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a komplex szám abszolút értéke a jel nagyságát (csúcsértékét), a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát adja meg.
Figyelem! Mivel a villamos hálózatoknál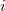 
az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt 
!
Az 2. ábrán látható fazorábrán szereplő jeleknek megfelelő komplex mennyiségek:
![\[\mathbf{I}=I\]](/images/math/d/b/3/db3b10836f663e18d0b2457c4f381161.png)
![\[\mathbf{U_{\rm R}}=U_{\rm R}=RI\]](/images/math/6/d/e/6dea4cee9d301924a744b4a8c84a41ec.png)
![\[\mathbf{U_{\rm L}}=jU_{\rm L}=j\omega LI\]](/images/math/4/0/4/404442f2e57583da99a06b8decbb04df.png)
![\[\mathbf{U_{\rm C}}=-jU_{\rm C}=I/j\omega C\]](/images/math/5/0/2/502eb5b1ee2c68e4c415bc5288d65148.png)
Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:
![\[\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= RI + j\omega LI + I/j\omega C\]](/images/math/6/6/4/6641a34eef0fb3219e31270b1ff325ca.png)
Az eredő feszültség nagysága (csúcsértéke) a komplex érték abszolút értéke:
![\[U=|\mathbf{U}|=\sqrt{R^2+(\omega L-1/\omega C)^2}I=ZI,\]](/images/math/a/4/c/a4cd1a16c71b0e334e88ba1acfcabfd1.png)
ahol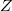 
az eredő ellenállás.
Az eredő feszültség fázisa a komplex feszültség arkusza:
![\[\varphi=\arccos\frac{R}{Z}.\]](/images/math/7/3/d/73dfbd65becf4c14d17054046e02c2d1.png)
A komplex áram és feszültség alapján azonban közvetlenül is fel tudjuk írni az áram és a feszültség időfüggvényét:
![\[i(t)=\rm{Re}\left(\mathbf{I}e^{j\omega t}\right)=I\cos \omega t\]](/images/math/b/6/8/b68fbcf4e38afed4b745c41ad35ae592.png)
![\[u(t)=\rm{Re}\left(\mathbf{U}e^{j\omega t}\right)=U\cos(\omega t+\varphi)=ZI\cos(\omega t+\varphi)\]](/images/math/d/7/b/d7bced5d7c0296acffc3b72671e50b2e.png)
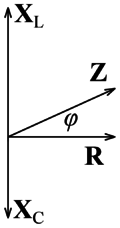
Ha az 2. ábrán látható fazorokat leíró komplex feszültségeket elosztjuk az áramerősség nagyságával, akkor ellenállás dimenziójú komplex mennyiségeket kapunk:
![\[\frac{\mathbf{U_{\rm R}}}{I}=\mathbf{R}=R\]](/images/math/2/0/d/20d4bff2b98a0110a9592b1262724367.png)
![\[\frac{\mathbf{U_{\rm L}}}{I}=\mathbf{X_{\rm L}}=j\omega L\]](/images/math/9/0/9/909749c3b65f94d726bfe561cccd17ed.png)
![\[\frac{\mathbf{U_{\rm C}}}{I}=\mathbf{X_{\rm C}}=1/j\omega C\]](/images/math/4/b/6/4b6488db0f72daa07f669e9634fad5ac.png)
![\[\frac{\mathbf{U}}{I}=\mathbf{Z}\]](/images/math/7/5/4/754bfd62ff79474ca4fe652ca9bf87df.png)
A komplex ellenállásokkal ugyanúgy számolhatunk egy váltóáramú körben, mint az ohmos ellenállásokkal egyenáramú hálózatok esetében.
A mi esetünkben a soros kapcsolás miatt az eredő (komplex) ellenállás az egyes (komplex) ellenállások összege:
![\[\mathbf{Z}=\mathbf{R}+\mathbf{X_{\rm L}}+\mathbf{X_{\rm C}}.\]](/images/math/3/4/8/348ecc64ebd75571a424645a09bb1775.png)
A komplex jelölésmóddal bármely áramköri elem leírása olyan, mintha egy ohmos ellenállás lenne:
![\[\mathbf{U_{\rm R}}=\mathbf{R}\mathbf{I}\]](/images/math/6/f/9/6f983d04136f9b37d69e64e469e822a4.png)
![\[\mathbf{U_{\rm L}}=\mathbf{X_{\rm L}}\mathbf{I}\]](/images/math/a/9/5/a95ad0be1fe4306378c8ec89f23f6bbf.png)
![\[\mathbf{U_{\rm C}}=\mathbf{X_{\rm C}}\mathbf{I}\]](/images/math/5/e/3/5e3f95af623562cd52e17a7ce9d424ae.png)
![\[\mathbf{U}=\mathbf{Z}\mathbf{I}\]](/images/math/9/d/8/9d836ab019d68fc534654b71bb9da238.png)
A komplex ellenállás abszolút értéke a skalár ellenállás értéket adja, míg arkusza azt mutatja meg, hogy az adott áramköri elem mennyivel tolja el a fázist.
Szűrő áramkörök
Szűrők segítségével egy különböző frekvenciájú rezgésekből álló elektromos jelből ki lehet szűrni bizonyos frekvenciatartományokat. Ezen a mérésen csak RC alul- és felüláteresztő szűrőket fog mérni, de itt néhány más kapcsolást is bemutatunk.
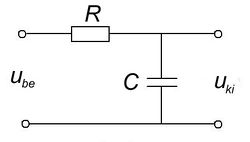
Aluláteresztő szűrők
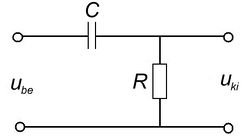
A 4/a és 4/b ábrákon látható kapcsolások kimenő feszültségeit a komplex jelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert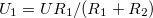 
feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!
 |
 |
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega RC} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega RC}\right|=\frac{1}{\sqrt{1+(\omega RC)^2}} \end{array} \]](/images/math/9/4/3/943854eb463ad63e4d67664743f7e96e.png) |
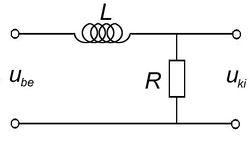
![\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{R}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega L/R} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega L/R}\right|=\frac{1}{\sqrt{1+(\omega L/R)^2}} \end{array} \]](/images/math/5/f/1/5f1da1dd24d313e4abefdadb0d7af81c.png) |
A kimeneti és bemeneti feszültségek hányadosa, a hálózatra jellemző, frekvenciafüggő kifejezés.
A két kifejezés formailag azonos, tehát a két kapcsolás azonos jellegű viselkedést mutat. Ameddig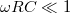 
vagy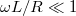 
, a kifejezések értéke 1; ha 
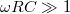vagy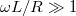 
, a hányados értéke 
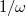szerint csökken. Ez azt jelenti, hogy adott , 
és 
esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
Felüláteresztő szűrő
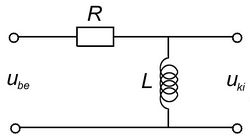
A 5/a és a 5/b ábrákon látható kapcsolásokat leíró egyenletek az előző pontban követett eljárás alapján az alábbiak szerint alakulnak.
 |
 |
![\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{R}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + 1/j\omega RC} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + 1/j\omega RC}\right|=\frac{1}{\sqrt{1+(1/\omega RC)^2}} \end{array} \]](/images/math/6/7/e/67eb7285e8d93596127be6e7771a16c0.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{j\omega L}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + R/j\omega L} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + R/j\omega L}\right|=\frac{1}{\sqrt{1+(R/\omega L)^2}} \end{array} \]](/images/math/b/0/d/b0d1a82212f3c504b48dcc32ffe04a9a.png) |
A kifejezésekből jól látszik, hogy a kapcsolások a kisfrekvenciás jeleket nem engedik a kimenetre, míg a nagyfrekvenciás jelek csillapítás nélkül jelennek meg a kimeneti pontokon. Ezek felüláteresztő szűrők.
Soros rezgőkör
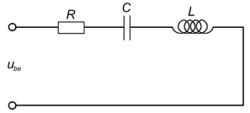
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (7. ábra).
Ha a kondenzátort feltöltenénk, majd a bemenetet rövidre zárnánk, akkor egy csillapodó rezgést figyelhetnénk meg. A nagy frekvencia és a gyors csillapodás miatt azonban ezt nehezebb megfigyelni, mint egy kitérített, és magára hagyott mechanikai rezgő rendszert.
Ha a bemenetre szinuszos gerjesztő feszültséget kapcsolunk, akkor viszont a kényszerrezgéssel teljesen analóg viselkedést figyelhetünk meg.
Ha a rezgőkörre kapcsolt feszültség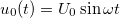 
, és a kondenzátor töltését az idő függvényében 
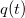írja le, akkor
![\[u_{\rm C}=q(t)/C\]](/images/math/6/e/5/6e557c5a7c02f41f9e8b70185a9b0687.png)
![\[i(t)=\dot{q}(t)\]](/images/math/3/4/5/345f04f2a83cf0399cf9dc740f7a3cc0.png)
![\[u_{\rm R}=Ri(t)=R\dot{q}(t)\]](/images/math/0/f/9/0f98abcde80a186b296ccde6f3a37145.png)
![\[u_{\rm L}=L\dot{i}(t)=L\ddot{q}(t)\]](/images/math/4/1/1/41175632a87ec6b612a0336e39d0926c.png)
![\[L\ddot{q}(t)+R\dot{q}(t)+q(t)/C=U_0\sin\omega t\]](/images/math/8/f/e/8fe0fb39e34df6fdeb9a07c794faa834.png)
![\[\ddot{q}(t)+\frac{R}{L}\dot{q}(t)+\frac{1}{LC}q(t)=\frac{U_0}{L}\sin\omega t.\]](/images/math/d/3/c/d3ce0c79341d4c23d3824118773ab42e.png)
Ez a differenciálegyenlet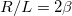 
és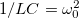 
jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.
Esetünkben a tranziens tag hamar elhal, és az állandósult tagot tanulmányozhatjuk. Az amplitúdó itt a kondenzátor töltése, de számunkra sokkal érdekesebb ennek deriváltja, a körben folyó áramerősség. Ez tehát az analógia alapján a mechanikai rezgés sebességrezonanciájával egyezik meg:
![\[I(\omega)=\frac{U_0}{L\sqrt{\left(\omega^2-\omega_0^2\right)^2+4\beta^2\omega^2}}.\]](/images/math/4/3/a/43a8a3f9f64b2cde816dccbf4d03ee63.png)
Ha behelyettesítjük és 
értékét, akkor
![\[I(\omega)=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}.\]](/images/math/b/7/f/b7f728d8b68397856b7e50ba9f6cea9a.png)
Ezt az eredményt azonban sokkal egyszerűbben megkapjuk a fentebb ismertetett komplex ellenállások felhasználásával. (Természetesen csak az állandósult állapotot vizsgálhatjuk így, a tranzienseket nem.)
A hálózat eredő impedanciája:
![\[\mathbf{Z}(\omega) = j\omega L + 1/j\omega C + R\]](/images/math/e/a/f/eaf39d1295bbd3bf4ce695878e668e42.png)
Az impedancia abszolút értéke és fázisszöge:
![\[Z(\omega) = \sqrt{(\omega L-1/\omega C)^2+R^2}\]](/images/math/a/f/b/afb8959afc8675cd549498ff967704b1.png)
![\[\varphi = \arccos\frac{R}{Z}\]](/images/math/7/2/9/729d8f49d530c5b193375ba76e77a481.png)
A körben folyó áram:
![\[I(\omega) = \frac{U_0}{Z}=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}\]](/images/math/e/1/3/e138a1c974541fd1854b72cad55d8434.png)
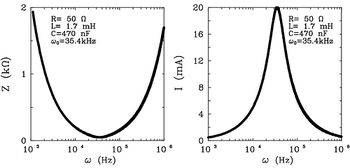
A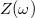 
és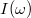 
függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (8. ábra).
Látható, hogy az eredő impedanciának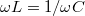 
esetén az
![\[\omega_0 = \frac{1}{\sqrt{LC}}\]](/images/math/a/d/4/ad4a43ecaf657200d72e8c141af15534.png)
körfrekvencián minimuma van, értéke valós, az ohmos (veszteségi) ellenállással egyezik meg. A jelenséget rezonanciának, -t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.
Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymáshoz viszonyítva 180°-os fázisban vannak, abszolút értékük pedig megegyezik (hiszen azonos áram folyik át rajtuk), így egymást kiegyenlítik.
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
Az áram- és feszültség- illetve az ellenállásmérésre alkalmas műszerekből és az áramköri elemekből a csatlakozózsinórok segítségével az áramköröket a hallgatók maguk állítják össze.
1. Ellenállások mérése multiméterrel
Válasszon ki négy darab tetszőleges ellenállást ügyelve arra, hogy ne legyen két egyforma köztük! Határozza meg az ellenállások értékeit és toleranciáját a színkód alapján, majd mérje meg a pontos ellenállásértéket egy multiméterrel!
- Az ellenállás színkód alapján történő meghatározásához itt talál információt.
- Becsülje meg az ellenállásmérés hibáját! Figyelje meg, mennyire stabil a mért jel! Jegyezze fel tapasztalatait! A mért és a színkód alapján meghatározott értékek a tolerancia/hibasávon belül vannak? Ugyanazt méri-e, ha egy másik műszert használ? Mekkora a vezetékek ellenállása?
2. Ellenállások mérése Ohm-törvény alapján
Mérje meg egy multiméterrel a rendelkezésre álló telep üresjárati feszültségét (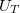
)! Válasszon ki két olyan ellenállást, amiket külön-külön a telepre kötve 20 mA alatti áramot várna az így létrehozott áramkörben! Ha nincs megfelelő ellenállás, akkor több ellenállást sorba kötve állítson be megfelelő értéket. Egy árammérő és egy feszültségmérő felhasználásával hozzon létre egy olyan kapcsolást, amellyel az adott ellenállások értékét meg tudja határozni.
- Hasonlítsa össze a kapott értékeket az előző feladatban mért értékekkel! Becsülje meg az ellenállás- feszültség- és árammérés hibáját és határozza meg az eltérés lehetséges okait! Állapítsa meg, hogy mekkora a telep és az árammérő belső ellenállása! Mi történik, ha az árammérőt, vagy a feszültségmérőt más méréshatárban használja?
A feladathoz kapcsolódóan mérje meg egy árammérő belső ellenállását! Ehhez használjon két multimétert, egyiket állítsa ellenállásmérésre, míg a másikat áramerősség-mérésre és kösse össze őket a megfelelő módon! Jegyezze fel a kapott ellenállásokat az árammérő minden méréshatára esetén!
3. Soros kapcsolás vizsgálata
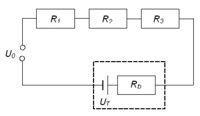
Válasszon ki három tetszőleges ellenállást majd kösse sorba őket egy teleppel (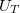) és egy tápegységgel () a 9.ábrának megfelelően! Mérje meg az egyes elemeken eső feszültséget és vizsgálja meg, hogy teljesül-e Kirchhoff második törvénye! Ezután fordítsa meg a telep polaritását és újra mérje meg az egyes elemeken eső feszültséget!
- A tápegységen 12V-os feszültséget állítson be!
- Tapasztalatait jegyezze le! Becsülje meg a mérés hibáját! Teljesül Kirchhoff második törvénye? A két mérésből határozza meg a telep belső ellenállását (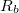) és elektromotoros erejét ()!
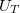4. Feszültségosztó méretezése izzó meghajtásához
Ebben a feladatban egy potenciométeres feszültségosztót méretezünk úgy, hogy segítségével egy 6 V, 1,2 W-os izzót működtethessünk 12 V-os feszültségforrással, majd megmérjük az izzón eső üzemi feszültséget és az átfolyó áramo. Végül a mérési eredményeket felhasználva határozzuk meg az izzószál üzemi hőmérsékletét!
a) Ohm-mérő segítségével mérje meg a kísérletben használt izzó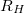 
hidegellenállását, illetve a megadott névleges feszültség és teljesítmény értékekből számolja ki az izzó üzemi ellenállását (
)!
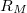- A mérésnél vegye figyelembe a vezetékek ellenállását!
b) Mérje meg a dobozba épített tolóellenállás (potenciométer)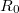 
ellenállását!
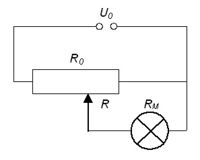
c) A 10. ábrán látható kapcsolás alapján számítsa ki, hogy a tolóellenállásból mekkora ellenállást kell az izzóval párhuzamosan kapcsolni, azaz hová kell állítani a csúszkát!
- Számításai szerepeljenek a mérési naplóban!
- Gondolja át a méréshez használt áramkört! Ahol szükséges, ott vegye figyelembe a műszerek belső ellenállását!
d) Ellenállásmérő segítségével állítsa be a megfelelő értéket, és állítsa össze az áramkört!
- A kapcsolási rajz (a műszerek bekötésével együtt) szerepeljen a mérési naplóban! Ha nincs ideje rajzot készíteni, akkor megfelelő megoldás, ha a leiratból bemásolja a kapcsolási rajzot és szóban leírja, hogy melyik műszert melyik ágba köti.
- Az áramerősségmérőt amperes (A) méréshatárban használja!
e) Az összeállított áramkörrel ellenőrizze számításai helyességét!
f) Állapítsa meg az izzólámpa tényleges üzemi paramétereit (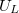
, 
, , 
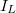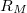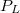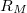)! a tényleges melegellenállás.
- Ha lényegesen eltérnek az előzetesen kiszámított értékektől, akkor ellenőrizze a számításait, és szükség esetén módosítson a beállításon!
g) Az izzólámpa 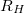hidegellenállásának és 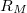melegellenállásának valamint a 
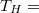300 K hideg hőmérsékletnek az ismeretében számítsa ki az izzószál üzemi hőmérsékletét! A volfrám hőfoktényezője 
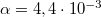1/K.
5. Ellenállásból és kondanzátorból álló aluláteresztő szűrő vizsgálata
Fakultatív feladat! (Ennek a feladatnak a megoldása nem kötelező, csak akkor foglalkozzon vele, ha marad elég idő rá.)
Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget függvényében! Ábrázolja a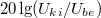 
– 
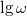függvényt! Illesszen a mért adatokra az elméletnek megfelelő görbét! Az illesztésből határozza meg a szűrőre jellemző 
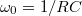körfrekvenciát, majd ebből az ellenállás ismeretében a kondenzátor kapacitását! (
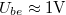legyen!)
- A multiméterekkel mérhető frekvenciatartomány: 5 Hz – 100 kHz. Az , értékeket úgy kell kiválasztani a panelen lévők közül, hogy
lehetőleg ennek a tartománynak a közepe táján (0,5-1 kHz körül) legyen. Figyelem! A képletekből -t számolunk, de a műszerek 
-et mérnek!
- A kondenzátor értékének meghatározásához itt talál információt.
- A mérési naplóban írja le, hogy milyen elemeket használt fel a kapcsolás összeállításához! Válaszát számítással indokolja.
- Mivel az eredményeket logaritmikus skálán fogja ábrázolni, érdemes nagyjából logaritmikusan egyenletes sűrűséggel felvenni az adatokat. Pl.: 5 Hz, 10 Hz, 20 Hz, 50 Hz, 100 Hz, ...
