Experiments with Polarized Light
Investigation of Liquid Crystal Displays
Liquid Crystals
Liquid crystal (LC) is a state of matter that is intermediate between the crystalline
solid and the amorphous liquid. The nematic LCs are organic compounds consisting of
long-shaped needle-like molecules. The orientation of the molecules can be easily aligned
and controlled by applying an electrical field. Uniform or well prescribed orientation of the
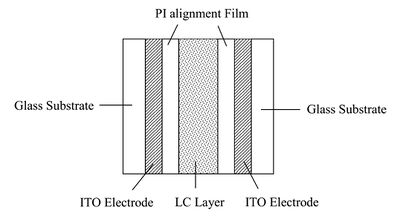
LC molecules is required in most LC devices. The structure of the LC cell used in this
experiment is shown in Fig 1. Rubbing the polyimide film can produce a well-aligned
preferred orientation for LC molecules on substrate surfaces, thus due to the molecular
interaction the whole slab of LC can achieve uniform molecular orientation. The local
molecular orientation is called the director of LC at that point.
The LC cell exhibits the so-called double refraction phenomenon with two principal
refractive indices. When light propagates along the direction of the director, all polarization
components travel with the same speed 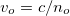 , where
, where 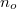 is called the ordinary index of
refraction. This propagation direction (direction of the director) is called the optical axis of
the LC cell. When a light beam propagates in the direction perpendicular to the optical axis,
in general, there are two speeds of propagation. The electric field of the light polarized
perpendicular (or parallel) to the optical axis travels with the speed of
is called the ordinary index of
refraction. This propagation direction (direction of the director) is called the optical axis of
the LC cell. When a light beam propagates in the direction perpendicular to the optical axis,
in general, there are two speeds of propagation. The electric field of the light polarized
perpendicular (or parallel) to the optical axis travels with the speed of 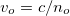 (or
(or
 , where
, where 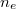 is called the extraordinary index of refraction). The birefringence
(optical anisotropy) is defined as the difference between the extraordinary and the ordinary
indices of refraction
is called the extraordinary index of refraction). The birefringence
(optical anisotropy) is defined as the difference between the extraordinary and the ordinary
indices of refraction  .
.
| Fig. 1. LC cell structure |
90o Twisted Nematic LC Cell
In the 90o twisted nematic (TN) cell shown in Fig. 2, the LC director of the back surface is twisted 90o with respect to the front surface. The front local director is set parallel to the transmission axis of the polarizer. An incident unpolarized light is converted into a linearly polarized light by the front polarizer.
| Fig. 2. 90o TN LC cell |
When a linearly polarized light traverses through a 90o TN cell, its polarization
follows the twist of the LC directors (polarized light sees 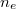 only) so that the output beam
remains linearly polarized except for that its polarization axis is rotated by 90o (it’s called
the polarizing rotary effect by
only) so that the output beam
remains linearly polarized except for that its polarization axis is rotated by 90o (it’s called
the polarizing rotary effect by 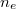 ; similarly we can also find polarizing rotary effect by
; similarly we can also find polarizing rotary effect by 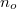 ).
Thus, for a normally black (NB) mode using a 90o TN cell, the analyzer’s (a second
polarizer) transmission axis is set to be parallel to the polarizer’s transmission axis, as
shown in Fig. 3. However, when the applied voltage V across the LC cell exceeds a critical
value
).
Thus, for a normally black (NB) mode using a 90o TN cell, the analyzer’s (a second
polarizer) transmission axis is set to be parallel to the polarizer’s transmission axis, as
shown in Fig. 3. However, when the applied voltage V across the LC cell exceeds a critical
value 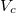 , the director of LC molecules tends to align along the direction of applied external
electrical field which is in the direction of the propagation of light. Hence, the polarization
guiding effect of the LC cell is gradually diminishing and the light leaks through the
analyzer. Its electro-optical switching slope
, the director of LC molecules tends to align along the direction of applied external
electrical field which is in the direction of the propagation of light. Hence, the polarization
guiding effect of the LC cell is gradually diminishing and the light leaks through the
analyzer. Its electro-optical switching slope 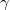 is defined as
is defined as 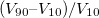 , where
, where  and
and
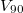 are the applied voltages enabling output light signal reaches up to 10% and 90% of its
maximum light intensity, respectively.
are the applied voltages enabling output light signal reaches up to 10% and 90% of its
maximum light intensity, respectively.
| Fig. 3. NB mode operation of a 90o TN cell |
Measurement Tasks
During the measurements a commercial 2 digit liquid crystal display is studied (Fig. 4.) such that the driving voltage is applied to all segments in parallel. The original polarizers of the display are removed, and replaced by rotatable polarizers. The measurements are performed both by white and laser light. In the latter case be very careful not to look into the laser beam directly! Note, that there are also beams reflected by the polarizers or other optical elements!
| Fig. 4. LC display |
- Assemble the optical setup with a white light source, the two polarizers, the LC cell, a lense and a screen. Project the image of the LC cell to the screen.
- Study the image of the LC cell at crossed and parallel polarizer directions. Investigate the image as the angle between the LC cell and the polarizer is rotated, such that the analyzer is always perpendicular/parallel to the polarizer. Discuss the observations!
- Repeat the previous task by gradually increasing the voltage on the LC cell. Always apply an a.c. voltage with ~100Hz frequency from a function generator, a d.c. voltage could destroy the cell. The voltage amplitude should not exceed 7V.
- To quantify the above experiments repeat them with a laser as the light source and a light sensor. (In this case the lense should be excluded.)
- Study the transmitted light intensity at zero driving voltage as a function of the angle between the LC cell and the polarizer. (In all cases keep the perpendicular/parallel orientation between the polarizer and the analyzer)
- Set the TN mode, and study the optical transmission as a function of the driving voltage amplitude. Determine the electro-optical switching slope.
- Set the polarizers such, that the vertical axis of the LC cell is in 45o angle with respect to the polarizer. The analyzer should be perpendicular/parallel to the polarizer. Study the transmission as a function of driving amplitude, and try to understand the observations!