Investigation of atomic contacts
The purpose of the measurement is to investigate the transport properties of atomic-sized contacts using a MyDAQ data acquisition card. For this purpose, the conductance curves of nanojunctions are recorded in the last moments before rupture, when only a few atoms connect the two sides. The acquired conductance traces are statistically examined using a conductance histogram.
Introduction: atomic sized contacts
Nowadays, an increasingly important and rapidly growing field of physics research is the study of various nanostructures with a typical width of several hundred - or as we will see - single atoms. Devices of nanometer scale exhibit many astonishing quantum physics processes, as the size of the system becomes comparable to the mean free path of electrons or even to the wavelength of the electrons, moreover in the case of very small, atomic systems, the atomic quantization of matter must be also taken into account. In addition to the study of quantum physical phenomena as part of basic research, nanostructures play an increasingly important role in the miniaturization and development of electronic devices. The fabrication of most nanostructures requires a strong technical background based on electron beam lithography, furthermore many quantum physics processes can only be studied at extremely low temperatures (4 K-10 mK). However in this measurement we study a nanophysical phenomenon that can be observed at room temperature with a relatively simple measurment system, even though the structure under investigation is probably one of the smallest nanostructures: a contact in which two electrodes are connected by a single atom.
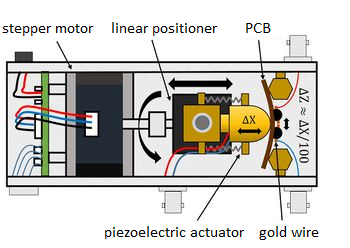
A single-atom contact is surprisingly easy to create, since at the last moment in the rupture of a metal wire usually only a single atom connects the two sides. However, the stabilization of the contact is a major challenge, since it's prerequisite is that the mechanical stability of the measuring device is significantly better than a typical atom to atom distance (~ 300 pm). Such conditions can be achieved with a high-stability low-temperature tunnel microscope or with the so-called MCBJ technique (Mechanically Controllable Break Junction technique). The principle of this method is illustrated in Figure 1. The contact is made of a simple metallic wire which is fixed with two adhesive dots on a bending beam. By bending the beam, the attachment points are moving apart so that the metallic wire can be broken. It follows from the mechanical arrangement of the instrument that, when the bending beam is bent in the centre by a smoothly movable axis, the relative displacement of the electrodes is around only 1/100 of the displacement of the axis. If measurements are made at extremely low temperatures, in a liquid helium environment and a finely tuneable piezo actuator is used to bend the beam, mechanical stability of up to a few pm can be achieved, which is by an order of magnitude better than what can be achieved using a scanning tunnel microscope.
| Figure 1: The sketch of the MCBJ setup. |
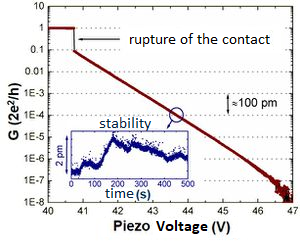
The stability of the system can be tested using a quantum mechanical effect. If the electrodes are gently moved closer after the rupture of the metallic wire even before direct contact occurs a tunnel current flows between the two sides, the magnitude of which is an exponential function of the electrode spacing. It is calculated that the tunnel current increases approximately tenfold when the electrodes are approached by 100 pm. In low temperature experiments, the exponential distance dependence can be detected through about six orders of magnitude (Figure 2), that is, the conductance increases by about one million times while the electrodes are only approached by 600 pm (two to three times the typical atomic distance). This phenomenon allows very sensitive detection of changes in the distance between the electrodes. The inset of Figure 2 shows that at a fixed piezo voltage, the electrode spacing changes by only 2 pm in ten minutes, which is about one hundredth of a typical atomic atom spacing. The figure also shows that as the electrodes are approached, a sudden jump is observed at a given point, followed by a conductivity plateau. This is the result of a direct metallic contact, which in most cases consists of a single atom.
| Figure 2: Tunnel current and mechanical stability test at 4K. |
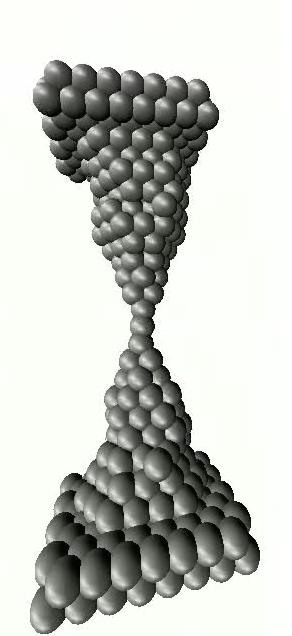
Let us now approach the formation of the atomic contact from the other side and examine the change in the conductivity as the metallic wire is broken. As the wire becomes thinner, we first experience a continuous decrease in conductivity. However, once the diameter of the contact reaches a few atoms, the conductivity can no longer change continuously due to granularity of material on atomic scale. Fig. 3a shows conductivity curves recorded during the rupture of nanocontacts. At first, when the two sides of the contact are pulled apart, the atoms move only elastically relative to one another, while the conductivity changes only moderately (plateau). However, after a certain amount of tension, the atoms rearrange abruptly, resulting in a more favourable configuration consisting fewer atoms at the narrowest part of the contact. Atomic rearrangements are reflected by a sudden change in conductance. At the last plateau before the rupture, usually there is only a single atom connecting the two sides. If the two electrodes are pushed together after rupture, the atoms on the broken surface will be reconnected, thus the rupture of the nanowire can be repeated over and over again (Fig. 3C). Naturally, the conductance curves look different, though similar in nature, for each nanocontact (see Figure 3a for different conductance traces). However the characteristic properties of nanocontacts made from a given material can be mapped using statistical methods. That is a histogram can be plotted from a large number of rupture conductance traces showing how often a given conductivity value was seen during the rupture (Fig. 3b). The peaks in the histogram show the conductance of stable, frequently occurring atomic configurations. The first peak of the histogram indicates the conductance of the single-atom contact. It is worth mentioning that in certain materials, e.g. in gold, a single-atom contact does not always break apart as a result of pulling, but it can form up to seven atoms in length and one atom wide atomic chain, as shown in the simulation of Fig. 3C and also by the large peak for the single atom contact in the histogram.
| Figure 3a: Conductance traces recorded during the breaking of a gold wire. The subsequent curves are similar in nature, but different in detail. After several breaking cycles the conductance histogram can be calculated and plotted as shown on panel b. The peaks in the histogram give the conductance value of frequently occurring atomic configurations | Figure 3c: Breaking of an atomic wire (computer simualtions). |
Understanding the conduction mechanism of a single atom requires a quantum mechanical approach, since the diameter of the contact is of the same order of magnitude as the wavelength of the electrons. Conductance takes place through quantized conduction channels whose conductivity must not exceed the quantum conductance unit, 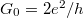 , where e is the electron charge and h is the plank constant.
, where e is the electron charge and h is the plank constant.
Figure 4:The conductance properties of atomic contacts can be modeled with two ideal leads separated by a scattering region. The n-th channel on the left is transmitted through the scattering region to the n-th mode on the right with a probability of  . .
|
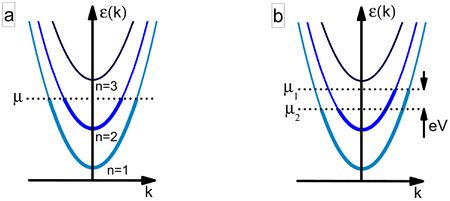
| Figure 5: (a)Dispersion relation in a nanowire. (b) The occupation in the dispersion relation changes due to the applied bias voltage. |
To understand why the conductance is quantized consider an ideal quantum conductor. (For a more detailed description see the Nanophysics Knowledge Base.) Imagine a ballistic wire connecting two parallel-walled electrodes which does not have any scattering centres such as the left or right side region on Figure 4. The motion of electrons in the conductor is described by the Schrödinger equation: transverse quantized modes are formed and electron waves propagate as longitudinal one-dimensional planar waves.
The dispersion relation is: 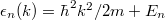 , where
, where 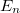 are the energies of transverse modes, k is the wavenumber and m is the mass of the electron (Fig.5a). The dispersions belonging to different quantized modes are called the conduction channels. We talk about an open channel if the dispersion relation intersects the chemical potential, otherwise for
are the energies of transverse modes, k is the wavenumber and m is the mass of the electron (Fig.5a). The dispersions belonging to different quantized modes are called the conduction channels. We talk about an open channel if the dispersion relation intersects the chemical potential, otherwise for  the channel is closed, that is, no electrons propagate in it. Let us calculate the conductance of the quantum wire for a single conduction channel. Applying voltage to the electrodes shifts the chemical potentials by
the channel is closed, that is, no electrons propagate in it. Let us calculate the conductance of the quantum wire for a single conduction channel. Applying voltage to the electrodes shifts the chemical potentials by  , thus states propagating from left to right have higher filling than states from right to left by
, thus states propagating from left to right have higher filling than states from right to left by  (Fig. 5b). Because of the shift of occupancy, the positive and negative currents are not equal, so in the wire a net current of
(Fig. 5b). Because of the shift of occupancy, the positive and negative currents are not equal, so in the wire a net current of 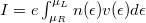 is present, where
is present, where 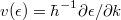 is the velocity of electrons,
is the velocity of electrons,  is the electron density, with
is the electron density, with 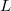 being the length of the wire and
being the length of the wire and 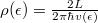 is the one dimensional density of states. After plugging these in:
is the one dimensional density of states. After plugging these in: 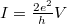 , which corresponds to one channel with a conductance of
, which corresponds to one channel with a conductance of 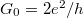 (or 12906 Ω resistance). This result can be generalized by considering several conducting channels and allowing a finite transmission probability in each channel (Figure 4). The system can be described in a suitable eigenbasis where electrons can only be scattered from the left n-th channel to the right n-th channel. Based on this, the conductance of any nanocontact can be described with the help of the Landauer formula:
(or 12906 Ω resistance). This result can be generalized by considering several conducting channels and allowing a finite transmission probability in each channel (Figure 4). The system can be described in a suitable eigenbasis where electrons can only be scattered from the left n-th channel to the right n-th channel. Based on this, the conductance of any nanocontact can be described with the help of the Landauer formula:
![\[G=\frac{2e^2}{h}\sum\limits_{n}{} T_n,\]](/images/math/d/5/6/d56db0d04c0942a7a2fc310e2d833b09.png)
where  is
is  -th transmission probability. A given nanocontact is well characterized by the number of conduction channels and the transmission probabilities of each channel, therefore the set of transmission coefficients is often referred to as the mesoscopic PIN code of the nanocontact.
-th transmission probability. A given nanocontact is well characterized by the number of conduction channels and the transmission probabilities of each channel, therefore the set of transmission coefficients is often referred to as the mesoscopic PIN code of the nanocontact.
The conductance traces and conductance histogram of Fig.3 shows that during the rupture of the contact, the last plateau corresponding to conductance of a single atom contact has a conductance of 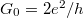 ,i.e. the conductance quantum. Strictly speaking, it cannot be concluded from this that a single, completely transmittable channel is responsible for the conduction, since several partially-transmitting channels may coincidentally result in a measured conductance of
,i.e. the conductance quantum. Strictly speaking, it cannot be concluded from this that a single, completely transmittable channel is responsible for the conduction, since several partially-transmitting channels may coincidentally result in a measured conductance of 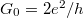 . To determine whether this is the case, additional measurements are needed which not only measure the sum of the transmission coefficients, but also provide additional information about the transmission coefficients. An example for this is the measurement of shot-noise: ff the temporal fluctuations of conductance are measured in addition to the average conductivity, then the quantity
. To determine whether this is the case, additional measurements are needed which not only measure the sum of the transmission coefficients, but also provide additional information about the transmission coefficients. An example for this is the measurement of shot-noise: ff the temporal fluctuations of conductance are measured in addition to the average conductivity, then the quantity 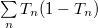 can also be determined. It can be seen that in the case of a single fully transmitting channel the shot noise disappears, whereas in the case of several partially transmitting channels finite noise is obtained. The noise measurements on the gold contact clearly showed that the conductance of the singe-atom gold contact with conductance of
can also be determined. It can be seen that in the case of a single fully transmitting channel the shot noise disappears, whereas in the case of several partially transmitting channels finite noise is obtained. The noise measurements on the gold contact clearly showed that the conductance of the singe-atom gold contact with conductance of 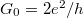 comes from a perfectly transmitting channel. This is due to the fact that only s electrons are involved in conduction of single atom gold contacts. However, in d-metals where d electrons also contribute to conduction of atomic contact, up to 5 partial transmission open channels can be observed. Note that this phenomenon strictly differs from the conductivity quantization observed in two-dimensional heterostructures or the quantum Hall effect, where only fully open and closed channels are present.
comes from a perfectly transmitting channel. This is due to the fact that only s electrons are involved in conduction of single atom gold contacts. However, in d-metals where d electrons also contribute to conduction of atomic contact, up to 5 partial transmission open channels can be observed. Note that this phenomenon strictly differs from the conductivity quantization observed in two-dimensional heterostructures or the quantum Hall effect, where only fully open and closed channels are present.
Measurement setup
| Figure 6: Metallic wire attached to a bendable substrate |
In lab course the conductance of single-atom contacts are investigated by repeatedly breaking and reconnecting a thin metallic wire. Since the conductance of a single-atom gold contacts is close to the conductance quantum, and gold is the least oxidizable of all metals, we make measurements on a gold sample. We use the MCBJ technique for controlled movement of the contact, and high purity gold fiber 100 μm in diameter attached to the bending beam.
The bending beam can be bent by means of a linear actuator controlled by a stepper motor and by a piezoelectric actuator. A bias voltage of 100 mV is applied to the sample using a NI myDAQ card, and the current flowing through the contact is measured with an I-V converter with a 10^5 current-voltage amplification.
As shown in Figure 1, the stepper motor, piezo actuator, and metal wire which is fixed to the flexible substrate are all mounted in an aluminium holder. The motor has to be connected to a power supply. Control of the motor and piezo actuator and conductance measurement are done entirely with a NI myDAQ card connected to a computer. The auxiliary circuits required for measurement are located on pre-assembled test circuit-boards.
The TRINAMIC - PD3-013-42 stepper motor is controlled via a four-pole microphone connector mounted on the aluminium frame. Three of the four poles are given digital signals from the measuring card. With one of the poles, the motor can be turned on and off (ENABLED), with an other pole, the motor rotation direction can be changed (DIRECTION), and by sending a short pulse to the third pole, the motor takes one step, e.g. about 0.1 degrees. The fourth pole is the Digital Ground (DGND). The motor is connected to the circuit using a special cable. The cable is colour coded as ENABLED - Blue, DIRECTION - Green, STEP - Orange, DGND - Brown. The ENABLED, DIRECTION, STEP, DGND signals are connected by the connector of the circuit-board to the DIO0, DIO1, DIO2 and DGND outputs of the card.
For smooth movement, we use the Piezomechanik PSt150 / 3.5x3.5 / 20 piezo actuator, which operates in the range of -30 to +150 V, the total voltage range corresponding to a movement of 28 μm. The piezo cannot be controlled directly from the measurement card as it would not be able to provide enough current, therefore we need to insert an amplifier. This amplifier circuit is also located on the assembled panel. The panel can be connected to a data acquisition card using a standard connector.
Measurement tasks
1. Familiarize yourself with the two panel MCBJ measurement program.
- The program should be able to do the followings:
- - Output a constant DC voltage. Measure the conductivity in through the timer cycle (for every different voltage on the piezo).
- - In every timer cycle outputs a triangular wave (output the triangular wave after the DC voltage, otherwise there will be an error).
- - Shows the measured data, but by clicking a button shows it only up to few
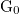 .
.
- - Shows the measured data, but by clicking a button shows it only up to few
- - Stores the data.
- - Calculates and updates the conductance histogram in every cycle.
The following steps will help in these tasks.
2. Based on this function generator program output one period of triangular wave with the amplitude of 10 V on the ao1 output of the NI myDAQ in every timer event (the wave should go like this: 0 V  10 V
10 V  -10 V
-10 V  0 V).
0 V).
3. Based on this oscilloscope program read the data on the ai0 input of the NI myDAQ in every timer event. Save the data to a file and plot it. To measure the conductance output a 100 mV DC voltage on the ao0 channel.
4. Implement a switchable software trigger: if the switch is on only plot N points after the trigger event. During the measurements the trigger level should be 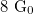 .
.
5. Write a routine which makes a histogram based on the measured curves, i.e., calculates the frequency of the different measured voltage points. It is recommended to think this step trough even before the start of the measurement, during the preparation for the laboratory practice. Save the histogram during/at the end of the measurement to a variable/file so it will be available for the report.
6. Plot on the panels both the measured conductivity and the cumulative histogram in 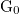 units.
units.
7. Assemble the measurement setup for the investigation of atomic contacts, and test it with a 12900 Ω resistor. Test the histogram making routine with a measurement on this resistor. The routine can be also tested on the triangular wave (on the corresponding array).
8. Switch the test resistance to the golden wire fixed on a bending beam. Rupture the junction with the stepper motor and record individual conductance traces. Save a few traces which show the conductance plateaus nicely. By using both the stepper motor and the piezoelectric actuator rupture the junction again and again and record at least 100 curves, calculate the cumulative histogram. Save this curves so they will be available for data analysis later.
Optional task 1: Investigate the push of the ruptured nano-contact. Record and plot the tunneling current. Plot the tunneling current also on logarithmic scale compare it to the expectations from the literature.
Optional task 2: By using the tunneling current control the distance of the electrodes. For this apply the well known PI control technique. Only use the piezo for the fine movement. Test the stability with different external effects (e.g. clapping, temperature fluctuation). Help:
In the report
- -Abstract
- -Theoretical introduction
- -Plot a few chosen rupture curves.
- -Sort the rupture and the push curves and plot the conductance histogram for each of them.
- -What is the difference between the two histogram?
- -What is the reason behind this differences?
- -Investigate the tunneling current part of a curve.
- -Find a physical quantity that can be determined from this and calculate it (there are multiple good answers).
- -Compare the calculated value to the one found in the literature or calculate it on another way.
- -Optional task: describe the basics of the PI control and how you realized it.
- -Discussion
Help
For the laboratory exercise an initial program is available here.