Kvantummechanika
Motiváció 60 évvel ezelőtt még hihetetlennek tűnt az, ami ma a számítástechnikában a valóság. A gyors és miniatűr logikai áramkörök (a legegyszerűbbtől a legbonyolultabbig) a napi életünk szerves részeivé váltak, akár tudunk erről, akár nem. A globalizáció eredményeként szinte nincsen a Világnak olyan eldugott helye, ahol ne lenne egy asztali számítógép internetes kapcsolat lehetőségével. Az információs társadalom ma már az Emberiség Információs Kultúrájává vált.
Ennek a hihetetlen és robbanásszerű (30-40 év) technológiai fejlődésnek a gyökerei a kvantummechanikában, az atomon belüli törvények felismerésében és alkalmazásában keresendők.
Az informatikai forradalom lényege: sok adat gyors, megbízható továbbítása (mozgatása) és kis helyen való biztonságos tárolása gyors hozzáféréssel.
Mindezekre a lehetőséget a Kvantummechanika egyik igen fontos alkalmazási területe, az elméleti és kísérleti Szilárdtestfizika teremtette meg. Az ezen alapuló technológiával (jelenleg) az IC-kben igen magas alkatrészsűrűséget értünk el. Az itt lévő logikai áramkörök azonban klasszikus módon működnek. A Kvantummechanika „csak” az elemi alkatrészek létrehozásában van jelen. David Deutch azon gondolkodott, mi történne, ha a kvantummechanika már a logikai műveletek szintjén megjelenne. Azaz a Boole-algebrát megvalósító „kétállpotú” rendszer kvatummechanikailag viselkedne.
Az elveket kidolgozta és ezzel útjára indult a Kvantuminformatika. Napjainkban az elmélet igen látványosan fejlődik. A kísérleti eredmények még lemaradtak (nyílvánvalóan a kérdéskör roppant bonyolultsága miatt). Senki nem engedheti meg magának, hogy kimaradjon az ez irányú kutatásokból. Ugyanis aki egy kvantumszámítógépet birtokol, annak számára a ma is használt titkosítási eljárások „csak pár percnyi” akadályt jelentenek. Nincsen előtte titok többé.
|
|
|
|
|
|
- A helytelenül értelmezett igazságok több kárt okozhatnak, mint az indokolt tévedések. (Thomas Huxley)
Bevezető gondolatok és kedvcsináló
Az érzékszerveink által érzékelt és az agyunkban leképzett klasszikus fizikai világ fogalmai a megszokott, változatlan formában használhatatlanok az atomi skálán lezajló fizikai folyamatok megértésében. Ezért a Fizikában egy valódi „szellemi forradalom” zajlott le a XX. század első harmadában. A „paradigmaváltás” ténylegesen megtörtént. Mindez érezteti hatását a klasszikus fizikai szemléletünkben is. Kétségtelen tény, hogy ma már a természettudós teljesen másképpen látja a világot, mint a száz évvel ezelőtt élt kollegája. Mindennap tapasztalhatjuk azt, hogy egy átlagos középfokú műveltséggel rendelkező ember fizikai szemlélete jó esetben is csak a XIX. század közepének megfelelő szinten van. Az a hatalmas technikai fejlődés, amely az elmúlt másfél száz évben végbement (a gőzgépektől a számítógép által vezérelt űrhajókig és atomreaktorokig, a postakocsitól a mobiltelefonig és a GPS-ig), egyértelműen a kvantummechanika megszületésének a következtében volt lehetséges. Elmondhatjuk tehát, hogy a kvantummechanika mint kezdetben „tiszta elméleti tudomány” olyan gyakorlati eredmények sokaságát produkálta, amelyek a technikai fejlődést alapvetően befolyásolták. Mindez átformálta mindennapjainkat is és így a Kvantummechanika a XX. századi civilizációnk és egyéni életünk szerves részévé vált akár tudatában vagyunk ennek, akár nem. A XXI. században dolgozó és alkotó mérnöknek (informatikusnak) valamilyen szinten igenis ismernie kell ezt a klasszikus szemléletünk számára idegen és furcsa, sokszor igen meghökkentő elméletet.
Másképpen látni a dolgokat, mint azok a felszínen látszanak, bepillantani a hétköznapi szemléletünk függönye mögé, az ember egyik alapvető pszichikai igénye. Ez a Kíváncsiság az, amely civilizációnk egyik hajtómotorja volt évezredeken át.
A természettudományos gondolkodás (és módszer) képes arra, hogy az Univerzum végtelennek tűnő bonyolultságában valamiféle rendet és szerkezetet fedezzen fel. Mindez természetesen a gondolkodásunknak csak egy magasabb absztrakciós szintjén lehetséges. Első pillanatra a kvantummechanika kijelentései meglehetősen misztikusnak tűnnek. De a kvantummechanika megérthető, ellenőrizhető, alkalmazható. Helyessége a mai mérnöki gyakorlatban az elektronikus alkatrészek előállítása során minden nap tapasztalható.
A kvantummechanika főleg szemléletében nyújt merőben újat. A használt matematikai apparátus (ebben a BSc kurzusban) lényegében megmarad a klasszikus analízis és lineáris algebra keretei között. A nehézség inkább abban van, hogy a klasszikus fizikai szemlélet számára szokatlan kijelentéseinket az egzakt matematika nyelvén kell megfogalmaznunk. Ez megkívánja a matematikai jelrendszer rutinos ismeretét és annak „könnyed” használatát.
Thomas Huxley (1825-1895) írta: A tudomány nagy tragédiája, ahogyan egyetlen rusnya tény lemészárol egy gyönyörű elméletet.
Valóban, a Fizika (mint a természettudományok általában) az elméleti modellek és a kísérleti eredmények állandó kölcsönhatásának eredményeképpen fejlődik. Minden elméleti állítás kísérleti igazolást követel és minden kísérleti eredmény elméleti magyarázatot igényel. A „Kísérlet” (azaz a „Valósággal való szembesülés”) ebben a kapcsolatrendszerben teljes „vétóval” rendelkezik.
„A tudomány története maga a tudomány”, szoktuk mondani, és ez különösen érvényes akkor, amikor egy eddig még ismeretlen, számunkra új területtel ismerkedünk meg. Nincsen ez másképpen a ma már több mint 100 éves kvantummechanikával sem.
A kvantummechanika kialakulását és történeti fejlődését az ábrán közölt hálódiagram szemlélteti. Világosan megmutatja a kísérleti eredmények (négyzet jelöli) és az elméleti modellek (pont jelöli) egymásra hatását. Ezen kurzus témája nem tudománytörténetet. Mégis, a kvantummechanika szemlétének a „megértését” megkönnyíti, ha kialakulásának történetét is ismerjük.
Az elmúlt 100 év hosszú idő a mindennapi életünket alapjaiban meghatározó technikai fejlődés skáláján. Gondoljunk csak arra, hogy a XIX század végén mennyire más volt az élet a mi kultúrkörünkbe tartozó Európában és Amerikában. A XX. század döntő változást hozott a fizika tudományában. A Világról alkotott képünk alapjaiban változott meg. Ezért a XIX. - XX. századforduló előtti fizikát klasszikus fizikának, az azt követő időszakét pedig modern fizikának szoktuk nevezni. A relativitáselmélet és a kvantummechanika az a két jellegzetes tudományterület, ahol szakítani kellett évszázadokon át jól bevált gondolati sémákkal és természetesnek tűnő szemléletekkel.
A „régi” kvantummechanika 1900. december 14-én született. Ekkor hangzott el a német Fizikai Társaság ülésén az akkor 42 éves (!) Max Planck előadása, amelynek a címe: „A normálspektrum energia-eloszlási törvényének az elmélete” volt. Ekkor ismertette a fekete test hőmérsékleti sugárzására vonatkozó elképzeléseit (a részleteket lásd késöbb). Ennek a legfontosabb megállapítása az volt, hogy egy  frekvenciájú (rezgésszámú) rezgő atom, ún. atomi oszcillátor energiája (szó szerint idézve): „meghatározott számú kicsiny egyforma részből áll. Erre a
frekvenciájú (rezgésszámú) rezgő atom, ún. atomi oszcillátor energiája (szó szerint idézve): „meghatározott számú kicsiny egyforma részből áll. Erre a  természeti állandó szolgál, amelyet a rezgésszámmal megszorozva az említett energiaelemet kapjuk”. Ez volt a kvantumhipotézis első megfogalmazása.
természeti állandó szolgál, amelyet a rezgésszámmal megszorozva az említett energiaelemet kapjuk”. Ez volt a kvantumhipotézis első megfogalmazása.
Ernest Rutherford mérései alapján kiderült, hogy egy atom atommagból és a körülötte „keringő” elektronokból áll (1911). Ettől kezdve beszélhetünk elektronfizikáról és atommagfizikáról. A kvantummechanika elsősorban az elektronok viselkedésének a vizsgálata során fejlődött. De a neutron felfedezése (Chadwick 1932) után az elmélet megfelelő általánosítással alkalmas volt az atommag modellek megalkotására is. A kvantummechanikai elmélet és a kísérletezés összhangjának diadala volt az első atomreaktor megépítése (Enrico Fermi, 1942) és a tranzisztor megalkotása (Bardeen, Shockley, Brattain, 1947). Egyik sem születhetett volna meg, a kvantummechanika elmélete nélkül.
„Semmi sem olyan gyakorlati, mint egy jó elmélet” mondotta Boltzmann. Technikai civilizációnk mindennapjai igazolják, hogy a kvantummechanika egy jó elmélet!
Már említettük, hogy a kvantummechanika fogalmi rendszere és szemlélete nagyon eltér a megszokott klasszikus fizikai gondolkodásunktól. Ezért a hétköznapi nyelvre „lefordított” állításait a „józan ész” sokszor képtelenségnek ítéli. Létezik azonban egy olyan univerzális „formális rendszer” egy egzakt nyelv, amellyel fizikai állításainkat egyértelműen kifejezhetjük. Ez a „nyelv” a Matematika. Ezzel kapcsolatosan hadd idézzünk egy-két igen találó gondolatot R. P. Feynman-tól:
- ...Én azonban a matematika kikerülését nem tartom lehetségesnek, mivel a matematika nem csak egyszerűen egy másik nyelv. A matematika nyelv plusz gondolkodásmód, nyelv és logika egysége.... Pedig a fizika nem matematika, mint ahogy a matematika sem fizika. A fizikában érteni kell az egyes szavak kapcsolatát a valóságos világgal.... ...A matematika lényeges szerepet játszik a természet leírásában, és nem lehetnek eredményesek az olyan próbálkozások, amelyek a természetet filozófiai elvekkel, vagy csupán ösztönös megérzésekkel akarják kifejezni.
Izgalmas filozófiai kérdés az, hogy mi lehet az oka annak, hogy a matematika ilyen jól használható a természetben tapasztalható jelenségek leírásában és megértésében (lásd Wigner Jenő ide vonatkozó cikkét). Tény azonban, hogy szinte egyetlen mód a természeti törvények pontos megfogalmazására az, ha azt a matematikai állítások (egyenletek) formájában adjuk meg. A hétköznapi szemlélet hiánya miatt a kvantummechanikában erre különösen nagy szükség van. Bár a Fizika nem matematika, de nem lehet meg a Matematika nélkül. Ahogyan azt először Galileo Galilei megfogalmazta:
- A Természet a matematika nyelvét beszéli.
(Ekkor a XVII. század elejét mutatta a naptár.)
A Kvantummechanika születése
A hőmérsékleti sugárzás
A hőmérsékleti sugárzás jelenségét a hétköznapokban is mindenki tapasztalhatja. Minden  hőmérsékletű test elektromágneses hullámok formájában energiát sugároz. Ennek oka a testet felépítő atomokban lévő elektromos töltések (gyorsuló, pl. rezgő) mozgása. A jelenséget találóan hőmérsékleti sugárzásnak nevezzük. Tudjuk, hogy az elektromágneses hullámok (EMH)
hőmérsékletű test elektromágneses hullámok formájában energiát sugároz. Ennek oka a testet felépítő atomokban lévő elektromos töltések (gyorsuló, pl. rezgő) mozgása. A jelenséget találóan hőmérsékleti sugárzásnak nevezzük. Tudjuk, hogy az elektromágneses hullámok (EMH)  frekvenciája igen sokféle lehet (a vákuumban folytonos spektruma van). Értelmes kérdés, hogy milyen a test által kisugárzott EMH-ok frekvencia szerinti eloszlása.
frekvenciája igen sokféle lehet (a vákuumban folytonos spektruma van). Értelmes kérdés, hogy milyen a test által kisugárzott EMH-ok frekvencia szerinti eloszlása.
A megmérhető mennyiség az 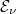 spektrális energiasűrűség. Ennek definíciója a következő:
spektrális energiasűrűség. Ennek definíciója a következő:
![\[ {\rm d}E = {\cal E}_{\nu} \, {\rm d}\nu \, {\rm d}F \, {\rm d}\Omega \, {\rm d}t, \]](/images/math/7/8/9/7895c85c704b3669caece96382a53dd0.png)
azaz a 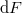 felületeről, a felületre merőleges irány körüli
felületeről, a felületre merőleges irány körüli 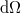 térszögben,
térszögben, 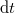 idő alatt,
idő alatt,  és
és 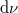 frekvenciatartományban kisugárzott elektromágneses hullám energiája. A hétköznapokban azonban röviden csak azt mondjuk, hogy „
frekvenciatartományban kisugárzott elektromágneses hullám energiája. A hétköznapokban azonban röviden csak azt mondjuk, hogy „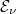 a
a  frekvencián kisugárzott energia”. Azt is tapasztaljuk, hogy ez az energia függ a felület „mikroszkopikus szerkezetétől” is (például hogy síma, rücskös, festett stb. a felület). Ezt a tulajdonságot (makroszkopikusan) a felület abszorpciós (fényelnyelési) tulajdonságával jellemezzük. Ez azt jelenti, hogy a felületre beeső
frekvencián kisugárzott energia”. Azt is tapasztaljuk, hogy ez az energia függ a felület „mikroszkopikus szerkezetétől” is (például hogy síma, rücskös, festett stb. a felület). Ezt a tulajdonságot (makroszkopikusan) a felület abszorpciós (fényelnyelési) tulajdonságával jellemezzük. Ez azt jelenti, hogy a felületre beeső 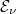 energia egy részét az
energia egy részét az  felület elnyeli, a maradékot pedig visszaveri. Azaz Elnyelt energia
felület elnyeli, a maradékot pedig visszaveri. Azaz Elnyelt energia 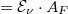 , Visszavert energia
, Visszavert energia 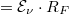 , és
, és
![\[ A_F + R_F = 1, \]](/images/math/8/d/2/8d2d5fa4d11c4659379b6c2c6a189a55.png) |
(1) |
ahol 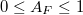 -et abszorpciós tényezőnek és
-et abszorpciós tényezőnek és 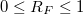 -et reflexiós tényezőnek hívjuk.
-et reflexiós tényezőnek hívjuk.
Abszolút fekete testnek azt a testet nevezzük, amely a ráeső elektromágneses sugárzást teljes egészében elnyeli, azaz amelyre 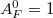 . Ennek a fogalomnak kulcsfontosságú szerepe lesz az elmélet kidolgozásában. Ennek oka a következő. Helyezzünk el egymással mellett két, azonos
. Ennek a fogalomnak kulcsfontosságú szerepe lesz az elmélet kidolgozásában. Ennek oka a következő. Helyezzünk el egymással mellett két, azonos  hőmérsékletű (végtelen nagy) testet amelyeknek a sík felülete párhuzamos egymással. Az egyik test abszorpciója
hőmérsékletű (végtelen nagy) testet amelyeknek a sík felülete párhuzamos egymással. Az egyik test abszorpciója 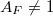 , a másik legyen egy abszolút fekete test.
, a másik legyen egy abszolút fekete test.
A két test az általuk kisugárzott és elnyelt EMH révén kapcsolatban van egymással. Mivel mindkét test hőmérséklete ugyanaz a  , így termikus egyensúlyban vannak. Ez azt jeleni, hogy mindegyikük külön-külön ugyanannyi energiát ad le, mint amennyit felvesz. Azaz az ábra szerint
, így termikus egyensúlyban vannak. Ez azt jeleni, hogy mindegyikük külön-külön ugyanannyi energiát ad le, mint amennyit felvesz. Azaz az ábra szerint
![\[ {\cal E}_\nu = {\cal E}^0_\nu \cdot A_F, \]](/images/math/a/a/8/aa8c8f7f8a443cc9152f4a7386dd070f.png) |
(2) |
![\[ {\cal E}^0_\nu = {\cal E}_\nu + {\cal E}^0_\nu \cdot R_F. \]](/images/math/4/3/b/43b6208c0fd1d77074a137e40c013617.png) |
(3) |
A (1) figyelembevételével (3) átrendezése után éppen (2)-t kapjuk. Tehát, mint az várható volt, a két egyenlet ekvivalens egymással. Mindez pedig azt jelenti, hogy
![\[ \frac{{\cal E}_\nu}{A_F} = \frac{{\cal E}_\nu^0}{A_F^0} = {\cal E}_\nu^0. \]](/images/math/5/6/1/5619a69dcdeffac89a4d5b560abbac56.png) |
(4) |
Ez az összefüggés tetszőleges 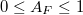 minőségű felületre igaz. Tehát az
minőségű felületre igaz. Tehát az 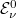 egy univerzális függvény. Ezt nevezik a fekete test sugárzási görbéjének. Ha ezt megmérjük, akkor a hőmérsékleti sugárzásnak egy univerzális tulajdonságát mérjük meg.
egy univerzális függvény. Ezt nevezik a fekete test sugárzási görbéjének. Ha ezt megmérjük, akkor a hőmérsékleti sugárzásnak egy univerzális tulajdonságát mérjük meg.
Az abszolút fekete test egy tetszőleges minőségű szilárd anyagba vájt, tetszőleges alakú üreg elegendően kicsiny kivezető nyílásával valósítható meg.
Ugyanis a nyíláson bejutó fény (elektromágneses sugárzás) elvileg végtelen sok reflexió után érné el ismét a lyuk kivezető nyílását. Ekkorra azonban (az egyes reflexióknál elnyelődött energiák következtében) az intenzitása gyakorlatilag zérusra csökken. Így a nyíláson belépett fény teljesen elnyelődött. Pontosan ez a fekete test definíciója. Ha az üreget tartalmazó szilárd anyag hőmérséklete  , akkor a nyíláson át („abszolút fekete test”) távozó EMH-ok spektrális (frekvencia szerinti) eloszlása éppen az
, akkor a nyíláson át („abszolút fekete test”) távozó EMH-ok spektrális (frekvencia szerinti) eloszlása éppen az 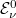 -t adja. Ez megmérhető:
-t adja. Ez megmérhető:
A mérés eredményeként adódó jellegzetes, „harang alakú” görbét nevezik még normál spektrumnak is.
A  hőmérsékleten kisugárzott
hőmérsékleten kisugárzott 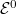 összenergia nagyságát a Stefan-Boltzmann törvény adja meg (1884):
összenergia nagyságát a Stefan-Boltzmann törvény adja meg (1884):
![\[ {\cal E}^0 = \int_{0}^{\infty} \, {\rm d}\nu {\cal E}_{\nu}^0 = \sigma T^4. \]](/images/math/6/7/9/67994b65108ad7776a53616f689a7dde.png)
A XIX. század végén a fizikusok sikertelenül próbálkoztak avval, hogy elméleti számításokkal megadják a görbe matematikai alakját. A Maxwell-egyenleteket, a termodinamika és a statisztikus fizika ismert törvényeit alkalmazva rendre rossz eredmények születtek (pl. J. W. S. Rayleigh és J. H. Jeans vagy W. Wien).
Az alkalmazandó fizikai modell egyértelműen adódik az abszolút fekete test fent említett „üreges” realizációjából. Valamely  hőmérséklet esetén az üreg falában az elektromos töltéssel rendelkező atomok (a statisztikus fizikában tanultak szerint) termikus mozgást végeznek. Ezek a
hőmérséklet esetén az üreg falában az elektromos töltéssel rendelkező atomok (a statisztikus fizikában tanultak szerint) termikus mozgást végeznek. Ezek a  frekvenciával rezgő atomok, ún. atomi oszcillátorok, mint piciny (atomi) antennák, elektromágneses hullámot sugároznak be az üregbe. Ugyanakkor (az üregből) rájuk eső elektromágneses sugárzást el is nyelik. Egyensúly esetén az atomok által elnyelt és kisugárzott energia egymással megegyezik. Mindezek eredőjeként az üregben elektromágneses hullámok formájában
frekvenciával rezgő atomok, ún. atomi oszcillátorok, mint piciny (atomi) antennák, elektromágneses hullámot sugároznak be az üregbe. Ugyanakkor (az üregből) rájuk eső elektromágneses sugárzást el is nyelik. Egyensúly esetén az atomok által elnyelt és kisugárzott energia egymással megegyezik. Mindezek eredőjeként az üregben elektromágneses hullámok formájában 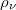 homogén energiasűrűségű és izotrop elektromágneses tér van jelen. A nyíláson keresztül eltávozó energia evvel arányos kell, hogy legyen. Azaz
homogén energiasűrűségű és izotrop elektromágneses tér van jelen. A nyíláson keresztül eltávozó energia evvel arányos kell, hogy legyen. Azaz
![\[ {\cal E}_{\nu}^0 \sim \rho_\nu, \]](/images/math/0/0/2/00296206fc717111008047a27f405652.png)
ahol 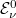 spektrális energiasűrűség megmérhető és a
spektrális energiasűrűség megmérhető és a 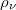 térfogati energiasűrűség elméletileg meghatározható. Ezzel megteremtettük a kapcsolatot a mérés és az elméleti számolás között.
térfogati energiasűrűség elméletileg meghatározható. Ezzel megteremtettük a kapcsolatot a mérés és az elméleti számolás között.
Könnyen belátható, hogy 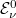 független az üreget tartalmazó test anyagától és az üreg alakjától. Ezt a törvényt első megfogalmazójáról (Gustav Robert Kirchhoff, 1862) Kirchhoff-féle sugárzási törvénynek nevezzük. A bizonyítása igen egyszerű. Helyezzünk el szorosan, egymással szembe két, különböző anyagú szilárd testbe vájt különböző alakú üreget:
független az üreget tartalmazó test anyagától és az üreg alakjától. Ezt a törvényt első megfogalmazójáról (Gustav Robert Kirchhoff, 1862) Kirchhoff-féle sugárzási törvénynek nevezzük. A bizonyítása igen egyszerű. Helyezzünk el szorosan, egymással szembe két, különböző anyagú szilárd testbe vájt különböző alakú üreget:
Legyen a testek hőmérséklete azonos. Ekkor a termodinamika nulladik főtétele szerint a két test termikus egyensúlyban van egymással, így eredő energiaáramlás nem jöhet létre. Azaz az üregek közös nyílásán átáramló energia (előjeles) összege zérus kell, hogy legyen. Tehát
![\[ {\cal E}_{\nu}^0(1) = {\cal E}_{\nu}^0(2). \]](/images/math/2/0/5/20507f409f4284fa220f494c6aaa9f10.png)
Ezzel a Kirchhoff-törvényt igazoltuk.
Most rátérhetünk 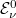 kiszámítására, ami tulajdonképpen
kiszámítására, ami tulajdonképpen 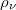 meghatározását jelenti. Válasszuk ki az üreg falában lévő, (tetszőleges)
meghatározását jelenti. Válasszuk ki az üreg falában lévő, (tetszőleges)  frekvenciával rezgő atomokat. Ezek átlagos energiája legyen
frekvenciával rezgő atomokat. Ezek átlagos energiája legyen 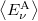 . Az üregben lévő, ugyancsak
. Az üregben lévő, ugyancsak  frekvenciájú EMH-ok sokasága módusok formájában van jelen. Egy módus egy
frekvenciájú EMH-ok sokasága módusok formájában van jelen. Egy módus egy  frekvenciájú és
frekvenciájú és 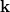 hullámszám-vektorú EMH-ot jelent.
hullámszám-vektorú EMH-ot jelent.
Tudjuk, hogy EMH esetén (vákuumban)
![\[ \nu = \frac{c}{\lambda} = \frac{c}{2\pi} k, \]](/images/math/f/8/2/f823fcbb181a6d5338638f69a9200b87.png) |
(5) |
ahol 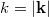 . Ezért a
. Ezért a  és
és 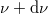 frekvenciatartományban rezgő módusok
frekvenciatartományban rezgő módusok 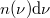 száma arányos lesz a
száma arányos lesz a  és
és 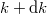 tartományba eső
tartományba eső 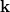 vektorok számával, azaz
vektorok számával, azaz
![\[ n(\nu) {\rm d}\nu \sim 4\pi k^2 {\rm d} k. \]](/images/math/4/6/a/46ac0e0d92335e5adb9a370e7d2512d4.png) |
(6) |
(5) alapján 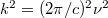 és
és 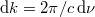 . Ezért aztán
. Ezért aztán 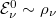 miatt
miatt
![\[ n(\nu) \sim \nu^2. \]](/images/math/1/5/a/15a851d62c9b215f129049915b1a66cc.png) |
(7) |
Mindezek ismeretében pedig a 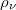 energiasűrűségre kapjuk, hogy
energiasűrűségre kapjuk, hogy
![\[ \rho_\nu \sim n(\nu) \left< E_\nu^{\rm M} \right>, \]](/images/math/b/a/8/ba8ae37539cdf2992b928a119f3d9874.png)
ahol 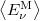 a
a  frekvenciájú módusok átlagos energiáját jelenti.
frekvenciájú módusok átlagos energiáját jelenti.
Az üregben lévő EMH és a falban lévő rezgő atomok között akkor van termikus egyensúly, ha az átlagos energiájuk megegyezik, azaz
![\[ \left< E_\nu^{\rm M} \right> = \left< E_\nu^{\rm A} \right>. \]](/images/math/c/b/e/cbe7d79f8a7b67de43eca9d34ace1894.png)
Végül is (4), (6) és (7) felhasználásával adódik, hogy
![\[ {\cal E}_{\nu}^0 = A n(\nu) \left< E_\nu^{\rm A} \right>. \]](/images/math/f/e/4/fe423f4899ffd0709fe0bc876be6b661.png)
A Termodinamikában tanultak szerint, az ekvipartíció tételének értelmében
![\[ \left< E_\nu^{\rm A} \right> = {\rm k}T. \]](/images/math/5/5/0/55046f97eb5c0540801eaf6d49396a81.png)
Vigyázat!  a hullámszám-vektor nagysága,
a hullámszám-vektor nagysága, 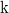 pedig a Boltzmann-állandó. Mivel
pedig a Boltzmann-állandó. Mivel 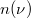
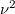 -tel arányos,
-tel arányos,
![\[ {\cal E}_\nu^0 = A \nu^2 {\rm k}T \equiv {\cal E}_\nu^{\rm RJ}. \]](/images/math/6/0/7/60738a2282fb5a17edce171eff2861c4.png)
Ennek a neve Rayleigh–Jeans-féle sugárzási törvény (1900). Látható, hogy ez „kis” frekvenciákon jól visszaadja a mért értékeket, „nagy” frekvenciákon azonban teljesen rossz eredményt szolgáltat.
Látható az is, hogy a kisugárzott összenergiára 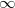 adódik, hiszen:
adódik, hiszen:
![\[ {\cal E}^0 = \int_0^\infty {\rm d}\nu {\cal E}_\nu^{\rm RJ} = A \int_0^\infty \nu^2 {\rm d}\nu {\rm k}T \to \infty. \]](/images/math/b/8/e/b8eaeb2f33706ec3172b538fd942c3dc.png)
Miután ezen eredményért a Rayleigh–Jeans formula nagyfrekvenciás viselkedése (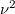 ) a felelős, ennek a neve ultraibolya katasztrófa.
) a felelős, ennek a neve ultraibolya katasztrófa.
A sikeres megoldás Max Planck nevéhez fűződik (1900). Ez a Fizika egyik legtanulságosabb „háromfelvonásos” felfedezéstörténete, amely alapjaiban változtatta meg a Természetről alkotott képünket.
Az első felvonásra 1900. október 19-én, a Német Fizikai Társaság (DPG) ülésén került sor. Max Planck ekkor mutatott be egy „próbálgatással” (interpolációval) kapott matematikai függvényt, amelyik csak egyetlen  illesztőparamétert tartalmazott.
illesztőparamétert tartalmazott.
![\[ {\cal E}_{\nu}^{\rm PL} = A \frac{h\nu^3}{\exp (h\nu/{\rm k}T ) - 1}. \]](/images/math/b/5/b/b5be5c5432d9b0c62b241c02172a4ed7.png)
Ez az 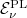 függvény a
függvény a 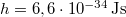 értéknél tökéletesen megadta a fekete test sugárzási spektrumát minden
értéknél tökéletesen megadta a fekete test sugárzási spektrumát minden  frekvencián. Látható, hogy „kis” frekvenciákon, amikor
frekvencián. Látható, hogy „kis” frekvenciákon, amikor
![\[ h\nu \ll {\rm k}T, \]](/images/math/5/9/0/590bd27242f7a074ebebcd394f060e49.png)
a nevezőben lévő exponenciális függvény Taylor-sorba fejthető és az 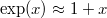 közelítés alkalmazható. Ekkor visszakapjuk a Rayleigh–Jeans féle sugárzási törvényt:
közelítés alkalmazható. Ekkor visszakapjuk a Rayleigh–Jeans féle sugárzási törvényt:
![\[ \lim_{h\nu \ll {\rm k}T} {\cal E}_{\nu}^{\rm PL} = {\cal E}_{\nu}^{\rm RJ} = A\nu^2 {\rm k}T. \]](/images/math/2/7/5/27540430fc588a89b71db299b3b2a407.png)
Az 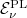 Planck-féle sugárzási törvény korrekt fizikai magyarázatára a történet „második felvonásában”, 1900. december 14-én (ugyanott) került sor. Ekkor ismertette Planck azt a fizikai modelljét, amelynek eredményeként az „októberi formula” megkapható.
Planck-féle sugárzási törvény korrekt fizikai magyarázatára a történet „második felvonásában”, 1900. december 14-én (ugyanott) került sor. Ekkor ismertette Planck azt a fizikai modelljét, amelynek eredményeként az „októberi formula” megkapható.
Elképzelése a következő volt. A fentiekben használt „üreg modell” szerint az üregből távozó energia spektrális sűrűségére egy általános formula adódott. Eszerint
![\[ {\cal E}_{\nu}^0 = An(\nu) \left<E_\nu^{\rm A} \right>. \]](/images/math/c/6/c/c6cb5044d187ff7b001833960ee23b87.png)
Az EMH módusok számát megadó 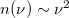 összefüggésen nincsen mit változtatni, mert ezt az EMH-okra általánosan jellemző
összefüggésen nincsen mit változtatni, mert ezt az EMH-okra általánosan jellemző 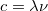 kapcsolatból adódik. Planck eddigre már sokat foglakozott a termodinamika (nevezetesen az entrópia) statisztikus hátterével, így nem véletlen, hogy a megoldás kulcsát az atomi oszcillátorok
kapcsolatból adódik. Planck eddigre már sokat foglakozott a termodinamika (nevezetesen az entrópia) statisztikus hátterével, így nem véletlen, hogy a megoldás kulcsát az atomi oszcillátorok 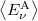 átlagenergiájának a meghatározásában vélte felismerni. A kérdése az volt, hogy mit kell az előző egyenletben
átlagenergiájának a meghatározásában vélte felismerni. A kérdése az volt, hogy mit kell az előző egyenletben 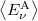 helyére írni, hogy az
helyére írni, hogy az 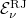 helyett az
helyett az 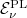 adódjon. A válasz triviális:
adódjon. A válasz triviális:
![\[ \left<E_\nu^{\rm A} \right>^{\rm PL} = \frac{h\nu}{\exp(h\nu/{\rm k}T) - 1}. \]](/images/math/7/7/1/771b70d2ceee08279957b14c41ee3443.png)
Ekkor ugyanis írható, hogy:
![\[ {\cal E}_{\nu}^{\rm PL} = A\nu^2\left<E_\nu^{\rm A} \right>^{\rm PL}. \]](/images/math/6/3/5/63551f13d86a8b9beaa6641676d3dda1.png)
Látható, hogy kis  frekvenciákon visszakapjuk az ekvipartíció-tétel által jósolt klasszikus értéket:
frekvenciákon visszakapjuk az ekvipartíció-tétel által jósolt klasszikus értéket:
![\[ \left<E_\nu^{\rm A} \right>^{\rm PL} \rightarrow \left<E_\nu^{\rm A} \right> = {\rm k}T, \quad \text{ha } \quad h\nu \ll {\rm k}T. \]](/images/math/1/1/0/110e1423c2b78f8fc546841a69d2d849.png)
Ezek után Planck számára feladat az atomi oszcillátorok fizikai tulajdonságainak a vizsgálatára redukálódott. A kérdést a következőképpen lehet feltenni: milyen különleges tulajdonsággal kell rendelkezniük az atomi méretű oszcillátoroknak ahhoz, hogy az átlagenergiájuk a 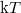 helyett
helyett 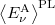 legyen? A kérdésre adódott válasz amilyen egyszerű, olyan megdöbbentő volt. A két ülés közti két hónapban (októbertől decemberig) Planck elméleti számításokkal kimutatta, hogy csakis egy esetben kapható meg a kívánt
legyen? A kérdésre adódott válasz amilyen egyszerű, olyan megdöbbentő volt. A két ülés közti két hónapban (októbertől decemberig) Planck elméleti számításokkal kimutatta, hogy csakis egy esetben kapható meg a kívánt 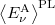 átlagenergia: ha feltételezi, hogy az atomi oszcillátorok
átlagenergia: ha feltételezi, hogy az atomi oszcillátorok  energiája nem lehet tetszőleges. Pontosabban, egy atomi méretű,
energiája nem lehet tetszőleges. Pontosabban, egy atomi méretű,  frekvenciával rezgő tömegpont energiája csak a
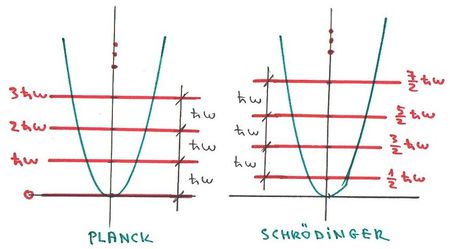
frekvenciával rezgő tömegpont energiája csak a 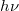 energia adag („energiakvantum”) egész számú többszöröse lehet (ld. ábra, alább). Azaz
energia adag („energiakvantum”) egész számú többszöröse lehet (ld. ábra, alább). Azaz
![\[ E \equiv E_n = n\cdot h\nu, \quad \text{ahol } n=0,1,2,... . \]](/images/math/0/4/c/04ca975071c3735eff1daaefb9a524cb.png)
Tehát egy mechanikai oszcillátor energiája (a klasszikus szemlélet számára igen furcsa módon) nem folytonosan változik, hanem „kvantált”. A  -nak Planck a hatáskvantum nevet adta. Ezzel megszületett a Kvantummechanika.
-nak Planck a hatáskvantum nevet adta. Ezzel megszületett a Kvantummechanika.
Elvileg mindez igaz egy makroszkopikus méretű rezgő tömeg esetén is. Ekkor a jellemző makroszkopikus mozgások energiája olyan nagy, hogy a  kicsiny értéke miatt az energiaszintek kvantáltsága klasszikus mechanikai mérésekkel nem mutatható ki.
kicsiny értéke miatt az energiaszintek kvantáltsága klasszikus mechanikai mérésekkel nem mutatható ki.
A felfedezés harmadik (sok év hosszú) felvonása legalább olyan tanulságos, mint az első kettő volt. A klasszikus fizikán nevelkedett és abban dolgozó Planck maga (is) nehezen fogadta el a kapott eredményt. Ezt írta erről visszaemlékezésében:
- Rövidesen próbálkozni kezdtem, hogy a
 hatáskvantumot valamiképpen bekényszerítsem a klasszikus elmélet kereteibe, de ez minden ilyen kísérletnek makacsul ellenszegült. Hiábavaló fáradozásaim több éven át elhúzódtak és igen sok munkámba kerültek. Néhány kollegám valami tragikust látott ebben. Nekem más a véleményem. Számomra értékesebb volt a nyereség, amelyet ez az alapos feltárás hozott. Ma már tudom, hogy a
hatáskvantumot valamiképpen bekényszerítsem a klasszikus elmélet kereteibe, de ez minden ilyen kísérletnek makacsul ellenszegült. Hiábavaló fáradozásaim több éven át elhúzódtak és igen sok munkámba kerültek. Néhány kollegám valami tragikust látott ebben. Nekem más a véleményem. Számomra értékesebb volt a nyereség, amelyet ez az alapos feltárás hozott. Ma már tudom, hogy a  hatáskvantum a fizikában sokkal jelentősebb szerepet játszik, mint ahogyan azt kezdetben gondoltam. Látom, milyen elkerülhetetlenül szükséges, hogy atomi problémák tárgyalásánál teljesen új szemléletet, teljesen új számítási módszert vezessünk be.
hatáskvantum a fizikában sokkal jelentősebb szerepet játszik, mint ahogyan azt kezdetben gondoltam. Látom, milyen elkerülhetetlenül szükséges, hogy atomi problémák tárgyalásánál teljesen új szemléletet, teljesen új számítási módszert vezessünk be.
Mint láttuk, a  karrierje igen látványos. Megszületésekor pusztán csak egy illesztési paraméter volt. A későbbiek során (éppen magának Plancknak az ez irányú erőfeszítései eredményeként) derült ki az, hogy a
karrierje igen látványos. Megszületésekor pusztán csak egy illesztési paraméter volt. A későbbiek során (éppen magának Plancknak az ez irányú erőfeszítései eredményeként) derült ki az, hogy a  nem csupán csak egy paraméter, hanem egy új természeti állandó, ugyanis nem fejezhető ki a már ismert klasszikus természeti állandókkal. A
nem csupán csak egy paraméter, hanem egy új természeti állandó, ugyanis nem fejezhető ki a már ismert klasszikus természeti állandókkal. A  mindig megjelenik az elméleti modelljeinkben, ha azok atomi szinten lezajló kvantumos jelenségeket írnak le.
mindig megjelenik az elméleti modelljeinkben, ha azok atomi szinten lezajló kvantumos jelenségeket írnak le.
Az 1918-as fizikai Nobel-díjat Max Planck kapta a „hatáskvantum felfedezéséért”.
Megszületett tehát a Kvantummechanika, amely a XX. század legnagyobb és legsikeresebb szellemi alkotásának bizonyult. Létrejöttével egy teljesen új természetszemlélet és a hétköznapi eszközök soha nem sejtett sokasága jelenik majd meg.
Sőt, száz év múlva maga a Planck formula perdöntő szerephez jutott az Univerzum létét firtató alapvető kérdés eldöntésében: „mindig létezett-e, avagy valamikor keletkezett?” Mindezt azonban akkor még senki nem sejthette.
Vége a harmadik felvonásnak, a függöny legördült.
- ...Látom, milyen elkerülhetetlenül szükséges, hogy atomi problémák tárgyalásánál teljesen új szemléletet, teljesen új számítási módszert vezessünk be.

|
| Max Planck (1858-1947)
Nobel díj (1965): „a hatáskvantum felfedezéséért” |
Az adódó matematikai összefüggések egyszerűsítése miatt a továbbiakban a  helyett sokszor a
helyett sokszor a 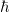 -t (kiejtése: „há vonás”) fogjuk használni. Ennek értéke
-t (kiejtése: „há vonás”) fogjuk használni. Ennek értéke 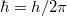 . Ez az ún. redukált Planck-állandó, de a hétköznapokban ezt is csak Planck-állandónak nevezzük.
. Ez az ún. redukált Planck-állandó, de a hétköznapokban ezt is csak Planck-állandónak nevezzük.
A Planck-féle sugárzási görbe és az Univerzum
A hőmérsékleti sugárzás és ezáltal maga a Planck formula a születése után 100 évvel ismét a tudományos érdeklődés középpontjába került. 1989. november 18-án indították útnak azt az űrszondát, amelynek faladata a kozmikus háttérsugárzás nagypontosságú megmérése volt. A program a COBE nevet kapta (COsmic Background Explorer).
A kozmikus háttérsugárzást véletlenül fedezte fel 1964-ben Arno Penzias és Robert Wilson, akik egy igen jó minőségű (zajmentes) rádiótávcsövet akartak készíteni. A teleszkóp azonban állandóan mutatott egy kb. 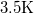 hőmérsékletű „zajt”. Mint később kiderült, a zajforrás nem a készülékükben, hanem az Univerzumban volt. A mindenütt jelen lévő, homogén és izotrop mikrohullámú háttérsugárzás az Ősrobbanás (Big Bang) maradványának, „visszfényének” bizonyult. Ennek várható spektrális sűrűségét (hőmérsékletét) 1940-ben George Gamow (1904-1968) már kiszámította. Ő volt ugyanis ennek az elméletnek egyik kidolgozója.
hőmérsékletű „zajt”. Mint később kiderült, a zajforrás nem a készülékükben, hanem az Univerzumban volt. A mindenütt jelen lévő, homogén és izotrop mikrohullámú háttérsugárzás az Ősrobbanás (Big Bang) maradványának, „visszfényének” bizonyult. Ennek várható spektrális sűrűségét (hőmérsékletét) 1940-ben George Gamow (1904-1968) már kiszámította. Ő volt ugyanis ennek az elméletnek egyik kidolgozója.

|

|
| George Gamow
1904-1968 |
Gamow Georges Lemaitre 1930-as ötletét elevenítette fel és az azóta kapott megfigyelési adatok birtokában már számításokat is végzett. Így kapta meg az 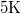 körüli háttérsugárzást. Az 1960-as években még vitatott volt ez a kozmológiai modell. Vetélytársa az állandó állapotú Univerzum elmélet volt. Ez is számot adott az akkori kísérleti eredményekről. A Hubble-féle vörös eltolódást az ún. „folytonos teremtés” ötletével magyarázta. Eszerint az Univerzum álladóan tágul ugyan, de az állapota (pl. sűrűsége) azért nem változik, mert átlagosan,
körüli háttérsugárzást. Az 1960-as években még vitatott volt ez a kozmológiai modell. Vetélytársa az állandó állapotú Univerzum elmélet volt. Ez is számot adott az akkori kísérleti eredményekről. A Hubble-féle vörös eltolódást az ún. „folytonos teremtés” ötletével magyarázta. Eszerint az Univerzum álladóan tágul ugyan, de az állapota (pl. sűrűsége) azért nem változik, mert átlagosan, 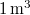 térfogatban,
térfogatban, 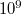 évenként 1 db hidrogén atom keletkezik. Ugyanakkor nem volt képes előre megjósolni a „háttérsugárzás” jelenlétét. Ezt (utólag) a távoli galaxisok „szórt fényével” magyarázta.
évenként 1 db hidrogén atom keletkezik. Ugyanakkor nem volt képes előre megjósolni a „háttérsugárzás” jelenlétét. Ezt (utólag) a távoli galaxisok „szórt fényével” magyarázta.
Penzias és Wilson 1978-as fizika Nobel-díja egyben a Big Bang elmélet elfogadását is jelentette. A rohamosan szaporodó és egyre pontosabb csillagászati mérések következtében az 1970-es évekre a Big Bang egyre inkább nyerő pozícióba került. A Hubble űrtávcső mért adatai végleg eldöntötték a modellek között folyó vitát. Mára az állandó állapotú Univerzum modell megszűnt létezni.

|

|

|
| Arno Penzias és Robert W. Wilson | Hubble űrteleszkop
1990 |
Edwin Powell Hubble
1889-1957 |
A COBE adatai alapján az Univerzum „születési anyakönyve” kb. így nézhet ki:
- Született 13.7 milliárd évvel ezelőtt a Big Bang alkalmával.
- Jelenlegi hőmérséklete:
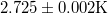 .
.
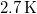 -os homogén, izotrop sugárzás
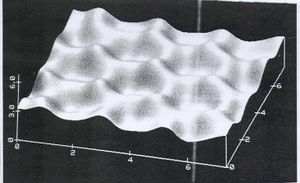
-os homogén, izotrop sugárzás- Ez a 300 000 éves csecsemő fényképe:
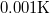 -os inhomogenitások
-os inhomogenitásokA mérhető, véletlenszerű, térbeli 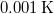 nagyságrendű hőmérsékletingadozások a születendő galaxisok „csírái”, köztük van a mi mostani Tejútrendszerünk is.
nagyságrendű hőmérsékletingadozások a születendő galaxisok „csírái”, köztük van a mi mostani Tejútrendszerünk is.
Az Ősrobbanás kozmológiai elmélete tehát újabb megerősítést kapott. A mért eredmények tökéletesen visszaadják az elmélet által jósolt adatokat. Pontos, számszerű értékei beépültek az elmélet kvantitatív adatai közé. Ezzel a Big Bang a precízen ellenőrizhető (egzakt) elméletek sorába lépett. Ez volt a Nobel-díj Bizottság kimondott véleménye is, ugyanis a 2006-os fizikai Nobel díjat megosztva John C. Mather és George Smoot kapta „a mikrohullámú kozmikus háttérsugárzás feketetest jellegének és anizotrópiájának felfedezéséért”.

|

|
| John C. Mather
1946- |
George Smoot
1945- |
A fényelektromos jelenség (fotoeffektus)
A kvantummechanika kialakulásának fontos állomása volt a fényelektromos jelenség magyarázata. Ezt a több, mint száz éve ismert effektust hétköznapjainkban is gyakran használjuk, valahányszor egy fotocella-vezérelt ajtón átmegyünk.
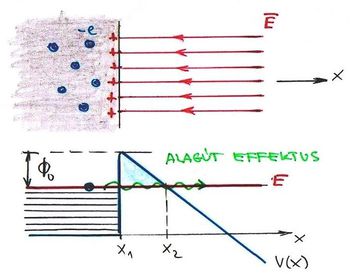
A XIX. század utolsó harmadában a szikra- illetve gázkisülések vizsgálata (különböző minőségű, illetve kis nyomású) gázokban igen érdekes, és ugyanakkor egy kísérleti fizikus számára izgalmas kihívást jelentő tudományos kutatás volt. 1888-ban Wilhelm Hallwachs (is) azt tapasztalta, hogy ha a negatív töltésű elektródát ultraibolya fény éri, akkor a szikrakisülés „könnyebben” jön létre. Ebből ő arra a következtetésre jutott, hogy bizonyára az elektródából a fény hatására negatív töltések lépnek ki. Mindez még közel 10 évvel az elektron felfedezése előtt történt.
Ma már tudjuk, hogy a fémekben könnyen mozgó elektronok vannak, amelyeket onnan ki is lehet „szabadítani”. A kísérleti tapasztalatok szerint tehát, ha egy fémlapra fény (elektromágneses hullám) esik, akkor a fémből elektronok lépnek ki.
A Maxwell-féle elektrodinamika törvényei szerint, ha a fény kölcsönhatásba lép a pontszerűnek feltételezett elektronnal, akkor a fémből kilépő elektron kinetikus energiája a fény intenzitásával lesz arányos. Mindez könnyen belátható. Az elektromágneses hullámban oszcilláló 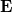 elektromos térerősség hatására gyorsul fel az elektron. Minél nagyobb ez a térerősség, az elektron annál nagyobb sebességre tesz szert, azaz annál nagyobb mozgási energiával fogja elhagyni a fémet.
elektromos térerősség hatására gyorsul fel az elektron. Minél nagyobb ez a térerősség, az elektron annál nagyobb sebességre tesz szert, azaz annál nagyobb mozgási energiával fogja elhagyni a fémet.
Legyen a fényhullámban az 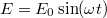 elektromos térerősség
elektromos térerősség  irányú. Ekkor a fémben lévő szabad elektron mozgásegyenlete
irányú. Ekkor a fémben lévő szabad elektron mozgásegyenlete
![\[ m\ddot z = -{\rm e}E_0 \sin(\omega t). \]](/images/math/c/8/d/c8d63b5f3efefeb9cf70ed00db5361d6.png)
Ennek triviális megoldása egy harmonikus rezgőmozgás:
![\[ z = z_0 \sin(\omega t). \]](/images/math/e/1/2/e128ea7b11972ff53b0424697515507d.png)
Beírva ugyanis ezt a mozgásegyenletbe, kapjuk, hogy:
![\[ -m \omega^2 z_0 \sin(\omega t) = -{\rm e}E_0 \sin(\omega t). \]](/images/math/8/2/6/826e7676b6879d402e45dc7ef28f61e0.png)
Ezért a mozgás amplitúdójára adódik, hogy
![\[ z_0 = \frac{\rm e}{m\omega^2}E_0. \]](/images/math/4/e/4/4e4029fc5d4cc40d82ede6b757a05d8b.png)
A rezgés energiája egyben a maximális kinetikus energiát is jelenti, tehát
![\[ E_{\rm KIN}^{\rm max} = \frac{1}{2}m\omega^2 z_0^2 = \frac{{\rm e}^2}{2m\omega^2}E_0^2. \]](/images/math/b/5/9/b5920a08b98ee5ad505ec3971457cabe.png)
Tudjuk, hogy a fény (EMH) intenzitását a Poynting-vektor időbeli átlaga határozza meg, azaz
![\[ I_{\rm FENY} = \left< S \right> = c\varepsilon_0 \left< E^2 \right> = \frac{1}{2} c\varepsilon_0 E_0^2. \]](/images/math/b/8/8/b88c0965a83fede040a79dabf0183e36.png)
Ezt beírva a maximális kinetikus energia egyenletébe, kapjuk, hogy:
![\[ E_{\rm KIN}^{\rm max} = \frac{e^2}{c\varepsilon_0 m\omega^2} I_{\rm FENY} \sim \frac{I_{\rm FENY}}{\nu^2}. \]](/images/math/c/7/9/c79bde614efdaf927f5bc27afeaf095f.png) |
(8) |
Ezzel a fenti állításunkat igazoltuk. A fotoeffektust a fentebb bemutatott ábrán látható kísérleti elrendezéssel mérjük. A kísérleti eredmények az imént ismertetett klasszikus elképzeléssel szemben merőben más eredményt mutatnak.
Ha a két elektróda között mozgó elektronra fékező tér hat, akkor elérhető egy olyan 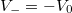 feszültség, amely esetén az árammérő éppen
feszültség, amely esetén az árammérő éppen 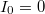 áramot jelez. Ez azt jelenti, hogy a fém elektródából kilépő, maximális kinetikus energiával rendelkező elektronok sem érik el a
áramot jelez. Ez azt jelenti, hogy a fém elektródából kilépő, maximális kinetikus energiával rendelkező elektronok sem érik el a 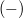 elektródát (ld. A ábra). Tehát
elektródát (ld. A ábra). Tehát
![\[ E_{\rm KIN}^{\rm max} = eV_0. \]](/images/math/9/1/7/917fed68d835b243f4ee52156c1fbf01.png)
Ha az elektronokra gyorsító tér hat, akkor minden 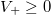 feszültségnél az összes kilépő elektron eljut az anódra. Azaz egy
feszültségnél az összes kilépő elektron eljut az anódra. Azaz egy 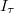 telítési áram folyik, amelynek értéke nem függ az aktuális
telítési áram folyik, amelynek értéke nem függ az aktuális 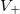 értéktől. Ha adott
értéktől. Ha adott  frekvencia mellett növeljük a beeső fény
frekvencia mellett növeljük a beeső fény 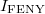 intenzitását, akkor az
intenzitását, akkor az 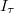 telítési áram is (vele arányosan) növekszik. (ld. B ábra). Ha változatlan
telítési áram is (vele arányosan) növekszik. (ld. B ábra). Ha változatlan 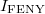 mellett növeljük a beeső fény
mellett növeljük a beeső fény  frekvenciáját, akkor egyre növekvő
frekvenciáját, akkor egyre növekvő 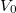 értéknél lehet elérni az
értéknél lehet elérni az 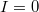 áramot (ld. B ábra). Ez azt jelenti, hogy a fémből kilépő elektronok kinetikus energiája a beeső fény frekvenciájától függ. Sőt mitöbb, minden fémre létezik egy reá jellemző
áramot (ld. B ábra). Ez azt jelenti, hogy a fémből kilépő elektronok kinetikus energiája a beeső fény frekvenciájától függ. Sőt mitöbb, minden fémre létezik egy reá jellemző 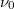 küszöbfrekvencia. Ez azt jelenti, hogy ha a beeső fény
küszöbfrekvencia. Ez azt jelenti, hogy ha a beeső fény  frekvenciája ennél kisebb (
frekvenciája ennél kisebb (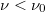 ), akkor nincsen elektron emisszió, bármilyen nagy is legyen a beeső fény intenzitása. Azaz
), akkor nincsen elektron emisszió, bármilyen nagy is legyen a beeső fény intenzitása. Azaz
![\[ E_{\rm KIN}^{\rm max} = {\rm konst}\cdot(\nu-\nu_0) \geq 0. \]](/images/math/8/3/0/8307a77f69196381e5bd97699c3baa0f.png)
| A ábra: | B ábra: |
Az A ábra szerint a fény intenzitásával az 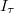 áram, azaz a fémből (időegység alatt) kilépő
áram, azaz a fémből (időegység alatt) kilépő 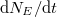 elektronok száma arányos:
elektronok száma arányos:
![\[ I_{\rm FENY} \sim \frac{{\rm d}N_E}{{\rm d}t}. \]](/images/math/2/0/6/2069a6c4f8ab912de40c19a89e081889.png)
Világosan látható, hogy a fotoeffektus mérési eredményei teljesen mások, mint a Maxwell-egyenletek által megjósolt (8) összefügés.
A mérési eredmények korrekt magyarázata 1905-ben született meg. Az Annalen der Physik neves, nívós fizikai folyóirat (volt). A 17. kötete (1905. év) különösen érdekes! Ebben a kötetben ugyanis (a 132., 549. és 851. oldalon) három igen fontos cikk jelent meg. Mindegyik a kialakulóban lévő modern fizika egy-egy kulcsfontosságú alapkövét tette le. Az egyik a Brown-mozgás elméletét tárgyalta, és így a statisztikus fizika fejlődéséhez járult hozzá. A második a mozgó testek elektrodinamikájáról szólt és a modern tér-idő fogalmunk megszületését jelentette. A harmadik a fényelektromos jelenség igen ötletes magyarázatát adta, hozzájárulva ezzel a kvantummechanika kialakulásához, ugyanakkor már a kvantumelektrodinamika csíráját is magába rejtette.
Már az sem mindennapi (még egy ilyen neves tudományos folyóirat életében sem), hogy egyetlen kötetében (alig több mint 700 oldalon belül) ennyi zseniális és újszerű gondolat jelenjen meg. De sokkal meglepőbb a helyzet, ha figyelembe vesszük, hogy mindhárom cikk fejlécén ugyanaz az (addig gyakorlatilag ismeretlen) név szerepelt. A név viselője egy akkor 26 éves fiatalember, a Berni Szabadalmi Hivatal köztisztviselője volt. Neve ma már szinte a legismertebb tudós név még a közember számára is. Ő volt Albert Einstein!

|
| Albert Einstein
1879-1955 |
A fényelektromos jelenség magyarázatát tehát Albert Einstein adta meg (1905).
Feltételezte, hogy a  frekvenciájú fény az elektronnal való kölcsönhatás során az elektronnak csak
frekvenciájú fény az elektronnal való kölcsönhatás során az elektronnak csak 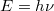 nagyságú energiát adhat át. Ezt az energia adagot („fénykvantumot”) fotonnak nevezte el. Ha ez az energia kisebb, mint az elektront a fémfelülethez kötő
nagyságú energiát adhat át. Ezt az energia adagot („fénykvantumot”) fotonnak nevezte el. Ha ez az energia kisebb, mint az elektront a fémfelülethez kötő 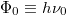 maximális energia (ezt igen találóan kilépési munkának nevezzük) akkor az elektron nem tud kilépni a fémből. A mérési eredmények szerint az
maximális energia (ezt igen találóan kilépési munkának nevezzük) akkor az elektron nem tud kilépni a fémből. A mérési eredmények szerint az 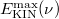 egyenes meredeksége független a fém minőségétől és a
egyenes meredeksége független a fém minőségétől és a  Planck állandóval egyezik meg:
Planck állandóval egyezik meg:
![\[ E_{\rm KIN}^{\rm max}(\nu) = h\nu - \Phi_0 = h(\nu - \nu_0). \]](/images/math/b/7/2/b72754ea207ce2cbc795be773e92a20e.png)
Alkalmazva a relativisztikus mechanika összefüggéseit, Einstein a fotonhoz egy impulzust is rendelt. A motiváció nyilvánvaló. Már a klasszikus elektrodinamikában is megmutatható az, hogy egy töltött részecskére eső EMH impulzust ad át a részecskének.
Ismeretes, hogy a speciális relativitáselmélet szerin egy részecske  energiája mind a
energiája mind a 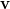 sebességével, mind pedig a
sebességével, mind pedig a 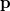 impulzusával megadható (lásd a Speciális relativitáselmélet részt):
impulzusával megadható (lásd a Speciális relativitáselmélet részt):
![\[ E = \frac{m_0 c^2}{\sqrt{1-v^2/c^2}} = \sqrt{m_0^2 c^4 + c^2 p^2}. \]](/images/math/9/3/8/9380704669f03787a1e3e31439a016de.png) |
(9) |
Az 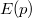 függvényt az alábbi ábrán mutatjuk be.
függvényt az alábbi ábrán mutatjuk be.
Látható, hogy a függvény aszimptotája
![\[ \lim_{p\to\infty} E=cp. \]](/images/math/2/1/0/2104b31e2acac1d60161c8527c4d00ca.png)
Ez éppen megfelel egy 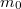 nyugalmi tömegű részecske
nyugalmi tömegű részecske 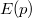 függvényének. Eddig nem találtunk olyan objektumot, amelyik ennek felelt volna meg. De most itt van a foton! Ha ezt egy
függvényének. Eddig nem találtunk olyan objektumot, amelyik ennek felelt volna meg. De most itt van a foton! Ha ezt egy 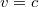 sebességgel mozgó „részecskének” tekintjük, akkor (9) értelmében (mivel
sebességgel mozgó „részecskének” tekintjük, akkor (9) értelmében (mivel 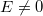 )
) 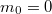 kell, hogy legyen. Feltesszük természetesen, hogy ekkor a
kell, hogy legyen. Feltesszük természetesen, hogy ekkor a 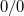 -t véges mennyiségnek, jelesül
-t véges mennyiségnek, jelesül 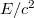 -nek definiáljuk. Mindenesetre a foton egy lehetséges „realizációja” lehet egy
-nek definiáljuk. Mindenesetre a foton egy lehetséges „realizációja” lehet egy 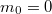 tömegű, fénysebességgel mozgó objektumnak. Ekkor tehát
tömegű, fénysebességgel mozgó objektumnak. Ekkor tehát 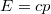 , és az előzőek alapján
, és az előzőek alapján 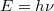 . A kettőt összevetve kapjuk, hogy
. A kettőt összevetve kapjuk, hogy
![\[ h \nu = cp. \]](/images/math/e/5/d/e5d86f8d2e1e2ed468fb5cb6d7de0ea0.png)
Mivel pedig a fényhullámokra igaz az, hogy 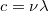 , ez utóbbi kettő összefüggésből adódik a következő alapvető összefüggés:
, ez utóbbi kettő összefüggésből adódik a következő alapvető összefüggés:
![\[ p = h/\lambda. \]](/images/math/a/e/d/aed7a793f6ed27299192bd308dbc2283.png)
Ezzel Einstein a fotont egy olyan részecske tulajdonságaival ruházta fel, aminek a nyugalmi tömege zérus.
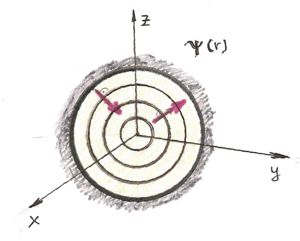
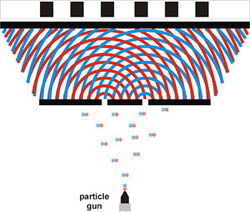
A foton fogalma nem egyszerű. A hétköznapi értelemben vett szemléletes képet igen nehéz alkotni róla. Kezdetben Einstein véges hosszúságú, igen keskeny hullámvonulatnak képzelte. Ezt szemléletesen a fény „tűsugárzás” elméletének nevezték. Azonban 1911-ben a magyar Selényi Pál elsőként kísérletileg bebizonyította, hogy az atomi fénykibocsátás gömbhullám formájában történik (ld. ábra).
Ezt a „hullámképet” igen nehéz összeegyeztetni a foton „részecske” képével. Nem véletlenül mondta Peter Debye:
- A fizikusok nagy szerencséje, hogy Selényi a kísérletét nem néhány évvel korábban végezte el. Akkor talán meg sem születhetett volna a fénykvantumok elmélete.
A foton fogalmának a kezdeti, kétkedő (elutasító) fogadtatására Planck mondatai is jellemzőek, eszerint:
- Einstein nagyságából mit sem von le az a körülmény, hogy más tanulmányaiban kalandos és megalapozatlan hipotézisekbe bocsátkozik. Egyik ilyen hipotézise fénykvantumok létezésének a feltételezése.
Ekkor 1914-et írtak.
Az 1921-es fizikai Nobel-díjat Albert Einstein kapta „érdemdús matematikai-fizikai kutatásaiért, különös tekintettel a fényelektromos jelenség törvényének a felfedezésére”.
A fotonimpulzus (mint részecsketulajdonság) közvetlen bizonyítékát Arthur Holly Compton mérései szolgáltatták 1923-ban. A róla elnevezett Compton-effektus felfedezéséért 1927-ben Nobel díjat kapott.

|
Arthur Holly Compton 1892-1962
He identified the Compton Effect (increase of wavelength of X-rays and gamma rays under certain conditions), sharing the Nobel Prize in 1927. Worked on the Manhattan Project, and was Chancellor of Washington University in St. Louis (1945-53) |
Az effektus során beeső fotonok elektronokkal ütköznek. Az elektront meglökő szórt foton megváltozott energiával halad tovább. A kölcsönhatás során a rendszer (elektron - foton páros) energiája és impulzusa állandó marad. A foton hullámhossz-változása számítható és mérhető, ugyanis az energiamegmaradás tétele szerint:
![\[ h\nu = h\nu' + \frac{(p_{\rm e}')^2}{2m_{\rm e}}, \]](/images/math/7/9/0/790f74d1d70f7b4161a5fe57ec864cdc.png) |
(10) |
ahol 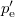 a meglökött elektron impulzusa. Az impulzusmegmaradás tétele pedig
a meglökött elektron impulzusa. Az impulzusmegmaradás tétele pedig 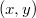 komponensekkel felírva:
komponensekkel felírva:
![\[ p_{\rm f} = p_{\rm f}' \cos \vartheta + p_{\rm e} \cos \phi, \quad 0 = p_{\rm f}' \sin \vartheta - p_{\rm e} \sin \phi. \]](/images/math/1/a/f/1afd72271d292f064760918c3220228b.png) |
(11) |
Tudjuk, hogy a foton energiája és impulzusa között fennáll, hogy
![\[ h\nu = cp_{\rm f} \quad \text{és} \quad h\nu' = cp_{\rm f}'. \]](/images/math/0/2/2/0223492a88e8374ffb44fcc68fde0320.png)
Ez öt darab ismeretlen mennyiséget jelent (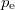 ,
, 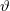 ,
, 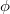 ,
, 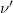 ,
, 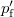 ), és van öt darab egyenletünk is. Ebből azonban minket csak a szórt foton (fény) hullámhossza (
), és van öt darab egyenletünk is. Ebből azonban minket csak a szórt foton (fény) hullámhossza (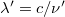 ) érdekel, mert ezt tudjuk megmérni. Az egyenletrendszer a szokásos algebrai módszerekkel megoldható és végeredményül kapjuk, hogy
) érdekel, mert ezt tudjuk megmérni. Az egyenletrendszer a szokásos algebrai módszerekkel megoldható és végeredményül kapjuk, hogy
![\[ \Delta\lambda \equiv \lambda' - \lambda = \Lambda(1-\cos\vartheta), \]](/images/math/9/2/4/924bdd1ffc71e9c59f7c4c71de2e0c39.png)
ahol 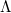 egy természeti állandókból álló konstans, melynek neve Compton hullámhossz és értéke:
egy természeti állandókból álló konstans, melynek neve Compton hullámhossz és értéke:
![\[ \Lambda\equiv\frac{h}{m_{\rm e}c} = 2,4\cdot 10^{-12} \, {\rm m}. \]](/images/math/e/3/d/e3d6aeec911233740a7a411646cc1dd7.png)
A foton tehát egy olyan „valami”, amely energiát és impulzust hordoz: az elektromágneses kölcsönhatások során energiát és impulzust ad át a töltött részecskéknek. Tehát úgy viselkedik mintha egy részecske volna ő is. Tovább erősödik bennünk ez a kép, ha a foto-effektusra gondolunk. Mint azt láttuk, ekkor (a mérések szerint) a fémből kilépő elektronok száma a beeső fény intenzitásával arányos. Ugyanakkor egy fotont mindig egy elektron „nyeli el”. Tehát a (fémből) kilépő elektronok száma meg kell, hogy egyezzék a beeső fény fotonjainak a számával, azaz
![\[ N_{\rm E} = N_{\rm foton}. \]](/images/math/b/d/0/bd0d9fd0fbc00bf75b0dd2b7758781f5.png)
Tudjuk, hogy (definíció szerint) mindegyik foton 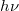 energiát hordoz. Ugyanakkor a foto-effektusnál tapasztaltak szerint
energiát hordoz. Ugyanakkor a foto-effektusnál tapasztaltak szerint
![\[ I_{\rm feny} \sim \frac{\rm d}{{\rm d}t} N_{\rm E}. \]](/images/math/7/5/b/75b6528da21eb32f65600eff6df442e0.png) |
(12) |
(12) és (10) alapján írható, hogy a 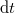 idő alatt a
idő alatt a 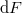 felületre beeső fény energiája
felületre beeső fény energiája
![\[ I_{\rm feny} \, {\rm d}t \, {\rm d}F = {\rm d} N_{\rm foton} h \nu \, {\rm d}F. \]](/images/math/0/4/e/04ed7febd8303eaabafb9c272276928b.png)
Így tehát a nagy intenzitású fény sok fotont jelent. Azaz nagy intenzitású fény detektálása sok foton (időegység alatti) elnyelését jelenti. Ma már tudjuk ugyan, hogy vannak kétfotonos effektusok is de ezek nagyon ritkák.
Ettől kezdve a foton fogalma végleg meggyökeresedett a fizikában. A kvantummechanika, majd a (relativisztikus-)kvantumelektrodinamika fejlődésével egyre bonyolultabbá vált, de mára már a mindennapi fizikai gondolkodásunk szerves része.
Mi a fény és mi a foton?
A fény a Maxwell-féle elektrodinamika szerint elektromágneses hullám.
Ezt a hullámtermészetet az interferenciajelenségek egyértelműen igazolják. Ugyanakkor a foto-effektus és a Compton szórás azt mutatja, hogy a fénnyel való kölcsönhatás csak a részecske tulajdonságú fotonokkal magyarázható. Ezzel megszületett a híres (és azóta is gyakran félreértett) „hullám-részecske kettős természet” ideája. Természetesen a fénynek nincsen kettős természete. A fénynek nagyon is egységes a természete, méghozzá az, hogy ő fény! Az más kérdés, hogy a kísérletek egyik részét hulláminterferenciaként, a másik részét pedig részecske kölcsönhatásként tudjuk értelmezni. De ezek sohasem egyszerre vannak jelen.
A fény úgy terjed, mint a hullám. Ezért a megtett optikai út végén interferencia hozható létre. De a felfogó ernyőn már fotonokat detektálunk.
A fény tehát úgy terjed, mint a hullám és úgy észleljük mint foton. De amikor éppen terjed, akkor nem észleljük és amikor detektáljuk, akkor már nem terjed.
Ebben áll a „hullám-részecske kettősség” lényege. Egymást kizáró effektusokról van tehát szó. Ez a „kettősség” végleg eltűnik, ha figyelembe vesszük azt is, hogy ahol nagy a fény intenzitása, ott sok foton van és fordítva [ld. (12)]. Tehát a „világos” (fényes) interferenciacsíkoknál sok fotont, a „sötéteknél” pedig igen kevés (esetleg nulla) számú fotont detektálunk.
Ha ezt a jelenséget az egyedi fotonok szemszögéből nézzük, akkor a nagy fényintenzitású helyeken a foton megtalálási valószínűsége nagy, a sötéteknél kicsi (esetleg zérus).
Joggal mondhatjuk tehát, hogy a Maxwell-egyenletek valójában igen nagyszámú foton (makroszkopikus) mozgásának időbeni és detektálásának térbeli sajátosságait írja le.
Az elektromágneses mező kvantummechanikájával (relativisztikus kvantumelektrodinamika) nem foglakozunk. Annyit azonban érdemes tudni, hogy az elektromágneses mező egy igen bonyolult anyagi szerkezetű valami. A Maxwell-egyenletekben ennek a fizikai mezőnek a makroszkopikus méretskálán jelentkező (átlagokban megnyilvánuló) tulajdonságait fogalmazzuk meg. A mikroszkopikus tartományban történő elektromágneses kölcsönhatásokat a „foton” jeleníti meg.
A makroszkopikus világban tapasztalt szemléletes kölcsönhatások között a testek ütközésekor tapasztaljuk az energia- és a impulzusátadást. Így a fejünkben ez a jelenség óhatatlanul is a részecske képhez kötődik. Ezért aztán a „fotont” apró golyócskának képzeljük el, amely energiát és impulzust ad át a vele ütköző töltött részecskéknek. Ezzel a „szemléletes” képpel nincsen semmi baj, ha tudjuk, hogy ez csak igen korlátozottan (az energia- és az impulzuscsere alkalmával) használható. Azaz nem szabad túl komolyan venni!
„Igazi képe” a Kvantumelektrodinamika matematikai modelljébe zárva rejtőzik.
A Kvantummechanika kialakulása és a hidrogén atommodell fejlődése
Az elektron felfedezése
Mint már az előzőekben említettük, a gázkisülések és ezen belül a katódsugárzás vizsgálata a XIX. század végén érdekes tudományos munka volt. Lassan kialakult a sejtés, hogy talán a katódsugarakban addig ismeretlen, elektromos töltéssel rendelkező részecskék áramlanak.
J. J. Thomson a katódsugarak elhajlását vizsgálta elektromos térben. Sikerült bebizonyítania, hogy a katódsugárzás valóban negatív töltések áramlásából áll, amelyeket negatronnak nevezett el. 1881-ben G. Johnstone Stoney (1853–1928) kb. hat éven át tartó kísérleti munka eredményeként sikeresen kiszámította ezen töltésegységeknek a nagyságát. Ez a mai SI egységre átszámolva 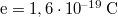 -nak adódott. Pár évvel később ennek az
-nak adódott. Pár évvel később ennek az  -nek az elektron nevet adta (G. J. Stoney, Philosophical Magazine, 1895, 40. kötet, 372. oldal).
-nek az elektron nevet adta (G. J. Stoney, Philosophical Magazine, 1895, 40. kötet, 372. oldal).
1897-ben J. J. Thomson feltételezte, hogy a katódsugárban repülő negatív  töltések tömeggel is rendelkeznek és sikerült megmérnie a tömeg-töltés arányt. A kísérlet részleteiből azt a következtetést vonta le, hogy az elektronnak (amely most már egy tömeggel bíró töltés volt) egy univerzális és elemi részecskének kell lennie. Az elektron léte fizikai realitássá vált. Ezt írta:
töltések tömeggel is rendelkeznek és sikerült megmérnie a tömeg-töltés arányt. A kísérlet részleteiből azt a következtetést vonta le, hogy az elektronnak (amely most már egy tömeggel bíró töltés volt) egy univerzális és elemi részecskének kell lennie. Az elektron léte fizikai realitássá vált. Ezt írta:
- ... Ilyen módon a katódsugarak az anyag új állapotát jelentik, egy olyan állapotot, amelyben az anyag részekre bomlása sokkal magasabb fokú, mint a közönséges gázállapotban: ez egy olyan állapot, melyben minden anyag – származzon az hidrogénből, oxigénből vagy bármely más forrásból – már egy és ugyanazon fajta; lévén ez az a szubsztancia, amelyből az összes kémiai elem felépül.
Valószínűleg még senki nem sejtette azt, hogy a felfedezett elektron, a XX. század alapvető objektuma lesz és egész iparágak épülnek majd rá.
1906-ban a fizikai Nobel-díj nyertese az első elemi részecske felfedezője J. J. Thomson volt.

|

|
| Joseph John, „J. J.” Thomson
1856-1940 |
A katódsugárcsö, amellyel J. J. a kísérleteit végezte |
Spektroszkópia
1814-ben Joseph von Fraunhofer felfedezte, hogy a Napsugárzás spektrumában bizonyos frekvenciák hiányoznak az amúgy folytonos spektrumból (fekete vonalak látszódnak). Ugyanis (első ránézésre) a Nap fénysugárzásának a spektruma egy 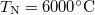 -os fekete test spektrális (folytonos) energiasűrűségével egyezik meg.
-os fekete test spektrális (folytonos) energiasűrűségével egyezik meg.
Gustav Kirchhoff (aki az elektromos áramokat is vizsgálta) 1858-ban észrevette, hogy a gázok fénye vonalas spektrummal rendelkezik. A fényt egy prizma segítségével színeire bontotta, és így a felfogó ernyőn a hullámhosszak jobban láthatóak voltak. Akkoriban (prizma helyett) különféle színű szűrőket használtak, amelyek csökkentették a vizsgált fény intenzitását. De a fényforrásul használt égő láng túl fényesnek bizonyult és ez akadályozta a pontos mérést. Robert Bunsen (1811-1899) az egyes kémiai elemek elégetésekor kisugárzott fény spektrumát vizsgálta. Speciális égőt dolgozott ki, amely magas hőfokon (kb. 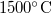 ) égette el a kémiai anyagokat, de kevés fényt bocsátott ki (1858). Ezt úgy érte el, hogy a kémiai elemet a levegővel először összekeverte és utána égette el. A Bunsen-égő ma is a kémia laborok elengedhetetlen kelléke.
) égette el a kémiai anyagokat, de kevés fényt bocsátott ki (1858). Ezt úgy érte el, hogy a kémiai elemet a levegővel először összekeverte és utána égette el. A Bunsen-égő ma is a kémia laborok elengedhetetlen kelléke.
A két kísérleti szakember egyesítette eljárását. Bunsen égőjét a fény keltésére, a prizmát a fény felbontására használták. Később a prizmát az optikai rács váltotta fel, amely a nagyobb felbontás miatt sokkal pontosabb méréseket tett lehetővé. Ezzel megszületett az első spektrográf.
Rájöttek, hogy minden elemnek egyedi spektruma van. A spektrumvonalak szerkezete minden elem „újjlenyomata”. Katalógusba foglalták az akkor ismert kémiai elemeket. 1860-61-ben kettő újat is fölfedeztek: a céziumot és a rubídiumot. Meg tudták állapítani, hogy a Nap atmoszférájában hidrogén, hélium, nátrium és egyéb földi elemek is vannak. Ez bizonyította be először, hogy a Föld és a Nap azonos elemekből áll. Ezzel megszűnt a Föld egyediségébe vetett hitünk.
A spektroszkópiával a csillagok fényét is lehetett vizsgálni. Kiderült, hogy még a sok milliárd fényév távolságra lévő égitestekben is ugyanazok az elemek találhatók, mint itt a Földön. Az Univerzum atomi egységessége lassan nyilvánvalóvá vált. Ennek természetfilozófiai jelentőségét nem lehet eléggé túlbecsülni. A Föld csak egy az Univerzum milliárdszor milliárd számú égiteste közül, melyek ugyanazon kémiai elemekből épülnek fel.
J. J. Thomson joggal gondolta azt, hogy a katódsugárcsőben mozgó elektronok csakis az elektróda anyagát felépítő atomokból származhatnak. Így az addig „oszthatatlannak” (ez az „atom” szó eredeti jelentése) gondolt atom valójában egy elemibb részletekkel bíró objektum, azaz valamilyen szerkezete van. A XIX-XX. század fordulójára (az addigi tapasztalatok alapján) megszületett a Thomson-féle hidrogén atommodell. Az atom méretét abból az ismert tényből határozhatjuk meg, hogy 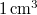 folyadék kb egy mól, azaz éppen
folyadék kb egy mól, azaz éppen 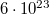 darab atomot tartalmaz. Eszerint az atom egy kb.
darab atomot tartalmaz. Eszerint az atom egy kb. 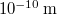 átmérőjű, gömb alakú egyenletes pozitív töltéseloszlás, amelynek közepében egy pontszerű elektron rezeg.
átmérőjű, gömb alakú egyenletes pozitív töltéseloszlás, amelynek közepében egy pontszerű elektron rezeg.
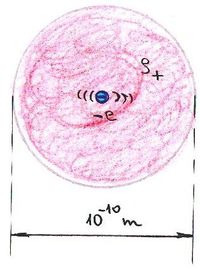
Thomson-modell |
Egyenletesen töltött gömb 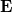 tere: tere:
|
Ugyanis (mint azt az elektrosztatikában megtanultuk) egy (a térfogatában) egyenletesen töltött gömb belsejében a térerősség (a centrumtól távolodva) lineárisan növekszik. Így pedig a középpontjában lévő elektronra ható erő is lineárisan növekszik. Maximális értékét a gömb határán éri el, utána 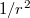 szerint csökken. Ha az elektron rezgési amplitudója nagyobb, mint a gömb sugara, akkor ő elszakadhat a gömbtől. Az elektron szabaddá válván az atom ionizálódott.
szerint csökken. Ha az elektron rezgési amplitudója nagyobb, mint a gömb sugara, akkor ő elszakadhat a gömbtől. Az elektron szabaddá válván az atom ionizálódott.
A következő években a kvantummechanika fejlődését a hidrogén atom modell kidolgozása is inspirálta. A hidrogén atom sugárzási spektrumának a pontos és részletes megmérése igazi kihívás volt a kor kísérleti fizikusainak a számára. A kísérleti adatokat sokan és sokszor ellenőrizték és így igen megbízhatóak voltak. Ezért aztán minden elméleti ötletet (anyagmodellt) a hidrogén atomon próbáltak ki. Ez volt minden elmélet próbaköve.
Ernest Rutherford angol fizikus közvetlen mérésekkel szerette volna ellenőrizni a Thomson-modell helyes voltát. Ezért elektronjuktól megfosztott 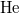 (hélium) atomokat (
(hélium) atomokat ( -részecskéket) lőtt vékony fémfóliára.
-részecskéket) lőtt vékony fémfóliára.
Egy 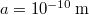 sugarú gömbben lévő
sugarú gömbben lévő  pozitív töltéseloszlás a gömbfelületénél produkálja a legnagyobb térerősséget. Ennek értéke jól ismert:
pozitív töltéseloszlás a gömbfelületénél produkálja a legnagyobb térerősséget. Ennek értéke jól ismert:
![\[ E_{\rm MAX} = \frac{Q}{4\pi\varepsilon_0} \frac{1}{a^2}. \]](/images/math/1/1/b/11baf4d4b892acf57650a16b3b0d541c.png)
Ha a 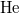 ion áthalad a fémfólián, akkor a reá ható maximális erő csak
ion áthalad a fémfólián, akkor a reá ható maximális erő csak 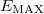 -ból adódhat. Nyilvánvaló az, hogy a visszapattanó
-ból adódhat. Nyilvánvaló az, hogy a visszapattanó 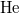 atomra hatott a maximális erő. Ezért a visszapattanó (azaz a „nagyszögű szórást” szenvedő) és a fólián szinte akadálytalanul áthatoló
atomra hatott a maximális erő. Ezért a visszapattanó (azaz a „nagyszögű szórást” szenvedő) és a fólián szinte akadálytalanul áthatoló 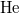 -lövedékek arányából
-lövedékek arányából 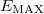 meghatározható.
meghatározható.
A kapott kísérleti eredmény azt mutatta, hogy a Thomson-féle atommodell nem helyes (1907, 1911). A szóráskísérletek eredménye szerint az atomban a pozitív töltés csak egy „kicsiny” térrészben, egy kb. 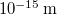 átmérőjű gömbben koncentrálódik. Ezen kísérleti tény alapján Rutherford egy új atommodellt alkotott. Eszerint az atom egy kb.
átmérőjű gömbben koncentrálódik. Ezen kísérleti tény alapján Rutherford egy új atommodellt alkotott. Eszerint az atom egy kb. 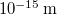 átmérőjű pozitív töltésű atommagból és körülötte mozgó elektronokból áll. A továbbra is pontszerűnek képzelt elektronok, a Coulomb vonzás következtében, az atommag körül keringenek egy kb.
átmérőjű pozitív töltésű atommagból és körülötte mozgó elektronokból áll. A továbbra is pontszerűnek képzelt elektronok, a Coulomb vonzás következtében, az atommag körül keringenek egy kb. 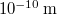 sugarú pályán. Ugyanis a modellnek kell tükröznie az atom korábbi „mértét” is.
sugarú pályán. Ugyanis a modellnek kell tükröznie az atom korábbi „mértét” is.
A hidrogén atom a periódusos rendszer első eleme. Ha megfosztjuk az egyetlen elektronjától, akkor egy még elemibb objektumot kapunk, amelyik így az „első előtt álló” (görögül protosz) lesz. Rutherford ezért a hidrogén atom magját protonnak nevezte el.

|
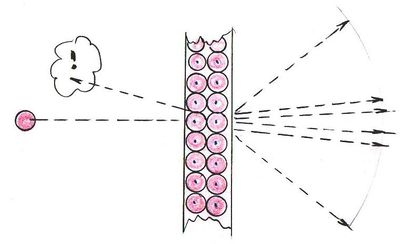
|
| Ernest Rutherford
1871-1937 |
Nagyszögű szóráskísérlet
1907-11 |
Rutherford atommodellje a kvantummechanika kialakulásának egyik gerjesztője volt, és mint ilyen, fizikatörténeti jelentősége óriási. A kémiai Nobel-díjat (nem ezért, hanem még korábban) 1908-ban, a rádióaktivitással kapcsolatos kutatásaiért kapta (többek között az „alfa” és a „béta” sugárzás azonosítása és elnevezése is tőle származik).
A Rutherford-féle atommodell megfelelt ugyan a korabeli kísérleti tényeknek, de alapvető elméleti hiányossága is volt: ha az elektron kering az atommag körül, akkor centripetális gyorsulással rendelkezik. Ekkor azonban – az elektrodinamika törvényei szerint – elektromágneses hullámot kellene gerjesztenie és így energiát kellene állandóan kisugároznia. Az elektron – az energiamegmaradás elve értelmében – állandóan veszítene az energiájából és rövid idő alatt beleesne az atommagba (elméleti becslések szerint ez kb. 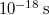 ). Azaz az atom nem lenne stabil. Ugyanakkor igaz az is, hogy a spektroszkópiai megfigyelések szerint az atomok bizonyos körülmények között elektromágneses hullámot bocsátanak ki. A kisugárzott energia frekvencia szerinti eloszlása minden fajta atomra (sőt molekulára) különböző. Közös jellegzetességük a diszkrét frekvencia eloszlás. Ezt vonalas spektrumnak hívjuk.
). Azaz az atom nem lenne stabil. Ugyanakkor igaz az is, hogy a spektroszkópiai megfigyelések szerint az atomok bizonyos körülmények között elektromágneses hullámot bocsátanak ki. A kisugárzott energia frekvencia szerinti eloszlása minden fajta atomra (sőt molekulára) különböző. Közös jellegzetességük a diszkrét frekvencia eloszlás. Ezt vonalas spektrumnak hívjuk.
A legegyszerűbb atom a hidrogén atom. Ezért célszerű, ha először a hidrogén atom spektrumát próbáljuk megérteni. Kezdetben csak a négy látható vonal (frekvencia illetve hullámhossz érték) volt ismeretes. Az 1860-as évektől a spektroszkópia megfigyelések során hatalmas mennyiségű kísérleti adat gyűlt össze. A hidrogén atom látható négy spektrumvonalát igen nagy pontossággal Anders Angström mérte meg.
A kísérleti spektroszkópia fejlődése lehetővé tette, hogy a megfigyeléseket kiterjesszék mind az infravörös, mind pedig az ultraibolya tartományba is. Így „láthatóvá vált” a hidrogén atom többi (rendkívül sok) spektrumvonala is.
Az IQ tesztek egyik közkedvelt feladata, amikor szabályosságot kell felfedezni egy adott számsor elemei között. Például az
![\[ 1, 2, 3, 5, 8, ... \]](/images/math/d/6/3/d6302d72f87af7445820fd3a6171618b.png)
feladatot az emberek döntő többsége könnyedén megoldja. Valamivel nehezebb lenne a következő:
![\[ 1, 7/2, 7, 23/2, ... \]](/images/math/6/b/2/6b2c67c34308f16b1966106495739ce9.png)
Érdekes feladatnak mutatkozik a
![\[ 1, 9/8, 5/4, 4/3, 3/2, ... \]](/images/math/4/7/c/47c9fb843a27b7c02736024530b9b46b.png)
számsor is. Erre csak akkor tudunk könnyen válaszolni, ha „segítségként” felírjuk: c, d, e, f, g, a, ... . Szinte rögtön felismerjük, a C-dur hangsor alaphanghoz viszonyított frekvenciáit.
Mindezen előkészítés azt a célt szolgálta, hogy kellően felmérjük annak a feladatnak a nehézségét, amelyben szabályosságot kell felfedezni a
![\[ 6562.1, 4860.74, 4340.10, 4101.20, ... \]](/images/math/0/2/6/026729b72e6045abd7acbe6b519e71aa.png)
számadatok között. Az első ránézésre a megoldás meglehetősen komplikáltnak ígérkezik. Hacsak nem találunk valamiféle vezérfonalat, (hasonlóan a C-dur skálához) a megoldás szinte reménytelennek tűnik. Pedig ezt a feladatot már megoldotta valaki...

|

|
| Johann Jakob Balmer
1825-1898 |
1885 |
Az illető Johann Jacob Balmer, svájci középiskolai tanár volt. A meglepően egyszerű megoldás a bázeli leányiskola évkönyvében látott először napvilágot, majd 1885-ben egy rövid közlemény formájában az Annalen der Physik-ben, a kor vezető európai tudományos folyóiratában is megjelent. A közlemény címe: „Megjegyzések a hidrogén atom színképvonalaihoz”. A megadott számsor ugyanis a hidrogén atom által kibocsátott látható fény hullámhosszait jelenti 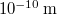 egységben. A négy számot összekötő formula pedig:
egységben. A négy számot összekötő formula pedig:
![\[ \nu = R\left( \frac{1}{4} - \frac{1}{n^2} \right), \quad \text{ahol} \quad n = 3,4,5,6. \]](/images/math/c/8/0/c8090ad8e8dab01cbe1ae3ee205606a7.png)
Ebből a keresett hullámhosszak a 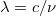 hányados segítségével megkaphatók.
hányados segítségével megkaphatók.
J. J. Balmer ábrázoló geometriát tanított. A geometria nemcsak önmagában érdekelte, de foglalkoztatta annak építészeti és művészeti vonatkozása is. Szerteágazó érdeklődési köre tette őt alkalmassá arra, hogy igen egyszerű formulát kapjon a hidrogén atom fent megadott spektrum vonalainak a megadására. A fizikatörténet bizonyítja, hogy egy új tudományterület kezdeti szakaszában elsősorban a széleskörű ismerteken alapuló analógiaérzék lehet igen gyümölcsöző, természetesen csak akkor, ha mindez logikai igényességgel is társul. Ez történt Balmer esetében is. Filozófiai beállítottságát tekintve Pitagorász (Pithagoras) követői közé tartozott, aki hitt abban, hogy a világ jelenségei összefüggő harmóniát alkotnak és ez a harmónia egész számokkal kifejezhető. Feltételezte ezért, hogy hasonlóan a C-dur skálához a hidrogén atom spektruma is egész számokkal megadható. Maga a módszer, ahogyan Balmer a végső felismeréshez eljutott igen eredeti és intuitív, de most nem fontos.
A lényeg az, hogy végül is a hidrogén atom látható frekvenciaspektrumára megkapta a fent közölt összefüggést. Ez a zárt matematikai forma azt üzente, hogy a hidrogén atom belsejében szigorú törvények uralkodnak, amelyek ezt a „szabályos” spektrumot produkálják. A kor fizikusainak nagy feladata éppen ezen törvények megfejtése volt. Mint tudjuk, ennek a „kihívásnak” sikerrel eleget is tettek. A siker eredményeként épült ki az a Kvantummechanika, amely még ma is eszközül szolgál a mikrovilág jelenségeinek sikeres megértésében, a „kvarkoktól a fotonokig”. Azaz az atommag belsejétől az Univerzum mélységéig.
Balmer formulája és neve csaknem 20 évre feledésbe merült. Csak akkor fedezték fel újra, amikor Rydberg (1890) és Ritz (1906) munkássága következtében nyilvánvalóvá vált az, hogy kellő általánosítással, a képlet segítségével az összes (ultraibolya és infravörös tartományban lévő „végtelen sok”) frekvenciaérték is kiszámítható.
![\[ \nu_{mn} = R\left( \frac{1}{m^2} - \frac{1}{n^2} \right), \quad \text{ahol} \quad m = 1,2,3,... \quad \text{és} \quad n = m+1, m+2, m+3, ... . \]](/images/math/c/d/e/cde9e13afb159e2d6bfe5f38d4f09168.png)
Az első lépést megtenni mindig nehéz. A fenti általános formulát is Balmer-formulának nevezi az első felfedezőt tisztelő utókor. A benne szereplő  neve viszont Rydberg-állandó. A Balmer-formula megadta ugyan a hidrogén atom teljes sugárzási spektrumát, de azt megmagyarázni nem tudta.
neve viszont Rydberg-állandó. A Balmer-formula megadta ugyan a hidrogén atom teljes sugárzási spektrumát, de azt megmagyarázni nem tudta.
A hidrogén atom modell fejlődéstörténete igen tanulságos a természettudományos megismerés mechanizmusát megérteni akarók számára. Rajta keresztül figyelemmel kísérhetjük egy „tudományos forradalom” paradigmaváltását. Azt is láthatjuk, hogy az új kísérleti eredmények hogyan épülnek be az elméleti modellbe és az új elméleti modell miként generál még újabb ellenőrző kísérleteket. A tudományos előrehaladás a „kísérlet” és az „elmélet” dinamikus egymásrahatásának az eredménye, ahol a döntő szó mindig a tapasztalaté (azaz a kísérleti eredményeké).
Azt is megfigyelhetjük, hogy egy „jó” elmélet mindig csak a lehető legkevesebb számú „önkényes feltevést” viszi be a modellbe. Éppen annyit, amennyire az „újdonsághoz” szüksége van. Ennek a gondolkodási stratégiának a neve Occam borotvája, amely végigvonul a fizika egész történetén.
Didaktikusan így mondhatnánk: Ugyanazon jelenséget magyarázó két különböző elmélet közül azt válaszd, amelyik a kevesebb számú önkényes feltevést tartalmazza!
- Esentia non sunt multiplicanda praeter necessitatem.

|

|

|
| William Ockham
1285–1349 |
Ockham borotvája | és a „modern változat” |
A „proton” kísérleti felfedezése és a Rutherford-féle atommodell nyilvánvaló hiányosságai csak tovább növelték az érdeklődést a hidrogén atom irányában. A fizikusok slágertémája a hidrogén atom „rejtélyének” a megfejtése volt. Ki kellett találni egy olyan modellt, amely minimális számú alapfeltevésből kiindulva (Occam borotvája) koherens egységbe rendezi a kísérleti eredményeket. Lényegében a hidrogén atom sugárzását (annak vonalas spektrumát) kellett megmagyarázni, de úgy, hogy az ne a klasszikus elektrodinamika szerint történjék.
Végül Niels Bohr dán fizikus volt az, aki három egyszerű, de nagyon merész posztulátum (alapfeltevés) segítségével matematikai levezetését adta a Balmer-formulának (Koppenhága, 1913. április). Ezzel a spektroszkópiai megfigyelések elméleti magyarázatot nyertek.
A Bohr-modell
A Bohr-féle atommodell alapfeltevései (posztulátumai) a következők.
- 1. posztulátum. Az elektron a hidrogén atomban csak meghatározott
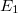 ,
, 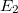 ,
, 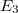 , ... energiájú pályákon tud sugárzás nélkül keringeni. Ezek a (kör)pályák tehát stabilak.
, ... energiájú pályákon tud sugárzás nélkül keringeni. Ezek a (kör)pályák tehát stabilak.
- 2. posztulátum. Ha az elektron egy magasabb energiájú pályáról egy alacsonyabb energiájú pályára „ugrik”, akkor az energiakülönbséget egy
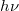 energiájú foton kibocsátásával leadja:
energiájú foton kibocsátásával leadja: 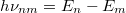 .
.
- 3. posztulátum. Csak azok a (kör)pályák stabilak, amelyen az elektron pályamozgásból adódó perdülete a
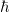 -nak egész számú többszöröse, azaz
-nak egész számú többszöröse, azaz 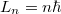 , ahol
, ahol 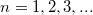 .
.
Világosan látszik, hogy az egyes posztulátumok miként támaszkodnak az akkori modern ismeretekre. Az 1. posztulátum stabil pályái az atomi Planck-oszcillátor diszkrét energiaszintjeire emlékeztetnek. A 2. posztulátum szerint a hidrogén atom az energiáját az Einstein által bevezetett fotonok alakjában adja le. A 3. posztulátum azonban teljes egészében Bohr „ötlete”. Megmutatjuk, hogy alkalmas nézőpontot választva a körpályák és az atomi oszcillátor kvantálása ugyanannak az általános elvnek a következménye. Bohr és Sommerfeld érdeme, hogy rátaláltak erre a szemléletmódra.

|
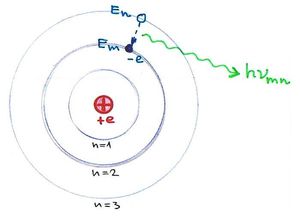
|
| Niels Henrik David Bohr
1885 – 1962 |
A Bohr-model |
Mint az ismeretes, a lineáris oszcillátor energiaszintjeire vonatkozó Planck-féle kvantálási törvény:
![\[ E_n = n\cdot h\nu, \quad \text{ahol} \quad n=1,2,3,... . \]](/images/math/4/8/4/4840c42fe17c694148d18473691f993d.png)
A körmozgásra vonatkozó Bohr-féle kvantálás a perdületre vonatkozik:
![\[ L_n = n\cdot \hbar, \quad \text{ahol} \quad n=1,2,3,... . \]](/images/math/b/3/1/b31fa12cef28d61dc15093a34bf7aedd.png)
Ez a két törvény formailag nagyon különbözik egymástól. Mi lehet az az általános kvantálási törvény, amely minden esetben érvényes? A választ Bohr és Sommerfeld adta meg 1916-ban.
Az általánosítás alapja a következő. Egyetlen tömegpont egydimenziós mozgását vizsgáljuk. Mint tudjuk ezt a Newton-féle mozgásegyenlet szabályozza. Ha megadjuk a  időpillanatban a részecske
időpillanatban a részecske  helyét és
helyét és 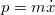 impulzusát, akkor az
impulzusát, akkor az  erőhatás ismeretében meg tudjuk mondani a részecske egész (mechanikai) jövőjét:
erőhatás ismeretében meg tudjuk mondani a részecske egész (mechanikai) jövőjét:
![\[ \dot p = F, \quad x(0) = x_0, \quad p(0) = p_0. \]](/images/math/1/8/3/183ae322fa495b31ce90638e05fa7c9c.png)
Tehát a részecske „életét” az 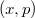 síkon egy görbe fogja jellemezni (ezek neve fázissík és fázisgörbe v. trajektória). Nézzük meg, mi lesz a fázisgörbe egy harmonikus oszcillátor esetén. Ehhez írjuk fel az oszcillátor összenergiáját:
síkon egy görbe fogja jellemezni (ezek neve fázissík és fázisgörbe v. trajektória). Nézzük meg, mi lesz a fázisgörbe egy harmonikus oszcillátor esetén. Ehhez írjuk fel az oszcillátor összenergiáját:
![\[ \frac{p^2}{2m} + \frac{x^2}{2/D} = E, \quad \text{amiből} \quad \frac{p^2}{2mE} + \frac{x^2}{2E/D} = 1. \]](/images/math/e/2/a/e2afb3ca0e311a21d04dccd7da7e707b.png)
Ez pedig egy ellipszis egyenlete a fázissíkban.
Számítsuk ki ennek az ellipszisnek a területét:
![\[ \oint p \, {\rm d} x = \pi \sqrt{2mE} \cdot \sqrt{2E/D} = 2\pi E \sqrt{m/D} = \frac{2\pi E}{\omega} = \frac{E}{\nu}. \]](/images/math/2/8/9/289b930149697e0d27c0afab33ff60a3.png)
Az atomi oszcillátorok energiaszintjeit megadó Planck-féle törvény alapján
![\[ \oint p \, {\rm d} x = nh, \quad \text{ahol} \quad n = 1,2,3,... . \]](/images/math/c/9/d/c9ddc556a357ac1e87f8effdf668c86e.png)
Látjuk tehát, hogy egy tetszőleges (egydimenziós) periodikus mozgást végző tömegpont mozgását (az impulzus és a koordináta által definiált) fázispont zárt trajektorián történő mozgásával adhatjuk meg. A kvantálási törvény az, hogy ezen zárt görbe által határolt terület a  Planck-állandó egész számú többszöröse lehet csak. A törvény általánosítható tetszőleges szabadságfokú mozgás esetére is.
Planck-állandó egész számú többszöröse lehet csak. A törvény általánosítható tetszőleges szabadságfokú mozgás esetére is.
Alkalmazzuk ezt egy körmozgásra. Ez is egy periodikus mozgás és a fázisgörbe most is zárt kell, hogy legyen. Az adott  sugarú egyenletes körmozgás esetén a körpályán megtett utat tekinthetjük a pont
sugarú egyenletes körmozgás esetén a körpályán megtett utat tekinthetjük a pont  koordinátájának. A pont pálya menti
koordinátájának. A pont pálya menti 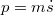 impulzusa a mozgás során állandó marad. A fázisgörbe egy téglalap lesz.
impulzusa a mozgás során állandó marad. A fázisgörbe egy téglalap lesz.
A fázisintegrál könnyen kiszámítható:
![\[ \oint p \, {\rm d} s = p\cdot 2\pi r = 2\pi L = n\cdot h. \]](/images/math/f/1/d/f1d8267fb9851943072d9605347872be.png)
Ebből pedig egyszerű átrendezéssel kapjuk, hogy
![\[ L_n = n\hbar, \quad \text{ahol} \quad n=1,2,3,... . \]](/images/math/1/9/8/19863060a553b394f5bcdc83688b3507.png)
Ez pedig éppen a Bohr-féle körpályák kvantálási törvénye.
A következőkben a Bohr-modell alapján meghatározzuk a Balmer-formulát. A Bohr-féle 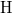 atomban az elektron a proton körül
atomban az elektron a proton körül  sugarú körpályán kering. Az elektron centripetális gyorsulását a Coulomb-erő biztosítja:
sugarú körpályán kering. Az elektron centripetális gyorsulását a Coulomb-erő biztosítja:
![\[ \frac{e^2}{4\pi\varepsilon_0} \frac{1}{r^2} = \frac{mv^2}{r}. \]](/images/math/e/5/e/e5e41500147e5970c8ad3fc1f4258329.png) |
(13) |
A lehetséges körpályákat a kvantálási törvény választja ki, amely most a következő alakú:
![\[ mvr = n\hbar, \quad \text{ahol} \quad n=1,2,3,... . \]](/images/math/b/5/d/b5d2de41bb17a44d52f30d8e046c5315.png) |
(14) |
A (13) egyenletet 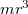 -el bővítve és (14)-et felhasználva kapjuk, hogy
-el bővítve és (14)-et felhasználva kapjuk, hogy
![\[ n^2 \hbar^2 = m^2 v^2 r^2 = \frac{m{\rm e}^2}{4\pi\varepsilon_0} r. \]](/images/math/2/4/d/24d07bed468525d3fc9a2d99c83baf62.png)
Ebből adódnak a lehetséges Bohr-pálya sugarak:
![\[ r_n = a_0 n^2, \quad n=1,2,3, ... ., \]](/images/math/3/b/a/3ba1cc1842951cde177101e3e3fea314.png)
ahol 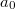 a Bohr sugár vagy Bohr hosszúság:
a Bohr sugár vagy Bohr hosszúság:
![\[ a_0 = \frac{4\pi\varepsilon_0}{m{\rm e}^2}\hbar^2 \approx 0,529\cdot 10^{-10} \, {\rm m}. \]](/images/math/4/4/1/441412cbd8deed3be6a7df4d283d5671.png)
A fizikusok nagyon gyakran az atomi tartományokban ezt a hosszúságegységet használják, amely a legkisebb Bohr-pálya sugarával egyezik meg.
Könnyen megkapható a körpályán mozgó elektron sebessége is: 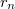 kifejezését behelyettesítve (14)-be, kapjuk, hogy
kifejezését behelyettesítve (14)-be, kapjuk, hogy
![\[ v_n = n \frac{\hbar}{mr_n} = \frac{1}{n} \frac{\hbar}{m a_0} = \frac{v_0}{n}, \quad \text{ahol} \quad v_0 = \frac{{\rm e}^2}{4\pi\varepsilon_0\hbar} = \frac{\hbar}{m a_0} = 2,2\cdot 10^6 \frac{\rm m}{\rm s}. \]](/images/math/0/b/1/0b1629e97ccaea561c4ab02b4c9e7e16.png)
A Bohr-atomban a leggyorsabban a legkisebb sugarú pályán lévő elektron mozog. Ennek a sebessége a fénysebességhez képest kicsi:
![\[ \alpha = \frac{v_0}{\rm c} = \frac{1}{4\pi\varepsilon_0} \frac{{\rm e}^2}{\hbar {\rm c}} = \frac{1}{137,036} \approx \frac{1}{137}. \]](/images/math/0/9/0/09075997c371a76709276770c75d90e9.png)
Tehát a Bohr-modell egy nem-relativisztikus atommodell. A végeredményei nincsenek ellentmondásban a kiindulási feltételezésekkel. Erre azt szoktuk mondani, hogy a modell „konzisztens” (ellentmondásmentes).
Az  neve finomszerkezeti állandó. Érdekessége az, hogy egy (mértékegység nélküli) szám. Azaz a mértékegység választásától függetlenül ugyanakkora az értéke (még az esetleges UFO-knál is ennyi lenne). Három fontos természeti állandót köt össze:
neve finomszerkezeti állandó. Érdekessége az, hogy egy (mértékegység nélküli) szám. Azaz a mértékegység választásától függetlenül ugyanakkora az értéke (még az esetleges UFO-knál is ennyi lenne). Három fontos természeti állandót köt össze:  -t,
-t,  -t és
-t és 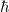 -t. Az elektrodinamika, a speciális relativitáselmélet és a kvantummechanika jellegzetes állandói határozzák meg az értékét. Mint olyan, a Természet egyik fontos és jellemző adatát kapjuk meg. Mindenhol előfordul, ahol az atomi világ és az elektrodinamika találkozik.
-t. Az elektrodinamika, a speciális relativitáselmélet és a kvantummechanika jellegzetes állandói határozzák meg az értékét. Mint olyan, a Természet egyik fontos és jellemző adatát kapjuk meg. Mindenhol előfordul, ahol az atomi világ és az elektrodinamika találkozik.
Meghatározhatjuk még pl. a Bohr-pályán mozgó elektron keringési körfrekvenciáját is. Ez nyilvánvalóan
![\[ \omega_n = \frac{v_n}{r_n} = \frac{1}{n^3} \frac{v_0}{a_0} \equiv \frac{\omega_0}{n^3}, \]](/images/math/d/b/c/dbc279303ac9d9d7beb5aa2d3a6d54c3.png)
ahol az előzőek alapján
![\[ \omega_0 = \frac{\hbar}{m a_0^2}. \]](/images/math/0/4/0/040f61c27f490af2977071418af3a76c.png)
A Bohr-pályákon keringő elektronok diszkrét energiaszintjei definíciószerűen adódnak:
![\[ E_n = E^{\rm kin}_n + E^{\rm pot}_n = \frac{1}{2}mv_n^2 - \frac{{\rm e}^2}{4\pi\varepsilon_0} \frac{1}{r_n} = \frac{1}{2} mv_0^2 \frac{1}{n^2} - \frac{{\rm e}^2}{4\pi\varepsilon_0 a_0} \frac{1}{n^2}. \]](/images/math/a/5/c/a5c3ce0c173116497f8c6f304817a9d2.png)
A kinetikus energiatagban szereplő 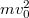 együttható
együttható 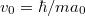 felhasználásával átalakítható:
felhasználásával átalakítható:
![\[ mv_0^2 = m \frac{\hbar^2}{m^2 a_0^2} = \frac{\hbar^2}{m} \frac{m{\rm e}^2}{4\pi\varepsilon_0} \frac{1}{a_0} = \frac{{\rm e}^2}{4\pi\varepsilon_0 a_0}. \]](/images/math/d/0/3/d030f452684fb8e1ff7d19d7a151cadd.png)
és ezzel kapjuk, hogy
![\[ E_n = \frac{1}{n^2} \left ( \frac{1}{2} \frac{{\rm e}^2}{4\pi\varepsilon_0 a_0} - \frac{{\rm e}^2}{4\pi\varepsilon_0 a_0} \right ) = - \frac{1}{n^2} \frac{{\rm e}^2}{8\pi\varepsilon_0 a_0}, \quad E_0 \equiv \frac{{\rm e}^2}{8\pi\varepsilon_0 a_0}, \]](/images/math/6/c/e/6cee04a00d4af9921d57129df93e8d63.png)
![\[ E_n = -\frac{E_0}{n^2}, \quad n=1,2,3,... . \]](/images/math/c/c/5/cc59f2efccbf4ed6e9f340cd93c7e8e0.png)
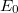 számértéke:
számértéke:
![\[ E_0 = 13,6 {\rm eV}. \]](/images/math/0/5/b/05b6e0b9388b0d28b796b8e17f008a3d.png)
Ezek az első Bohr-posztuátumban szereplő 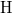 atom diszkrét energiaszintjei. Az atom által kisugárzott EMH frekvenciák pedig a 2. posztulátum szerint adódnak:
atom diszkrét energiaszintjei. Az atom által kisugárzott EMH frekvenciák pedig a 2. posztulátum szerint adódnak:
![\[ h\nu_{mn} = E_n - E_m, \]](/images/math/1/e/a/1eaae32e7518da0658ad2217f36760bf.png)
és így
![\[ \nu_{mn} = \frac{E_n - E_m}{h} = \frac{E_0}{h} \left( \frac{1}{m^2} - \frac{1}{n^2} \right). \]](/images/math/f/c/8/fc8241f98eb20f93645fc23c7b850f0c.png)
Ez pedig a Balmer-formula. Ebből leolvasható az 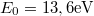 energia fizikai tartalma is. Ugyanis ha
energia fizikai tartalma is. Ugyanis ha 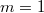 és
és 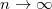 , akkor a
, akkor a 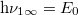 eredményt kapjuk. Ez azt jelenti, hogy ha az
eredményt kapjuk. Ez azt jelenti, hogy ha az 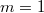 alapállapotú elektronnak
alapállapotú elektronnak 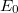 energiát adunk, akkor az elhagyja az atomot (
energiát adunk, akkor az elhagyja az atomot (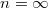 ). Tehát az (alapállapotú) hidrogén atom ionizációs energiája
). Tehát az (alapállapotú) hidrogén atom ionizációs energiája 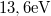 . A Bohr-modell lehetőséget ad a Rydberg-féle empirikus állandó kiszámítására is:
. A Bohr-modell lehetőséget ad a Rydberg-féle empirikus állandó kiszámítására is: 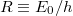 . A számítások pontosan visszaadták a kísérleti adatokat. A Bohr-modell győzelme vitathatatlan volt.
. A számítások pontosan visszaadták a kísérleti adatokat. A Bohr-modell győzelme vitathatatlan volt.
A Bohr-modell és a korrespondencia-elv
A speciális relativitáselmélet kapcsán már foglakoztunk a korrespondencia-elvvel. Idézzük most fel az ott olvasottakat:
- Van még egy fontos támpontunk. Ez az ún. „korrespondencia-elv”. Ezt a Fizikai törvények megalkotásánál igen gyakran használjuk. Azt mondja ki, hogy egy adott jelenségre vonatkozó „új” törvénynek határesetben mindig vissza kell adnia a „régit”. Ugyanis az „új” törvény mindig megváltoztatja a „réginek” az érvényességi körét. Ettől még a régi állítások nem válnak hamissá, hiszen azokat továbbra is a „régi” feltételek között használjuk.
A mostani esetben ez azt jelenti, hogy „makroszkópikus” skálán a Bohr-modellnek vissza kell adnia a klasszikus elektrodinamikai jelenségeket. Azaz az 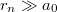 makroszkopikus nagyságú körpályán mozgó elektronnak elektromágneses hullámokat kell sugároznia. A klasszikus elektrodinamika szerint ennek a körfrekvenciája éppen a mozgó töltés keringési körfrekvenciájával (ez most
makroszkopikus nagyságú körpályán mozgó elektronnak elektromágneses hullámokat kell sugároznia. A klasszikus elektrodinamika szerint ennek a körfrekvenciája éppen a mozgó töltés keringési körfrekvenciájával (ez most 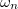 ) kell megegyeznie, ha
) kell megegyeznie, ha 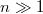 . A kérdés az, kiadja-e a Bohr modell ezt az eredményt
. A kérdés az, kiadja-e a Bohr modell ezt az eredményt 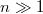 esetén?
esetén?
A Bohr-modell második feltevése szerint a kisugárzott energia
![\[ \hbar\omega = E_{n+1} - E_n = E_0 \left[ \frac{1}{n^2} - \frac{1}{(n+1)^2} \right]. \]](/images/math/6/c/6/6c621af6806cdd4518a86389a6336598.png)
Tehát
![\[ \omega = \frac{E_0}{h} \left[ \frac{1}{n^2} - \frac{1}{(n+1)^2} \right] = \frac{E_0}{h} \left[ \frac{2n+1}{n^4 + 2n^3 + n^2} \right]. \]](/images/math/e/3/9/e39af19ea8ec806b9da393c9eaf7377b.png)
A klasszikus határesetet nagyon nagy kvantumszámok jelentik, tehát ha  , akkor:
, akkor:
![\[ \omega = \frac{2E_0}{h} \frac{1}{n^3}. \]](/images/math/6/8/2/682b8b1f6a034f124e64e755c07bc9fc.png)
De az előzőekben láttuk, hogy 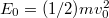 és
és 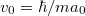 . Ezekkel adódik, hogy a kisugárzott foton frekvenciája
. Ezekkel adódik, hogy a kisugárzott foton frekvenciája
![\[ \omega = \frac{mv_0^2}{\hbar} \frac{1}{n^3} = \frac{ma_0^2 \omega_0^2}{\hbar} \frac{1}{n^3} = \frac{\omega_0}{n^3} = \omega_n. \]](/images/math/2/d/b/2db3d2bfaafb7bdba55719e196b56133.png)
Ez pedig megegyezik az elektron keringési körfrekvenciájával. Tehát megkaptuk a klasszikus elektrodinamika eredményét. A Bohr-modell eleget tesz a korrespondencia-elvnek, ahogyan annak lenni is kell.
Később megszületett a modell egy továbbfejlesztett változata is, amelyben az elektron (az általánosabbnak tekinthető) ellipszis pályákon is mozoghat. Ez volt a Bohr-Sommerfeld modell. Ennek ma már inkább csak fizikatörténeti jelentősége van, ezért ezzel nem foglalkozunk.
Niels Bohr a fizikai Nobel-díjat 1922-ben kapta meg, az indoklás szerint: „Az atomok szerkezetének és az azokból eredő sugárzásoknak a vizsgálataiért”. Modelljének merész újdonsága döntő lépés volt abba az irányba, amely szakítást jelentett a megszokott klasszikus fogalmakkal. Bohr ennek tudatában volt. 1913 decemberében ezzel kapcsolatosan a következőket mondta:
- ...remélem, elég világosan fejeztem ki magam ahhoz, hogy önök is megértsék, milyen merev ellentétben állnak az előadott elgondolások a fogalmaknak azon csodálatra méltó, összefüggő rendszerével, melyet joggal a „klasszikus” elektrodinamikának nevezünk.
Bohr szakítását a „csodálatra méltó” klasszikus elektrodinamikával joggal nevezhetjük forradalmi lépésnek és ez a forradalmi gondolat igen hasznosnak is bizonyult.
A fizikusok feltételezték, hogy minden atom szerkezete a hidrogén atoméhoz hasonló. A diszkrét energiaszintek közvetlen mérését James Franck és Gustav Ludwig Hertz valósította meg 1913-ban, hat hónappal (!) a Bohr-modell megszületése után.

|

|
| James Franck
1882–1964 |
Gustav Ludwig Hertz
1887–1975 |
A mérés elve az volt, hogy megmérték a higany-atomokkal ütköző elektronok ütközés utáni kinetikus energiáját. A higany atom tömege kb. nyolcvanezerszer nagyobb, mint az elektron tömege és a kísérletben az átlagsebessége az elektronokéhoz képest elhanyagolható. Ha az ütközés során az ütköző elektron kinetikus energiája lecsökken (azaz az ütközés rugalmatlan), akkor ez azt jelenti, hogy a higany atom valamelyik elektronjának az energiája megnövekedett. Ha az atomban az energiaszintek diszkrétek, akkor az ütköző elektronok energiacsökkenése nem lehet akármekkora. A mérési elrendezés vázlata az ábrán látható.
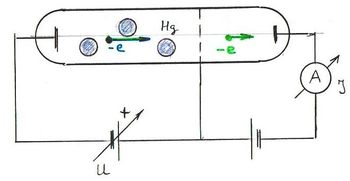
|
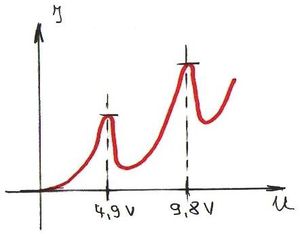
|
| A Franck-Hertz kísérlet vázlata | |
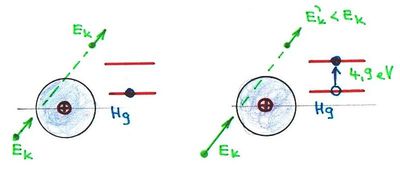
| |
| A rugalmas és a rugalmatlan ütközés | |
A katódból kiinduló elektronokat a változtatható  feszültségforrás segítségével gyorsítjuk. Az elektronok az ebben a térrészben lévő higanygőz atomjaival ütköznek. Ha az elektronok nem adnak át energiát az atomnak, akkor az ütközés rugalmas és az elektronok energiaveszteség nélkül haladnak tovább. A tartály közepén egy olyan vékony háló van, amelyen az elektronok át tudnak menni, de a hozzá képest sokkalta nagyobb
feszültségforrás segítségével gyorsítjuk. Az elektronok az ebben a térrészben lévő higanygőz atomjaival ütköznek. Ha az elektronok nem adnak át energiát az atomnak, akkor az ütközés rugalmas és az elektronok energiaveszteség nélkül haladnak tovább. A tartály közepén egy olyan vékony háló van, amelyen az elektronok át tudnak menni, de a hozzá képest sokkalta nagyobb  atomok már nem. A rácson átjutott elektronokat egy fékező tér lelassítja. Az itt mért
atomok már nem. A rácson átjutott elektronokat egy fékező tér lelassítja. Az itt mért  áram egyben az anódhoz érkező elektronok kinetikus energiáját méri. Pl. ha az áram éppen zérus (lenne), akkor egy elektron sem érte el az anódot.
áram egyben az anódhoz érkező elektronok kinetikus energiáját méri. Pl. ha az áram éppen zérus (lenne), akkor egy elektron sem érte el az anódot.
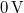 -ról indulva, az
-ról indulva, az  gyorsító feszültség növekedésével nő a rácshoz érkező elektronok (maximális) kinetikus energiája. Ha ez akkora, hogy éppen gerjeszteni tudja a
gyorsító feszültség növekedésével nő a rácshoz érkező elektronok (maximális) kinetikus energiája. Ha ez akkora, hogy éppen gerjeszteni tudja a 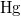 atom legkülső elektronját akkor az ütköző elektron kinetikus energiája lecsökken (majdnem nullára). Ez legelőször éppen a „rácsnál” fog bekövetkezni. Ekkor az
atom legkülső elektronját akkor az ütköző elektron kinetikus energiája lecsökken (majdnem nullára). Ez legelőször éppen a „rácsnál” fog bekövetkezni. Ekkor az  áram látványosan lecsökken.
áram látványosan lecsökken.
Ha tovább növeljük az  -t, akkor az
-t, akkor az  térerősség olyan nagy lesz, hogy az elektronoknak már a katód-rács távolság felénél elegendően nagy energiájuk lesz a
térerősség olyan nagy lesz, hogy az elektronoknak már a katód-rács távolság felénél elegendően nagy energiájuk lesz a 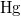 atomok gerjesztéséhez. Majd a hátralévő úton történő gyorsulás ismét elegendő lesz egy újabb rugalmatlan ütközésre (a rácsnál). Ekkor az
atomok gerjesztéséhez. Majd a hátralévő úton történő gyorsulás ismét elegendő lesz egy újabb rugalmatlan ütközésre (a rácsnál). Ekkor az 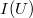 görbe már „két púpot” fog mutatni. És így tovább. Két szomszédos púp közötti feszültségkülönbségnek mindig ugyanakkorának kell lenni. Ez ugyanis éppen a
görbe már „két púpot” fog mutatni. És így tovább. Két szomszédos púp közötti feszültségkülönbségnek mindig ugyanakkorának kell lenni. Ez ugyanis éppen a 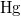 atom gerjesztési energiájával egyezik meg. Ez
atom gerjesztési energiájával egyezik meg. Ez 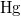 esetén kb
esetén kb 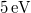 -nak adódott. Ha az energiaszintek nem lennének kvantáltak, akkor a „púpos görbe” helyett egy sima grafikont kaptunk volna.
-nak adódott. Ha az energiaszintek nem lennének kvantáltak, akkor a „púpos görbe” helyett egy sima grafikont kaptunk volna.
1925-ben a fizikai Nobel-díjat megosztva J. Franck és G. L. Hertz kapta „az elektronok és az atomok egymás közötti ütközés törvényeinek a felfedezésért”.
Ezzel a Bohr-modell újabb kísérleti megerősítést kapott.
Az elektron „vezérhullám elmélete”
Louis de-Broglie 1923-ban (majd az 1924-ben megvédett doktori dolgozatában) egy igen furcsa hipotézist dolgozott ki. Arra gondolt, hogy ha az elektromágneses tér hullámszerű tulajdonságot (pl. diffrakció, interferencia stb) és részecske jellegű tulajdonságot (foton!) is mutat, akkor ez a „kettősség” esetleg az elektronokra is igaz. Azaz az elektron mozgásához egy valamiféle hullám rendelhető. Később így emlékezett vissza azokra az időkre:
- ...Nem könnyű szívvel, hanem vonakodva és kényszer hatására hagytam el a klasszikus fizika hagyományos pozícióit, ez a megállapítás talán megmutatja a hitetlenkedőknek, hogy a hagyományos pozíciók mennyire védhetetlenekké váltak.
- ...aki egy új elmélet alapvető gondolatait kifejti, nem mindig veszi észre rögtön annak minden következményét. Személyes meglátásai alapján irányítva, a matematikai hasonlóságok belső ereje által indíttatva, szinte önmaga ellenére kényszerül új útra, amelyről maga sem tudja, hogy tulajdonképpen hova vezet... . Lassanként olyan értelmezésekre kényszerül, amelyekre eredetileg nem is gondolt...
- Minthogy a fényelmélet keretében össze kellett házasítani a megfelelően értelmezett hullám- és részecske-fogalmat, szükségszerűen felmerült a következő kérdés: vajon az elektronnak, akárcsak a fénynek, a jól ismert korpuszkuláris természeten kívül nincsen-e hullám természete is, amely a hullámoptikához hasonló jelenségekben nyilvánul meg? ... 1923-ban ennek a kérdésnek a felvetése igen merész dolog volt, mert akkor még semmi sem mutatott arra, hogy az elektronnak hullámtermészete is van. De ha az ember elgondolkozott a kvantumelmélet által bevezetett új fogalmakon, akkor lehetett találni néhány bizonyítékot, amely az elgondolás helyessége mellett szólt. Például: ...Planck, Bohr és Sommerfeld által bevezetett kvantumfeltételekben egész számok szerepelnek, ami az anyagi pont dinamikájában még sohasem fordult elő, de egészen megszokott olyan problémákban, amelyekben hullámokról van szó (interferencia, rezonancia stb)...
De Broglie ezt a hullámot igen találóan vezérhullámnak nevezte el és meglehetős óvatossággal fogalmazott:
- Az anyagi részecskék lehetséges megnyivánulásainak térbeli eloszlását ekkor a részecskékhez társuló hullám terjedése kell, hogy leírja...
A mindennapokban a fizikusok ezt a vezérhullámot elektronhullámnak szokták hívni. Ez azonban azt a hamis képet sugallja, mintha „az elektron maga hullámzana”. Mint az majd később ki fog derülni, ez nincsen így. Mindenesetre a félreértések elkerülése végett mi az elkövetkezőkben a de Broglie-hullám elnevezést fogjuk használni.

|
|
| Louis-(Victor-Pierre-Raymond, 7th duc) de Broglie
1892–1987 |
De Broglie állóhullámok a hidrogén atomban
1923-24 |
Már a foton esetében láttuk, hogy a speciális relativitáselmélet miként „veszi egy kalap alá” a véges 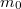 nyugalmi tömegű részecskéket és az
nyugalmi tömegű részecskéket és az 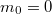 tömegű,
tömegű,  sebességgel mozgó fotont. Az energia-impulzus kapcsolat volt erre alkalmas:
sebességgel mozgó fotont. Az energia-impulzus kapcsolat volt erre alkalmas:
![\[ E = \sqrt{m_0^2 {\rm c}^4 + {\rm c}^2 p^2}. \]](/images/math/c/d/5/cd596a018fc16ac8ab7e6a6691e0d3eb.png)
Foton esetén 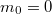 , és ezért
, és ezért
![\[ E=cp. \]](/images/math/0/2/1/0218ff05515a58ca031eb082a65608c7.png)
De ha a speciális relativitáselmélet szerint a foton és az elektron ugyanúgy viselkedik, mint a tömegpont, akkor de Broglie joggal feltételezte, hogy ez hasonlóság érvényes lehet a jelenségek más körére is. Láttuk már, hogy az elektromágneses hatás hullámként terjed és fotonként hat kölcsön a környezetével. De Broglie feltevése szerint legyen ugyanez igaz az ismert mikrorészecskékre, így az elektronra is. Az általa bevezetett hullám frekvenciája és hullámhossza az elektron energiájából és impulzusából ugyanúgy számítható ki, mint ahogyan azt a foton esetében láttuk. Azaz
![\[ E = \hbar\omega, \quad {\bf p} = \hbar{\bf k}. \]](/images/math/5/3/3/533181aa7a0274e9a9aacc79d7a61b4d.png)
Ennek az igen furcsa hullám-modellnek a meghökkentő eredménye az volt, hogy segítségével a Bohr-féle harmadik (kvantálási) hipotézis igen szemléletes jelentést kapott. Tekintsük a Hidrogén atom 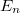 energiájú elektronját. Ekkor a körpálya sugara
energiájú elektronját. Ekkor a körpálya sugara 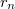 és az impulzusa
és az impulzusa 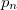 . Az elektron perdülete ekkor
. Az elektron perdülete ekkor
![\[ L_n = r_n\cdot p_n. \]](/images/math/6/b/b/6bb2b8be7428fc59de569fb6b3d07b29.png)
A 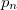 impulzusú elektron de Broglie hullámhossza
impulzusú elektron de Broglie hullámhossza
![\[ \lambda_n = \frac{h}{p_n}. \]](/images/math/0/6/6/066b2c482e85ab35bf148e09f10fb10a.png)
Stabil állapot akkor alakul ki, ha a körpályán mozgó elektronhoz rendelt (vezér)hullám önmagával interferálva állohullámot alakít ki. Azaz a de Broglie-hullámhossz egész számszor ráfér a pálya kerületére:
![\[ 2\pi r_n = n \lambda_n. \]](/images/math/1/6/7/16796660dcf1617ac2626689b5d46f04.png)
Beírva ide 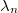 kifejezését, kapjuk, hogy:
kifejezését, kapjuk, hogy:
![\[ 2\pi r_n = n\frac{h}{p_n}. \]](/images/math/7/2/0/720f3a5a8234ef34879e3716ee9193f3.png)
Átrendezés után, pedig kapjuk, hogy
![\[ 2\pi r_n p_n = n\cdot h. \]](/images/math/2/a/3/2a3a50442cffc7c7073764b5e1deeeee.png)
Mivel most csak és kizárólag körpályákról van szó, ezért a perdület nyilvánvalón
![\[ L_n = r_n p_n = n \frac{h}{2\pi} = \hbar n. \]](/images/math/4/2/7/42735f5a08ab1c04c44d356f177e2df9.png)
Ez pedig nem más, mint a Bohr-féle kvantálási törvény. Tehát csak azok a pályák stabilak, amelyeken az elektronhoz rendelt vezérhullám önmagával interferálva állóhullámot alakit ki.
Az 1929-ben kiosztott fizikai Nobel-díj tulajdonosa Louis de Broglie lett „...az elektron hullámtermészetének a felfedezéséért”.
A részecskék „hullámtermészetének” az ötlete tetszetős volt és a Bohr-modellben igen szemléletessé vált. De bármilyen „szép vagy vonzó” egy elmélet, mit sem ér ha közvetlen kísérleti megerősítés nélkül marad. Mint azt többször említettük, a végső szó mindig a tapasztalaté. Az elektron hullámtulajdonságának a közvetlen kimutatása C. J. Davisson és munkatársa L. H. Germer (1927) amerikai fizikusok nevéhez fűződik. Nikkel kristály felületéről szóródó elektronnyaláb intenzitás-eloszlását vizsgálták. Ez olyan volt, hogy az csak az elektronokhoz rendelt de Broglie-féle hullámoknak a kristályatomokon történő diffrakciójával volt magyarázható. Hasonlóan a röntgen sugárzás Bragg-féle reflexiójához. Ez azt jelenti, hogy egy kristály röntgendiffrakciós és elektrondiffrakciós képe megtévesztően hasonló. Tőlük függetlenül G. P. Thomson (Aberdeen, 1928) arany, platina és alumínium filmeken áthaladó elektronnyaláb diffrakciós képeit hozta létre.
Mivel ezek a kísérletek alapvetően hozzájárultak a kvantummechanikai gondolkodásmód fejlődéséhez, az 1937-es fizikai Nobel-díjat megosztva C. J. Davisson és G. P. Thomson kapta.

|
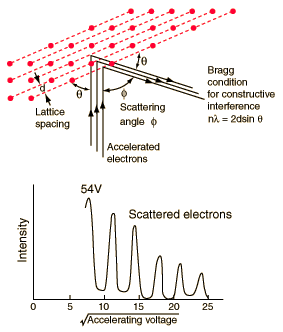
|
| C. J. Davisson (1881–1958) és
L. H. Germer (1896 –1971) |
Elektrondiffrakciós kísérlet (1927) |
Tudománytörténeti érdekesség, hogy G. P. Thomson, aki az elektronhullám kísérleti kimutatásáért nyerte el a legnagyobb tudományos díjat, annak a J. J. Thomsonnak a fia, aki 31 évvel előtte az elektron mint elemi részecske kimutatásáért kapta meg ugyanezt a tudományos elismerést.
Ezzel az elektronhoz rendelt „hullám-kép” ugyanúgy elfogadottá vált, mit a fényhullámhoz rendelt „foton-kép”.
Joggal merül fel a kérdés: valójában mi is az, ami hullámzik? Erre a nyilvánvaló kérdésre azonban még nem volt válasz! De Broglie szavait idézve:
- A hullám-részecske dualitás helyes értelmezését azonban nem láttam világosan és továbbra is foglalkoztatott a kérdés.
Tegyük hozzá: ebbéli gondjaiban nem volt egyedül!
A de Broglie-féle hullámok értelmezésére tett próbálkozások megértése céljából nézzük meg, hogy mit mond a klasszikus fizika a hullámok viselkedéséről.
Hullámcsomag a klasszikus mechanikában
Mint azt a (klasszikus) hullámtanból tudjuk, elemi síkhullámok szuperpozíciójaként egy ún. hullámcsomag állítható elő, amelyik a tér (tetszőlegesen kicsiny) véges tartományába lokalizálható. Ezt most egy egyszerű (klasszikus) mechanikai modellen mutatjuk be.
Mozogjon az  tengely mentén két, közel azonos hullámhosszúságú (
tengely mentén két, közel azonos hullámhosszúságú (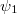 és
és 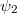 ) klasszikus „szinuszos” hullám. Az egyes hullámok haladási sebességét fázissebességnek hívjuk. Legyen a két hullám fázissebessége ugyanaz. A két hullám összeadódik. Az effektus neve szuperpozíció. Az összeadandó hullámok halmazát az eredő hullám spektrumának nevezzük. Határozzuk meg a szuperponálódott hullámok
) klasszikus „szinuszos” hullám. Az egyes hullámok haladási sebességét fázissebességnek hívjuk. Legyen a két hullám fázissebessége ugyanaz. A két hullám összeadódik. Az effektus neve szuperpozíció. Az összeadandó hullámok halmazát az eredő hullám spektrumának nevezzük. Határozzuk meg a szuperponálódott hullámok 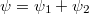 eredőjét. Az egyszerűség végett legyen a két összetevő hullám
eredőjét. Az egyszerűség végett legyen a két összetevő hullám 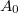 amplitúdója azonos. A klasszikus fizikai ismereteink alapján Írhatjuk tehát, hogy:
amplitúdója azonos. A klasszikus fizikai ismereteink alapján Írhatjuk tehát, hogy:
![\[ \psi_1(x,t) = A_0 \sin (k_1 x - \omega_1 t), \quad \psi_2(x,t) = A_0 \sin (k_2 x - \omega_2 t). \]](/images/math/0/4/2/04250a57ad06955449d9c4cd98541b53.png)
A fázissebességek azonosak, tehát 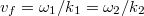 . A szuperponált, eredő hullám:
. A szuperponált, eredő hullám:
![\[ \psi = \psi_1 + \psi_2 = A_0 \left[ \sin (k_1 x - \omega_1 t) + \sin (k_2 x - \omega_2 t) \right] \equiv A_0 \left( \sin \varphi_1 + \sin \varphi_2 \right). \]](/images/math/1/9/4/19405c01ff7ab00617f94d34aff873e2.png)
Ezen eredő hullám (hullámszám) spektruma tehát 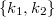 .
Alkalmazva a jól ismert „addíciós formulát” azt kapjuk, hogy
.
Alkalmazva a jól ismert „addíciós formulát” azt kapjuk, hogy
![\[ \psi = 2A_0 \sin \left( \frac{\varphi_1 + \varphi_2}{2} \right) \cos \left( \frac{\varphi_2 - \varphi_1}{2} \right). \]](/images/math/2/0/9/2092fb7a35ff1f1b9a47fde0d70af0f9.png)
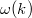
A későbbi általánosíthatóság végett célszerű bevezetni a következő fogalmakat:
![\[ k_1 \equiv k_0 - \frac{\Delta k}{2}, \quad k_2 \equiv k_0 + \frac{\Delta k}{2}. \]](/images/math/2/d/d/2dd7f1188962d6e1834db4f0a75dab41.png)
![\[ k_0 \equiv \frac{k_2 + k_1}{2}, \quad \Delta k \equiv k_2 - k_1. \]](/images/math/a/7/f/a7f7bc675101a1a8bf89298ce3a4c4d5.png)
Ennek megfelelően
![\[ \omega_0 \equiv v_f \cdot k_0, \quad \omega_1 \equiv v_f \cdot k_1, \quad \omega_2 \equiv v_f \cdot k_2, \]](/images/math/7/5/6/756419d91380dcacdc308b895b7e9b6c.png)
![\[ \Delta\omega \equiv \omega_2 - \omega_1 = v_f (k_1 - k_2) = v_f \Delta k, \]](/images/math/7/6/5/7654bdfaaefe5ed6e3dd72d9a33bdae9.png)
és ezért
![\[ \omega_1 = v_f \left( k_0 - \frac{\Delta k}{2} \right) = v_f k_0 - \frac{v_f \Delta k}{2} \equiv \omega_0 - \frac{\Delta\omega}{2}, \]](/images/math/5/5/d/55d2d350d545691c2ff015317322a664.png)
![\[ \omega_1 = v_f \left( k_0 + \frac{\Delta k}{2} \right) = v_f k_0 + \frac{v_f \Delta k}{2} \equiv \omega_0 + \frac{\Delta\omega}{2}. \]](/images/math/b/8/1/b8117a1c2478ef398e28a23078e86b74.png)
Így a 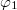 és
és 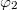 fázisok kombinációjára kapjuk, hogy:
fázisok kombinációjára kapjuk, hogy:
![\[ \frac{\varphi_1 + \varphi_2}{2} = \frac{k_1 + k_2}{2} x - \frac{\omega_1 + \omega_2}{2} t \approx k_0 x - \omega_0 t, \]](/images/math/8/5/d/85d2b412c30a2e255ea00f933da6c4fd.png)
![\[ \frac{\varphi_1 - \varphi_2}{2} = \frac{k_1 - k_2}{2} x - \frac{\omega_1 - \omega_2}{2} t \approx \frac{\Delta k}{2} x - \frac{\Delta \omega}{2} t. \]](/images/math/6/6/2/662c9e1400655b62a8beb4b2f94b0c30.png)
Ezzel az eredő (szuperponált) hullám a következő:
![\[ \psi(x,t) = 2A_0 \cos \left( \frac{\Delta k}{2} x - \frac{\Delta\omega}{2} t \right) \cdot \sin \left( k_0 x - \omega_0 t \right) \equiv A(x,t) \cdot \sin \left( k_0 x - \omega_0 t \right), \]](/images/math/1/b/8/1b8f19162373864c080a04575525a47a.png)
ahol
![\[ A(x,t) \equiv 2A_0 \cos \left( \frac{\Delta k}{2} x - \frac{\Delta\omega}{2} t \right). \]](/images/math/9/3/a/93aaa2aecc6159ae40d88b70f8d0d984.png)
Az eredő hullám tehát egy 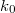 és egy
és egy 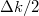 hullámszámú haladó hullám szorzata. A kérdés mármost az, hogy hogyan néz a
hullámszámú haladó hullám szorzata. A kérdés mármost az, hogy hogyan néz a 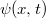 függvény? Legyen a két hullámhossz közel azonos, azaz
függvény? Legyen a két hullámhossz közel azonos, azaz
![\[ \frac{\Delta k}{2} \ll k_0 , \quad \frac{\Delta\omega}{2} \ll \omega_0, \]](/images/math/0/a/7/0a756aade833b6226a11076e44fb8d0f.png)
ezért
![\[ \Lambda \equiv 2\pi\frac{2}{\Delta k} \gg \frac{2\pi}{k_0} = \lambda_0. \]](/images/math/4/c/e/4ce286df3a873e657a81b17273c34853.png)
Tehát az 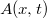 valóban egy váltózó amplitúdónak fogható föl, aminek
valóban egy váltózó amplitúdónak fogható föl, aminek  térbeli és
térbeli és  időbeli változása sokkal lassabb, mint a
időbeli változása sokkal lassabb, mint a 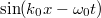 alaphullám tér és időbeli oszcillációja. A szemléletessége miatt nagyon gyakran azt mondjuk, hogy az
alaphullám tér és időbeli oszcillációja. A szemléletessége miatt nagyon gyakran azt mondjuk, hogy az 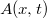 amplitúdó függvény a
amplitúdó függvény a 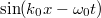 alap függvény burkológörbéje.
alap függvény burkológörbéje.
A burkológörbe haladási sebessége a 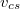 csoportsebesség. Ennek a kiszámítása igen egyszerű és nyilvánvaló szemléletességén alapul. Válasszuk ki a (periódikusan változó) burkoló görbe egyik maximális értékét és nézzük meg, hogy ez mekkora sebességgel halad. Erre az adódik, hogy
csoportsebesség. Ennek a kiszámítása igen egyszerű és nyilvánvaló szemléletességén alapul. Válasszuk ki a (periódikusan változó) burkoló görbe egyik maximális értékét és nézzük meg, hogy ez mekkora sebességgel halad. Erre az adódik, hogy
![\[ A(x,t) = 2A_0 \cos \left[ \frac{1}{2} (\Delta k x - \Delta \omega t) \right] = 2A_0, \]](/images/math/3/c/f/3cfbea0f537a6bf2daa62a3e2a694ccc.png)
azaz
![\[ \cos \left[ \frac{1}{2} (\Delta k x - \Delta \omega t) \right] = 1. \]](/images/math/d/2/3/d23257aae7c37f7597b6c25a93e9051a.png)
És ezért pl.
![\[ \Delta k x - \Delta \omega t = 0. \]](/images/math/c/b/9/cb96dce3897f3d1d3b7edf04ef37c052.png)
Így aztán nyilvánvaló, hogy ennek a maximumnak a helyét a következő 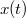 függvény adja meg:
függvény adja meg:
![\[ x = \frac{\Delta\omega}{\Delta k} t. \]](/images/math/3/c/b/3cb7fcffaa319c4c35740ea2b430c907.png)
Ebből adódik, hogy a maximum haladási sebessége (azaz a csoportsebesség) tehát (az idő szerinti deriválás után)
![\[ v_{cs} = \frac{{\rm d} x}{{\rm d} t} = \frac{\Delta\omega}{\Delta k}. \]](/images/math/9/1/e/91e0c92055bf749eee7e3918e629eeb1.png)
Jelen esetben a kétfajta (fázis- és csoport-) sebesség megegyezik
![\[ v_{cs} = \frac{\Delta\omega}{\Delta k} = \frac{\omega}{k} = v_f. \]](/images/math/c/7/2/c720a55afe88cb6fdccb0de96c65fd20.png)
Az eddigiek szemléletes értelmezése az, hogy a szuperpozíció eredményeként, az  térben „periódikusan” ismétlődő
térben „periódikusan” ismétlődő 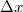 széles „hullámcsomagok” sokasága halad tovább éppen a
széles „hullámcsomagok” sokasága halad tovább éppen a 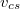 sebességgel. Ahol, mint az megfigyelhető:
sebességgel. Ahol, mint az megfigyelhető:
![\[ \Delta x = \frac{\Lambda}{2}. \]](/images/math/2/5/9/2595b21a9515d55c34e38fa9204b3fc4.png)
A 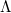 ismeretében írható, hogy
ismeretében írható, hogy
![\[ \Delta x = \frac{2\pi}{\Delta k}, \quad \text{azaz} \quad \Delta x \Delta k = 2\pi. \]](/images/math/4/a/f/4aff2d02f30a5591f9bd11b4c01360bc.png)
Ennek az összefüggésnek az értelmezése triviális. Szavakban: minél keskenyebb a spektrum, a hullámcsomag annál szélesebb.
Az eddigieket általánosíthatjuk úgy, hogy végtelen sok fázishullámot adunk össze. Azaz pl. a 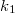 és a
és a 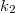 közé betesszük az összes (kontinuum számosságú)
közé betesszük az összes (kontinuum számosságú)  hullámot. Ekkor kapjuk, hogy:
hullámot. Ekkor kapjuk, hogy:
![\[ \psi(x,t) = \int_{k_1}^{k_2} A \cos[kx - \omega(k) t] \, {\rm d} k. \]](/images/math/2/a/d/2adc7e0160bfba476bc704d0e4306b4b.png)
Tudjuk, hogy az egyes összetevők fázissebessége 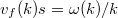 . Tegyük fel most is, hogy az összetevő hullámok egyforma sebességgel haladnak, azaz
. Tegyük fel most is, hogy az összetevő hullámok egyforma sebességgel haladnak, azaz 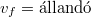 . Ekkor írható, hogy
. Ekkor írható, hogy
![\[ \psi(x,t) = \int_{k_1}^{k_2} A \cos[k (x - v_f t) ] \, {\rm d} k. \]](/images/math/9/c/e/9cea90c9d14e6dc515fd5e0d78e0e13e.png)
A  szerinti integrálás egyszerűen elvégezhető:
szerinti integrálás egyszerűen elvégezhető:
![\[ \psi(x,t) = A_0 \left[ \frac{\sin k (x - v_f t)}{x - v_f t} \right]_{k_1}^{k_2}, \]](/images/math/e/3/2/e328d6e1172e4d12023ca5211eca924c.png)
és ezért az integrálási határok beírása után kapjuk, hogy
![\[ \psi(x,t) = A_0 \left[ \frac{\sin k_2 (x - v_f t) - \sin k_1 (x - v_f t)}{x - v_f t} \right]. \]](/images/math/5/3/7/53745412dc33030f9fc5e69f5b28c26a.png)
Alkalmazzuk a jól ismert trigonometrikus azonosságot, nevezetesen:
![\[ \sin \varphi_{2} - \sin \varphi_1 = 2 \cos \frac{\varphi_2 + \varphi_1}{2} \cos \frac{\varphi_2 - \varphi_1}{2}. \]](/images/math/0/d/5/0d560e05bf086164968cb54e36886d8a.png)
Ekkor kapjuk, hogy
![\[ \psi(x,t) = 2A_0 \cos \left[ \frac{k_2 + k_1}{2} (x - v_f t) \right] \frac{\sin \left[ \frac{k_2 - k_1}{2} (x - v_f t) \right]}{x - v_f t}. \]](/images/math/5/f/8/5f804a94feb249330bc8126494650668.png)
Tudjuk azonban, hogy:
![\[ \frac{k_1 + k_2}{2} = k_0, \quad \frac{k_2 - k_1}{2} = \frac{\Delta k}{2}, \]](/images/math/4/5/a/45af4ee3d50a99a2b7cbf136e9a3b630.png)
és ezért
![\[ \psi(x,t) = 2A_0 \cos k_0 (x - v_f t) \frac{\sin \left[ \frac{\Delta k}{2} (x - v_f t) \right] }{x - v_f t}. \]](/images/math/6/9/c/69c654d9c9e76e91e327e2f14225ab5f.png)
Mivel a 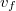 fázissebesség minden
fázissebesség minden  esetén ugyanaz, ezért (mint azt már láttuk)
esetén ugyanaz, ezért (mint azt már láttuk) 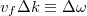 . Ezt beírva az egyenletbe, adódik, hogy
. Ezt beírva az egyenletbe, adódik, hogy
![\[ \psi(x,t) = 2A_0 \cos k_0 (x - v_f t) \frac{\sin \left[ \frac{1}{2}(\Delta k x - \Delta\omega t) \right]}{x - (\Delta\omega / \Delta k) t}. \]](/images/math/d/0/5/d056b260c5c3b6f46ab1ec1b1f400309.png)
Ebből 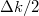 -vel való bővítés után kapjuk, hogy:
-vel való bővítés után kapjuk, hogy:
![\[ \psi(x,t) = A_0 \cos k_0 (x - v_f t) \Delta k \frac{\sin \left[ \frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) \right] }{\frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) }. \]](/images/math/0/0/2/002f4517b6098b0f6f2a0533e16ee6d8.png)
Hasonlóan a „kéthullámos” esethez, ez a 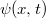 függvény is úgy fogható fel, mint egy
függvény is úgy fogható fel, mint egy 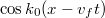 fázishullám, amelyet egy
fázishullám, amelyet egy 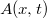 burkológörbe borít, ahol
burkológörbe borít, ahol
![\[ A(x,t) = A_0 \Delta k \frac{\sin \left[ \frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) \right] }{\frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) }. \]](/images/math/a/0/b/a0b176da0d5bb35c908aa6e597670a24.png)
Ez már nem egy periódikus függvény (mint az az előző esetben volt) hanem egyetlen 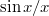 típusú, harangszerű görbe.
típusú, harangszerű görbe.
Mint azt az elemi matematikából tudjuk, ennek a burkológörbének a maximális értékét minden  időpillanatban a következő egyenlet definiálja:
időpillanatban a következő egyenlet definiálja:
![\[ \frac{\sin \left[ \frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) \right] } {\frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) } = 1. \]](/images/math/3/e/2/3e25a70c0330bcb42479697092e15be0.png)
Mint az ismeretes, ez akkor teljesül, ha
![\[ \frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) = 0. \]](/images/math/4/2/b/42b84db18d6c064609858de48db12aa5.png)
Elvégezve az idő szerinti deriválást, megkapjuk a burkológörbe maximumának a haladási sebességét, azaz a csoportsebességet:
![\[ \frac{\Delta k}{2} \left( \frac{{\rm d} x}{{\rm d} t} - \frac{\Delta\omega}{\Delta k} t \right) = 0. \]](/images/math/2/a/b/2abcea341130d1d37a2dec4c83f62308.png)
Ezért adódik, hogy:
![\[ v_{cs} = \frac{{\rm d} x}{{\rm d} t} = \frac{\Delta\omega}{\Delta k}, \]](/images/math/9/6/7/967ad746dd47a36672e931124d680a4e.png)
és most 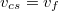 .
.
A hullámcsomaggal való „játékunk” tovább általánosítható, ha feltesszük, hogy 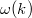 egy nem lineáris függvény. Ekkor ez azt jelenti, hogy a
egy nem lineáris függvény. Ekkor ez azt jelenti, hogy a 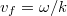 módon definiált fázissebesség függni fog a
módon definiált fázissebesség függni fog a  hullámszámtól, azaz
hullámszámtól, azaz
![\[ \omega(k) = k v_f(k). \]](/images/math/0/c/9/0c952502a53ede0e20203fd8ae96e8b3.png)
Könnyen belátható, hogy ebben az esetben a 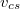 csoportsebesség korrekt definíciója az eddigi
csoportsebesség korrekt definíciója az eddigi 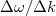 helyett, ennek általánosításaként
helyett, ennek általánosításaként 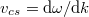 , helyesebben a
, helyesebben a
![\[ v_{cs} = \left[ \frac{{\rm d}\omega}{{\rm d} k} \right]_{k_0} \]](/images/math/7/c/0/7c0e7ea67572071fbc1119389150a2d4.png)
kifejezés lesz.
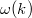
Összefoglalva az eddigieket azt kaptuk, hogy
![\[ \psi(x,t) = A_0 \cos k_0 (x - v_f t) \cdot \Delta k \cdot \frac{ \sin \left[ \frac{\Delta k}{2} (x - v_{cs} t) \right] }{ \frac{\Delta k}{2} (x - v_{cs} t) }. \]](/images/math/b/6/d/b6dcac008000f7e3865da852a2201882.png)
Ez a függvény egy 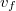 sebességgel haladó,
sebességgel haladó, 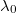 hullámhosszúságú szinusz-hullám, amelyet egy
hullámhosszúságú szinusz-hullám, amelyet egy 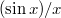 típusú függvény burkol. Ez a burkoló
típusú függvény burkol. Ez a burkoló 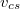 sebességgel mozog. Tehát amíg két hullám szuperpozíciója hullámcsomagok sokaságát adta, addig végtelen sok hullám eredője egyetlen „lokalizált hullámcsomag” lett. A „lokalizált” jelző itt a véges térbeli kiterjedésre utal. A hullámcsomag szélessége a „főmaximum” szélességével definiálható. Ez a burkoló függvény „első zérus helyéből” megkapható. Az „első zérus hely” a
sebességgel mozog. Tehát amíg két hullám szuperpozíciója hullámcsomagok sokaságát adta, addig végtelen sok hullám eredője egyetlen „lokalizált hullámcsomag” lett. A „lokalizált” jelző itt a véges térbeli kiterjedésre utal. A hullámcsomag szélessége a „főmaximum” szélességével definiálható. Ez a burkoló függvény „első zérus helyéből” megkapható. Az „első zérus hely” a 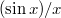 típusú függvény esetén azt jelenti, hogy
típusú függvény esetén azt jelenti, hogy 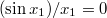 . Ez pedig az
. Ez pedig az 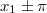 pontokban van. Alkalmazva ezt a mostani
pontokban van. Alkalmazva ezt a mostani 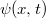 függvényre, kapjuk, hogy:
függvényre, kapjuk, hogy:
![\[ \frac{ \sin \left[ \frac{\Delta k}{2} \left( x - \frac{\Delta\omega}{\Delta k} t \right) \right] }{ \frac{\Delta k}{2} (x - v_{cs} t) } = 0, \]](/images/math/7/9/1/791aa07649e779da60cd9589e2ee415a.png)
és ezért
![\[ \frac{\Delta k}{2} \left( x_{\pm 1} - \frac{\Delta\omega}{\Delta k} t \right) = \pm \pi, \]](/images/math/c/2/3/c23c9a8b736b37318ed599a274e944a0.png)
azaz
![\[ x_{\pm 1} = \pm \frac{2\pi}{\Delta k} + \frac{\Delta\omega}{\Delta k} t. \]](/images/math/f/e/d/fed57deaa23becde4b7a2e22f54f0d34.png)
A hullámcsomag 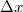 szélessége definíciószerűen tehát
szélessége definíciószerűen tehát
![\[ \Delta x \equiv x_{+1} - x_{-1} = \frac{4\pi}{\Delta k}. \]](/images/math/7/d/3/7d378c88df80d0d62d4d9e8365f83a89.png)
A hullámcsomag ezen véges kiterjedése, azaz a „lokalizáltsága” és az összetevő hullámok spektrális tulajdonsága között a következő összefüggést jelent:
![\[ \Delta x \, \Delta k = 4\pi. \]](/images/math/0/f/5/0f528beea1f04cee36a8f3a40cf8e56d.png)
Ez jellegében ugyanaz, mint a kételemű spektrum esetén kaptunk. Az értelmezése is azonos.
A de Broglie-féle hullámcsomag
Az előzőekben láttuk, hogy a klasszikus mechanikában homogén és izotróp közegben (azaz, ahol nincsen kitüntetett hely és irány) kis amplitúdójú hullámok fázissebessége állandó. Azaz
![\[ v_f = \frac{\omega(k)}{k} = {\rm c} = \text{konst}. \]](/images/math/b/4/c/b4c73731fc72fbe88cc5cfad01207831.png)
Ezért aztán 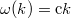 , és így a csoportsebesség
, és így a csoportsebesség
![\[ v_{cs} = \frac{{\rm d} \omega(k)}{{\rm d} k} = {\rm c}. \]](/images/math/8/c/e/8ceb2599ddd74e431195fa335ea32511.png)
Tehát a fázissebesség megegyezik csoportsebességgel. (Ugyanezt tapasztaljuk a vákuumban terjedő elektromágneses hullámoknál is.) Azt is láttuk, hogy hullámcsomag esetén, a „lokalizáltság miatt” megjelent egy „részecske jellegű” tulajdonság is.
Alkalmazzuk a ezeket az eredményeket a de Broglie-hullámok esetére! Ekkor egy szabadon mozgó elektron (kinetikus) energiáját kifejezhetjük a hozzá rendelhető de Broglie-hullám 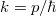 hullámszámával is, azaz
hullámszámával is, azaz
![\[ E = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m}. \]](/images/math/5/d/3/5d35ee3c517bd0338669d2b9d05471f3.png)
Ugyanakkor már láttuk, hogy a fotonhoz hasonlóan 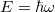 . E két energiakifejezést egybevéve kapjuk, hogy:
. E két energiakifejezést egybevéve kapjuk, hogy:
![\[ \omega = \frac{\hbar k^2}{2m}. \]](/images/math/8/6/4/864ad58ed85328d5c44ebcd5b0bbe936.png)
Mint az ismeretes, a  hullámszámú (azaz a
hullámszámú (azaz a  hullámhosszúságú) hullám (fázis)sebessége:
hullámhosszúságú) hullám (fázis)sebessége:
![\[ v_f = \frac{\omega}{k} = \frac{\hbar k}{2m} = \frac{1}{2} \frac{p}{m} = \frac{v}{2}. \]](/images/math/1/b/c/1bc07fe7b1fc22ede6e5c208467ca42b.png)
Azt kaptuk tehát, hogy egy  tömegű, egyenletes
tömegű, egyenletes  sebességgel (szabadon) mozgó részecskéhez rendelt de Broglie síkhullám
sebességgel (szabadon) mozgó részecskéhez rendelt de Broglie síkhullám 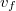 sebessége a részecske sebességének a felével egyenlő. Az eredmény meglehetősen „furcsa” és az
sebessége a részecske sebességének a felével egyenlő. Az eredmény meglehetősen „furcsa” és az 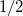 -es szorzót semmiféle „fizikai szemlélet” nem indokolja.
-es szorzót semmiféle „fizikai szemlélet” nem indokolja.
Határozzuk meg a de Broglie-hullámok csoportsebességét! A 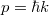 miatt
miatt
![\[ v_{cs} = \frac{{\rm d} \omega}{{\rm d} k} = \frac{\hbar k}{m} = \frac{p}{m} = v. \]](/images/math/8/f/0/8f02d549f76d221410221fcda66bc716.png)
Tehát egy lokalizált de Broglie hullámcsomag haladási sebessége éppen a részecske sebessége lesz. Ez már egy elfogadható eredmény. Azaz a „hullám” és a „részecske” tulajdonságok összebékülni látszanak.
Ekkor azonban újabb, súlyos értelmezési probléma lép fel. Mint azt látjuk, a de Broglie-hullámok esetén a 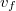 fázissebesség függ magának a (sík)hullámnak a
fázissebesség függ magának a (sík)hullámnak a  hullámszámától és így az
hullámszámától és így az  körfrekvenciától. Azaz nem ugyanaz minden síkhullámra. Így a hullámcsomagot előállító fázishullámok mindegyike más-más sebességgel mozog. Ezáltal az összetevő fázishullámok fáziskülönbsége állandóan változik. Ennek az eredménye az lesz, hogy a kezdetben jól lokalizált hullámcsomag igen rövid idő alatt szétfolyik. Ezt a „szemléletes” effektust csak akkor lehetne számszerű formába önteni, ha ismernénk a de Broglie-hullámok időfüggését. Ehhez pedig ismernünk kellene a de Broglie-hullámokat meghatározó hullámegyenletet is. De Broglie azonban ilyen egyenletről nem beszélt.
körfrekvenciától. Azaz nem ugyanaz minden síkhullámra. Így a hullámcsomagot előállító fázishullámok mindegyike más-más sebességgel mozog. Ezáltal az összetevő fázishullámok fáziskülönbsége állandóan változik. Ennek az eredménye az lesz, hogy a kezdetben jól lokalizált hullámcsomag igen rövid idő alatt szétfolyik. Ezt a „szemléletes” effektust csak akkor lehetne számszerű formába önteni, ha ismernénk a de Broglie-hullámok időfüggését. Ehhez pedig ismernünk kellene a de Broglie-hullámokat meghatározó hullámegyenletet is. De Broglie azonban ilyen egyenletről nem beszélt.
Milyen ez a hullámegyenlet? Ezt a kérdést Schrödingernek is feltették annak idején (1926). Az erre adott válasza a kvantumelmélet fejlődésében egy igen jelentős előrelépést jelentett.
A Schrödinger-egyenlet és a hullámfüggvény
A történet szerint a kvantummechanika egyik alapegyenletének a megalkotása a Zürichi Egyetem egyik elméleti fizika szemináriumán elhangzott, ártatlannak tűnő kérdéssel vette kezdetét.
Ebben az időben (1925-26) Peter Debye a zürichi Műszaki Főiskola tanára volt. Rendszeresen szervezett közös szemináriumokat az Egyetem fizikusaival. Ő javasolta (az ott elméleti fizikát tanító, akkor 39 éves) Ervin Schrödingernek, hogy egy ilyen közös szeminárium keretében ismertesse Louis de Broglie (1924) doktori dolgozatát. Annak feltételezése, hogy az elektron valamiféle „hullám jellegű tulajdonságokkal” is rendelkezik, nem kis meglepetést okozott a kor fizikusainak. A fiatalság (mint mindig) most is nagy érdeklődéssel fordult az új és igencsak „furcsa” elmélet felé. A szeminárium végén Peter Debye feltette a kérdést az előadónak: Ha van hullám, akkor hullámegyenletnek is kell lennie! Milyen ez az egyenlet? Természetesen az azonnali válasz elmaradt, hiszen de Broglie publikált dolgozatában erről nem esett szó. Schrödingert azonban elgondolkoztatta a feltett kérdés és maga próbált meg rá válaszolni. Pár hét múlva megszületett a Schrödinger-egyenlet.
Az Annalen der Physik (1926. január, február, május és júniusi számában) összesen négy cikk jelent meg (gyors egymásutánjában) amely a témával foglalkozott. Schrödinger először egy relativisztikus egyenletet (a későbbi, ún. Klein–Gordon egyenletet) konstruálta meg, de ez nem adta meg jól a „próbakőnek” tekintett hidrogén atom sugárzási spektrumát. Végül is ennek egy nem-relativisztikus közelítése vezetett a helyes eredményre. A későbbiekben ezt az egyenletet nevezték el Schrödinger-egyenletnek.
Hamarosan kiderült, hogy a Schrödiger-egyenlet a kvantummechanika egyik alapfeltevésének (azaz axiómájának) tekinthető. Megalkotóját (P. A. M. Dirac-kal együtt) az 1933. évi fizikai Nobel-díjjal tüntették ki „az atomelmélet új és gyümölcsöző megfogalmazásainak a megalkotásáért”.
Nem ennek a kurzusnak a témája, hogy tudománytörténeti hitelességgel kövessük a Schrödinger-egyenlet megszületésének minden részletét. Erre nincs is szükség, mert ma már számtalan visszaemlékezés és önéletrajzi írás jelent meg, amely a „fizika újkori” forradalmával, a modern fizika megszületésével foglalkozik. Az előtanulmányaink hiányos volta miatt még vázlatosan sem mutathatjuk be azt a gondolatmenetet, amelyet Schrödinger követett. Helyette egy sokkal egyszerűbb, didaktikus utat fogunk követni.
Jelen (BSc) kurzus keretei között csak a legelemibb ismeretek elsajátítására van lehetőség. Ennek megfelelően mi a következőkben a Schrödinger-egyenlet egy egyszerűbb alakjával, az ún. időtől független Schrödinger-egyenlettel fogunk megismerkedni. Ez a mikroszkopikus rendszerek (atomok, molekulák, szilárd testek stb) állandósult (stacionárius) állapotait írja le, de az állapotok időbeli változásaival (mint azt a neve is mutatja) már nem foglakozik. Erre az ún. időtől függő Schrödinger-egyenlet az alkalmas.
Az elkövetkezőkben (a rövidség kedvéért) Schrödinger-egyenleten mindig az időtől független Schrödinger-egyenletet fogjuk érteni.
Megjegyzés. A fent említet didaktikai tárgyalási mód azonban nem csökkenti az eredmény hitelességét, sőt, rámutat a Fizika, mint tudomány egységére és gondolati koherenciájára. Ezen azt kell érteni, hogy utólag visszatekintve, immáron sokkal több ismeret birtokában, egyszerűbb és rövidebb utakat fedezünk fel, amin jöhettünk volna. Azaz ugyanarra az objektív eredményre többféleképpen is eljuthatunk. Így pillanthatjuk meg a „törvény szövedékét”!
A kvantummechanika mélyebb kifejtésére csak a magasabb (MSc) tanulmányok során kerülhet majd sor. Ennek ellenére már BSc szinten is sok (a mérnöki területen) használható ismeretre tehetünk szert.
A Schödinger-egyenlet megalkotása (a hullámmechanika egyik axiómája)
Az egyszerűség végett az egydimenziós egyenletet fogjuk „kitalálni”, majd ezt általánosítjuk háromdimenziós (térbeli) problémákra. Az általánosítás lehetősége nyilvánvaló lesz.
Mint az ismeretes, a de Broglie által bevezetett (anyag)hullámhipotézis mellett szóló alapvető érv az volt, hogy segítségével indokolni lehetett a Bohr-féle hidrogén atom modell (perdületre vonatkozó) kvantálási törvényét (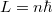 ,
, 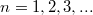 ). A bizonyítás lényege az az állítás volt, hogy a stabil körpályán mozgó elektron de Broglie-hulláma önmagával interferálva állóhullámot kell, hogy eredményezzen. Ellenkező esetben a hullám önmagát kioltja azaz ilyen állapot nem létezhet. Ezt a gondolatmenetet fogjuk követni most is.
). A bizonyítás lényege az az állítás volt, hogy a stabil körpályán mozgó elektron de Broglie-hulláma önmagával interferálva állóhullámot kell, hogy eredményezzen. Ellenkező esetben a hullám önmagát kioltja azaz ilyen állapot nem létezhet. Ezt a gondolatmenetet fogjuk követni most is.
Tekintsünk egy ún. egydimenziós potenciáldobozt. Ez azt jelenti, hogy a részecske az  tengely mentén mozog egy
tengely mentén mozog egy  hosszúságú „merev falakkal” határolt tartományban. A klasszikus dinamika szerint a tömegpont a két fal között „pattogva”, egyenletes mozgást végez. A sebességének, és így impulzusának is a nagysága a mozgás során állandó marad. Felhasználva a hidrogén atom de Broglie-modellnél alkalmazott okoskodásunkat, a részecske stacionárius (stabil) állapotainak állóhullámoknak kell lenniük.
hosszúságú „merev falakkal” határolt tartományban. A klasszikus dinamika szerint a tömegpont a két fal között „pattogva”, egyenletes mozgást végez. A sebességének, és így impulzusának is a nagysága a mozgás során állandó marad. Felhasználva a hidrogén atom de Broglie-modellnél alkalmazott okoskodásunkat, a részecske stacionárius (stabil) állapotainak állóhullámoknak kell lenniük.
Legyen ebben az állapotban a részecske (állandó nagyságú) impulzusa  , és így a hozzá rendelt de-Broglie hullámhossz:
, és így a hozzá rendelt de-Broglie hullámhossz: 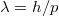 . A továbbiak miatt célszerű bevezetni az alábbi jelöléseket:
. A továbbiak miatt célszerű bevezetni az alábbi jelöléseket:
![\[ k \equiv 2\pi / \lambda, \quad \hbar = h/2\pi, \]](/images/math/9/7/c/97ca4c6ab6c0fbd1d5a5e3b8d66824b8.png)
ahol, mint az ismeretes,  a hullámszám és
a hullámszám és 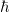 neve redukált Planck-állandó, de mi ezt is csak röviden Planck-állandónak fogjuk hívni. Így a részecske impulzusára adódik, hogy:
neve redukált Planck-állandó, de mi ezt is csak röviden Planck-állandónak fogjuk hívni. Így a részecske impulzusára adódik, hogy:
![\[ p = \hbar k. \]](/images/math/b/c/d/bcd7ad797b9ae65f32dd8afd262ac27b.png)
Megjegyzés. Ennek a felírásnak az a nagy előnye, hogy síkhullámok esetén a hullámszám valójában egy vektor mennyiség. Iránya merőleges a hullámfrontra. Így aztán az impulzusvektor nyilvánvalóan 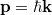 alakba írható.
alakba írható.
Mármost a szóban forgó potenciáldobozban csak azok a de Broglie-hullámok fognak állóhullámot alkotni, amelyek esetén a doboz  hossza a fél hullámhossz egész számú többszöröse (ld. előző ábra). Így a
hossza a fél hullámhossz egész számú többszöröse (ld. előző ábra). Így a  hullámhosszra fennáll, hogy:
hullámhosszra fennáll, hogy:
![\[ L = \frac{\lambda}{2}n, \quad \text{ahol} \quad n=1,2,3,... . \]](/images/math/7/7/c/77c48d59280ba84c6abfe6f94e41bd62.png)
Ebből pedig az adódik, hogy:
![\[ \lambda = \frac{2L}{n}, \quad \text{illetve} \quad k = \frac{2\pi}{\lambda} = \frac{n \pi}{L}, \quad \text{és ezért} \quad p = \hbar k = n\frac{\hbar\pi}{L}, \quad n = 1,2,3,... . \]](/images/math/3/7/c/37c8de3a5442c9ba8d9d52ad72d78906.png)
Ezzel megkaptuk a részecske stacionárius (de Broglie-féle) állapotainak kvantált energiaszintjeit is. Ugyanis (most) a részecske (kinetikus) energiája a mozgás során állandó:
![\[ E = \frac{p^2}{2m}. \]](/images/math/f/5/e/f5e3a4ae165f08660c5d27c0961fac6c.png)
Beírva ide az impulzusra kapott értékeket az adódik, hogy:
![\[ E = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m} = \frac{\hbar^2 \pi^2}{2mL^2}, \quad n = 1,2,3,... . \]](/images/math/e/6/1/e61e3d671f94ef58d4d9d43c0c153665.png)
Tehát a „dobozba zárt” részecske energiája kvantált lesz, hasonlóan a „Bohr-féle rezgő atom”, vagy a „hidrogénba zárt elektron” energiájához. Természetesen az energia kvantálási törvénye minden esetben más és más, de ez a modellek fizikai különbségéből adódik.
Ahogyan már említettük, most a jelenség időfüggését nem vizsgáljuk. Így (a hullámoknál tanultak szerint) az állóhullám  koordinátától függő részének a matematikai alakja a következő kell, hogy legyen:
koordinátától függő részének a matematikai alakja a következő kell, hogy legyen:
![\[ \psi_0 (x) = A \sin \left( \frac{2\pi}{\lambda} x \right) = A \sin (kx). \]](/images/math/5/a/d/5ad33a5cc07d7753a6314927dd551508.png) |
(15) |
Mármost a feladatunk az, hogy megválaszoljuk Peter Debye hajdani kérdését, azaz kitaláljuk azt az egyenletet, amelynek a megoldása éppen ez a függvény lesz. A matematikából tudjuk, hogy olyan egyenlet, amelynek megoldásai függvények, többek között egy differenciálegyenlet lehet. A mi esetünkben ez éppen a keresett Schrödinger-egyenlet lesz.
A fizikai alapegyenleteknek az előállítása (megkonstruálása) végigkíséri a Fizika történetét Newtontól napjainkig. Egy „alapegyenlet” nem más, mint a tapasztalat (illetve kísérletek) által igazolt alapvető fizikai törvény matematikai alakban történő megfogalmazása. Tulajdonképpen Galileo Galilei (1623) felismerését követjük, mely szerint:
- A filozófia abban a nagy könyvben van írva, amely nyitva áll mindenkor szemeink előtt: az Univerzumra gondolok. De nem olvashatjuk mindaddig, míg meg nem tanuljuk a nyelvét, és nem barátkozunk meg a jelekkel, amelyekkel írva van. A matematika nyelvén van írva, és a betűi háromszögek, körök és más geometriai alakzatok, amelyek ismerete nélkül lehetetlen egyetlen szót is megérteni.
Az ilyenfajta konstrukció soha nem egy szigorú matematikai „levezetés” eredménye. Ha ez így volna, akkor ismernünk kellene azt a még általánosabb törvényt, amelynek a folyománya lenne az éppen megalkotni vágyott összefüggés. Azaz értelemszerűen ez már nem lenne egy „alapegyenlet”. Ilyen esetekben tehát (szükségképpen) mindig valamiféle heurisztikus utat kell követnünk. Ez amolyan „intuitív” eljárás. Nem a matematikai szigor, hanem inkább az ötletes játékosság vezérli. A következőkben azt fogjuk mondani, hogy ez egy „konstitutiv” eljárás, amelynek eredménye egy „konstitutív alapegyenlet”. Ha valóban sikerült felismernünk a „Természet egy alapvető sajátosságát” akkor ez a „konstitutív egyenlet” az axióma rangjára emelkedik.
„Konstitutiv” latin eredetű szó. Jelentése : alkotó, szerves.
Az alábbiakban egy „konstitutív” eljárással fogjuk kitalálni a Schrödinger-egyenlet. Mint azt mindjárt látni fogjuk ez az eljárás sikeres lesz. Ezért aztán a későbbiekben is gyakran fogjuk használni.
A nem-relativisztikus newtoni mechanikából kell kiindulnunk, hiszen a Schrödinger-egyenlet nem más, mint a dinamika alapegyenletének mikroszkopikus méretekben érvényes megfogalmazása. Tudjuk, hogy a tömegpontnak képzelt részecske  energiája és
energiája és  impulzusa közötti kapcsolatot az energiamegmaradás tétele adja meg, azaz:
impulzusa közötti kapcsolatot az energiamegmaradás tétele adja meg, azaz:
![\[ \frac{p^2}{2m} + V_0 = E. \]](/images/math/a/a/9/aa9dcd25de54b52c3a6894848d04396b.png)
Jelen esetben a ![\setbox0\hbox{$[0,L]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/7/0/8/70825939347b3e5f3ba78a5ab898969d.png) tartományban a potenciális energia
tartományban a potenciális energia 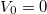 és a de Broglie-hullám definíciója szerint
és a de Broglie-hullám definíciója szerint 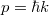 . Így a fenti összefüggés a következő alakra írható át:
. Így a fenti összefüggés a következő alakra írható át:
![\[ \frac{\hbar^2 k^2}{2m} + V_0 = E. \]](/images/math/0/1/c/01c42dec4032cdf87042426f86bbe6c5.png) |
(16) |
Ezek után tehát egy olyan differenciálegyenletet kell keresnünk, amelynek megoldása a (15) által megadott 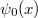 állóhullám és amely egyben kielégíti az
állóhullám és amely egyben kielégíti az  energia és a
energia és a  hullámszám között fennálló fenti összefüggést is. Ennek differenciálegyenletnek szükségképpen tartalmaznia kell a
hullámszám között fennálló fenti összefüggést is. Ennek differenciálegyenletnek szükségképpen tartalmaznia kell a 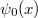 megoldásfüggvény
megoldásfüggvény  -szerinti deriváltját. Ez nagyon jó, hiszen az (16)-ban szereplő
-szerinti deriváltját. Ez nagyon jó, hiszen az (16)-ban szereplő  hullámszám a
hullámszám a 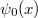 -ből deriválással „kinyerhető”. Képezzük ugyanis az állapotfüggvény
-ből deriválással „kinyerhető”. Képezzük ugyanis az állapotfüggvény  szerinti második deriváltját:
szerinti második deriváltját:
![\[ \frac{{\rm d}^2}{{\rm d} x^2} \psi_0 = -k^2 \psi_0. \]](/images/math/e/8/6/e86eecf89235d20ca9f477f2b495eb3e.png)
Ennek alapján tehát:
![\[ k^2 = -\frac{1}{\psi_0} \frac{{\rm d}^2}{{\rm d} x^2} \psi_0. \]](/images/math/6/1/c/61c41ad49d6f938208c27bb9c7f48254.png)
Ezt beírva (16)-ba adódik, hogy:
![\[ -\frac{\hbar^2}{2m} \frac{{\rm d}^2}{{\rm d} x^2} \psi_0 + V_0\psi_0 = E\psi_0. \]](/images/math/2/b/e/2be19e5da8c576c9702ffafc35318679.png)
Az így kapott másodrendű differenciálegyenlet tehát megadja az egydimenziós potenciáldobozban mozgó részecskéhez rendelt (de Broglie-féle) állóhullámot.
Az axióma rangú Schrödinger-egyenletre úgy jutunk, ha feltesszük, hogy ez az egyenlet általánosan is érvényes. Azaz olyan esetekben is, amikor a részecske környezetével tetszőleges kölcsönhatásban van. Ekkor az egyenletben szereplő 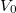 potenciális energia helyére egy valamilyen
potenciális energia helyére egy valamilyen 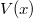 függvényt kell írunk. Értelemszerűen ez jellemzi a részecske és a környezete között fellépő mindenkori fizikai kölcsönhatást. Ekkor már az egyenlet megoldása nem az eddigi
függvényt kell írunk. Értelemszerűen ez jellemzi a részecske és a környezete között fellépő mindenkori fizikai kölcsönhatást. Ekkor már az egyenlet megoldása nem az eddigi 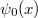 állóhullám, hanem valamilyen
állóhullám, hanem valamilyen 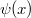 függvény lesz. A keresett Schrödinger-egyenlet tehát:
függvény lesz. A keresett Schrödinger-egyenlet tehát:
![\[ -\frac{\hbar^2}{2m} \frac{{\rm d}^2}{{\rm d} x^2} \psi +V(x) \psi = E\psi. \]](/images/math/6/3/2/632c47c11bfa7806a64dd1891c80a5df.png) |
(17) |
Az egyenlet megoldását adó 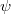 függvényt (mivel a részecske mozgásállapotát határozza meg) állapotfüggvénynek, vagy (utalva az eredetére) hullámfüggvénynek hívjuk. Az így felépített Schrödinger-féle mechanikát igen találóan hullámmechanikának hívjuk.
függvényt (mivel a részecske mozgásállapotát határozza meg) állapotfüggvénynek, vagy (utalva az eredetére) hullámfüggvénynek hívjuk. Az így felépített Schrödinger-féle mechanikát igen találóan hullámmechanikának hívjuk.
Az imént alkalmazott általánosítás természetesen nem egy egzakt logikai lépés volt, azaz nem kell, hogy szükségképpen helyes legyen. Az egyenlet „sikere” vagy „sikertelensége” dönti majd el azt, hogy valóban a Természet egy alapvető törvényszerűségét fedeztük-e fel.
Mint említettük már, BSc szinten a Schrödinger-egyenlet a Kvantummechanika egyik alaptörvényének tekinthető.
Ezt a „heurisztikus” gondolkodást a Fizikában gyakran használjuk, amikor új, alapvető törvények felfedezése a cél. A módszer neve „induktív módszer”. Ennek során néhány egyszerű esetben felismert törvényszerűségről feltesszük, hogy nagy általánosságban is igaz. Ezt a feltevésünket (posztulátum) addig tartjuk fenn, amíg nem találunk olyan (az általánosítás körébe eső) jelenséget, amely megcáfolja azt. Ekkor korlátozzuk a feltételezett törvény érvényességi körét, vagy (alapvető ellentmondás esetén) elvetjük azt. Az ebből származtatható törvényeket logikai úton (a Fizikában ez a matematika) levezetjük és kísérlettel ellenőrizzük. Ez a „dedukció”. A fizikában tehát a tudományos felfedezések az „indukció és a dedukció harmóniájából” születnek.
A kapott egydimenziós (17) differenciálegyenlet természetes módon általánosítható háromdimenziós esetre is. Ekkor az állapotfüggvény az 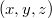 koordináták függvénye lesz, azaz
koordináták függvénye lesz, azaz 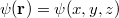 alakba írható. A
alakba írható. A 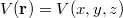 potenciális energia szintén mindhárom Descartes-koordináta függvénye lesz. Természetes tehát, hogy a Schrödinger-egyenletben meg kell jelennie mind a három változónak, azaz írható, hogy:
potenciális energia szintén mindhárom Descartes-koordináta függvénye lesz. Természetes tehát, hogy a Schrödinger-egyenletben meg kell jelennie mind a három változónak, azaz írható, hogy:
![\[ -\frac{\hbar^2}{2m} \left( \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2} \right) + V\cdot\psi = E\cdot\psi. \]](/images/math/c/9/1/c91bee7fd0c6175e1012469dca349f0f.png)
Az így megalkotott egyenletünk formálisan igen egyszerű alakba irható fel, ha a
![\[ \Delta\psi \equiv \left( \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2} \right) \]](/images/math/c/8/d/c8dff662724bc7bd73c9e3e1b08c36d4.png)
definícióval bevezetjük az ún. Laplace operátort. Ennek jele a nagy görög „delta” betű: 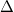 .
.
Általában operátoroknak nevezzük egyértelműen definiált matematikai műveletek együttesét. Ez azt jelenti, hogy a szóban forgó függvényen végre kell hajtani azokat a műveleteket amelyeket az illető operátor előír.
Rögtön látható, hogy ekkor a Schrödinger-egyenletünk a következő egyszerű alakot ölti:
![\[ -\frac{\hbar^2}{2m} \Delta\psi + V\cdot\psi = E\cdot\psi. \]](/images/math/6/4/0/64079ee682a327d9b1ea0eb2fbb12c74.png)
Ez az „egyszerűség” természetesen csak az egyenlet külső megjelenésére vonatkozik. Bonyolult, mély fizikai tartalmán semmiféle „formális bűvészkedés” nem változtat.
A kapott Schrödinger-egyenlet (1926) egy többváltozós (jelen esetben háromváltozós) parciális differenciálegyenlet. Az ilyen típusú egyenletek megoldása általában igen bonyolult matematikai és számítástechnikai feladat. Jócskán lecsökkennek a nehézségek, ha sikerül a keresett többváltozós függvényt egyváltozós függvények szorzataként felírni, azaz
![\[ \psi(x,y,z) = \psi_a (x) \, \psi_b(y) \, \psi_c(z) \]](/images/math/5/9/c/59c0504ff56393df66b454c3d3e929f7.png)
alakban. Ekkor ugyanis az egyes tényezőket már csak egyváltozós (ún. közönséges) differenciálegyenletek határozzák meg, amelyek megoldása lényegesen egyszerűbb matematikai feladat. Ezt a műveletet szeparálásnak, azaz a változók szétválasztásának nevezzük.
A Schrödinger-egyenlet „próbaköve” a hidrogén atom (volt). Ekkor a 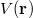 potenciális energia helyére a proton és az elektron közötti
potenciális energia helyére a proton és az elektron közötti 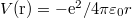 Coulomb-potenciált kell írni. Az így kapott egyenlet részletes megoldása eléggé munkaigényes és meghaladja ennek a kurzusnak a színvonalát. Egy-két alapvető dolgot azonban ismernünk kell. Fontos tudni pl. azt, hogy megoldva a Schrödinger-egyenletet, az
Coulomb-potenciált kell írni. Az így kapott egyenlet részletes megoldása eléggé munkaigényes és meghaladja ennek a kurzusnak a színvonalát. Egy-két alapvető dolgot azonban ismernünk kell. Fontos tudni pl. azt, hogy megoldva a Schrödinger-egyenletet, az  energiára megkapjuk a Bohr-elméletből jól ismert energiaszinteket.
energiára megkapjuk a Bohr-elméletből jól ismert energiaszinteket.
Mint az ismeretes, ezek helyességét a Balmer-formula spektroszkópiai igazolása jelentette. Tehát a Schrödinger-egyenlet a hidrogén atom esetén a következő:
![\[ -\frac{\hbar^2}{2m} \Delta\psi + \left( - \frac{{\rm e}^2}{4\pi\varepsilon_0 r} \right)\psi = - \frac{13,6 {\rm eV}}{n^2} \quad n=1,2,3,... . \]](/images/math/b/5/e/b5ecf9a64dbf7ac65e4ffd9f94a8670a.png)
Magáról a 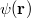 hullámfüggvényről most nem tudunk semmit, hiszen ahhoz meg kellene oldanunk magát az egyenletet.
hullámfüggvényről most nem tudunk semmit, hiszen ahhoz meg kellene oldanunk magát az egyenletet.
A továbbiakban evvel az egyenlettel még sokat foglalkozunk majd. Anélkül, hogy részletesen megoldanánk, igen fontos fizikai eredményeket fogunk kiolvasni belőle.
Láttuk, hogy a Bohr-féle hidrogén atomban az elektron diszkrét (kvantált) energiaszintjei a perdületre kirótt 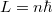 „kvantálási hipotézis” felhasználásával adódnak. De Broglie ezt az általa kitalált „vezérhullám” elmélettel indokolta. Láttuk, hogy itt csak a vezérhullám térbeli struktúrája volt a fontos (
„kvantálási hipotézis” felhasználásával adódnak. De Broglie ezt az általa kitalált „vezérhullám” elmélettel indokolta. Láttuk, hogy itt csak a vezérhullám térbeli struktúrája volt a fontos (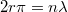 ). Az „állóhullám” időbeni oszcillálása nem számított. Így arról nem is tudunk semmit mondani. Ennek megfelelően, láthatjuk, hogy a bevezetett Schrödinger-egyenlet sem tartalmazza a
). Az „állóhullám” időbeni oszcillálása nem számított. Így arról nem is tudunk semmit mondani. Ennek megfelelően, láthatjuk, hogy a bevezetett Schrödinger-egyenlet sem tartalmazza a  időt. Annak ellenére van ez így, hogy a
időt. Annak ellenére van ez így, hogy a 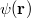 hullámfüggvény a részecske dinamikáját hivatott leírni. Ez az „ellentmondás” feloldható lesz, miután felismerjük az állapotfüggvény fizikai jelentését.
hullámfüggvény a részecske dinamikáját hivatott leírni. Ez az „ellentmondás” feloldható lesz, miután felismerjük az állapotfüggvény fizikai jelentését.
Létezik egy időfüggő Schrödinger-egyenlet is amelyik az időtől is függő 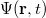 állapotfüggvények kiszámítására szolgál. Evvel azonban ebben a kurzusban mi, nem foglalkoztunk.
állapotfüggvények kiszámítására szolgál. Evvel azonban ebben a kurzusban mi, nem foglalkoztunk.
A hullámfüggvény fizikai jelentése
Megszületett tehát a Schrödinger-egyenlet (1926) amelyet minden fizikus rögtön használni tudott. De egy alapvető kérdés még válasz nélkül maradt: mi az ami hullámzik, azaz mi az állapotfüggvény fizikai jelentése?
Először maga Schrödinger is arra gondolt, hogy létezik valamiféle „anyagi közeg” (az elektron anyaga), amelyben a létrejövő és tovahaladó „gerjesztést” (lokalizált hullámot), mint egy elektront érzékeljük (ezt sugallta a de Broglie-hullámok „anyaghullám” megnevezése is). Azonban ez az amúgy tetszetősnek tűnő elképzelés tarthatatlannak bizonyult.
Láttuk, hogy ha egy hullámcsomagot készítünk, azaz sok hullámot összeadunk (összekeverünk), akkor ezek az összetevők más-más sebességgel fognak haladni. Némely részhullám gyorsabban, mások lassabban mozognak. Ezért a közöttük lévő fáziskülönbség időben változni fog. Ennek az lesz a következménye, hogy a hullámcsomag lokalizáltsága megnövekszik. Azt mondjuk, hogy a hullámcsomag „szétfolyik”. A részletes számolás azt mutatja, hogy egy  tömegű részecske esetén a de Broglie-féle hullámcsomag szélessége (mérete)
tömegű részecske esetén a de Broglie-féle hullámcsomag szélessége (mérete) 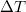 időközönként „megduplázódik” és
időközönként „megduplázódik” és
![\[ \Delta T \approx \frac{m}{\hbar} (\Delta x_0)^2, \]](/images/math/e/5/e/e5e6c087f53f6ad374a0c504da6ccdc6.png)
ahol 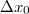 a hullámcsomag kezdeti szélessége. Ezért az adott
a hullámcsomag kezdeti szélessége. Ezért az adott  időpillanatban a hullámcsomag
időpillanatban a hullámcsomag 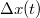 szélessége a következő lesz:
szélessége a következő lesz:
![\[ \Delta x(t) = \Delta x_0 \cdot 2^{t/\Delta T}. \]](/images/math/e/4/c/e4c0886b19d78f8e50a14ea8859f6d48.png)
Két egyszerű példa igen szemléletesen bemutatja ezt a jelenséget. Egy makroszkopikus mérető golyó átmérője legyen 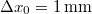 és a tömege
és a tömege 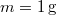 . Ebben az esetben
. Ebben az esetben 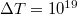 év adódik. Azaz a „szétfolyás” gyakorlatilag nem létezik. Egy elektron esetén azonban drasztikusan más az eredmény. Ekkor
év adódik. Azaz a „szétfolyás” gyakorlatilag nem létezik. Egy elektron esetén azonban drasztikusan más az eredmény. Ekkor 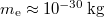 és jobb híján legyen az elektron „atomnyi” méretű, azaz
és jobb híján legyen az elektron „atomnyi” méretű, azaz 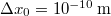 . Most az adódik, hogy
. Most az adódik, hogy 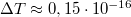 . Ez azt jelenti, hogy ha egy szoba
. Ez azt jelenti, hogy ha egy szoba 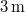 , a kezdetben mikroszkopikus méretű elektron
, a kezdetben mikroszkopikus méretű elektron
![\[ t = \Delta T \log_2 \left( \frac{3 \, {\rm m}}{10^{-10} \, {\rm m}} \right) \approx 5\cdot 10^{-15} \, {\rm s} \]](/images/math/f/3/2/f3211dd57f8ec39524e428d9d4fe0043.png)
idő múlva szobányi méretűvé dagad. Ezt az eredményt azonban a hétköznapi tapasztalat egyértelműen cáfolja. Senki nem látott még szobaméretű elektront!
Megjegyzés. Mint az ismeretes, az optikában az 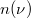 törésmutató függ a fény frekvenciájától. Ez az oka annak, hogy a prizmával a fehér fény összetevőire (azaz a szivárvány színeire) bontható. A törőközegben mozgó rövid fényimpulzus „szétfolyása” (diszperziója) jól ismert jelenség. Mechanizmusa ugyanaz, mint az imént elmondott de Broglie-féle esetben.
törésmutató függ a fény frekvenciájától. Ez az oka annak, hogy a prizmával a fehér fény összetevőire (azaz a szivárvány színeire) bontható. A törőközegben mozgó rövid fényimpulzus „szétfolyása” (diszperziója) jól ismert jelenség. Mechanizmusa ugyanaz, mint az imént elmondott de Broglie-féle esetben.
A későbbiekben a határozatlansági reláció ismeretében egy igen szemléletes magyarázatot adunk a hullámcsomag szétfolyására. Ezzel azonban még várnunk kell.
Végül is a hullámfüggvény fizikai értelmezésére vonatkozó, mindent kielégítő megoldást Max Born találta meg (1926). Szerinte
-
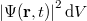 annak a valószínűségét adja, hogy a pontszerű elektron az
annak a valószínűségét adja, hogy a pontszerű elektron az  helyvektor
helyvektor 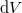 környezetében van (azaz ott megtalálható).
környezetében van (azaz ott megtalálható).
BSc szinten a Born-féle értelmezés tekinthető a Kvantummechanika másik axiómájának.
Megjegyzés. A 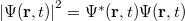 kifejezés az „abszolút érték négyzetet” jelenti, ahol
kifejezés az „abszolút érték négyzetet” jelenti, ahol 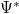 a komplex konjugáltat jelöli. Ez valós függvények esetén ugyanaz, mint a függvény négyzete, komplex esetben azonban
a komplex konjugáltat jelöli. Ez valós függvények esetén ugyanaz, mint a függvény négyzete, komplex esetben azonban 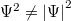 . A kvantummechanika egyik jellegzetessége éppen az, hogy itt a
. A kvantummechanika egyik jellegzetessége éppen az, hogy itt a 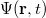 függvények komplex függvények is lehetnek (sőt, lényegében mindig azok). Ekkor pedig
függvények komplex függvények is lehetnek (sőt, lényegében mindig azok). Ekkor pedig 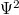 maga is egy komplex mennyiség, aminek nem lehet fizikai tartalmat tulajdonítani. Ugyanis minden fizikai mennyiségnek kísérletileg ellenőrizhetőnek, azaz mérhetőnek kell lennie. Egy mérés eredménye pedig szükségképpen mindig egy valós szám. Ezért szerepel a fenti „Born-féle értelmezésben” a
maga is egy komplex mennyiség, aminek nem lehet fizikai tartalmat tulajdonítani. Ugyanis minden fizikai mennyiségnek kísérletileg ellenőrizhetőnek, azaz mérhetőnek kell lennie. Egy mérés eredménye pedig szükségképpen mindig egy valós szám. Ezért szerepel a fenti „Born-féle értelmezésben” a 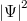 , ami valós mennyiség és így lehet hozzá fizikai tartalmat rendelni. További fontos részleteket az MSc kurzusban tudhatunk majd meg.
, ami valós mennyiség és így lehet hozzá fizikai tartalmat rendelni. További fontos részleteket az MSc kurzusban tudhatunk majd meg.
Born javaslata rendkívül szokatlan, a klasszikus fizikai szemléletünkkel és ismeretelméleti elképzelésünkkel nehezen összeegyeztethető volt. Nem véletlen, hogy a kvantummechanika „nagy öregjei” közül jó néhányan nem tudták elfogadni azt. Mára már a sok kísérleti tapasztalat egyértelműen igazolta a borni hipotézis helyességét, és ennek következtében beépült a fizikusi szemléletünkbe. Tekintsük most ezt az intuitív kijelentést egy axióma jellegű állításnak, azaz minden különösebb indoklás nélkül fogadjuk el! Kísérleti eredmények sokasága válik ezzel értelmezhetővé, amely igazolja majd feltevésünk helyességét.
Az előzőekben említett hullámcsomag-szétfolyás tehát a megtalálási valószínűség időbeli szétterülését jelenti, ami pedig fizikailag igen szemléletes és érthető. Ezzel egy csapásra megszűnt a „hullám-részecske kettősség” feloldhatatlannak tűnő „misztikus” önellentmondása. Pontszerű részecskék vannak és a kvantummechanika ezen pontszerű részecskék megtalálási valószínűségét határozza meg a Schrödinger-egyenlet segítségével. A kvantummechanikának ezt (a ma is elfogadott) értelmezését koppenhágai értelmezésnek nevezik.
Ezt a fizikai interpretációt támasztja alá az a szórás-kísérlet is, amikor vékony fémfólián elektronokat egyenként lövünk át. A fólia mögött elhelyezett felfogó ernyőn lehet a szóródó elektronok becsapódását detektálni. A kezdetben szabálytalanul elhelyezkedő becsapódási pontok nagyszámú egyedi elektron-becsapódás után szabályos interferencia gyűrűkké olvadnak össze. Az adott helyre beérkező elektronok száma az ottani megtalálási valószínűséggel lesz arányos. Mindezt az alábbi ábra szemlélteti.
Az következő kísérleti ábra is igen meggyőző:
A baloldali röntgensugárral részült. A röntgensugárzás egy olyan elektromágneses hullám, amelynek hullámhossza a kristályrácsban lévő atomok egymásközti távolságának a nagyságrendjébe esik. A baloldali diffrakciós képet egy elektronsugár produkálta. A hasonlóság nyilvánvaló, az elektron „hullámszerű viselkedése” mintegy „szemmel látható”.
Max Born (1882-1970) széleskörű matematikai ismeretekkel rendelkező fizikus volt. A „matematikusok Mekkájában”, Göttingenben olyan nagyhírű „proféták” előadásait hallgatta, mint Felix Klein, David Hilbert és Hermann Minkowski. A doktori munkáját a neves elméleti csillagász, Karl Schwarzschild vezetése alatt írta. Valószínűleg ennek a matematikai tudásának köszönhette, hogy a „hullámfüggvény valószínűségi értelmezése” éppen az ő ötlete volt. Mindezekkel kapcsolatban a következőket írja:
- Schrödinger az elektront nem részecskének, hanem az általa felírt hullámfüggvény
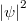 négyzetével meghatározott sűrűségeloszlásnak tekintette. ...Én azonban naponta láttam, hogy Franck atomi és molekuláris ütközési kísérleteiben milyen termékeny szerepet játszik a részecske fogalom és meg voltam győződve, hogy a részecskéket nem lehet egyszerűen kiebrudalni. Módot kell találni a részecskék és a hullámok összebékítésére. Az összekötő láncszemet én a valószínűség fogalmában láttam. ...A hipotézist sikerült igazolni az ütközési folyamatoknak hullámok szóródásával való leírásával és más eljárásokkal. ...A
négyzetével meghatározott sűrűségeloszlásnak tekintette. ...Én azonban naponta láttam, hogy Franck atomi és molekuláris ütközési kísérleteiben milyen termékeny szerepet játszik a részecske fogalom és meg voltam győződve, hogy a részecskéket nem lehet egyszerűen kiebrudalni. Módot kell találni a részecskék és a hullámok összebékítésére. Az összekötő láncszemet én a valószínűség fogalmában láttam. ...A hipotézist sikerült igazolni az ütközési folyamatoknak hullámok szóródásával való leírásával és más eljárásokkal. ...A 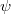 függvény általában adott statisztikus értelmezése csupán az első lépés volt az atomfizikában a részecskék és a hullámok közötti kapcsolat megértésében. ...Noha ezeket az elgondolásokat a fizikusok döntő többsége elfogadta, mindig volt néhány kivétel, közöttük olyan nagy nevek, mint Planck, Einstein, de Broglie és Schrödinger. Ez a magyarázata, hogy miért tartott huszonnyolc esztendeig amíg munkásságomért megkaptam a Nobel-díjat.
függvény általában adott statisztikus értelmezése csupán az első lépés volt az atomfizikában a részecskék és a hullámok közötti kapcsolat megértésében. ...Noha ezeket az elgondolásokat a fizikusok döntő többsége elfogadta, mindig volt néhány kivétel, közöttük olyan nagy nevek, mint Planck, Einstein, de Broglie és Schrödinger. Ez a magyarázata, hogy miért tartott huszonnyolc esztendeig amíg munkásságomért megkaptam a Nobel-díjat.
Az 1954-es fizikai Nobel-díj átvételekor Max Born 72 éves (!) volt. Az indoklásban ez állt: „alapvető kvantummechanikai munkásságáért, különös tekintettel a hullámfüggvény statisztikus interpretációjára”. Planck akkor már 7 éve halott, De Broglie 62, Einstein 75, Schrödinger 67 éves volt.
- Valamely tudományos igazság nem oly módon szokott érvényre jutni, hogy ellenfeleit meggyőzik és azok meggyőzöttnek jelentik ki magukat, hanem inkább úgy, hogy az ellenfelek lassanként kihalnak és a következő generáció kezdetektől fogva ezt az igazságot ismeri meg.
E kijelentés igazsága szépen igazolódott a kvantummechanika fejlődése során, a Planck-féle  „hatáskvantum” bevezetésétől kezdve egészen a borni interpretációig. Az idézett sorok írója éppen Max Planck volt...
„hatáskvantum” bevezetésétől kezdve egészen a borni interpretációig. Az idézett sorok írója éppen Max Planck volt...
A felsorolt „nagy nevek” is mutatják, hogy a kvantummechanika alapjában valószínűségi szemlélete nem tartozik a könnyen elfogadható fizikai interpretációk közé. Einstein közkedveltté vált mondását szabadon idézve: nehezen elfogadható, hogy az „Isten kockajátékos” lenne.
Max Born kedvelte a filozófiát és megfelelő alapképzettséget is szerzett benne. Átérezte hipotézisének természet-filozófiai vonatkozásait is. Nem véletlenül írta a következőket:
- Még ha figyelmen kívül hagyjuk is a filozófiai szempontokat, a fizikában a sugárzás korpuszkuláris és hullámtulajdonságai közötti ellentmondás a statisztikus nézőpont nélkül nem oldható fel. ...Noha az új elmélet kísérletileg jól megalapozottnak látszik, mégis felvethető a kérdés, vajon az elmélet nem tehető-e ismét determinisztikussá a jövőben, további kiterjesztéssel vagy finomítással? Erre ezt válaszolhatjuk: egzakt matematikai számításokkal bebizonyítható, hogy a kvantummechanika ma elfogadott formalizmusa nem tesz lehetségessé ilyen kiegészítést. Ha tehát meg akarjuk őrizni a reményt, hogy a determináció egy napon visszatér, úgy a mai elméletet alapvetően tévesnek kell minősítenünk. Vagyis az elmélet egyes állításait kísérletekkel kellene megcáfolni. A deterministának tehát nem tiltakoznia, hanem kísérleteznie kell, ha meg akarja téríteni a statisztikus elmélet híveit.
Tegyük hozzá, hogy a Kvantummechanika eddigi, több mint 100 éves történetében még senki sem tudott olyan jelenséget mutatni, amelyik ezt az elméletet cáfolta volna. Az új próbálkozások (pl. a divatos „húrelmélet”) is lényegét tekintve „ugyanezen a színpadon játszódnak”. De természetesen nem láthatunk a Jövőbe!
Tudománytörténeti érdekesség, hogy a „kvantummechanika” elnevezést először Max Born használta egy 1924-ben megjelent dolgozatában. Személyében tehát a névadó „keresztapát” is tisztelhetjük.
Az alábbi ábra a hidrogén atommodell változását mutatja be a Thomson-féle modellhez képest:
Az előbbi szerint a negatív töltésű, pontszerű elektron rezeg gömb alakú pozitív töltéseloszlásban, az utóbbi szerint pedig a pozitív töltésű atommag körül található meg a negatív töltésű elektron 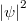 valószínűséggel.
valószínűséggel.
A hullámfüggvény matematikai tulajdonságai
Tekintsük az egydimenziós (időfüggetlen) Schrödinger-egyenletet!
![\[ - \frac{\hbar^2}{2m} \psi'' + V\psi = E\psi. \]](/images/math/5/2/c/52c358cd41f376e41551bfe32f6fc8b9.png)
Az egyszerűség végett a második deriváltat 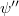 -vel jelöltük. Első ránézésre ez egy igen „furcsa” egyenlet, hiszen két ismeretlen mennyiséget tartalmaz: az egyenletben sem a
-vel jelöltük. Első ránézésre ez egy igen „furcsa” egyenlet, hiszen két ismeretlen mennyiséget tartalmaz: az egyenletben sem a 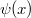 állapotfüggvényt, sem pedig az
állapotfüggvényt, sem pedig az  energiaértéket nem ismerjük. A feladat éppen ezek meghatározását jelenti. Az ilyen típusú egyenletek speciális megoldási technikát követelnek.
energiaértéket nem ismerjük. A feladat éppen ezek meghatározását jelenti. Az ilyen típusú egyenletek speciális megoldási technikát követelnek.
Vizsgáljuk meg először is, hogy mik lesznek a 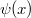 általános matematikai tulajdonságai. Erre már a
általános matematikai tulajdonságai. Erre már a 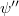 előjeléből is következtethetünk. Átrendezés után kapjuk, hogy
előjeléből is következtethetünk. Átrendezés után kapjuk, hogy
![\[ \psi'' = \frac{2m}{\hbar^2} [V(x) - E]\psi. \]](/images/math/0/4/a/04a9f976ea821fee3f69db61eb5f56da.png)
A szigorú matematikai precizitás mellőzésével gondoljuk végig a következőket! Már a klasszikus mechanikában láttuk, hogy pl. egy másodrendű deriváltakat (is) tartalmazó (közönséges) differenciálegyenlet pontos megoldásához meg kell adnunk egy (tetszőleges) pontban a keresett függvény értékét és a deriváltjának az értékét is. Ezt nevezzük kezdeti feltételnek (ha a változó a  idő) vagy peremfeltételnek (ha a változó pl. az
idő) vagy peremfeltételnek (ha a változó pl. az  térkoordináta).
térkoordináta).
Tekintsük tehát az egydimenziós Schrödinger-egyenletet. Vizsgálni fogjuk a kötött állapotokhoz tartozó állapotfüggvények matematikai jellegzetességeit.
Az ábrán egy tipikus 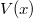 potenciálfüggvény látható.
potenciálfüggvény látható.
A newtoni (klasszikus) mechanika szerint (a tér bármely pontjában) egy tömegpont  összenergiája a
összenergiája a 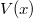 potenciális energiájának és a kinetikus energiájának az összege. Mivel a kinetikus energia (definíció szerint) soha nem lehet negatív (
potenciális energiájának és a kinetikus energiájának az összege. Mivel a kinetikus energia (definíció szerint) soha nem lehet negatív (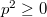 ), a tömegpont csak abban az
), a tömegpont csak abban az 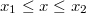 tartományban mozoghat, ahol a potenciális energiája kisebb, mint az
tartományban mozoghat, ahol a potenciális energiája kisebb, mint az  összenergiája (klasszikusan megengedett tartomány). Ezért azt a tartományt (
összenergiája (klasszikusan megengedett tartomány). Ezért azt a tartományt (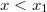 és
és 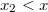 ), ahol a részecske potenciális energiája nagyobb, mint az összenergiája, klasszikusan tiltott tartománynak nevezzük. Azokat a helyeket, ahol a potenciális energia éppen egyenlő az összenergiával (
), ahol a részecske potenciális energiája nagyobb, mint az összenergiája, klasszikusan tiltott tartománynak nevezzük. Azokat a helyeket, ahol a potenciális energia éppen egyenlő az összenergiával (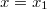 és
és 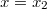 ), visszafordulási pontnak hívjuk. A szemléletes elnevezés onnan ered, hogy ezek a pontok választják el egymástól a (klasszikus) mozgás számára megengedett és tiltott tartományokat. Nyilvánvaló, hogy egy részecske akkor van kötött állapotban, ha a klasszikus mozgási tartománya véges nagyságú. Ennek legegyszerűbb esetét fogjuk most tárgyalni.
), visszafordulási pontnak hívjuk. A szemléletes elnevezés onnan ered, hogy ezek a pontok választják el egymástól a (klasszikus) mozgás számára megengedett és tiltott tartományokat. Nyilvánvaló, hogy egy részecske akkor van kötött állapotban, ha a klasszikus mozgási tartománya véges nagyságú. Ennek legegyszerűbb esetét fogjuk most tárgyalni.
Fontos megvizsgálni azt, hogy tudunk-e általában mondani valamit az egydimenziós, kötött állapotban lévő részecskék állapotfüggvényéről. Vannak-e esetleg olyan matematikai jellegzetességei, amelyek fontos fizikai tulajdonságokat tükröznek?
Először is tegyük fel, hogy a 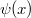 függvények valósak. Ha találunk valós megoldásokat és azokat értelmezni is tudjuk, akkor a feladatunkat megoldottuk. Ha nem, akkor próbálkozhatunk komplex megoldások keresésével is. A BSc tanulmányaink során mi csak olyan esetekkel foglalkozunk, amikor a
függvények valósak. Ha találunk valós megoldásokat és azokat értelmezni is tudjuk, akkor a feladatunkat megoldottuk. Ha nem, akkor próbálkozhatunk komplex megoldások keresésével is. A BSc tanulmányaink során mi csak olyan esetekkel foglalkozunk, amikor a 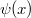 megoldásfüggvények valósak.
megoldásfüggvények valósak.
Bár – mintegy ízelítőnek – a későbbiekben találunk majd egy igen „egyszerű” mozgásállapotot, amelyhez komplex állapotfüggvény tartozik.
Mint azt a matematikai analízisben megtanultuk, egy (valós) egyváltozós függvény konvex vagy konkáv voltát a függvény (helyszerinti) második deriváltja határozza meg. A mi esetünkben látható, hogy:
![\[ \psi'' = \frac{2m}{\hbar^2}[V(x) - E]\psi. \]](/images/math/c/8/1/c81c7da9db901b2c629a1a007417ce65.png) |
(18) |
Tekintsük először a klasszikusan megengedett tartományokat (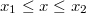 , lásd előző ábra). Ekkor:
, lásd előző ábra). Ekkor:
![\[ V(x) < E, \quad \text{és ezért} \quad \psi'' = \begin{cases} >0 & \text{ha $\psi<0$}, \\ <0 & \text{ha $\psi>0$}. \end{cases} \]](/images/math/a/5/f/a5f1e1a44eb1f15f3bdee00bbae99139.png)
Azaz ebben az esetben a 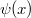 (az
(az  -tengely felől nézve) konkáv (homorú) függvény lesz. A klasszikusan tiltott tartományokban:
-tengely felől nézve) konkáv (homorú) függvény lesz. A klasszikusan tiltott tartományokban:
![\[ V(x) > E, \quad \text{és ezért} \quad \psi'' = \begin{cases} >0 & \text{ha $\psi>0$}, \\ <0 & \text{ha $\psi<0$}. \end{cases} \]](/images/math/4/f/3/4f36f513ae0f92b7902901a7839edcac.png)
Azaz ebben az esetben a 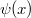 (az
(az  –tengely felöl nézve) konvex (domború) függvény lesz.
–tengely felöl nézve) konvex (domború) függvény lesz.
A klasszikus visszafordulási pontokban (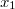 és
és 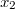 ) az állapotfüggvénynek inflexiója van, hiszen:
) az állapotfüggvénynek inflexiója van, hiszen:
![\[ V(x) = E, \quad \text{és ezért} \quad \psi'' = 0. \]](/images/math/3/a/2/3a201ab1d9edeabb608cb7b86ee8b422.png)
Hasonlóan zérus lesz a második derivált, ha
![\[ \psi(x) = 0, \quad \text{és ezért} \quad \psi'' = 0. \]](/images/math/9/4/c/94c9674c92e4b2996829e28761617a3e.png)
Mindebből az alábbi következtetésekre juthatunk. A hullámfüggvény (Born-féle) fizikai értelmezése szerint
![\[ \int_{-\infty}^{+\infty} \left| \psi \right|^2 \, {\rm d} x = 1, \]](/images/math/d/8/3/d83ad06e7b1d45059e78640f1ab007d6.png)
hiszen az elektron a teljes térben 1 valószínűséggel található meg. Ezt úgy mondjuk, hogy „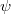 normája (definíciószerűen) egységnyi” és normálási feltételként fogunk rá hivatkozni. Könnyen belátható, hogy a normálási feltétel miatt
normája (definíciószerűen) egységnyi” és normálási feltételként fogunk rá hivatkozni. Könnyen belátható, hogy a normálási feltétel miatt
![\[ \lim_{x \to \pm \infty} \psi(x) = 0 \]](/images/math/9/9/3/993e3fd04f168fff392850247849adf0.png)
kell, hogy legyen, hiszen csak így lehet a (jelen esetben valós) állapotfüggvény négyzetének az integrálja egységnyi.
Mivel kötött állapotok esetén az 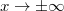 a klasszikusan tiltott tartományba esik, ezért a
a klasszikusan tiltott tartományba esik, ezért a 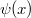 hullámfüggvény konvex módon, monoton tart a nullához. A klasszikus mozgás tartományában az állapotfüggvény (az
hullámfüggvény konvex módon, monoton tart a nullához. A klasszikus mozgás tartományában az állapotfüggvény (az  tengely felöl nézve) konkáv, és ha metszi az
tengely felöl nézve) konkáv, és ha metszi az  tengelyt, akkor ott inflexiós pontja van. Ezért az állapotfüggvény ebben a tartományban az
tengelyt, akkor ott inflexiós pontja van. Ezért az állapotfüggvény ebben a tartományban az  tengely körül oszcillálni fog. Inflexiója van a függvénynek a visszafordulási pontokban is. Ez teszi lehetővé, hogy a konvex és a konkáv hullámfüggvény-szakaszok egymáshoz kapcsolódjanak. Azt is megtudhatjuk, hogy mitől függ az, hogy hány oszcillációt végez a függvény a klasszikus mozgás tartományában. Ugyanis ahhoz, hogy a hullámfüggvény sok oszcillációt végezzen, az kell, hogy a függvény deriváltja az
tengely körül oszcillálni fog. Inflexiója van a függvénynek a visszafordulási pontokban is. Ez teszi lehetővé, hogy a konvex és a konkáv hullámfüggvény-szakaszok egymáshoz kapcsolódjanak. Azt is megtudhatjuk, hogy mitől függ az, hogy hány oszcillációt végez a függvény a klasszikus mozgás tartományában. Ugyanis ahhoz, hogy a hullámfüggvény sok oszcillációt végezzen, az kell, hogy a függvény deriváltja az  tengely mentén „gyorsan” változzon. Azaz a második deriváltja mindenhol „nagy” legyen.
tengely mentén „gyorsan” változzon. Azaz a második deriváltja mindenhol „nagy” legyen.
Az (18) összefüggésből nyilvánvalóan látható, hogy minél magasabb az  energiaszint, annál nagyobb lesz a
energiaszint, annál nagyobb lesz a 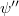 értéke. Így minél nagyobb energiaszinthez tartozó állapotfüggvényt tekintünk, az annál több oszcillációval fog rendelkezni. A fellépő zérushelyek (csomópontok) száma mindig egész számmal változik, ha az egyik energiaszintről egy másikra térünk át.
értéke. Így minél nagyobb energiaszinthez tartozó állapotfüggvényt tekintünk, az annál több oszcillációval fog rendelkezni. A fellépő zérushelyek (csomópontok) száma mindig egész számmal változik, ha az egyik energiaszintről egy másikra térünk át.
Az energiaszintek emelkedő sorrendben megszámozhatók:
![\[ E_1 < E_2 < E_3 < ... < E_i < ... . \]](/images/math/2/9/5/2959d42b73d0be54862d8b15abde83d7.png)
A hozzájuk tartozó állapofüggvények legyenek 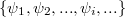 . Ezek a (klasszikusan megengedett) véges
. Ezek a (klasszikusan megengedett) véges 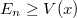 tartományban rendre
tartományban rendre  ,
,  ,
,  , ...,
, ..., 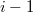 , ... darab csomóponttal rendelkező valós függvények lesznek. Mindezeket az alábbi ábrán szemléltettük.
, ... darab csomóponttal rendelkező valós függvények lesznek. Mindezeket az alábbi ábrán szemléltettük.
Az elmondottak alapján a megoldás módszere tehát a következő. Beírunk a Schrödinger-egyenletbe egy tetszőleges  értéket, és egy kiinduló (amúgy tetszőleges) peremfeltételt megadva meghatározzuk (pl. numerikusan) az ismeretlen
értéket, és egy kiinduló (amúgy tetszőleges) peremfeltételt megadva meghatározzuk (pl. numerikusan) az ismeretlen 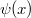 függvényt. Így formálisan megkaptuk a választott
függvényt. Így formálisan megkaptuk a választott  –hez tartozó
–hez tartozó 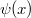 matematikai „megoldásfüggvényt”. Ezek után megvizsgáljuk, hogy ez a matematikai megoldásfüggvény teljesíti-e azokat a feltételeket, amelyek ahhoz kellenek, hogy ő fizikailag értelmezhető legyen. Azaz teljesül-e például az, hogy
matematikai „megoldásfüggvényt”. Ezek után megvizsgáljuk, hogy ez a matematikai megoldásfüggvény teljesíti-e azokat a feltételeket, amelyek ahhoz kellenek, hogy ő fizikailag értelmezhető legyen. Azaz teljesül-e például az, hogy
![\[ \lim_{x\to \pm\infty}\psi(x) = 0. \]](/images/math/8/4/6/8463f88b4029aae482c547d16c3fc5a3.png)
Hiszen csak ebben az esetben teljesül a normálási feltétel, ami pedig feltétlenül szükséges ahhoz, hogy a 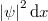 kifejezést valószínűségként értelmezhessük. Ha a kapott
kifejezést valószínűségként értelmezhessük. Ha a kapott 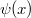 a fenti feltételeknek nem felel meg, akkor egy újabb
a fenti feltételeknek nem felel meg, akkor egy újabb  értékkel próbálkozunk. Ez a látszólag „próba-szerencse” módszer természetesen „automatikussá” tehető és a megfelelő (elméleti és gyakorlati) számítási algoritmusok kidolgozásával és használatával a kvantummechanikai problémák megoldhatók. Mindezt az alábbi ábrán szemléltetjük.
értékkel próbálkozunk. Ez a látszólag „próba-szerencse” módszer természetesen „automatikussá” tehető és a megfelelő (elméleti és gyakorlati) számítási algoritmusok kidolgozásával és használatával a kvantummechanikai problémák megoldhatók. Mindezt az alábbi ábrán szemléltetjük.
Látható, hogy a választott 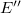 energia túl nagy, mert a hozzá tartózó
energia túl nagy, mert a hozzá tartózó 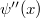 függvény (vigyázat, most a
függvény (vigyázat, most a 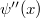 nem deriválást jelent) az
nem deriválást jelent) az 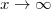 esetén „elszáll” a végtelenbe. Hasonló módon
esetén „elszáll” a végtelenbe. Hasonló módon 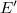 pedig túl kis érték, ugyanis
pedig túl kis érték, ugyanis 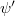 -vel ugyanilyen gondok vannak. Azonban a kettő között lévő
-vel ugyanilyen gondok vannak. Azonban a kettő között lévő 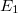 éppen az első energiaszintet adja, hiszen az általa meghatározott
éppen az első energiaszintet adja, hiszen az általa meghatározott 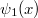 teljesíti a szükséges határfeltételeket.
teljesíti a szükséges határfeltételeket.
A Schrödinger-egyenlet megoldása során tehát a lehetséges (formális) matematikai megoldások közül (a peremfeltételek teljesítésével) kiválasztjuk a fizikailag értelmezhető megoldásokat. Valójában ezeket nevezzük a „Schrödinger-egyenlet megoldásának”.
Mint azt az előzőekben említettük, az adott fizikai problémára felírt Schrödinger-egyenletnek természetesen több (akár végtelen sok) megoldása is lehet. Ezek közül mi főleg azokkal az esetekkel foglalkozunk, amikor az energiaszintek halmaza „diszkrét sokaságot” alkot, azaz „megszámlálható”. Ekkor azt mondjuk, hogy az „energiaspektrum diszkrét”, illetve, hogy „az energiaszintek kvantáltak”. Ekkor a 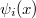 ,
, 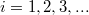 állapotfüggvények ismeretében minden további nélkül meg tudjuk határozni a részecske
állapotfüggvények ismeretében minden további nélkül meg tudjuk határozni a részecske 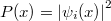 megtalálási valószínűség(sűrűség)ét a térben, azaz az
megtalálási valószínűség(sűrűség)ét a térben, azaz az  tengely mentén.
tengely mentén.
Láttuk, hogy a klasszikusan tiltott tartományban a hullámfüggvény véges értékű, így a 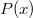 megtalálási valószínűség ezekben a tartományokban sem lesz nulla, azaz (például a fent tárgyalt esetben):
megtalálási valószínűség ezekben a tartományokban sem lesz nulla, azaz (például a fent tárgyalt esetben):
![\[ \int_{-\infty}^{x_1} \left| \psi(x) \right|^2 \, {\rm d}x > 0, \quad \text{és} \quad \int_{x_2}^{+\infty} \left| \psi(x) \right|^2 \, {\rm d}x > 0. \]](/images/math/9/f/4/9f4df6c7e970bb1638f29dca67202f6e.png)
Ez arra a meglepő eredményre vezet, hogy a kvantummechanika szerint a részecske véges valószínűséggel tartózkodhat abban a térrészben is ahol a (klasszikus értelemben vett) mozgási energiája negatív (!) lenne. Ezen „misztikusnak tűnő” tény pusztán „csak” annyit jelent, hogy egy mikrorészecskére (pl. elektron, proton, neutron stb) nem érvényesek a klasszikus mechanika fogalmai és törvényei. Ezen részecskék dinamikai viselkedését csak a kvantummechanika segítségével tudjuk megérteni. Ezt a következő ábrán szemléltetjük, ahol bejelöltük a klasszikus mechanika szerinti 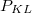 megtalálási valószínűségsűrűség függvényt is.
megtalálási valószínűségsűrűség függvényt is.
Láttuk tehát, hogy a mikrorészecske képes behatolni a klasszikusan tiltott tartományba. Ha ez a tartomány véges szélességű, akkor ezt potenciálgátnak hívjuk. Az elmondottakból következik tehát, hogy egy részecske képes „átjutni” ezen a potenciálgáton. Ezt a jelenséget alagúteffektusnak nevezzük és ma már számtalan kísérleti bizonyíték áll rendelkezésre, amely az effektus valódi voltát igazolja.
Nyilvánvaló a kérdés, hogy vajon mekkora a valószínűsége annak, hogy a részecske „átjut” a potenciálgáton. Jelen esetben ezt még nem tudjuk kiszámítani. A későbbiek során majd erre is lehetőségünk nyílik majd. Ehhez azonban még meg kell ismerkednünk egy-két új fogalommal.
Természettudományos ismeretelméleti kitérő
A kvantummechanika a Fizika egyik axiomatikusan felépített fejezetének tekinthető.
A Matematikában már megismerkedtünk az axióma fogalmával. A Matematika egy szigorú „deduktív” rendszer. A „...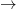 tétel
tétel 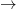 bizonyítás
bizonyítás 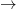 tétel
tétel 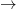 bizonyítás
bizonyítás  ...” logikai láncolat első elemei azok az alaptörvények (görögül axiómák, latinul posztulátumok), amelyeket közvetlen bizonyítás nélkül el kell fogadnunk igaznak és amelyekből így minden más törvény (állítás) levezethető. Az axiómák helyességét az egész rendszer együttese igazolja. A Matematikában az alaptörvények kimondása néha „önkényesnek”, szubjektívnek tűnhet. Azt sugallja, mintha a Matematikát „kitalálnánk” és nem „felfedeznénk”. Erről a kérdésről már sokan és sokat értekeztek filozófusok és matematikusok egyaránt. Mindenesetre elgondolkoztató az a tény, hogy a Matematika az az egyetlen „nyelv”, amely a Természet leírásában igen nagy hatásfokkal („adekvát módon”) használható.
...” logikai láncolat első elemei azok az alaptörvények (görögül axiómák, latinul posztulátumok), amelyeket közvetlen bizonyítás nélkül el kell fogadnunk igaznak és amelyekből így minden más törvény (állítás) levezethető. Az axiómák helyességét az egész rendszer együttese igazolja. A Matematikában az alaptörvények kimondása néha „önkényesnek”, szubjektívnek tűnhet. Azt sugallja, mintha a Matematikát „kitalálnánk” és nem „felfedeznénk”. Erről a kérdésről már sokan és sokat értekeztek filozófusok és matematikusok egyaránt. Mindenesetre elgondolkoztató az a tény, hogy a Matematika az az egyetlen „nyelv”, amely a Természet leírásában igen nagy hatásfokkal („adekvát módon”) használható.
Ez a „HIFI” nem lehet csupán csak „a véletlen műve”, ezért a fizikus inkább a matematikai törvények „felfedezésére” voksolna.
A Fizikában a helyzet kissé más! Itt az önkényesség és a szubjektivitás fel sem merülhet. Itt az alaptörvényeket nem mi találjuk ki, hanem a természeti jelenségek megfigyelése alapján felfedezzük. A természettudomány Mottója ez lehetne:
- A Természet nem kitalálható, hanem felfedezhető!
Ezen a következőt kell érteni. A Világban rengeteg, szinte megszámlálhatatlan mennyiségű tényt észlelünk és tapasztalunk. Azt vesszük észre, hogy ezek a tények egy „ok-okozati” hálóba rendezhetők. Azaz a Természetben valamiféle „rend, szabályosság, mintázat” van. Mármost azt vettük észre, hogy a rengeteg megfigyelt tényből kiválasztható néhány, amelyekből kiindulva a többi tény logikai úton (matematika) is megkapható. Ezeket a kiinduló tényeket nevezzük axiomáknak. Tehát a fizikai axiomákat a közvetlen megfigyelés és a tapasztalat igazolja. A többi természettörvényt ezekből logikai úton levezethetjük, a többi jelenséget ezek segítségével értelmezhetjük és helyességüket a tapasztalat igazolja vagy cáfolja. Sőt, az általa előre megjósolt jelenségeket a mérések utólag igazolják.
Mindebből látható, hogy a természettudomány tényeket tényekkel magyaráz.
Tehát nem filozófiai alapelvekből kiindulva magyarázza meg a tényeket. Ez utóbbi inkább a bölcseleti tudományokra (pl. filozófia) és a vallási rendszerekre jellemző. Nyílválóan ennek is megvan a maga szerepe az Emberiség kultúrtörténetében és kollektív „okosságában”, de a természettudományokban nem.
A szuperpozíció elve a kvantummechanikában
A Kvantummechanika axiómarendszerének a precíz tárgyalására majd az MSc kurzuson belül kerül sor. Itt és most ebből csak annak a három alaptörvénynek az egyszerűsített változatával ismerkedünk meg, amelyek a továbbiakban a tárgyalásra kerülő jelenségek megértése szempontjából nélkülözhetetlenek. Ezek
- a.) az (időfüggetlen) Schrödinger-egyenlet,
- b.) a hullámfüggvény fizikai jelentése,
- c.) ---------------------
Az első kettőt már részletesen megbeszéltük. Ennek a fejezetnek a valódi célja a harmadik törvény ismertetése és „megértetése”. Foglaljuk össze röviden az a.) és b.) posztulátumokat!
a.) Az (időfüggetlen) Schrödinger-egyenlet
Láttuk, hogy konzervatív rendszerek esetén a részecske kvantummechanikai viselkedését a Schrödinger-egyenlet segítségével határozzuk meg.
![\[ -\frac{\hbar^2}{2m} \left( \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2} \right) + V(x,y,z)\cdot\psi = E\cdot\psi. \]](/images/math/9/7/e/97ecf6f635a96108ec5c9d3f3c52c5a9.png)
Az egyenletben megjelenő  fizikai jelentése az elektron energiája. Az egyenletben szereplő
fizikai jelentése az elektron energiája. Az egyenletben szereplő 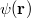 függvényt a részecske állapotfüggvényének neveztük. Mi (az egyszerűség végett) csak olyan eseteket vizsgálunk, amikor
függvényt a részecske állapotfüggvényének neveztük. Mi (az egyszerűség végett) csak olyan eseteket vizsgálunk, amikor 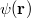 valós függvény. Tudnunk kell azonban, hogy az egyenlet legáltalánosabb megoldásaihoz akkor jutunk, ha
valós függvény. Tudnunk kell azonban, hogy az egyenlet legáltalánosabb megoldásaihoz akkor jutunk, ha 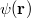 -t a komplex függvények halmázában keressük.
-t a komplex függvények halmázában keressük.
b.) A hullámfüggvény fizikai jelentése (a Born-féle hipotézis)
Az állapotfüggvény fizikai tartalmát a 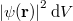 adja meg. Mint azt már láttuk, ennek a Born-féle értelmezése az elektron „megtalálási valószínűsége”.
adja meg. Mint azt már láttuk, ennek a Born-féle értelmezése az elektron „megtalálási valószínűsége”.
Térjünk át a harmadikra! Az első kettő klasszikus szemléletünkkel is „elfogadható”, abban az értelemben, hogy differenciálegyenletekkel eddig is találkoztunk és valószínűségi fizikai eseményekkel is foglalkoztunk már.
Mint azt látni fogjuk, a most következő (harmadik) posztulátum állítása a tömegpontok mechanikájában a klasszikus fizikai szemlélettel értelmezhetetlen.
c.) Az állapotok szuperpozíciójának elve
Ezen kvantummechanikai alapelv megvilágítása egy „egyszerű” kísérlet megtárgyalásán keresztül történhet. A kísérlet didaktikai jelentőségét legtalálóbban R. P. Feynman fogalmazta meg. Idézzük fel idevonatkozó véleményét!
R. P. Feynman: Mai Fizika 3. kötet, 144. oldal
- Mivel az atomok viselkedése az általános, közvetlen tapasztalatoktól olyannyira elüt, nehéz hozzáidomítani gondolkodásunkat. Ezért tűnik különösnek, szinte misztikusnak mind a kezdő, mind a tapasztalt fizikus számára. Még a szakemberek sem értik meg oly mértékben, ahogyan szeretnék, de teljesen logikus, hiszen az ember minden közvetlen tapasztalata és sejtése a nagyméretű tárgyakhoz kapcsolódik. A közönséges méretű tárgyakról előre meg tudjuk jósolni, hogyan viselkednek adott körülmények között, de a kis méretek világában másképp folynak a dolgok. Ezért bizonyos absztrakcióval vagy még inkább képzelő erővel kell tanulmányoznunk a jelenségeket, s nem társíthatjuk őket közvetlen tapasztalatainkkal.
- Ebben a fejezetben azonnal e titokzatos viselkedés leglényegesebb alapelemét igyekszünk megragadni, annak legfurcsább alakjában. Vizsgálódásunk célpontjául azt a jelenséget választjuk, amelyet semmiféle klasszikus módon nem lehet – abszolúte lehetetlen – megmagyarázni, s amely ugyanakkor magában rejti a kvantummechanika lényegét is. Valójában ez a jelenség tartalmazza az egyetlen rejtélyt. Ezt a rejtélyt nem tudjuk abban az értelemben megvilágítani, hogy „elmagyarázzuk”. Egyszerűen csak elmondjuk, miképpen „működik”. S miközben erről beszélünk, nagyjából már megismertetjük az Olvasót az egész kvantummechanika alapvető sajátosságaival.
R. P. Feynman: A fizikai törvények jellege, 161. oldal
- Nagyfokú képzelőerőt igényel hát annak megértése, hogy valójában hogyan is viselkednek (mármint az elektronok, O. L.), mivel ez semmi eddig látotthoz nem hasonlítható. Ez az előadás lesz tehát a legnehezebben érthető, abban az értelemben, hogy nagyon elvont, és távol esik a kézzelfogható tapasztalatok körétől. De ezt nem kerülhetem el.
- A fizikai törvények jellegéről szólva nem hallgathatok arról, hogy a kis méretek világában hogy írható le a részecskék viselkedése – megfutamodás volna elkerülni ezt a kérdést. Ez a természet valamennyi részecskéjének jellegzetes és egyetemes tulajdonsága, és ezért ha a fizika alaptörvényeit akarjuk megismerni, beszélnünk kell ezekről a tulajdonságokról is. Nem lesz könnyű. De a nehézség valójában pszichológiai eredetű, abból ered, hogy örökösen azzal a kérdéssel gyötrik magukat: „De hát hogy lehet ez ilyen?” És ez nem más, mint a kifejezése annak a ki nem mondott és hiábavaló óhajuknak, hogy szeretnénk a dolgokat valami jól ismert, kézzelfogható tapasztalattal párhuzamba állítani. Nos, én nem fogok semmi efféle hasonlatot mondani, egyszerűen csak leírom a jelenségeket úgy, ahogy vannak.
- Volt idő, amikor az újságok arról cikkeztek, hogy csupán tizenkét ember érti a relativitáselméletet. Én nem hiszem, hogy ez valaha is így volt. Lehetett olyan időszak, amikor csak egyetlen ember értette – mert történetesen ő fedezte fel –, de miután ezt a cikkben is közölte, így vagy úgy, de sokan mások is megértették a leírtakat: tizenkettőnél bizonyára jóval többen. Ezzel szemben azt hiszem, nyugodtan állíthatom, hogy a kvantummechanikát senki sem érti. Ezért ne vegyék ezt az előadást túlságosan komolyan, s ne érezzék úgy, hogy meg kell érteniük valamilyen modellel mindazt, amiről beszélni fogok: inkább engedjék el magukat, s élvezzék gondtalanul, amit hallani fognak! El fogom mondani, hogy viselkedik a természet. Ha csak elfogadják, hogy ez lehetséges, máris gyönyörűségesnek és elbájolónak fogják találni. Hacsak tudják, próbálják elkerülni, hogy folytonosan kérdezgessék önmagukat: „De hát miképp lehetséges ez?”, mert akkor lezuhanunk egy sötét szakadékba, ahonnan még senkinek sem sikerült kijutnia. Kérdésükre a választ senki sem tudja.
Mint azt már számtalanszor megbeszéltük, a Fizika nem nélkülözheti a matematika nyelvezetét. A jelenségek pontos „megértése” csak matematikai modelleken keresztül lehetséges. Különösen így van ez a Kvantummechanika esetében. A beszélgetéseinkben használt szavak csak a „képi metaforák” verbális megfogalmazására szolgálnak. A háttérben egy igen bonyolult, egzakt matematikai modell van. Természetesen ez nem férhet bele egy BSc kurzus szűk keretei közé. Itt csak egy igen leegyszerűsített változatról lehet szó. Így az elkövetkező „szemléletes” képeket kellő kritikával kell fogadnunk.
Mint azt láttuk, a kvantummechanikában egy elektron állapotát valamilyen 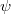 függvénnyel írjuk le. Ezt a függvényt pl. a Schrödinger-egyenlet segítségével tudjuk meghatározni és ennek ismeretén ki tudjuk számítani azt, hogy az elektron a tér egy adott tartományában milyen valószínűséggel tartózkodik.
függvénnyel írjuk le. Ezt a függvényt pl. a Schrödinger-egyenlet segítségével tudjuk meghatározni és ennek ismeretén ki tudjuk számítani azt, hogy az elektron a tér egy adott tartományában milyen valószínűséggel tartózkodik.
Legyen adott a 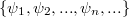 állapotfüggvényeknek egy
állapotfüggvényeknek egy  halmaza! Legyenek ezek a függvények olyanok, hogy (a Born-féle valószínűségi értelmezésnek megfelelően) teljesüljön rájuk a normálási feltétel:
halmaza! Legyenek ezek a függvények olyanok, hogy (a Born-féle valószínűségi értelmezésnek megfelelően) teljesüljön rájuk a normálási feltétel:
![\[ \int_{\infty} \left| \psi_n \right|^2 \, {\rm d} V = 1, \quad n = 1,2,3,... . \]](/images/math/7/d/2/7d2245a2d679301d6c7e501e982c2f49.png)
Matematikailag nyilvánvaló, hogy bármelyik függvényt megszorozhatjuk valamilyen 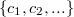 (komplex) számmal és két függvényt össze is adhatjuk. Azaz pl. ha
(komplex) számmal és két függvényt össze is adhatjuk. Azaz pl. ha 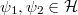 , akkor
, akkor
![\[ \psi = c_1\psi_1 + c_2\psi_2 \in {\cal H}. \]](/images/math/e/9/e/e9eae1b589a412557a3dc52674e0480f.png) |
(19) |
Az is látható, hogy a 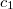 és
és 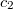 számok megválaszthatók úgy, hogy
számok megválaszthatók úgy, hogy 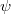 -re is igaz legyen a Born-féle valószínűségi értelmezésből adódó normálási feltétel: teljesülnie kell, hogy
-re is igaz legyen a Born-féle valószínűségi értelmezésből adódó normálási feltétel: teljesülnie kell, hogy
![\[ \left| c_1 \right|^2 + \left| c_2 \right|^2 = 1. \]](/images/math/1/c/0/1c00e55416828de2cef4865b7e1a7f15.png)
A kérdés mármost az, hogy létezik-e olyan állapot, amelyiket az így konstruált 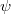 függvény jellemez? A kvantummechanikai kísérletek azt mutatják, hogy igenis létezik ilyen állapot!
függvény jellemez? A kvantummechanikai kísérletek azt mutatják, hogy igenis létezik ilyen állapot!
Ezt a tapasztalati tényt a Kvantummechanika újabb alaptörvénye, a szuperpozíció elve fogalmazza meg. Ez azt jelenti, hogy ha például van az elektronnak két különböző állapota, amelyhez a 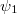 illetve a
illetve a 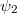 (komplex) állapotfüggvények rendelhetők, akkor léteznie kell egy olyan elektronállapotnak is, amelyet a
(komplex) állapotfüggvények rendelhetők, akkor léteznie kell egy olyan elektronállapotnak is, amelyet a 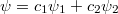 (komplex) állapotfüggvény reprezentál.
(komplex) állapotfüggvény reprezentál.
Az állítás fordítva is igaz. Azaz ha egy 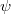 állapotfüggvényt sikerül felbontani két olyan (komplex) függvény összegére (
állapotfüggvényt sikerül felbontani két olyan (komplex) függvény összegére (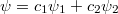 ), amelyek egyenként is teljesítik a normálási feltételt, akkor létezik két olyan elektronállapot, amelyet ez a két (komplex) függvény ír le.
), amelyek egyenként is teljesítik a normálási feltételt, akkor létezik két olyan elektronállapot, amelyet ez a két (komplex) függvény ír le.
Az, hogy a mikrofizika világában két fizikai állapot között ilyen kapcsolat is lehetséges, azaz olyan, amelyet a (komplex) állapotfüggvények kombinálásával jellemezhetünk, nem egy könnyen emészthető gondolat. Mint azt hamarosan látni is fogjuk, ennek „megértése” és „intellektuális elfogadása” a klasszikus fizikáétól alapvetően eltérő szemléletet igényel. Ugyanis a (mozgás)állapotoknak ilyen jellegű összefüggése a klasszikus pontmechanikában ismeretlen. (Lásd a fenti Feynman idézetet!)
Ugyanakkor a (folytonos anyageloszlást feltételező) hullámjelenségek körében ez a fajta kapcsolat megszokott. Mint azt már láttuk, a folytonosnak tekinthető (kontinuum) közegekben tapasztalható hullámterjedés leírásakor teljesen hasonló jelenséggel találkoztunk. Például a felületi vízhullámokkal végrehajtott kísérletek igen szemléletesen mutatják a hullámok körében megnyilvánuló szuperpozíció elvének az érvényességét. Két koherens hullám (külön-külön) az illető közeg egy-egy rezgési állapotát adja meg. A két állapot lineáris kombinációja útján kapott állapotot a két hullám együttes hatásaként kialakuló interferenciakép szolgáltatja.
Valami hasonlót tapasztaltunk a klasszikus elektrodinamikában is. Itt a helyzet kissé bonyolultabb. Gondoljunk pl. a két koherens fényforrásból induló elektromágneses hullámnál fellépő interferenciajelenségére.
Mint az már az optikai tanulmányainkból jól ismert, ennek egyik lehetséges megvalósítása a Young–féle kétréses kísérlet. Ebben az esetben a közvetlenül mérhető mennyiség a fény intenzitása. A térben megjelenő 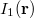 intenzitáseloszlás jeleníti meg számunkra az
intenzitáseloszlás jeleníti meg számunkra az 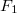 résből (fényforrásból) származó elektromágneses tér energiaállapotát. Hasonló módon az
résből (fényforrásból) származó elektromágneses tér energiaállapotát. Hasonló módon az 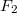 résből (egy, az előzővel koherens fényforrásból) származó elektromágneses tér energiaviszonyait az
résből (egy, az előzővel koherens fényforrásból) származó elektromágneses tér energiaviszonyait az 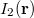 intenzitás eloszlásként érzékeljük.
intenzitás eloszlásként érzékeljük.
Ha mind a két rés nyitva van (mindkét koherens fényforrás be van kapcsolva) akkor azt tapasztaljuk, hogy a térben megjelenő 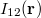 intenzitásra a szuperpozíció elve nem érvényes, azaz
intenzitásra a szuperpozíció elve nem érvényes, azaz
![\[ I_{12}({\bf r}) \neq I_1({\bf r}) + I_2({\bf r}). \]](/images/math/1/b/0/1b05f183e125e1bfa883019e4c83a353.png)
Érvényes viszont az elektromos térerősségekre (azaz a térben mindenhol teljesül az), hogy
![\[ {\bf E}_{12}({\bf r}) = {\bf E}_1({\bf r}) + {\bf E}_2({\bf r}). \]](/images/math/2/e/7/2e78a3d6939e91d3d50c1f10e4385e5f.png) |
(20) |
Mint azt tanultuk, energetikai okok miatt az elektromágneses hullám intenzitását az elektromos tér négyzetével definiáljuk. A definíció helyességét (azaz a használhatóságát) a tapasztalatok igazolják. Így az intenzitásra a tér bármelyik  pontjában azt kapjuk, hogy:
pontjában azt kapjuk, hogy:
![\[ I_{12} = {\bf E}^2 = {\bf E}_1^2 + {\bf E}_2^2 + 2{\bf E}_1 {\bf E}_2 = I_1 + I_2 + 2{\bf E}_1 {\bf E}_2. \]](/images/math/3/a/7/3a7f3ea0732e8debecd1bff7c45c57dc.png)
Mondhatjuk tehát, hogy az interferenciáért a 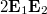 tag a felelős. Ez a tag azonban közvetlenül nem érzékelhető, hiszen a méréskor (pl. az interferenciacsíkok rögzítésekor egy fotolemezen) mindig az eredő
tag a felelős. Ez a tag azonban közvetlenül nem érzékelhető, hiszen a méréskor (pl. az interferenciacsíkok rögzítésekor egy fotolemezen) mindig az eredő  intenzitást mérjük. Ebben az esetben az interferencia jelenségének a megértése nem jelent gondot, hiszen magáról az
intenzitást mérjük. Ebben az esetben az interferencia jelenségének a megértése nem jelent gondot, hiszen magáról az 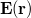 térerősségről határozott fizikai elképzelésünk van.
térerősségről határozott fizikai elképzelésünk van.
Megjegyzés. Fontos emlékeznünk arra is, hogy ha a két fényforrás független egymástól (azaz nem koherensek), akkor az intenzitások valóban összeadódnak, azaz
![\[ I_{12} = I_1 + I_2 \quad \text{(inkoherens forrásokra!)} \]](/images/math/c/1/a/c1a5576e8b1ee8adec16b0359f2ac950.png)
Ennek az oka az, hogy bár a térerősségek most is összeadódnak, a források inkoherenciája (függetlensége) miatt az interferencia tag időbeli átlaga zérus lesz. Ugyanis az interferencia tagot definiáló skalárszorzat (véletlenszerűen) pozitív és negatív értéket is felvehet.
Nézzük meg ezek után, hogy mi a helyzet a kvantummechanikában! Itt a 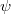 állapotoknak (általában komplex függvényeknek) nincsen közvetlen fizikai tartalma. Mint azt az előzőekben már láttuk, fizikai tartalmat a
állapotoknak (általában komplex függvényeknek) nincsen közvetlen fizikai tartalma. Mint azt az előzőekben már láttuk, fizikai tartalmat a
![\[ P({\bf r}) = \left| \psi({\bf r}) \right|^2 = \psi^*({\bf r}) \psi({\bf r}) \]](/images/math/f/2/c/f2c9bb7baadfb2dfb705f2bbb5fadcf1.png)
(abszolút érték négyzet) kifejezésnek tulajdonítunk. Ez megadja egy adott állapotú részecske (pl. elektron) megtalálási valószínűség(sűrűség)ét a térben. Ez pedig detektálható.
Alkalmazzuk a szuperpozíció elvét a fentiekben tárgyalt általános (matematikai) formában [ld. (19)]! Azaz tegyük fel, hogy a 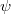 állapotfüggvény két másik állapot (
állapotfüggvény két másik állapot (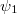 és
és 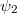 ) szuperpozíciójaként előállítható, azaz:
) szuperpozíciójaként előállítható, azaz:
![\[ \psi = c_1\psi_1 + c_2\psi_2. \]](/images/math/8/2/3/823cf91d1e0a55abf5bb3e1a4bb0df3c.png)
Ekkor a tér tetszőleges  pontjában kapjuk, hogy:
pontjában kapjuk, hogy:
![\[\begin{aligned} P = \left| \psi \right|^2 &= (c_1\psi_1 + c_2\psi_2)^* (c_1\psi_1 + c_2\psi_2) = \\ &= \left| c_1 \right|^2 \left| \psi_1 \right|^2 + \left| c_2 \right|^2 \left| \psi_2 \right|^2 + \Re \lbrace c_1^* c_2 \psi_1^* \psi_2 \rbrace = \\ &= \left| c_1 \right|^2 P_1 + \left| c_2 \right|^2 P_2 + \Re \lbrace c_1^* c_2 \psi_1^* \psi_2 \rbrace. \\ \end{aligned}\]](/images/math/1/c/1/1c14fa0d02f16c087edc0b1f9fe633e9.png)
Nyilvánvaló, hogy a részecske  megtalálási valószínűségsűrűsége sok részecske esetén azonosítható az
megtalálási valószínűségsűrűsége sok részecske esetén azonosítható az  intenzitással, azaz az adott helyen, egységnyi idő alatt detektált részecskék számával. Ismeretes ugyanis, hogy „a relatív gyakoriság határértéke a valószínűség”. Láthatóan itt is fellép egy kísérletileg ellenőrizhető interferencia tag. Azaz a szuperpozíció elve a mérhető megtalálási valószínűségekre (vagyis sok részecske esetén) a részecskék hely szerinti sűrűségeloszlására (az intenzitásokra) nem érvényes.
intenzitással, azaz az adott helyen, egységnyi idő alatt detektált részecskék számával. Ismeretes ugyanis, hogy „a relatív gyakoriság határértéke a valószínűség”. Láthatóan itt is fellép egy kísérletileg ellenőrizhető interferencia tag. Azaz a szuperpozíció elve a mérhető megtalálási valószínűségekre (vagyis sok részecske esetén) a részecskék hely szerinti sűrűségeloszlására (az intenzitásokra) nem érvényes.
A szuperpozíció elve „csak” meglehetősen absztrakt formában, a (komplex) állapotfüggvények halmazán érvényes (éppen ez ennek az axiómának a lényege). Ennek következményei a mérésekben ellenőrizhető módon megmutatkoznak.
Az állapotok szuperpozíciójának legegyszerűbb személtetése a kétréses kísérlettel történhet. Ez tulajdonképpen az optikából ismert Young-féle „kétréses kísérlet” elektronokkal elvégzett változata.
Mint azt már láttuk, az eredeti optikai kísérlet a hullámoptikai ismereteinkkel helyesen és igen szemléletesen megérthető és magyarázható. A szemléletbeli „nehézségek” akkor léptek fel, amikor a kísérletet a fotonokkal kellett értelmeznünk. Ekkor a (20) szerint megadott  intenzitás az időegység alatt detektált fotonok számát jelenti. A dolog természetéből adódik, hogy ugyanezek a szemléletbeli problémák lépnek fel, ha a kísérletet másfajta részecskékkel, például elektronokkal végezzük el.
intenzitás az időegység alatt detektált fotonok számát jelenti. A dolog természetéből adódik, hogy ugyanezek a szemléletbeli problémák lépnek fel, ha a kísérletet másfajta részecskékkel, például elektronokkal végezzük el.
Összehasonlítás végett nézzük meg először, hogy mi történne, ha a kétréses kísérletet klasszikus részecskékkel végeznénk el, azaz olyanokkal, amelyekre a Newton-féle mozgástörvények érvényesek.
Tekintsünk tehát egy adott (egyforma) sebességű tömegpontokból álló homogén részecskenyalábot, amelyik két réssel ellátott árnyékoló lapra esik. A rések előtt legyen egy-egy takaró lapocska, amellyel a réseket zárni (Z), illetve nyitni (NY) lehet. A résekkel szemben egy felfogó ernyő helyezkedik el, amellyel detektálni lehet az ernyő adott pontjára időegység alatt becsapódó tömegpontok számát, azaz a  függvényt. Ekkor az alábbi „triviális” kísérleti eredmény adódik:
függvényt. Ekkor az alábbi „triviális” kísérleti eredmény adódik:
| 1. rés | 2. rés | a mért intenzitás |
| Ny | Z | 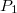
|
| Z | Ny | 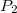
|
| Ny | Ny | 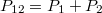
|
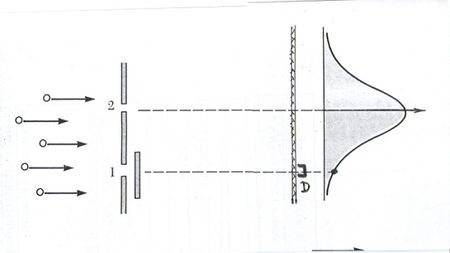
Az ernyőn mért intenzitáseloszlás |
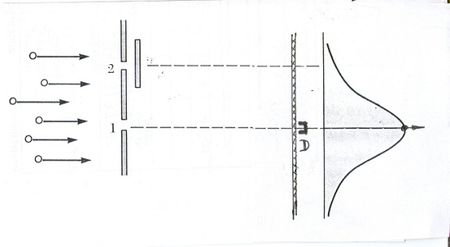
Az ernyőn mért intenzitáseloszlás |
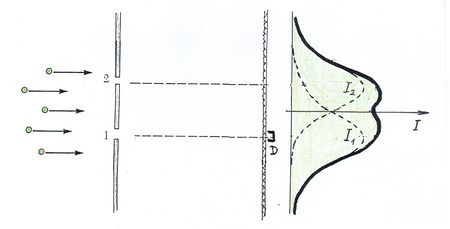
Az ernyőn mért intenzitáseloszlás |
Ezek után térjünk át a kvantummechanikára! Tekintsünk most is egy adott energiájú, homogén elektronnyalábot, amelyik az imént megadott, két réssel ellátott árnyékoló lapra esik. A rések természetesen szükségesen kicsiny méretűek azért, hogy a kvantumos effektusok a mérés szintjén is érvényesüljenek. A résekkel szemben elhelyezett „felfogó ernyő” olyan, hogy alkalmas az ernyőre becsapódó elektronok detektálására (foto-lemez, szcintillációs ernyő stb).
A „kísérlet” maga azt jelenti, hogy a rések különböző (zárt vagy nyitott) állapotai mellett megmérjük az ernyőre (adott idő alatt) becsapódó elektronok  eloszlását. Elvégezve a kísértet, eredményül a következőt kapjuk:
eloszlását. Elvégezve a kísértet, eredményül a következőt kapjuk:
| 1. rés | 2. rés | a mért intenzitás |
| Ny | Z | 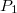
|
| Z | Ny | 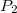
|
| Ny | Ny | 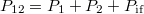
|
Az elektronokkal elvégzett kísérlet eredménye a klasszikus (részecske)szemléletünk számára azért „furcsa”, mert megjelent az interferenciára jellemző 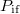 tag. A „zavart” az okozza a fejünkben, hogy nem tudjuk elképzelni azt, hogy vajon, amikor a pontszerűnek gondolt elektron átmegy az egyik résen, miként „érzékeli” azt, hogy a másik rés ugyanakkor nyitva van-e avagy zárva? Márpedig ezt valamiféleképpen „tudnia kell”, hiszen a képernyőn az eloszlás teljesen más akkor, amikor mind a két rés nyitva van, mint akkor amikor csak az egyik!
tag. A „zavart” az okozza a fejünkben, hogy nem tudjuk elképzelni azt, hogy vajon, amikor a pontszerűnek gondolt elektron átmegy az egyik résen, miként „érzékeli” azt, hogy a másik rés ugyanakkor nyitva van-e avagy zárva? Márpedig ezt valamiféleképpen „tudnia kell”, hiszen a képernyőn az eloszlás teljesen más akkor, amikor mind a két rés nyitva van, mint akkor amikor csak az egyik!
Gondolhatnánk esetleg arra, hogy az elektron „valami módon kettéhasad és így egyszerre mind a két résen átmegy”. Igaz ugyan, hogy ez meglehetősen vad ötletnek tűnik, de nem vethető el teljesen. Kísérletileg kell ellenőriznünk, hogy ez lehetséges-e vagy sem. Ennek megfelelően tegyünk egy-egy érzékelő detektort közvetlenül a rések után. Ez akkor fog jelezni, ha egy elektron átmegy az adott résen. Ha történetesen az elektron (eléggé fura módon, de) „egyszerre menne át mind a két résen”, akkor a két detektor „egyszerre jelezne”. Bocsássunk ismét egy elektronnyalábot a résekre! Azt tapasztaljuk, hogy vagy az egyik, vagy a másik detektor jelez, de a kettő egyszerre sohasem!
Ezt szemléletesen csak úgy tudjuk interpretálni (értelmezni), hogy az elektron egyszerre csak az egyik résen megy át. Ennek fényében különösen „érthetetlen” az interferencia tag megjelenése. Idézzük fel ismét Feynman mondatait!
- Hacsak tudják, próbálják elkerülni, hogy folytonosan kérdezgessék önmagukat: „De hát miképp lehetséges ez?”, mert akkor lezuhanunk egy sötét szakadékba, ahonnan még senkinek sem sikerült kijutnia. Kérdésükre a választ senki sem tudja.
A jelenség „megértése” a kvantummechanika (előzőekben bemutatott) „szuperpozíció elvének” az alkalmazásával válik lehetővé. Az alábbi táblázatban megadtuk a lehetséges 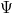 állapotokat és az azokhoz tartozó, a felfogó ernyőn mérhető elektron becsapódások
állapotokat és az azokhoz tartozó, a felfogó ernyőn mérhető elektron becsapódások  intenzitását.
intenzitását.
| 1. rés | 2. rés | az állapotfv. | a mért intenzitás |
| Ny | Z | 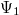
|
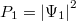
|
| Z | Ny | 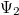
|
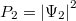
|
| Ny | Ny | 
|
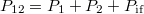
|
Hiszen a „valószínűségi” értelmezés axiómája szerint:
![\[\begin{aligned} P_{12} = \left| \Psi_{12} \right|^2 &= \left| \Psi_1 + \Psi_2 \right|^2 = \\ &= \left| \Psi_1 \right|^2 + \left| \Psi_2 \right|^2 + 2 \Re \lbrace \Psi_1^* \Psi_2 \rbrace = \\ &= P_1 + P_2 + P_{\rm if}. \end{aligned}\]](/images/math/9/b/f/9bf2eaf92e5a67b0861cad80737f5c26.png)
Az előzőekben használt 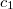 és
és 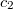 konstansoktól most eltekintettünk, ugyanis ez nem változtat a jelenség lényegi, kvalitatív magyarázatán. A
konstansoktól most eltekintettünk, ugyanis ez nem változtat a jelenség lényegi, kvalitatív magyarázatán. A  konstansok fizikai jelentésének a megtárgyalása szintén az MSc tanulmányok feladata.
konstansok fizikai jelentésének a megtárgyalása szintén az MSc tanulmányok feladata.
Ezzel kapcsolatban írja R. P. Feynman a következőket (R. P. Feynman: Mai Fizika, 3. kötet, 155. oldal):
- Akadhat valaki, akinek a kíváncsisága ezek után sem nyugszik meg: „Miért van így mindez? Milyen mechanizmus áll a törvény mögött?” Senkinek sem sikerült semmiféle mechanizmust találnia a törvény mögött. Senki sem tudja a dolgot szemernyivel sem jobban megmagyarázni, mint ahogyan mi „megmagyaráztuk” az imént.
- S eddig még senki nem talált kiutat ebből a talányból. Így hát jelenleg a valószínűségek kiszámítására kell korlátozódnunk. Azt mondjuk, hogy „jelenleg”, de erősen gyanítjuk, hogy ez már mindig így lesz, hogy ez a talány megoldhatatlan. És a Természet valójában így működik.
Bevezető (BSc) szinten tehát a Kvantummechanika három (egyszerűsített) alaptörvénye a következő:
a.) az (időfüggetlen) Schrödinger-egyenlet,
b.) a hullámfüggvény fizikai jelentése,
c.) az állapotok szuperpozíciójának az elve.
Az alaptörvények néhány fontos következménye
Az alagúteffektus elméleti háttere (nem kötött állapotok tárgyalása)
A szabadon mozgó elektron állapotfüggvénye
Az alábbiakban egy igen fontos állapotfüggvény megkeresésére vállalkozunk. A dobozba nem zárt, azaz az egész térben szabadon mozgó elektron állapotfüggvényét a szuperpozíció elvének a felhasználásával fogjuk megalkotni. Az egyszerűség végett egydimenziós esetet vizsgálunk.
Mint azt láttuk, az egydimenziós,  nagyságú potenciáldobozba zárt elektron állapotfüggvénye a következő:
nagyságú potenciáldobozba zárt elektron állapotfüggvénye a következő:
![\[ \psi_0(x) = A\sin \left( \frac{2\pi}{\lambda_n} x\right) = A \sin(kx), \quad \text{ahol} \]](/images/math/0/3/9/03981455355ac0dbd2a6ccf536a0075e.png)
![\[ k = \frac{2\pi}{\lambda_n} = \frac{\pi}{L} n, \quad n = 1,2,3,... , \]](/images/math/7/6/4/7644f23edfecb962130fdb4db9db3f1e.png)
és mint tudjuk, az elektron impulzusa 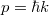 . A matematikai ismereteink alapján tudjuk, hogy a szinuszfüggvény felírható két komplex függvény összegeként:
. A matematikai ismereteink alapján tudjuk, hogy a szinuszfüggvény felírható két komplex függvény összegeként:
![\[ \sin (kx) = \frac{1}{2{\rm i}} \left[ \exp(+{\rm i}kx) - \exp(-{\rm i}kx) \right], \quad \text{ahol} \quad {\rm i} = \sqrt{-1}. \]](/images/math/9/2/4/924571ae501129544deab2492f912ab4.png)
Ennek ismeretében a megadott 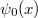 valós állapotfüggvény két komplex állapotfüggvény szuperpozíciójaként is felfogható. Tekintsünk el ismét a
valós állapotfüggvény két komplex állapotfüggvény szuperpozíciójaként is felfogható. Tekintsünk el ismét a  konstansoktól. Ekkor írható, hogy:
konstansoktól. Ekkor írható, hogy:
![\[ \psi_0(x) = A\sin(kx) = \varphi_{+}(x) + \varphi_{-}(x), \quad \text{ahol} \]](/images/math/5/2/5/52559cd698056f1d18cfa9a6f600c275.png)
![\[ \varphi_{+}(x) = \frac{A}{2{\rm i}}\exp(+{\rm i}kx) \quad \text{és} \quad \varphi_{-}(x) = -\frac{A}{2{\rm i}}\exp(-{\rm i}kx). \]](/images/math/c/c/f/ccf3a38ce8eec0503519e8aba3f0af73.png)
A kérdés mármost az, hogy mi lehet az a két fizikai állapot, amelyet a 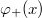 és a
és a 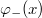 függvény leír. A kiindulásul megadott
függvény leír. A kiindulásul megadott 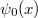 egy dobozba zárt elektron állapotát jellemzi. Ezen elektron impulzusának a nagysága
egy dobozba zárt elektron állapotát jellemzi. Ezen elektron impulzusának a nagysága 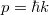 és az energiája
és az energiája  , valamint tudjuk, hogy
, valamint tudjuk, hogy 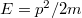 . Láthatóan eddig egyáltalában nem esett szó arról, hogy milyen az impulzus iránya, azaz az elektron a
. Láthatóan eddig egyáltalában nem esett szó arról, hogy milyen az impulzus iránya, azaz az elektron a 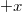 avagy a
avagy a  irányban halad-e. Hiszen:
irányban halad-e. Hiszen:
![\[ p^2 = 2mE, \quad \text{és ezért} \quad p = \pm \sqrt{2mE}. \]](/images/math/d/f/c/dfce3edab53472532ba05ae145f7846d.png)
Ezt végiggondolva, nyilvánvalóan adódik a jogos feltételezés, hogy a 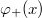 állapotot a
állapotot a 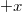 és a
és a 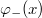 állapotfüggvényt a
állapotfüggvényt a  irányba haladó részecske állapotának tekintsük. Hasonlóan ahhoz, ahogyan a hullámtanban az állóhullámok kialakulása két ellentétes irányban mozgó haladó hullám szuperpozíciójaként adódik. Ha a Born-féle valószínűségi értelmezést alkalmazzuk, akkor kapjuk, hogy
irányba haladó részecske állapotának tekintsük. Hasonlóan ahhoz, ahogyan a hullámtanban az állóhullámok kialakulása két ellentétes irányban mozgó haladó hullám szuperpozíciójaként adódik. Ha a Born-féle valószínűségi értelmezést alkalmazzuk, akkor kapjuk, hogy
![\[ P_{+}(x) = \left| \varphi_{+}(x) \right|^2, \quad P_{-}(x) = \left| \varphi_{-}(x) \right|^2. \]](/images/math/d/3/b/d3b9337533d1c82d1bd6ba9ceb03b6af.png)
Adódik tehát, hogy
![\[ P_{+}(x) = P_{-}(x) = \frac{A^2}{4} = \text{állandó.} \]](/images/math/d/e/e/dee06b736992a2fe829133efe571310a.png)
Ez pontosan megfelel a várakozásunknak. Ugyanis, ha egy részecske szabadon és minden korlátozás nélkül mozog az  tengely mentén, akkor őt mindenhol egyforma valószínűséggel kell megtalálnunk. Ez az egyenletes mozgás „szimmetriájából” következik. Ugyanakkor
tengely mentén, akkor őt mindenhol egyforma valószínűséggel kell megtalálnunk. Ez az egyenletes mozgás „szimmetriájából” következik. Ugyanakkor
![\[\begin{aligned} P_{\pm}(x) \equiv \left| \Psi_0(x) \right|^2 &= \left| \varphi_{+}(x) + \varphi_{-}(x) \right|^2 = \\ &= \left| \varphi_{+}(x) \right|^2 + \left| \varphi_{-}(x) \right|^2 + 2\Re \lbrace \varphi_{+}^* \varphi_{-} \rbrace. \end{aligned}\]](/images/math/e/a/0/ea056914caa9bd30dcd1d737a4693bef.png)
Beírva ide az állapotfüggvényeket, adódik, hogy:
![\[\begin{aligned} P_{\pm}(x) &= \frac{A^2}{4} + \frac{A^2}{4} + 2\Re\left\lbrace -\frac{A^2}{4}\exp(-{\rm i} 2kx ) \right\rbrace = \\ &= \frac{A^2}{4} + \frac{A^2}{4} - 2 \frac{A^2}{4} \cos(-2kx). \end{aligned}\]](/images/math/7/f/5/7f5f8a36170dc85a00695427bd204d02.png)
Átalakítva a „kettős szögfüggvényt”, kapjuk, hogy:
![\[ \cos(-2kx) = \cos(2kx) = \cos^2(kx) - \sin^2(kx) = 2\cos^2(kx) - 1, \]](/images/math/d/4/f/d4f08e2a9365bb7f6e427ecdee40e910.png)
és így
![\[\begin{aligned} P_{\pm}(x) &= \frac{A^2}{4} + \frac{A^2}{4} - \frac{A^2}{2} \left[ 2\cos^2(kx) - 1 \right] = \\ &= \frac{A^2}{4} + \frac{A^2}{4} + \frac{A^2}{2} - 2\frac{A^2}{2}\cos^2(kx) = \\ &= A^2\left[ 1 - \cos^2(kx) \right] \\ &= A^2\sin^2(kx) = \\ &= \left| \psi_0(x) \right|^2, \end{aligned}\]](/images/math/8/1/9/8190c25c98b36527321b2aadfa392e79.png)
ahogyan azt vártuk is. Mármost (az előzőeknek megfelelően) ezt a kifejezést át kell írni a megszokott „szemléletes” formába, azaz:
![\[ P_{\pm}(x) = P_{+}(x) + P_{-}(x) + P_{if}(x). \]](/images/math/0/5/1/051bed289ab19c5bdd677cc5fa5aaa01.png)
Látható tehát, hogy adott mozgási energiájú részecskének két állapota van. Az egyik a „jobbra” a másik a „balra” való egyenletes mozgáshoz rendelhető. Mindkét állapotban a részecske megtalálási valószínűségsűrűsége (ugyanaz a 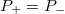 ) az
) az  mentén állandó lesz. Ha a részecskét egy potenciáldobozba zárjuk, akkor visszaverődve a falakról hol „balra”, hol pedig „jobbra” fog mozogni. Így a kvantummechanika alaptörvénye (axiómája) szerint a részecske állapotát ezen kétféle mozgást megadó hullámfüggvény összege fogja szolgáltatni. A két állapot interferenciája miatt a részecske
mentén állandó lesz. Ha a részecskét egy potenciáldobozba zárjuk, akkor visszaverődve a falakról hol „balra”, hol pedig „jobbra” fog mozogni. Így a kvantummechanika alaptörvénye (axiómája) szerint a részecske állapotát ezen kétféle mozgást megadó hullámfüggvény összege fogja szolgáltatni. A két állapot interferenciája miatt a részecske 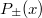 megtalálási valószínűségsűrűsége „ingadozni” fog. A méréskor ez (az
megtalálási valószínűségsűrűsége „ingadozni” fog. A méréskor ez (az  tengely mentén elhelyezett) „detektor ernyőn” interferenciacsíkok formájában fog megjelenni.
tengely mentén elhelyezett) „detektor ernyőn” interferenciacsíkok formájában fog megjelenni.
Látható tehát, hogy:
![\[ P_{\pm} \neq P_{+} + P_{-}, \quad \text{hiszen} \quad \left| \psi_0 \right|^2 \neq \left| \varphi_{+} \right|^2 + \left| \varphi_{-} \right|^2. \]](/images/math/5/9/3/593402b89f6d120c1b4e68cb9c8ccd8a.png)
Ezen vizsgálódásunk igen fontos eredménye az, hogy ha adott egy, a teljes térben szabadon mozgó tömegpont (azaz amelynek mozgása nem korlátozódik a tér egy véges tartományára), akkor ennek az állapotát egy komplex függvény adja meg. Nevezetesen:
![\[ \varphi_{+}(x) = A_{+} \exp(+{\rm i} kx) \quad \text{ha a részecske a $+x$ irányban mozog}, \]](/images/math/a/7/2/a721c48b8cdf48690492b58787d884e2.png)
![\[ \varphi_{-}(x) = A_{-} \exp(-{\rm i} kx) \quad \text{ha a részecske a $-x$ irányban mozog}. \]](/images/math/0/e/c/0ec24862e004994163cb2d1ce53cd1ef.png)
Ne felejtsük el, hogy ebben a kurzusban mi csak időfüggetlen állapotokat vizsgálunk! Ezért ezek az állapotfüggvények nem függnek az időtől.
Az 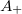 és
és 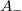 állandók számszerű meghatározására tudnunk kellene a kombinációs együtthatók fizikai jelentését. Ennek a kifejtésére azonban már csak az MSc kurzuson kerülhet sor.
állandók számszerű meghatározására tudnunk kellene a kombinációs együtthatók fizikai jelentését. Ennek a kifejtésére azonban már csak az MSc kurzuson kerülhet sor.
Mármost az így definiált 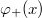 és
és 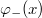 állapotokat általánosíthatjuk arra az esetre is, amikor a potenciáldobozunk nagyon nagy (
állapotokat általánosíthatjuk arra az esetre is, amikor a potenciáldobozunk nagyon nagy (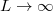 ). Ekkor egy szabadon mozgó részecskéhez jutunk, ún. nem kötött állapotok alakulnak ki. Mivel a falak végtelen távol vannak, nincsen visszaverődés és a részecske szabadon mozog vagy jobbra, vagy balra. Mivel a részecske nem pattog a két fal között, nem lép fel a
). Ekkor egy szabadon mozgó részecskéhez jutunk, ún. nem kötött állapotok alakulnak ki. Mivel a falak végtelen távol vannak, nincsen visszaverődés és a részecske szabadon mozog vagy jobbra, vagy balra. Mivel a részecske nem pattog a két fal között, nem lép fel a 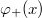 és a
és a 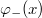 állapotok szuperpozíciója sem. Ez azért fontos, mert ha a
állapotok szuperpozíciója sem. Ez azért fontos, mert ha a 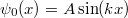 kötött állapotot tekintjük, akkor értelmezési nehézségekbe ütközünk: a klasszikusan megengedett tartomány végtelen nagy mérete miatt a hullámfüggvény már nem négyzetesen integrálható és így a (kötött állapotok esetén definiált) valószínűségi értelmezés (minden további nélkül) már nem lehetséges. Az elmondottak szemléltetésére vegyük a jól ismert egydimenziós potenciáldoboz esetét. Mint azt láttuk, ezen alapult az egydimenziós Scrödinger-egyenlet megalkotása. Egy adott energiánál az előzőek szerint
kötött állapotot tekintjük, akkor értelmezési nehézségekbe ütközünk: a klasszikusan megengedett tartomány végtelen nagy mérete miatt a hullámfüggvény már nem négyzetesen integrálható és így a (kötött állapotok esetén definiált) valószínűségi értelmezés (minden további nélkül) már nem lehetséges. Az elmondottak szemléltetésére vegyük a jól ismert egydimenziós potenciáldoboz esetét. Mint azt láttuk, ezen alapult az egydimenziós Scrödinger-egyenlet megalkotása. Egy adott energiánál az előzőek szerint
![\[ E = \frac{p^2}{2m}, \quad \text{ahol} \quad p = \hbar k \quad \text{és} \quad k = \frac{\pi}{L} n. \]](/images/math/a/c/3/ac37f1866f3103025afa618de03c9e8d.png)
Az állapotfüggvény pedig
![\[ \psi_0(x) = \sqrt{\frac{2}{L}} \sin(k x). \]](/images/math/9/d/3/9d32448b1cda8ef9a91c02cdf1a7b9b4.png)
A fentiek értelmében nem kötött állapothoz jutunk, ha 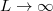 . Látható, hogy ekkor
. Látható, hogy ekkor
![\[ \lim_{L\to\infty} E = 0, \quad \lim_{L\to\infty} \psi_0(x) = 0, \]](/images/math/2/b/4/2b4f67ce70f7280c5e13bdf7531b8520.png)
és ezért
![\[ \lim_{L\to\infty} \left| \psi_0(x) \right|^2 \equiv 0. \]](/images/math/d/4/3/d4394c1603ffb8fdf66e938c45f1a143.png)
Ez pedig fizikailag értelmetlen állapotot jelent. A precíz kvantummechanikai elmélet igazolja a fenti gondolatmenetet.
A valószínűségi áramsűrűség
A hullámfüggvény fizikai jelentésének általánosításához meg kell szabadulnunk a négyzetesen integrálhatóságtól és új fogalmat kell bevezetnünk. Ez az új fogalom – a klasszikus fizikából jól ismert konvektív áramsűrűség mintájára – a valószínűségi áramsűrűség.
Megtanultuk, hogy ha valamilyen 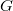 fizikai mennyiségre tudjuk értelmezni annak
fizikai mennyiségre tudjuk értelmezni annak 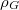 térbeli sűrűségét, akkor ez azt jelenti, hogy a
térbeli sűrűségét, akkor ez azt jelenti, hogy a 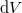 térfogatban ebből
térfogatban ebből 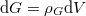 van jelen.
van jelen. 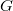 lehet tömeg, elektromos töltés, energia stb, és ennek megfelelően van tömegsűrűség, elektromos töltéssűrűség és energiasűrűség. Mindegyikkel találkoztunk már. Ha ez a
lehet tömeg, elektromos töltés, energia stb, és ennek megfelelően van tömegsűrűség, elektromos töltéssűrűség és energiasűrűség. Mindegyikkel találkoztunk már. Ha ez a 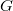 most
most 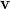 sebességgel áramlik, akkor definiálható a
sebességgel áramlik, akkor definiálható a 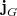 áramsűrűség is:
áramsűrűség is:
![\[ {\bf j}_G = {\bf v} \rho_G. \]](/images/math/4/7/c/47ce19cb97198205c7dc3fd45d8a574b.png)
Ennek megfelelően ismeretes, hogy van pl. tömegáram-sűrűség, töltés-áramsűrűség és energia-áramsűrűség.
Szemléltető példaként kiszámíthatjuk egy szabadon mozgó részecske esetén a valószínűségi áramsűrűséget. Mint azt megtanultuk, (pl. az  tengely mentén) szabadon mozgó elektron impulzusa (a mozgás irányától függően)
tengely mentén) szabadon mozgó elektron impulzusa (a mozgás irányától függően) 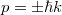 . Ekkor a
. Ekkor a 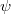 állapotfüggvény egy síkhullám. A megtalálási valószínűségsűrűség
állapotfüggvény egy síkhullám. A megtalálási valószínűségsűrűség 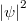 (ez lesz most a
(ez lesz most a 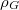 ). Az általa definiált (valószínűségi) áramsűrűség egyszerűen meghatározható:
). Az általa definiált (valószínűségi) áramsűrűség egyszerűen meghatározható:
![\[ J_\psi = v \left| \psi \right|^2 = \frac{p}{m} \left| \psi \right|^2 = \pm\frac{\hbar k}{m} \left| \psi \right|^2. \]](/images/math/e/7/2/e7247cd3368388580a0b0c27135724e9.png)
Az így kapott 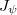 már alkalmas lesz arra, hogy a szabadon mozgó részecske dinamikáját helyesen leírjuk.
már alkalmas lesz arra, hogy a szabadon mozgó részecske dinamikáját helyesen leírjuk.
A valószínűségi áramsűrűség fogalma definiálható nem csak a szabad részecskékre, hanem tetszőleges 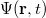 állapot esetére is. Ehhez azonban a jelenleginél mélyebb kvantummechanikai ismertekre lenne szükségünk. Így most ezzel tovább nem foglalkozunk.
állapot esetére is. Ehhez azonban a jelenleginél mélyebb kvantummechanikai ismertekre lenne szükségünk. Így most ezzel tovább nem foglalkozunk.
Áthaladás potenciálgáton (közelítő számítás)
Láttuk azt, hogy egy részecske (pl. elektron) behatolhat a klasszikusan tiltott tartományba is. Ha ez a tartomány véges szélességű, akkor az elektron véges valószínűséggel át is tud jutni rajta. Ezt a jelenséget nevezzük alagúteffektusnak. Mivel a részecske összenergiája mindvégig állandó marad, nem mondhatjuk azt, hogy ő mintegy „átugorja” a potenciálgátat. A jelenség tisztán kvantummechanikai, így magyarázata csakis a kvantummechanika törvényeivel lehetséges. Kvantitatív jellemzőként bevezetjük a  transzmissziós tényező fogalmát. A
transzmissziós tényező fogalmát. A 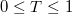 annak a valószínűsége, hogy a részecske áthalad a gáton. Ennek a kiszámításához fogjuk használni a valószínűségi áramsűrűséget.
annak a valószínűsége, hogy a részecske áthalad a gáton. Ennek a kiszámításához fogjuk használni a valószínűségi áramsűrűséget.
A jelenséget egy egyszerű modellen fogjuk bemutatni. Tekintsünk egy ún. egydimenziós „négyszögletes” potenciálgátat. Ez azt jelenti, hogy az  tengely mentén a potenciális energia azonosan nulla, kivéve egy
tengely mentén a potenciális energia azonosan nulla, kivéve egy 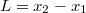 hosszúságú tartományt. Ebben a tartományban a potenciális energia legyen
hosszúságú tartományt. Ebben a tartományban a potenciális energia legyen 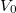 . A feladatunk a következő. Határozzuk meg, hogy egy (az
. A feladatunk a következő. Határozzuk meg, hogy egy (az  tengely mentén mozgó)
tengely mentén mozgó) 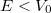 kinetikus energiájú részecske mekkora valószínűséggel jut át ezen a
kinetikus energiájú részecske mekkora valószínűséggel jut át ezen a 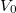 magasságú és
magasságú és  szélességű potenciálgáton. A feladatot ún. Gamow-közelítéssel lehet könnyen megoldani. Ekkor az áthaladás valószínűségének a közelítő értékét
szélességű potenciálgáton. A feladatot ún. Gamow-közelítéssel lehet könnyen megoldani. Ekkor az áthaladás valószínűségének a közelítő értékét 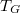 -vel fogjuk jelölni.
-vel fogjuk jelölni.
A potenciálgátra balról beeső részecske bizonyos valószínűséggel áthalad illetve visszaverődik a potenciálgáton. A beeső, a visszaverődő és az átjutás után eltávozó szabadon mozgó részecske kvantummechanikai leírása a megfelelő valószínűségi áramsűrűségekkel történik. A 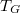 transzmissziót az eltávozó
transzmissziót az eltávozó 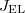 és a beeső
és a beeső 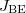 valószínűségi áramsűrűségek hányadosaként definiáljuk:
valószínűségi áramsűrűségek hányadosaként definiáljuk:
![\[ T_G = \frac{J_{\rm EL}}{J_{\rm BE}}, \quad \text{ahol} \quad J_{\rm BE} = \frac{\hbar k}{m} \left| \psi_1(x) \right|^2, \quad J_{\rm EL} = \frac{\hbar k}{m} \left| \psi_3(x) \right|^2. \]](/images/math/6/7/9/679cdecfccdd91035a0dce08ae73bc16.png)
A potenciálgát szimmetrikus alakja miatt a gát mindkét oldalán a részecske sebessége ugyanakkora. Így az a számítás során kiesik. Értelemszerűen, az áramsűrűségeket a potenciálgát 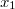 és
és 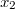 szélein érdemes megadni. Ezzel kapjuk, hogy:
szélein érdemes megadni. Ezzel kapjuk, hogy:
![\[ T_G = \left| \frac{\psi_3(x_2)}{\psi_1(x_1)} \right|^2. \]](/images/math/d/d/e/dde80f9999b177acbfd194ca79ded8b9.png)
A hullámfüggvény folytonossága miatt
![\[ \psi_1(x_1) = \psi_2(x_1) \quad \text{és} \quad{} \psi_3(x_2) = \psi_2(x_2), \]](/images/math/9/c/9/9c9632edefda9ebd8f79eef9405e6a07.png)
ezért a transzmissziót a gáton belül számított 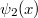 hullámfüggvény határozza meg. Azaz
hullámfüggvény határozza meg. Azaz
![\[ T_G = \left| \frac{\psi_2(x_2)}{\psi_2(x_1)} \right|^2. \]](/images/math/a/8/f/a8f62dc545d940b117dd7b3dbc47dc6a.png)
A 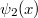 a 2-es tartományban felírható Schrödinger-egyenlet megoldásaként adódik:
a 2-es tartományban felírható Schrödinger-egyenlet megoldásaként adódik:
![\[ -\frac{\hbar^2}{2m} \psi_2''(x) + V_0\cdot\psi_2(x) = E\cdot \psi_2(x), \]](/images/math/7/5/e/75ed4f9a072da42ab7915b8625c9098f.png)
azaz
![\[ \psi_2''(x) = \frac{2m}{\hbar^2}(V_0 - E)\psi_2(x). \]](/images/math/9/b/7/9b7c41f5a19d3fb664b1426043fe3cf6.png)
Mivel a jobb oldalon a 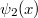 együtthatója állandó, az egyenlet két megoldása egyszerűen adódik:
együtthatója állandó, az egyenlet két megoldása egyszerűen adódik:
![\[ \psi_2(x) \sim \exp\left\lbrace \pm \sqrt{\frac{2m}{\hbar^2}(V_0 - E) \cdot x} \right\rbrace. \]](/images/math/7/5/0/7507f7824b656e8264f55b75cb576019.png)
Mivel 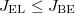 ezért
ezért 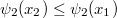 és
és 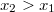 . Így tehát
. Így tehát 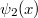 -nek az exponenciálisan csökkenő függvényt kell választanunk. Ezzel pedig adódik, hogy
-nek az exponenciálisan csökkenő függvényt kell választanunk. Ezzel pedig adódik, hogy
![\[ T_G = \exp\left\lbrace -2\sqrt{\frac{2m}{\hbar^2}(V_0 - E)} \cdot (x_2 - x_1)\right\rbrace. \]](/images/math/5/a/7/5a73d407bd45975efa70466392e16799.png)
A hullámfüggvény deriváltjára (a gát széleinél) semmiféle kikötést nem tettünk, ezért az eredményünk csak egy közelítő érték lehet. Ez a Gamow-köelítés lényege. Láthatóan, a potenciálgát 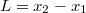 szélességének a növelésével az átjutás valószínűsége exponenciálisan csökken.
szélességének a növelésével az átjutás valószínűsége exponenciálisan csökken.
Annak egyik jele, hogy a kapott összefüggés csakis egy közelítés lehet többek között az, hogy 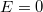 esetén
esetén 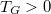 . Az az állítás, hogy (szemléletesen szólva) egy álló részecske is átjuthat a gáton, még a kvantummechanikai szemléletünk szerint is hamis kell, hogy legyen.
. Az az állítás, hogy (szemléletesen szólva) egy álló részecske is átjuthat a gáton, még a kvantummechanikai szemléletünk szerint is hamis kell, hogy legyen.
A négyszögletes potenciálgátra kapott Gamow-féle eredmény segítségével közelítően meghatározhatjuk egy tetszőleges alakú potenciálgáton való áthaladás valószínűségét is. A tetszőleges alakú potenciálgát ugyanis igen kicsiny 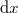 szélességű négyszögletes gátak együtteseként fogható fel.
szélességű négyszögletes gátak együtteseként fogható fel.
Feltételezhetjük, hogy az egyes elemi gátakon való 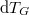 áthaladási valószínűsége egymástól független eseményeknek tekinthetők. Ezért ezek a
áthaladási valószínűsége egymástól független eseményeknek tekinthetők. Ezért ezek a 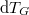 -k összeszorzódnak (független események együttes bekövetkezése):
-k összeszorzódnak (független események együttes bekövetkezése):
![\[ {\rm d} T_G = \exp \left\lbrace -2\sqrt{\frac{2m}{\hbar^2}[V(x) - E]} \, {\rm d}x \right\rbrace. \]](/images/math/5/7/1/5716e8de3101e3cb24c8ddea394a6577.png)
Mivel a 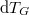 elemi valószínűségek exponenciális kifejezések, a szorzatuk is exponenciális kifejezés lesz. A kitevők összeadódnak és az eredő kitevő a gát alakjától és a részecske összenergiájától függő integrál lesz. Tehát
elemi valószínűségek exponenciális kifejezések, a szorzatuk is exponenciális kifejezés lesz. A kitevők összeadódnak és az eredő kitevő a gát alakjától és a részecske összenergiájától függő integrál lesz. Tehát
![\[ T_G = \prod {\rm d}T_G = \exp\left\lbrace -2\int_{x_1}^{x_2} \sqrt{\frac{2m}{\hbar^2}[V(x) - E]} \, {\rm d}x \right\rbrace. \]](/images/math/5/f/d/5fdf61c2fa99c0c805db2022c5104c18.png)
Alagúteffektus a gyakorlatban (mérés, elektronikus eszközök)
Az alagúteffektus történeti példájaként az „ősproblémát” kell említenünk. Ugyanis Gamow a módszerét az  -bomlás elméleti vizsgálatára dolgozta ki. Az ötlete szerint az atommagból az igen stabil 2 protonból és 2 neutronból álló
-bomlás elméleti vizsgálatára dolgozta ki. Az ötlete szerint az atommagból az igen stabil 2 protonból és 2 neutronból álló 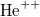 az atommagból alagúteffektus révén jut ki.
az atommagból alagúteffektus révén jut ki.
A másik (technikai-gyakorlati) példa a hideg- (vagy tér-) emisszió jelensége, amikor elektrosztatikus tér hatására a fémből elektronok lépnek ki. Ennek régen az elektronforrások fejlesztésében volt nagy szerepe (rádiócsövek, elektronágyúk stb). A fém felületére merőleges, homogén, sztatikus elektromos tér potenciálja a fémen kívül lineáris lesz. A fémen belül az elektromos tér nulla. A fotóeffektusnál bevezetett potenciállépcső ennek megfelelően fog módosulni. A transzmissziós tényező az előzőekben tárgyalt Gamow-közelítéssel kiszámítható.
A transzmissziós tényező (értelemszerűen) az  árammal, az alkalmazott elektromos térerősség pedig a rendszerre kapcsolt
árammal, az alkalmazott elektromos térerősség pedig a rendszerre kapcsolt  feszültséggel arányos. A számolás elemi módon elvégezhető. Az
feszültséggel arányos. A számolás elemi módon elvégezhető. Az 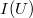 függvényre adódik, hogy
függvényre adódik, hogy
![\[ I = I(t) \exp \left( - \text{áll} \frac{\Phi_0^{3/2}}{ \left| {\bf E} \right| } \right). \]](/images/math/4/f/4/4f45581f110165197fbc7a17ee96c7bc.png)
Ez az ún. Fowler-Nordheim formula. A számítások megegyeznek a mérési eredményekkel.
A formula aktualitása napjainkban látványosan megnőtt. A félvezető alkatrészek egy részében ez a fajta alagutazási effektus igen gyakori és az eszköz működésének az alapját jelenti (pl. MOS, flash memory). Ezekre a későbbekben még majd visszatérünk.
Az alagúteffektus a klasszikus fizika számára értelmezhetetlen jelenség. A mérési eredmények fényesen igazolják a kvantummechanikai szemléletünk helyességét. Létezése ma már trivialitás.
Az alagúteffektus dinamikáját csak az időtől függő Schrödinger-egyenlet alkalmazásával lehet korrektül tárgyalni. Ez azonban már csak az MSc szak keretei között lehetséges. Mindemellett az imént tárgyalt „statikus” modell is képes bemutatni az effektus elvi lényegét. Erre a későbbiekben kerül sor.
Alagúteffektus a laboratóriumban
A jól ismert alagút dióda (tunnel dióda, Leo Esaki, Nobel díj 1973.), mint azt a neve is mutatja, ezt a kvantummechanikai jelenséget használja ki.

|
Leo Esaki (1925-)
Nobel-díj: 1973 Egyetemi tanulmányit Tokióban végezte. Doktori dolgozata a Sony cégnél, 1957-ben folytatott kísérleti munkájának a feldolgozása és értékelése volt. Ez az erősen adalékolt germánium p-n átmenetében létrehozott alagúteffektusról szólt. Ezek az eredmények alapozták meg az alagút dióda létrejöttét. A megosztott Nobel díjat „a félvezetőkben lévő alagút-jelenségekkel kapcsolatos kísérleti felfedezésekért” kapta 1973-ban. Partnerei (Ivar Giaever és Brian David Josephson) a szupravezetőkben zajló alagúteffektusokkal kapcsolatos kísérleti és elméleti munkát végeztek. |
A pásztázó alagútmikroszkóp vagy STM (1985, Gerd Binnig, Heinrich Rohrer. Nobel díj 1986!) volt az az eszköz, amellyel valójában először „pillanthattuk meg” az atomokat. Ernst Mach („pozitivista”) „álma” (70 évvel az 1916-ban bekövetkezett halála után) végre valahára teljesült.
Az STM működésének alapja az alagúteffektus. A vizsgálandó felület egy atomja és a „vizsgáló tű” egy atomja között (lokális, atomi „keresztmetszetű felületen” átfolyó) alagútáram alakul ki.
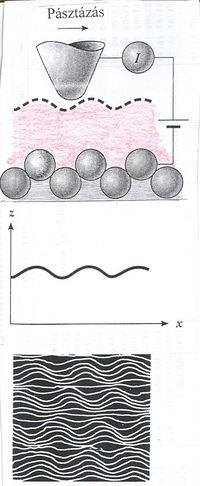
|
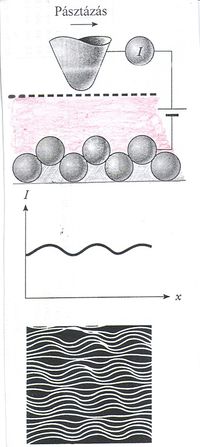
|

Az STM elektronikája által szolgáltatott „rajzolat”
A számítógépes „manipuláció” eredményeként adódó „szemléletes” kép |
A tűt a felület felett vízszintes (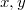 ) irányban, atomi „lépésekben” mozgatják. Az alagútáramot állandónak tarják úgy, hogy a tűt (függőleges
) irányban, atomi „lépésekben” mozgatják. Az alagútáramot állandónak tarják úgy, hogy a tűt (függőleges 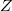 irányban) közelítik, vagy távolítják a felülethez. Ezt az igen finom (az atomi méret töredékét jelentő) mozgatást egy „piezoelektromos karral” lehet megoldani. A tűnek ez a finom mozgása mintegy letapogatását jelenti a felület „elektronsűrűségének”, ami korrelál a felületet alkotó atomok elrendezésével (struktúrájával). A
irányban) közelítik, vagy távolítják a felülethez. Ezt az igen finom (az atomi méret töredékét jelentő) mozgatást egy „piezoelektromos karral” lehet megoldani. A tűnek ez a finom mozgása mintegy letapogatását jelenti a felület „elektronsűrűségének”, ami korrelál a felületet alkotó atomok elrendezésével (struktúrájával). A 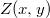 függvényt elektronikusan feldolgozzák és számítógépes programokkal „atomi felbontású felületté” alakítják. A készüléket lehet olyan „üzemmódban” is működtetni, hogy
függvényt elektronikusan feldolgozzák és számítógépes programokkal „atomi felbontású felületté” alakítják. A készüléket lehet olyan „üzemmódban” is működtetni, hogy 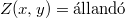 legyen. Ekkor a pásztázás során az alagútáram fog változni, az
legyen. Ekkor a pásztázás során az alagútáram fog változni, az 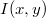 függvény fogja a felület atomi felbontású „képét” szolgáltatni. Egy ilyen kép látható a mellékelt ábrán is.
függvény fogja a felület atomi felbontású „képét” szolgáltatni. Egy ilyen kép látható a mellékelt ábrán is.
A készülék maga meglepően egyszerű és „biztonságos” működésű. Előállítása olcsó, így ma már minden „valamire való” egyetemi Fizika labor hallgatói mérésének a része.

|
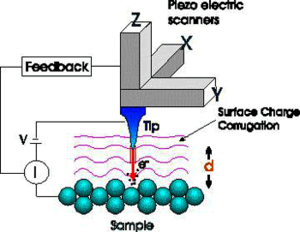
|

| |
Összefoglalásul (ismét) megállapíthatjuk tehát, hogy a mikrorészecskék fentiekben bemutatott viselkedése a newtoni tömegpont-mechanika szerint teljesen érthetetlen. Mindez azt sugallja, hogy szakítanunk kell a hagyományos tömegpont-modellel és gyökeresen új szemléletet kell kialakítanunk! Ez pedig a Kvantummechanika!
A határozatlansági reláció
A szükséges valószínűségszámítási fogalmak
| Relatív gyakoriság: | 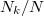
|
| Valószínűségi változó: | 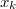 , , 
|
| Valószínűség(sűrűség): | 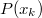 , , 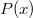
|
| Várható érték: | 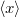
|
| Négyzetes szórás: | 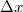
|
| A valószínűség és a relatív gyakoriság kapcsolata: | ![\[ \lim_{n\to\infty} \frac{N_k}{N} = P(x_k) \]](/images/math/6/1/0/61006e685d6011e734a572648dcaeff5.png) |
| A diszkrét és folytonos valószínűségi változó: | ![\[ P(x_k) \to P(x) \]](/images/math/b/0/a/b0ad5e1ffa9112c58171aed0021f3e68.png) |
| A várható érték: | ![\[ \left< x \right> = \sum_k x_k P(x_k), \quad \left< x \right> = \int_{-\infty}^{+\infty} x P(x) \, {\rm d} x \]](/images/math/2/e/7/2e7480a3654d1346a432784812bfead8.png) |
| Négyzetes szórás: | ![\[ \Delta x = \sqrt{\left< (x - \left< x \right>)^2 \right>} = \sqrt{\left< x^2 \right> - \left< x \right>^2 } \]](/images/math/8/a/4/8a40d97985ea119a06c02dade4b9a4bd.png) |
A Heisenberg-féle határozatlansági reláció fizikai tartalma
A Heisenberg-féle határozatlansági reláció fizikai tartalma (BSc szinten) csak a „szuperpozíció” elvének a tükrében érthető meg igazán.

|
Werner Heiseberg (1901-1976)
Nobel-díj (1932/33): „a kvantummechanika megalkotásáért és alkalmazásáért, amely többek között a hidrogénmolekula allotrop módosulatának a felfedezéséhez vezetett”. Egyetemi tanulmányait Münchenben végezte. 24 éves korában írta azt a cikkét, amely megvetette a kvantummechanika alapjait. Max Born és Niels Bohr munkatársaként is dolgozott. A II. világháború alatt Németországban maradt, de a Náci-rendszerrel nem szimpatizált. Az USA-ban dolgozó fizikusok attól tartottak, hogy ő is az atombomba megvalósításán dolgozik. Ismerve a zsenialitását, úgy gondolták, hogy sikerrel járhat. Csak a háború után derült ki, hogy Heisenberg ez irányú munkája során „téves utat” követett. Ennek okairól megoszlanak a vélemények. Egy azonban biztos, a német nukleáris fegyver nem készült el. A neutron felfedezése után, 1932-ben ő javasolt először egy kvantummechanikai atommagmodellt. A róla elnevezett határozatlansági reláció a „koppenhágai iskola” filozófiai nézetének egyik alapköve lett. A Valóságról vallott elképzelésünk alapjait érintette, így ismeretelméleti hatása óriási. |
Kiindulásul tekintsük a „középiskolás fokon” megfogalmazott szöveges változatát és alkalmazzuk egy konkrét egyszerű esetre:
- egy részecske helyének és impulzusának egyidejű mérésekor a határozatlanságok szorzata nagyobb vagy olyan nagyságrendű, mint a
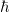 szám.
szám.
Ezzel a mondattal kapcsolatosan legalább két fogalmat kell tisztázni! Mit jelent az, hogy egyidejű mérésekor és határozatlanságok? Az egzakt kvantummechanika szerint a „helyes” összefüggés a következő:
![\[ \Delta x \Delta p_x \geq \frac{\hbar}{2}. \]](/images/math/b/7/a/b7a01829c6cd834d2c0cbe3aea069e27.png)
Elöljáróban le kell szögeznünk, hogy a határozatlansági reláció a részecskéken végzett mérések „objektív” sajátosságáról nyilatkozik. Ez azt jelenti, hogy a reláció „igazsága vagy hamissága” nem függ a mérőműszereink technikai fejlettségétől, azaz „ideális” mérőműszereket feltételez.
Ideális az a mérőműszer, amelyik az ismert természeti törvényeknek megfelelően működik, azokat nem sérti meg, de a mérnöki megvalósításból adódó „pontatlanságokkal” nem rendelkezik. Azaz „elvileg” tetszőlegesen nagy pontossággal méri meg azt a fizikai mennyiséget, amelyiknek a detektálására készítették.
A Fizikában gondolatkísérletnek nevezzük az imént definiált ideális műszerekkel konstruált méréseket. Ezek „sajnos” a megadott idealizációk miatt ténylegesen nem végezhetők el éppen a valóságos mérőműszereink technikai korlátjai miatt. Mégis igen hasznos „elméleti eszköznek” bizonyulnak abban a tudományos megismerési folyamatban, melynek célja a fizikai törvények egymásra épülésének a feltárása és az adott jelenségkör minél pontosabb (adekvát) elvi modelljének a megalkotása.
Megjegyzés. Az egyik legismertebb és méltán legnépszerűbb gondolatkísérlet-sorozat Albert Einstein nevéhez fűződik. A speciális relativitáselméletet népszerűsítő könyvében használt „vonatkísérletek” egyszerűsége és „szemléletessége” sokat segített a valójában igen elvont és forradalmian új gondolatokat tartalmazó elmélet elterjedésében. Mit sem von le ennek értékéből az a tény, hogy a „kísérlet” túlságosan is jól sikerült. Az elméletet éppen a tárgyalásból fakadó látszólagos „egyszerűsége” miatt sokan (többnyire nem szakmabeli, lelkes amatőrök) alaposan félreértelmezik. Az ilyen irányú úgymond „kritikai elmélkedések” bőséges irodalmát nyújtja az igen agresszíven nyomuló áltudományos irodalom.
A könyvesboltok polcai roskadoznak ezen tudományosnak tűnő „irodalmi alkotások” sokaságától. A XXI. század BSc mérnökének ezeket illene (sőt, hitünk szerint kötelessége lenne) felismerni. Hasonló a helyzet (ha nem rosszabb) a Kvantummechanikával is.
Mindezek előrebocsátása után, most egy igen egyszerű gondolatkísérlettel megmutatjuk, hogy a határozatlansági reláció fenti megfogalmazása legalább is félreérthető. Márpedig ami félreérthető, azt félre is fogják érteni (à la Murphy). Így van ez a Heisenberg-féle határozatlansági relációval is.
Megjegyzés. Különösen élenjárnak ebben némely „filozófusok” (nincsenek is olyan kevesen!), akik a Világ „megismerhetetlenségének” misztikus korlátját vélik felfedezni ebben. Nem árt, ha kellő kritikával és óvatossággal közelítünk eme filozófiai eszmefuttatásokhoz!
Ha „szó szerint” értelmezzük a tankönyvből idézett megfogalmazást, akkor bajba jutunk, ugyanis könnyen mutathatunk olyan példát, amikor az állítás nyilvánvalóan nem teljesül. Vegyük egy (egydimenziós)  hosszúságú potenciáldobozba zárt részecskét. Legyen ez alapállapotban, azaz az energiája egy határozott
hosszúságú potenciáldobozba zárt részecskét. Legyen ez alapállapotban, azaz az energiája egy határozott 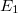 érték. Ekkor az impulzusa is ismert:
érték. Ekkor az impulzusa is ismert: 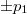 . Helyezzünk el egy részecskeérzékelő detektort a doboz valamely
. Helyezzünk el egy részecskeérzékelő detektort a doboz valamely  pontjába. Állítsuk be a detektor mérőfejét úgy, hogy csak a „balról-jobbra” mozgó részecske becsapódásakor adjon ki egy jelet.
pontjába. Állítsuk be a detektor mérőfejét úgy, hogy csak a „balról-jobbra” mozgó részecske becsapódásakor adjon ki egy jelet.
Mármost, ha a detektorunk jelez, akkor ez azt jelenti, hogy a tér  pontjában egy
pontjában egy 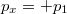 impulzusú részecske van (volt). Mivel az impulzus jelen esetben egy határozott (elvileg pontos) érték, így a mérésének a bizonytalansága elvileg
impulzusú részecske van (volt). Mivel az impulzus jelen esetben egy határozott (elvileg pontos) érték, így a mérésének a bizonytalansága elvileg 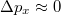 .
.
Megjegyzés. A dolog ennél sokkal bonyolultabb. A 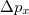 -be beleszól az „Energia és az Idő” között fennálló határozatlansági reláció is. Ennek a precíz megtárgyalása bőven meghaladja egy BSc kurzusnak a matematikai lehetőségeit, így erre majd az MSc Fizika tantárgyon belül kerülhet sor.
-be beleszól az „Energia és az Idő” között fennálló határozatlansági reláció is. Ennek a precíz megtárgyalása bőven meghaladja egy BSc kurzusnak a matematikai lehetőségeit, így erre majd az MSc Fizika tantárgyon belül kerülhet sor.
A részecske helymérésének a pontossága „csak” a detektor érzékelő felületének a pontos lokalizálhatóságától függ. Ezt pedig a „mérőfej” technikai megvalósítása korlátozza. Ez azonban, mint azt a bevezetőben említettük, „csak” műszaki probléma, amely ezen a méretskálán elvileg mindig egyre pontosabbá tehető. Azaz 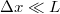 , ami azt jelenti, hogy
, ami azt jelenti, hogy 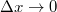 .
.
Tehát (a vizsgált állítással ellentétben) sikerült tetszőleges pontossággal „egyszerre megmérnünk” a részecske helyét ( ) és az impulzusát (
) és az impulzusát (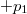 ). Csakhogy a Heisenberg-féle határozatlansági reláció egyáltalán nem azt jelenti, mint amit az imént elmondtunk. Valódi fizikai tartalmát az alábbiakban tesszük érthetővé.
). Csakhogy a Heisenberg-féle határozatlansági reláció egyáltalán nem azt jelenti, mint amit az imént elmondtunk. Valódi fizikai tartalmát az alábbiakban tesszük érthetővé.
Vegyük ismét az egydimenziós,  szélességű potenciáldobozba zárt elektronunkat. Mint azt láttuk, (megoldva a Schrödinger-egyenletet) a részecske lehetséges energiaszintjeire és állapotaira azt kaptuk, hogy:
szélességű potenciáldobozba zárt elektronunkat. Mint azt láttuk, (megoldva a Schrödinger-egyenletet) a részecske lehetséges energiaszintjeire és állapotaira azt kaptuk, hogy:
![\[ E_n = \frac{\hbar^2 \pi^2}{2mL^2}n^2, \quad \varphi_n (x) = \sqrt{\frac{2}{L}} \sin\left( \frac{\pi}{L} nx \right), \quad n = 1,2,3,... . \]](/images/math/2/e/6/2e6cd375c9f79b5edea28a968081b0e3.png)
Legyen az elektron éppen alapállapotban. Ekkor, mivel a kvantumszám értéke 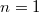 , az energiája nyilvánvalóan
, az energiája nyilvánvalóan
![\[ E_1 = \frac{\hbar^2 \pi^2}{2mL^2}, \]](/images/math/6/c/4/6c4d11da7eec475df30f45f195b413c2.png)
az állapotfüggvénye pedig
![\[ \varphi_1(x) = \sqrt{\frac{2}{L}} \sin\left( \frac{\pi}{L} x \right). \]](/images/math/1/1/0/110d0e6e8d692fd2d7693f6903ffab98.png)
Az állapotfüggvény Born-féle értelmezése szerint (b. axióma) az elektron megtalálási valószínűségsűrűsége ekkor
![\[ P(x) = \left| \varphi_1 (x) \right|^2 = \frac{2}{L} \sin^2 \left( \frac{\pi}{L} x \right). \]](/images/math/2/3/0/23092aaf895a84b296b50a2e7642aca8.png)
Tehát az elektron helyével kapcsolatosan csak annyit tudunk mondani, hogy milyen valószínűséggel található meg ő az  pont infinitezimálisan kicsiny környezetében. Az elektron
pont infinitezimálisan kicsiny környezetében. Az elektron 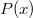 megtalálási valószínűségsűrűsége ekvivalens az
megtalálási valószínűségsűrűsége ekvivalens az  (mint) valószínűségi változó
(mint) valószínűségi változó 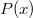 sűrűségfüggvényével. Tehát sokszor (
sűrűségfüggvényével. Tehát sokszor (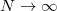 ) megmérve a
) megmérve a 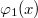 állapotú elektron helyét, a helymérés „határozatlanságát” a mérés „négyzetes szórásával” kell definiálnunk:
állapotú elektron helyét, a helymérés „határozatlanságát” a mérés „négyzetes szórásával” kell definiálnunk:
![\[ (\Delta x)^2 = \left< x^2 \right> - \left< x \right>^2. \]](/images/math/2/0/8/208af7d53774d3b8a77940754210bbf0.png)
Ennek megfelelően adódik tehát, hogy 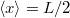 , valamint
, valamint
![\[\begin{aligned} \left< x^2 \right> &= \int_0^L x^2 \left| \varphi_1 \right|^2 \, {\rm d} x = \\ &= \int_0^L x^2 \left| \sqrt{\frac{2}{L}} \sin \left( \frac{\pi}{L} x \right) \right|^2 \, {\rm d}x = \\ &= \frac{2}{L} \int_0^L x^2 \sin^2 \left( \frac{\pi}{L} x \right) \, {\rm d} x = ... = \\ &= L^2 \left( \frac{1}{3} - \frac{1}{2\pi^2} \right). \end{aligned}\]](/images/math/8/7/f/87fbacc1c392171f46d7fd6aaf92cc31.png)
A kijelölt integrálás könnyen elvégezhető. A számolás részleteinek a kidolgozásánál a Tisztelt Olvasó szorgalmára hagyatkozunk!
Így tehát a helymérés „bizonytalanságára” azt kapjuk, hogy
![\[ \Delta x = \sqrt{\left< x^2 \right> - \left< x \right>^2} = L \sqrt{\frac{1}{12} + \frac{1}{2\pi^2}}. \]](/images/math/f/1/0/f101d88b43c71728966d40a88c567f68.png)
Most térjünk rá a 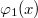 alapállapotú elektron impulzusának a megmérésre. Mivel az elektron energiája ebben az állapotban egy pontos érték és definíció szerint
alapállapotú elektron impulzusának a megmérésre. Mivel az elektron energiája ebben az állapotban egy pontos érték és definíció szerint 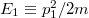 , így adódik, hogy
, így adódik, hogy
![\[ \pm p_1 = \pm\sqrt{2mE_1} = \hbar \left(\pm k_1 \right) = \pm \hbar k_1. \]](/images/math/9/a/2/9a2a3887c61e26b00400082ac734f757.png)
A kétféle előjel azt jelenti, hogy az impulzus (vektor lévén) előjeles mennyiség. Hiszen az elektron az  tengely mentén vagy „balról jobbra”, vagy pedig ezzel ellentétes irányban „jobbról-balra” haladhat.
tengely mentén vagy „balról jobbra”, vagy pedig ezzel ellentétes irányban „jobbról-balra” haladhat.
Megjegyzés: Mint azt tudjuk, egydimenziós esetben nem szoktuk használni a vektor jelet (például 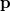 ). Helyette a vektor abszolút értéke elé tett
). Helyette a vektor abszolút értéke elé tett 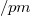 előjellel fejezzük ki a vektor irányát.
előjellel fejezzük ki a vektor irányát.
Mindez nem érinti az állapotfüggvény fizikai jelentését, hiszen
![\[ \varphi_1(x) = \sqrt{\frac{2}{L}} \sin(\pm k_1 x) = \pm\sqrt{\frac{2}{L}}\sin(k_1 x), \]](/images/math/c/2/5/c25a0d1125752e217d3eec3a68756b8a.png)
és így
![\[ \left| \varphi_1(x) \right|^2 = \left| \pm\sqrt{\frac{2}{L}} \sin(k_1 x) \right|^2 = \frac{2}{L} \sin^2 (k_1 x). \]](/images/math/b/5/b/b5bff3a1f3885f5f67c4bb571ea14317.png)
Azaz fizikailag ugyanarról az állapotról van szó.
A mozgás szimmetriájából következően nyugodtan feltételezhetjük, hogy megmérve a 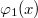 alapállapotú elektron impulzusát, egyforma valószínűséggel fogunk nála „balról-jobbra”, illetve „jobbról-balra” történő mozogást detektálni.
alapállapotú elektron impulzusát, egyforma valószínűséggel fogunk nála „balról-jobbra”, illetve „jobbról-balra” történő mozogást detektálni.
A valószínűségek nyelvén kifejezve ez azt jelenti, hogy
![\[ P(+\hbar k) = P(-\hbar k) = \frac{1}{2}. \]](/images/math/2/2/5/22557fffa4df06b334c7f207c9a64a58.png)
Az impulzus átlagértékére nyilvánvalóan az adódik, hogy
![\[ \left< p_x \right> = P(+\hbar k)(+\hbar k) + P(-\hbar k)(-\hbar k) = +\frac{1}{2}\hbar k = 0. \]](/images/math/3/d/a/3dad3e61dac2b8def86aaeba6407bdb8.png)
Az impulzus négyzetének az átlaga pedig
![\[\begin{aligned} \left< p_x^2 \right> &= P(+\hbar k)(+\hbar k)^2 + P(-\hbar k)(-\hbar k)^2 = \\ &= +\frac{1}{2}(+\hbar k)^2 + \frac{1}{2}(-\hbar k)^2 = \\ &= (\hbar k)^2. \end{aligned}\]](/images/math/a/c/8/ac82b9b31e3bca4e92ebda8b704f469a.png)
Az impulzus mérésének a szórása tehát
![\[ \Delta p_x = \sqrt{\left< p_x^2 \right> - \left< p_x \right>^2} = \sqrt{(\hbar k_1)^2 - 0} = \hbar k_1 = \hbar\frac{\pi}{L}. \]](/images/math/0/a/b/0ab500cc4a4e719cb952bdea43ba85a9.png)
Azaz végül is kapjuk, hogy
![\[\begin{aligned} \Delta p_x \Delta x &= \hbar \frac{\pi}{L} L \sqrt{\frac{1}{12} - \frac{1}{2\pi^2}} = \hbar\sqrt{\frac{\pi^2}{12} - \frac{1}{2}} = \\ &= \hbar\sqrt{0,8224 - 0,5} = \\ &= \hbar \cdot 0,5678 \geq \frac{\hbar}{2}. \end{aligned}\]](/images/math/7/9/2/79295e9886ec7f2f510a682724eb46c2.png)
Tehát a Heisenberg-féle határozatlansági reláció valóban teljesül.
Kimondhatjuk tehát, hogy az egyszerre történő mérés ugyanabban az állapotban történő sok (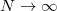 ) elemi mérést jelent. A mérés pontosságán pedig sok elemi mérés statisztikus eredményeiből számított szórásokat kell érteni.
) elemi mérést jelent. A mérés pontosságán pedig sok elemi mérés statisztikus eredményeiből számított szórásokat kell érteni.
A mérés elvégzése az előzőekben megadott „műszerrel” a következő módon történhet. Vegyük a részecskedetektorunkat és lássuk el olyan mérőfejjel, amelyik megkülönböztetve detektálja a „jobbról”, illetve a „balról” érkező elektronokat. Ezek után a 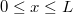 mentén, apró lépésekkel mozgatva vigyük végig a detektort a doboz belsejében. Jegyezzük fel, hogy az egyes
mentén, apró lépésekkel mozgatva vigyük végig a detektort a doboz belsejében. Jegyezzük fel, hogy az egyes  pontokban hány „jobbról” érkező (azaz
pontokban hány „jobbról” érkező (azaz 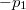 impulzusú) és hány „balról” érkező (azaz
impulzusú) és hány „balról” érkező (azaz 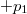 impulzusú) elektront detektáltunk.
impulzusú) elektront detektáltunk.
Mindig tudunk „kellően sok”  pontban és ott „megfelelően sokszor” mérni, hogy (az adott
pontban és ott „megfelelően sokszor” mérni, hogy (az adott  hosszúságskálán) az elektron „helymérését” már folytonosnak lehessen tekinteni. Azaz, hogy kellő pontossággal megkapjuk a
hosszúságskálán) az elektron „helymérését” már folytonosnak lehessen tekinteni. Azaz, hogy kellő pontossággal megkapjuk a 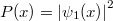 folytonos valószínűségeloszlást.
folytonos valószínűségeloszlást.
Nyilvánvaló, hogy a jelen állapotban az „impulzusmérés” diszkrét eloszlást eredményez, hiszen vagy csak 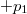 vagy csak
vagy csak 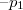 értéket detektálhatunk. Természetesen mindvégig biztosítani kell, hogy a dobozban mindig legyen
értéket detektálhatunk. Természetesen mindvégig biztosítani kell, hogy a dobozban mindig legyen 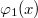 alapállapotú elektron.
alapállapotú elektron.
A mérés eredményét az alábbi ábrán láthatjuk.
Bejelöltük az előzőekben elmondott „helytelen mérés” hisztogramját is.
Összefoglalásul megadjuk a Heisenberg-féle határozatlansági reláció (jelen esetre vonatkozó) „precíz” megfogalmazását:
- Egy részecske helyének és impulzusának egy adott állapotban történő mérésekor a mérések négyzetes szórásának a szorzata nagyobb vagy egyenlő, mint
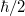 .
.
Ennek értelmében tehát a Természetben létezik olyan állapotú elektron, amelynek a helyét tetszőlegesen kicsiny szórással (pontossággal) meg tudjuk mérni (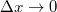 ), de akkor ebben az állapotban az impulzusmérés nagyon nagy szórást fog mutatni (
), de akkor ebben az állapotban az impulzusmérés nagyon nagy szórást fog mutatni (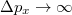 ). Hasonlóképpen létezik olyan állapot is, amelynél ez éppen fordítva van, azaz amikor az impulzusnak van egy határozott, „pontos” értéke (
). Hasonlóképpen létezik olyan állapot is, amelynél ez éppen fordítva van, azaz amikor az impulzusnak van egy határozott, „pontos” értéke (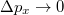 ) és az elektron helymérése mutat nagy eltéréseket (
) és az elektron helymérése mutat nagy eltéréseket (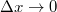 ). Olyan állapot azonban nem létezik a természetben, amely esetén az elektronnak mind a helye, mind pedig az impulzusa tetszőlegesen kicsiny szórással mérhető (
). Olyan állapot azonban nem létezik a természetben, amely esetén az elektronnak mind a helye, mind pedig az impulzusa tetszőlegesen kicsiny szórással mérhető (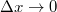 és
és 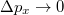 ).
).
A kvantummechanikai szemlélet „ismeretelméleti” vonatkozásai
(O. L. szubjektív eszmefuttatása, amely lehet, hogy nem is olyan szubjektív (Ars Poetica)!)
Az emberi megismerés korlátoltsága (agnoszticizmus) vagy korlátlansága (gnoszticizmus) örök elvi problémája (volt) a Filozófiának.
A Heisenberg-féle határozatlansági reláció a klasszikus méréseknél megszokott szemlélet szerint meglehetősen „furcsa” állítás. Hiszen a klasszikus mechanikában a mérés célja mindig is a mérendő mennyiség minél pontosabb meghatározása volt. A mérés pontosságát a mérési eljárás és a mérőműszer egyedi sajátosságának tekintettük, és így a klasszikus szemlélet szerint az objektív valóság ettől független kell, hogy legyen. Ezzel szemben a Kvantummechanikában a mérés pontossága a Valóság szerves részeként jelenik meg.
Mindez természetesen semmiféle „agnosztikus” világszemléletet nem sugall. Pusztán ismét csak arról van szó, hogy a mikrorészecskék nem úgy viselkednek, mint ahogyan azt a makroszkopikus világban tapasztaltak szerint elvárnánk.
A mikrovilág objektumait teljesen másfajta törvények irányítják. Az itteni világot a saját törvényei szerint kell és lehet „megérteni”. Ehhez azonban nem alkalmasak a hétköznapok megszokott fogalmi képei. Ez a Kvantummechanika világa, amelyet ugyanolyan szigorú törvények uralnak, mint a makroszkopikus világét. Mindez pedig a megszokott gondolkodás számára teljesen „furcsa”, és furcsaságában „idegen”.
Az „emberi méretskálán” az érzékszerveink alapján kialakult „szemléletünk” rabjai vagyunk Ettől nem tudunk, de nem is kell megszabadulni. Hiszen mi magunk is éppen a megismerni kívánt Természeti Törvények következtében létezünk. „Szerencsénkre” az absztrakciós készségünk, azaz a Matematika nyelvezete átsegít minket minden nehézségen.
A természettudományos megismerést tehát legjobb egy folyamatként (és nem egy állapotként) definiálni. A megalkotott elméleti modelljeink egyre pontosabbak, és ennek a pontosságnak nincsen elvi korlátja. Ebben az értelemben a természettudomány inkább gnosztikus (azaz megismerhetőség-párti). Bár azt is tudjuk, hogy a Modell soha nem ekvivalens a Valósággal, és így ebben az értelemben agnosztikusak vagyunk.
Ezt a „dialektikát” (a dialektikus gondolkodás „atyja” Hegel volt!) talán így fogalmazhatnánk meg legtalálóbban:
- a Természet megismerhető, bár soha nem fogjuk megismerni! Hiszen az Emberi Civilizáció várhatóan véges élettartama Objektív Természeti Törvénynek tűnik! (O. L.)
A megismerés folyamata nem ütközik semmiféle korlátba. Azonban ahogyan egyre „távolodunk” a megszokott világunk tapasztalati szintjétől (egyre kisebb, vagy egyre nagyobb méretek felé, vagy az egyre nagyobb sebességek birodalmába), a Természet viselkedéséről nyert információkhoz egyre „drágábban” jutunk.
A megismerés folyamata nem áll meg! Az emberi kíváncsiság és intellektuális kalandvágy egyre „idegenebb és izgalmasabb” tájakra vezet bennünket. A Természet „végtelen bonyolultsága” és az a „Rend”, amely ebben felismerhető, az egyre „hűbb” megismerés vágyával töltheti meg „arasznyi létünket”. Ez pedig egy értelmes Célként jelenhet meg az Emberiség amúgy „céltalan” élettörténetében!
Kiegészítő megjegyzések
- Hibás dolog lenne a kvantummechanikai szemlélet minden „létező dologra” történő általánosítása. A Kvantummechanika az atomnál is kisebb (ún. szubatomi) részecskék dinamikáját megadó tudomány. A Newton-féle mechanika a makroszkopikus testek viselkedését adja meg. Mindkét elmélet igaz a maga méretskáláján, de elveszti értelmét ha ebből kilépünk. A Newtoni mechanikánál ez „természetes”, hiszen az atomi méretekben való kudarca vezetett el minket a kvantummechanikai törvények felismeréséhez. De a dolog „fordítva” is igaz: makroszkopikus testek esetén soha nem tapasztalunk „kvantumos” effektusokat. Például soha nem tapasztaltuk még az „egyenletes mozgás” és az „egyenletesen gyorsuló mozgás” szuperpozícióját, valamint a falnak sem tanácsos nekimenni, mert az „alagúteffektus” ebben a mérettartományban gyakorlatilag soha nem fordulhat elő.
- A természettudományos megismerés stratégiája az elmúlt két és félezer év tapasztalata alatt fejlődött ki és alakította ki „mai” formáját. Sikerét az alkalmazhatósága igazolja, melynek eredménye a XXI. század technikai civilizációja. Számtalan működő eszközt alkottunk meg, amely körülvesz minket és átalakította életünket. A természeti törvények megismerésének sikerét így a mindennapokban (is) tapasztalhatjuk. A Kvantummechanika egyik alapvető jellegzetessége a Heisenberg-féle határozatlansági reláció. Ugyanez a Kvantummechanika jelenti a mai elektronikai ipar elméleti alapjait is. Ami a klasszikus fogalmak szintjén a „korlátozott” megismerhetőség benyomását kelti, az a gyakorlati alkalmazás területén tökéletesen alkalmas a mikrofizikai jelenségeken alapuló eszközök adott célú megtervezéséhez és megépítéséhez. Mindez pedig a Természet megismerésének adekvát voltát közvetlenül és tényszerűen igazolja.
A korrespondencia-elv teljesülése potenciáldoboz esetén
Láttuk, hogy a kvantummechanikában a részecske megtalálási valószínűségét tudjuk meghatározni. Az egyszerűség végett most csak egydimenziós esetet vizsgálunk. Az eredményünk „értelemszerűen” általánosíthatók három dimenzióra is. Ekkor, mint azt tudjuk:
![\[ P_{\rm KM} = \left| \psi(x) \right|^2. \]](/images/math/d/b/2/db2485bc8784c9b839d24e9383429136.png)
Ennek a korrekt értelmezéséhez hozzátartozik a klasszikus eredményekkel való összehasonlítás is. A klasszikus mechanikában egy pont megtalálási valószínűségét a következő „természetes” módon érdemes definiálni. Annak a valószínűsége, hogy egy részecskét a 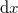 tartományban megtalálunk azzal a
tartományban megtalálunk azzal a 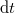 időtartammal arányos, amannyit ott eltölt. Azaz:
időtartammal arányos, amannyit ott eltölt. Azaz: 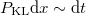 . Ennek megfelelően írható, hogy
. Ennek megfelelően írható, hogy
![\[ P_{\rm KL} = A_0 \frac{{\rm d} t}{{\rm d} x} = \frac{A_0}{{\rm d}x / {\rm d}t} = \frac{A_0}{\dot{x}}. \]](/images/math/3/8/0/3800c46cde007580ba83f2b94b801059.png)
Az 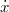 sebesség pedig az
sebesség pedig az  energiájú részecske kinetikus energiájából meg tudjuk határozni:
energiájú részecske kinetikus energiájából meg tudjuk határozni:
![\[ \dot x = \sqrt{\frac{2}{m} \left[ E - V(x) \right] }. \]](/images/math/a/1/1/a117ddbed7bdd1876462112c40f33f6f.png)
Ezzel pedig a keresett valószínűség(sűrűség):
![\[ P_{\rm KL} (x) = \frac{A}{\sqrt{E - V(x)}}. \]](/images/math/d/b/1/db11c2b4b04d7b1cdc5ed790a9ed8441.png)
Az itt szereplő  állandót a valószínűségre vonatkozó normálási feltételből határozzuk meg, azaz:
állandót a valószínűségre vonatkozó normálási feltételből határozzuk meg, azaz:
![\[ \int_{-\infty}^{+\infty} P_{\rm KL} \, {\rm d} x = A \int_{-\infty}^{+\infty} \frac{1}{\sqrt{E - V(x)}} \, {\rm d} x = 1. \]](/images/math/1/6/d/16d6e088ba377aeef3ef10786a6641bf.png)
Az egydimenziós potenciáldobozban mozgó részecske a klasszikus tárgyalásban két fal között pattogó tömegpontnak felel meg. Az  hosszúságú doboz belsejében a potenciális energia állandó (nevezetesen zérus), így a részecskére nem hat erő. Ezért a sebessége állandó. Ebből az következik, hogy a tömegpont mindenhol ugyanakkora valószínűséggel található meg. Tehát
hosszúságú doboz belsejében a potenciális energia állandó (nevezetesen zérus), így a részecskére nem hat erő. Ezért a sebessége állandó. Ebből az következik, hogy a tömegpont mindenhol ugyanakkora valószínűséggel található meg. Tehát 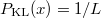 , hiszen valóban
, hiszen valóban
![\[ \int_0^L P_{\rm KL} (x) \, {\rm d} x = \int_0^L \frac{1}{L} \, {\rm d} x = 1. \]](/images/math/0/b/1/0b1de88653e94b6a48fd27140d64519d.png)
Az állapotfüggvény (hullámfüggvény) ismeretében a részecske megtalálási valószínűsége is meghatározható:
![\[ P_{\rm KV} (x) = \left| \psi_n(x) \right|^2 = \frac{2}{L} \sin^2 \left( n \frac{\pi}{L} x \right). \]](/images/math/e/d/c/edc3455ba4882a0140b86819e37d4d1a.png)
A részecske energiája pedig
![\[ E_n = E_0 n^2, \quad n = 1,2,3,... . \]](/images/math/1/2/8/1289197ec3a7bddf63719375ddc8bee4.png)
Eredményül tehát azt kaptuk, hogy a kvantummechanikai valószínűségsűrűség a klasszikus körül oszcillál, méghozzá annál nagyobb térfrekvenciával, minél nagyobb a részecske energiája. Ez az észrevételünk általában is igaznak fog bizonyulni. Ezek a kvantummechanikai eredmények első pillantásra meglehetősen idegenek a klasszikus szemléletünk számára.
A makroszkopikus világban a newtoni fizika eredményeit tapasztaljuk. Ezért joggal elvárhatjuk, hogy a kvantummechanika valamiképpen adja vissza a klasszikus mechanika eredményeit (ezt nevezzük makroszkopikus határesetnek). Érdemes tehát ezt megvizsgálni ebben a jelenlegi, igen egyszerű és szemléletes esetben. A klasszikus határeset a mikroszkopikus energiaszintekhez képest nagy(?) energiát jelent. Ez azt jelenti, hogy a klasszikus mechanikával tárgyalható részecske 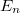 energiája sokkal nagyobb, mint az alapállapoti
energiája sokkal nagyobb, mint az alapállapoti 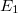 energia (az első energiaszint). Azaz az
energia (az első energiaszint). Azaz az  kvantumszám sokkal nagyobb, mint 1. A kvantummechanika sajátossága az energiaszintek kvantáltsága. Azaz
kvantumszám sokkal nagyobb, mint 1. A kvantummechanika sajátossága az energiaszintek kvantáltsága. Azaz
![\[ \Delta E_n = E_{n+1} - E_n \neq 0. \]](/images/math/5/3/8/538613410940c9ca858efc6ecdb20a3c.png)
Ezen 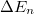 -nek így „önmagában” nincsen sok értelme. Értelmetlen dolog arról beszélni, hogy egy mért fizikai mennyiség „nagy” vagy „kicsi”. Minden mennyiség valamihez képest kicsi vagy nagy, ezért az energiaszintek kvantáltságát a „relatív kvatáltsággal” kell jellemeznünk, azaz
-nek így „önmagában” nincsen sok értelme. Értelmetlen dolog arról beszélni, hogy egy mért fizikai mennyiség „nagy” vagy „kicsi”. Minden mennyiség valamihez képest kicsi vagy nagy, ezért az energiaszintek kvantáltságát a „relatív kvatáltsággal” kell jellemeznünk, azaz 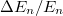 . Jelen esetben ennek értéke:
. Jelen esetben ennek értéke:
![\[ \frac{\Delta E_n}{E_n} = \frac{E_{n+1} - E_n}{E_n} = \frac{E_0 \left[ (n+1)^2 - n^2 \right] }{E_0 n^2} = \frac{2n + 1}{n^2}. \]](/images/math/8/2/0/820ad61ad3a89104fab0d62b702a9cc4.png)
„Nagy” energiaszinteknél, 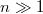 esetén írható, hogy
esetén írható, hogy
![\[ \frac{\Delta E_n}{E_n} = \frac{2}{n} \to 0, \quad \text{ha} \quad n \to \infty. \]](/images/math/9/1/1/91195ebc36af58d09c97686771b0b0fc.png)
Minden makroszkopikus mérés csak valamilyen véges relatív pontossággal végezhető el. Ez a mérőműszerek tulajdonsága. A makroszkopikus fizika szerint egy mérőműszer pontossága elvileg tetszőlegesen csökkenthető, de mindig véges marad. Ennek pusztán technikai okai vannak. Tehát egy „energiamérő” műszer 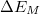 pontossága mindig véges. A fentiek értelmében minden (tetszőlegesen kicsiny)
pontossága mindig véges. A fentiek értelmében minden (tetszőlegesen kicsiny) 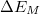 értékhez található akkora
értékhez található akkora 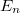 energiaszint, amely esetén a
energiaszint, amely esetén a 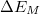 tartományban már nagyon sok diszkrét energiaszint esik. Így makroszkopikus esetben az energia kvantáltsága kimérhetetlen lesz, azaz folytonos energiaskálát tapasztalunk.
tartományban már nagyon sok diszkrét energiaszint esik. Így makroszkopikus esetben az energia kvantáltsága kimérhetetlen lesz, azaz folytonos energiaskálát tapasztalunk.
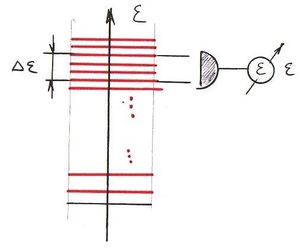
Energia |
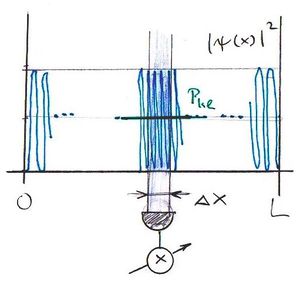
Állapotfüggvéy |
| Korrespondencia-elv potenciádoboz esetén | |
Az állapotfüggvények szempontjából a nagy kvantumszám nagyon sűrű térbeli oszcillációt jelent. Ekkor a makroszkopikus helymérés pontatlansági tartományában a hullámfüggvénynek igen nagyszámú oszcillációja esik. Így a kvantummechanikai megtalálási valószínűség erre a tartományra vett átlaga éppen a klasszikus értéket adja. Azaz a klasszikus mechanika eredményeit fogjuk a makroszkopikus hosszúságskálán is tapasztalni.
Azt a kívánalmat, hogy az általánosabbnak és alapvetőbbnek tekintett kvantummechanika határesetben adja vissza a klasszikus mechanika eredményeit, korrespondencia-elvének hívjuk és gyakran használjuk eredményeink globális ellenőrzésére. Azaz egy mikrofizikai modell helyességének ez szükséges feltétele.
A háromdimenziós potenciáldoboz
A háromdimenziós potenciáldoboz az egydimenziósnak a kézenfekvő általánosítása. Egy  élhosszúságú kocka alakú tartomány belsejében a potenciális energia zérus, azon kívül pedig végtelen. Ez a legegyszerűbb háromdimenziós probléma, amely analitikus módon megoldható.
élhosszúságú kocka alakú tartomány belsejében a potenciális energia zérus, azon kívül pedig végtelen. Ez a legegyszerűbb háromdimenziós probléma, amely analitikus módon megoldható.
Az egydimenziós esetben láttuk, hogy egy mikrorészecske (pl. az elektron) nem tud behatolni olyan térrészbe, ahol a potenciális energia végtelen nagy. Ez nyilván érvényes a jelen esetben is: 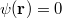 az
az 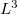 potenciáldobozon kívül (azaz, ha
potenciáldobozon kívül (azaz, ha 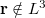 ). Így a Schrödinger-egyenletet csak a dobozon belül kell megoldanunk. Mivel az
). Így a Schrödinger-egyenletet csak a dobozon belül kell megoldanunk. Mivel az 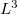 dobozon belül a potenciál
dobozon belül a potenciál 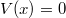 , ezért írható, hogy
, ezért írható, hogy
![\[ \frac{\hbar^2}{2m} \left( \frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2} \right) = E\psi. \]](/images/math/2/2/a/22a4835840c2d1a1afde1e896aa65202.png)
A szimmetria miatt feltehetjük, hogy az egyenletet kielégítő 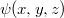 állapotfüggvény az egydimenziós potenciáldoboz általánosításaként adódó „állóhullámok” lesznek, azaz
állapotfüggvény az egydimenziós potenciáldoboz általánosításaként adódó „állóhullámok” lesznek, azaz
![\[ \psi(x,y,z) = \sqrt{\frac{8}{L^3}} \cdot\sin\left( \frac{n_x \pi}{L}x \right) \cdot\sin\left( \frac{n_y \pi}{L}y \right) \cdot\sin\left( \frac{n_z \pi}{L}z \right), \quad n_x, n_y, n_z = 1,2,3,... . \]](/images/math/9/a/d/9adca38e1e3b2b69ece30eec150a77a5.png)
Közvetlen behelyettesítéssel (a parciális deriválások elvégzése után) azt kapjuk, hogy ez az állapotfüggvény valóban megoldása a Schrödinger-egyenletnek és az energiára az
![\[ E = \frac{\hbar^2 \pi^2}{2mL^2} \left( n_x^2 + n_y^2 + n_z^2 \right) \equiv E_0 \left( n_x^2 + n_y^2 + n_z^2 \right) \]](/images/math/d/e/0/de0e05f593ffab8e0e9fa3acd3b7f1a2.png) |
(1) |
kifejezés adódik. Az egydimenziós doboznál tanultakhoz képest a hasonlóságokon túl van némi eltérés is. Az alapállapoti energiára most 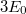 adódik, hiszen ebben az esetben
adódik, hiszen ebben az esetben 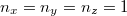 .
.
Nézzünk két egyszerű számszerű példát a szemléletesség végett!
Zárjuk be az elektront egy atomnyi méretű potenciáldobozba (azaz 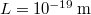 )! Ekkor az elektron alapállapoti (kinetikus) energiája
)! Ekkor az elektron alapállapoti (kinetikus) energiája 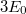 lesz. Ennek értékére
lesz. Ennek értékére 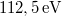 adódik. Ez az atomok és molekulák világában elég nagy érték.
adódik. Ez az atomok és molekulák világában elég nagy érték.
Szokásos még ún. „félklasszikus” számolásokat is elvégezni. Jelen esetben kiszámolható, hogy mekkora lenne annak a pontszerű (klasszikus mechanika szerint mozgó) elektronnak a sebessége, amelyiknek a kinetikus energiája éppen az imént kapott 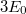 volna. Erre a sebességére
volna. Erre a sebességére 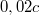 adódik.
adódik.
A középiskolai tanulmányainkból tudjuk, hogy az atommagok [elektron  –bomlásakor] a magból elektron távozik. Számítsuk ki, hogy mekkora lenne egy atommagnyi dobozba zárt elektron alapállapoti kinetikus energiája és a sebessége. (1) alapján kapjuk, hogy
–bomlásakor] a magból elektron távozik. Számítsuk ki, hogy mekkora lenne egy atommagnyi dobozba zárt elektron alapállapoti kinetikus energiája és a sebessége. (1) alapján kapjuk, hogy
![\[ E_{\rm alap} = C_0 \frac{3}{L^2} = 1,13\cdot 10^{12} \, {\rm eV} = 1,13\cdot 10^6 \, {\rm MeV}. \]](/images/math/7/f/4/7f45f433411303c947fec025f00f0b3d.png)
Ez sokkal nagyobb, mint a  -sugárzás elektronjainak a maximális energiája. (Ennek tipikus értéke
-sugárzás elektronjainak a maximális energiája. (Ennek tipikus értéke 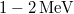 !) Az elektron sebességére pedig:
!) Az elektron sebességére pedig:
![\[ v_{\rm alap} = \sqrt{\frac{2E_{\rm alap}}{m}} \approx 1000 c \]](/images/math/0/3/f/03fbac058c18b55d956e8c2d39002217.png)
adódik. Ez nyilvánvalóan fizikailag lehetetlen. Az eredmény azt mutatja, hogy itt már a relativisztikus effektusok messze nem hanyagolhatóak el. Mivel a Schrödinger-egyenlet nem relativisztikus, így nyilván nem adhat még helyes becslést sem ebben az esetben.
Végül is arra a következtetésre kell jutnunk, hogy szabad elektron nem lehet az atommagban. Valójában, a neutron bomlik el protonra, elektronra és antineutrinóra. Ez a jelenség azonban már nem magyarázható az eddig használt kvantummechanikai modellel. Itt már a „részecskefizika” fogalomrendszerét és matematikai eszközeit kell alkalmazni, amely (formáját tekintve) meglehetősen eltér az eddig tanultaktól.
Mint azt láttuk, egy dobozba zárt elektron állapotát és energiáját három egész (kvantum)számmal jellemezhetjük. Különböző 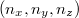 kvantumszám-hármasok különböző állapotfüggvényeket adnak meg. Ugyanakkor (1) alapján látható, hogy létezhetnek olyan különböző kvantumszám-hármasok, amelyek ugyanakkora energiát adnak. Azaz előfordulhat, hogy egy energiaértékhez (energiaszinthez) több különböző állapotfüggvény tartozik. Ezt nevezzük az állapotok elfajulásának, vagy degenerációnak. A degeneráció fokát pedig az adott energiaszinthez tartozó különböző állapotok számával definiáljuk.
kvantumszám-hármasok különböző állapotfüggvényeket adnak meg. Ugyanakkor (1) alapján látható, hogy létezhetnek olyan különböző kvantumszám-hármasok, amelyek ugyanakkora energiát adnak. Azaz előfordulhat, hogy egy energiaértékhez (energiaszinthez) több különböző állapotfüggvény tartozik. Ezt nevezzük az állapotok elfajulásának, vagy degenerációnak. A degeneráció fokát pedig az adott energiaszinthez tartozó különböző állapotok számával definiáljuk.
Erre már láttunk példát a hidrogén atom esetében. Itt az energiát az  főkvantumszám határozza meg, de az elektronállapot megadásához az
főkvantumszám határozza meg, de az elektronállapot megadásához az  -en kívül még az
-en kívül még az  mellékkvantumszám és az
mellékkvantumszám és az 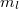 mágneses kvantumszám is szükséges.
mágneses kvantumszám is szükséges.
Egy adott energiájú héjhoz tehát többféle (nevezetesen 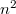 db.) pályaállapot tartozik. Egy adott pályaállapothoz pedig két spinállapot (
db.) pályaállapot tartozik. Egy adott pályaállapothoz pedig két spinállapot (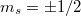 ) is tartozik. Ezért a degeneráció foka valójában
) is tartozik. Ezért a degeneráció foka valójában 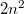 lesz.
lesz.
Térjünk vissza a térbeli potenciáldobozhoz!
Az állapotfüggvények és az energiaszintek azonosítása a kvantumszámokon keresztül történik. Emiatt a szokásos jelölés az, hogy a három kvantumszám értékét az állapotfüggvény alsó indexébe írjuk, pl. 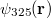 . Ez egy olyan állapotot jelöl, amelynek kvantumszámai rendre
. Ez egy olyan állapotot jelöl, amelynek kvantumszámai rendre 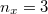 ,
, 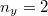 ,
, 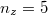 . Az energiája pedig nyilvánvalóan
. Az energiája pedig nyilvánvalóan 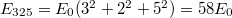 . Triviálisan adódik, hogy pl. a
. Triviálisan adódik, hogy pl. a 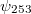 és a
és a 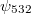 állapotok energiája is ennyi. Az is látható, hogy jelen esetben
állapotok energiája is ennyi. Az is látható, hogy jelen esetben 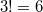 ilyen különböző állapotot találhatunk, amelyek energiája
ilyen különböző állapotot találhatunk, amelyek energiája 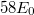 .
.
Az első öt energiaszinthez tartozó degenerált (elfajult) állapot:
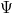
|
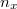
|
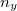
|
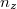
|

|
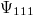
|

|

|

|
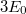
|
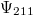
|

|

|

|
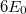
|
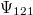
|

|

|

|
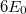
|
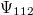
|

|

|

|
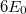
|
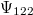
|

|

|

|
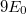
|
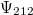
|

|

|

|
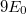
|
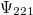
|

|

|

|
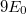
|
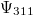
|
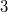
|

|

|
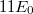
|
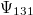
|

|
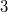
|

|
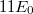
|
|

|

|
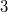
|
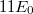
|
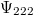
|

|

|

|
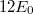
|
Az egyes (degenerált) állapotokhoz tartozó megtalálási valószínűségsűrűség-függvényt ábrázoltuk a következő ábrákon. Az egy- és kétdimenziós eseteket is közöltük, mert a többi struktúra megértéséhez fontos lesz.
Mint azt láttuk, egy dimenzióban:
![\[ \psi_n (x) = \sqrt{\frac{2}{L}} \sin\left( n \frac{\pi}{L} x \right) \quad \text{és} \quad n = 1,2,3, ... . \]](/images/math/e/7/1/e716f88c2db612716d346a97f6d260ef.png)
Az ábrán a 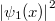 és
és 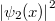 valószínűségsűrűségek láthatók. A „csomópont(ok)” (
valószínűségsűrűségek láthatók. A „csomópont(ok)” (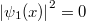 ) helyét is bejelöltük.
) helyét is bejelöltük.
A kétdimenziós potenciáldobozban lévő elektron állapotfüggvényei a következők:
![\[ \psi_{n_x,n_y}(x) = \sqrt{\frac{4}{L^2}} \sin\left( n_x \frac{\pi}{L} x \right) \sin\left( n_y \frac{\pi}{L} y \right) \quad \text{és} \quad n_x, n_y = 1,2,3, ... . \]](/images/math/9/5/2/95261be128b826065150fe30bb63c933.png)
Az ábrán 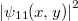 , valamint
, valamint 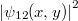 és
és 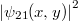 , illetve a csomóvonalak (
, illetve a csomóvonalak (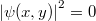 ) helyzete látható:
) helyzete látható:
A háromdimenziós esetben az állapotfüggvények általános matematikai alakja a következő:
![\[ \psi_{n_x,n_y,n_z}(x) = \sqrt{\frac{8}{L^3}} \sin\left( n_x \frac{\pi}{L} x \right) \sin\left( n_y \frac{\pi}{L} y \right) \sin\left( n_z \frac{\pi}{L} z \right) \quad \text{és} \quad n_x, n_y, n_z = 1,2,3, ... . \]](/images/math/6/8/0/68099d2e7ffb04e41f9bb015952bab30.png)
A háromdimenziós esetben az ábrázolás már nem ilyen egyszerű. Ekkor „alkalmasan” választott szintfelületeket használunk. Az ábrán az 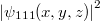 alapállapot és a második energiaszint állapotai,
alapállapot és a második energiaszint állapotai, 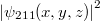 ,
, 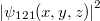 és
és 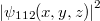 láthatók. A csomósíkok helyzete (
láthatók. A csomósíkok helyzete (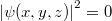 ) jól tükrözi az állapotok szimmetriatulajdonságait.
) jól tükrözi az állapotok szimmetriatulajdonságait.
Nagyon magas energiaszintek degenerációs fokának a kiszámítása már nem egy egyszerű számelméleti feladat. Látható ugyanis, hogy a permutációkon kívül elvileg lehet más egész számhármas is, amelyek négyzetösszege ugyanazt az értéket adja (pl. 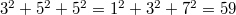 ). Ezek megkeresése nem könnyű, de mint azt majd látni fogjuk, nem is szükséges.
). Ezek megkeresése nem könnyű, de mint azt majd látni fogjuk, nem is szükséges.
A degeneráció fokának a közelítő megadása nagy energiaszintek esetén igen egyszerű. Erről a fémek szabadelektron-elméletének a kapcsán fogunk beszélni.
A szimmetriák szerepe a (modern, atom-) Fizikában
Az elektronállapotok degenerációja a vizsgált rendszer (térbeli) szimmetriájának a következménye. Ez a kapcsolat olyan szoros és jellegzetes, hogy a rendszer szimmetriájának az ismeretében következtetni lehet az állapotfüggvények matematikai alakjára is. Ez a fontos észrevétel a magyar származású Wigner Jenő érdeme.
Wigner Jenő a kvantummechanika közismerten nagy egyénisége. A szimmetria meggondolásai annyira alapvetőnek bizonyultak, hogy a kidolgozott módszere a későbbiek során a kvantummechanikai számítások (az atomi elektronhéj és az atommagok) fontos eszközévé vált.
A szimmetriatulajdonságok matematikai tárgyalása a csoportelmélets segítségével történik. A csoportelmélet alapjait az 1832-ben, a 21 éves korában párbajban megölt zseniális francia matematikus, Evariste Galois (ejtése: GALOÁ) tette le. A csoportelméletet Galois az ötöd- és magasabb fokú egyenletek algebrai megoldhatatlanságának problémája vizsgálatához teremtette meg, amely azután hamarosan nélkülözhetetlenné vált a matematika egész területén és a XX. századi modern fizikában is.
A wigneri felismerés a csoportelmélet továbbfejlődésének az ösztönzőjévé vált. Mára már egy igen hatékony matematikai apparátust sikerült kiépíteni. Napjainkban a szimmetriacsoportok használata az elemi részek fizikájának alapvető eszközévé vált. („Éjszakánk erdejében sárga láng”)
| William Blake
(1757-1827) |
William Blake
The Ancient of Days |
| „Tigris! Tigris! Éjszakánk
erdejében sárga láng, mely örök kéz szabta rád rettentő szimmetriád?” Ford: Szabó Lőrinc (1900-1957) |

|
Az 1963. évi fizikai Nobel-díjat Wigner Jenő kapta, indoklásul: „az atommagok és az elemi részek elméletének fejlesztéséért, kivált az alapvető szimmetriaelvek felfedezéséért és alkalmazásáért”.
- A matematikának a természettudományok terén való hasznossága a csodával határos. Nincs is rá racionális magyarázat. Mert semmiképpen sem természetes, hogy legyenek "természeti törvények", és még kevésbé kézenfekvő, hogy az ember felfedezhesse őket. Az a tény, hogy a matematika nyelve alkalmas a fizikai törvények megfogalmazására, csodálatos ajándék, amelyet soha nem leszünk képesek igazán megérteni vagy kiérdemelni. (Wigner Jenő)
A következőkben az állapotfüggvény és a rendszer szimmetriájának a kapcsolatát fogjuk szemléltetni a jelenlegi ismereteinknek megfelelő, lehető legegyszerűbb szinten.
Tekintsük a háromdimenziós, kocka alakú potenciáldobozban lévő elektron (részecske) esetét. A rendszer szimmetriája azt jelenti, hogy ha egy geometriai transzformációval (forgatás, tükrözés) a kockát önmagába transzformáljuk, akkor ez semmiféle fizikai változást nem eredményez. Meg fogjuk nézni, hogy mi történik egy állapotfüggvénnyel a szimmetriatranszformációk során.
Egy adott energiaszinthez tartozó 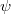 hullámfüggvény ismeretében a részecske
hullámfüggvény ismeretében a részecske 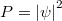 megtalálási valószínűségsűrűsége meghatározható. A
megtalálási valószínűségsűrűsége meghatározható. A 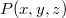 háromváltozós függvény ábrázolására az ún. szintfelületeket használjuk. Szintfelületnek nevezzük azon térbeli pontok összességét, amelyek kielégítik a
háromváltozós függvény ábrázolására az ún. szintfelületeket használjuk. Szintfelületnek nevezzük azon térbeli pontok összességét, amelyek kielégítik a 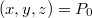 egyenletet. Ezek a pontok egy térbeli felületet adnak. Mármost a
egyenletet. Ezek a pontok egy térbeli felületet adnak. Mármost a 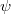 állapotfüggvény ábrázolása esetén felrajzoljuk azt a szintfelületet, amelyen belül az elektron „közel egy” (pl. 95%) valószínűséggel található meg.
állapotfüggvény ábrázolása esetén felrajzoljuk azt a szintfelületet, amelyen belül az elektron „közel egy” (pl. 95%) valószínűséggel található meg.
A potenciáldoboz esetén a 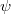 hullámfüggvények matematikai alakja jól ismert. Ezek vizsgálata alapján a következőket vehetjük észre:
hullámfüggvények matematikai alakja jól ismert. Ezek vizsgálata alapján a következőket vehetjük észre:
- alapállapotban minden szimmetriatranszformáció során a
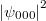 szintfelület önmagába transzformálódik,
szintfelület önmagába transzformálódik,
- a második energiaszinthez tartozó három (degenerált) állapotfüggvény olyan, hogy minden szimmetriatranszformáció során a
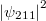 ,
, 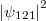 ,
, 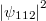 szintfelületek egymásba transzformálódnak.
szintfelületek egymásba transzformálódnak.
A harmonikus lineáris oszcillátor
A (z egydimenziós) harmonikus lineáris oszcillátor esetén a potenciális energia az egyensúlyi helyzettől való eltérés (legyen ez  ) négyzetével arányos. A klasszikus mechanikai tulajdonságai már jól ismertek. A mechanikában széles körben használjuk, aminek oka a következő. Bármely két test közötti kölcsönhatás taszító és vonzó erők együttes fellépésének a következménye. E két erőhatás eredményeként a két test között stabil vagy instabil egyensúlyi állapot jöhet létre.
) négyzetével arányos. A klasszikus mechanikai tulajdonságai már jól ismertek. A mechanikában széles körben használjuk, aminek oka a következő. Bármely két test közötti kölcsönhatás taszító és vonzó erők együttes fellépésének a következménye. E két erőhatás eredményeként a két test között stabil vagy instabil egyensúlyi állapot jöhet létre.
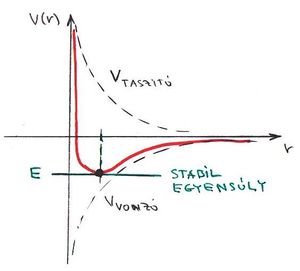
Vonzás + Taszítás = stabil egyensúly |
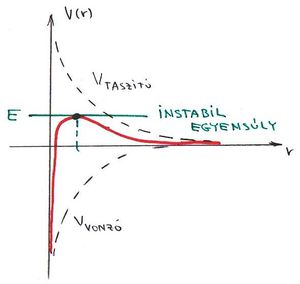
Vonzás + Taszítás = instabil egyensúly |
A továbbiakban minket csak a stabil egyensúlyi állapot érdekel, hiszen ez az egyik szükséges feltétele annak, hogy részecskék sokaságából álló nagy (mechanikai) rendszerek épülhessenek fel. Könnyű belátni, hogy ha rövid távolágon a taszító és nagy távolságokon a vonzó erőhatás dominál, akkor stabil egyensúlyi állapot alakulhat ki. Ebben az esetben a potenciálfüggvénynek az egyensúlyi helyzetben minimuma van. Az egyensúlyi helyzettől való kis kitérések esetén a potenciálfüggvény egy parabolával közelíthető. Azaz a rendszer egy oszcillátornak tekinthető. Ez pedig modellezhető egy  rugóból és egy
rugóból és egy  tömegű pontból álló „oszcillátorral”. A modell akkor korrekt, ha az oszcillátorok (a modell és a valóság) frekvenciája megegyezik.
tömegű pontból álló „oszcillátorral”. A modell akkor korrekt, ha az oszcillátorok (a modell és a valóság) frekvenciája megegyezik.
A klasszikus megoldás jól ismert. Mivel a potenciális energia
![\[ V(x) = \frac{1}{2} Dx^2, \]](/images/math/f/0/d/f0dc16695d14852c384e0e1bc3be1223.png)
ezért a tömegpontra ható erő
![\[ F = -\frac{\rm d}{{\rm d} x}V(x) = -Dx. \]](/images/math/a/6/2/a6258467b0cd1feaa34be630d46d8543.png)
A mozgásegyenlet tehát
![\[ m\ddot{x} = -Dx, \quad \text{azaz} \quad \ddot{x} = -\omega^2 x, \quad \text{ahol} \quad \omega \equiv \sqrt{\frac{D}{m}}. \]](/images/math/0/e/1/0e1579193668e6c7ea3e0b8c24b10442.png)
Az egyenlet megoldása:
![\[ x(t) = a\cdot \sin(\omega t + \alpha), \]](/images/math/3/d/5/3d58d8144564cfad07afe4120ae3ff01.png)
Ahol az  és
és  értékeket a kezdeti feltételek (pl.
értékeket a kezdeti feltételek (pl. 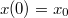 és
és 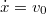 ) határozzák meg. Mivel az oszcillátor konzervatív rendszer, ezért az
) határozzák meg. Mivel az oszcillátor konzervatív rendszer, ezért az  összenergiája a mozgás során állandó:
összenergiája a mozgás során állandó:
![\[ E = \frac{1}{2} m\dot{x}^2 + \frac{1}{2}m\omega^2 x^2. \]](/images/math/9/4/8/948b53145ea7215164367dcbf7294039.png)
Itt most felhasználtuk azt, hogy 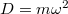 , így formálisan sikerült megszabadulnunk a túlságosan „realisztikus rugótól”. A szélső kitéréseknél (
, így formálisan sikerült megszabadulnunk a túlságosan „realisztikus rugótól”. A szélső kitéréseknél (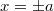 ) a tömegpont sebessége zérus (
) a tömegpont sebessége zérus (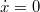 ), tehát az összenergia értékére írható, hogy
), tehát az összenergia értékére írható, hogy
![\[ E = \frac{1}{2} m \omega^2 a^2. \]](/images/math/d/c/6/dc6f19ac219570f9bb428839648af039.png)
Mivel a klasszikus mechanikában az  amplitúdó bármekkora lehet, így az oszcillátor energiája „folytonos spektrumot” ad. (Spectrum latin szó, jelentése: „széles választék, sok lehetőség”.)
amplitúdó bármekkora lehet, így az oszcillátor energiája „folytonos spektrumot” ad. (Spectrum latin szó, jelentése: „széles választék, sok lehetőség”.)
A kvantummechanikai tárgyalás esetén a Schrödinger-egyenletet kell megoldanunk. A potenciális energia helyére ekkor a parabolikus (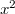 -től függő) függvényt kell beírnunk. Azaz:
-től függő) függvényt kell beírnunk. Azaz:
![\[ -\frac{\hbar^2}{2m} \frac{{\rm d}^2}{{\rm d}x^2}\psi + \frac{1}{2} m \omega^2 x^2 \psi = E\cdot \psi. \]](/images/math/3/e/b/3eb7ca08a4af1bc569be1cc9e4117f1d.png)
Ismeretlen az  energia és a
energia és a 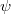 állapotfüggvény. Egyszerű algebrai átalakítással a következő differenciálegyenletet kapjuk:
állapotfüggvény. Egyszerű algebrai átalakítással a következő differenciálegyenletet kapjuk:
![\[ \frac{{\rm d}^2}{{\rm d}x^2}\psi + \left( \frac{2mE}{\hbar^2} - \frac{m^2 \omega^2}{\hbar^2} x^2 \right) \psi = 0. \]](/images/math/b/1/2/b12754ea8d9edb56342b1cdf4a1f1a46.png)
Bár a differenciálegyenlet egyszerűnek látszik, megoldása az eddigi matematikai ismereteink alapján meglehetősen nehéz lenne. Támaszkodhatunk azonban arra, amit a Schrödinger-egyenlet általános matematikai vizsgálata során tapasztaltunk. Láttuk, hogy kötött állapotban az energiaszintek kvantáltak és egydimenziós esetben a 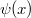 állapotfüggvény valós függvény. Azt is megmutattuk, hogy a „megtalálási valószínűségsűrűség-függvény” (
állapotfüggvény valós függvény. Azt is megmutattuk, hogy a „megtalálási valószínűségsűrűség-függvény” (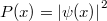 ) „egypúpú”, „kétpúpú”, „hárompúpú" stb. függvény lesz.
) „egypúpú”, „kétpúpú”, „hárompúpú" stb. függvény lesz.
Mivel jelen esetben a potenciális energia szimmetrikus (páros függvény), könnyű belátni, hogy a (valós) állapotfüggvények páros és páratlan függvények lesznek. Ennek bizonyítása igen egyszerű. „Tükrözzük” a rendszerünket, azaz hajtsuk végre a 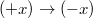 transzformációt. Ekkor
transzformációt. Ekkor
![\[ \frac{{\rm d}^2}{{\rm d}x^2} \to \frac{{\rm d}^2}{{\rm d}(-x)^2} \quad \frac{1}{2}m\omega^2 x^2 \to \frac{1}{2}m\omega^2 (-x)^2 \equiv \frac{1}{2} m \omega^2 x^2. \]](/images/math/a/a/6/aa6c04895d8ebddc6c6461577adf601f.png)
Tehát a Schrödinger-egyenlet alakja nem változik meg. Ekkor viszont az állapotfüggvény 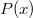 „fizikai tartalmának” sem szabad megváltoznia. Ezért írható, hogy:
„fizikai tartalmának” sem szabad megváltoznia. Ezért írható, hogy:
![\[ P(-x) = P(+x), \quad \text{azaz} \quad \psi(x)^2 = \psi(-x)^2. \]](/images/math/2/f/d/2fd8ab1267065167676cf15695036c4c.png)
Így tehát ha mind a két oldalának a négyzetgyökét vesszük, azt kapjuk, hogy:
![\[ \psi(x) = \pm\psi(-x). \]](/images/math/a/a/3/aa31de63af6b12d78cb1f1c94574c060.png)
Ez pedig éppen a páros és a páratlan függvények definíciója. Ezzel a fenti állításunkat bizonyítottuk.
A legalacsonyabb 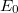 energiaszinthez (az alapállapothoz) tartozó
energiaszinthez (az alapállapothoz) tartozó 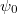 függvény tehát egy „egypúpú” páros függvény kell, hogy legyen. Keressük ezt egy
függvény tehát egy „egypúpú” páros függvény kell, hogy legyen. Keressük ezt egy 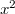 -től függő exponenciális függvény (az ún. Gauss függvény) alakjában. Azaz legyen
-től függő exponenciális függvény (az ún. Gauss függvény) alakjában. Azaz legyen
![\[ \psi_0(x) = A_0 \exp(-\alpha x^2). \]](/images/math/0/e/7/0e77a3a2462d10837580f824e08dc908.png)
Közvetlen behelyettesítéssel nézzük meg, hogy a feltételezésünk helyes-e? Azaz ellenőrizzük, hogy a Gauss függvény tényleg megoldása-e az egydimenziós oszcillátor Schrödinger-egyenletének. Képezni kell 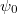 második deriváltját:
második deriváltját:
![\[ \psi_0(x)' = (-2\alpha x) \cdot\psi_0, \quad \psi_0(x)'' = -2\alpha\psi_0 + (-2\alpha x)\cdot \psi_0'. \]](/images/math/a/d/9/ad9bdc188e9885c3766111a001dd0cec.png)
A kettő összevonásával kapjuk, hogy:
![\[\begin{aligned} \psi_0(x)'' &= -2\alpha\psi_0 + (-2\alpha x)(-2\alpha x)\psi_0 = \\ &= -2\alpha\psi_0 + (2\alpha x)^2 \psi_0 = \\ &= \left[ -2\alpha + (2\alpha x)^2 \right] \psi_0. \end{aligned}\]](/images/math/5/9/6/596d2146fd633e1e0e2043be6004d588.png)
Beírva 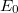 -t és
-t és 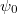 -t a Schrödinger-egyenletbe, adódik, hogy
-t a Schrödinger-egyenletbe, adódik, hogy
![\[ \psi_0'' + \left( \frac{2mE_0}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2} x^2 \right) \psi_0 = 0, \]](/images/math/2/4/3/243250839e14a1e2ec25902380f6b35a.png)
azaz:
![\[ \left[ -2\alpha + (2\alpha x)^2 \right] \psi_0 + \left( \frac{2mE_0}{\hbar^2} - \frac{m^2 \omega^2}{\hbar^2} x^2 \right)\psi_0 = 0.\]](/images/math/3/b/4/3b4a1dfee39d374774e342636e9a69cc.png)
Átrendezés (kiemelés) után kapjuk, hogy:
![\[ \left[ \left( \frac{2mE_0}{\hbar^2} - 2\alpha \right) + \left( 4\alpha^2 - \frac{m^2\omega^2}{\hbar^2} \right) x^2 \right] \psi_0 = 0. \]](/images/math/5/6/1/5615ab7f22d686e2978e1ae7ccc49c05.png)
Ennek a tér minden  pontjában teljesülnie kell. Mivel
pontjában teljesülnie kell. Mivel 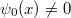 , ezért a másik tényezőnek kell zérusnak lennie, azaz:
, ezért a másik tényezőnek kell zérusnak lennie, azaz:
![\[ \left( \frac{2mE_0}{\hbar^2} - 2\alpha \right) + \left( 4\alpha^2 - \frac{m^2\omega^2}{\hbar^2} \right) x^2 = 0. \]](/images/math/a/7/1/a71b25a446d2dc6a6bea20bda5cffdba.png)
Ez egy polinom, amely csak akkor lesz zérus, ha a polinom minden egyes tagjában az együttható zérus! Azaz
![\[ \frac{2mE_0}{\hbar^2} - 2\alpha = 0 \quad \text{és} \quad 4\alpha^2 - \frac{m^2\omega^2}{\hbar^2} = 0. \]](/images/math/d/d/3/dd3ac099f5bf5a4440677b620613643f.png)
A második egyenletből kapjuk, hogy:
![\[ \alpha = \pm\frac{m\omega}{2\hbar}. \]](/images/math/6/9/8/698c07920902b8d3fff69bd6338a8104.png)
Tudjuk, hogy minden állapotfüggvénynek teljesítenie kell a
![\[ \lim_{x\to\pm\infty} \psi(x) = 0 \]](/images/math/3/2/8/328c65b0b97f2fdb10da26cbe17b6efa.png)
határfeltételt, mert csak ekkor lehetséges a „valószínűségi” értelmezés, azaz csak ekkor teljesülhet a normálási feltétel:
![\[ \int_{-\infty}^{+\infty} \left|^2 \psi(x) \right| \, {\rm d}x = 1. \]](/images/math/3/2/9/32950b41972eb2c47d7ed64d343cead9.png)
Ezért a 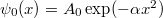 állapotfüggvényben csak az
állapotfüggvényben csak az 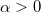 lehetséges. Ezt beírva a fenti
lehetséges. Ezt beírva a fenti 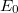 -t tartalmazó egyenletbe, a következő adódik:
-t tartalmazó egyenletbe, a következő adódik:
![\[ \frac{2mE_0}{\hbar^2} - \frac{m\omega}{\hbar} = 0. \]](/images/math/4/6/f/46f319f7d8b11c406d45c83f441909d6.png)
Ezzel megkaptuk az alapállapot energiáját:
![\[ E_0 = \frac{1}{2} \hbar\omega. \]](/images/math/a/9/7/a97f4ecb2eb9a7589fae585ff61debd8.png)
A 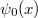 -ben lévő
-ben lévő 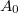 együtthatót a normálási feltételből tudjuk kiszámítani.
együtthatót a normálási feltételből tudjuk kiszámítani.
Tovább is próbálkozhatunk az állapotfüggvények szemléleten alapuló megkonstruálásával. Jelöljük a második energiaszintet 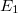 -el és a hozzátartozó állapotfüggvényt
-el és a hozzátartozó állapotfüggvényt 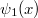 -el! Könnyen belátható, hogy megfelelő szimmetriájú és alakú állapotfüggvényt kapunk a
-el! Könnyen belátható, hogy megfelelő szimmetriájú és alakú állapotfüggvényt kapunk a
![\[ \psi_1(x) = a_1 x \psi_0(x), \]](/images/math/1/8/1/181a72c457c49b23696c94267417c48f.png)
szorzattal, ahol 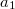 -et a
-et a 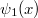 -re vonatkozó normálási feltétel határozza meg.
-re vonatkozó normálási feltétel határozza meg.
Nézzük meg, hogy „eltaláltuk-e” a megoldást, azaz kielégül-e a Schrödinger-egyenlet?
![\[ \psi_1'' + \left( \frac{2mE_1}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2} x^2 \right) \psi_1 = 0. \]](/images/math/f/d/f/fdfaa27c1c849fb33fd2f6514c97afc6.png)
Képeznünk kell tehát a 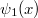 második deriváltját. Ismeretes, hogy egy szorzatfüggvény második deriváltja a következő:
második deriváltját. Ismeretes, hogy egy szorzatfüggvény második deriváltja a következő:
![\[ (fg)'' = f'' g + 2f'g' + fg''. \]](/images/math/5/d/9/5d94a5aecb20646e6fbb34c12e8e3fb4.png)
Ezt alkalmazva 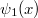 -re azt kapjuk, hogy
-re azt kapjuk, hogy
![\[ \psi_1'' = a_1 (x'' \psi_0 + 2x'\psi_0' + x\psi_0'') = a_1 (2\psi_0' + x\psi_0''). \]](/images/math/e/c/0/ec0a006214c41a94c72cb48e565287d9.png)
Ugyanakkor már láttuk, hogy
![\[ \psi_0' = -2\alpha x\cdot \psi_0. \]](/images/math/0/9/3/0933f520856b7122451ff8b2c1ceada9.png)
Ezzel adódik, hogy
![\[ \psi_1'' = a_1(2\psi_0' + x\psi_0'') = a_1 \cdot x \cdot (-4\alpha\psi_0 + \psi_0''). \]](/images/math/b/f/a/bfad2ff73daf2556f154d33dcbb2b377.png)
Ezt beírva a szóban forgó Schrödinger-egyenletbe, kapjuk, hogy:
![\[ a_1 x (-4\alpha\psi_0 + \psi_0'') + \left( \frac{2mE_1}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2}x^2 \right) a_1 x \psi_0 = 0, \]](/images/math/b/2/e/b2eba429f944a4feeba94f0a0e88eb6b.png)
azaz
![\[ a_1 x \left[ (-4\alpha\psi_0 + \psi_0'') + \left( \frac{2mE_1}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2}x^2 \right) \psi_0 \right] = 0. \]](/images/math/4/8/c/48cd89c8dfac812f6fea8ce73573e8f2.png)
Felhasználva, hogy 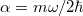 , az egyenlet algebrai átrendezésével adódik, hogy
, az egyenlet algebrai átrendezésével adódik, hogy
![\[ a_1 x \left\lbrace (+\psi_0'') + \left( -2\frac{m\omega}{\hbar} + \frac{2mE_1}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2}x^2 \right) \psi_0 \right\rbrace = 0. \]](/images/math/8/1/e/81e9ed7793e503dc82cc8c00c483aa85.png)
A kapcsos zárójel belsejében felismerhetjük az alapállapoti Schrödinger-egyenletet. Ugyanis fentebb már láttuk, hogy
![\[ \psi_0'' + \left( \frac{2mE_0}{\hbar^2} - \frac{m^2\omega^2}{\hbar^2}x^2 \right) \psi_0 = 0. \]](/images/math/1/a/1/1a1e3ef93fddba04a056f86a3c18ec50.png)
Ezért aztán
![\[ -2\frac{m\omega}{\hbar} + \frac{2mE_1}{\hbar^2}, \]](/images/math/a/b/9/ab961a8efac6d0eab5a4098a88832717.png)
ebből pedig kapjuk, hogy
![\[ E_1 = E_0 + \hbar\omega, \quad \text{és így} \quad E_1 = \frac{3}{2}\hbar\omega. \]](/images/math/e/5/d/e5d6fe63180429d8d2bc069d1919f4c2.png)
Tovább folytatva ezt a heurisztikus módszert, az adódna, hogy az energiaszintek a következők:
![\[ \frac{1}{2}\hbar\omega, \quad \frac{3}{2}\hbar\omega, \quad \frac{5}{2}\hbar\omega, \quad \frac{7}{2}\hbar\omega, ... \quad \text{stb}. \]](/images/math/4/b/7/4b7739d854dd2ad6c3edd7c1e65de2a3.png)
Kimondhatjuk tehát, hogy a harmonikus lineáris oszcillátor energiaszintjeit az
![\[ E_n = \hbar\omega\left( n + \frac{1}{2} \right), \quad n = 0,1,2,3,... \]](/images/math/5/0/6/5063592d6e152d4b1a60a5fecb0208b6.png)
összefüggés adja meg. Látható, hogy most az 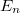 és a
és a 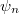 „indexeibe” az
„indexeibe” az  kvantumszámot (és nem a sorszámot) írtuk be. Az alapállapoti energia (
kvantumszámot (és nem a sorszámot) írtuk be. Az alapállapoti energia (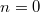 ) nem nulla, hanem véges érték. Ezt nevezik nullaponti energiának. Mivel ez a legalacsonyabb energia, ezért ez az oszcillátorból nem vonható el. Ez azt is jelenti, hogy az oszcillátor soha nincsen nyugalomban, kis, ún. alapállapoti (nullaponti) rezgést mindig végez. Hiszen ekkor a megtalálási valószínűség(sűrűség) nem egy „pontszerű függvény”, hanem „elmosódik”:
) nem nulla, hanem véges érték. Ezt nevezik nullaponti energiának. Mivel ez a legalacsonyabb energia, ezért ez az oszcillátorból nem vonható el. Ez azt is jelenti, hogy az oszcillátor soha nincsen nyugalomban, kis, ún. alapállapoti (nullaponti) rezgést mindig végez. Hiszen ekkor a megtalálási valószínűség(sűrűség) nem egy „pontszerű függvény”, hanem „elmosódik”:
![\[ \left| \psi_0 \right|^2 = A_0^2\exp(-2\alpha x^2). \]](/images/math/7/e/6/7e6babee62867b3972b432d831775595.png)
A magasabb kvantumszámokhoz tartozó állapotfüggvények az eddigiekhez hasonlóan állíthatók elő:
![\[ \psi_n(x) = H_n(x)\cdot \psi_0(x), \]](/images/math/5/b/b/5bb094d5ffd3c138d42cae1764cdf49e.png)
ahol az előzőek értelmében a 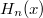 egy páros vagy páratlan polinom. Ebből az első kettőt az előzőekben már használtuk:
egy páros vagy páratlan polinom. Ebből az első kettőt az előzőekben már használtuk:
![\[ H_0(x) = 1, \quad H_1(x) = a_1 x. \]](/images/math/f/1/3/f13637148f4f6c6fd9f8675a56fc0944.png)
A többi értelemszerűen a következő:
![\[ H_2(x) = a_0 + a_2 x^2, \quad H_3(x) = a_1 + a_3 x^3, \quad \text{stb}. \]](/images/math/e/1/9/e1967be7c5de14d7c7df5627f9333514.png)
Természetesen az 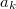 ,
, 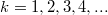 együtthatók minden polinomban mások és mások. Ezek kiszámítása jelenti a
együtthatók minden polinomban mások és mások. Ezek kiszámítása jelenti a 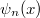 állapotfüggvények meghatározását. Az egydimenziós potenciáldobozhoz hasonlóan most is a kvantummechanikai megtalálási valószínűség(sűrűség) a klasszikus eredmény körül ingadozik.
állapotfüggvények meghatározását. Az egydimenziós potenciáldobozhoz hasonlóan most is a kvantummechanikai megtalálási valószínűség(sűrűség) a klasszikus eredmény körül ingadozik.
Az energiaszintek egymástól egyenlő távolságra helyezkednek el. Ez a távolság éppen 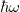 . Tehát az oszcillátor csak
. Tehát az oszcillátor csak 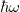 nagyságú energiát tud leadni, vagy felvenni. Az eredményt érdemes összevetni a Planck-féle oszcillátor modellel. Mint azt láttuk, Planck-féle hipotézis szerint
nagyságú energiát tud leadni, vagy felvenni. Az eredményt érdemes összevetni a Planck-féle oszcillátor modellel. Mint azt láttuk, Planck-féle hipotézis szerint
![\[ E_n = n\cdot\hbar\omega \quad n = 0,1,2,3,... . \]](/images/math/3/e/2/3e2573146b2dc370fad7f1cc65040c1a.png)
Láthatóan az 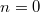 alapállapoti energia ebben az esetben
alapállapoti energia ebben az esetben 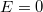 , ellentétben a Schrödinger-féle egzakt eredménnyel, amely szerint ez az érték
, ellentétben a Schrödinger-féle egzakt eredménnyel, amely szerint ez az érték 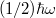 . Mint láttuk, a Planck-modellnek ez a „hiányossága” nem volt zavaró. Ennek oka egyszerű. Planck az oszcillátor és az elektromágneses tér termikus egyensúlyát vizsgálta. Ekkor azonban csak a leadott és a felvett energia számít. Ez pedig mind a két esetben
. Mint láttuk, a Planck-modellnek ez a „hiányossága” nem volt zavaró. Ennek oka egyszerű. Planck az oszcillátor és az elektromágneses tér termikus egyensúlyát vizsgálta. Ekkor azonban csak a leadott és a felvett energia számít. Ez pedig mind a két esetben 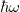 .
.
Elektron a Hidrogén atomban
A kapott eredmény általánosabb, mint azt az elején definiáltuk. Ugyanis egy háromdimenziós térben haladó síkhullám esetén a terjedés iránya egy kitüntetett irány. Ez az irány tekinthető a 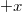 tengelynek, hiszen a fizikai számítások eredményei nem függhetnek a koordinátarendszer megválasztásától. Mivel az
tengelynek, hiszen a fizikai számítások eredményei nem függhetnek a koordinátarendszer megválasztásától. Mivel az 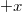 irányba haladó síkhullámnál az
irányba haladó síkhullámnál az 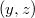 síkkal párhuzamos hullámfrontnak minden pontjában egyforma fizikai viszonyok uralkodnak, így írható, hogy
síkkal párhuzamos hullámfrontnak minden pontjában egyforma fizikai viszonyok uralkodnak, így írható, hogy
![\[ \varphi({\rm r}) = A\exp\lbrace + {\rm i} kx \rbrace. \]](/images/math/1/a/f/1af12fe31be578667ae21cae865169f8.png)
A fenti gondolatmenet alkalmazható a térben bármilyen irányban mozgó elektron állapotfüggvényének a meghatározására is. Ez már „valódi” háromdimenziós feladat lesz. A hidrogén atom tárgyalásakor tanultunk már a Schrödinger-egyenlet térbeli polárkoordinátákkal felírt alakjáról. Írjuk fel ezt az egyenletet egy  sugarú gömbalakú potenciáldobozra. Azaz legyen a
sugarú gömbalakú potenciáldobozra. Azaz legyen a 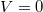 a gömbön belül és
a gömbön belül és 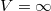 a gömbön kívül. A feladat tehát gömbszimmetrikus.
a gömbön kívül. A feladat tehát gömbszimmetrikus.
Keressük meg a Schrödinger-egyenlet „gömbszimmetrikus” megoldásait. Ilyennek biztosan kell lennie, hiszen (mint azt láttuk) a hidrogén atom  állapotai szintén gömbszimmetrikusak. A megoldást tehát a következő alakban kell keresnünk:
állapotai szintén gömbszimmetrikusak. A megoldást tehát a következő alakban kell keresnünk:
![\[ \Psi({\bf r}) = \Psi(r,\vartheta,\varphi) = R(r). \]](/images/math/e/c/b/ecbde1974058cff66b7d96ab3b8550b3.png)
Mivel az állapotfüggvény nem függ a szögektől, adódik, hogy
![\[ \Delta\Psi({\bf r}) = \Delta R(r) = \frac{1}{r^2} \frac{\rm d}{{\rm d} r} \left( r^2 \frac{{\rm d}R}{{\rm d}r} \right) = \frac{2}{r} \frac{{\rm d}R}{{\rm d}r} + \frac{{\rm d}^2 R}{{\rm d}r^2} \equiv \frac{2}{r}R' + R''. \]](/images/math/b/5/f/b5ff886e9388e3a1189647a7ae1285b4.png)
Az egyszerűbb írás végett a „deriválást” most a (szokásos) „vesszővel” jelöltük. A kapott kifejezés tovább alakítható a következőképpen:
![\[ \Delta\Psi({\bf r}) = \Delta R(r) = \frac{1}{r} (2R' + rR'') = \frac{1}{r} (rR)''. \]](/images/math/a/5/f/a5f5fc1ca9bf3e7af01d3256f08ae544.png)
Ezen átírás előnye azonnal szembeötlő lesz, ha felírjuk a megadott potenciálgömbbe zárt elektronra vonatkozó Schrödinger-egyenletet. Azaz a gömbön belül:
![\[ -\frac{\hbar^2}{2m}\Delta R - E\cdot R = 0, \]](/images/math/1/8/7/1878de53c97f309c2d55221388c03770.png) |
(21) |
és ahogyan az az egydimenziós potenciáldoboznál is volt, a gömbön kívül
![\[ \Psi(r) \equiv R(r) \equiv 0. \]](/images/math/4/4/7/44754d2c62b2a928414d8f54f774b54a.png)
Szorozzuk be  -rel a (21) egyenlet mindkét oldalát! Ekkor adódik, hogy
-rel a (21) egyenlet mindkét oldalát! Ekkor adódik, hogy
![\[ -\frac{\hbar^2}{2m} r\cdot \Delta R - E\cdot rR = 0. \]](/images/math/e/1/2/e12d8f72204c94c3ad9fe0fc8d028fbb.png)
Mármost, ha bevezetjük a
![\[ P_{\rm rad} \equiv r\cdot R(r), \]](/images/math/0/d/f/0df613f5d235e16e3d0a921577eeaa83.png)
radiális állapotfüggvényt, akkor a fentiek alapján kapjuk, hogy
![\[ -\frac{\hbar^2}{2m} P''_{\rm rad} + E\cdot P_{\rm rad} = 0, \]](/images/math/c/5/e/c5eb3afbb547b7d6e6da850acdbdb7df.png)
azaz
![\[ P''_{\rm rad} = -\frac{2mE}{\hbar^2}\cdot P_{\rm rad}. \]](/images/math/1/9/0/190f0bee4a96ab96873c28ea97a146ec.png)
Ez pedig matematikailag a következő jól ismert egyenletet jelenti:
![\[ P''_{\rm rad} = -k^2 \cdot P_{\rm rad}, \quad \text{ahol} \quad k^2 = \frac{2mE}{\hbar^2}. \]](/images/math/b/0/7/b074d8ee7c7a7b02b8260ed32fccde8c.png)
Ez ugyanolyan alakú egyenlet, mint az egydimenziós potenciáldoboz esetében volt. A peremfeltételek is azonosak, azaz
![\[ R(a) = 0, \quad \text{és legyen} \quad R(0) = 0. \]](/images/math/0/e/9/0e9dd20ed45cb8b5c507ecdf08110211.png)
Az első nyilvánvaló, hiszen a gömbön kívül az állapotfüggvény mindenhol zérus. A második már nem ilyen egyszerű, de fogadjuk el, és akkor a megoldás fizikai értelmezése maga fogja igazolni a feltevésünk helyességét.
A fentiek értelmében az állapotfüggvényre adódó megoldás tehát
![\[ P_{\rm rad}(r) = A\sin(kr). \]](/images/math/8/d/c/8dc1d15d4c7f42092a498348c8048e72.png)
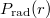 definíciója alapján pedig írható a következő:
definíciója alapján pedig írható a következő:
![\[ \Psi(r) = R(r) = \frac{1}{r} \cdot P_{\rm rad}(r) \equiv \frac{A}{r}\sin(kr). \]](/images/math/d/9/a/d9ad9d62c461b844f0ad92794d5f2f53.png)
Az „elemi” valószínűségek képzésénél célszerű figyelembe venni azt, hogy a 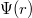 állapotfüggvény gömbszimmetrikus. Ezért az az elemi
állapotfüggvény gömbszimmetrikus. Ezért az az elemi 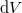 térfogat, amelyen belül a
térfogat, amelyen belül a 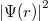 állandónak tekinthető egy
állandónak tekinthető egy  sugarú
sugarú 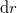 vastagságú gömbhéj. Így tehát
vastagságú gömbhéj. Így tehát 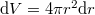 . Ennek megfelelően kapjuk, hogy
. Ennek megfelelően kapjuk, hogy
![\[ \left| \Psi(r) \right|^2 {\rm d}V = \left| \Psi(r) \right|^2 4\pi r^2 {\rm d} r = 4\pi \left| A \right|^2 \sin^2 (kr) {\rm d} r. \]](/images/math/b/a/5/ba5dcbb96ffcc249e0c9764a6b39b134.png)
Az ezt bemutató interferenciacsíkokat az előző ábrán láthatjuk. Alkalmazzuk a szuperpozíció elvét a 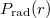 állapotfüggvényre:
állapotfüggvényre:
![\[ P_{\rm rad} (r) = \frac{A}{2{\rm i}}\exp({\rm i}kr) - \frac{A}{2{\rm i}}\exp(-{\rm i}kr). \]](/images/math/1/b/d/1bde0e5246e9c6a3f5a1350e58dd3102.png)
Követve az egydimenziós potenciáldoboznál alkalmazott gondolatmenetet, a 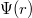 állapotfüggvény egy „befutó” és egy „kifutó” gömbhullám szuperpozíciójaként adható meg:
állapotfüggvény egy „befutó” és egy „kifutó” gömbhullám szuperpozíciójaként adható meg:
![\[ \Psi(r) = C_{-} \frac{1}{r}\exp(-{\rm i}kr) + C_{+} \frac{1}{r}\exp(+{\rm i}kr) \equiv \Psi_{\rm be}(r) + \Psi_{\rm ki}(r). \]](/images/math/4/a/d/4ade258f77c79b303cfb30646e268648.png)
Látható tehát, hogy
![\[ \left| \Psi_{\rm be}(r) \right|^2 {\rm d} V = \left| \Psi_{\rm be} \right|^2 4\pi r^2 {\rm d}r = 4\pi\left| C_{-} \right|^2 {\rm d}r = \text{állandó} \cdot {\rm d}r, \]](/images/math/f/5/a/f5a79e84984c82aff8331f21b0c6cd5b.png)
és ugyanígy
![\[ \left| \Psi_{\rm ki}(r) \right|^2 {\rm d} V = \left| \Psi_{\rm ki} \right|^2 4\pi r^2 {\rm d}r = 4\pi\left| C_{+} \right|^2 {\rm d}r = \text{állandó} \cdot {\rm d}r, \]](/images/math/e/8/f/e8faf40764820f1eacb1e6b5f00958bb.png)
Tehát erőmentes, nem korlátozott mozgás esetén (azaz amikor nincsenek visszaverő falak) a térben az elektron egyenletes valószínűségsűrűséggel, bárhol megtalálható. Mindez egybevág a fizikai „szimmetriaérzékünkkel”.
Tudománytörténeti kitekintés
Az „Einstein tudós-portréja” és a mi mögötte van
A közvélemény Einsteinről alkotott képét nagyrészt közepes tehetségű emberek alakították ki. Az újságírók örökké interjúért zaklatták, könyveket írtak életéről és eredményeiről, úgy tettek, mintha megértenék azokat a problémákat, amelyekkel birkózott. Az így létrejött közvéleménykép messze állott a valóságtól.
- Elég nehéz dolog egy olyan géniuszt értékelni, aki ilyen egyedülálló adottságokkal rendelkezik és ilyen egyedüli helyet foglal el a tudománytörténetben...
- írta róla a magyar származású Lánczos Kornél, aki 1928-29-ben Einstein közvetlen munkatársa és így személyes, jó ismerőse volt. Nyilvánvaló, hogy a Térről és az Időről mint alapvető fogalomról mindnyájunknak van valamilyen (a hétköznapok tapasztalatán alapuló) elképzelése. Annyira megszoktuk már ezeket a fogalmakat, amelyek a maguk módján beépültek a szemléletünkbe, hogy minden ettől eltérő állítás mélyen meghökkent minket. Nem meglepő tehát, hogy az einsteini Téridő fogalom forradalmian új struktúrája és a hozzá kapcsolódó speciális relativitáselmélet volt az, amely Einsteint közismertté tette. Pedig a valóban eredeti alkotása a foton fogalma volt!
A „különc, tudós professzor sztereotípiája” Einsteinben látszott testet ölteni. Sok személyéhez kötődő „story” él és terjed róla, amelyeknek nagy részét éppoly meghökkentő „legendává” alakította a szájhagyomány, mint amilyen elméletének furcsasága volt. Ezek egy része nélkülözi a valóságos alapokat, de ahogyan mondani szokás „ha nem is igaz, jól ki van találva”!
- Nem volt csodagyerek, bár a természet titkai már igen hamar érdekelni kezdték. Az ötéves korában ajándékba kapott iránytű rendkívüli módon lenyűgözte és erősen hatott rá az az elemi geometriai kézikönyv, ami tizenkét éves korában került a kezébe. Az iskolák nemigen feleltek meg Einstein vérmérsékletének, és tanárai gyakran fegyelmezetlennek találták. Egyik elkeseredett tanára egyszer meg is jósolta nem túl találóan: «Einstein, Einstein, maga semmire sem fogja vinni az életben!»
- írta róla ugyancsak Láczos Kornél. Később, egyetemi évei alatt sem tűnt ki a társai közül.
- Egyik matematikaprofesszora az a Hermann Minkowski volt, aki később a speciális relativitáselmélet geometriai értelmezésének úttörője lett. Amikor elolvasta Einstein 1905-ös tanulmányát, igen meg volt lepve. «Ez ugyanaz az Einstein lenne – kérdezte egyik barátjától –, aki néhány éve a diákom volt? Akkor úgy látszott, hogy nagyon keveset tud!» (L. K.)
A társadalmi átlagra tervezett intézményes oktatás és a különlegesen gondolkodó Einstein konfliktusa szükségképpen végig kísérte az életét. Nem volt „jó” diák és egyetemi tanársága idején nem szeretett tanítani sem. Bár mindez igen izgalmas lehet az utca emberének, de a „zseniális bukott diák” legendája csak a középszerűség önámításának tekinthető.
A Schrödinger-egyenlet és Lánczos Kornél
A Zeitschrift für Physik fizikai folyóirat szerkesztőségébe 1925. december 22-én beérkezett egy cikk, melynek szerzője Cornelius Lanczos volt. Többek között ezt írta :
- Heisenberg nagyhatású gondolatmenete úttörő jelentőségűnek tűnik a kvantumkutatás számára. A következetesen diszkrét adatokat használó elmélet csak távolról korrespondál a klasszikus fogalmainkkal. Eleve saját külön útjának vág neki, gyökeresen új értelmet adván a régi szimbólumoknak. Az új alapvetés a kvantumelmélet korábban nem sejtett elmélyítését hozta meg.
- Itt most azt fogjuk megmutatni, hogy a kvantumelmélet minden eredménye integrálegyenlettel is- kifejezhető. Ily módon annak egy olyan megfogalmazását kapjuk, amely közelebb áll az analitikus módszerekhez szokott fizikushoz, mint a mátrixos ábrázolás. Ezáltal egy kontinuum felfogáshoz jutunk, amely a diszkrét mátrix-leírással egyenrangúan használható. A két módszer matematikailag teljesen egyenértékű.
- Ami a kvantumok mélyebb értelmét illeti, nincs kizárva, hogy a mátrix-megfogalmazásnál esetleg értékesebb lesz az integrálos megfogalmazás, hiszen ez utóbbi közvetlenül összeegyeztethető a térelméleti gondolkodással, amitől pedig a mátrixos megfogalmazás teljesen idegen.

|
Cornelius Lanczos 1893-1974
Albert Einstein ajánlása: Lánczos Kornél úr kétségkívül tehetséges és önálló elméleti fizikus, aki alkalmas egyetemi tanárnak. Alaposan ismeri a relativitáselméletet, de a kvantummechanikában is eredményesen dolgozik. Külön kiemelendő, hogy mindig a nehéz kérdések ragadják meg érdeklődését, nem pedig a könnyen elérhető célok. |
Lánczos Kornél a kidolgozta fent vázolt elképzelését. 1926-ban egy hónappal megelőzve Erwin Schrödinger differenciálegyenletét a Zeitschrift für Physik hasábjain közzétette integrálegyenletét. A két egyenlet ugyanannak a fizikai problémának matematikailag ekvivalens megfogalmazása. Lánczos „pechére” a fizikusok a differenciálegyenletek nyelvén beszéltek. Így sem őt, sem pedig Heisenberget nem értették meg. Ezért aztán Lánczos-egyenlet helyett Schrödinger-egyenletről beszélünk.
Természetesen ma már a kvantummechanikai alkalmazások során mindhárom féle „reprezentációt” használjuk. Lánczos neve azonban még ma sem hangzik el a kvantummechanika előadásokon. Az ő nevét a matematikai alkotásai miatt idézik a matematikusok (pl. Lánczos-közelítés, -algoritmus, -szigma faktor, -tenzor, -szűrő). Hárommondatos életrajza a kor történelmét is tükrözi:
- Cornelius Lanczos (Lánczos Kornél) született Lőwy Kornél, 1893 Székesfehérvár, Magyarország.
- 1974-ben szívroham következtében hunyt el, amikor hazalátogatott Budapestre.
- Egész életét külföldön töltötte.
Werner Heisenberg és a mátrixmechanika
A 24 éves(!) Werner Heisenberget (aki ekkor Göttingenben magántanárként dolgozott) nagyon zavarta az, hogy a Bohr-féle atommodell túl szemléletes. Olyan sajátosságokat tulajdonít az elektronnak, amit közvetlenül még soha senki nem mért meg (pl. a pontszerű elektron az atomban kering). Ezért kigondolt egy olyan számítási módszert, amely kiindulásul csak a hidrogén atom megmérhető adatait tartalmazta (a Balmer-féle frekvenciákat). Ezeket az adatokat táblázatokba rendezte és a táblázatokkal igen furcsa, általa definiált műveleteket kellett végezni. Mint utóbb kiderült ezek mátrixműveletek voltak. Megszületett az ún. mátrixmechanika (1925), egy eredeti módszer, amit senki sem értett meg igazán!
Amúgy Heisenberg a XX. századi fizika egyik nagy egyénisége. A Kvantummechanika egyik kidolgozója, aki a szilárdtestfizikában (ferromágnesség elmélete) és az atommagfizikában (atommagmodellek) is sokat és maradandót alkotott. Késöbb még találkozunk a nevével! A fizikai Nobel-díjat 1933-ban kapta meg.
Erdős Pál véleménye a Matematikáról
„Minden, ami emberi, akár rossz, akár jó, előbb-utóbb véget ér. Kivéve a matematikát.”
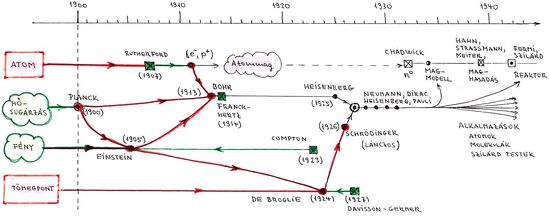
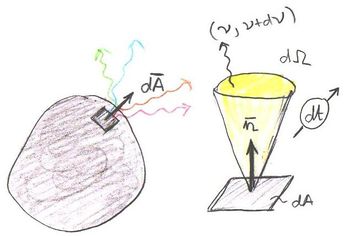
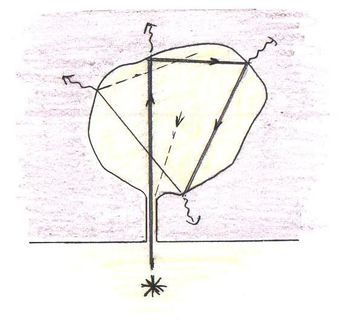
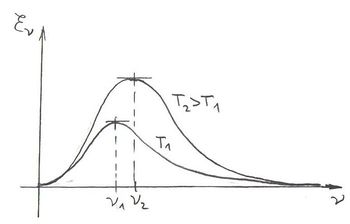
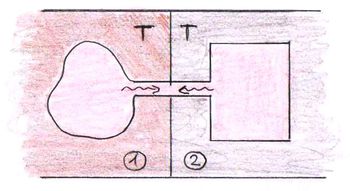
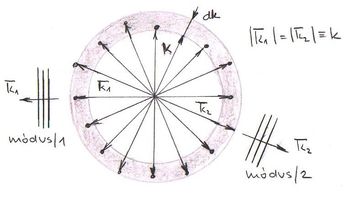
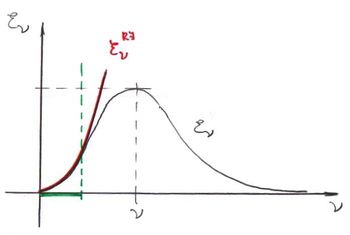
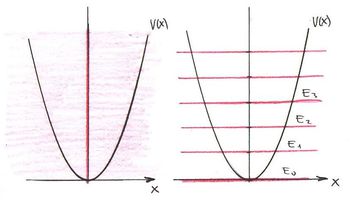

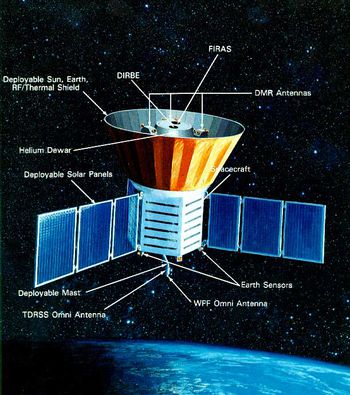
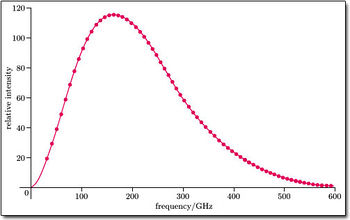
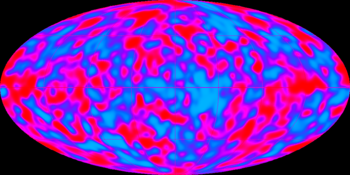
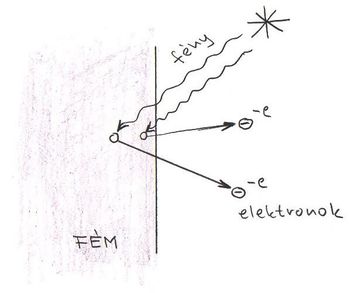
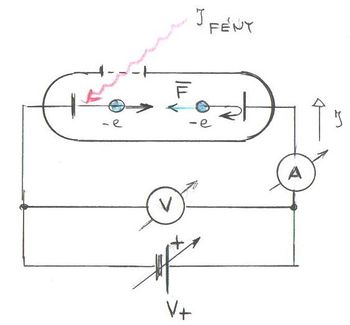
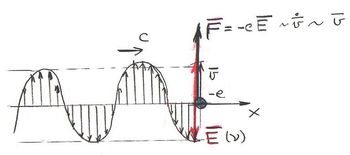
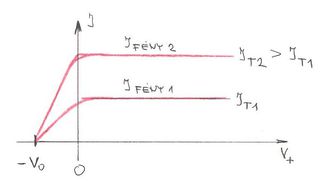
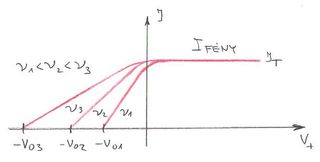
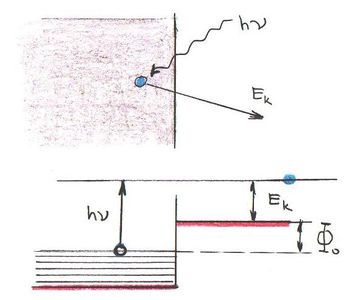
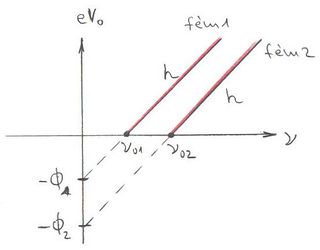
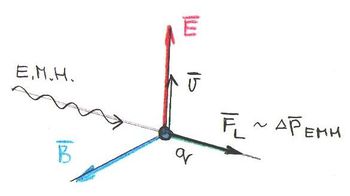
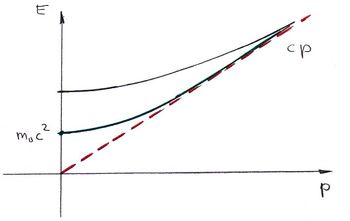
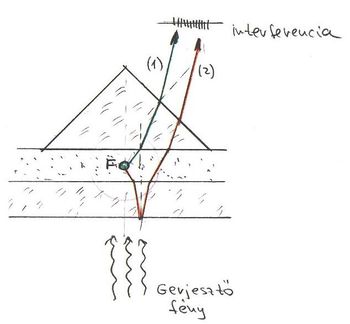
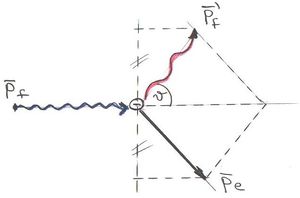
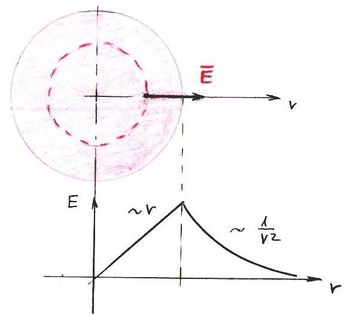
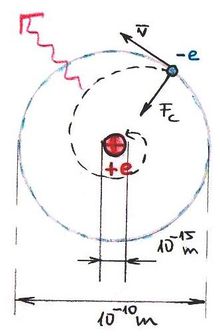
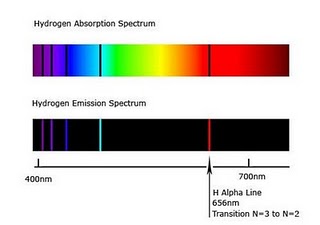
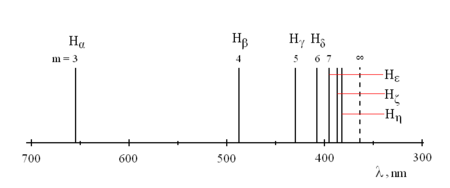
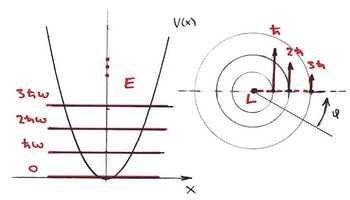
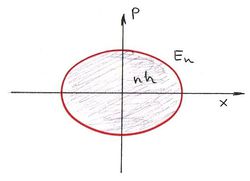
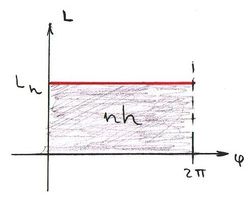
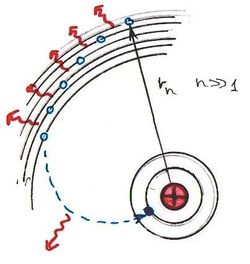
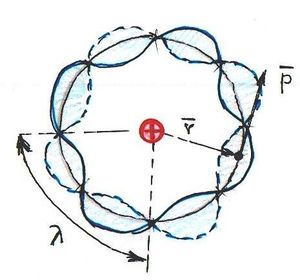
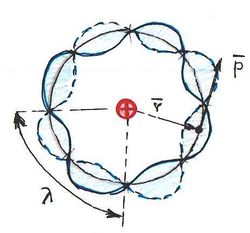


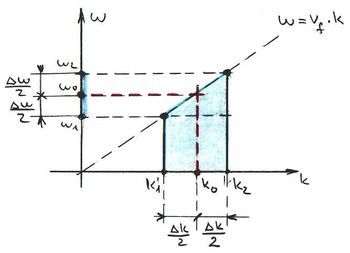
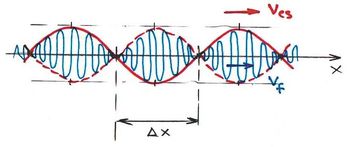
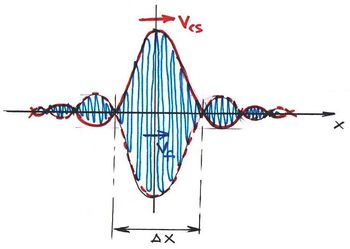
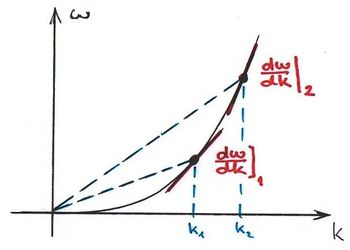

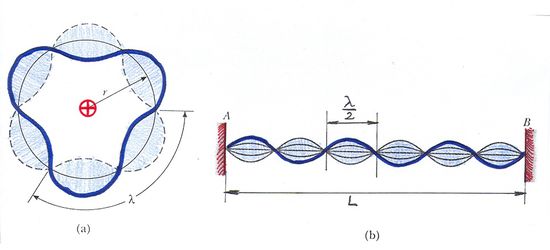
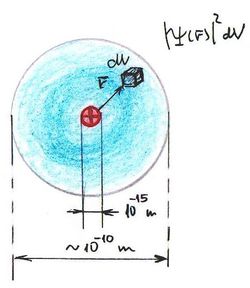
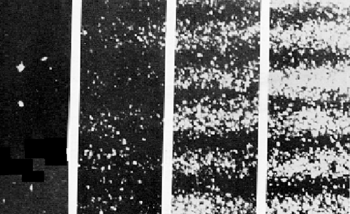
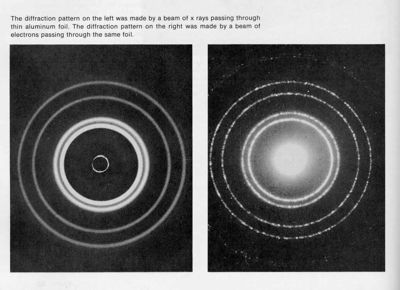
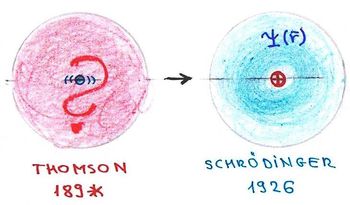
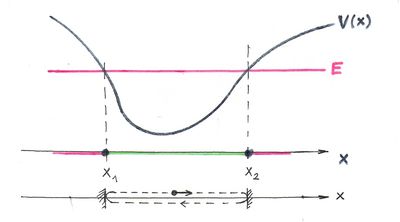
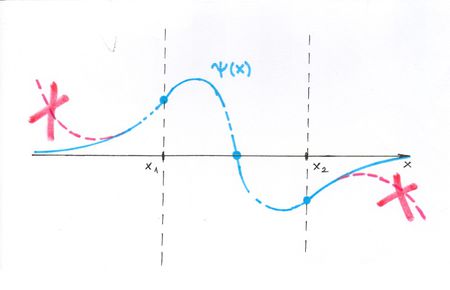
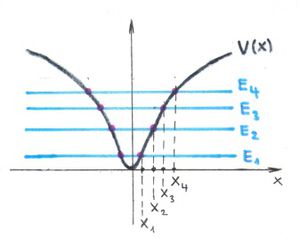
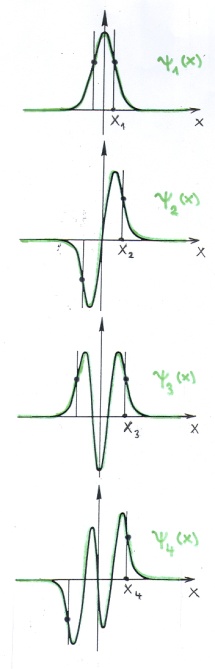
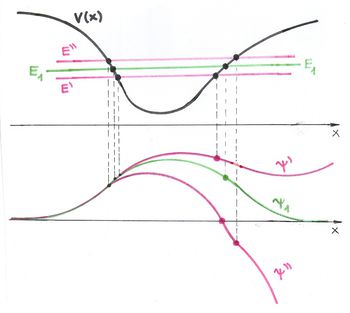
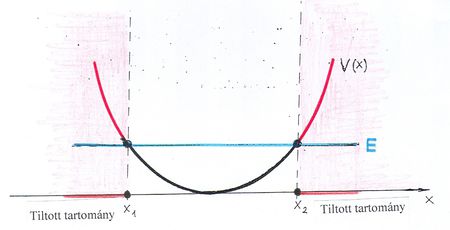
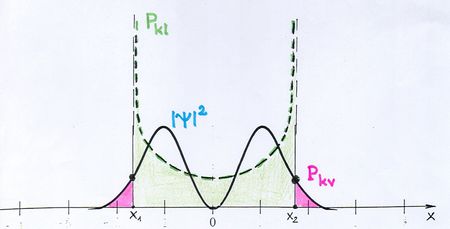
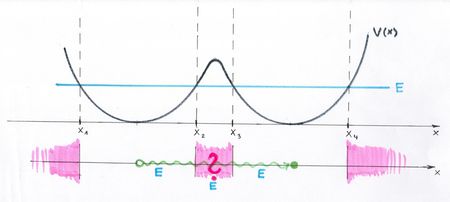
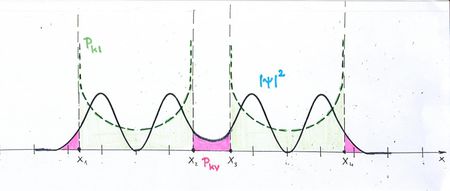


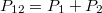 , abban az esetben, ha mind a két rés nyitva van
, abban az esetben, ha mind a két rés nyitva van