Méréstechnika szerkesztőlap
Tartalomjegyzék[elrejtés] |
Spektrumanalízis
Egy 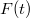 időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg:
időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg:
![\[f(\omega)=\int_{-\infty}^{\infty} F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t.\]](/images/math/5/9/5/595ba94d38747532dc0a86ce5c451009.png)
Egy valós mérésnél a Fourier-transzformált függvényt csak közelítőleg tudjuk megadni, hiszen egyrészt véges ideig tart a mérésünk, másrészt a mérési adatok csak diszkrét időfelbontással álnak rendelkezésre. Először nézzük meg a véges idejű mérés hatását a Fourier-transzformáltra.
A véges idejű mérés megfelel annak, mintha az eredeti függvényt megszoroznánk a mérési intervallumnak megfelelő 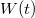 ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki:
ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki:
![\[f_W(\omega)=\int_{-\infty}^{\infty} W(t)\cdot F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,\]](/images/math/8/3/d/83d2a1130cc875baedfb60e75dbff165.png)
ahol a 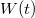 függvény
függvény 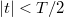 esetén
esetén 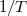 , ezen
, ezen  hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz:
hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz:
![\[ f_W(\omega)=\int_{-\infty}^{\infty} f(\omega ')w(\omega - \omega ')\frac{\mathrm{d}\omega}{2\pi},\ \ \ \ \mathrm{ahol}\ \ \ w(\omega)=\int_{-\infty}^{\infty} W(t)\mathrm{e}^{-i\omega t}\mathrm{d}t. \]](/images/math/0/5/8/0582a6df73925371593d682d300af119.png)
Nézzünk egy egyszerű példát, legyen 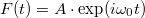 egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény:
egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény: 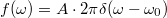 . Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján
. Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján 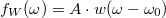 , azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az
, azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az  középfrekvenciához eltolva. A fent definiált téglalap ablak esetén (azaz amikor
középfrekvenciához eltolva. A fent definiált téglalap ablak esetén (azaz amikor 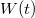 egy
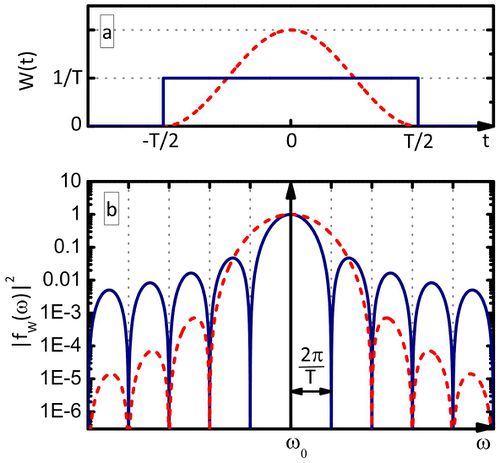
egy  szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja
szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja 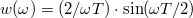 , azaz
, azaz 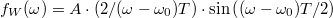 (5b. ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az
(5b. ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az  középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az
középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az 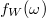 függvény
függvény  melletti első zérushelyeinek a távolsága
melletti első zérushelyeinek a távolsága 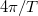 , így az
, így az  körüli csúcs szélessége
körüli csúcs szélessége 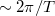 . Tehát az első fontos konklúzió, hogy véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg
. Tehát az első fontos konklúzió, hogy véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg 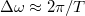 frekvenciafelbontással látjuk!
frekvenciafelbontással látjuk!
5. ábra. a) 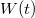 ablakfüggvény téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. b) ablakfüggvény téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. b) 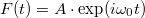 harmonikus jel Fourier-transzformáltjának abszolút érték négyzete téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. A téglalap ablakot Hanning ablakra cserélve az harmonikus jel Fourier-transzformáltjának abszolút érték négyzete téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. A téglalap ablakot Hanning ablakra cserélve az  körüli csúcs kiszélesedik, azaz romlik a frekvenciafelbontás, azonban az körüli csúcs kiszélesedik, azaz romlik a frekvenciafelbontás, azonban az  -tól távolabbi mellékcsúcsok amplitúdója lecsökken, azaz csökken a spektrális szivárgás. -tól távolabbi mellékcsúcsok amplitúdója lecsökken, azaz csökken a spektrális szivárgás.
|
Érdemes megjegyezni, hogy a fent említett téglalap ablak helyett választhatunk más ablakfüggvényt is, például 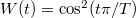 ún. Hanning-ablak esetén a mért jelben elnyomjuk a
ún. Hanning-ablak esetén a mért jelben elnyomjuk a 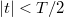 mintavételezési időablak széleihez közeli részeket (5a. ábra, piros szaggatott vonal). Ebben az esetben az
mintavételezési időablak széleihez közeli részeket (5a. ábra, piros szaggatott vonal). Ebben az esetben az  körfrekvenciás jel Fourier-transzformáltjában
körfrekvenciás jel Fourier-transzformáltjában  körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az
körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az  -tól távolabbi oszcillációk amplitúdója (az ún. spektrális szivárgás) lecsökken (5b. ábra, piros szaggatott vonal).
-tól távolabbi oszcillációk amplitúdója (az ún. spektrális szivárgás) lecsökken (5b. ábra, piros szaggatott vonal).
Következő lépésként nézzük meg, hogy mi a hatása annak, hogy a jelünket nem folytonosan látjuk, hanem csak diszkrét mintavételezési időpontokban. Emiatt a jel Fourier-transzformáltját a folytonos integrál helyett kénytelenek vagyunk egy diszkrét összeggel, az ún. diszkrét Fourier-transzformálttal (DFT) közelíteni:
![\[ f_W(\omega)=\sum_{n=0}^{N-1} W(n\cdot \Delta t)F(n\cdot \Delta t) \mathrm{e}^{-i\omega n \Delta t}\Delta t, \]](/images/math/1/c/2/1c29d0a765e68527b917bd9e7cc0b666.png)
ahol  a szomszédos mérési pontok közötti idő,
a szomszédos mérési pontok közötti idő, 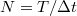 pedig a mintavételezett pontok száma.
Az ún. Nyquist-Shannon mintavételezési törvény szerint
pedig a mintavételezett pontok száma.
Az ún. Nyquist-Shannon mintavételezési törvény szerint  sűrűségű mintavételezés esetén a jelet
sűrűségű mintavételezés esetén a jelet 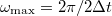 maximális körfrekvenciáig tudjuk rekonstruálni.
maximális körfrekvenciáig tudjuk rekonstruálni.
Könnyen belátható, hogy a diszkrét Fourier-transzformált fenti képlet szerinti kiértékelése  mérési pont esetén
mérési pont esetén 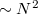 művelet (
művelet (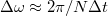 frekvenciafelbontás és
frekvenciafelbontás és 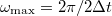 maximális felbontható frekvencia esetén csak
maximális felbontható frekvencia esetén csak 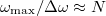 diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián
diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián 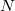 művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa (
művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa (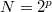 ), és a frekvenciatérben
), és a frekvenciatérben  diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma
diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma 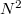 -ről
-ről 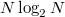 -re csökken, ami nagy N esetén lényeges különbség.
-re csökken, ami nagy N esetén lényeges különbség.
A Fourier-transzformáció nem csak a jel frekvenciájának a vizsgálatára alkalmas, hanem a jel amplitúdójának a mérésére is. A fenti képletek szerint egy 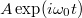 harmonikus jel téglalap ablakkal vett Fourier transzformáltja az
harmonikus jel téglalap ablakkal vett Fourier transzformáltja az  körfrekvenciánál pontosan
körfrekvenciánál pontosan  amplitudóval rendelkezik. Az
amplitudóval rendelkezik. Az  amplitúdót azonban csak akkor kapjuk vissza, ha a jel körfrekvenciája megegyezik az FFT valamelyik frekvenciapontjával (
amplitúdót azonban csak akkor kapjuk vissza, ha a jel körfrekvenciája megegyezik az FFT valamelyik frekvenciapontjával (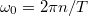 ), ami akkor teljesül, ha a jelnek pontosan egész számú periódusa fér el a
), ami akkor teljesül, ha a jelnek pontosan egész számú periódusa fér el a  mintavételezési ablakban. (Érdemes megjegyezni, hogy ebben az esetben az FFT összes többi frekvenciapontja a téglalapablakkal számolt Fourier-transzformált zérushelyeivel esik egybe, azaz a spektrális szivárgás is megszűnik.) Azonban ha a mérési ablak szélessége nem egyezik meg a jel periódusidejének egész számú többszörösével, akkor az FFT-algoritmus által számolt frekvenciapontok biztosan eltérnek a mért jelünk frekvenciájától, így az amplitúdóra is pontatlan értéket kapunk. Ha a jel amplitúdója érdekel minket, akkor olyan ablakfüggvényt érdemes választni, melynek a Fourier-transzormáltja a centrális csúcs körüli
mintavételezési ablakban. (Érdemes megjegyezni, hogy ebben az esetben az FFT összes többi frekvenciapontja a téglalapablakkal számolt Fourier-transzformált zérushelyeivel esik egybe, azaz a spektrális szivárgás is megszűnik.) Azonban ha a mérési ablak szélessége nem egyezik meg a jel periódusidejének egész számú többszörösével, akkor az FFT-algoritmus által számolt frekvenciapontok biztosan eltérnek a mért jelünk frekvenciájától, így az amplitúdóra is pontatlan értéket kapunk. Ha a jel amplitúdója érdekel minket, akkor olyan ablakfüggvényt érdemes választni, melynek a Fourier-transzormáltja a centrális csúcs körüli 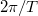 szélességű tartományban minél kevesebbet változik. Téglalapablak esetén az amplitúdópontosság mintegy 36%, Hanning-ablak esetén pedig 15%. Speciális, ún. Flattop-ablakot választva ennél sokkal jobb, mintegy 0.01%-os amplitúdópontosság is elérhető, viszont cserébe lényegesen leromlik a frekvenciafelbontásunk.
szélességű tartományban minél kevesebbet változik. Téglalapablak esetén az amplitúdópontosság mintegy 36%, Hanning-ablak esetén pedig 15%. Speciális, ún. Flattop-ablakot választva ennél sokkal jobb, mintegy 0.01%-os amplitúdópontosság is elérhető, viszont cserébe lényegesen leromlik a frekvenciafelbontásunk.
A zaj
A zaj definíciója
Egy 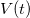 időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy
időben fluktuáló zaj jellegű (azaz széles frekvenciaspektrumú) jelet egy  középfrekvencia körüli
középfrekvencia körüli  szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány
szélességű sávszűrűn keresztül vizsgálva azt találjuk, hogy a szűrt jel szórásnégyzete arányos a frekvenciatartomány  szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectral Density - PSD):
szélességével, az arányossági tényező a feszültségzaj spektrális sűrűsége (spectral density of noise), azaz a teljesítmény spektrális sűrűsége (Power Spectral Density - PSD):
![\[\left\langle (\Delta V(t|f_0,\Delta f))^2 \right\rangle=s_V(f_0)\Delta f.\]](/images/math/f/c/e/fcef50d6c156742a0f491cc490623688.png)
Ez a zaj kísérleti definíciója. A feszültség szórásnégyzete a zajsűrűség teljes frekvenciatartományra vett integráljával egyenlő.
![\[\langle(\Delta V(t))^2 \rangle=\int_{0}^{\infty} df s_V(f).\]](/images/math/4/e/5/4e5f54e003163e2b26ac0e5c132ede8d.png)
Ez a képlet közvetlenül is használható a zajspektrum kísérleti meghatározásához, azonban emellett jó kiindulópontként szolgál más fizikai mennyiségekkel való kapcsolatának vizsgálatára is. Érdemes megvizsgálni a zajsűrűség és a feszültség korrelációs függvény kapcsolatát. Ez utóbbi a következőképpen definiálható:
![\[C(\Delta t)=\langle\Delta V(t)\cdotp\Delta V(t+\Delta t) \rangle=\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int_{0}^{T}dt\Delta V(t)\cdotp\Delta V(t+\Delta t).\]](/images/math/2/2/4/2249b4df683368d4b8351cadfb3df188.png)
Könnyen belátható, hogy a korrelációs függvény 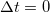 -ban megegyezik a feszültség szórásnégyzetével.
-ban megegyezik a feszültség szórásnégyzetével.
![\[C(0)=\langle(\Delta V(t))^2 \rangle.\]](/images/math/a/b/5/ab573547effc08d355afcf78edbf2b69.png)
Most fejezzük ki a korrelációs függvényt a Fourier-transzformáltja segítségével:
![\[C(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega e^{i\omega t}c(\omega).\]](/images/math/9/2/d/92d0898595e749cda299df5939826fab.png)
Ez alapján a feszültség szórásnégyzete:
![\[\langle(\Delta V(t))^2 \rangle=C(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega c(\omega)=\frac{1}{\pi}\int_{0}^{\infty}d\omega c(\omega),\]](/images/math/1/e/f/1eff86c194f06c16f8941773197552b2.png)
mivel 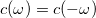 .
Másrészt a szórásnégyzet és a zaj közötti összefüggésből következik:
.
Másrészt a szórásnégyzet és a zaj közötti összefüggésből következik:
![\[\langle(\Delta V(t))^2 \rangle=\frac{1}{2\pi} \int_{0}^{\infty} d\omega s_V(\omega).\]](/images/math/7/9/7/7975f3b4b9d91fc7591790411d47208e.png)
Az utóbbi két egyenletből látható, hogy a zaj teljesítménysűrűsége a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
Sikerült kapcsolatot teremteni a zajsűrűség és a feszültség korrelációs függvény között. Most vizsgáljuk meg a feszültség korrelációs függvény és a feszültség mint mérhető fizikai mennyiségek kapcsolatát. A feszültség átlagtól való eltérésének (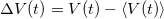 ) a Fourier-transzformáltja szerint:
) a Fourier-transzformáltja szerint:
![\[\Delta v(\omega)= \int_{-\infty}^{\infty} dt \Delta V(t)e^{-i\omega t}.\]](/images/math/2/9/6/2965fd4ba4a7bbef8a3053293de74505.png)
Vizsgáljuk ezen Fourier-transzformált abszolút érték négyzetének várható értékét:
![\[\langle|(\Delta v(\omega))|^2 \rangle= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} dt' dt \langle\Delta V(t)\Delta V(t') \rangle e^{-i\omega t} e^{i\omega t'}.\]](/images/math/4/c/e/4ce29a8e2825fd676032ef5e4d3274cb.png)
Az egyenlet jobb oldalán látható korrelációs függvény kifejezhető a következőképpen:
![\[ \langle\Delta V(t)\Delta V(t')\rangle=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega'c(\omega')e^{i\omega'(t-t')}.\]](/images/math/0/2/0/020ed4a8570c778e72bfcb56197a4710.png)
Továbbá az exponenciális tagokat átcsoportosítva a következő tag integrálja egy Dirac-deltát ad:
![\[\int_{-\infty}^{\infty}dt'\frac{e^{i(\omega+\omega')t'}}{2\pi}=\delta(\omega+\omega').\]](/images/math/0/9/5/095ca08f79957cdab9fa2f6b7d38b462.png)
Így a feszültség Fourier-transzformált abszolút érték négyzetének várható értéke könnyen belátható, hogy arányos a korrelációs függvény Fourier-transzformáltjával, illetve az időablak szélességével:
![\[\langle|(\Delta v(\omega))|^2 \rangle= c(\omega) \int_{-\infty}^{\infty} dt.\]](/images/math/b/e/7/be72f26b149e5ab64d53d20f46b4bc31.png)
Innen könnyen kifejezhető a zaj teljesítménysűrűsége, felhasználva, hogy az a feszültség korrelációs függvény Fourier-transzformáltjának kétszerese.
![\[s_V(\omega)=\lim\limits_{T->\infty} \frac{2}{T}\left\langle |\int_{-T/2}^{T/2} dt \Delta V(t)e^{-i\omega t}|^2\right\rangle.\]](/images/math/f/6/2/f62535c4ffea081a318dd4bd7ac2a654.png)
A mérésünk során diszkrét pontokon történik a mintavételezés, így ugyanez a számolás DFT segítségével a következő módon fejezhető ki:
![\[s_V(\omega)\approx\frac{2}{N\Delta t}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}\Delta t|^2=\frac{2\Delta t}{N}|\sum_{n=0}^{N-1} \Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/6/0/3/603ab5b3fd96cfbcbb85edb29268c6af.png)
A fentiekben sikerült megállapítanunk, hogy a vizsgált 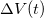 jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
jel Fourier-transzformáltjából hogyan számolható a zaj spektrális sűrűsége. Azonban ennél a számolásnál nem vettünk figyelembe ablakfüggvényt, vagy fogalmazhatunk úgy is, hogy téglalap ablakkal számoltunk.
Nézzük meg, hogy egy tetszőleges ablakfüggvény esetén hogyan származtatható a zajsűrűség. Sajnos tetszőleges spektrumú zajra és tetszőleges ablakfüggvényre általános összefüggés nem adható, viszont ha 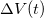 fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor.
fehér zaj, akkor tetszőleges ablakfüggvényre egyszerűen számolható a konverziós faktor.
Az ablakfüggvénnyel szorzott jel Fourier-transzformáltja:
![\[\Delta v_W(\omega)=\int_{-\infty}^{\infty}dt\Delta V(t)W(t)e^{-i\omega t}.\]](/images/math/7/e/f/7efc09e6fe1e8b10c418e39ae67c31c9.png)
Vizsgáljuk meg ezen Fourier-transzformált abszolút érték négyzetének várható értékét, ekkor a következőt kapjuk:
![\[\langle|\Delta v(\omega)|^2\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dtdt'W(t)W(t')\langle\Delta V(t)\Delta V(t')\rangle e^{-i\omega t}e^{-i\omega t'}.\]](/images/math/7/d/3/7d3c7333af2e34f077367ef15237c488.png)
A fehér zaj jellegéből következik, hogy:
![\[\langle\Delta V(t)\Delta V(t')\rangle=C(t-t')=\frac{s_0}{2}\delta(t-t').\]](/images/math/7/2/c/72c3ab5d9e5160ea1cc93ce4aa1e97ae.png)
Így a Fourier-transzformált abszolút érték négyzetének várható értéke a következőképpen egyszerűsödik:
![\[\langle|\Delta v_W(\omega)|^2\rangle=\frac{s_0}{2}\int_{-\infty}^{\infty}W^2(t)dt.\]](/images/math/6/3/5/6356a96296e2b3eca8d114d91dae4d48.png)
Azaz a zajsűrűség számolása:
![\[s_0=\frac{2\langle|v_W(\omega)|^2\rangle}{\int_{-\infty}^{\infty}W^2(t)dt}.\]](/images/math/9/1/7/917c7b49524f91ef5d3aee98385f13b5.png)
A feszültségzaj spektrális sűrűsége egy normálási faktor erejéig egyenlő a mért feszültségpontok diszkrét Fourier-transzformáltjának abszolútérték-négyzetének kétszeresével. A normálási faktor az ablakfüggvény négyzetének a mérési időablakra vett integrálja. Láttuk, hogy ez téglalap ablakkal számolva  . Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye:
. Most vizsgáljuk meg a zajméréshez leggyakrabban használt Hanning-ablakot, melynek ablakfüggvénye:
![\[W(t)=2\sin^2\left(\frac{t\pi}{T}\right).\]](/images/math/d/5/8/d58104d67248c78d0d25e0feb8d3b3ac.png)
A zajsűrűség Hanning-ablakot használva:
![\[s_0=\frac{4\langle|v_W(\omega)|^2\rangle}{3T}.\]](/images/math/b/d/e/bdee8db481fad34233895abf370d61ae.png)
Diszkrét mérési pontok esetén a következőképpen módosul a kifejezés:
![\[s_0\approx\dfrac{2}{\sum_{n=0}^{N-1}W^2(n\Delta t)\Delta t}|\sum_{n=0}^{N-1}W(n\Delta t) V(N\Delta t)e^{-i\omega n\Delta t}\Delta t|^2.\]](/images/math/c/7/9/c798b690d1d9023a3a2741285d12ca1c.png)
Hanning-ablakkal számolva:
![\[s_0\approx\frac{4\Delta t}{3N}|\sum_{n=0}^{N-1}W(n\Delta t)\Delta V(n\Delta t)e^{-i\omega n\Delta t}|^2.\]](/images/math/e/1/1/e11505f5d483e5c169ac48ae35cc33ba.png)
Így frekvenciafüggetlen zajsűrűségek esetén sikerült analitikusan meghatározni, hogy a mérési pontokból miképpen számolható ki a zaj spektrális sűrűsége.
Termikus zaj
Egy kristályban lévő elektronok termikus fluktuációi miatt külső feszültség nélkül az áram időátlaga nulla, azonban az adott időpillanatokban véletlen irányokba mutató áramokból áramfluktuációk alakulnak ki.
Ezt, az elektronok termikus fluktuációjából adódó zajt nevezzük termikus zajnak. Jellegét tekintve ez a zaj egy fehér zaj, azaz a zajsűrűsége független a frekvenciától.
A Drude-modell értelmében az elektronok elektromos tér által nyert impulzusát a kristályráccsal történő ütközése (szóródás, rácsrezgés keltése) során veszíti el. A modell értelmében a fajlagos vezetőképesség ( ) arányos az elektronok átlagos sűrűségével (
) arányos az elektronok átlagos sűrűségével ( ), töltésük négyzetével (
), töltésük négyzetével ( ) és az átlagosan két ütközés között eltelt idővel (
) és az átlagosan két ütközés között eltelt idővel ( ), továbbá fordítottan arányos az elektron tömegével (
), továbbá fordítottan arányos az elektron tömegével ( ):
):
![\[\sigma=\frac{ne^2\tau}{m}.\]](/images/math/d/2/7/d272d9a77f5c05c819ce3d63089929dc.png)
Most vizsgáljuk meg ugyanezen rendszer áramzaját külső feszültség nélkül. (Tételezzük fel, hogy a vizsgált vezető mintánk két végét egy árammérővel összekötve mérjük az áramfluktuációkat.) A  karakterisztikus időnként elszenvedett ütközések miatt az áram korrelációja is elvész. Ezt egy
karakterisztikus időnként elszenvedett ütközések miatt az áram korrelációja is elvész. Ezt egy  időállandóval jellemzett exponenciálisan lecsengő korrelációs függvénnyel modellezzük:
időállandóval jellemzett exponenciálisan lecsengő korrelációs függvénnyel modellezzük:
![\[C(\Delta t)=C_0e^{-\frac{|\Delta t|}{\tau}}.\]](/images/math/8/c/b/8cb50ea92d26e5cfbf8154d9b6460f95.png)
Ilyen korrelációs függvény esetén a zajsűrűségre a következő érték adódik:
![\[s_I(\omega)=2c(\omega)=2\int_{-\infty}^{\infty}dte^{-i\omega t}C_0e^{-\frac{|\Delta t|}{\tau}}=\frac{4C_0\tau}{1+\omega^2\tau^2}.\]](/images/math/2/0/7/20768e384b97f92ab829ba61c33e9941.png)
A feladat tehát nem más, mint a 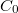 érték, azaz az áram teljes szórásnégyzetének a meghatározása a Drude-modell segítségével.
Vizsgáljunk egy
érték, azaz az áram teljes szórásnégyzetének a meghatározása a Drude-modell segítségével.
Vizsgáljunk egy  keresztmetszetű,
keresztmetszetű,  hosszúságú téglalap alakú dobozt. Ebben egy elektron árama a következőképpen fejezhető ki:
hosszúságú téglalap alakú dobozt. Ebben egy elektron árama a következőképpen fejezhető ki:
![\[I_1=-Anev_x(t)=-\frac{e}{L}v_x(t),\]](/images/math/4/e/b/4ebadeb87b1e436313b4ff6c953affdf.png)
ahol 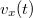 a részecske
a részecske  irányú, azaz a doboz hosszanti irányába mutató sebessége adott
irányú, azaz a doboz hosszanti irányába mutató sebessége adott  időpillanatban.
Innen következik egy elektron áram-áram korrelációs függvénye:
időpillanatban.
Innen következik egy elektron áram-áram korrelációs függvénye:
![\[\langle (\Delta I_1(t))^2\rangle=\frac{e^2}{L^2}\langle v_x^2(t)^2\rangle.\]](/images/math/9/f/b/9fb04c1d2167158df99085550836afbd.png)
N független elektronra a szórásnégyzetek összeadódnak:
![\[\langle (\Delta I(t))^2\rangle=C_0=N\langle (\Delta I_1(t))^2\rangle=N\frac{e^2}{L^2}\langle v_x^2(t)\rangle.\]](/images/math/c/6/9/c69c4ba2e2224f9544750bd1347d921e.png)
Bővítsük a törtet 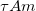 -mel, hogy észrevegyük benne a Drude-modell vezetőképességét:
-mel, hogy észrevegyük benne a Drude-modell vezetőképességét:
![\[C_0=\frac{N}{AL}\frac{e^2\tau}{m}\frac{A}{L}\frac{1}{\tau}m\langle v_x^2(t)\rangle =\frac{G}{\tau}m\langle v_x^2(t)\rangle.\]](/images/math/b/f/3/bf3b4bc698599d537c0d1d7b318041cc.png)
Tovább egyszerűsödik a képlet a klasszikus ekvipartíciós tételt alkalmazva:
![\[C_0=\frac{G}{\tau}k_BT.\]](/images/math/e/0/c/e0c9b547ca4a0e0d53c308478bda303b.png)
Ezt felhasználva, továbbá élve azzal a közelítéssel, hogy a frekvencia sokkal kisebb az átlagos ütözkési idő reciprokánál, adódik a termikus áramzaj spektrális sűrűsége:
![\[s_I(\omega)=\frac{4C_0\tau}{1+\omega^2\tau^2}=\frac{4k_BTG}{1+\omega^2\tau^2}\approx 4k_BTG.\]](/images/math/c/f/6/cf603a783cd205ed68579aa19284d006.png)
Felhasználva, hogy 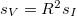 a feszültségzaj spektrális sűrűsége:
a feszültségzaj spektrális sűrűsége:
![\[s_V=4k_BTR.\]](/images/math/9/d/5/9d568e509d842e9eba8731ca66db5a51.png)
Ezzel számítással is beláttuk a termikus zaj fehér zaj jellegét, továbbá azt is látjuk, hogy a zaj mértéke arányos a hőmérséklettel és az ellenállás nagyságával.
Meg kell jegyezni továbbá, hogy a számolás két helyen sem volt teljesen korrekt. Egyrészt csak a Fermi-energia körüli 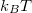 energiasávban lévő elektronok tekinthetők valamilyen szinten függetlennek, a mélyebb energiákon lévő elektronállapotok mindegyike teljesen betöltött, így az áramfluktuációjuk zérus. Másrészt a Fermi-Dirac-eloszlást követő elektronok sebességét nem írhatjuk le az ekvipartíció tétellel, hanem a zajhoz járulékot adó részlegesen betöltött elektronállapotok alapvetően a Fermi-sebességgel mozognak.
Ez a két hiba kompenzálja egymást, és korrekt szilárdtestfizikai számításokkal is a végeredményben kapott képlettel azonos eredményre jutunk.
energiasávban lévő elektronok tekinthetők valamilyen szinten függetlennek, a mélyebb energiákon lévő elektronállapotok mindegyike teljesen betöltött, így az áramfluktuációjuk zérus. Másrészt a Fermi-Dirac-eloszlást követő elektronok sebességét nem írhatjuk le az ekvipartíció tétellel, hanem a zajhoz járulékot adó részlegesen betöltött elektronállapotok alapvetően a Fermi-sebességgel mozognak.
Ez a két hiba kompenzálja egymást, és korrekt szilárdtestfizikai számításokkal is a végeredményben kapott képlettel azonos eredményre jutunk.
Poisson zaj
A Poisson-zaj az elektronok diszkrét töltéséből fakadó áramzajnak, azaz a sörétzaj egy speciális fajtája. A Poisson-zaj specialitását az egymástól független elektronok detektálása jelenti. Az elnevezése is innen származik, hiszen ahogyan a klasszikus példában a véletlen időközönként elsütött puskagolyók, úgy az egymástól függetlenül kilépő elektronok száma is Poisson-eloszlást mutat. A Poisson-eloszlás sörétzaj szempontjából fontos tulajdonsága, hogy a várható értéke megegyezik a szórásnégyzetével:
![\[\langle N\rangle=\langle (\Delta N)^2\rangle.\]](/images/math/0/c/b/0cbf76e8a53c85f26d6b4cbeaafb2b77.png)
Tegyük fel, hogy  idő alatt átlagosan N elektron lép ki az egyik elektródából. Ekkor az áram várható értéke a következőképpen definiálható:
idő alatt átlagosan N elektron lép ki az egyik elektródából. Ekkor az áram várható értéke a következőképpen definiálható:
![\[\langle I\rangle=\langle N\rangle\frac{e}{\Delta t}.\]](/images/math/4/3/1/43134253ea237625df6026d88d1889a6.png)
Az áram szórásnégyzete pedig felhasználva a várható érték és szórásnégyzet közötti egyenlőséget:
![\[\langle (\Delta I)^2\rangle=\langle (\Delta N)^2\rangle\left(\dfrac{e}{\Delta t}\right)^2=\langle I\rangle\frac{e}{\Delta t}.\]](/images/math/9/e/5/9e543806163d27007b6da7d9ad38faa8.png)
Ebben az esetben azonban a  nem a fentebb definiált két diszkrét mintavételezés között eltelt időt jelenti, hanem azt az időintervallumot, amelyen belül az áram várható értéke
nem a fentebb definiált két diszkrét mintavételezés között eltelt időt jelenti, hanem azt az időintervallumot, amelyen belül az áram várható értéke 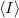 , illetve szórásnégyzete
, illetve szórásnégyzete 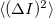 .
.
Határozzuk meg ebben az időintervallumban az átlagos áramot. Ehhez a jelünket konvolváljuk össze egy 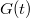 függvénnyel, amely egyenlő
függvénnyel, amely egyenlő 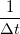 -vel, ha
-vel, ha 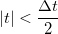 , egyébként nulla.
, egyébként nulla.
![\[I_{out}(t)=\int_{-\infty}^{\infty}dt'I_{in}(t')G(t-t')=\frac{1}{\Delta t}\int_{t-\frac{\Delta t}{2}}^{t+\frac{\Delta t}{2}}dt'I_{in}(t').\]](/images/math/f/d/d/fdda2738e77acc0eb16abe5aa0d08a3d.png)
A konvolúció Fourier-transzformáltja a Fourier-transzformáltak szorzatával egyenlő:
![\[i_{out}(\omega)=i_{in}(\omega)g(\omega).\]](/images/math/8/2/9/829367a8b41b6331e7bc923cc438ff6e.png)
Ez az összefüggés azt sejteti, hogy a konvolváló függvény szűrőként viselkedik. Mivel a zaj az áram Fourier-transzformáltjának négyzetével arányos az áramzajok aránya a szűrő karakterisztika Fourier-transzformáltjának négyzete lesz:
![\[s_{out}(\omega)=s_{in}(\omega)g^2(\omega).\]](/images/math/7/5/9/759ca2234c0102cf091504ed2482f1c8.png)
Vizsgáljuk meg a szűrő karakterisztikáját:
![\[g(\omega)=\int_{-\infty}^{\infty}dtg(t)e^{-i\omega t}=\frac{1}{\Delta t}\int_{-\frac{\Delta t}{2}}^{+\frac{\Delta t}{2}}dte^{-i\omega t}=\frac{2}{\omega \Delta t}sin\left(\frac{\omega \Delta t}{2}\right).\]](/images/math/2/6/9/269f158eea7317a97e5628f40d665bef.png)
A továbbiakhoz bevezetjük az ekvivalens zaj sávszélesség (Equivalent Noise Bandwidth, ENBW) fogalmát. Az ENBW az a sávszélesség, amelyen fehér zajt feltételezve ugyanakkorának adódik az áram szórásnégyzete, mint a szűrőnkön mérve.
![\[\langle (\Delta I)^2\rangle=\frac{1}{2\pi}\int_{0}^{\infty}d\omega s_{out}(\omega)=\frac{s_0}{\pi \Delta t}\int_{0}^{\infty}\frac{sin^2(x)}{x^2}=\frac{s_0}{2\Delta t}=s_0f_{max}.\]](/images/math/c/a/2/ca22cb4ebe7355290d5225c1e22fd173.png)
Azaz az ekvivalens zaj sávszélesség:
![\[ENBW=\frac{1}{2\Delta t}.\]](/images/math/7/c/e/7ce1c947eb5c347f8259226055c573ec.png)
Ez az összefüggés érezhetően összecseng a Nquist-Shannon mintavételezési törvénnyel. Ha egy  időablakra átlagolunk egy jelet, az a konvolúció egy olyan szűrőként viselkedik a frekvenciatérben, melyen keresztül fehér zajt mérve az áram szórásnégyzet egyenlő lesz egy
időablakra átlagolunk egy jelet, az a konvolúció egy olyan szűrőként viselkedik a frekvenciatérben, melyen keresztül fehér zajt mérve az áram szórásnégyzet egyenlő lesz egy 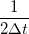 tökéletes sávszűrőn mért szórásnégyzettel.
tökéletes sávszűrőn mért szórásnégyzettel.
Most vizsgáljuk az áram szórásnégyzetét:
![\[\langle (\Delta I)^2\rangle=\langle I\rangle\dfrac{e}{\Delta t}=\int_{0}^{\infty}s_I(f)g(f)df=\int_{0}^{\frac{1}{2\Delta t}}s_I(f)df.\]](/images/math/c/2/0/c20ebbde3fd6c7b498184f399cf0c8ab.png)
Ez bármely  szélességű átlagolási időre csak akkor teljesülhet, ha a zajsűrűség független a frekvenciától, értéke pedig:
szélességű átlagolási időre csak akkor teljesülhet, ha a zajsűrűség független a frekvenciától, értéke pedig:
![\[s_I(f)=2e\langle I\rangle.\]](/images/math/0/b/7/0b7c201ad4cc0af42ed36530052db89f.png)
Aliasing jelenség
A DFT a mért jel spektrumát  és
és 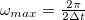 frekvenciák közötti diszkrét pontokon értékeli ki. Felmerül a kérdés, hogy egy
frekvenciák közötti diszkrét pontokon értékeli ki. Felmerül a kérdés, hogy egy 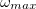 -nál nagyobb frekvenciakomponenseket tartalmazó jelnél mi történik a magas frekvenciakomponensekkel.
-nál nagyobb frekvenciakomponenseket tartalmazó jelnél mi történik a magas frekvenciakomponensekkel.
Vizsgáljunk egy  frekvenciájú tiszta szinuszos jelet:
frekvenciájú tiszta szinuszos jelet:
![\[F(t)=A_0e^{i\omega_0t}.\]](/images/math/2/4/5/245b0442ddc0df9d07406191c01c8389.png)
Vegyük ennek a jelnek a Fourier-transzformáltját:
![\[f(\omega)=\int_{-\infty}^{\infty}A_0e^{i\omega_0t}e^{-i\omega t}dt=A_02\pi\delta(\omega-\omega_0).\]](/images/math/8/8/7/88791b26a657f44c0a4a149987bb78bc.png)
A jel Fourier-transzformáltja tehát a várakozásnak megfelelően egy Dirac-delta. Most nézzük meg, hogy a DFT számolása során hogyan változik a spektrum meghatározása a gyakorlatban.
![\[DFT(\omega_k)=\sum_{n=0}^{N-1}A_0e^{i\omega_0n\Delta t}W(n\Delta t)e^{-i\omega_k n\Delta t}\Delta t.\]](/images/math/7/7/4/77454b64a192deb67b7e8ea793f4485d.png)
Vegyük észre, hogy
![\[DFT(\omega_k)=DFT\left(\omega_k+\frac{2\pi m}{\Delta t}\right),\]](/images/math/f/d/3/fd376985dc4b0bb692451f12d2b4dc6c.png)
ahol  egész szám. Másrészt
egész szám. Másrészt
![\[DFT(\omega_k)=DFT^*(-\omega_k),\]](/images/math/5/e/6/5e6d6b14e0209e2955a599f2e5c37a67.png)
azaz
![\[\left|DFT(\omega_k)\right|=|DFT(-\omega_k)|.\]](/images/math/8/0/d/80ddbb4ed0ee9ca1958dfae37b6c7c3e.png)
Így belátható, hogy tetszőleges magas körfrekvenciájú jelet úgy látunk, mint ha az a ![\setbox0\hbox{$\left[0,\omega_{max}=\dfrac{2\pi}{2\Delta t}\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/1/d/5/1d5edc142dda0da53e19be6704cd946e.png) tartományban lévő jel lenne a saját
tartományban lévő jel lenne a saját 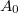 amplitúdójával.
amplitúdójával.
A 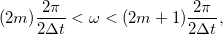
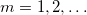 frekvenciatartományokban lévő komponensek az
frekvenciatartományokban lévő komponensek az 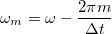 frekvencián jelennek meg a spektrumban, míg a
frekvencián jelennek meg a spektrumban, míg a 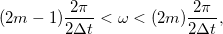
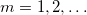 tartományokban lévők a
tartományokban lévők a 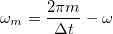 frekvencián.
frekvencián.
A fentiekkel beláttuk, hogy minden 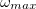 -nál nagyobb frekvenciatag megjelenik a DFT-t követően a diszkrét frekvenciákat tartalmazó
-nál nagyobb frekvenciatag megjelenik a DFT-t követően a diszkrét frekvenciákat tartalmazó ![\setbox0\hbox{$[0,\omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/5/8/9/589da9a19c34b829d19740c9873851cf.png) tartományban. Gondoljuk át, hogy a végeredményben kapott DFT spektrum
tartományban. Gondoljuk át, hogy a végeredményben kapott DFT spektrum 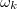 pontjában összeadódnak-e a
pontjában összeadódnak-e a 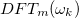 tagok amplitúdói
tagok amplitúdói 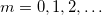 értékekre. Mivel ezen frekvenciatagok fázisai nem azonosak, így a különböző
értékekre. Mivel ezen frekvenciatagok fázisai nem azonosak, így a különböző  értékekhez tartozó amplitúdók nem adhatóak össze.
értékekhez tartozó amplitúdók nem adhatóak össze.
Később látni fogjuk, hogy a zajsűrűség számításához a DFT abszolútérték négyzetére van szükség, amely azonban a véletlenszerű, egymástól független fázisok miatt egyenlő a különböző  értékekre vett amplitúdók négyzeteivel:
értékekre vett amplitúdók négyzeteivel:
![\[|DFT(\omega_k)|^2=\left(\sum_{m}^{} DFT_m(\omega_k)\right)\left(\sum_{m}^{} DFT^*_m(\omega_k)\right)=\sum_{m}^{}|DFT_m(\omega_k)|^2.\]](/images/math/1/7/b/17bbdbf920eb8fad23dd47b01b2d3d7f.png)
A leképezés leginkább úgy képzelhető el, mint a magas frekvenciás tartományok 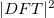 -einek a
-einek a ![\setbox0\hbox{$[0,\omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/5/8/9/589da9a19c34b829d19740c9873851cf.png) intervallumra történő visszahajtogatása. Az
intervallumra történő visszahajtogatása. Az 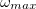 fölötti részt visszahajtjuk
fölötti részt visszahajtjuk ![\setbox0\hbox{$[-\infty; \omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/7/e/1/7e1583c668f4dc9fea3cf73d3c7fb0ab.png) intervallumra. Majd ezt a visszahajtott spektrumot 0
intervallumra. Majd ezt a visszahajtott spektrumot 0 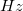 -nél előrehajtjuk, stb. Ezt mindaddig folytatjuk, amíg minden jelentős frekvenciakomponenst be nem hajtottunk a
-nél előrehajtjuk, stb. Ezt mindaddig folytatjuk, amíg minden jelentős frekvenciakomponenst be nem hajtottunk a ![\setbox0\hbox{$[0,\omega_{max}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/5/8/9/589da9a19c34b829d19740c9873851cf.png) intervallumba.
intervallumba.
Beláttuk, hogy a magas komponensű jelek fals spektrumot okozhatnak, így gondoskodni kell kiszűrésükről egy aluláteresztő szűrővel. Ezt a jelenséget aliasingnak, azaz magas frekvenciájú komponensek beszűrődésének nevezzük. Fontos megjegyezni, hogy az aliasing kialakulásának az oka a DFT diszkrét mintavételezése, és független a mérési pontok  számától. A gyakorlatban a legtöbbször az erősítők, vagy a mérőkártyák rendelkeznek anti-aliasing szűrővel, ami a maximális frekvencia fölött rendszerint élesen levágja a spektrumot.
számától. A gyakorlatban a legtöbbször az erősítők, vagy a mérőkártyák rendelkeznek anti-aliasing szűrővel, ami a maximális frekvencia fölött rendszerint élesen levágja a spektrumot.