Matlab szimulációk
Tartalomjegyzék |
MATLAB programok
A fizikában tanultak mélyebb elsajátítása érdekében érdemes az itt található MATLAB programok lefuttatása, értelmezése, és módosítása. A programok MATLAB Version 7.3.0.267 (R2006b)-nal készültek. A függvények és szkriptek a MATLAB 7.xx verzióval lefutnak. A különálló felhasználói felületnél erősebb a verzió függés.
A programok forráskódja tartalmazza a probléma rövid leírását - ahol szükséges - utalást a megoldási módszerre. Egyes esetekben külön feladatok is találhatók a forráskódban.
A továbbiak röviden bemutatják az egyes MATLAB programokat.
Hajítás
A MATLAB program azt az esetet vizsgálja, amikor a közegellenállás nem elhanyagolható. Ez előfordulhat például abban az esetben, amikor nagy a vizsgált test sebessége, nem pontszerű a test, a közeg viszkozitása számottevő stb.. Ebben az esetben az egyik lehetséges megközelítés a sebesség valamely hatványával arányos fékező erő feltételezése. Természetesen különböző sebesség tartományban más és más lehet a fékező erő alakja. Kvalitatíve azt lehet mondani, hogy kis sebességeknél a fékező erőt elhanyagoljuk, nagy sebességeknél a sebesség nagyságának első hatványával arányos. Még nagyobb sebességeknél már a második hatvány jelenik meg. Általában érdemes ún. szélcsatornában végzett mérésekkel meghatározni a fékező erőt a sebesség függvényében.
Jelen MATLAB program azt az esetet kezeli, amikor a fékező erő a sebesség nagyságának négyzetével arányos. A program a légellenállási paraméter nullának való választásakor a vákuumban történő hajítást modellezi. A program könnyen módosítható a sebesség nagyságától lineárisan függő fékező erő leírására.
Rezgőmozgás
A MATLAB program segítségével a szabad rezgéseket és a gerjesztett rezgéseket tanulmányozhatjuk. A fizikai probléma a tömegpontok egydimenziós mozgásának témakörébe tartozik (Lásd Rezgések). Inerciarendszerben felírt mozgásegyenlet matematikai szempontból másodrendű közönséges differenciál-egyenlet kezdetiérték problémájának megoldására vezet.
MATLAB programban ez az ODE megoldó függvények segítségével történhet a legegyszerűbben (ODE45, OE15s stb.). Természetesen mindegyik megoldó esetén érdemes elolvasni a MATLAB dokumentációt (pl. be kell írni: doc ode45). Mivel másodrendű differenciálegyenletet kell megoldani, ezért egy adott időpillanatban meg kell adni a tömegpont kitérését és sebességét egyidejűleg.
A különböző szimulált esetek:
Szabad rezgések: harmonikus rezgőmozgás, sebességgel arányos csillapítás. Harmonikus rezgőmozgás esetén érdemes változtatni a kezdeti feltételeket, a tömeget, a rugóállandót. A fenti paraméterek változtatása esetén érdemes megnézni, hogyan változik az idő függvényében a sebesség és kitérés. Sebességgel arányos csillapítás esetén a rugóállandó, a tömeg és a csillapításra jellemző együttható megfelelő értekei mellett jól megfigyelhető három fizikai szempontpontból különböző eset: rezgő mozgás, aperiodikus mozgás, aperiodikus határeset. Ne feledjük, hogy a tömegpont aperiodikus határesetben éri el leghamarabb az egyensúlyi helyzetet. Ez az eset hasznos a mérőműszerek kényelmes és pontos leolvasásakor.
Gerjesztett rezgőmozgás: A gerjesztett rezgőmozgás során a tömegpontra a következő erők hatnak: lineáris rugó erő, sebességgel arányos csillapító erő és harmonikus gerjesztőerő. A szimulációs program futtatásakor érdemes változtatni a gerjesztő frekvenciát, megkeresni azt a gerjesztő frekvencia értéket, amikor maximális a kitérés amplitúdó, vagy a sebesség amplitúdó időben állandósult esetben.
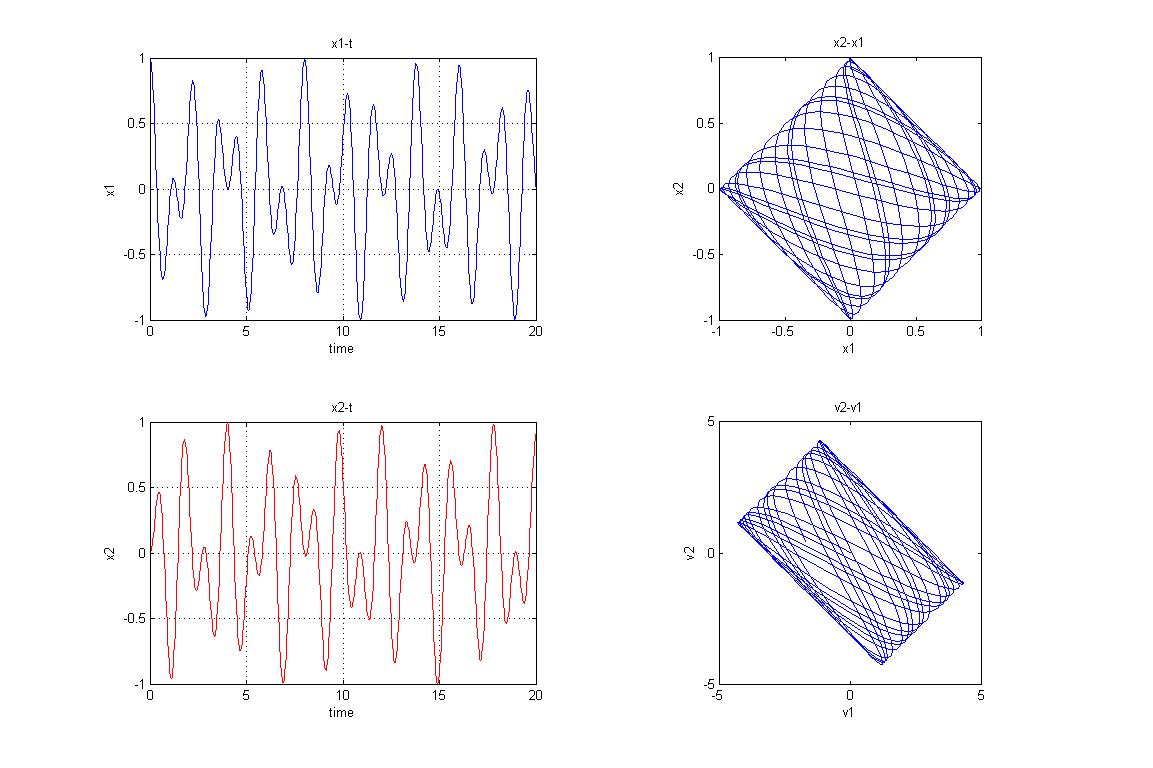
Csatolt rezgés: Két tömegpont csatolt rezgése során az egyes tömegpontokra egyrészt lineáris rugóerő hat, valamint egymásra való kölcsönhatásukat, ún. csatolásukat szintén lineáris rugóerővel írjuk le. Természetesen általánosabb esetben nem szükségszerű, hogy az erőhatások az egyensúlyi helyzettől való kitéréssel arányosak, vagyis lineárisak legyenek. A csatolt rezgés MATLAB programjában ez könnyen megváltoztatható, és az ODE típusú numerikus MATLAB megoldók ezt általában minden további nélkül sikeresen kezelik. A mozgásegyenlet csatolt közönséges differenciál egyenlet rendszerre vezet.
![\[ m_{1} \ddot x_{1}=-D_{1} x_{1} + D (x_{2}-x_{1}) \]](/images/math/8/d/2/8d2d6a5bb242ef12267fc8d9c1e1f545.png)
![\[ m_{2} \ddot x_{2}=-D_{2} x_{2} + D (x_{1}-x_{2}), \]](/images/math/9/9/5/99521b69443e9e0eccf0e33bb595e7f0.png)
Az indexek az 1-es ill. 2-es tömegpontra utalnak.  a tömeg,
a tömeg,  az egyensúlyi helyzettől való kitérés,
az egyensúlyi helyzettől való kitérés, 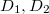 az 1-es ill. 2-es tömegpontra ható lineáris erő rugóállandója,
az 1-es ill. 2-es tömegpontra ható lineáris erő rugóállandója,  rugóállandó a két tömegpont kölcsönhatása során fellépő erőt jellemző rugóállandó. Ha
rugóállandó a két tömegpont kölcsönhatása során fellépő erőt jellemző rugóállandó. Ha 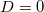 , akkor a két tömegpont között nincs kölcsönhatás. Az egyes tömegpontok mozgása egymástól független. Ha
, akkor a két tömegpont között nincs kölcsönhatás. Az egyes tömegpontok mozgása egymástól független. Ha  értékét növeljük, akkor a tömegpontok egyre inkább befolyásolják egymás mozgását. Természetesen a különböző kezdeti feltételek igen eltérő mozgást eredményezhetnek. Ezek mind megfigyelhetők a MATLAB program futtatásakor.
értékét növeljük, akkor a tömegpontok egyre inkább befolyásolják egymás mozgását. Természetesen a különböző kezdeti feltételek igen eltérő mozgást eredményezhetnek. Ezek mind megfigyelhetők a MATLAB program futtatásakor.
Rezgések összetevése
Képzeljük el, hogy egy tömegpontra több erő hat. Ebben az esetben a szuperpozíció elve alapján a tömegpont eredő mozgását úgyis meg tudjuk adni, hogy az egyes erők által okozott mozgásokat összegezzük. Két alapvetően különböző eset van. Az egyik esetben a tömegpontra ható erők hatásvonala párhuzamos, ekkor a létrejött rezgések is egy irány mentén történnek. A másik esetben nem áll fenn ez a párhuzamosság. Ekkor vektoriális összegzéssel jutunk eredményre. A MATLAB program az első esetben két egyirányú rezgés összetevését vizsgálja, amelyet a rezgések párhuzamos összetevésének nevezünk. A másik esetben két egymásra merőleges rezgés összetevését adja meg. Természetesen a MATLAB programkód továbbfejleszthető kettőnél több rezgés összetevésének elemzésére is.
Hullámmozgás
1D hullám terjedése rugalmas közegben
Hullám rugalmas közegben történő egydimenziós terjedését a következő parciális differenciál egyenlet írja le:
![\[ \frac{\partial^{2}\Psi}{\partial t^{2}}=c^{2}\frac{\partial^{2}\Psi}{\partial x^{2}},\]](/images/math/e/d/7/ed770eaaab8c1549ee1e0bcad7d0b7c6.png)
ahol 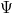 a helytől (
a helytől ( ) és időtől (
) és időtől ( ) függő hullámfüggvény,
) függő hullámfüggvény,  a hullám terjedési sebessége.
A probléma ún. vegyes probléma.
a hullám terjedési sebessége.
A probléma ún. vegyes probléma.
- Meg kell adni a kezdeti időpontban a hullámfüggvényt és annak idő szerinti deriváltját. (Pl. egy Gauss-féle hullámcsomag, és annak idő szerinti deriváltja.)
- Meg kell adni a vizsgált időtartományban a perempontokban a hullámfüggvény értékét. (Pl. a végeken rögzített értékű hullámfüggvény, ez felel meg a befogott húr esetének.)
A fenti hullámegyenlet megoldása explicit véges differencia sémával történik a mellékelt MATLAB programban.
Jól megfigyelhető a hullámcsomag terjedése, a rögzített végeken történő 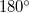 -os fázisugrás.
-os fázisugrás.