Piezoelektromos anyagok
==Piezoelektromos állandók mérése==
A mérés célja: megismertetni a hallgatókat a
-piezoelektromos effektusokkal,
-a piezoelektromos állandók értelmezésével,
-illetve azok kísérleti meghatározási módszereivel.
A cél érdekében
- értelmezzük a piezoelektromos állandókat,
- ismertetjük a kísérleti meghatározás lehetőségeit,
- ismertetjük a mérés során alkalmazott vizsgálati módszereket, a mérőkészülék felépítését és működését,
- megmérjük kerámia minták piezoelektromos állandóit.
== 1. Elméleti ismeretek == (Szerkesztés alatt!)
Ha egy anyagot valamilyen külső hatás ér, akkor abban különböző változások jönnek létre, az anyag valamilyen módon „reagál” a külső hatásokra, amit megfigyelőként a hatástól függő jelenségként észlelünk. Mind az anyagot ért hatások, mind pedig az anyagban ilyenkor észlelhető jelenségek fizikai szempontból valamilyen fizikai mennyiséggel – illetve annak megváltozásával – jellemezhetők. Az, hogy meghatározott körülmények között egy hatás milyen erősségű változást (jelenséget) hoz létre, függ a vizsgált anyagtól, pontosabban az anyagnak az adott jelenség szempontjából fontos tulajdonságától.
Például: ha egy anyagot melegítünk, akkor az anyagot ért hatás a hőmérséklet változásával jellemezhető, a hőmérsékletváltozás által kiváltott egyik lehetséges jelenség pedig az, hogy megváltozik az anyag térfogata. Ugyanolyan hőmérsékletváltozás azonban különböző anyagokban különböző térfogatváltozást okoz, vagyis a jelenség „mértéke” az anyagi minőségtől függ és az anyag egy tulajdonságával – a térfogati hőtágulási együtthatóval – jellemezhető. Egy másik ismert példa, hogy egy szigetelőanyag elektromos tér hatására polarizálódik. Itt a hatás az elektromos térerősségvektorral, a jelenség a polarizáció-vektorral, a jelenségnek az anyagi minőségtől való függése pedig egy tenzorral, a dielektromos szuszceptibilitás tenzorával jellemezhető. Hasonlóan: egy test erőhatás következtében létrejövő alakváltozása esetén a hatás a feszültségtenzorral, a jelenség az alakváltozási tenzorral, az anyag tulajdonságai pedig a rugalmas együtthatókkal (amelyek ugyancsak tenzort alkotnak) jellemezhető.
A jelenségek számszerű leírásának alapvető feltétele az, hogy a vizsgált esetre vonatkozóan ismerjük a hatást, a jelenséget és a tulajdonságot jellemző fizikai mennyiségek közötti összefüggést. Szerencsére számos olyan jelenséget ismerünk amelynél – nem túl nagy hatások esetén – ez az összefüggés igen egyszerű formában írható fel. A pontos megfogalmazást egyenlőre mellőzve, azt mondhatjuk, hogy a hatást és a jelenséget jellemző mennyiségek között egyfajta lineáris összefüggés áll fenn, amely szimbolikusan az alábbi alakban írhatunk fel:jelenség= tulajdonság* hatás (1)
Itt a „jelenség”, „tulajdonság”, „hatás” elnevezés fizikai mennyiségeket jelöl, amelyek matematikai szempontból skaláris- vektor- vagy tenzormennyiségek lehetnek. Ennek megfelelően a „*” jel is különböző műveleteket jelenthet.
Az említett példák közül az állandó nyomás (P) mellett végbemenő hőtágulás esetében a hatás a hőmérsékletváltozás, a jelenség a térfogatváltozás, a tulajdonság pedig az térfogati hőtágulási együttható. Az említett mennyiségek között az egyszerű
(2)
tapasztalati összefüggés áll fenn (itt mindhárom mennyiség skalár). A másik példában a hatást jellemző E tér-erősség-vektor és a jelenséget jellemző P polari-záció-vektor kapcsolata – a vektorok derékszögű koordinátarendszerbeli komponenseit 1, 2, 3-mal jelölve – az alábbi lineáris egyenletekkel adható meg
(3)
Az egyenletben szereplő mennyiségek egy másodrendű tenzor komponensei, amelyet a
(4)
szimbólummal jelölhetünk. Ezzel a jelöléssel a (3) egyenleteket sűrített formában gyakran az alábbi módón írják fel.:
P = E (5)
Ez az írásmód egy ilyen – másodrendű tenzort -tartalmazó egyenletnél még egyértelmű, maga-sabb rendű tenzorok esetén azonban nem derül ki belőle a szereplő tenzorok rendje, ezért he-lyette rendszerint az egyenleteket – bizonyos megállapodásokkal – rövidített indexes alakban használják. A (3) egyenlet ilyen indexes alakja:
(6)
azzal a megállapodással, hogy az egyenletben ugyanazon tagban előforduló, megegyező inde-xekre (a (6) egyenletben tehát j-re) összegezni kell, a magában álló index (i) helyébe pedig az 1, 2, vagy 3 érték helyettesítendő be ( így kapunk 3 egyenletet). Ugyanilyen alakban írható fel a másodrendű tenzorral jellemezhető mechanikai feszültség ( ) és a deformáció ( ) közötti kapcsolatot megadó általános Hooke-törvény is:
(7)
ahol a mennyiségek egy negyedrendű tenzor komponensei, amelyeket rugalmas állan-dóknak neveznek. Ugyanez a törvény úgy is felírható, hogy a deformációkat fejezzük ki a feszültségekkel, azaz
(8)
Az itt szereplő mennyiségek szintén egy ne-gyedrendű tenzort alkotnak, amelyeket merev-ségi együtthatóknak neveznek. Mivel gyakran előfordul, hogy ugyanazt a je-lenséget többféle hatás is létrehozhatja, fontos megadni, hogy a jelenség milyen feltételek kö-zött ment végbe. Ennek megfelelően a fenti egyenletek csak akkor érvényesek, ha a jelensé-get a vizsgált esetekben csak az egyenletekben szereplő egyetlen hatás váltja ki. A továbbiakban vizsgálandó jelenségek éppen azzal kapcsolato-sak, hogy bizonyos anyagokban elektromos po-larizációt nem csak az elektromos tér, hanem más hatások is létrehozhatnak, illetve hogy egy anyag deformációja nem csak mechanikai fe-szültség, hanem más hatások eredménye is lehet, és ilyenkor a (6) és a (8) egyenletet módosítani kell. A tapasztalat azt mutatja, hogy polarizáció- változást – az elektromos tér mellett - létrehoz-hat hőmérsékletváltozás és mechanikai feszült-ség is. Azt a jelenséget, melynek során egy anyag polarizációja megváltozik, piroelektromos ef-fektusnak nevezik. A hőmérsékletváltozás ( ) által létrehozott polarizáció a már említett lineá-ris séma szerint fejezhető ki a hőmérsékletválto-zással:
, (9)
ahol a mennyiségek a piroelektromos együtt-hatók, amelyek egy vektor (elsőrendű tenzor) komponensei. Bizonyos anyagokban polarizáció-változást mechanikai feszültség is eredményezhet. Ezt a jelenséget piezoelektromos effektusnak neve-zik, és a mechanikai feszültség által létrehozott polarizációra szintén a fentiekhez hasonló lineá-ris törvény érvényes:
. (10)
A mennyiségek egy harmadrendű tenzort alkotnak, amelyeket piezoelektromos modulu-soknak neveznek. A piezoelektromos effektust mutatóanyagok a piezoelektromos anyagok. Az elektromos tér, hőmérsékletváltozás és mechanikai feszültség együttes hatása miatt lét-rejött polarizációt a szuperpozíció elvének al-kalmazásával a (6), (9), és (10) egyenletekből kapjuk meg:
. (11)
A három effektus közül a továbbiakban a piezo-elektromos effektussal foglalkozunk, és feltéte-lezzük, hogy a másik két hatás által okozott po-larizáció elhanyagolható, vagyis a (11) általános egyenlet helyett a (10) egyenlet használható. Tapasztalatból tudjuk, hogy egy test defor-mációja nem csak mechanikai feszültség, hanem hőmérsékletváltozás és – bizonyos anyagokban – elektromos tér hatására is létrejöhet. A hőtágulás jelensége eléggé ismert, anizotróp anyagokban azonban a hőtágulás is irányfüggő lehet, így a jelenséget leíró egyenlet az alábbi alakban írható fel:
. (12)
Az konstansok hőtágulási együtthatók, ame-lyek egy másodrendű tenzort alkotnak. Piezoelektromos anyagokban deformáció lét-rejöhet elektromos tér hatására is. Ez a jelenség az inverz piezoelektromos effektus, amelynek leírása a szokásos lineáris egyenletekkel történik:
(13)
Ebben az egyenletben ugyanazok az állandók szerepelnek, mint a piezoelektromos effektust leíró (10) egyenletben. A három hatás együttes eredményeként létre-jött deformációt az alábbi összefüggés adja meg
(14)
A továbbiakban ezek közül a jelenségek közül csak az inverz piezoelektromos effektussal fog-lalkozunk, és feltételezzük, hogy a deformáció egyedüli oka az elektromos tér, vagyis használ-hatjuk a speciális estre vonatkozó (13) össze-függést.
A piezoelektromos effektusok (piezoelekt-romos- és inverz piezoelektromos effektus) gya-korlati felhasználása azon alapul, hogy egy test felületén külső mechanikai hatás következmé-nyeként megváltozik az elektromos töltéselosz-lás, illetve a külső elektromos tér a testet defor-málja. A gyakorlatban az ilyen anyagok egyre nagyobb szerepet kapnak, mint erő- és elmozdu-lás érzékelők, rezgéskeltők, nagypontosságú mechanikai helyzetbeállítók, stb. A kristályos anyagok jelentős része mutat pi-ezoelektromos tulajdonságokat, gyakorlati al-kalmazhatóságuk e jelenség mértékétől függ, ami számszerűen a piezomodulusokkal jelle-mezhető. A piezoelektromos modulus-tenzornak 27 eleme van, de szerencsére egy anyag – még a legáltalánosabb esetben is – ennél jóval kevesebb számú piezomodulussal jel-lemezhető. Tudjuk, hogy a feszültségtenzor és az alakváltozási tenzor szimmetrikus, azaz érvényes a és az összefüggés. Ez azt jelenti, hogy a test egy pontjában a fe-szültség és az alakváltozás jellemzésére csak 6-6 mennyiségre van szükség, ezért bevezették a következő indexelési konvenciót: a főátló elemei rendre 1, 2, 3, míg az azon kívüli elemek, tehát a vegyes indexű tagok a 4, 5, 6, indexeket kapják. Ezáltal a két tenzor a alábbi, 6-6 különböző elemet tartalmazó két mátrix formájában írható fel:
A mátrixokból az átindexelés pontos sémája le-olvasható. Kimutatható, hogy a fenti két tenzor szim-metrikus volta miatt a piezomodulus-tenzor elemeire is fennáll egyfajta szimmetria (a máso-dik és harmadik indexek felcserélhetők):
, (15)
aminek alapján az elemek száma itt is csökkent-hető. A tenzorkomponensek második és harma-dik indexeire alkalmazva a feszültség- és alak-változási tenzornál megismert átindexelést (111, 222, 333, 234, 135, 126), a 27 elemet tartalmazó harmadrendű kétindexes mátrix formájába írható át:
A fenti mátrixok segítségével a piezoelekt-romos effektust leíró egyenletek az eredeti (10) egyenleteknél egyszerűbb
( i= 1, 2, 3; j= 1, 2, …6) (16)
alakba írhatók. Hasonló módon egyszerűsíthetők az inverz piezoelektromos effektus (13) egyenletei is:
( i= 1, 2, 3; j= 1, 2, …6) (17)
A (16) és (17) egyenletek tovább egyszerű-södnek a vizsgált anyag kristálytani szimmetriái következtében. A kristály szimmetriáitól függő-en ugyanis a mátrix egyes elemei nullává válhatnak, illetve bizonyos elemek egymással megegyezhetnek, ami tovább csökkenti az anyag piezoelektromos tulajdonságainak jellemzéséhez szükséges független állandók és az egyenletek-ben fellépő tagok (esetleg az egyenletek) számát. A mai gyakorlatban a kristályos piezoelekt-romos anyagok közül leggyakrabban a kvarccal találkozunk (kvarcórák rezonátora), de a legna-gyobb mennyiségben alkalmazott piezoelektro-mos anyagok az ólom-cirkonát-titanát (PZT) alapú kerámiák, amelyek bizonyos területeken az olcsóbb, tömeggyártásra alkalmas technoló-giájuknak köszönhetően, az egykristályokat szinte teljesen kiszorították. A piezokerámiák polikristályos anyagok, így szerkezetükben a krisztallitok rendezetlen irányítottsággal helyez-kednek el. A gyártás során a kerámiai anyagot polarizálják, más szóval maradandó elektromos anizotrópiát alakítanak ki a szerkezetében. A polarizálás megfelelően nagy (az átütési szilárd-ságot megközelítő) elektromos térrel történik, aminek hatására a véletlenszerűen elhelyezkedő kristályszemcsék polarizációvektorai többé ke-vésbé rendeződnek, és így az anyagban mak-roszkopikus elektromos polarizáció alakul ki. Ha a 3 tengely a polarizáció irányába mutat, akkor egy ilyen polarizált kerámiában a piezo-elektromos modulus egyszerűsített mátrixa a következőképpen alakul:
A és , valamint a és elemek ér-tékei egymással megegyeznek, ezért a kerámia piezoelektromos szempontból a , , három független állandóval jellemezhető. A piezoelektromos effektust leíró egyenletek ebben az esetben tehát így alakulnak:
(18)
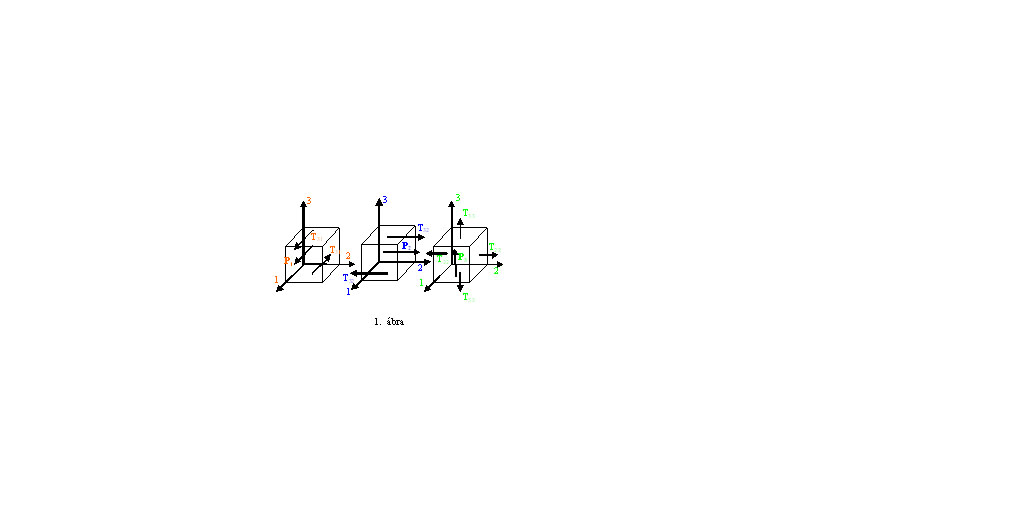
Az első egyenlet a 3 irányra merőleges síkban működő 1 irányú nyírófeszültség ( ) által az 1 irányban-, a második egyenlet a 3 irányra merőleges síkban működő 2 irányú nyírófe-szültség ( ) által a 2 irányban-, a harma-dik egyenlet pedig a három tengely irányában ható normális feszültségek ( , , ) által a 3 irányban létrehozott polari-zációt adja meg. A fentiekből látható, hogy a piezomodulus-mátrix elemeinek első indexe mindig az elektromos tér, a második pedig a mechanikai hatás irányát mutatja meg. A fe-szültségek és a létrehozott polarizáció közötti kapcsolatot az 1. ábrán mutatjuk be.
Hasonló módon kaphatók meg az inverz pie-zoelektromos effektus egyenletei, amelyek eb-ben az esetben az alábbi alakot öltik:
(19)
Mint látható, itt a piezomodulus-mátrix elemei-ben az első index a térerősség-, a második pedig a deformáció irányát mutatja meg. A állandók egysége C/N vagy az ezzel egyenértékű m/V, ami szemléletesen fejezi ki, hogy hány coulomb töltés jelenik meg 1N terhe-lőerő esetén egy hasáb alakú piezoelektromos test két szemben lévő felületén elhelyezett elekt-ródokon, illetve az inverz piezoelektromos ef-fektust kihasználva, mekkora deformációt szen-ved a test, ha az elektródokra 1V feszültséget kapcsolunk. Megjegyzendő, hogy a piezoelektromos anyagok egy részénél a fenti egyenletek nagy térerősségeknél nem használhatók, mert ilyenkor a polarizáció - mechanikai feszültség, illetve a deformáció – elektromos térerősség összefüggés nem lineáris, és a permittivitás függ a térerősség-től.