Relativitás elmélet
Törölni!!! Speciális relativitáselmélet címen új cikket hoztam létre (Sz.Zsolt)
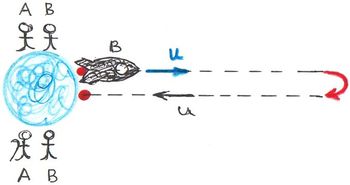
A hírek, azaz az információ megszerzése és továbbítása az Emberiség történelmének egyik fontos tényezője volt. Győzelem vagy vereség függött a gyors, pontos információáramlástól. De lehet-e vajon tetszőleges gyorsasággal hírt közölni? Az elektrodinamikából tudjuk, hogy a csillagos égbolt éppen  fénysebességgel küld felénk információt az Univerzum állapotáról. Ha „távolra” nézünk, egyben a „múltba” is tekintünk. Mit „látnánk”, ha utolérnénk a fényt? Vajon lehetséges-e kitalálni egy fénynél sebesebb információközlési módszert? Vagy talán a fénysebesség valóban egy „objektív” áttörhetetlen korlát?
fénysebességgel küld felénk információt az Univerzum állapotáról. Ha „távolra” nézünk, egyben a „múltba” is tekintünk. Mit „látnánk”, ha utolérnénk a fényt? Vajon lehetséges-e kitalálni egy fénynél sebesebb információközlési módszert? Vagy talán a fénysebesség valóban egy „objektív” áttörhetetlen korlát?
Tartalomjegyzék[elrejtés] |
Elvek (posztulátumok)
Inerciarendszer a Newtoni mechanikában
Mint azt a klasszikus mechanikában már megtanultuk, a Newton-féle tér- és időszemlélet tükrözi a hétköznapi, egyszerű elképzelésünket. Azt gondoljuk, hogy létezik egy végtelen nagy (az egész Univerzumra kiterjedő) „álló” inerciarendszer, azaz van egy univerzális „Színpad” (tér) amelyen a Világ eseményei megtörténnek. Ebben mozognak a galaxisok, ebben mozog a Földünk is és a Föld felszínén lévő testek mozgását is ehhez az abszolút rendszerhez kellene viszonyítanunk. Valamint létezik (egy nagyon absztrakt) „valami”, amit időnek nevezünk. Ez „egyenletesen telik” a végtelen távoli múlttól a „jelen pillanatig” és tudjuk, hogy ezt teszi a jövőben is „az idők végezetéig”. Az abszolút inerciarendszerben a távolságokat (azaz a „Teret”) méterrúddal mérjük, az „Időt” pedig órával. Mindezt eleve (a priori) adottnak, mintegy természetesnek vesszük.
- Nem vitatjuk e szemlélet jogosságát. Pedig megtehetnénk, ugyanis mindez csupán egy kulturális örökség és így meglehetősen speciális. A görögöktől kapott Euklideszi geometria a végtelen (homogén) tér szemléletét hagyta ránk. A geometriai törvények szigorú (logikai) rendje szinte evidensé teszi a térszemléletünk helyességét. A kereszténység (teremtéselméletén alapuló) lineáris időszemlélete hosszú generációkon keresztül ivódott belénk. Tudjuk, hogy más kultúrákban az időt más tulajdonságúnak képzelik az emberek. Például a hinduk időszemléletét a linearitás helyett a periodikusság jellemzi. Ennek vallási vetülete pl. a reinkarnációban való hit is.
Az álló, univerzális (abszolút) inerciarendszerhez képest minden egyenletes sebességgel mozgó vonatkoztatási rendszer szintén inerciarendszer. Azaz, ha létezik egy inerciarendszer, akkor végtelen sok is létezik! A Newton axiómák inerciarendszerekben érvényesek. Ez fordítva is igaz: (definíciószerűen) inerciarendszerek azok, amelyekben a Newton axiómák teljesülnek. Ez azt jelenti, hogy ha bezárkózunk egy inerciarendszerbe, akkor semmiféle mechanikai kísérlettel nem tudjuk eldönteni, hogy az abszolút rendszerben vagyunk-e vagy pedig nem. De ez azt is jelenti, hogy bármelyik inerciarendszert tekinthetjük állónak. Ezt egyszerűsített formában úgy mondjuk, hogy mechanikai kísérlettel nem tudjuk eldönteni, hogy állunk-e vagy mozgunk. Természetesen „mozgó” rendszeren mindig egyenletesen mozgót kell érteni.
Ezen az egyáltalán nem triviális problémán már Galileo Galilei is gondolkodott és tökéletesen megfogalmazta az inerciarendszerek ekvivalenciáját. Gondolatait a „Discorsi e dimostrazioni matematiche, intorno due nuove scienze attenenti alla mecanica & i movimenti locali” (Matematikai érvelések és bizonyítások) című 1638-ban kiadott művében igen részletesen és precízen fejtette ki. Ez még Isaac Newton előtt volt, így itt „csak” (!) a mozgások matematikai leírását adja meg (pl. a jól ismert 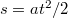 itt szerepel először a fizika történetében). A „tehetetlenség” törvényének az első megfogalmazását is itt találhatjuk meg. Newton ezeket már „készen kapta”. Az ő érdeme ezen gondolatok matematizálása és egységbe foglalása volt (Newton axiómák).
itt szerepel először a fizika történetében). A „tehetetlenség” törvényének az első megfogalmazását is itt találhatjuk meg. Newton ezeket már „készen kapta”. Az ő érdeme ezen gondolatok matematizálása és egységbe foglalása volt (Newton axiómák).
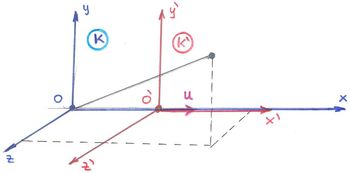
Az elmondottakból következik, hogy elegendő csak két (tetszőleges) inerciarendszert vizsgálni. A kettő közül az egyiket (bármelyiket) tekinthetjük állónak és a másikat (ehhez épest) mozgónak. Az, hogy melyik melyik, pusztán megállapodás kérdése. Az állónak tekintett rendszert  -val, mozgónak tekintett rendszert
-val, mozgónak tekintett rendszert  -vel szoktuk jelölni. Az élő beszédben pedig „vesszős” és „vesszőtlen” rendszert mondunk. Ezek után azt vizsgáljuk, hogy ugyanazt a mechanikai jelenséget milyennek észleli a
-vel szoktuk jelölni. Az élő beszédben pedig „vesszős” és „vesszőtlen” rendszert mondunk. Ezek után azt vizsgáljuk, hogy ugyanazt a mechanikai jelenséget milyennek észleli a  -ban illetve a
-ban illetve a  -ben lévő megfigyelő. Ezeket gyakran „álló megfigyelőnek” illetve „mozgó megfigyelőnek” hívjuk. Mármost azt várjuk, hogy bizonyos mért adatok (pl. a hely, a sebesség) a két inerciarendszerben ugyan mások lesznek, de ezek egymásba átszámolhatók. Ezt az átszámolási technikát nevezzük Galilei-féle transzformációnak.
-ben lévő megfigyelő. Ezeket gyakran „álló megfigyelőnek” illetve „mozgó megfigyelőnek” hívjuk. Mármost azt várjuk, hogy bizonyos mért adatok (pl. a hely, a sebesség) a két inerciarendszerben ugyan mások lesznek, de ezek egymásba átszámolhatók. Ezt az átszámolási technikát nevezzük Galilei-féle transzformációnak.
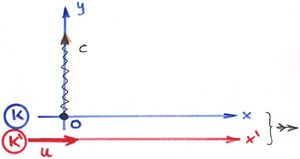
A konkrét matematikai tárgyalás érdekében (a szokásos módszert követve) definiálnunk kell mind az álló, mind pedig a mozgó inerciarendszerben egy-egy koordinátarendszert. Célszerű lesz a „legegyszerűbb”, Descartes koordináták választása.  -ban a koordinátákat és az időt
-ban a koordinátákat és az időt  -vel és
-vel és 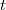 -vel,
-vel,  -ben
-ben 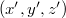 -vel és
-vel és 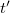 -vel jelöljük. Mivel a fizikai eredmény nem függ sem a koordinátarendszer konkrét helyzetétől, sem az időszámítás kezdetétől, ezeket úgy válaszjuk meg, hogy:
-vel jelöljük. Mivel a fizikai eredmény nem függ sem a koordinátarendszer konkrét helyzetétől, sem az időszámítás kezdetétől, ezeket úgy válaszjuk meg, hogy:
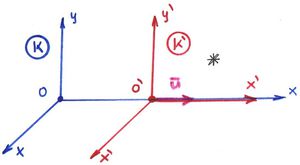
- a megfelelő koordinátatengelyek egymással párhuzamosak,
- az
 és
és 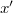 tengelyek abba az irányba mutatnak, amit a két rendszer egymáshoz képesti (egyenletes,
tengelyek abba az irányba mutatnak, amit a két rendszer egymáshoz képesti (egyenletes, 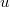 nagyságú) sebessége kitüntet,
nagyságú) sebessége kitüntet,
- a
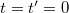 időpillanatban a koordinátarendszerek origója (
időpillanatban a koordinátarendszerek origója (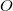 és
és 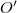 ) egybeesik (következésképpen az
) egybeesik (következésképpen az  és
és 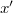 tengelyek minden időpillanatban egybeesnek).
tengelyek minden időpillanatban egybeesnek).
Az elkövetkezőkben mindig ezt a konvenciót fogjuk követni. Modern szóval élve ez lesz a default vagy az „alapértelmezés”. A relativitáselmélet szakirodalmában ezt standard boost-nak hívják.
Egy valamilyen erő hatására mozgó tömegpont esetében a Galilei-transzformáció a következő (triviális) összefüggéseket jelenti (lásd a 2.ábra):
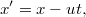
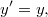
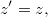
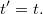
<<2. abra>>
Az utolsó egyenlet azt a természetes tényt rögzíti, hogy az időt mindkét inerciarendszerben ugyanolyan módon mérjük (ugyanazt a naptárt és órát használjuk). A sebességek és a gyorsulások egyszerű 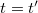 szerinti deriválással kaphatók:
szerinti deriválással kaphatók:
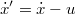 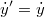 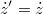 |
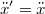 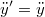 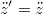 |
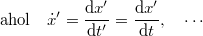 |
Tehát a sebesség nem, de a gyorsulás mindkét rendszerben ugyannak adódik. Tegyük fel (mert igazából semmi nem indokolná az ellenkezőjét), hogy a pont 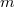 tömege és a rá ható
tömege és a rá ható 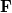 erő mindkét rendszerből mérve ugyanaz. Így valóban a Newton-féle mozgásegyenlet (mind a vesszős, mind pedig a vesszőtlen rendszerben) ugyanolyan alakú lesz:
erő mindkét rendszerből mérve ugyanaz. Így valóban a Newton-féle mozgásegyenlet (mind a vesszős, mind pedig a vesszőtlen rendszerben) ugyanolyan alakú lesz:
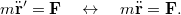
Ezt nevezzük Galilei-féle relativitás elvnek. Nyilvánvaló, hogy ha egyetlen tömegpont mozgástörvényét ismerjük, akkor nagyon sok, egymással kölcsönható tömegpontokból álló rendszer mozgását is meg tudjuk határozni (lásd: merev testek, folyadékok, gázok mechanikáját). Ezek után megállapíthatjuk, hogy a Galilei-féle relativitási elv szerint:
A mechanika törvényei minden inerciarendszerben ugyanazok (azaz egyforma matematikai alakban fogalmazhatók meg).
A speciális relativitáselmélet posztulátumai
A leggyorsabb haladás érdekében az „axiomatikus utat” fogjuk követni: egy egyszerűsített „felvezetés” után kimondjuk a speciális relativitáselmélet alaptörvényeit (ezek neve „Einstein-posztulátumok”) majd ezek következményeit részletesen megtárgyaljuk. A kapott „relativisztikus” effektusok mindegyikét (közvetlen vagy közvetett) kísérletek sokasága igazolja illetve (és ez a fontosabb) az elmúlt 100 évben még nem találkoztunk olyan természeti jelenséggel, amely cáfolta volna ezen törvények valamelyikét.
Hiba! Nincs fentebb említve semmi!
- A fentebb említett „áltudományos” művekkel kapcsolatban célszerű egy igen egyszerű „prakticista” álláspontra helyezkedni. A Természetet semmiféle filozófiai okoskodással nem lehet kitalálni. Ezért ne filozofálgassunk a relativitáselméletről! Elegendő csupán az, ha valaki elvégez egyetlen egy olyan kísérletet, amely az einsteni posztulátumok bármelyikét egyértelműen és reprodukálható módon megcáfolja. Azaz mér egy
 -nél nagyobb hatásterjedési sebességet vagy egy fizikai méréssel megállapítja, hogy mozog-e vagy nyugalomban van! Ennél több nem is kell! Minden egyéb csak szócséplés és üres „filozofálgatás”!
-nél nagyobb hatásterjedési sebességet vagy egy fizikai méréssel megállapítja, hogy mozog-e vagy nyugalomban van! Ennél több nem is kell! Minden egyéb csak szócséplés és üres „filozofálgatás”!
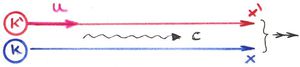
Galilei (1564-1642) és Newton (1642-1727) után mintegy 200 évvel James Clerk Maxwell (1831-1879) megalkotta az elektrodinamika alaptörvényeit, az ún. Maxwell egyenleteket. Az 1864-ben megjelent művének a címe: „Az elektromágneses mező dinamikájának elmélete”. Joggal merülhet fel a kérdés, hogy vajon ezek az egyenletek melyik vonatkoztatási rendszerben érvényesek. Ha következetesek akarunk lenni, akkor azt kell mondanunk, hogy természetesen a Newton-féle Univerzális (abszolút) Rendszerben (a Világszínpadon) biztosan jónak kell lennie. Hiszen ezért fogadjuk el alaptörvénynek. De mi a helyzet a többi (mozgó) inerciarendszerrel? Vajon ezek az „új” törvények ugyanúgy viselkednek, mint a Newton-féle mechanika, vagy esetleg másképpen? Azaz változatlanok maradnak-e, ha az abszolút rendszerből áttérünk egy mozgó rendszerre. Erre csak a tapasztalat adhatja meg a választ!
Mint azt már láttuk, a Maxwell-egyenletek szerint léteznie kell elektromágneses hullámoknak (EMH). Mivel a vákuum homogén és izotróp, így az EMH-k terjedése is ilyen kell hogy legyen. Valóban, Heinrich Hertz (1857-1894) kísérletileg kimutatta ezek létezését (1885-1889) ami még érdekesebbé tette a fenti kérdést. Ugyanis a klasszikus tapasztalatok szerint egy hullámjelenség mindig valamilyen anyagi közegben lép fel. Jól ismert példaként a hanghullámokat (levegőben), a rugalmas hullámokat (szilárd anyagban) vagy a felületi vízhullámokat említhetnénk. Így aztán nyilvánvaló volt, hogy az elektromágneses hullámnak is valamilyen anyagi közegre van szüksége. Ez a közeg azonban (a mechanikai szemlélet szerint) igen szokatlan tulajdonságú. Láttuk, hogy a (sík) EMH szerkezete olyan, hogy a térben és időben változó („hullámzó”) elektromos és mágneses térerősség merőleges a terjedési irányra, azaz ún. tranzverzális hullámról van szó.
A mechanikában tranzverzális hullámok csak szilárd anyagokban (ahol nyírási erőhatások ébredhetnek) lépnek fel. Az EMH-t hordozó közeg tehát a szilárd anyagokra emlékeztet. Ugyanakkor ebben a közegben a testek akadálytalanul mozoghatnak (pl. az égitestek), így ez a közeg a tömeggel bíró testek számára érzékelhetetlen. Ezért elnevezték „éternek”. Az éter görög szó (aithér). A mitológia szerint földi levegő felett lévő (könnyű, fénylő és tiszta) égi levegő, amelyben az istenek laknak.
Tehát – gondolták a régiek – az abszolút, álló Univerzális Rendszert kitölti az éter és az EMH (pl. a fény) ebben terjed éppen  sebességgel. Az EMH pedig a töltések között fellépő elektromágneses kölcsönhatások hordozója, közvetítője. Mint azt láttuk, a Maxwell-egyenletekben egyetlen sebességadat szerepel, ezt jelöltük
sebességgel. Az EMH pedig a töltések között fellépő elektromágneses kölcsönhatások hordozója, közvetítője. Mint azt láttuk, a Maxwell-egyenletekben egyetlen sebességadat szerepel, ezt jelöltük  -vel. Az egyenletekből levezethető hullámegyenletben éppen ez a
-vel. Az egyenletekből levezethető hullámegyenletben éppen ez a  jelenik meg. Ennek megoldásaként adódó EMH sebességére is ugyanez a
jelenik meg. Ennek megoldásaként adódó EMH sebességére is ugyanez a  adódik. Mindezt már részletesen tárgyaltuk az elektrodinamikában. A kérdés mármost az, hogy mekkora lesz az
adódik. Mindezt már részletesen tárgyaltuk az elektrodinamikában. A kérdés mármost az, hogy mekkora lesz az  tengely mentén pozitív irányban haladó EMH sebessége, ha az éterhez képest mozgó inerciarendszerben mérjük azt meg (alapértelmezés!). A hullámoknál tapasztaltak szerint ennek különböznie kell a
tengely mentén pozitív irányban haladó EMH sebessége, ha az éterhez képest mozgó inerciarendszerben mérjük azt meg (alapértelmezés!). A hullámoknál tapasztaltak szerint ennek különböznie kell a  -től. Valóban, ha a Maxwell egyenletekből levezethető hullámegyenletet a fenti módon áttranszformáljuk a mozgó rendszerbe, akkor az új hullámegyenlet megoldására egy
-től. Valóban, ha a Maxwell egyenletekből levezethető hullámegyenletet a fenti módon áttranszformáljuk a mozgó rendszerbe, akkor az új hullámegyenlet megoldására egy 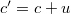 , illetve
, illetve 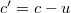 sebességű fényhullámot kapunk, attól függően, hogy szembe mozgunk-e a fénnyel (
sebességű fényhullámot kapunk, attól függően, hogy szembe mozgunk-e a fénnyel ( ) vagy vele egyező irányban (
) vagy vele egyező irányban (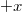 ). De ez azt is jelentené, hogy ami a mechanikában lehetetlen volt, az most lehetővé válik: egy egyszerű fénysebesség méréssel meg tudnánk mondani, hogy „állunk-e vagy mozgunk”.
). De ez azt is jelentené, hogy ami a mechanikában lehetetlen volt, az most lehetővé válik: egy egyszerű fénysebesség méréssel meg tudnánk mondani, hogy „állunk-e vagy mozgunk”.
Van azonban egy érdekes tény! Ugyanis, ha a Maxwell-egyenleteken (külön-külön mind a négyen) végrehajtjuk az 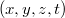 -re vonatkozó Galilei-transzformációt, akkor olyan „új” tagok jelennek meg az egyenletekben, amelyet semmiféle kísérlet nem igazol. Az érdekesség az, hogy ezek a „felesleges tagok” a hullámegyenlet képzésekor éppen kiesnek! Ezért ez ott nem okozott gondot. Kimondhatjuk tehát, hogy a Galilei-transzformáció alkalmazása az elektrodinamikában rossz eredményt ad. De ez egyben azt is jelenti, hogy a mozgó rendszerben kapott
-re vonatkozó Galilei-transzformációt, akkor olyan „új” tagok jelennek meg az egyenletekben, amelyet semmiféle kísérlet nem igazol. Az érdekesség az, hogy ezek a „felesleges tagok” a hullámegyenlet képzésekor éppen kiesnek! Ezért ez ott nem okozott gondot. Kimondhatjuk tehát, hogy a Galilei-transzformáció alkalmazása az elektrodinamikában rossz eredményt ad. De ez egyben azt is jelenti, hogy a mozgó rendszerben kapott 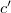 sebességérték sem helyes. Erre a problémára a legegyszerűbb választ Albert Einstein adta meg.
sebességérték sem helyes. Erre a problémára a legegyszerűbb választ Albert Einstein adta meg.
Tételezzük fel – mondta –, hogy a Maxwell-egyenletek minden inerciarendszerben ugyanolyan alakúak. Tehát minden inerciarendszerben az EMH (fény) sebessége ugyanaz a  érték. Ekkor viszont az abszolút nyugvó éter fogalma tarthatatlanná válik. Mondjuk tehát ki, hogy az éter nem létezik! Mindezekből következik, hogy nem csak mechanikai, hanem elektrodinamikai kísérlettel sem lehet eldönteni, hogy „nyugvó, vagy pedig mozgó” rendszerben vagyunk. Az inerciarendszerek ezen egyenértékűsége és a
érték. Ekkor viszont az abszolút nyugvó éter fogalma tarthatatlanná válik. Mondjuk tehát ki, hogy az éter nem létezik! Mindezekből következik, hogy nem csak mechanikai, hanem elektrodinamikai kísérlettel sem lehet eldönteni, hogy „nyugvó, vagy pedig mozgó” rendszerben vagyunk. Az inerciarendszerek ezen egyenértékűsége és a  , mint az elektromágneses kölcsönhatások terjedési sebességének állandósága (invarianciája) nem lehet véletlen. Einstein azt javasolta, hogy legyenek ezek alapvető természeti törvények. Az elmondottak lehető legszélesebb körű általánosítása vezet az Einstein-féle posztulátumokhoz. Ezek szerint
, mint az elektromágneses kölcsönhatások terjedési sebességének állandósága (invarianciája) nem lehet véletlen. Einstein azt javasolta, hogy legyenek ezek alapvető természeti törvények. Az elmondottak lehető legszélesebb körű általánosítása vezet az Einstein-féle posztulátumokhoz. Ezek szerint
- a Természettörvények minden inerciarendszerben ugyanolyan alakúak,
- bármilyen fizikai hatás maximum
 sebességgel terjedhet.
sebességgel terjedhet.
A  (homogén, izotrop) sebesség invarianciáját nem kell külön kimondani, mert ez az első posztulátumnak a következménye. Ha ez nem így volna, akkor fénysebesség méréssel különbséget tudnánk tenni két inerciarendszer között. Ha ezt a két alaptörvényt elfogadjuk, akkor ebből az egész speciális relativitáselmélet felépíthető: minden törvénye igazolható vagy cáfolható.
(homogén, izotrop) sebesség invarianciáját nem kell külön kimondani, mert ez az első posztulátumnak a következménye. Ha ez nem így volna, akkor fénysebesség méréssel különbséget tudnánk tenni két inerciarendszer között. Ha ezt a két alaptörvényt elfogadjuk, akkor ebből az egész speciális relativitáselmélet felépíthető: minden törvénye igazolható vagy cáfolható.
Mint azt tudjuk, a Fizikában a természeti jelenségek leírása úgy történik, hogy a kiválasztott térrész minden 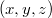 pontjában és minden
pontjában és minden 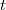 időpontban meghatározzuk valamely
időpontban meghatározzuk valamely 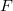 fizikai mennyiség értékét. Ez szükségképpen mindig egy skalár mennyiség (szám + mértékegység). Az ismert természettörvények segítségével az
fizikai mennyiség értékét. Ez szükségképpen mindig egy skalár mennyiség (szám + mértékegység). Az ismert természettörvények segítségével az 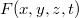 függvény kiszámítható és az eredmény mérésekkel ellenőrizhető. A speciális relativitáselmélet arról szól, hogy milyen kapcsolat van az állónak tekintett
függvény kiszámítható és az eredmény mérésekkel ellenőrizhető. A speciális relativitáselmélet arról szól, hogy milyen kapcsolat van az állónak tekintett  és a mozgó
és a mozgó  rendszerben meghatározott adatok között:
rendszerben meghatározott adatok között:
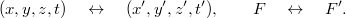
Láttuk, hogy a mechanikában az álló és a mozgó megfigyelő által mért helykoordináta és idő adatok között a Galilei-transzformáció teremt kapcsolatot. Az erő komponensek és a tömeg pedig ugyanaz mind a két rendszerben (azaz nem transzformálódik). Az már rögtön látszik, hogy a Galilei-transzformáció nem teljesíti azt a posztulátumot, amely szerint a fénysebesség minden inerciarendszerben ugyanaz a  érték. Ez a már bemutatott sebesség összeadási formulából következik (
érték. Ez a már bemutatott sebesség összeadási formulából következik (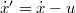 ). Ezért egy új transzformációt kell keresnünk. Ezt a transzformációt már Einsteintől függetlenül Hendrik Antoon Lorentz és Henri Poincaré megtalálta. Ők arra a transzformációra jöttek rá, amely a Maxwell-egyenleteket változatlanul hagyja. Tehát egy speciális jelenségkört, az elektrodinamikát vizsgálták. Ezt a transzformációt a fizikus társadalom Lorentz-transzformációnak nevezte el. Einstein egyik nagy érdeme többek között az, hogy meglátta ennek a transzformációnak az alapvető és univerzális voltát, amely gyökeresen megváltoztatta a térről és az időről alkotott newtoni szemléletünket. És ennek megfelelően a természeti törvények fontos szimmetriatulajdonságára mutatott rá (lásd Einstein első posztulátumát).
). Ezért egy új transzformációt kell keresnünk. Ezt a transzformációt már Einsteintől függetlenül Hendrik Antoon Lorentz és Henri Poincaré megtalálta. Ők arra a transzformációra jöttek rá, amely a Maxwell-egyenleteket változatlanul hagyja. Tehát egy speciális jelenségkört, az elektrodinamikát vizsgálták. Ezt a transzformációt a fizikus társadalom Lorentz-transzformációnak nevezte el. Einstein egyik nagy érdeme többek között az, hogy meglátta ennek a transzformációnak az alapvető és univerzális voltát, amely gyökeresen megváltoztatta a térről és az időről alkotott newtoni szemléletünket. És ennek megfelelően a természeti törvények fontos szimmetriatulajdonságára mutatott rá (lásd Einstein első posztulátumát).
A jelen tanulmányink során mi csak a relativisztikus kinematikával és a relativisztikus dinamikával tudunk foglalkozni. Az elektrodinamika relativisztikus tárgyalása (azaz az elektromos és a mágneses térerősség komponensek transzformációs tulajdonságainak ismertetése) már jócskán meghaladja e kurzus színvonalát.
A Lorentz transzformáció
Az első feladatunk tehát az, hogy meghatározzuk azt a transzformációt, amelyik változatlanul hagyja a fény  sebességét, ha az egyik inerciarendszerből egy másikra térünk át. Ezt a Maxwell-egyenletek nélkül is meg lehet csinálni (ez is Einstein ötlete volt!).
sebességét, ha az egyik inerciarendszerből egy másikra térünk át. Ezt a Maxwell-egyenletek nélkül is meg lehet csinálni (ez is Einstein ötlete volt!).
A gondolatmenet a következő. Tekintsük az álló és a mozgó vonatkoztatási rendszert az alapértelmezés szerinti Descartes koordinátákkal ellátva.
A koordinátatengelyek kalibrálása (azaz tetszőleges méretű egyforma szakaszok kijelölése az  ,
,  ,
,  tengelyeken) geometriai feladat és így egzaktul megoldható.
tengelyeken) geometriai feladat és így egzaktul megoldható.
Alapvetően más a helyzet az időt mérő órákkal. Pontos órát igen sokféle módon lehet készíteni. A technikatörténet a görögök által használt vízi óráktól kezdve az inga-, a rugós- és a kvarcórákon át a mai modern atomórákig (lásd GPS) rengeteg fajta megoldást ismer. Ezek működésében a Fizika szinte minden ismert törvénye jelen van. Mondhatjuk tehát, hogy egy óra használata a természeti törvények „használatát” (is) jelenti. Egy adott rendszeren belül lévő óráknak pontosan egyformán kell járniuk. Nem kell, hogy ugyanolyan típusúak legyenek, de az időt egyformán kell mutatniuk. Ez egyszerű „kalibrálással” megoldható: az órákat egy „etalon” órához („ősórához”) kell igazítani. Hasonlóan ahhoz, mint amikor a hosszúság mérés etalonjának az „Ősmétert” használtuk. Így az órák használata (ami az Idő mérésének egyedüli lehetséges módja) a természeti törvények objektív megnyilvánulását jelenti. Hiszen minden óra (bármilyen típusú is legyen) a természeti törvényeknek megfelelően működik.
- Ez egy alapvetően fontos gondolat! Ezzel ugyanis megszabadítottuk az „Idő” fogalmát azoktól a szubjektív elemektől amelyeket az életünk során a mindennapi élményeink vetítettek rá. Hála a kísérleti pszichológia fejlődésének mára már könyvtárnyi irodalom tárgyalja az emberi időérzékelés pszichés folyamatait. A természeti törvények szerint működő órák által definiált idő a természeti jelenségek objektív tulajdonságát tükrözik. Ezért mondhatjuk, hogy ezek az órák valóban az „Időt” mérik. Azt a valamit, ami a természeti jelenségek egymásutániságának a mértékét tükrözik. Mivel a biológiában is a Természet törvényei érvényesülnek így pl. a biológiai öregedés folyamatát is egy „óraként” lehet értelmezni. Világítsuk meg ezt egy igen egyszerű példával! Tegyük fel, hogy egy kutya az álló rendszerben lévő óra szerint 10 évig élt, és a mozgó rendszerben egy macska az ottani óra szerint szintén 10 évig élt. Ekkor joggal mondjuk azt, hogy a két állat ugyanolyan hosszú életet élt, függetlenül attól, hogy a két óra melyik rendszerben mérte az időt. A gazdik egymásnak elküldött táviratában ugyanaz az „élt 10 évig” mondat fog szerepelni.
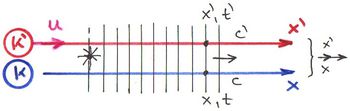
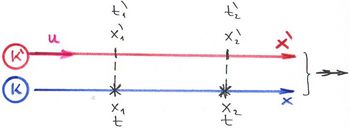
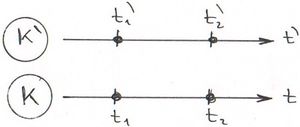
Vizsgáljuk meg, hogy mit kell tapasztalnia az álló és a mozgó megfigyelőnek, ha az Einstein-posztulátumok valóban jól tükrözik a Természet „működését”. Mint tudjuk, az alapértelmezés (sztenderd elrendezés) szerint az időszámítás kezdete mindkét rendszerben ugyanaz az esemény definiálja. Nevezetesen, amikor az origók éppen fedték egymást, azaz:

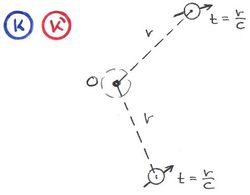
Az ábrán a következő kísérlet elvi vázlata látható. Indítsunk el egy fényjelet a 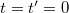 időpillanatban és nézzük meg, hogy a megfigyelőknek a posztulátumok érvényességének a következtében mit kell tapasztalniuk.
időpillanatban és nézzük meg, hogy a megfigyelőknek a posztulátumok érvényességének a következtében mit kell tapasztalniuk.
A válasz egyszerű: az álló megfigyelő azt látja, hogy az  helyen lévő óra
helyen lévő óra 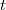 időt mutat, a mozgó megfigyelő pedig azt tapasztalja, hogy az
időt mutat, a mozgó megfigyelő pedig azt tapasztalja, hogy az 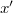 helyen lévő óra
helyen lévő óra 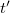 időt jelez. És természetesen a fénysebesség állandósága szerint
időt jelez. És természetesen a fénysebesség állandósága szerint

Természetesen ugyanez a helyzet, ha a tér bármely 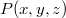 illetve
illetve 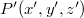 pontját tekintjük, Ekkor értelemszerűen a
pontját tekintjük, Ekkor értelemszerűen a
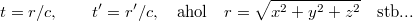
összefüggések érvényesek (lásd ábra).
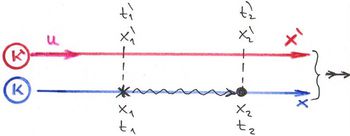
Ezt a kísérletet felfoghatjuk úgy is, hogy ellenőriztük az órák (relativisztikusan) helyes működését. Azaz megnéztük, hogy mind az álló, mindpedig a mozgó rendszerben lévő órák eleget tesznek-e az Einsteini posztulátumoknak, azaz valóban teljesül-e a 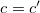 feltétel? Ránézésre látszik, hogy a Galilei-transzformáció ezt nem elégíti ki. Az első egyenletét (
feltétel? Ránézésre látszik, hogy a Galilei-transzformáció ezt nem elégíti ki. Az első egyenletét (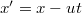 ) osztva
) osztva  -vel azt kapjuk, hogy
-vel azt kapjuk, hogy
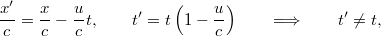
és ez ellentmondásban van a negyedik egyenlettel (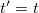 ). Tehát a Galilei-transzformáció és a fénysebesség invarianciája egyszerre nem lehet igaz! Nincsen más választás, mint feladni a Galilei-transzformációt és egy olyan másikat keresni, amely ezt a feltételt teljesíti.
). Tehát a Galilei-transzformáció és a fénysebesség invarianciája egyszerre nem lehet igaz! Nincsen más választás, mint feladni a Galilei-transzformációt és egy olyan másikat keresni, amely ezt a feltételt teljesíti.
Van még egy fontos támpontunk, amit a fizikai törvények megalkotásánál igen gyakran használunk: az ún. korrespondencia-elv. Ez azt mondja ki, hogy egy adott jelenségre vonatkozó „új” törvénynek határesetben mindig vissza kell adnia a „régit”. Ugyanis az „új” törvény mindig megváltoztatja a „réginek” az érvényességi körét. Ettől még a régi állítások nem válnak hamissá, hiszen azokat továbbra is a „régi” feltételek között használjuk.
Jelen esetben ez azt jelenti, hogy ha a mechanikát a  -hez mérten kis sebességeknél vizsgáljuk, akkor nyugodtan használhatjuk a Galilei-transzformációt. Például az előbbi esetben az
-hez mérten kis sebességeknél vizsgáljuk, akkor nyugodtan használhatjuk a Galilei-transzformációt. Például az előbbi esetben az 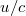 arány sokkal kisebb lesz mint egy. Ezért határesetben (pl.
arány sokkal kisebb lesz mint egy. Ezért határesetben (pl. 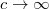 ) visszakapjuk a Galilei féle
) visszakapjuk a Galilei féle 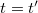 összefüggést.
összefüggést.
Az előzőekben már megbeszéltük, hogy két inerciarendszer a természeti jelenségek leírása szempontjából ekvivalens egymással. Ezért az „álló” és a „mozgó” szerepek kijelölése önkényes. Így, ha az egyik a másikhoz képest 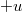 sebességgel mozog, akkor a másik az egyikhez képest
sebességgel mozog, akkor a másik az egyikhez képest 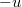 -val fog mozogni. Az eddig elmondottaknak megfelelően kézenfekvőnek tűnik, ha az „új” transzformációt következő alakban keressük:
-val fog mozogni. Az eddig elmondottaknak megfelelően kézenfekvőnek tűnik, ha az „új” transzformációt következő alakban keressük:
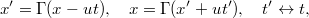
ahol a korrespondencia-elv következtében a még ismeretlen 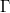 -ra teljesülnie kell annak, hogy
-ra teljesülnie kell annak, hogy
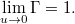
Végezzük el most is a fenti óraellenőrzési kísérletet és nézzük meg, hogy miként kezeli ezt a mostani transzformáció! Írjuk be a 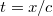 és
és 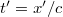 kifejezéseket a transzformációba. Azt kapjuk, hogy:
kifejezéseket a transzformációba. Azt kapjuk, hogy:
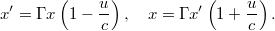
Összeszorozva a két egyenletet az 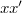 szorzat kiesik az egyenletből és
szorzat kiesik az egyenletből és 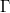 meghatározható:
meghatározható:
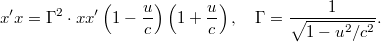
A korrespondencia tényleg teljesül, hiszen:
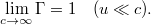
Ezek után áttérhetünk az idő transzformációjának a meghatározására (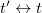 ).
). 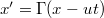 -t beírva az
-t beírva az 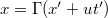 egyenletbe,
egyenletbe, 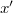 -t ki tudjuk ejteni. Azt kapjuk, hogy
-t ki tudjuk ejteni. Azt kapjuk, hogy
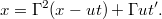
Ebből 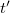 kifejezhető és átrendezés után megkapjuk az idő transzformációs tulajdonságát (a részletek házi feladat):
kifejezhető és átrendezés után megkapjuk az idő transzformációs tulajdonságát (a részletek házi feladat):
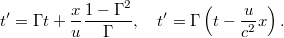
Erre is teljesül a korrespondencia elv, hiszen
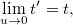
azaz visszakaptuk a Galilei-féle abszolút idő fogalmát. Ezzel megszületett a Lorentz transzformáció:
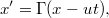
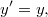
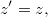
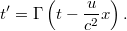
A következőkben megvizsgáljuk, hogy milyen következményei vannak ennek az új, relativisztikus szemléletnek. Az alkalmazások megkövetelik egy régi-új fogalom bevezetését. Ez az esemény. Ez azt jelenti, hogy a tér egy  pontjában (ez az esemény helye) a
pontjában (ez az esemény helye) a  időpillanatban (ez az esemény időpontja) az
időpillanatban (ez az esemény időpontja) az 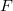 fizikai mennyiség felvesz egy értéket (ez maga az esemény).
fizikai mennyiség felvesz egy értéket (ez maga az esemény).
Ahhoz tehát, hogy egy eseményt meghatározzunk, a tér minden pontjához hozzárendeljük az ő helyét meghatározó Descartes koordinátákat és elhelyezünk egy („pontszerű”) órát, amelyiket az imént bemutatott szinkronizálási eljárással kalibráltunk. Ez mutatja az adott pontban a mindenkori 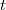 időpontot. Ugyanezt az
időpontot. Ugyanezt az 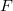 eseményt szemlélhetjük a mozgó rendszerből is. Ekkor természetesen
eseményt szemlélhetjük a mozgó rendszerből is. Ekkor természetesen 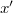 ,
, 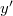 ,
, 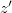 ,
, 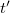 és
és 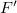 értékeket mérünk. Minden természeti jelenség ilyen elemi események sokaságából épül fel. Ezért (az általánosság minden csorbítása nélkül) elegendő az adott fajta események közül csak egynek a transzformációs tulajdonságait megvizsgálni.
értékeket mérünk. Minden természeti jelenség ilyen elemi események sokaságából épül fel. Ezért (az általánosság minden csorbítása nélkül) elegendő az adott fajta események közül csak egynek a transzformációs tulajdonságait megvizsgálni.
Ha rátekintünk a Lorentz transzformációra, láthatjuk, hogy a 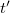 meghatározásához nem csak a
meghatározásához nem csak a  -re, de még az
-re, de még az  -re is szükségünk van. Azaz nem csak az számít, hogy mikor, hanem az is, hogy hol történik az az esemény, amelynek a mozgó rendszerbeni időpontját meg szeretnénk tudni. Az Időnek ez a furcsa tulajdonsága azt mutatja, hogy az idő és a térkoordináták mintegy „összefonódnak” és egységes egészként transzformálódnak. Ezért a
-re is szükségünk van. Azaz nem csak az számít, hogy mikor, hanem az is, hogy hol történik az az esemény, amelynek a mozgó rendszerbeni időpontját meg szeretnénk tudni. Az Időnek ez a furcsa tulajdonsága azt mutatja, hogy az idő és a térkoordináták mintegy „összefonódnak” és egységes egészként transzformálódnak. Ezért a 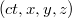 számnégyest a „Téridő” egy pontjának nevezzük. Olyan tulajdonságai vannak, mint egy négydimenziós vektortérnek. Az események tehát a téridőben zajlanak. A
számnégyest a „Téridő” egy pontjának nevezzük. Olyan tulajdonságai vannak, mint egy négydimenziós vektortérnek. Az események tehát a téridőben zajlanak. A  -ból a
-ból a  -be való átszámolás a téridő transzformációs tulajdonsága. Ez az amit Lorentz-transzformációnak neveztünk. A téridő igen szemléletes geometriai reprezentációját Hermann Minkowski (1907) alkotta meg.
-be való átszámolás a téridő transzformációs tulajdonsága. Ez az amit Lorentz-transzformációnak neveztünk. A téridő igen szemléletes geometriai reprezentációját Hermann Minkowski (1907) alkotta meg.
Mint említettük, mi csak a kinematikával és a dinamikával fogunk foglalkozni. Ekkor az 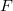 mennyiség felépíthető az
mennyiség felépíthető az 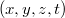 mennyiségekből (sebesség, gyorsulás). Mivel a „tér+idő” adatok (Lorentz) transzformációja ismert, így az ezekből származtatott
mennyiségekből (sebesség, gyorsulás). Mivel a „tér+idő” adatok (Lorentz) transzformációja ismert, így az ezekből származtatott 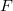 transzformációja definíció szerint meghatározható. A következőkben ezt részletesen is tárgyalni fogjuk. Minden más esetben (pl. erőkomponensek, elektromos és mágneses térerősség komponensei stb) az
transzformációja definíció szerint meghatározható. A következőkben ezt részletesen is tárgyalni fogjuk. Minden más esetben (pl. erőkomponensek, elektromos és mágneses térerősség komponensei stb) az 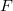 transzformációját külön meg kell határozni. A fizikusok kidolgoztak erre egy „koherens” és „szisztematikus” módszert, de ez meghaladja ennek a kurzusnak a lehetőségeit.
transzformációját külön meg kell határozni. A fizikusok kidolgoztak erre egy „koherens” és „szisztematikus” módszert, de ez meghaladja ennek a kurzusnak a lehetőségeit.
A számolásaink tovább egyszerűsödnek, ha figyelembe vesszük azt a tényt, hogy az alapértelmezés (standard boost) szerint az 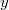 és
és  koordináta adatok nem transzformálódnak. Így az esemény tér-idő adatait
koordináta adatok nem transzformálódnak. Így az esemény tér-idő adatait 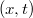 fogja jelenteni.
fogja jelenteni.
A Lorentz transzformáció a kinematikában (relativisztikus kinematika)
A hosszkontrakció
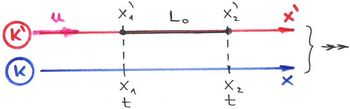
Tekintsük a következő feladatot! Az álló  rendszerben lévő megfigyelő mérje meg a mozgó
rendszerben lévő megfigyelő mérje meg a mozgó  rendszer
rendszer 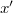 tengelyén fekvő,
tengelyén fekvő, 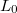 hosszúságú rúdnak a hosszát. A rúd végeinek koordinátáit jelölje
hosszúságú rúdnak a hosszát. A rúd végeinek koordinátáit jelölje 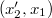 .
.
Einstein szemléletes példájával élve az a kérdés, hogyan lehet meghatározni egy száguldó vonat hosszát a sínpár mellett állva? A megoldás igen egyszerű. Állítsunk fel a sín mentén (egy sorban) nagyon sok megfigyelőt, akik szorosan egymás mellett állnak. Minden megfigyelőnek a kezében legyen egy óra. Minden megfigyelőnek az a feladata, hogy állítsa meg az óráját, amikor a vonat eleje éppen elhalad az orra előtt. Mi is álljunk be a sorba és állítsuk meg az óránkat, ha megpillantjuk a vonat végét. Amikor a vonat elrobog a sor előtt, minden megfigyelő (magunkat is beleértve) megállítja az óráját a kapott utasításnak megfelelően. Nyílvánvaló, hogy csak egyetlen olyan megfigyelő lesz, akinek az órája éppen a mi óránkkal egyező időpontot mutat. Ennek a megfigyelőnek a tőlünk mért távolsága lesz a mozgó vonat hossza. Hiszen ugyanabban a pillanatban láttuk meg mi a vonat végét, mint amikor a másik megfigyelő a vonat elejét. Azt mondjuk, hogy ez a két megfigyelés egy időben történt. Az elmondottak könnyen lefordíthatók az „események nyelvére” a következőképen.
Az álló rendszerben a rúd hosszát két esemény definiálja. Az egyik amikor megpillantjuk a rúd elejét 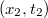 , a másik, amikor a végét
, a másik, amikor a végét 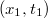 . A két esemény egyidejű, tehát
. A két esemény egyidejű, tehát 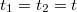 . A mozgó rúd hosszát a
. A mozgó rúd hosszát a  rendszerben az
rendszerben az 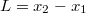 kifejezés definiálja. A rúd hossza a (vele együtt) mozgó
kifejezés definiálja. A rúd hossza a (vele együtt) mozgó  rendszerben nyilvánvalóan
rendszerben nyilvánvalóan 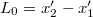 . Ezt nevezzük nyugalmi hossznak, hiszen ekkor a szakaszhoz képest nyugalomban vagyunk.
. Ezt nevezzük nyugalmi hossznak, hiszen ekkor a szakaszhoz képest nyugalomban vagyunk.
A két esemény kapcsolata a Lorentz transzformációnak megfelelően:

A fent bevezetett jelöléseket használva
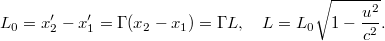
A jelenség neve hosszkontrakció. Eszerint egy mozgó rúd hossza a mozgás irányában „megrövidül”. Az inerciarendszerek ekvivalenciájából következik, hogy mindez „fordítva” is igaz: ha ugyanekkor elhelyezünk egy 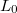 nyugalmi hosszúságú rudat az álló
nyugalmi hosszúságú rudat az álló  rendszer
rendszer  tengelye mentén, akkor ennek a hosszát a mozgó rendszerből mérve észleljük rövidebbnek.
tengelye mentén, akkor ennek a hosszát a mozgó rendszerből mérve észleljük rövidebbnek.
Joggal felmerülhet a kérdés, hogy mármost kinek van igaza? Az eddigiek szellemében csak azt mondhatjuk, hogy mindkét megfigyelőnek igaza van! Ezen nem kell csodálkozni, hiszen a két mérés teljesen másképpen történt. A „nyugalmi hossz” és a „mozgási hossz” meghatározása valójában két különböző típusú mérés volt. A „hagyományos eljárás”, azaz a rudak közvetlen összehasonlítása lehetetlen, hiszen nem tudunk „átugrani” (kezünkben a rúddal)  -ból
-ból  -be!
-be!
Természetesen, az iménti levezetés akkor is elvégezhető, ha nincsenek jelen a merev (fizikai) rudak, csak a kijelölt  és
és 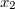 koordinátapontok. Ezért azt mondhatjuk, hogy a hosszkontrakció nem az anyagi rudak tulajdonsága, hanem magának a Térnek a sajátossága.
koordinátapontok. Ezért azt mondhatjuk, hogy a hosszkontrakció nem az anyagi rudak tulajdonsága, hanem magának a Térnek a sajátossága.
Erre a merész következtetésre Einstein jutott először. Lorerntz-Fitzgerald ugyanis a rudak… Pozitivizmus…
!!! Befejezni !!!
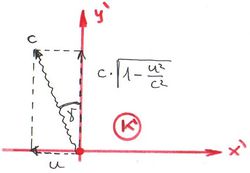
Az idődilatáció
Mint az eddig kiderült, a relativitáselmélet megfosztotta az Időt a rárakodott pszichológiai és az ebből fakadó filozófiai rétegektől és egzaktul mérhető mennyiséggé tette. Az Idő az a paraméter, amely a lezajló események sorrendiségét regisztrálja. Az Időt órával mérjük. Egy órát bármilyen objektummal megvalósíthatunk, ha az eleget tesz a méréseknél használt általános követelményeknek. Az óra lehet tehát akár fizikai, kémiai, vagy biológiai képződmény (szerkezet) is.
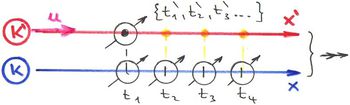
Helyezzünk el a mozgó  rendszer
rendszer 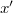 koordinátájú pontjába egy órát (lásd ábra). Az óra által mért egységnyi időtartamot jelölje
koordinátájú pontjába egy órát (lásd ábra). Az óra által mért egységnyi időtartamot jelölje 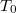 . Azaz adjon az óra jeleket a
. Azaz adjon az óra jeleket a 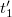 ,
, 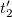 ,
, 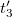 , … időpontokban, amelyek
, … időpontokban, amelyek 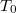 -al követik egymást. A jelek tetszőlegesek: ketyegés, mutató elmozdulás, digitális kijelzés stb. Ezek a jelek az események.
-al követik egymást. A jelek tetszőlegesek: ketyegés, mutató elmozdulás, digitális kijelzés stb. Ezek a jelek az események.
A kérdés az, hogy milyen 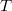 egység időtartamot mér az álló megfigyelő? Nyilvánvalóan elegendő csak két egymást követő eseményt vizsgálni. Azaz határozzuk meg, hogy az álló megfigyelő milyen adatokat detektál az
egység időtartamot mér az álló megfigyelő? Nyilvánvalóan elegendő csak két egymást követő eseményt vizsgálni. Azaz határozzuk meg, hogy az álló megfigyelő milyen adatokat detektál az 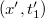 és az
és az 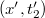 eseményeket mérve. Az álló megfigyelő azt látja, hogy az óra
eseményeket mérve. Az álló megfigyelő azt látja, hogy az óra  koordinátája állandóan változik. Azaz a szóban forgó két esemény tér-idő adatait
koordinátája állandóan változik. Azaz a szóban forgó két esemény tér-idő adatait 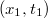 illetve
illetve 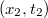 lesznek.
lesznek.
Mint tudjuk, az álló és a mozgó megfigyelő adatai között a Lorentz transzformáció teremt kapcsolatot. Azaz írhatjuk, hogy:
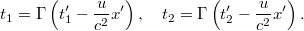
Majd ebből kapjuk, hogy:
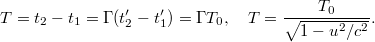
Látható tehát, hogy 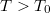 , azaz az álló megfigyelő szerint a mozgó óra lassabban jár. Például ha
, azaz az álló megfigyelő szerint a mozgó óra lassabban jár. Például ha 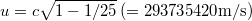 , az álló megfigyelő óráján
, az álló megfigyelő óráján 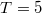 óra telik el, amíg a mozgó óra csak
óra telik el, amíg a mozgó óra csak 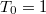 órát megy tovább. Az inerciarendszerek ekvivalenciája miatt a mozgó megfigyelő ugyanezt állítja az álló óráról. Természetesen jelen esetben is mindkét állítás helyes. Ezen most sem kell csodálkoznunk, hiszen mérési eljárás most is más volt az álló rendszerben, mint a mozgóban. Mint azt láttuk, egyrészt ugyanazon mozgó óra által mutatott két időpontot (
órát megy tovább. Az inerciarendszerek ekvivalenciája miatt a mozgó megfigyelő ugyanezt állítja az álló óráról. Természetesen jelen esetben is mindkét állítás helyes. Ezen most sem kell csodálkoznunk, hiszen mérési eljárás most is más volt az álló rendszerben, mint a mozgóban. Mint azt láttuk, egyrészt ugyanazon mozgó óra által mutatott két időpontot (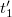 ,
, 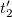 ) határoztunk meg. Másrészt az álló rendszerben történt méréskor két különböző helyen (
) határoztunk meg. Másrészt az álló rendszerben történt méréskor két különböző helyen (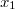 ,
, 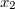 ) lévő, két különböző óra által mutatott (
) lévő, két különböző óra által mutatott (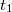 ,
, 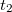 ) időpontokat kellett használnunk. Az álló és a mozgó óra közvetlen összehasonlításra most sincsen lehetőség, hiszen a megfigyelők (zsebükben az óráikkal) nem hagyhatják el a saját rendszerüket.
) időpontokat kellett használnunk. Az álló és a mozgó óra közvetlen összehasonlításra most sincsen lehetőség, hiszen a megfigyelők (zsebükben az óráikkal) nem hagyhatják el a saját rendszerüket.
Ha az órák közvetlen összehasonlítását is lehetővé tesszük, akkor egy másik problémához jutunk, amelynek a találó neve „ikerparadoxon”.
Paradoxonnak egy elméleten belüli látszólagos ellentmondást nevezünk. Azért látszólagos, mert abból fakad, hogy valami lényeges tényt nem vettünk figyelembe vagy valamit rosszul értelmeztünk. A paradoxonok feloldása azért nehéz, mert rutinszerű gondolkodunk. Például hallgatólagosan olyan dolgokat feltételezünk, amelyek esetleg ellentmondanak az elmélet tételeinek. A relativitáselmélet állításai igen szokatlanok (pl. hoszkontrakció, idődilatáció) a hétköznapi tapasztalatoknak ellentmondanak. Ezért megszületésekor paradoxonok sokaságával próbálták cáfolni állításait. Mivel a relativitáselmélet jól tükrözi a Természetben lezajló jelenségeket (azaz egy „jó elmélet”) így a paradoxonok mind feloldhatóak voltak. Némelyik olyan „szellemes”, hogy ma is használjuk az elmélet jobb megértetésének a céljából. Az egyik ezek közül éppen az „ikerparadoxon”.
Az ikerparadoxon
25 évesen válnak el
A: a Földön 50 év telik el és A úgy számolja, hogy az űrhajón csak 20.
B: ha az úrhajón 20 év telik el, B úgy számolja, hogy a Földön csak 8.
A gondolatmenete:
A: 25 50 75 B: 25 35 45
B gondolatmenete:
B: 25 35 45 A: 25 29 33
Képzeljünk el egy (egypetéjű) ikerpárt. Legyen a nevük 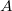 (pl. Aladár) és
(pl. Aladár) és 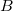 (pl. Béla). 25 éves korukban
(pl. Béla). 25 éves korukban 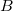 beül egy űrhajóba és közel fénysebességgel, egyenletesen mozogva távolodik a Földtől, majd (a megbeszélt terv szerint) megfordul és ugyanazzal az állandó sebességgel visszatér a Földre. Mit vár
beül egy űrhajóba és közel fénysebességgel, egyenletesen mozogva távolodik a Földtől, majd (a megbeszélt terv szerint) megfordul és ugyanazzal az állandó sebességgel visszatér a Földre. Mit vár 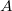 és mit vár
és mit vár 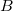 amikor újra találkoznak és mit fognak valójában tapasztalni?
amikor újra találkoznak és mit fognak valójában tapasztalni?
Tegyük fel, hogy az űrhajó sebessége akkora, hogy 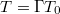 szerint
szerint 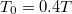 . Ez kb.
. Ez kb. 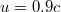 sebességnek felel meg.
sebességnek felel meg.
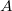 gondolatmenete a következő.
gondolatmenete a következő. 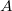 a Földet természetesen állónak tekinti. Tudja jól, hogy a testvére,
a Földet természetesen állónak tekinti. Tudja jól, hogy a testvére, 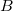 , lassabban öregszik, mert megtanulta, hogy a mozgó óra lassabban jár mint az álló. Amikor
, lassabban öregszik, mert megtanulta, hogy a mozgó óra lassabban jár mint az álló. Amikor 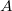 50 éves,
50 éves, 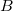 még csak 35 (ugyanis
még csak 35 (ugyanis 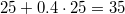 ). A terveknek megfelelően ekkor az űrhajó visszafordul és ugyanazzal az egyenletes sebességgel a Föld felé tart.
). A terveknek megfelelően ekkor az űrhajó visszafordul és ugyanazzal az egyenletes sebességgel a Föld felé tart. 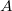 szerint a testvére továbbra is lassabban öregszik.
szerint a testvére továbbra is lassabban öregszik. 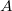 éppen 75 éves, amikor
éppen 75 éves, amikor 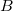 megérkezik. A visszaút
megérkezik. A visszaút 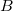 számára ugyanolyan hosszú volt, mint az elmenetele, azaz szintén 10 évig tartott.
számára ugyanolyan hosszú volt, mint az elmenetele, azaz szintén 10 évig tartott. 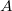 arra számít, hogy
arra számít, hogy 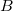 éppen 45 évesen száll ki az űrhajóból. Így egy 45 éves és egy 75 éves ikerpár fog összeölelkezni.
éppen 45 évesen száll ki az űrhajóból. Így egy 45 éves és egy 75 éves ikerpár fog összeölelkezni.
Ezek után lássuk, a történetet  szemszögéből! Ő szintén önmagát tekinti állónak. Egyenletes sebességgel távolodik tőle a Föld, ahol testvére
szemszögéből! Ő szintén önmagát tekinti állónak. Egyenletes sebességgel távolodik tőle a Föld, ahol testvére  lassabban öregszik mint ő. Ezt
lassabban öregszik mint ő. Ezt  logikusnak tarja, hiszen az egyenletesen mozgó Földön az órák lassabban járnak. Amikor
logikusnak tarja, hiszen az egyenletesen mozgó Földön az órák lassabban járnak. Amikor  35 éves,
35 éves, 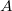 csak 29 (hiszen
csak 29 (hiszen 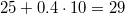 ). Ekkor
). Ekkor 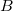 megfordul és változatlan nagyságú, egyenletes sebességgel hazafelé tart. 10 év múlva megérkezik a Földre. Ekkor tehát 45 éves. De a visszaút alatt a testvére,
megfordul és változatlan nagyságú, egyenletes sebességgel hazafelé tart. 10 év múlva megérkezik a Földre. Ekkor tehát 45 éves. De a visszaút alatt a testvére, 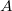 , szintén csak 4 évet öregedett, azaz 33 évesnek kell lennie.
, szintén csak 4 évet öregedett, azaz 33 évesnek kell lennie.  azt várja, hogy amikor 45 évesen kiszáll az űrhajóból, a 33 éves (fiatalabb) ikertestvérét fogja megölelni.
azt várja, hogy amikor 45 évesen kiszáll az űrhajóból, a 33 éves (fiatalabb) ikertestvérét fogja megölelni.
Ez nyilvánvaló ellentmondás (paradoxon), hiszen a 45 éves  vagy a 75 éves, vagy a 33 éves
vagy a 75 éves, vagy a 33 éves  -val találkozik. A két gondolatmenet egyszerre nem lehet igaz! Az eredmény azonban ténykérdés és az összeölelkezéskor kiderül, hogy melyikük gondolkodott helyesen. A paradoxon feloldása viszonylag egyszerű.
-val találkozik. A két gondolatmenet egyszerre nem lehet igaz! Az eredmény azonban ténykérdés és az összeölelkezéskor kiderül, hogy melyikük gondolkodott helyesen. A paradoxon feloldása viszonylag egyszerű.  gondolatmenete azért helytelen, mert az űrhajó az utazása során nem mindig viselkedett inerciarendszerként. Az elindulás, a fordulás és a fékezés alatt az űrhajó gyorsuló mozgást végzett. Ezzel a szimmetria megtört. Tehát egy 45 és egy 75 éves ember fog találkozni.
gondolatmenete azért helytelen, mert az űrhajó az utazása során nem mindig viselkedett inerciarendszerként. Az elindulás, a fordulás és a fékezés alatt az űrhajó gyorsuló mozgást végzett. Ezzel a szimmetria megtört. Tehát egy 45 és egy 75 éves ember fog találkozni.
A tárgyalt probléma egy új fogalom bevezetését generálja. Ez a sajátidő. A sajátidő a megfigyelővel együtt mozgó óra által mért idő, bármilyen is legyen a megfigyelő mozgása. Jelen estben az 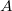 sajátideje 75 év, a
sajátideje 75 év, a 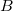 -jé 45 év volt.
-jé 45 év volt.
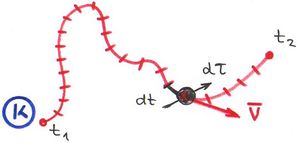
A sajátidő
Nézzük meg a sajátidő fogalmát általános esetben is. Mozogjon egy pont tetszőleges térbeli pályán!
A pálya két végpontja adott (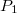 ,
, 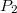 ). A pont végighalad a teljes pályán és a vele együtt mozgó megfigyelő méri a
). A pont végighalad a teljes pályán és a vele együtt mozgó megfigyelő méri a 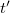 időt a nála lévő órával. Ez lesz a sajátidő, amelynek értéke legyen most
időt a nála lévő órával. Ez lesz a sajátidő, amelynek értéke legyen most 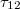 . Ugyanezt a mozgást nagyon sok inerciarendszerből megvizsgálhatjuk. Nyilvánvaló, hogy a mozgó óra által mutatott
. Ugyanezt a mozgást nagyon sok inerciarendszerből megvizsgálhatjuk. Nyilvánvaló, hogy a mozgó óra által mutatott 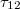 időtartam egyértelmű fizikai tény és ez nem függ attól, hogy a mozgást melyik inerciarendszerből figyeljük. Válasszunk ki tetszőlegesen két inerciarendszert és jelöljük őket
időtartam egyértelmű fizikai tény és ez nem függ attól, hogy a mozgást melyik inerciarendszerből figyeljük. Válasszunk ki tetszőlegesen két inerciarendszert és jelöljük őket  -val és
-val és  -vel. A szokásos alapértelmezés szerint definiáljuk a Descartes koordinátákat és a rendszeridőket. Az itt lévő megfigyelők a mozgó órát különböző képen látják mozogni. Ki-ki a saját rendszerében meg tudja mérni a mozgó óra futási idejét, legyen ez
-vel. A szokásos alapértelmezés szerint definiáljuk a Descartes koordinátákat és a rendszeridőket. Az itt lévő megfigyelők a mozgó órát különböző képen látják mozogni. Ki-ki a saját rendszerében meg tudja mérni a mozgó óra futási idejét, legyen ez 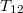 és
és 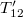 . Ugyanakkor mind a ketten ki tudják számítani a
. Ugyanakkor mind a ketten ki tudják számítani a 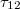 is, amelyre ugyanazt a (helyes) értéket fogják kapni. Azt mondjuk, hogy a
is, amelyre ugyanazt a (helyes) értéket fogják kapni. Azt mondjuk, hogy a 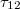 sajátidő egy invariáns mennyiség, azaz nem függ attól, hogy melyik inerciarendszerből nézve határozzuk meg az értékét.
sajátidő egy invariáns mennyiség, azaz nem függ attól, hogy melyik inerciarendszerből nézve határozzuk meg az értékét.
A  -beli megfigyelő számolási módja a következő. Osszuk fel a pályát infinitezimális (egyenesnek tekinthető) szakaszokra!
-beli megfigyelő számolási módja a következő. Osszuk fel a pályát infinitezimális (egyenesnek tekinthető) szakaszokra!
Egy ilyen kicsiny szakasz megtételéhez a  -beli megfigyelő szerint
-beli megfigyelő szerint 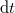 idő kell. A pályán mozgó óra ezalatt
idő kell. A pályán mozgó óra ezalatt 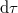 időt mér. Ezen infinitezimális szakaszon a pont (és az óra) mozgási sebessége állandónak tekinthető, így az idődilatáció
időt mér. Ezen infinitezimális szakaszon a pont (és az óra) mozgási sebessége állandónak tekinthető, így az idődilatáció 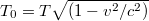 formulája használható:
formulája használható:
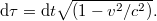
Mármost (a  -ból mérve) legyen a mozgó óra a pálya kezdeti pontjában
-ból mérve) legyen a mozgó óra a pálya kezdeti pontjában 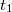 időpillanatban és a végpontban
időpillanatban és a végpontban 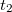 pillanatban! Így a következő írható:
pillanatban! Így a következő írható:
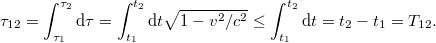
Ugyanez a számolás megtehető a másik  inerciarendszerben is. Természetesen mindenhol a vesszős rendszerben lévő megfigyelő által mért vesszős adatokat (
inerciarendszerben is. Természetesen mindenhol a vesszős rendszerben lévő megfigyelő által mért vesszős adatokat (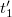 ,
, 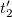 ,
, 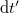 ,
, 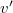 ,
, 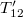 ) kell használni. Ezek ugyan mások, mint a
) kell használni. Ezek ugyan mások, mint a  -beliek, de a mozgó óra
-beliek, de a mozgó óra 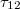 sajátidejére ugyanazt fogjuk kapni.
sajátidejére ugyanazt fogjuk kapni.
(29)
Az egyidejűség relativitása
Mint azt már a bevezetésben említtettük, a speciális relativitáselmélet megalapozásában sokan részt vettek. Lorentz és Poincare munkái vezettek a legmesszebbre. Az elektrodinamika Maxwell egyenleteinek a vizsgálata során ők is eljutottak az idő „relatív” voltáig: az álló és a mozgó inerciarendszerben mért idők transzformációs tulajdonságához. Ezek az eredmények azonban mintegy „be voltak zárva” az elektrodinamikába. Albert Einstein volt az, aki mindezt a teljes általánosság szintjére emelte. Felismerte azt, hogy itt alapvető természeti törvényekről van szó, amelyek (többek között) a Térről és az Időről tesznek alapvető kijelentéseket és száműzte az éter fogalmát a Fizikából. Ennek megfelelően ő volt az, aki egyszerű, áttekinthető, logikus rendszerbe (axiómák) szervezte a relativisztikus törvényeket. Ezért aztán (természetesen elismerve az elődök munkáit is) méltán beszélünk Einstein-féle speciális relativitáselméletről.
Az elődökön való túllépést jelenti az az igen fontos einsteini felismerés is, hogy az egyidejűség is relatív fogalom. Nincsen „abszolút” egyidejűség: ha két esemény az egyik inerciarendszerben egy időben történik, akkor (lehetséges), hogy egy másikban a két esemény két különböző időpontban következik be. Sőt még az események sorrendje is megváltozhat. A következőkben erről lesz szó.
Tekintsünk az álló rendszerben két eseményt, amelyeket az 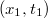 és az
és az 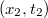 téridő adatokkal adunk meg. Ugyanezen két eseményt a mozgó rendszerben
téridő adatokkal adunk meg. Ugyanezen két eseményt a mozgó rendszerben 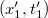 és az
és az 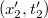 mennyiségek jellemzik.
mennyiségek jellemzik.
Az időviszonyokat külön is ábrázolhatjuk. A következőkben ezt vizsgáljuk.
Írjuk fel a két esemény időadatainak a Lorentz transzformációját:

A két egyenletet vonjuk ki egymásból. Ekkor megkapjuk az események közötti időkülönbségek kapcsolatát, tehát
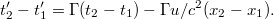
Legyen a két esemény egyidejű az álló rendszerben! Ez azt jelenti, hogy 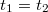 . Ezért aztán adódik, hogy
. Ezért aztán adódik, hogy
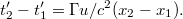
Látható, hogy két egyidejű esemény akkor lesz egyidejű a mozgó rendszerben is, ha az álló rendszerben egy helyen történtek: 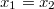 és
és 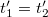 . Az egyidejű események sorrendje a mozgó rendszerben az események álló rendszerbeli helyétől függ, azaz az
. Az egyidejű események sorrendje a mozgó rendszerben az események álló rendszerbeli helyétől függ, azaz az 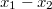 előjelétől.
előjelétől.
Az ok-okozat relativisztikus tárgyalása
Tekintsünk két (nem egy helyen és nem egy időben történő) eseményt!
Az események időadatainak Lorentz transzformációját kivonva egymásból, átrendezéssel az adódik, hogy
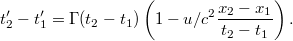
A kapott algebrai kifejezésnek igen szemléletes fizikai jelentése van. Tegyük fel, hogy 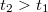 , azaz az első esemény előbb történik meg, mint a második. Ekkor létezik egy olyan mozgó rendszer, amelyben a két esemény sorrendje megcserélődik. Ez akkor következik be, ha a második szorzótényező értéke negatív. Ez a tény azonban felvet egy alapvető problémát. Ha ugyanis a két esemény ok-okozati viszonyban van egymással (azaz az első esemény okozza a másodikat) akkor a sorrendcsere fizikai lehetetlenség. Hiszen nem létezhet olyan inerciarendszer, amelyben az okozat megelőzi az okot (pl. előbb törik össze a pohár és csak utána esik le)! Látható, hogy ez a paradoxon akkor következne be, ha
, azaz az első esemény előbb történik meg, mint a második. Ekkor létezik egy olyan mozgó rendszer, amelyben a két esemény sorrendje megcserélődik. Ez akkor következik be, ha a második szorzótényező értéke negatív. Ez a tény azonban felvet egy alapvető problémát. Ha ugyanis a két esemény ok-okozati viszonyban van egymással (azaz az első esemény okozza a másodikat) akkor a sorrendcsere fizikai lehetetlenség. Hiszen nem létezhet olyan inerciarendszer, amelyben az okozat megelőzi az okot (pl. előbb törik össze a pohár és csak utána esik le)! Látható, hogy ez a paradoxon akkor következne be, ha
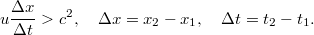
Ennek pedig az a szükséges feltétele, hogy 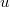 és
és 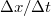 közül valamelyik, esetleg mindkettő nagyobb legyen
közül valamelyik, esetleg mindkettő nagyobb legyen  -nél. A második axióma szerint
-nél. A második axióma szerint  minden hatás terjedési sebességének a felső határa. Ez alapján
minden hatás terjedési sebességének a felső határa. Ez alapján 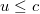 triviális, mivel
triviális, mivel 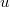
 sebessége
sebessége  -ban,
-ban, 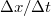 pedig annak a hatásnak az átlagsebessége, amelyet az első esemény elindít és amely aztán előidézi a második bekövetkezését, tehát ennek is
pedig annak a hatásnak az átlagsebessége, amelyet az első esemény elindít és amely aztán előidézi a második bekövetkezését, tehát ennek is  -nél kisebb-egyenlőnek kell lennie. Ezzel tulajdonképpen igazoltuk a második axióma jogosságát.
-nél kisebb-egyenlőnek kell lennie. Ezzel tulajdonképpen igazoltuk a második axióma jogosságát.
A sebességek relativisztikus összegződése
Eddig a téridő pontjainak transzformációjával és ennek a fizikai értelmezésével foglakoztunk. Most rátérünk a sebesség, mint alapvető kinematikai mennyiség transzformációs tulajdonságainak a tárgyalására.
Tekintsünk egy pontot, amelynek mozgását a téridő négy koordinátájával adunk meg. A pont mozgását vizsgáljuk a szokásos álló és mozgó rendszerben.
Mint tudjuk, a sebesség az elmozdulás-vektor idő szerinti deriváltja, amelyet a Descartes komponenseivel (is) megadhatunk. Mivel a Lorentz transzformáció lineáris művelet, így változatlanul igaz lesz infinitezimális koordináta- és idő megváltozásokra is:
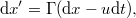
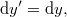
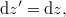
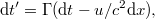
ahol 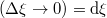 és
és 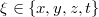 . Az infinitezimálisok „hányadosai” (definíciószerűen) éppen a klasszikus analízis deriváltjait adja. Az
. Az infinitezimálisok „hányadosai” (definíciószerűen) éppen a klasszikus analízis deriváltjait adja. Az  komponensre kapjuk tehát, hogy
komponensre kapjuk tehát, hogy
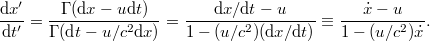
Az 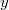 komponensre pedig:
komponensre pedig:
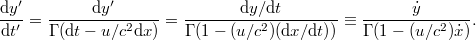
Látható, hogy kis sebességek esetén éppen a jól ismert Galilei-féle sebességösszeadási formulát kapjuk. A kapott eredményeket két feladattal világítjuk meg.
Első példa a sebességek összeadására
Mozogjon egy fénysugár  sebességgel az álló
sebességgel az álló  rendszer
rendszer 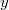 tengelye mentén. Határozzuk meg a fénysugár sebességét a mozgó
tengelye mentén. Határozzuk meg a fénysugár sebességét a mozgó  rendszerhez képest! Az álló rendszerben a sebességadatok a következők:
rendszerhez képest! Az álló rendszerben a sebességadatok a következők:

Így a mozgó rendszerben mért sebesség komponensek relativisztikus összegződés alapján:
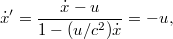
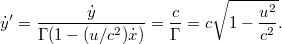
A fénysugár sebességének a nagysága az  és az
és az 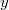 sebességkomponensekből adódik:
sebességkomponensekből adódik:
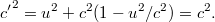
Tehát a fény a posztulátumoknak megfelelően, a mozgó rendszerben is  sebességgel terjed, de az iránya egy kissé megváltozik.
sebességgel terjed, de az iránya egy kissé megváltozik.
A csillagászatból jól ismert jelenségről van szó. A mozgó Földön lévő megfigyelő éppen ezt a szögelhajlást tapasztalja, amikor az állócsillagok helyét (fél év időkülönbséggel, Föld sebességére merőleges irányban) pl. tavasszal és ősszel megméri. Ennek az effektusnak a neve csillagászati aberráció.
Második példa a sebességek összeadására
Indítsunk el egy fénysugarat a mozgó  rendszer
rendszer 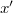 tengelye mentén.
tengelye mentén.
Mekkora ennek a sebessége az álló  rendszerben?
rendszerben?
A mozgó rendszerben mérhető sebességadatok a következők:
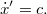
A relativisztikus sebességösszeadás értelmében az álló rendszerben azt kapjuk, hogy
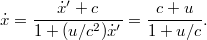
Tehát ismét teljesül az einsteni axióma. Sőt, ez még akkor is igaz, ha a mozgó rendszer fénysebességgel halad az állóhoz képest, azaz 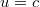 .
.
A következőkben három olyan kinematikai kísérletet mutatunk be, amelyek megerősítik a speciális relativitáselmélet téridővel kapcsolatos állításait.
Fény mozgása áramló folyadékban
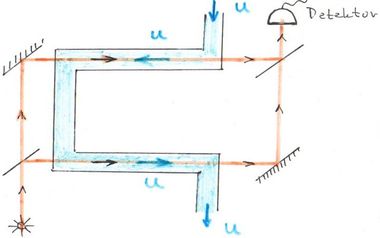
Ezt a kísérletet Hippolyte Fizeau már 1851-ben elvégezte. Korrekt magyarázatot a speciális relativitáselmélet sebességösszeadási technikája szolgáltatja. A mérés vázlata az ábrán látható.
Az „U” alakúra hajlított üvegcsőben 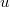 sebességgel folyadék áramlik. A félig áteresztő tükörrel két részre osztott fénynyaláb az egyik ágban a folyadék áramlásával egy irányban, a másik ágban vele szemben halad. Így a fénysugarak a két ágban, tükrökhöz képest különböző sebességgel mennek. Az ágak geometriai hossza (elvileg) megegyezik. Az üvegcsövet elhagyó nyalábokat egy másik féligáteresztő tükörrel újra egyesítjük. A sebességkülönbségekből adódó optikai úthossz-különbség miatt az egyesülő nyalábok interferenciavonalakat hoznak létre a felfogó ernyőn (ez a detektor). Ezt az optikai elrendezést Fabry-Perot interferométernek hívják.
sebességgel folyadék áramlik. A félig áteresztő tükörrel két részre osztott fénynyaláb az egyik ágban a folyadék áramlásával egy irányban, a másik ágban vele szemben halad. Így a fénysugarak a két ágban, tükrökhöz képest különböző sebességgel mennek. Az ágak geometriai hossza (elvileg) megegyezik. Az üvegcsövet elhagyó nyalábokat egy másik féligáteresztő tükörrel újra egyesítjük. A sebességkülönbségekből adódó optikai úthossz-különbség miatt az egyesülő nyalábok interferenciavonalakat hoznak létre a felfogó ernyőn (ez a detektor). Ezt az optikai elrendezést Fabry-Perot interferométernek hívják.
Alkalmazzuk a relativitáselméletet a jelen kísérletre! A tükrök és a detektor alkotják az álló  rendszert. Az áramló folyadék lesz a mozgó
rendszert. Az áramló folyadék lesz a mozgó  rendszer. Ebből kettő is van, az interferométer két ágában. Elegendő csak az egyiket megvizsgálni, mert a másik (fizikailag) ugyanilyen, csak a végső formulában folyadék sebességének az előjelét kell megváltoztatni (
rendszer. Ebből kettő is van, az interferométer két ágában. Elegendő csak az egyiket megvizsgálni, mert a másik (fizikailag) ugyanilyen, csak a végső formulában folyadék sebességének az előjelét kell megváltoztatni (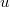 helyett
helyett 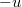 ).
).
Alkalmazva a relativisztikus sebességösszeadási formulát, kapjuk, hogy
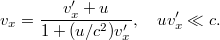
Mivel a sebességek jóval  alatt vannak, ezért a nevező sorfejtéssel közelíthető:
alatt vannak, ezért a nevező sorfejtéssel közelíthető:
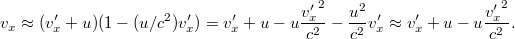
A fény terjedési sebessége a folyadékban az 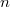 törésmutatótól függ
törésmutatótól függ
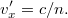
Ezt felhasználva, megkapjuk a fény sebességét az interferométer tükreihez képest:
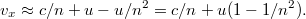
Ugyanez igaz a másik ágban is, de ekkor az 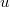 helyére
helyére 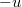 -t kell írnunk:
-t kell írnunk:
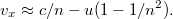
A két ágban fellépő sebességkülönbség optikai úthossz különbséget ad. Ezt már az interferométer ki tudja mutatni.
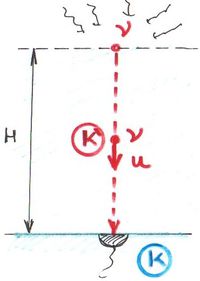
A mű-mezon (műon) bomlása
A „μ-mezon” vagy „műon” egy instabil (szubatomi, azaz a protonnál kisebb, de az elektronnál nagyobb) részecske, amely 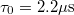 alatt elbomlik. Ezek a részecskék a Föld felső légkörében,
alatt elbomlik. Ezek a részecskék a Föld felső légkörében, 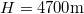 magasan keletkeznek, a kozmikus sugárzás eredményeképpen. A mérések azt mutatják, hogy a Föld felszínén is detektálunk mű-mezonokat. Ez azért meglepő, mert a részecske átlagsebessége
magasan keletkeznek, a kozmikus sugárzás eredményeképpen. A mérések azt mutatják, hogy a Föld felszínén is detektálunk mű-mezonokat. Ez azért meglepő, mert a részecske átlagsebessége
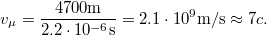
Ez pedig a relativitáselmélet axiómája szerint lehetetlen. A kérdés mármost az, miként magyarázható ez a mérési eredmény?
A válasz az idődilatációban és/vagy a hosszkontrakcióban rejlik. A szóban forgó jelenséget mind a Földhöz rendelt álló  , mind pedig a Föld felszíne felé száguldó mű-mezonhoz rögzített mozgó
, mind pedig a Föld felszíne felé száguldó mű-mezonhoz rögzített mozgó  (inercia)rendszerből is megvizsgáljuk.
(inercia)rendszerből is megvizsgáljuk.
A földi megfigyelő szerint azért éri el a mezon a Föld felszínét, mert a  -ban
-ban  sebességgel mozgó
sebességgel mozgó  -ben az idő lassabban telik. Azaz
-ben az idő lassabban telik. Azaz 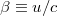 szerint
szerint
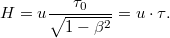
A mű-mezon szempontjából, a Föld mozog 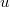 sebességgel, így a hosszkontrakció miatt a
sebességgel, így a hosszkontrakció miatt a 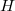 távolságot a mezonnal együtt mozgó megfigyelő (ez maga a mű-mezon) rövidebbnek méri, azaz
távolságot a mezonnal együtt mozgó megfigyelő (ez maga a mű-mezon) rövidebbnek méri, azaz
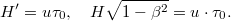
Rögtön látható, hogy az utolsó két formula pontosan ugyanaz. Számítsuk még ki a mezon sebességét! Átrendezés és 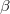 beírása után kapjuk, hogy
beírása után kapjuk, hogy
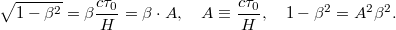
Ebből az ismereten 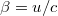 kiszámítható:
kiszámítható:
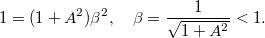
Az 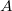 értékére kapjuk, hogy:
értékére kapjuk, hogy:
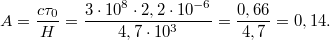
Mivel 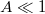 ezért jó közelítéssel
ezért jó közelítéssel
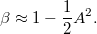
És így 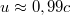 . Ez pedig eleget tesz az einsteini axiómának!
. Ez pedig eleget tesz az einsteini axiómának!
A Doppler-effektus
Az akusztikában már hallottunk a Doppler-effektusról. A közeledő hangforrás frekvenciáját magasabbnak, a távolodóét alacsonyabbnak halljuk. A hang sebessége hat nagyságrenddel kisebb, mint  , ezért a relativisztikus tárgyalás gyakorlatilag érdektelen. Egészen más a helyzet a fénnyel. Mivel a sebessége
, ezért a relativisztikus tárgyalás gyakorlatilag érdektelen. Egészen más a helyzet a fénnyel. Mivel a sebessége  , csakis a relativisztikus számolás adhat helyes eredményt!
, csakis a relativisztikus számolás adhat helyes eredményt!
Tekintsük a szokásos (standard,  ,
,  ) koordinátarendszereket. A fényforrás legyen a
) koordinátarendszereket. A fényforrás legyen a  -ban és haladjon a fény (sík)hullám a
-ban és haladjon a fény (sík)hullám a 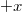 tengely mentén.
tengely mentén.
A kérdés az, hogy mekkora frekvenciájú fényt érzékel a (fényforráshoz képest) mozgó megfigyelő?
Mint azt az elektrodinamikából tudjuk, a fényhullámot alkotó elektromos és mágneses mező bármelyik (Descartes) komponense ugyanolyan függvény szerint változik. Jelölje ezt 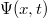 . A hullámfüggvény matematikai alakja a
. A hullámfüggvény matematikai alakja a  -ban:
-ban:
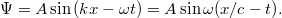
A Lorentz transzformáció szerint 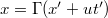 és
és 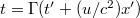 , így a hullámfüggvény a mozgó
, így a hullámfüggvény a mozgó  -ben így írható fel:
-ben így írható fel:
![\displaystyle \Psi' = A' \sin{\left[ \omega\Gamma\left( \frac{x'}{c} + \frac{u}{c}t' - t' - \frac{u}{c^2}x' \right) \right]}.](/images/math/0/e/e/0ee0ac23ef78b6a42ab7af8ebb9e770e.png)
A szinusz függvény argumentuma csak egy szám (fizikai skalár) lehet, hiszen pl. a 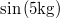 -nak nincsen értelme. Az előző egyenletben szereplő szinusz függvény argumentuma tehát skalár, ezért egy invariáns mennyiség, azaz minden inerciarendszerben ugyanaz az értéke. Például „3 darab alma” bármelyik inerciarendszerből megszámolva mindig 3 darab lesz. Az egyenletben található zárójeles kifejezés átalakítható (a részletek házi feladat):
-nak nincsen értelme. Az előző egyenletben szereplő szinusz függvény argumentuma tehát skalár, ezért egy invariáns mennyiség, azaz minden inerciarendszerben ugyanaz az értéke. Például „3 darab alma” bármelyik inerciarendszerből megszámolva mindig 3 darab lesz. Az egyenletben található zárójeles kifejezés átalakítható (a részletek házi feladat):
![\displaystyle \Psi' = A' \sin{\left[ \omega\Gamma \left( 1 - \frac{u}{c} \right) \left( \frac{x'}{c} - t' \right) \right]}.](/images/math/c/2/b/c2b5d59c354b592a14b925979096152c.png)
Ezt összevetve 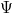
 -beli alakjával:
-beli alakjával:
![\displaystyle \omega' = \omega\Gamma \left( 1 - \frac{u}{c} \right) = \omega \sqrt{\frac{c-u}{c+u}}, \quad \Psi' = A' \sin{\left[ \omega' \left( \frac{x'}{c} - t' \right) \right]}.](/images/math/7/2/6/7267d0dd9a3395ed7b8f758d3b3bca1f.png)
Ez tehát az optikai Doppler-effektus. Kis sebességeknél visszakapjuk a „klasszikus” Doppler-formulát:
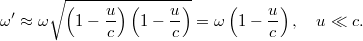
Ha a fénnyel szemben mozgunk, akkor 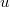 helyett
helyett 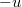 -t kell írnunk és ezért kapjuk, hogy
-t kell írnunk és ezért kapjuk, hogy
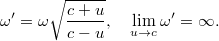
A Mechanika (Dinamika) relativisztikus törvényei
Az előzőekben megtanultuk, hogyan kell átformálnunk a Térről és az Időről alkotott hétköznapi elképzelésünket. Megértettük, hogy mi az oka annak, hogy szakítanunk kellett a Newton által definiált abszolút Tér és abszolút Idő szemléletes fogalmával. Elcsodálkoztunk a kinematikai effektusokon amelyek ennek a szakításnak az eredményeképpen szükségszerűen adódtak. Csodálkoztunk, mert a hétköznapi mozgások világában ezek megnyilvánulása 6-7 nagyságrenddel kisebbek az érzékszerveink által észlelhető effektusoknál. Így a szokatlanságuk a tapasztalat (szükségképpeni) hiányából fakad.
Előítéleteink rabjai vagyunk. Azon előítéleteké, amelyeket születésünktől fogva az érzékszervi észlelések (létfenntartó) sokasága épített ki bennünk. De hála absztrakciókészségünknek, a „függöny mögé pillanthatunk”. A Matematika pedig megadja azt az igen hatékony szerszámot, amellyel a dolgok (Természeti jelenségek rendszere) mélyére áshatunk.
A következőkben (a relativisztikus kinematikára támaszkodva) megnézzük, hogy a dinamikai törvények hogyan teljesítik az Einstein-féle posztulátumokat.
A klasszikus mechanika Newton-féle axiómarendszerének az ellenőrzésére legalkalmasabb módszer két tömegpont ütközésének a vizsgálata (volt). Ütközés előtt a két tömegpont egyenes vonalú egyenletes mozgást végez (Newton 1). Ütközéskor a tömegpontokra ható erők nagysága egyenlő (Newton 3). A tökéletesen rugalmas ütközés (igen rövid) ideje alatt az impulzusok megváltoznak (Newton 2), a rendszer összimpulzusa azonban állandó marad (impulzustétel). Az ütközés után a tömegpontok által (egy adott időtartam alatt) megtett távolságok aránya a tömegek reciprok arányával egyenlő (dinamikus tömegfogalom és mérése). Tökéletesen rugalmatlan ütközéskor (a tömegpontok összetapadnak) a mechanikai (kinetikus) energia nem lesz állandó a folyamat során, de impulzustétel továbbra is érvényes marad.
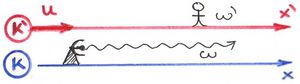
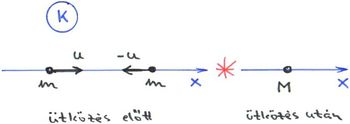
A nagyobb általánossága miatt célszerű az impulzustételt megvizsgálni a speciális relativitáselmélet eddig megtanult fogalmi rendszerén belül. Az álló  rendszer
rendszer  tengelye mentén két, azonos nagyságú,
tengelye mentén két, azonos nagyságú, 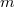 tömegű, pontszerű test
tömegű, pontszerű test 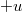 és
és 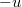 sebességgel egymással szembe halad. Összeütköznek és összetapadnak. Az ütközés tökéletesen rugalmatlan.
sebességgel egymással szembe halad. Összeütköznek és összetapadnak. Az ütközés tökéletesen rugalmatlan.
Az ütközés előtt a rendszer összimpulzusa zérus (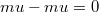 ) és az impulzusmegmaradás tétele miatt az ütközés után továbbra is nulla marad. Következésképpen az összetapadt tömeg nyugalomban lesz (
) és az impulzusmegmaradás tétele miatt az ütközés után továbbra is nulla marad. Következésképpen az összetapadt tömeg nyugalomban lesz (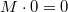 ).
).
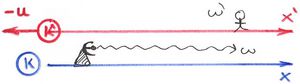
Rögzítsük a  koordinátarendszerünket a
koordinátarendszerünket a 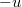 sebességgel mozgó tömegponthoz. Vizsgáljuk meg, hogy miként észleli az ütközés folyamatát ebben a mozgó rendszerben lévő (hipotetikus) megfigyelő. (Pl. ha most egy töréstesztben szereplő, két frontálisan ütköző gépkocsiról lenne szó, akkor az egyik próbabábú által regisztrált mérési adatokat akarjuk megjósolni. Mindezt azoknak a kinematikai és dinamikai mérési adatoknak az ismeretében, melyeket az ütközés során az álló laborban végeztünk el.)
sebességgel mozgó tömegponthoz. Vizsgáljuk meg, hogy miként észleli az ütközés folyamatát ebben a mozgó rendszerben lévő (hipotetikus) megfigyelő. (Pl. ha most egy töréstesztben szereplő, két frontálisan ütköző gépkocsiról lenne szó, akkor az egyik próbabábú által regisztrált mérési adatokat akarjuk megjósolni. Mindezt azoknak a kinematikai és dinamikai mérési adatoknak az ismeretében, melyeket az ütközés során az álló laborban végeztünk el.)
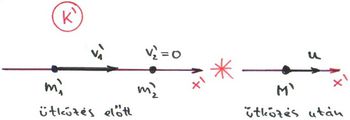
A matematikai általánosság végett a  rendszerben álló tömegpont tömegét
rendszerben álló tömegpont tömegét 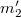 -vel, a mozgó pontét
-vel, a mozgó pontét 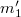 -vel, az ütközés utáni (összetapadt) tömeget pedig
-vel, az ütközés utáni (összetapadt) tömeget pedig 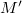 -vel fogjuk jelölni. Az
-vel fogjuk jelölni. Az 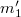 tömegpont ütközés előtti sebessége legyen
tömegpont ütközés előtti sebessége legyen 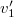 . Felírható az impulzusmegmaradás törvénye:
. Felírható az impulzusmegmaradás törvénye:
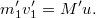
A tömeg(anyag-)megmaradás elve szerint pedig
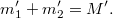
A két egyenletet összevonva, majd átrendezve, adódik, hogy:
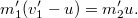
Ebből az ütközés előtti tömegek arányára kapjuk a következő összefüggést:
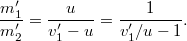
Alkalmazzuk ezt az eredményt a mostani példánkra! A Newton-féle dinamika szerint a tömegek ugyanazok, mint az álló rendszerben voltak, azaz 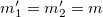 , ezért az előző egyenletből a tömegek kiesnek és
, ezért az előző egyenletből a tömegek kiesnek és 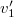 -re azt kapjuk, hogy
-re azt kapjuk, hogy
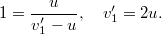
Tehát az impulzustétellel mintegy „levezettük” a Galilei-féle sebességösszeadási törvényt. Tudjuk azonban, hogy a relativisztikus sebességösszeadási formula szerint az eredmény más lesz, mégpedig a következő:
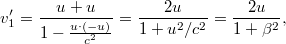
ahol 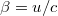 . Ha továbbra is newtoni tömegfogalmat használjuk, akkor nyilvánvalóan
. Ha továbbra is newtoni tömegfogalmat használjuk, akkor nyilvánvalóan 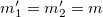 és
és 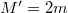 . Az impulzusmegmaradás tétele ekkor
. Az impulzusmegmaradás tétele ekkor
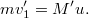
Beírva ide a relativisztikus sebesség értékét, azt kapjuk, hogy
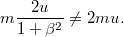
Tehát  koordinátarendszerben az impulzusmegmaradás tétele nem teljesül, csak kicsi sebességekre (
koordinátarendszerben az impulzusmegmaradás tétele nem teljesül, csak kicsi sebességekre (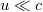 , azaz
, azaz 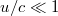 ). Mindez azonban ellentmond a relativitáselmélet első posztulátumának, azaz a természeti törvények invarianciájának. Ezért aztán nincsen más választásunk, mint a Newton-féle dinamika átalakítása. Ezt úgy kell megtennünk, hogy az impulzusmegmaradás törvénye mind a
). Mindez azonban ellentmond a relativitáselmélet első posztulátumának, azaz a természeti törvények invarianciájának. Ezért aztán nincsen más választásunk, mint a Newton-féle dinamika átalakítása. Ezt úgy kell megtennünk, hogy az impulzusmegmaradás törvénye mind a  , mind pedig a
, mind pedig a  rendszerben igaz legyen! Végigkövetve az eddigieket, látható, hogy a „tömeg” az az egyetlen szabad dinamikai mennyiség, amin (a siker reményében) változtatnunk kell. A következőkben ezt fogjuk megtenni. A relativisztikus sebesség kifejezése alapján határozzuk meg következő sebességarányt:
rendszerben igaz legyen! Végigkövetve az eddigieket, látható, hogy a „tömeg” az az egyetlen szabad dinamikai mennyiség, amin (a siker reményében) változtatnunk kell. A következőkben ezt fogjuk megtenni. A relativisztikus sebesség kifejezése alapján határozzuk meg következő sebességarányt:
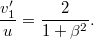
Beírva ezt a tömegarányt megadó összefüggésbe,
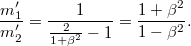
A szokásos jelölés bevezetésével legyen 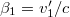 . A relativisztikus sebesség kifejezését felhasználva
. A relativisztikus sebesség kifejezését felhasználva
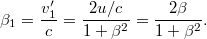
Képezzük az 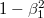 kifejezést:
kifejezést:
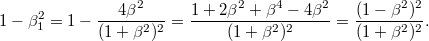
A gyökvonás elvégzése után, a (relativisztikus) tömegarányt kifejező összefüggés felhasználásával azt kapjuk, hogy
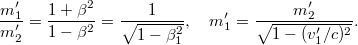
Látható azonban, hogy az 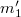 és
és 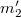 két ugyanakkora pontszerű testnek a tömege mozgó, illetve álló helyzetben. Tételezzük fel, hogy mindez teljes általánosságban (pl. egyetlen pontszerű testre) is igaz. Így, ha egy álló pontszerű test tömege
két ugyanakkora pontszerű testnek a tömege mozgó, illetve álló helyzetben. Tételezzük fel, hogy mindez teljes általánosságban (pl. egyetlen pontszerű testre) is igaz. Így, ha egy álló pontszerű test tömege 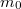 , akkor ugyanennek a testnek a tömege, ha az
, akkor ugyanennek a testnek a tömege, ha az  sebességgel mozog, a következő:
sebességgel mozog, a következő:
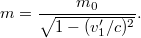
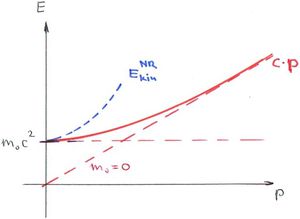
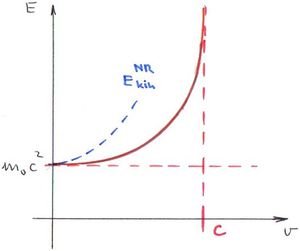
Ez az ún. relativisztikus tömegnövekedés. Az 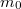 -t nyugalmi tömegnek nevezzük. (Lásd Tömeg a speciális relativitáselméletben (Wikipedia cikk))
-t nyugalmi tömegnek nevezzük. (Lásd Tömeg a speciális relativitáselméletben (Wikipedia cikk))
Tehát, a tömegpontok ütközése csak akkor zajlik le minden inerciarendszerben ugyanolyan törvények szerint (ami éppen a speciális relativitáselmélet első posztulátumának a követelménye), ha a relativisztikus kinematikát és a relativisztikus tömeg fogalmat használjuk. A kérdés ezek után az, hogy milyen lesz a relativisztikus mozgásegyenlet (axióma)? Természetesen ezt nem lehet „levezetni” semmiből! Ezt valami módon ki kell találni, hasonlóan mint azt tettük a Newton-féle 2. axióma esetén. A mérési tapasztalatok majd megerősítik vagy cáfolják a hipotézisünket. Kézenfekvő a feltevés, hogy a mozgásegyenlet formája legyen olyan mint a Newton-egyenlet, azaz
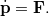
De most az impulzus a relativisztikus impulzus legyen, azaz
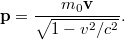
Látható, hogy a korrespondencia-elvnek megfelelően ha 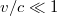 (vagy
(vagy 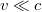 ), akkor az új egyenletünk átmegy a Newton-féle (nem-relativisztikus) mozgásegyenletbe.
), akkor az új egyenletünk átmegy a Newton-féle (nem-relativisztikus) mozgásegyenletbe.
Az elmúlt száz évben tapasztalati tények milliói támasztották alá a relativisztikus dinamika helyességét. Valamint nem találkoztunk egyetlen egy olyan reprodukálható kísérleti eredménnyel sem, amely ennek ellene mondott volna. A modern kísérleti technikában használt részecskegyorsítok százait építették meg ezen relativisztikus dinamika ismeretében. Mivel ezekkel a berendezésekkel a felgyorsított elektronok, protonok (töltött részecskék) közel fénysebességgel mozognak, a relativisztikus tömegnövekedés figyelembevétele a tervezői munka során kihagyhatatlan.
Mindezek alapján (nagyon nagy valószínűséggel) kijelenthetjük, hogy a Speciális Relativitáselméletben a Természet egyik alapvető (szimmetria-) tulajdonságát ismertük fel.
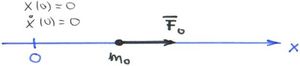
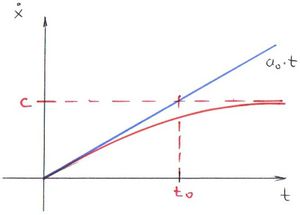
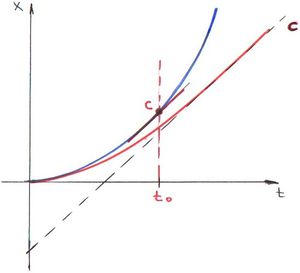
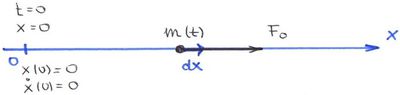
Tömegpont mozgása állandó erő hatására
Most egy jól ismert példán keresztül bemutatjuk a relativisztikus dinamika működését. Az álló  tengely mentén, az origóból, nyugalomból indulva egy tömegpont állandó
tengely mentén, az origóból, nyugalomból indulva egy tömegpont állandó 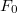 erő hatására mozog.
erő hatására mozog.
Határozzuk meg a kinematikai jellemzőit (sebesség, megtett út)!
Először elevenítsük föl a feladat jól ismert, klasszikus (newtoni dinamika) szerinti megoldását, így láthatjuk majd a lényegi különbséget, amit a relativisztikus mechanika jelent a klasszikussal szemben és ellenőrizhetjük a korrespondencia-elvet is.
A Newton-féle mozgástörvény szerint a tömegpont gyorsulása, sebessége és elmozdulása könnyen számolható. A kezdeti feltételeknek megfelelően („az origóból, nyugalomból indul”, 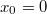 ,
, 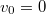 ) kapjuk, hogy:
) kapjuk, hogy:
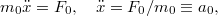
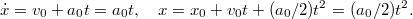
A relativisztikus tárgyalás matematikailag kissé bonyolultabb. A mozgásegyenlet összevetve a relativisztikus impulzus kifejezésével,
![\displaystyle \frac{\rm d}{{\rm d}t} \left[ \frac{m_0}{\sqrt{1-(\dot{x}/c)^2}} \dot{x} \right] = F_0.](/images/math/6/e/a/6eacf0e547849d2f97de5e7d30232fa3.png)
Mind a két oldal idő szerint könnyen integrálható
![\displaystyle \left[ \frac{m_0 \dot{x}}{\sqrt{1-(\dot{x}/c)^2}} \right]_{0}^{\dot{x}} = F_0 t.](/images/math/7/d/d/7dd5f3f5f38f1ecc17747f08b63ab54e.png)
Felhasználva a határfeltételeket, adódik, hogy:
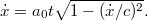
Négyzetre emelés után az egyenlet átrendezhető:
![\displaystyle \dot{x}^2 = \left( 1 - \frac{\dot{x}^2}{c^2} \right) a_0^2 t^2, \quad \dot{x}^2 \left[ 1 + (a_0 t/c)^2 \right] = a_0^2 t^2.](/images/math/b/a/3/ba3f555ee29e47c0ae328469ae76d625.png)
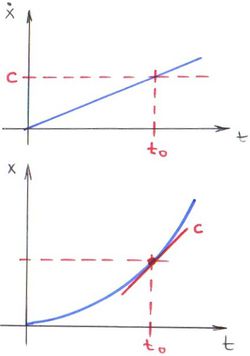
Innen a sebesség keresett időfüggvénye megkapható:
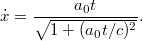
Látható, hogy 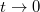 esetén, amikor még kicsi a sebesség, a newtoni eredmény adódik. A
esetén, amikor még kicsi a sebesség, a newtoni eredmény adódik. A 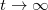 határérték pedig a fénysebességhez tart.
határérték pedig a fénysebességhez tart.
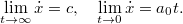
Ez eleget tesz a speciális relativitáselmélet Einstein-féle axiómáinak.
A sebesség ismeretében (integrálással) megkaphatjuk az elmozdulás 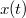 függvényt is.
függvényt is.
![\displaystyle [x]_0^t = \int_0^t \frac{a_0 t}{\sqrt{1 + (a_0 t/c)^2}} {\rm d}t = \left[ \frac{c^2}{a_0} \sqrt{1 + (a_0 t/c)^2} \right]_0^t.](/images/math/7/a/8/7a8c901f7cb490424bfe5ba9342af550.png)
A határfeltétel ismeretében adódik a végeredmény
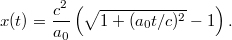
 az időnek hiperbolikus függvénye. Ennek a hiperbolának az aszimptotája egy
az időnek hiperbolikus függvénye. Ennek a hiperbolának az aszimptotája egy  meredekségű egyenes. Mint tudjuk, a klasszikus esetben az
meredekségű egyenes. Mint tudjuk, a klasszikus esetben az  parabola, amely nem rendelkezik ezzel az aszimptotikus tulajdonsággal. (29.ábra)
parabola, amely nem rendelkezik ezzel az aszimptotikus tulajdonsággal. (29.ábra)
A tömeg-energia ekvivalencia
Talán nincsen még egy olyan matematikai formula, amely annyit szerepelne a nyilvánosság előtt, mint az  . Található pólókra festve és a vicclapok karikatúráiban is. Nézzük meg, hogy miről is van szó.
. Található pólókra festve és a vicclapok karikatúráiban is. Nézzük meg, hogy miről is van szó.
Mozogjon egy tömegpont az  tengely mentén. A tömegpont nyugalomból indul és valamilyen tetszőleges
tengely mentén. A tömegpont nyugalomból indul és valamilyen tetszőleges  erő hatására gyorsul.
erő hatására gyorsul.
Számítsuk ki az 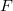 erő
erő 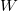 munkáját, mialatt a pont az álló helyzetéből
munkáját, mialatt a pont az álló helyzetéből  sebességűre gyorsul! A munkavégzés definíciója szerint
sebességűre gyorsul! A munkavégzés definíciója szerint
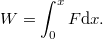
A tömegpont mindvégig a relativisztikus mozgásegyenletnek megfelelően viselkedik, azaz
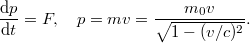
Ezt felhasználva a 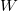 definíciós kifejezésében, kapjuk, hogy
definíciós kifejezésében, kapjuk, hogy
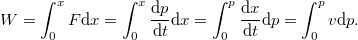
Az impulzus szerinti integrálásról áttérhetünk sebesség szerintire. A változócserét legegyszerűbben az infinitezimális 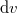 –vel való „bővítéssel” érhetjük el.
–vel való „bővítéssel” érhetjük el.
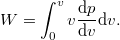
Ezután egy parciális integrálással léphetünk tovább. Tehát
![\displaystyle W = [pv]_0^v - m_0 \int_0^v p {\rm d}v.](/images/math/d/9/5/d95f516cf841c17e1c373e93cf7745cb.png)
A relativisztikus impulzus a  sebesség jól ismert függvénye, ezért írhatjuk, hogy
sebesség jól ismert függvénye, ezért írhatjuk, hogy
![\displaystyle W = [pv]_0^v - m_0 \int_0^v \frac{v}{1-(v/c)^2} {\rm d}v.](/images/math/2/a/0/2a041f85e01bdfbc0652319d6f6164c0.png)
A kijelölt integrálás könnyen elvégezhető, mert az integrálandó függvény primitív függvénye ismert:
![\displaystyle W = m_0 \frac{v^2}{\sqrt{1 - (v/c)^2}} - m_0 \left[ -c^2 \sqrt{1 - (v/c)^2} \right]_0^v = m_0 \frac{v^2}{\sqrt{1 - (v/c)^2}} + m_0 c^2 \sqrt{1 - (v/c)^2} - m_0 c^2.](/images/math/6/e/a/6ea023d336f338b2588798c42f27c62b.png)
Bevezethető a szokásos 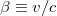 jelölés is. A nyilvánvaló adódó kiemelés után kapjuk, hogy
jelölés is. A nyilvánvaló adódó kiemelés után kapjuk, hogy
![\displaystyle W = m_0 c^2 \left[ \frac{\beta^2}{\sqrt{1-\beta^2}} + \sqrt{1-\beta^2} - 1 \right].](/images/math/e/e/3/ee30eeb270709b818b295014890abac9.png)
Elvégezve a zárójelben kijelölt műveletet, a következő kifejezésre jutunk:
![\displaystyle W = m_0 c^2 \left[ \frac{1}{\sqrt{1-\beta^2}} - 1 \right].](/images/math/f/8/e/f8e8dbe025ff0c6d5e79b2010b5ace3e.png)
Mint az jól ismert, a munkatétel szerint: egy tömegpont 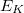 kinetikus energiájának a
kinetikus energiájának a 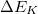 megváltozása egyenlő
a ponton ható erő
megváltozása egyenlő
a ponton ható erő 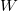 munkájával. Alkalmazzuk a munkatételt a mostani esetben is! Ekkor a
munkájával. Alkalmazzuk a munkatételt a mostani esetben is! Ekkor a 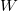 -re kapott kifejezés alapján írhatjuk, hogy
-re kapott kifejezés alapján írhatjuk, hogy
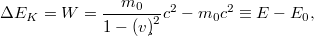
ahol definíció szerint megkapjuk a „híres összefüggést”:
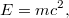
melynek neve: tömeg-energia ekvivalencia.
A newtoni mechanikához képest, a fogalmak szintjén megjelenik egy érdekes újdonság. Ez a 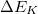 kifejezésében szereplő
kifejezésében szereplő 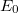 , amit nyugalmi energiának nevezünk. Evvel minden, nyugalomban lévő
, amit nyugalmi energiának nevezünk. Evvel minden, nyugalomban lévő 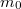 tömegű test rendelkezik. Ez joggal veti fel a kifejezés fizikai értelmezésének az igényét.
tömegű test rendelkezik. Ez joggal veti fel a kifejezés fizikai értelmezésének az igényét.
Mint azt tudjuk, a  fénysebesség egy invariáns skalár és egyben egy „természeti állandó” is. Az
fénysebesség egy invariáns skalár és egyben egy „természeti állandó” is. Az 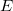 -vel jelölt energia bevezetése egy definícióval történt. Azaz a mozgó tömegpont kinetikus energiáját az
-vel jelölt energia bevezetése egy definícióval történt. Azaz a mozgó tömegpont kinetikus energiáját az 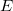 energia és az
energia és az 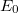 nyugalmi energiának a különbségeként definiáltuk. Tehát az
nyugalmi energiának a különbségeként definiáltuk. Tehát az 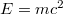 -ben az egyenlőség jel nem egy „ok-okozat” viszonyt fejez ki mint pl. az
-ben az egyenlőség jel nem egy „ok-okozat” viszonyt fejez ki mint pl. az 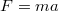 kifejezésben.
kifejezésben.
Mint azt tudjuk, az SI mértékegység rendszerben a ![c\approx 3\cdot 10^8 [{\rm m/s}]](/images/math/2/6/4/26497f6c4a4412d7475e6e7168fc07d2.png) . Választhatnánk olyan hosszúság- és időegységet, hogy
. Választhatnánk olyan hosszúság- és időegységet, hogy 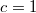 [hossz/idő] adódjék. Ekkor
[hossz/idő] adódjék. Ekkor 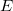 és
és 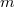 mindig ugyanaz a számérték lenne, de más mértékegységgel. Ez olyan, mintha ugyanarról a fizikai mennyiségről lenne szó, csak más mértékegységgel kifejezve. Ezért beszélhetünk „tömeg-energia ekvivalenciáról”.
mindig ugyanaz a számérték lenne, de más mértékegységgel. Ez olyan, mintha ugyanarról a fizikai mennyiségről lenne szó, csak más mértékegységgel kifejezve. Ezért beszélhetünk „tömeg-energia ekvivalenciáról”.
Einstein kiterjesztette ennek az érvényességét pontrendszerekre is. Egy pontrendszer nyugalmi energiája az összetevők kinetikus energiájának és (a részecskék kölcsönhatásából származó) potenciális energia(ák) összegéből áll. Így pl. a rendszer nyugalmi tömege változni fog, ha bármelyik belső energia (kinetikus, potenciális) megváltozik. Tehát nem arról van szó, hogy „a tömeg energiává alakul”, hanem arról, hogy az energia megváltozását egyben tömegváltozásként is detektálhatjuk.
- It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing – a somewhat unfamiliar conception for the average mind. Furthermore, the equation
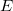 is equal to
is equal to 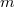
 -squared, in which energy is put equal to mass, multiplied by the square of the velocity of light, showed that very small amounts of mass may be converted into a very large amount of energy and vice versa. The mass and energy were in fact equivalent, according to the formula mentioned above. This was demonstrated by Cockcroft and Walton in 1932, experimentally. (Albert Einstein)
-squared, in which energy is put equal to mass, multiplied by the square of the velocity of light, showed that very small amounts of mass may be converted into a very large amount of energy and vice versa. The mass and energy were in fact equivalent, according to the formula mentioned above. This was demonstrated by Cockcroft and Walton in 1932, experimentally. (Albert Einstein)
Tömegdefektus
A fenti eredmények igen szépen igazolódnak az ún. „tömegdefektus” jelenségében. Ennek szerepe a nukleáris technikában alapvető.
Mint tudjuk, a Hélium atom magja két protonból és két neutronból áll. A tapasztalat szerint azonban két proton és két neutron tömegének az összege nagyobb, mint a Hélium atom magjáé. Vajon miért?
A megoldás a tömeg-energia ekvivalencia ténye. Ha a négy darab részecske egymástól végtelen (mikroszkopikus skálán nagyon nagy) távolságra van egymástól, akkor az így tekintett rendszer tömege a részecskék tömegének az összege lesz. Ha azonban a részecskék egy Hélium atommá állnak össze, akkor közöttük egy vonzó kölcsönhatásnak kell fellépni. Ez sokkal nagyobb kell, hogy legyen, mint a protonok közötti taszító Coulomb-erő. A vonzó kölcsönhatás távolságokban már igen nagy. Ezt az újfajta kölcsönhatást magerőnek hívjuk. Ez a nukleonok (neutronok és protonok) között hat. Mivel vonzó erőhatásról van szó, ez negatív potenciális energiát jelent, azaz lecsökken a rendszer (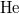 ) nyugalmi energiája.
) nyugalmi energiája.
Ez a tömegkülönbség (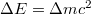 ) kb.
) kb. 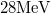 energiakülönbséget jelent. Egy mol (
energiakülönbséget jelent. Egy mol (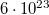 db)
db) 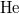 atom esetén ez
atom esetén ez 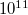 Joule energiát ad. Makroszkopikus skálán ez hatalmas mennyiség. Ezt az effektust használjuk fel a jövendő fúziós reaktoroknál.
Joule energiát ad. Makroszkopikus skálán ez hatalmas mennyiség. Ezt az effektust használjuk fel a jövendő fúziós reaktoroknál.
Az energia mint a sebesség és az impulzus függvénye
Ismeretes, hogy a klasszikus mechanikában az 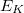 kinetikus energia definíció szerint
kinetikus energia definíció szerint 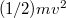 és/vagy
és/vagy 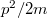 , ahol
, ahol 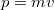 . Érdemes megkeresni ugyanezek megfelelőit a relativisztikus mechanikában!
. Érdemes megkeresni ugyanezek megfelelőit a relativisztikus mechanikában!
Az  valójában már ismert, hiszen
valójában már ismert, hiszen
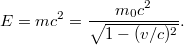
Könnyen belátható, hogy kis sebességeknél (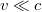 ) visszakapjuk klasszikus definíciót:
) visszakapjuk klasszikus definíciót:
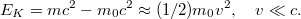
Az 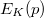 kiszámítása már bonyolultabb (a tömeg időfüggő!). Ezért itt csak azt bizonyítjuk, hogy a megadott formula teljesíti a korrespondencia-elvet, azaz „kis” impulzusok (
kiszámítása már bonyolultabb (a tömeg időfüggő!). Ezért itt csak azt bizonyítjuk, hogy a megadott formula teljesíti a korrespondencia-elvet, azaz „kis” impulzusok ( ) esetén visszakapjuk a klasszikus eredményt. Tehát
) esetén visszakapjuk a klasszikus eredményt. Tehát
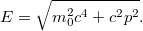
és így
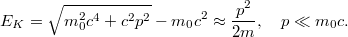
Mint azt vártuk, a  sebesség (kinetika) mindig kisebb, mint
sebesség (kinetika) mindig kisebb, mint  , de az impulzus (dinamika) tetszőlegesen nagy lehet.
, de az impulzus (dinamika) tetszőlegesen nagy lehet.