Spektrumanalízis heterodin méréstechnikával
A mérési feladatot összeállította: Simon Ferenc és Halbritter András, BME Fizika Tanszék (2015)
A jegyzettel kapcsolatos javításokat, javaslatokat köszönettel vesszük a és az
címre.
A laborgyakorlat célja, hogy a nagyfrekvenciás méréstechnikában széleskörben alkalmazott Fourier-analízis és heterodin méréstechnika alapjait bemutassa. A laborgyakorlat nagyban támaszkodik a korábbi Méréstechnika tárgyra, ezért az ott elsajátított ismeretek átismétlése erősen ajánlott.
Bevezetés és történeti háttér
Az adatátvitel alapfeladata, hogy a lehető legtöbb információt juttassunk el két pont között az információt minél jobban megtartva. Napjainkban amikor a környezetünk zsúfolva van különböző információtovábbító elektromágneses sugárzással, különösen fontos ez a kérdés. Az egyik elterjedt megoldás a különböző információk különböző frekvenciákhoz való rendelése (ún. frekvenciaosztásos multiplexelés). Ez eredményezi a manapság ismert különböző frekvenciájú rádióadások jelenlétét, ahol mindegyik rádiócsatorna adott (vivő)frekvencián sugározza az adását. Az adások információtartalma különböző módon van a vivőhullámba belekódolva. Itt a két legfontosabbat említjük csak, amivel a gyakorlaton is megismerkedünk: AM (amplitúdómoduláció) és FM (frekvenciamoduláció).
Belátható, hogy a továbbított információ mennyisége és az adott jelhez tartozó sávszélesség ( ) egymással egyenesen arányos. Például egy állandó frekvenciájú sugárzással - melynek sávszélessége nulla - semmilyen információt nem tudunk továbbítani, de például egy 1 kHz frekvenciával modulált 100 MHz-es vivőhullámmal már tudunk 1 kbit/s információtovábbítást elérni. (Képzeljük el, hogy egy állandó frekvenciájú, időben állandó nagyságú elektromágneses jellel próbálunk információt közvetíteni. Ennek Fourier-transzformáltja egy Dirac-delta függvény, azaz nulla sávszélessége van. Azonban ennek a jelnek az információtartalma is nulla. A legegyszerűbb Morse-adatátvitelhez is már ki-be kell kapcsolgatnunk ezt a jelet, ami már természetesen nem lesz egy állandó frekvenciájú időben állandó nagyságú jel, és így a Fourier-transzformáltja sem lesz Dirac-delta.) Nem véletlen, hogy a hétköznapi gyakorlatban mindeki csak sávszélességről beszél mialatt a továbbított információ mennyiségére utal, miközben ez a fogalom alapvetően a továbbított jel frekvenciaspektrumának szélességére utal. Ebben a jegyzetben mi a hagyományos értelmeben vett (frekvencia-)sávszélességre utalunk.
) egymással egyenesen arányos. Például egy állandó frekvenciájú sugárzással - melynek sávszélessége nulla - semmilyen információt nem tudunk továbbítani, de például egy 1 kHz frekvenciával modulált 100 MHz-es vivőhullámmal már tudunk 1 kbit/s információtovábbítást elérni. (Képzeljük el, hogy egy állandó frekvenciájú, időben állandó nagyságú elektromágneses jellel próbálunk információt közvetíteni. Ennek Fourier-transzformáltja egy Dirac-delta függvény, azaz nulla sávszélessége van. Azonban ennek a jelnek az információtartalma is nulla. A legegyszerűbb Morse-adatátvitelhez is már ki-be kell kapcsolgatnunk ezt a jelet, ami már természetesen nem lesz egy állandó frekvenciájú időben állandó nagyságú jel, és így a Fourier-transzformáltja sem lesz Dirac-delta.) Nem véletlen, hogy a hétköznapi gyakorlatban mindeki csak sávszélességről beszél mialatt a továbbított információ mennyiségére utal, miközben ez a fogalom alapvetően a továbbított jel frekvenciaspektrumának szélességére utal. Ebben a jegyzetben mi a hagyományos értelmeben vett (frekvencia-)sávszélességre utalunk.
Az emberi hang torzításmentes továbbításához (mono adás esetén) kb. 20 kHz sávszélességre van szükség. A gyakorlatban az egyes rádióadók frekvenciáját a zavaró interferencia elkerülése végett ennél távolabbra állítják be, ezért találunk a mindenki által ismert FM sávban (87,5-108 MHz között) kb. 100 kHz-enként rádióállomásokat.
Egy másik gyakorlati megfontolás ami korlátozza az átvihető információ és így a sávszélesség nagyságát, az a zaj kérdése. A Méréstechnika tárgyban ismertetett módon az ún. Johnson-Nyquist vagy termikus zaj teljesítménye és a sávszélesség közötti kapcsolat:
![\[P_{\text{JN-zaj}}=4 k_{\text{B}}T\Delta f\]](/images/math/6/3/4/634a973a440068cc792e939eb2d83b23.png)
ahol 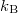 a Boltzmann-állandó,
a Boltzmann-állandó,  az abszolút hőmérséklet és
az abszolút hőmérséklet és  a sávszélesség.
a sávszélesség.
- A Méréstechnika tárgyban tanultak szerint egy
 ellenálláson eső feszültség szórásnégyzete egy
ellenálláson eső feszültség szórásnégyzete egy  sávszélességű frekvenciaablakban mérve a termikus zaj miatt
sávszélességű frekvenciaablakban mérve a termikus zaj miatt 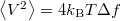 , így a termikus zaj teljesítménye
, így a termikus zaj teljesítménye 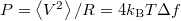 . A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon.
. A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon.
Eszerint minél nagyobb az elvárt sávszélesség, annál nagyobb lesz a zaj teljesítménye is. A telekommunikációban a termikus zajteljesítmény nagyságára 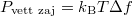 képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára
képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára 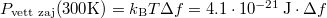 adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben
adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben 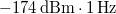 .
.
- A dBm egység definíciója:
![\setbox0\hbox{$P[\text{dBm}]=10\cdot \log_{10}(P/1\text{mW}).$}% \message{//depth:\the\dp0//}% \box0%](/images/math/c/a/d/cada73ee7df8a16390c26128fefd9511.png)
A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés.
A jelmoduláció alapjai
A vivőhullám mint harmonikus rezgés általános alakja: 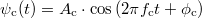 . Lehetőség van mindhárom paraméter (
. Lehetőség van mindhárom paraméter (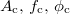 ) modulálására (itt
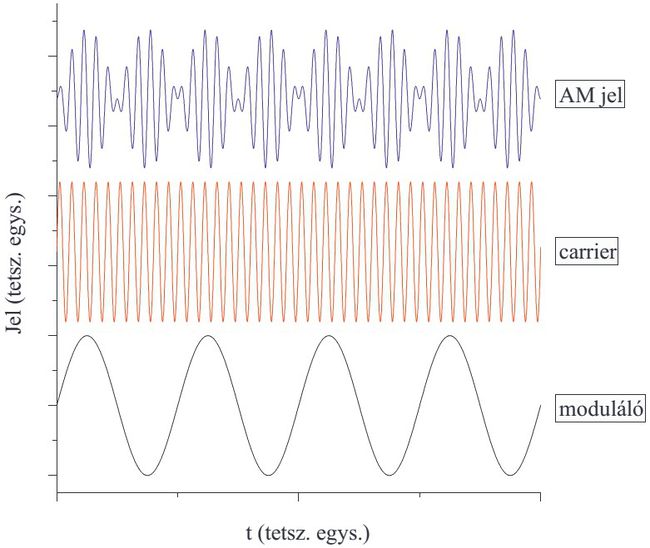
) modulálására (itt 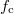 jelöli a vivőhullám/carrier frekvenciáját), amit amplitúdó- (AM), frekvencia- (FM), ill. fázismodulálásnak (PM) nevezünk. Itt csak az AM technikával foglalkozunk. Az AM jelet mutatja az 1. ábra.
jelöli a vivőhullám/carrier frekvenciáját), amit amplitúdó- (AM), frekvencia- (FM), ill. fázismodulálásnak (PM) nevezünk. Itt csak az AM technikával foglalkozunk. Az AM jelet mutatja az 1. ábra.
| 1. ábra. Az amplitúdómodulált jel. |
Az AM jelet felfoghatjuk úgy, hogy a vivőjelet a moduláló jellel összeszorozzuk. Amennyiben a moduláló jel is tiszta harmonikus hullám: 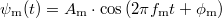 (itt az
(itt az  index a modulálásra vonatkozik), a trigonometrikus azonosságok alapján
index a modulálásra vonatkozik), a trigonometrikus azonosságok alapján
![\[\psi_{\text{c}}(t)\cdot\psi_{\text{m}}(t)=\frac{\cos\big(2\pi(f_{\text{c}}+f_{\text{m}}) t+\phi_{\text{c}}+\phi_{\text{m}}\big)+\cos\big(2\pi(f_{\text{c}}-f_{\text{m}}) t+\phi_{\text{c}}-\phi_{\text{m}}\big)}{2}\]](/images/math/b/6/a/b6a6996a6175713220164eb8e337cf2f.png)
látszik, hogy a két jel szorzata két szintén harmonikus hullám összege, melyek frekvenciája:  (feltéve, hogy
(feltéve, hogy 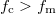 ). A későbbiekben bemutatjuk, hogyan valósítható meg a szorzás művelete, amit keverésnek is nevezünk. A jel demodulálása (azaz a lényeges információ előállítása) szintén szorzással valósítható meg: amennyiben az AM jelet újra beszorozzuk az
). A későbbiekben bemutatjuk, hogyan valósítható meg a szorzás művelete, amit keverésnek is nevezünk. A jel demodulálása (azaz a lényeges információ előállítása) szintén szorzással valósítható meg: amennyiben az AM jelet újra beszorozzuk az 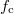 frekvenciájú jellel a kapott jelben 3 harmonikus hullám összege jelenik meg:
frekvenciájú jellel a kapott jelben 3 harmonikus hullám összege jelenik meg: 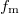 ,
, 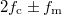 . Ezek közül értelemszerűen az első komponens az érdekes, a két másik nagyfrekvenciájú komponens kiszűrése (pl. aluláteresztő szűrővel) után az információt tartalmazó moduláló jel előáll. A tényleges kommunikációban a moduláló jel (pl. AM rádióadásban a továbbított hang) nem egyetlen harmonikus hullámból, hanem különböző frekvenciájú komponensek szuperpozíciójából áll. Látható, hogy ebben az esetben a demodulált jel az eredeti hangot adja vissza. Ezt a technikát nevezik szorzásos vagy heterodin (angolul heterodyne) detektálásnak.
. Ezek közül értelemszerűen az első komponens az érdekes, a két másik nagyfrekvenciájú komponens kiszűrése (pl. aluláteresztő szűrővel) után az információt tartalmazó moduláló jel előáll. A tényleges kommunikációban a moduláló jel (pl. AM rádióadásban a továbbított hang) nem egyetlen harmonikus hullámból, hanem különböző frekvenciájú komponensek szuperpozíciójából áll. Látható, hogy ebben az esetben a demodulált jel az eredeti hangot adja vissza. Ezt a technikát nevezik szorzásos vagy heterodin (angolul heterodyne) detektálásnak.
Korábban (kb. 50 évvel ezelőttig) az AM jelek demodulálását egyenirányítással (ún. detektoros vétellel) oldották meg (http://en.wikipedia.org/wiki/Envelope_detector). Ez azt használja ki, hogy az amplitúdómodulált vivőjelet egyenirányítva és a nagyfrekvenciás komponenst kiszűrve előáll a moduláló burkoló jel. Ezt a technikát nevezik burkoló detektoros vételnek is. Ennek előnye, hogy a vevőegység és hangszóró nem igényel extra energiaforrást (bár a jel persze igen halk lesz) hanem az energiát a vivőjelből veszi. Mára a szorzásos módszer vált a rádiótechnikában egyeduralkodóvá a következő részben ismertetett okoknál fogva.
Frekvenciaszelektív detektálás, mixerek
A burkoló detektoros demodulálás hátránya, hogy amennyiben több rádióadás van jelen egyszerre mindegyiket demodulálja, ezért nehéz egy tiszta jelet kapni. Ezen kicsit segíthet az, ha a vevő detektor előtt van egy sávszűrő, ami csak a kívánt vivőfrekvenciát és annak szűk tartományát engedi át. Ennek a megvalósításnak a hátránya, hogy a sávszűrő megépítése és különböző frekvenciákra hangolása nehézkes.
A heterodin detektálási technikában nincs szükség hangolható sávszűrőre, hanem csak egy fix aluláteresztő szűrőre. A kívánt vivőfrekvencia kiválasztását a demodulálásnál lekeveréshez használt frekvencia változtatásával érjük el. Az eddigiekben az a kérdés még nyitva maradt, hogyan érjük el az előző részben ismertetett, harmonikus hullámok összeszorzását.
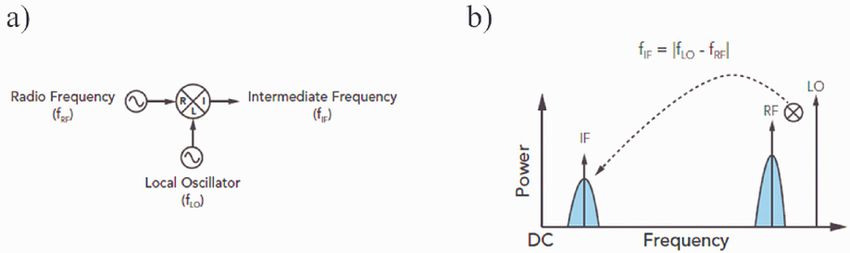
Az összeszorzás eszköze a keverő vagy mixer. Ez egy olyan félvezető eszköz aminek az áram-feszültség karakterisztikája erősen nemlineáris, emiatt két ráadott váltakozó áramú jel szorzata jelenik meg rajta. A mixer sematikáját 2a. ábra mutatja, a portok elnevezéseinek jelöléseivel. A 2b. ábra mutatja a mixert lekeverőként használva a frekvencia spektrumban milyen változás történik: az LO egy jól definiált frekvenciájú referenciajel, míg az RF egy modulált, ezért szélesebb frekvenciaspektrumú jel. Az IF porton a két frekvencia különsége jelenik meg, ami jellegében az RF spektrum tulajdonságait hordozza.
| 2. ábra. a) A mixert jelölő szimbólum és a ki-bemeneti portok jelei (LO bemenet: lokál-oszcillátor, RF bemenet: rádiófrekvenciás jel, IF kimenet: közbülső frekvencia), b) a mixert lekeverőként használva ilyen frekvencia konverzió valósul meg: az IF porton az LO és RF frekvenciák különbsége jelenik meg. |
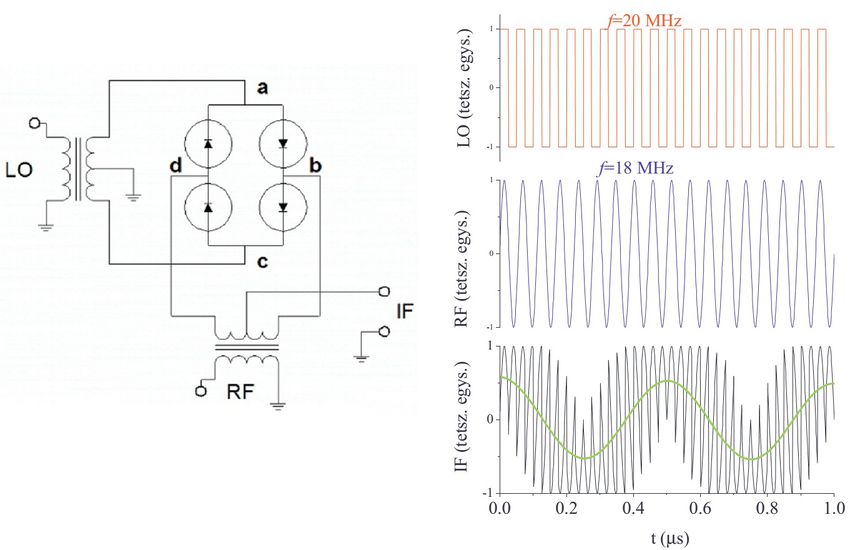
A mixer egy lehetséges megvalósítását és működését szemléltetjük a 3. ábrán. Amikor az LO feszültség olyan, hogy az a-c pontok között pozitív feszültség van (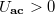 ), akkor a baloldali két dióda lezár, míg a jobboldali kettő nyitva van. Ekkor a d pont lebeg (feszültségét az RF port feszültsége adja) míg a b pont a földön van. Ezért az RF bemenetre adott feszültség közvetlenül, azonos előjellel megjelenik az IF kimeneten. Amikor
), akkor a baloldali két dióda lezár, míg a jobboldali kettő nyitva van. Ekkor a d pont lebeg (feszültségét az RF port feszültsége adja) míg a b pont a földön van. Ezért az RF bemenetre adott feszültség közvetlenül, azonos előjellel megjelenik az IF kimeneten. Amikor 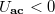 , akkor a baloldali két dióda nyit ki, ezért a d pont lesz leföldelve, míg a jobboldali két dióda lezár, ezért ekkor az RF bemenetre adott feszültség -1 szerese jelenik meg az IF kimeneten.
, akkor a baloldali két dióda nyit ki, ezért a d pont lesz leföldelve, míg a jobboldali két dióda lezár, ezért ekkor az RF bemenetre adott feszültség -1 szerese jelenik meg az IF kimeneten.
| 3. ábra. Bal panel: A mixer egy lehetséges megvalósításának sematikája az ún. átkapcsoló-mixer (switching-mixer). Jobb panelen: a mixerre kapcsolt jelalakok egy példán. LO: 20 MHz-es jel, RF: 18 MHz-es jel, az IF kimeneten kialakuló jel, ill. annak simított (alul áteresztővel megszűrt) változata (zöld folytonos vonal). |
Ezt a viselkedést szemlélteti a 3. ábra jobb oldali panele. A kapcsoló-mixer úgy viselkedik mintha az LO jel +1 és -1 közötti értékével szorzódna be az RF feszültség ami megjelenik az IF kimeneten. Az ábrán mutatott példában LO frekvenciája 20 MHz, RF frekvenciája 18 MHz és a szorzás után megjelenik az IF kimeneten egy alacsony (2 MHz-es) frekvenciával modulált 38 MHz-es jel. Ha ezt a jelet aluláteresztő szűrővel szürjük (példánkban numerikus csúszóátlagolást végeztünk) akkor jól látható az IF kimeneten megjelenő alacsony frekvencia. Ez a leírás egyben azt is megmutatja, hogy az LO feszültség nagyságától nem függ a kimeneti feszültség értéke, de az RF és IF feszültségek egymással arányosak (nem pontosan egyenlők mivel az eszköznek van egy kis vesztesége).
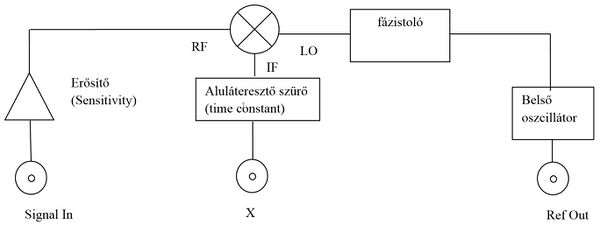
A Lock-in erősítő
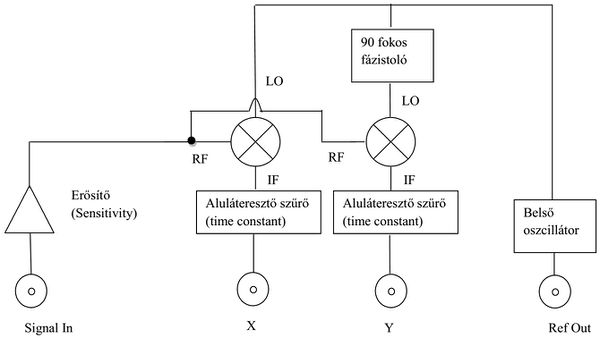
A kétcsatornás fázisérzékeny egyenirányító vagy lock-in erősítő blokkdiagrammját a 4. ábra mutatja. Ez lényegében két lekeverő mixerből áll, az IF kimenetet aluláteresztő szűrők követik. A két csatorna azt jelenti, hogy a bejövő RF jelnek mérjük két komponensét: az egyik amelyik fázisban van az LO-val és a másik amelyik 90 fokkal eltolt fázisban van. Előfordulhatna ugyanis, hogy a bejövő RF jel fázisa 90 fokos szöget zár be az LO-éval, ezáltal az IF jel kisfrekvenciás komponense 0 lenne. A két mért csatorna miatt lehetőség van a két kimenet négyzetösszegének meghatározására: 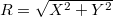 ami azért előnyős, mert a bejövő jel fázisa a belső oszcillátorhoz képest általában nem ismert, az
ami azért előnyős, mert a bejövő jel fázisa a belső oszcillátorhoz képest általában nem ismert, az  mennyiség azonban nem függ a fázistól. Az két kimenet (
mennyiség azonban nem függ a fázistól. Az két kimenet (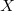 ,
, 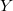 ) alapján a meghajtó jel és a mért jel közötti fázistolás is meghatározható, így ellenőrizhetjük, hogy a mért rendszerünk az elvárásnak megfelelő fázistolást mutatja-e (pl. kondenzátor vagy induktivitás
) alapján a meghajtó jel és a mért jel közötti fázistolás is meghatározható, így ellenőrizhetjük, hogy a mért rendszerünk az elvárásnak megfelelő fázistolást mutatja-e (pl. kondenzátor vagy induktivitás 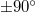 -os fázistolása.
-os fázistolása.
| 4. ábra. A kétcsatornás lock-in erősítő blokkdiagrammja (felül); az egycsatornás lock-in erősítő blokkdiagramja (alul). |
Az egyszerűbb lock-in erősítők -így a mérési gyakorlaton összeállított lock-in erősítő is- csak egy mixert alkalmaznak, viszont a kimenetre adott meghajtó jel és a szorzásnál alkalmazott LO referenciajel közötti fázistolás hangolható. Ebben az esetben a fázistolás hangolásával megkeressük a legnagyobb kimeneti jelet, ami annak felel meg, amikor a mért jel és az LO jel fázisban vannak. Az így beállított fázistolás adja meg a meghajtó és a mért jel közötti fáziskülönbséget.
Nagyfrekvenciás jelek analízise, a Fourier-transzformáció
A heterodin detektálás megismerése után ismételjük át, hogy hogyan határozható meg egy jel frekvenciatérbeli felbontása.
Egy 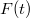 időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg:
időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg:
![\[f(\omega)=\int_{-\infty}^{\infty} F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t.\]](/images/math/5/9/5/595ba94d38747532dc0a86ce5c451009.png)
Egy valós mérésnél a Fourier-transzformált függvényt csak közelítőleg tudjuk megadni, hiszen egyrészt véges ideig tart a mérésünk, másrészt a mérési adatok csak diszkrét időfelbontással álnak rendelkezésre. Először nézzük meg a véges idejű mérés hatását a Fourier-transzformáltra.
A véges idejű mérés megfelel annak, mintha az eredeti függvényt megszoroznánk a mérési intervallumnak megfelelő 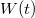 ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki:
ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki:
![\[f_W(\omega)=\int_{-\infty}^{\infty} W(t)\cdot F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,\]](/images/math/8/3/d/83d2a1130cc875baedfb60e75dbff165.png)
ahol a 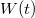 függvény
függvény 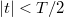 esetén
esetén 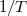 , ezen
, ezen  hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz:
hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz:
![\[ f_W(\omega)=\int_{-\infty}^{\infty} f(\omega ')w(\omega - \omega ')\frac{\mathrm{d}\omega}{2\pi},\ \ \ \ \mathrm{ahol}\ \ \ w(\omega)=\int_{-\infty}^{\infty} W(t)\mathrm{e}^{-i\omega t}\mathrm{d}t. \]](/images/math/0/5/8/0582a6df73925371593d682d300af119.png)
Nézzünk egy egyszerű példát, legyen 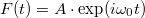 egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény:
egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény: 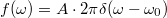 . Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján
. Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján 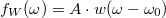 , azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az
, azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az  középfrekvenciához eltolva. A fent definiált téglalap ablak esetén (azaz amikor
középfrekvenciához eltolva. A fent definiált téglalap ablak esetén (azaz amikor 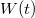 egy
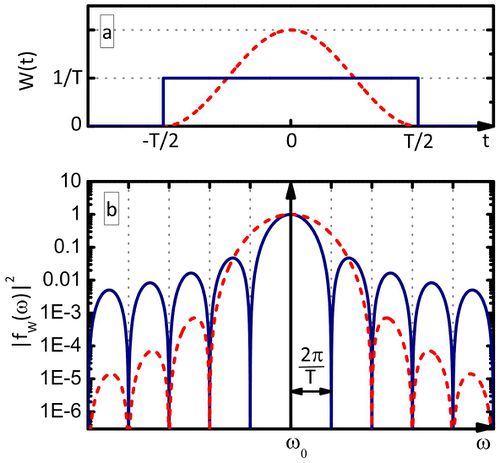
egy  szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja
szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja 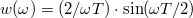 , azaz
, azaz 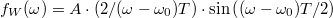 (5b. ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az
(5b. ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az  középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az
középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az 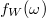 függvény
függvény  melletti első zérushelyeinek a távolsága
melletti első zérushelyeinek a távolsága 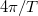 , így az
, így az  körüli csúcs szélessége
körüli csúcs szélessége 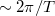 . Tehát az első fontos konklúzió, hogy véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg
. Tehát az első fontos konklúzió, hogy véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg 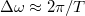 frekvenciafelbontással látjuk!
frekvenciafelbontással látjuk!
5. ábra. a) 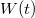 ablakfüggvény téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. b) ablakfüggvény téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. b) 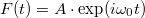 harmonikus jel Fourier-transzformáltjának abszolút érték négyzete téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. A téglalap ablakot Hanning ablakra cserélve az harmonikus jel Fourier-transzformáltjának abszolút érték négyzete téglalap ablak (kék folytonos vonal) és Hanning ablak (piros szaggatott vonal) esetén. A téglalap ablakot Hanning ablakra cserélve az  körüli csúcs kiszélesedik, azaz romlik a frekvenciafelbontás, azonban az körüli csúcs kiszélesedik, azaz romlik a frekvenciafelbontás, azonban az  -tól távolabbi mellékcsúcsok amplitúdója lecsökken, azaz csökken a spektrális szivárgás. -tól távolabbi mellékcsúcsok amplitúdója lecsökken, azaz csökken a spektrális szivárgás.
|
Érdemes megjegyezni, hogy a fent említett téglalap ablak helyett választhatunk más ablakfüggvényt is, például 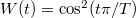 ún. Hanning-ablak esetén a mért jelben elnyomjuk a
ún. Hanning-ablak esetén a mért jelben elnyomjuk a 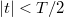 mintavételezési időablak széleihez közeli részeket (5a. ábra, piros szaggatott vonal). Ebben az esetben az
mintavételezési időablak széleihez közeli részeket (5a. ábra, piros szaggatott vonal). Ebben az esetben az  körfrekvenciás jel Fourier-transzformáltjában
körfrekvenciás jel Fourier-transzformáltjában  körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az
körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az  -tól távolabbi oszcillációk amplitúdója (az ún. spektrális szivárgás) lecsökken (5b. ábra, piros szaggatott vonal).
-tól távolabbi oszcillációk amplitúdója (az ún. spektrális szivárgás) lecsökken (5b. ábra, piros szaggatott vonal).
Következő lépésként nézzük meg, hogy mi a hatása annak, hogy a jelünket nem folytonosan látjuk, hanem csak diszkrét mintavételezési időpontokban. Emiatt a jel Fourier-transzformáltját a folytonos integrál helyett kénytelenek vagyunk egy diszkrét összeggel, az ún. diszkrét Fourier-transzformálttal (DFT) közelíteni:
![\[ f_W(\omega)=\sum_{n=0}^{N-1} W(n\cdot \Delta t)F(n\cdot \Delta t) \mathrm{e}^{-i\omega n \Delta t}\Delta t, \]](/images/math/1/c/2/1c29d0a765e68527b917bd9e7cc0b666.png)
ahol  a szomszédos mérési pontok közötti idő,
a szomszédos mérési pontok közötti idő, 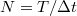 pedig a mintavételezett pontok száma.
Az ún. Nyquist-Shannon mintavételezési törvény szerint
pedig a mintavételezett pontok száma.
Az ún. Nyquist-Shannon mintavételezési törvény szerint  sűrűségű mintavételezés esetén a jelet
sűrűségű mintavételezés esetén a jelet 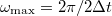 maximális körfrekvenciáig tudjuk rekonstruálni.
maximális körfrekvenciáig tudjuk rekonstruálni.
Könnyen belátható, hogy a diszkrét Fourier-transzformált fenti képlet szerinti kiértékelése  mérési pont esetén
mérési pont esetén 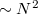 művelet (
művelet (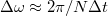 frekvenciafelbontás és
frekvenciafelbontás és 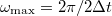 maximális felbontható frekvencia esetén csak
maximális felbontható frekvencia esetén csak 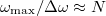 diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián
diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián 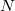 művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa (
művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa (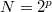 ), és a frekvenciatérben
), és a frekvenciatérben  diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma
diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma 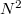 -ről
-ről 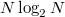 -re csökken, ami nagy N esetén lényeges különbség.
-re csökken, ami nagy N esetén lényeges különbség.
A mérőműszerek jelentős része, így a laborgyakorlaton használt digitális oszcilloszkóp is az FFT algoritmus numerikus kiértékelése alapján határozza meg a mért jel spektrumát. A legtöbb esetben a műszer nem adja meg külön a spektrum valós és képzetes részét, hanem csak a Fourier-transzformált abszolút érték négyzetét látjuk. Ezen kívül a mérőműszerek általában a frekvencia, és nem a körfrekvencia függvényében adják meg a spektrumot, erre érdemes odafigyelni a mérés kiértékelésénél.
A Fourier-transzformáció nem csak a jel frekvenciájának a vizsgálatára alkalmas, hanem a jel amplitúdójának a mérésére is. A fenti képletek szerint egy 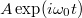 harmonikus jel téglalap ablakkal vett Fourier transzformáltja az
harmonikus jel téglalap ablakkal vett Fourier transzformáltja az  körfrekvenciánál pontosan
körfrekvenciánál pontosan  amplitudóval rendelkezik. Az
amplitudóval rendelkezik. Az  amplitúdót azonban csak akkor kapjuk vissza, ha a jel körfrekvenciája megegyezik az FFT valamelyik frekvenciapontjával (
amplitúdót azonban csak akkor kapjuk vissza, ha a jel körfrekvenciája megegyezik az FFT valamelyik frekvenciapontjával (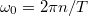 ), ami akkor teljesül, ha a jelnek pontosan egész számú periódusa fér el a
), ami akkor teljesül, ha a jelnek pontosan egész számú periódusa fér el a  mintavételezési ablakban. (Érdemes megjegyezni, hogy ebben az esetben az FFT összes többi frekvenciapontja a téglalapablakkal számolt Fourier-transzformált zérushelyeivel esik egybe, azaz a spektrális szivárgás is megszűnik.) Azonban ha a mérési ablak szélessége nem egyezik meg a jel periódusidejének egész számú többszörösével, akkor az FFT-algoritmus által számolt frekvenciapontok biztosan eltérnek a mért jelünk frekvenciájától, így az amplitúdóra is pontatlan értéket kapunk. Ha a jel amplitúdója érdekel minket, akkor olyan ablakfüggvényt érdemes választni, melynek a Fourier-transzormáltja a centrális csúcs körüli
mintavételezési ablakban. (Érdemes megjegyezni, hogy ebben az esetben az FFT összes többi frekvenciapontja a téglalapablakkal számolt Fourier-transzformált zérushelyeivel esik egybe, azaz a spektrális szivárgás is megszűnik.) Azonban ha a mérési ablak szélessége nem egyezik meg a jel periódusidejének egész számú többszörösével, akkor az FFT-algoritmus által számolt frekvenciapontok biztosan eltérnek a mért jelünk frekvenciájától, így az amplitúdóra is pontatlan értéket kapunk. Ha a jel amplitúdója érdekel minket, akkor olyan ablakfüggvényt érdemes választni, melynek a Fourier-transzormáltja a centrális csúcs körüli 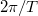 szélességű tartományban minél kevesebbet változik. Téglalapablak esetén az amplitúdópontosság mintegy 36%, Hanning-ablak esetén pedig 15%. Speciális, ún. Flattop-ablakot választva ennél sokkal jobb, mintegy 0.01%-os amplitúdópontosság is elérhető, viszont cserébe lényegesen leromlik a frekvenciafelbontásunk.
szélességű tartományban minél kevesebbet változik. Téglalapablak esetén az amplitúdópontosság mintegy 36%, Hanning-ablak esetén pedig 15%. Speciális, ún. Flattop-ablakot választva ennél sokkal jobb, mintegy 0.01%-os amplitúdópontosság is elérhető, viszont cserébe lényegesen leromlik a frekvenciafelbontásunk.
Spektrumanalizátorok típusai
Egy ismeretlen frekvenciaeloszlású bejövő jel spektrumanalízisére három módszer használatos:
- Az ún. DC körüli FFT-n alapuló spektrumanalízis.
- Az ún. sweepelt heterodin spektrumanalízis.
- Az ún. hibrid heterodin-FFT spektrumanalízis.
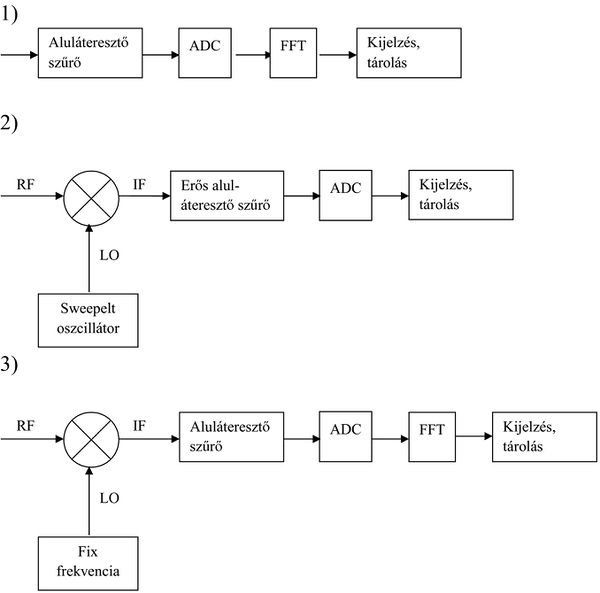
| 6. ábra. A háromfajta spektrumanalizátor sematikus blokkdiagrammja. |
Ezen módszerek sematikus blokk-diagrammjait mutatja 6. ábra. Az első módszerben a bejövő jelet FFT-zve adódik a frekvenciaspektrum (6a. ábra). Ez a módszer azonban lényegében csak DC körüli, pl. audió jelek spektrumanalízisére használatos, mivel ekkor a Fourier-spektrum mindenképpen DC-től indul, hiszen az FFT algoritmus akkor effektív, ha a teljes 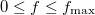 frekvenciasávra alkalmazzuk. (Pontosabban fogalmazva, kiszámolhatjuk az FFT-t egy szűkebb sávra is, de az gyakorlatilag ugyan annyi számítási művelet, mintha a teljes frekvenciatartományra számolnánk). Ez akkor nem jó módszer, ha pl. csak 100 MHz körüli spektrum érdekes egy szűk, mondjuk 10 kHz-es tartományban, amit viszont nagy frekvenciafelbontással szeretnénk megmérni.
frekvenciasávra alkalmazzuk. (Pontosabban fogalmazva, kiszámolhatjuk az FFT-t egy szűkebb sávra is, de az gyakorlatilag ugyan annyi számítási művelet, mintha a teljes frekvenciatartományra számolnánk). Ez akkor nem jó módszer, ha pl. csak 100 MHz körüli spektrum érdekes egy szűk, mondjuk 10 kHz-es tartományban, amit viszont nagy frekvenciafelbontással szeretnénk megmérni.
A második technika lényege, hogy egy olyan lokáloszcillátort használ aminek a frekvenciáját folyamatosan változtatjuk (sweepeljük), majd a kapott IF jelet aluláteresztve szűrjük, úgy hogy a lekevert jelnek gyakorlatilag csak a DC komponensét mérjük (6a. ábra). Az így kapott szűrt IF jel nagyságát ábrázolva az időben változó LO frekvencia függvényében megkapjuk az RF jel spektrumát. E módszer előnye, hogy viszonylag egyszerűen megvalósítható, lehetővé teszi a frekvenciaspektrum valósidejű vizsgálatát. Hátránya, hogy a sweepelt oszcillátorok frekvenciájának értékét nem könnyű pontosan meghatározni, ill. az, hogy egy időpillanatban csak 1 frekvenciaértéket mér. Azt is érdemes megjegyezni, hogy 6b. ábrán bemutatott elrendezésben csak a mért jelnek az LO jellel fázisban levő komponensét (azaz a valós részét) mérjük, ezért nevezzük ezt az elrendezést egycsatornás spektrumanalizátornak. A teljes Fourier-spektrum meghatározásához (és a Fourier-transzformált abszolút érték négyzetének meghatározásához is) ugyanezt a műveletet az LO jel 90 fokkal eltolt transzformáltjával is el kéne végezni, ami gyakorlatilag a lock-in erősítő 4. ábrán bemutatott blokkdiagramjának felel meg.
Az első két módszerből mindkettő legjobb tulajdonságait ötvözi a harmadik technika. Ebben egy fix frekvenciájú lokáloszcillátort használunk és a lekeverés után kapott IF jelet Fourier transzformáljuk FFT algoritmussal. Ezáltal tetszőleges frekvencia kis környezetét vizsgálhatjuk úgy, hogy egyszerre sok frekvenciát mérünk, ezt nevezik az FT módszer ún. multiplex tulajdonságának is. Emellett az LO frekvenciája nagyon stabil lehet, ezért a kapott frekvenciaspektrum nagyon pontosan kalibrált. Egyetlen hátránya, hogy az FFT művelet aránylag számolásigényes, azonban ez egyre kevésbé jelent limitációt a számítási kapacitás növekedése miatt.
A heterodin-FFT spektrumanalizátoroknál különösen fontos kérdés az IF frekvencia előjelének meghatározása, erre az ún. kvadratúra detektálás kínál megoldást. A probléma az, hogy a mixer fentebb említett tulajdonsága (azaz az LO és RF frekvenciák összegét és különbségét is előállítja) miatt 6c. ábrán mutatott blokkdiagram (ún. egycsatornás hibrid heterodin-FFT spektrumanalizátor) esetén pl. LO=100 MHz és RF=99.9 MHz mellett az IF jel 0.1 MHz-es frekvenciájú lesz. Erről a jelről az egycsatornás spektrumanalízis után nem tudjuk megmondani, hogy valójában -0.1 MHz frekvenciához, azaz RF=99.9 MHz-hez tartozik. Ha a lock-in kapcsán bemutatott elv szerint a bejövő RF jelet kettéosztjuk, majd két mixeren szorozzuk össze az LO-val és annak 90 fokos eltoltjával, akkor az így kapott két IF jelet Fourier-transzformálva az IF jel frekvenciája egyértelműen meghatározható. A modern spektrumanalizátorok, így pl. a Méréstechnika előadáson bemutatott Tektronix DPO/MSO oszcilloszkóp/jelanalizátor is kvadratúra üzemmódban működő heterodin-FFT elven alapulnak. A laborgyakorlat során a spektrumanalízist egyszerűbben oldjuk meg, az FM rádióadások vizsgálatánál az LO frekvenciáját 80 MHz-re állítjuk be. Mivel tudjuk, hogy a vizsgált rádióadások csak ennél nagyobb frekvenciákon vannak jelen (87.5-108 MHz között), ezért a kapott IF jelek frekvenciája egyértelmű.
Mérési feladatok
A mérési feladatok előtt gondosan olvassuk el a Függelékben az egyes műszerek használati útmutatóját. A mixer portjaira adott túl nagy feszültség a mixer meghibásodásához vezethet!
A mérés fontos részét képezi a modern függvénygenerátorok és digitális oszcilloszkópok funkcióinak megismerése, valamint az FFT spektrumanalízis, illetve a heterodin és lock-in méréstechnika elvének elsajátítása, így fordítsunk megfelelő időt a mérési feladatok végiggondolására, és az alkalmazott műszerek funkcióinak kipróbálására.
Minden releváns oszcilloszkópos mérés eredményét mentsük el a rendelkezésre álló segédprogram segítségével, és a jegyzőkönyvben szemléltessük az összes fontos részfeladat eredményét.
I. Függvénygenerátor és oszcilloszkóp beállításainak megismerése
- A jelgenerátoron állítsunk elő egy tetszőleges, 100kHz-1MHz közötti frekvenciájú szinuszjelet.
- Szinkronizáljuk az oszcilloszkópot a kiadott jelhez (trigger menü).
- Ellenőrizzük és értelmezzük az oszcilloszkóp bemenetének beállításait (1-es ill. 2-es jelű gomb), illetve az acquire menü beállításait.
- Becsüljük meg a jel amplitúdóját és periódusidejét a kurzorok segítségével.
- Próbáljuk ki az oszcilloszkóp measure funkcióit, mérjük meg pontosan a jel frekvenciáját, és peak-to-peak amplitudóját.
II. Fourier spektrum vizsgálata FFT algoritmussal
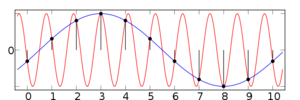
- Jelenítsük meg a korábban beállított szinuszjel FFT algoritmussal számított Fourier-transzformáltját. A Fourier-spektrum mellett jelenítsük meg a mért hullámformát is (FFT gomb, Source WFM On), használjunk téglalap ablakot (Window: Rectangular), és 1x-es FFT Zoom-ot. Milyen időalapot kell választani ahhoz, hogy a Fourier-spektrumból a szinuszjel frekvenciáját a legjobb frekvenciafelbontással meg tudjuk határozni? (Segítség: az oszcilloszkóp egy mintavételezés során mindig 2500 adatpontot vesz fel. A spektrumban látható csúcs szélességét az oszcilloszkóp cursor funkciójával csak pontatlanul lehet leolvasni, így érdemes a spektrumot számítógépre menteni, és Igor program segítségével elemezni.) Figyeljünk arra, hogy ha a szomszédos mintavételi pontok távolsága nagyobb, mint a jel periódusidejének a fele, akkor felléphet az "aliasing" jelensége (7. ábra).
- Továbbra is téglalap ablakot használva vizsgáljuk a FFT spektrumot a meghajtójel frekvenciájának finom (akár 0.01%-os felbontású) változtatása mellett. Az időalapot állítsuk be úgy, hogy kb. a jel 100 periódusa férjen el a mintavételezési ablakban. Rögzítsük, hogy milyen egymás utáni frekvenciaértékeknél kapunk éles (kiszélesedés nélküli) csúcsot a Fourier-spektrumban, értelmezzük az eredményeket. (Segítség: vegyük figyelembe, hogy az FFT-algoritmus mindig
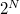 ponttal dolgozik.)
ponttal dolgozik.)
- Az előbbi mérést ismételjük meg Hanning és Flattop ablak segítségével is. Hasonlítsuk össze a három különböző ablakfügvénnyel kapott eredményt a frekvenciafelbontás, a spektrális szivárgás, és az amplitúdópontosság szempontjából, ehhez a felvett spektrumok releváns részeit még a helyszínen hasonlítsuk össze az Igor méréskiértékelő program segítségével. Az amplitúdópontosság vizsgálatához változtassuk a jel frekvenciáját, és vizsgáljuk meg, hogy eközben mennyit változik az FFT-spektrum csúcsának a magassága.
- Vizsgáljuk meg egy háromszögjel Fourier-spektrumát különböző aszimmetriaparaméterek mellett. A jegyzőkönyvben a kapott eredményeket hasonlítsuk össze az elméleti várakozásokkal szimmetrikus háromszögjel (asymmtry=50%) és fűrészfogjel (asymmtry=100%) esetén. Milyen ablakfüggvény esetén várjuk, hogy a Fourier-spektrum csúcsainak magassága leginkább megegyezik az elméleti várakozásokkal?
- A jelgenerátoron állítsunk be 100kHz-es szinuszjelet amit 1-20kHz-el amplitúdó modulálunk. Ehhez használjuk a jelgenerátor "Mod" gombját (AM Freq: 1-20kHz, AM depth: 100%). Vizsgáljuk meg a jel időfüggését és Fourier-spektrumát különböző modulációs jelalalkok mellett! A Fourier-spektrumokat mentsük is el és értelmezzük az oldalsávok helyét, számát és nagyságát!
| 7. ábra. "Aliasing" jelensége: a ritkán mintavételezett jel esetén teljesen fals jelforma alakulhat ki, hasonlóan ahhoz, mint amikor az egyre gyorsabban forgó autókereket egyszer csak visszafelé látjuk forogni. |
III. Demoduláció szorzó áramkör segítségével
- A jelgenerátorral előállított AM jelet demoduláljuk a AD831 mixer segítségével, a mérési elrendezést a fentiekben elsajátított ismeretek segítségével önállóan rakjuk össze! Legyen a vivőfrekvencia 1MHz és az AM moduláció pedig legyen 10-30kHz-es szimmetrikus háromszögjel. Ennek megfelelően az LO frekvencia is legyen 1MHz. Vegyük fel az IF kimenet Fourier-spektrumát, azonosítsuk a spektrumban a demodulált jelet. Milyen további frekvenciakomponensek jelennek meg a Fourier-spektrumban, amiket ideális esetben nem várnánk? Mi lehet ezen frekvenciakomponensek megjelenésének az oka? Nyomjuk el a nagyfrekvenciás komponenseket egy RC aluláteresztő szűrő segítségével. A szűrőbe egy 50
 -os ellenállás van forrasztva, ami kicsi az oszcillpszkóp 1M
-os ellenállás van forrasztva, ami kicsi az oszcillpszkóp 1M -os bemeneti ellenállásához képest. A szűrőben alkalmazott kapacitás értékét önállóan kell kiválasztani. Hasonlítsuk össze a szűrt jel időfüggését és Fourier-spektrumát a moduláló jelével, azaz ellenőrizzük, hogy sikerült-e a demoduláció, és megfelelő szűrést alkalmaztunk-e.
-os bemeneti ellenállásához képest. A szűrőben alkalmazott kapacitás értékét önállóan kell kiválasztani. Hasonlítsuk össze a szűrt jel időfüggését és Fourier-spektrumát a moduláló jelével, azaz ellenőrizzük, hogy sikerült-e a demoduláció, és megfelelő szűrést alkalmaztunk-e.
- Vizsgáljuk meg a 87.5-108 MHz frekvenciasávban található FM rádióadások spektrumát! Ez a frekvenciatartomány már meghaladja az oszcilloszkóp sávszélességét, így a spektrumok vizsgálatához lekeverést kell alkalmazni. A lekeveréshez a kifejezetten erre a frekvenciatartományra optimalizált HP passzív mixert használjuk. A rendelkezésre álló 80MHz-es oszcillátor kimenetét használjuk IF jelként, a mixer RF bemenete legyen a szobaantenna (erősítőjét kapcsoljuk be), az IF kimenetet pedig csatlakoztassuk az oszcilloszkópra! Utóbbi eszközt úgy állítsuk be, hogy ~50 MHz-es tartományt láthassunk az FT spektrumban. Azonosítsuk a látott FM csatornákat és a kapott eredményt hasonlítsuk össze a függelékben megadott táblázattal (ez tartalmaz szándékosan néhány kakukktojást is). Az azonos sugárzási helyről adott adások esetében a relatív intenzitás arányokat is mérjük meg és hasonlítsuk össze a táblázatban megadott értékekkel! (Az FM rádióadások demodulálása túlmutat a laborgyakorlat keretein).
IV. Szorzóáramkör használata lock-in erősítőként
- Állítsunk össze lock-in erősítőt az AD831 szorzóáramkör segítségével. Először használjuk a Siglent jelgenerátor két kimenetét referenciajelként (LO) és mért jelként (RF). Az IF kimenetet vizsgáljuk oszcilloszkóp, illetve GW Instek DC digitális multiméter segítségével. Állítsunk be 1MHz-es frekvenciát, és vizsgáljuk meg, hogy hogyan függ a lekevert, DC kimeneti jel a mért jel (RF) amplitudójától, és fázisától. Enyhén hangoljuk el a mért jelet a referenciajelhez képest, és vizsgáljuk meg, hogy hogyan tűnik el az IF kimeneten látható DC feszültség az elhangolás függvényében. Mi határozza meg az így összeállított lock-in erősítő időállandóját/sávszélességét?
- A 8. ábrán látható elrendezés szerint állítsunk össze egy differenciális induktív adót. A csévetest mindhárom részére elég egy réteg tekercset felcsévélni. A meghajtó tekercset hajtsuk 1MHz-es jellel a Siglent jelgenerátorról. Az ellentétes irányba tekercselt érzékelő tekercsek kimeneteit kössük a szorzóáramkör RF bemenetére, míg az LO bemenetre kössük a meghajtójelet referenciaként. Oszcilloszkópon ellenőrizzük a meghajtó és a mért jel fázisát, állítsuk fázisba őket. A vasmag mozgatása közben fázisérzékeny módon mérjük meg az induktív adó kimenő jelét, és specifikáljuk az így összeállított elmozdulásérzékelő távolságfelbontását. Gondoljuk végig, hogy miben változna a szenzor működése, ha a kimenő jelet a fázisérzékeny detektálás helyett egy egyszerű AC feszültségmérővel mérnénk.
- Szorgalmi feladat: A mellékelt nyáklap, illetve az összeállított lock-in erősítő segítségével állítsunk össze kapacitív érintésérzékelőt, és specifikáljuk annak működését! A lekeverő áramkör kalibrálása után a mérési eredményből határozzuk meg az érintésérzékelő kapacitását szabadon, illetve érintés közben.
- Szorgalmi feladat: A 8. ábrán látható, egymással szembefordított mikrométercsavaok segítségével szimuláljunk egy kapacitív távolságszenzort. Használjunk 1MHz-es meghajtójelet. Vizsgáljuk meg az IF kimeneten mért DC jel függését a mikrométerorsók végeinek távolságától, specifikáljuk a szenzor érzékenységét. Azonosítsuk be a mikrométerorsó pozíciójától független háttérjeleket, amik származhatnak szorzó áramkör offsetjéből, illetve áramkör vezetékei közötti áthallásból.
| 8. ábra. Fent: differenciális induktív adó: egy meghajtó tekercs és a két oldalán levő, sorba kötött, ellentétes irányban tekercselt érzékelő tekercs közötti kölcsönös indukciót mérjük, ami érzékenyen reagál a vasmag pozíciójára. A vasmag középső állásánál a két érzékelő tekercs jele kinullázza egymást. Lent: "Kapacitív távolságszenzor." |
Köszönetnyilvánítás
Köszönjük a jegyzet gondos átolvasását, javítását és az észrevételeket Fülöp Ferencnek, Bernáth Bencének, Márkus Bencének és Gubicza Ágnesnek. A laborgyakorlaton használt mérőprogram elkészítését Bernáth Bencének, az FM rádió állomások táblázatának elkészítését és a vehető állomások tesztelését Márkus Bencének köszönjük.
Ajánlott irodalom
- Simonyi Károly: Elméleti villamosságtan
- David M. Pozar: Microwave Engineering (4th Ed.)
Függelék
A Budapest körzetében fogható rádióadások
AM: Kossuth rádió 540 kHz, Solti Rádióadó, távolsága Budapesttől kb. 80 km (Európa legerősebb középhullámú rádióadója).
| f (MHz) | P (kW) | Rádió neve | Adó helye |
|---|---|---|---|
| 87.60 | nincs adat | Kontakt Rádió | Terézváros |
| 88.10 | 1 | InfóRádió | Nagyvárad tér, SOTE épület |
| 88.80 | 1 | Rádió C | Széchenyi-hegyi adótorony |
| 89.00 | 0.986 | MR2 Petőfi Rádió | Debrecen |
| 89.50 | 77.6 | Music FM | Széchenyi-hegyi adótorony |
| 90.20 | 8.3 | MR1 Kossuth Rádió | Nagykanizsa |
| 90.30 | 0.4 | Tilos Rádió | Gellért-hegy Citadella rádióadó állomás |
| 90.90 | 2 | 90.9 Jazzy | Sashegy adótorony |
| 91.40 | 1.2 | Dankó Rádió | Debrecen |
| 92.10 | 2.2 | Klasszik Rádió | Gellért-hegy, Citadella rádióadó állomás |
| 92.90 | 5 | Klub Rádió | Sashegy adótorony |
| 94.20 | 1 | Mária Rádió | Sashegy adótorony |
| 94.80 | 77.6 | MR2 Petőfi Rádió | Széchenyi-hegyi adótorony |
| 95.90 | 25.2 | MR1 Kossuth Rádió | Pécs |
| 96.70 | 37.1 | MR2 Petőfi Rádió | Komádi |
| 96.80 | 1 | Rádió 17 | XVII. Kerület, Rákosmente |
| 97.50 | 50.1 | MR1 Kossuth Rádió | Tokaj |
| 98.00 | 5 | Civil Rádió | Hármashatárhegy, Felso-Kecske-hegy |
| 98.20 | 7.5 | MR2 Petőfi Rádió | Tiszavasvári |
| 99.50 | 3 | Rádió Q | Sashegy 2 |
| 99.70 | 1.4 | MR1 Kossuth Rádió | Debrecen |
| 100.30 | 1 | Lánchíd Rádió | Nagyvárad tér, SOTE épület |
| 100.50 | 67.6 | Class FM | Kabhegy |
| 100.80 | 79.4 | MR Dankó Rádió | Széchenyi-hegyi adótorony |
| 102.00 | 22.4 | Class FM | Sopron |
| 102.10 | 0.741 | Magyar Katolikus Rádió | Széchenyi-hegyi adótorony |
| 102.70 | 30.2 | MR2 Petőfi rádió | Kékes |
| 103.30 | 81.3 | Class FM | Széchenyi-hegyi adótorony |
| 103.90 | 0.82 | Juventus Rádió | Széchenyi-hegyi adótorony |
| 104.80 | 0.3 | Budaörs Rádió | Budaörs |
| 105.30 | 81.3 | MR3 Bartók Rádió | Széchenyi-hegyi adótorony |
| 105.90 | 2 | Gazdasági Rádió | Gellért-hegy, Citadella rádióadó állomás |
| 106.20 | 23.4 | RTVS Rádio Regina BB | Besztercebánya, Száraz-hegy |
| 107.80 | 83.2 | MR1 Kossuth Rádió | Széchenyi-hegyi adótorony |
| 110.30 | 2 | Rádió 7 | Kőbánya, Határ úti adótorony |
A mérőeszközök és mérőprogram használata
Tektronix oszcilloszkóp
A digitális oszcilloszkóp alapvető használatát ismertnek tételezzük fel. A trigger gomb megnyomása után választható ki a csatorna amire triggerelünk (kijelző alatti gombokkal érhető el a trigger menü almenüjei), a vertical menu-ben a kijelzőtől jobbra elhelyezett gombokkal tudjuk a megfelelő kijelzett csatornákat beállítani. A Math gomb megnyomásával érjük el, hogy at FT spektrumot láthassuk. Gyakori hiba, hogy az FT spektrumban nem a kívánt tartományt látjuk hanem nagyságrendekkel más értékeket. Akkor kapunk jó FT spektrumot amikor az oszilloszkóp időalap értéke olyan, hogy egy periódikus jelből kb. 100 periódust is látunk (a képernyőn összefolyik).
Az FT spektrum vizsgálatakor nem látjuk az idő doménben mért adatokat. Ezért első lépésként mindíg győzödjünk meg arról, hogy ac coupled üzemmódban vannak és a feszültség értékek nem lógnak ki a képernyőről. Az adatok jel-zaj aránya javítható az Acquire menüben a 128 Average kiválasztásával. Az FT spektrum függőleges tengelye dBV egységekben van, ez a feszültség effektív (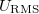 ) értékéből a következő módon származtatható:
) értékéből a következő módon származtatható:
![\[\mathrm{dBV}(U_{\text{RMS}})=20\log_{10}(U_{\text{RMS}}/1\,\text{V})\]](/images/math/f/f/a/ffabe7a8f2b1e905dc0657de6358ddcc.png)
A pontos feszültség (vagy dBV) és frekvencia értékek leolvasásához használjuk az oszcilloszkóp Cursor opcióját.
| 9. ábra. Tektronix digitális oszcilloszkóp. |
A Siglent SDG1020 jelgenerátor
A jelgenerátor két független kimenettel rendelkezik, melyeket a kimenet felett elhyelzkedő kapcsolóval lehet bekapcsolni. A billentyűzet bal felső sarkában lévő CH1/CH2 kapcsolóval lehet kiválasztani, hogy melyik csatorna értékét állítjuk be. Az aktuális csatornán beállított értékek (feszültség, frekvencia, kimenő impedancia) a képernyőn láthatók. Ebben a mérésben kimenő impedancia értékét célszerű high Z-re tenni, de az 50 Ohm sem okoz gondot. Az offset értéke legyen mindig 0. A frekvencia, jelamplitúdó, és jelalak (Sine, Square stb.) beállítása intuitív. A Mod gomb megnyomásával juthatunk a modulációs menühöz az adott csatornára, ha ez világít, akkor az aktuális csatornakimenet modulált.
| 10. ábra. Siglent jelgenerátor. |
Analog Devices AD831 aktív mixer és HP passzív mixer
A mixerek LO (AD) ill. L (HP) portja a lokál-oszcillátor bemenet, erre 0.5-1 V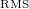 értéket adhatunk, a pontos értéktől a kimenet nagysága nem függ (ez csak a munkapontot állítja be). A mixert lekeverőként használva az RF (AD) és R (HP) port a meghajtó jel (bemenet) és az IF (AD) ill. X (HP) a lekevert jel (kimenet). A mixerek RF ill. R bemenetére adható feszültség ne haladja meg a 0.2 V
értéket adhatunk, a pontos értéktől a kimenet nagysága nem függ (ez csak a munkapontot állítja be). A mixert lekeverőként használva az RF (AD) és R (HP) port a meghajtó jel (bemenet) és az IF (AD) ill. X (HP) a lekevert jel (kimenet). A mixerek RF ill. R bemenetére adható feszültség ne haladja meg a 0.2 V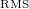 értéket!
értéket!
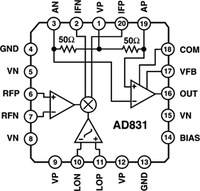
| 11. ábra. Analog Devices AD831 mixer (fölül és középen), illetve HP mixer (alul). |
Megfontolások a körfrekvencia "előjelével" kapcsolatban
A Fourier transzformáció definiciójánál azt látjuk, hogy a Fourier spektrum komplex mennyiség. Erre azért van szükség, hogy a különböző frekvenciájú harmonikus tagok fázisát is le tudjuk írni. Könnyen belátható, hogy amennyiben 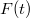 páros függvény (pl. cos), akkor a Fourier spektrum tisztán valós, amennyiben pedig
páros függvény (pl. cos), akkor a Fourier spektrum tisztán valós, amennyiben pedig 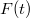 páratlan függvény (pl. sin), akkor a Fourier spektrum tisztán képzetes. Tetszőleges
páratlan függvény (pl. sin), akkor a Fourier spektrum tisztán képzetes. Tetszőleges 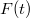 esetén pedig a Fourier spektrum tartalmaz valós és képzetes tagokat is. (Ilyen értelemben a komplex jelölésnek az a szerepe, hogy a leírást rövidítse, egyébként kétkomponensű vektorokat kellene írnunk.) Amennyiben a fázis ismerete nem lényeges és csak az egyes Fourier komponensek erősségére vagyunk kiváncsiak akkor a Fourier spektrum valós és képzetes részeinek négyzetösszegének gyökéből képezhetjük az ún. Fourier erősséget (Fourier magnitude).
esetén pedig a Fourier spektrum tartalmaz valós és képzetes tagokat is. (Ilyen értelemben a komplex jelölésnek az a szerepe, hogy a leírást rövidítse, egyébként kétkomponensű vektorokat kellene írnunk.) Amennyiben a fázis ismerete nem lényeges és csak az egyes Fourier komponensek erősségére vagyunk kiváncsiak akkor a Fourier spektrum valós és képzetes részeinek négyzetösszegének gyökéből képezhetjük az ún. Fourier erősséget (Fourier magnitude).
Egy kérdés azonban még nyitva maradt: amikor harmonikus rezgésről beszélünk gyakran mint cos, sin vagy 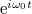 -ként hivatkozunk rá. Itt mi a komplex jelölés szerepe? Erre a rövid válasz az, hogy önmagában a cos vagy sin függvény nem adja meg a harmonikus rezgés frekvenciájának előjelét. Első hallásra meglepő, hogy harmonikus rezgés frekvenciájának előjele van, azonban gondoljunk csak a mixeres lekeverésre: amennyiben RF frekvenciája kisebb mint az LO frekvenciája, a kapott IF jel alacsonyfrekvenciás komponensének fekvenciája negatív. Az előjel elvesztésének bemutatására tekintsük először a
-ként hivatkozunk rá. Itt mi a komplex jelölés szerepe? Erre a rövid válasz az, hogy önmagában a cos vagy sin függvény nem adja meg a harmonikus rezgés frekvenciájának előjelét. Első hallásra meglepő, hogy harmonikus rezgés frekvenciájának előjele van, azonban gondoljunk csak a mixeres lekeverésre: amennyiben RF frekvenciája kisebb mint az LO frekvenciája, a kapott IF jel alacsonyfrekvenciás komponensének fekvenciája negatív. Az előjel elvesztésének bemutatására tekintsük először a 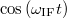 jelet, ennek a Fourier-transzformáltja valós és tartalmaz
jelet, ennek a Fourier-transzformáltja valós és tartalmaz 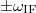 -nél is egy-egy pozitív csúcsot. Második példánkban tekintsük a
-nél is egy-egy pozitív csúcsot. Második példánkban tekintsük a 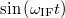 jelet, aminek Fourier transzformáltja képzetes és
jelet, aminek Fourier transzformáltja képzetes és 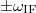 -nél mutat egy-egy ellentétes előjelű csúcsot. Tehát egyik példában sem tudjuk a jel frekvenciájának előjelét egyértelműen meghatározni. Ezzel szemben a
-nél mutat egy-egy ellentétes előjelű csúcsot. Tehát egyik példában sem tudjuk a jel frekvenciájának előjelét egyértelműen meghatározni. Ezzel szemben a 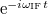 Fourier-transzformáltjának
Fourier-transzformáltjának 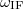 -nél (előjelhelyesen) van egy csúcsa, azaz nincs csúcsa
-nél (előjelhelyesen) van egy csúcsa, azaz nincs csúcsa 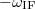 -nél.
-nél.
A 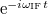 kifejezés valós és képzetes részei úgy viselkednek mint a trigonometrikus függvények definiciójakor használt egységkörön mozgó pont vetületei, ami foroghat pozitív és negatív körüljáráson is. Ezzel szemben külön-külön a cos és sin vetületek nem érzékenyek az egységkörön mozgó pont körüljárásának irányára.
kifejezés valós és képzetes részei úgy viselkednek mint a trigonometrikus függvények definiciójakor használt egységkörön mozgó pont vetületei, ami foroghat pozitív és negatív körüljáráson is. Ezzel szemben külön-külön a cos és sin vetületek nem érzékenyek az egységkörön mozgó pont körüljárásának irányára.
Már csak azt a kérdést kell megválaszolnunk, hogy méréstechnikában hogyan tudjuk ezt a 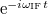 komplex időfüggő mennyiséget előállítani a mért valós jelekből. A válasz az, hogy a valós és képzetes részek a lock-in technikánál bemutatott kvadratúra detektálásból adódnak: azaz a bejövő jelet két, egymástól 90 fokban eltolt jellel keverjük le. Az így kapott két adatsort (
komplex időfüggő mennyiséget előállítani a mért valós jelekből. A válasz az, hogy a valós és képzetes részek a lock-in technikánál bemutatott kvadratúra detektálásból adódnak: azaz a bejövő jelet két, egymástól 90 fokban eltolt jellel keverjük le. Az így kapott két adatsort (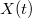 és
és 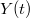 4. ábra jelöléseivel) tekintjük a bejövő lekevert jel valós és képzetes részeinek:
4. ábra jelöléseivel) tekintjük a bejövő lekevert jel valós és képzetes részeinek: 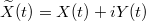 . Az FT után szintén két adatsort kapunk:
. Az FT után szintén két adatsort kapunk:
![\[ \widetilde{x}(\omega)=x(\omega)+i y(\omega)=\int_{-\infty}^{\infty} \widetilde{X}(t)\mathrm{e}^{-i\omega t}\mathrm{d}t, \]](/images/math/9/2/4/9249ed81b648f64a445c9b9663aec19f.png)
ezért ezt komplex vagy kétcsatornás Fourier transzformációnak nevezzük.
Ha a tagokat expliciten kiírjuk, akkor belátható, hogy e két adatsor a következőképpen adódik:
![\[ x(\omega)=\int_{-\infty}^{\infty} X(t)\cos(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\sin(\omega t)\mathrm{d}t,\\ y(\omega)=\int_{-\infty}^{\infty} -X(t)\sin(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\cos(\omega t)\mathrm{d}t. \]](/images/math/b/1/f/b1fe6427816a97f3bf2e8c54549a936e.png)
E két adatsor négyzetösszegének gyöke: 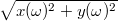 adja meg a különböző frekvenciájú komponensek erősségét a Fourier spektrumban.
adja meg a különböző frekvenciájú komponensek erősségét a Fourier spektrumban.