Termikus zaj szerkesztőlap
Termikus zaj
Egy kristályban lévő elektronok termikus fluktuációi miatt külső feszültség nélkül az áram időátlaga nulla, azonban az adott időpillanatokban véletlen irányokba mutató áramokból áramfluktuációk alakulnak ki.
Ezt, az elektronok termikus fluktuációjából adódó zajt nevezzük termikus zajnak. Jellegét tekintve ez a zaj egy fehér zaj, azaz a zajsűrűsége független a frekvenciától.
A Drude-modell értelmében az elektronok elektromos tér által nyert impulzusát a kristályráccsal történő ütközése (szóródás, rácsrezgés keltése) során veszíti el. A modell értelmében a fajlagos vezetőképesség ( ) arányos az elektronok átlagos sűrűségével (
) arányos az elektronok átlagos sűrűségével ( ), töltésük négyzetével (
), töltésük négyzetével ( ) és az átlagosan két ütközés között eltelt idővel (
) és az átlagosan két ütközés között eltelt idővel ( ), továbbá fordítottan arányos az elektron tömegével (
), továbbá fordítottan arányos az elektron tömegével ( ):
):
![\[\sigma=\frac{ne^2\tau}{m}.\]](/images/math/d/2/7/d272d9a77f5c05c819ce3d63089929dc.png)
Most vizsgáljuk meg ugyanezen rendszer áramzaját külső feszültség nélkül. (Tételezzük fel, hogy a vizsgált vezető mintánk két végét egy árammérővel összekötve mérjük az áramfluktuációkat.) A  karakterisztikus időnként elszenvedett ütközések miatt az áram korrelációja is elvész. Ezt egy
karakterisztikus időnként elszenvedett ütközések miatt az áram korrelációja is elvész. Ezt egy  időállandóval jellemzett exponenciálisan lecsengő korrelációs függvénnyel modellezzük:
időállandóval jellemzett exponenciálisan lecsengő korrelációs függvénnyel modellezzük:
![\[C(\Delta t)=C_0e^{-\frac{|\Delta t|}{\tau}}.\]](/images/math/8/c/b/8cb50ea92d26e5cfbf8154d9b6460f95.png)
Ilyen korrelációs függvény esetén a zajsűrűségre a következő érték adódik:
![\[s_I(\omega)=2c(\omega)=2\int_{-\infty}^{\infty}dte^{-i\omega t}C_0e^{-\frac{|\Delta t|}{\tau}}=\frac{4C_0\tau}{1+\omega^2\tau^2}.\]](/images/math/2/0/7/20768e384b97f92ab829ba61c33e9941.png)
A feladat tehát nem más, mint a 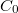 érték, azaz az áram teljes szórásnégyzetének a meghatározása a Drude-modell segítségével.
Vizsgáljunk egy
érték, azaz az áram teljes szórásnégyzetének a meghatározása a Drude-modell segítségével.
Vizsgáljunk egy  keresztmetszetű,
keresztmetszetű,  hosszúságú téglalap alakú dobozt. Ebben egy elektron árama a következőképpen fejezhető ki:
hosszúságú téglalap alakú dobozt. Ebben egy elektron árama a következőképpen fejezhető ki:
![\[I_1=-Anev_x(t)=-\frac{e}{L}v_x(t),\]](/images/math/4/e/b/4ebadeb87b1e436313b4ff6c953affdf.png)
ahol 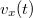 a részecske
a részecske  irányú, azaz a doboz hosszanti irányába mutató sebessége adott
irányú, azaz a doboz hosszanti irányába mutató sebessége adott  időpillanatban.
Innen következik egy elektron áram-áram korrelációs függvénye:
időpillanatban.
Innen következik egy elektron áram-áram korrelációs függvénye:
![\[\langle (\Delta I_1(t))^2\rangle=\frac{e^2}{L^2}\langle v_x^2(t)^2\rangle.\]](/images/math/9/f/b/9fb04c1d2167158df99085550836afbd.png)
N független elektronra a szórásnégyzetek összeadódnak:
![\[\langle (\Delta I(t))^2\rangle=C_0=N\langle (\Delta I_1(t))^2\rangle=N\frac{e^2}{L^2}\langle v_x^2(t)\rangle.\]](/images/math/c/6/9/c69c4ba2e2224f9544750bd1347d921e.png)
Bővítsük a törtet 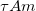 -mel, hogy észrevegyük benne a Drude-modell vezetőképességét:
-mel, hogy észrevegyük benne a Drude-modell vezetőképességét:
![\[C_0=\frac{N}{AL}\frac{e^2\tau}{m}\frac{A}{L}\frac{1}{\tau}m\langle v_x^2(t)\rangle =\frac{G}{\tau}m\langle v_x^2(t)\rangle.\]](/images/math/b/f/3/bf3b4bc698599d537c0d1d7b318041cc.png)
Tovább egyszerűsödik a képlet a klasszikus ekvipartíciós tételt alkalmazva:
![\[C_0=\frac{G}{\tau}k_BT.\]](/images/math/e/0/c/e0c9b547ca4a0e0d53c308478bda303b.png)
Ezt felhasználva, továbbá élve azzal a közelítéssel, hogy a frekvencia sokkal kisebb az átlagos ütözkési idő reciprokánál, adódik a termikus áramzaj spektrális sűrűsége:
![\[s_I(\omega)=\frac{4C_0\tau}{1+\omega^2\tau^2}=\frac{4k_BTG}{1+\omega^2\tau^2}\approx 4k_BTG.\]](/images/math/c/f/6/cf603a783cd205ed68579aa19284d006.png)
Felhasználva, hogy 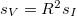 a feszültségzaj spektrális sűrűsége:
a feszültségzaj spektrális sűrűsége:
![\[s_V=4k_BTR.\]](/images/math/9/d/5/9d568e509d842e9eba8731ca66db5a51.png)
Ezzel számítással is beláttuk a termikus zaj fehér zaj jellegét, továbbá azt is látjuk, hogy a zaj mértéke arányos a hőmérséklettel és az ellenállás nagyságával.
Meg kell jegyezni továbbá, hogy a számolás két helyen sem volt teljesen korrekt. Egyrészt csak a Fermi-energia körüli 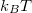 energiasávban lévő elektronok tekinthetők valamilyen szinten függetlennek, a mélyebb energiákon lévő elektronállapotok mindegyike teljesen betöltött, így az áramfluktuációjuk zérus. Másrészt a Fermi-Dirac-eloszlást követő elektronok sebességét nem írhatjuk le az ekvipartíció tétellel, hanem a zajhoz járulékot adó részlegesen betöltött elektronállapotok alapvetően a Fermi-sebességgel mozognak.
Ez a két hiba kompenzálja egymást, és korrekt szilárdtestfizikai számításokkal is a végeredményben kapott képlettel azonos eredményre jutunk.
energiasávban lévő elektronok tekinthetők valamilyen szinten függetlennek, a mélyebb energiákon lévő elektronállapotok mindegyike teljesen betöltött, így az áramfluktuációjuk zérus. Másrészt a Fermi-Dirac-eloszlást követő elektronok sebességét nem írhatjuk le az ekvipartíció tétellel, hanem a zajhoz járulékot adó részlegesen betöltött elektronállapotok alapvetően a Fermi-sebességgel mozognak.
Ez a két hiba kompenzálja egymást, és korrekt szilárdtestfizikai számításokkal is a végeredményben kapott képlettel azonos eredményre jutunk.