„Spektrumanalízis heterodin méréstechnikával” változatai közötti eltérés
| 25. sor: | 25. sor: | ||
A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés. | A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés. | ||
| + | </wlatex> | ||
| + | |||
| + | ==A jelmoduláció alapjai== | ||
| + | <wlatex> | ||
| + | A vivőhullám mint harmonikus rezgés általános alakja: $\psi(t)=A_{\text{c}} \cdot \exp\left[\mathrm{i}\left(2\pi f_{\text{c}} t+\phi_{\text{c}}\right)\right]$. Lehetőség van mindhárom paraméter ($A_{\text{c}},\,f_{\text{c}},\,\phi_{\text{c}}$) modulálására (itt $f_{\text{c}}$ jelöli a vivőhullám/carrier frekvenciáját), amit amplitúdó- (AM), frekvencia- (FM), ill. fázismodulálásnak (PM) nevezünk. Itt csak az AM technikával foglalkozunk. Az AM jelet mutatja az 1. ábra. | ||
| + | |||
| + | Az AM jelet felfoghatjuk úgy, hogy a vivőjelet a moduláló jellel összeszorozzuk. Amennyiben a moduláló jel is tiszta harmonikus hullám: $\psi_{\text{m}}(t)=A_{\text{m}} \cdot \exp\left(\mathrm{i}2\pi f_{\text{m}} t\right)$ (itt az $m$ index a modulálásra vonatkozik), a trigonometrikus azonosságok alapján | ||
| + | $$\cos(\omega_1 t)\cos(\omega_2 t)=\frac{\cos\big( \left( \omega_1+\omega_2\right) t\big)+\cos\big( \left( \omega_1-\omega_2\right) t\big)}{2}$$ | ||
| + | látszik, hogy a két jel szorzata két szintén harmonikus hullám összege, melyek frekvenciája: $f_{\text{c}} \pm f_{\text{m}}$ (feltéve, hogy $f_{\text{c}} > f_{\text{m}}$). A későbbiekben bemutatjuk, hogyan valósítható meg a szorzás művelete, amit keverésnek is nevezünk. A jel demodulálása (azaz a lényeges információ előállítása) szintén szorzással valósítható meg: amennyiben az AM jelet újra beszorozzuk az $f_{\text{c}}$ frekvenciájú jellel a kapott jelben 3 harmonikus hullám összege jelenik meg: $f_{\text{m}}$, $2f_{\text{c}} \pm f_{\text{m}}$. Ezek közül értelemszerűen az első komponens az érdekes, a két másik nagyfrekvenciájú komponens kiszűrése (pl. aluláteresztő szűrővel) után az információt tartalmazó moduláló jel előáll. A tényleges kommunikációban a moduláló jel (pl. AM rádióadásban a továbbított hang) nem egyetlen harmonikus hullámból, hanem különböző frekvenciájú komponensek szuperpozíciójából áll. Látható, hogy ebben az esetben a demodulált jel az eredeti hangot adja vissza. Ezt a technikát nevezik ''szorzásos'' vagy \emph{heterodin} (angolul ''heterodyne'') detektálásnak. | ||
| + | |||
| + | Korábban (kb. 50 évvel ezelőttig) az AM jelek demodulálását egyenirányítással (ún. detektoros vétellel) oldották meg (http://en.wikipedia.org/wiki/Envelope_detector). | ||
| + | Ez azt használja ki, hogy az amplitúdómodulált vivőjelet egyenirányítva és a nagyfrekvenciás komponenst kiszűrve előáll a moduláló burkoló jel. Ezt a technikát nevezik \emph{burkoló detektoros} vételnek is. Ennek előnye, hogy a vevőegység és hangszóró nem igényel extra energiaforrást (bár a jel persze igen halk lesz) hanem az energiát a vivőjelből veszi. Mára a szorzásos módszer vált a rádiótechnikában egyeduralkodóvá a következő részben ismertetett okoknál fogva. | ||
| + | </wlatex> | ||
| + | |||
| + | ==Frekvencia szelektív detektálás, mixerek== | ||
| + | <wlatex> | ||
| + | |||
| + | A burkoló detektoros demodulálás hátránya, hogy amennyiben több rádióadás van jelen egyszerre mindegyiket demodulálja, ezért nehéz egy tiszta jelet kapni. Ezen kicsit segíthet az, ha a vevő detektor előtt van egy sávszűrő, ami csak a kívánt vivőfrekvenciát és annak szűk tartományát engedi át. Ennek a megvalósításnak a hátránya, hogy a sávszűrő megépítése és különböző frekvenciákra hangolása nehézkes. | ||
| + | |||
| + | A heterodin detektálási technikában nincs szükség hangolható sávszűrőre, hanem csak egy fix aluláteresztő szűrőre. A kívánt vivőfrekvencia kiválasztását a demodulálásnál lekeveréshez használt frekvencia változtatásával érjük el. Az eddigiekben az a kérdés még nyitva maradt, hogyan érjük el az előző részben ismertetett, harmonikus hullámok összeszorzását. | ||
| + | |||
| + | Az összeszorzás eszköze a ''keverő'' vagy ''mixer''. Ez egy olyan félvezető eszköz aminek az áram-feszültség karakterisztikája erősen nemlineáris, emiatt két ráadott váltakozóáramú jel szorzata jelenik meg rajta. A mixer sematikáját 2a. ábra mutatja, a portok elnevezéseinek jelöléseivel. A mixereket használhatjuk le- ill.\ felkeverőként is. Előbbihez az RF bemenetként és IF kimenetként funkcionál, míg utóbbihoz az IF a bemenet és RF-en van a felkevert kimenő jel. A 2b. ábra mutatja a mixert lekeverőként használva a frekvencia spektrumban milyen változás történik: az LO egy jól definiált frekvenciájú jel, míg az RF egy modulált, ezért szélesebb frekvenciaspektrumú jel. Az IF porton a két frekvencia különsége jelenik meg, ami jellegében az RF spektrum tulajdonságait hordozza. Felkeverés esetén pedig az LO bemenetre csatlakozik a jól definiált frekvenciájú vivőhullám-jel, az IF bemenetre csatlakoztatjuk az alacsonyfrekvenciás moduláló jelet, és az RF kimeneten jelenik meg az amplitúdómodulált szorzatjel. | ||
| + | |||
| + | A mixer egy lehetséges megvalósítását és működését szemléltetjük \aref{mixer_mukodes_fig}. ábrán. Amikor az LO feszültség olyan, hogy az \textbf{a}-\textbf{c} pontok között pozitív feszültség van ($U_{\mathbf{ac}}>0$), akkor a baloldali két dióda lezár, míg a jobboldali kettő nyitva van. Ekkor a \textbf{d} pont lebeg (feszültségét az RF port feszültsége adja) míg a \textbf{b} pont a földön van. Ezért az RF bemenetre adott feszültség közvetlenül, azonos előjellel megjelenik az IF kimeneten. Amikor ($U_{\mathbf{ac}}<0$), akkor a baloldali két dióda nyit ki, ezért a \textbf{d} pont lesz leföldelve, míg a jobboldali két dióda lezár, ezért ekkor az RF bemenetre adott feszültség -1 szerese jelenik meg az IF kimeneten. | ||
| + | |||
| + | Ezt a viselkedést szemlélteti a 3. ábra jobb oldali panele. A kapcsoló-mixer úgy viselkedik mintha az LO jel +1 és -1 közötti értékével szorzódna be az RF feszültség ami megjelenik az IF kimeneten. Az ábrán mutatott példában LO frekvenciája 20 MHz, RF frekvenciája 18 MHz és a szorzás után megjelenik az IF kimeneten egy alacsony (2 MHz-es) frekvenciával modulált 38 MHz-es jel. Ha ezt a jelet aluláteresztő szűrővel szürjük (példánkban numerikus csúszóátlagolást végeztünk) akkor jól látható az IF kimeneten megjelenő alacsony frekvencia. Ez a leírás egyben azt is megmutatja, hogy az LO feszültség nagyságától nem függ a kimeneti feszültség értéke, de az RF és IF feszültségek egymással arányosak (nem pontosan egyenlők mivel az eszköznek van egy kis vesztesége). | ||
| + | </wlatex> | ||
| + | |||
| + | ==A Lock-in erősítő== | ||
| + | <wlatex> | ||
| + | A kétcsatornás fázisérzékeny egyenirányító vagy ''lock-in erősítő'' blokkdiagrammját a 4. ábra mutatja. Ez lényegében két lekeverő mixerből áll, az IF kimenetet aluláteresztő szűrők követik. A két csatorna azt jelenti, hogy a bejövő RF jelnek mérjük két komponensét: az egyik amelyik fázisban van az LO-val és a másik amelyik 90 fokkal eltolt fázisban van. Előfordulhatna ugyanis, hogy a bejövő RF jel fázisa 90 fokos szöget zár be az LO-éval, ezáltal az IF jel kisfrekvenciás komponense 0 lenne. A két mért csatorna miatt lehetőség van a két kimenet négyzetösszegének meghatározására: $R=\sqrt{X^2+Y^2}$ ami azért előnyős, mert a bejövő jel fázisa a belső oszcillátorhoz képest általában nem ismert, az $R$ mennyiség azonban nem függ a fázistól. | ||
| + | |||
| + | A gyakorlaton megismerkedünk a lock-in erősítő alapvető kezelésével, és azzal, hogy a segítségével az AM rádióadás közvetlenül demodulálható. Megjegyezzük, hogy a lock-in erősítő mint több milliós mérőeszköz használata a rádióadás vételére (amit egy filléres rádióval is megoldhatnánk) megmosolyogtató, azonban kiválóan alkalmas e műszer alapvető működésének demonstrációjára. | ||
| + | </wlatex> | ||
| + | |||
| + | ==Nagyfrekvenciás jelek analízise, a Fourier transzformáció== | ||
| + | |||
| + | A heterodin detektálás megismerése után ismételjük át, hogy hogyan határozható meg egy jel frekvenciatérbeli felbontása. | ||
| + | |||
| + | Egy $F(t)$ időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg: | ||
| + | $$f(\omega)=\int_{-\infty}^{\infty} F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t.$$ | ||
| + | Egy valós mérésnél a Fourier-transzformált függvényt csak közelítőleg tudjuk megadni, hiszen egyrészt véges ideig tart a mérésünk, másrészt a mérési adatok csak diszkrét időfelbontással álnak rendelkezésre. Először nézzük meg a véges idejű mérés hatását a Fourier-transzformáltra. | ||
| + | |||
| + | A véges idejű mérés megfelel annak, mintha az eredeti függvényt megszoroznánk a mérési intervallumnak megfelelő $W(t)$ ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki: | ||
| + | $$f_W(\omega)=\int_{-\infty}^{\infty} W(t)\cdot F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,$$ | ||
| + | ahol a $W(t)$ függvény $|t|<T/2$ esetén $1/T$, ezen $T$ hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz: | ||
| + | $$ | ||
| + | f_W(\omega)=\int_{-\infty}^{\infty} f(\omega ')w(\omega - \omega ')\frac{\mathrm{d}\omega}{2\pi},\ \ \ \ \mathrm{ahol}\ \ \ w(\omega)=\int_{-\infty}^{\infty} W(t)\mathrm{e}^{-i\omega t}\mathrm{d}t. | ||
| + | $$ | ||
| + | Nézzünk egy egyszerű példát, legyen $F(t)=A\cdot \exp(i\omega_0 t)$ egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény: $f(\omega)=A\cdot 2\pi\delta(\omega-\omega_0)$. Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján $f_W(\omega)=A\cdot w(\omega-\omega_0)$, azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az $\omega_0$ középfrekvenciához eltolva. A fent definiált \emph{téglalap ablak} esetén (azaz amikor $W(t)$ egy $T$ szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja $w(\omega)=(2/\omega T)\cdot \sin(\omega T/2)$, azaz $f_W(\omega)=\left(2/(\omega-\omega_0 ) T \right)\cdot \sin\left((\omega-\omega_0 ) T/2\right)$ (\ref{ablakfv_fig}b.\ ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az $\omega_0$ középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az $f_W(\omega)$ függvény $\omega_0$ melletti első zérushelyeinek a távolsága $4\pi/T$, így az $\omega_0$ körüli csúcs szélessége $\sim 2\pi/T$. Tehát az első fontos konklúzió, hogy {\bf véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg $\Delta \omega \approx 2\pi/T$ frekvenciafelbontással látjuk!} | ||
| + | |||
| + | Érdemes megjegyezni, hogy a fent említett téglalap ablak helyett választhatunk más ablakfüggvényt is, például $W(t)=\cos^2(t\pi/T)$ ún.\ Hanning-ablak esetén a mért jelben elnyomjuk a $|t|<T/2$ mintavételezési időablak széleihez közeli részeket (5a.\ ábra, piros szaggatott vonal). Ebben az esetben az $\omega_0$ körfrekvenciás jel Fourier-transzformáltjában $\omega_0$ körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az $\omega_0$-tól távolabbi oszcillációk amplitúdója (az ún.\ spektrális szivárgás) lecsökken (5b.\ ábra, piros szaggatott vonal). | ||
| + | |||
| + | Következő lépésként nézzük meg, hogy mi a hatása annak, hogy a jelünket nem folytonosan látjuk, hanem csak diszkrét mintavételezési időpontokban. Emiatt a jel Fourier-transzformáltját a folytonos integrál helyett kénytelenek vagyunk egy diszkrét összeggel, az ún.\ diszkrét Fourier-transzformálttal (DFT) közelíteni: | ||
| + | $$ | ||
| + | f_W(\omega)=\sum_{n=0}^{N-1} W(n\cdot \Delta t)F(n\cdot \Delta t) \mathrm{e}^{-i\omega n \Delta t}\Delta t, | ||
| + | $$ | ||
| + | ahol $\Delta t$ a szomszédos mérési pontok közötti idő, $N=T/\Delta t$ pedig a mintavételezett pontok száma. | ||
| + | Az ún.\ Nyquist-Shannon mintavételezési törvény szerint {\bf $\Delta t$ sűrűségű mintavételezés esetén a jelet $\omega_\mathrm{max}=2\pi/2\Delta t$ maximális körfrekvenciáig tudjuk rekonstruálni}. | ||
| + | |||
| + | Könnyen belátható, hogy a diszkrét Fourier-transzformált fenti képlet szerinti kiértékelése $N$ mérési pont esetén $\sim N^2$ művelet ($\Delta \omega \approx 2\pi/N\Delta t$ frekvenciafelbontás és $\omega_\mathrm{max}=2\pi/2\Delta t$ maximális felbontható frekvencia esetén csak $\omega_\mathrm{max}/\Delta \omega\approx N$ diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián $~N$ művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa ($N=2^p$), és a frekvenciatérben $\omega_k=2\pi k/N\Delta t,\ \ \ k=0,1,...,N/2$ diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma $N^2$-ről $N\log_2 N$-re csökken, ami nagy N esetén lényeges különbség. | ||
| + | |||
| + | A mérőműszerek jelentős része, így a laborgyakorlaton használt digitális oszcilloszkóp is az FFT algoritmus numerikus kiértékelése alapján határozza meg a mért jel spektrumát. A legtöbb esetben a műszer nem adja meg külön a spektrum valós és képzetes részét, hanem csak a Fourier-transzformált abszolút érték négyzetét látjuk. Ezen kívül a mérőműszerek általában a frekvencia, és nem a körfrekvencia függvényében adják meg a spektrumot, erre érdemes odafigyelni a mérés kiértékelésénél. | ||
| + | |||
| + | A Fourier transzformáció definiciójánál azt látjuk, hogy a Fourier spektrum komplex mennyiség. Erre azért van szükség, hogy a különböző frekvenciájú harmonikus tagok \emph{fázisát} is le tudjuk írni. Könnyen belátható, hogy amennyiben $F(t)$ páros függvény (pl. cos), akkor a Fourier spektrum tisztán valós, amennyiben pedig $F(t)$ páratlan függvény (pl. sin), akkor a Fourier spektrum tisztán képzetes. Tetszőleges $F(t)$ esetén pedig a Fourier spektrum tartalmaz valós és képzetes tagokat is\footnote{Ilyen értelemben a komplex jelölésnek az a szerepe, hogy a leírást rövidítse, egyébként kétkomponensű vektorokat kellene írnunk.}. Amennyiben a fázis ismerete nem lényeges és csak az egyes Fourier komponensek erősségére vagyunk kiváncsiak akkor a Fourier spektrum valós és képzetes részeinek négyzetösszegének gyökéből képezhetjük az ún. Fourier erősséget (\emph{Fourier magnitude}). | ||
| + | |||
| + | Egy kérdés azonban még nyitva maradt: amikor harmonikus rezgésről beszélünk gyakran mint cos, sin vagy $\mathrm{e}^{i\omega_0 t}$-ként hivatkozunk rá. Itt mi a komplex jelölés szerepe? Erre a rövid válasz az, hogy önmagában a cos vagy sin függvény nem adja meg a harmonikus rezgés frekvenciájának \emph{előjelét}. Első hallásra meglepő, hogy harmonikus rezgés frekvenciájának előjele van, azonban gondoljunk csak a mixeres lekeverésre: amennyiben RF frekvenciája kisebb mint az LO frekvenciája, a kapott IF jel alacsonyfrekvenciás komponensének fekvenciája \emph{negatív}. Az előjel elvesztésének bemutatására tekintsük először a $\cos\left( \omega_{\text{IF}}t\right)$ jelet, ennek \aref{FT_def}. képlet alapján a Fourier transzformáltja valós és tartalmaz $\pm \omega_{\text{IF}}$-nél is egy-egy pozitív csúcsot. Második példánkban tekintsük a $\sin\left( \omega_{\text{IF}}t\right)$ jelet, aminek Fourier transzformáltja képzetes és $\pm \omega_{\text{IF}}$-nél mutat egy-egy ellentétes előjelű csúcsot. Tehát egyik példában sem tudjuk a jel frekvenciájának előjelét egyértelműen meghatározni. Ezzel szemben a $\mathrm{e}^{-i\omega_{\text{IF}} t}$ Fourier transzformáltjának $\omega_{\text{IF}}$-nél (előjelhelyesen) van egy csúcsa\footnote{Azaz nincs csúcsa $-\omega_{\text{IF}}$-nél.}. | ||
| + | |||
| + | A $\mathrm{e}^{-i\omega_{\text{IF}} t}$ kifejezés valós és képzetes részei úgy viselkednek mint a trigonometrikus függvények definiciójakor használt egységkörön mozgó pont vetületei, ami foroghat pozitív és negatív körüljáráson is. Ezzel szemben külön-külön a cos és sin vetületek nem érzékenyek az egységkörön mozgó pont körüljárásának irányára. | ||
| + | |||
| + | Már csak azt a kérdést kell megválaszolnunk, hogy méréstechnikában hogyan tudjuk ezt a $\mathrm{e}^{-i\omega_{\text{IF}} t}$ komplex időfüggő mennyiséget előállítani a mért \emph{valós} jelekből. A válasz az, hogy a valós és képzetes részek a lock-in technikánál bemutatott kvadratúra detektálásból adódnak: azaz a bejövő jelet két, egymástól 90 fokban eltolt jellel keverjük le. Az így kapott két adatsort ($X(t)$ és $Y(t)$ \aref{LI_fig}. ábra jelöléseivel) \emph{tekintjük} a bejövő lekevert jel valós és képzetes részeinek: $\widetilde{X}(t)=X(t)+i Y(t)$. Az FT után szintén két adatsort kapunk \aref{FT_def}. képlet alapján: | ||
| + | |||
| + | |||
| + | $$ | ||
| + | \widetilde{x}(\omega)=x(\omega)+i y(\omega)=\int_{-\infty}^{\infty} \widetilde{X}(t)\mathrm{e}^{-i\omega t}\mathrm{d}t, | ||
| + | $$ | ||
| + | |||
| + | ezért ezt komplex vagy kétcsatornás Fourier transzformációnak nevezzük. | ||
| + | |||
| + | Ha a tagokat expliciten kiírjuk, akkor belátható, hogy e két adatsor a következőképpen adódik: | ||
| + | |||
| + | $$ | ||
| + | x(\omega)=\int_{-\infty}^{\infty} X(t)\cos(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\sin(\omega t)\mathrm{d}t,\\ | ||
| + | y(\omega)=\int_{-\infty}^{\infty} -X(t)\sin(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\cos(\omega t)\mathrm{d}t. | ||
| + | $$ | ||
| + | |||
| + | E két adatsor négyzetösszegének gyöke: $\sqrt{x(\omega)^2+y(\omega)^2}$ adja meg a különböző frekvenciájú komponensek erősségét a Fourier spektrumban. | ||
</wlatex> | </wlatex> | ||
A lap 2015. április 3., 12:38-kori változata
A mérési feladatot összeállította: Simon Ferenc és Halbritter András, BME Fizika Tanszék (2015)
A jegyzettel kapcsolatos javításokat, javaslatokat köszönettel kérjük az címre.
A laborgyakorlat célja, hogy a nagyfrekvenciás méréstechnikában széleskörben alkalmazott Fourier-analízis és heterodin méréstechnika alapjait bemutassa. A laborgyakorlat nagyban támaszkodik a korábbi Méréstechnika tárgyra, ezért az ott elsajátított ismeretek átismétlése elvárás.
Tartalomjegyzék |
Bevezetés és történeti háttér
Az adatátvitel alapfeladata, hogy a lehető legtöbb információt juttassunk el két pont között az információt minél jobban megtartva. Napjainkban amikor a környezetünk zsúfolva van különböző információtovábbító elektromágneses sugárzással, különösen fontos ez a kérdés. Az egyik elterjedt megoldás a különböző információk különböző frekvenciákhoz való rendelése (ún. frekvenciaosztásos multiplexelés). Ez eredményezi a manapság ismert különböző frekvenciájú rádióadások jelenlétét, ahol mindegyik rádiócsatorna adott (vivő)frekvencián sugározza az adását. Az adások információtartalma különböző módon van a vivőhullámba belekódolva. Itt a két legfontosabbat említjük csak, amivel a gyakorlaton is megismerkedünk: AM (amplitúdómoduláció) és FM (frekvenciamoduláció).
Belátható, hogy a továbbított információ mennyisége és az adott jelhez tartozó sávszélesség ( ) egymással egyenesen arányos. Például egy állandó frekvenciájú sugárzással - melynek sávszélessége nulla - semmilyen információt nem tudunk továbbítani, de például egy 1 kHz frekvenciával modulált 100 MHz-es vivőhullámmal már tudunk 1 kbit/s információtovábbítást elérni. (Képzeljük el, hogy egy állandó frekvenciájú, időben állandó nagyságú elektromágneses jellel próbálunk információt közvetíteni. Ennek Fourier-transzformáltja egy Dirac-delta függvény, azaz nulla sávszélessége van. Azonban ennek a jelnek az információtartalma is nulla. A legegyszerűbb Morse-adatátvitelhez is már ki-be kell kapcsolgatnunk ezt a jelet, ami már természetesen nem lesz egy állandó frekvenciájú időben állandó nagyságú jel, és így a Fourier-transzformáltja sem lesz Dirac-delta.) Nem véletlen, hogy a hétköznapi gyakorlatban mindeki csak sávszélességről beszél mialatt a továbbított információ mennyiségére utal, miközben ez a fogalom alapvetően a továbbított jel frekvenciaspektrumának szélességére utal. Ebben a jegyzetben mi a hagyományos értelmeben vett (frekvencia-)sávszélességre utalunk.
) egymással egyenesen arányos. Például egy állandó frekvenciájú sugárzással - melynek sávszélessége nulla - semmilyen információt nem tudunk továbbítani, de például egy 1 kHz frekvenciával modulált 100 MHz-es vivőhullámmal már tudunk 1 kbit/s információtovábbítást elérni. (Képzeljük el, hogy egy állandó frekvenciájú, időben állandó nagyságú elektromágneses jellel próbálunk információt közvetíteni. Ennek Fourier-transzformáltja egy Dirac-delta függvény, azaz nulla sávszélessége van. Azonban ennek a jelnek az információtartalma is nulla. A legegyszerűbb Morse-adatátvitelhez is már ki-be kell kapcsolgatnunk ezt a jelet, ami már természetesen nem lesz egy állandó frekvenciájú időben állandó nagyságú jel, és így a Fourier-transzformáltja sem lesz Dirac-delta.) Nem véletlen, hogy a hétköznapi gyakorlatban mindeki csak sávszélességről beszél mialatt a továbbított információ mennyiségére utal, miközben ez a fogalom alapvetően a továbbított jel frekvenciaspektrumának szélességére utal. Ebben a jegyzetben mi a hagyományos értelmeben vett (frekvencia-)sávszélességre utalunk.
Az emberi hang torzításmentes továbbításához (mono adás esetén) kb. 20 kHz sávszélességre van szükség. A gyakorlatban az egyes rádióadók frekvenciáját a zavaró interferencia elkerülésére végett ennél távolabbra állítják be, ezért találunk a mindenki által ismert FM sávban (87,5-108 MHz között) kb. 100 kHz-enként rádióállomásokat.
Egy másik gyakorlati megfontolás ami korlátozza az átvihető információ és így a sávszélesség nagyságát, az a zaj kérdése. A Méréstechnika tárgyban ismertetett módon az ún. Johnson-Nyquist vagy termikus zaj teljesítménye és a sávszélesség közötti kapcsolat:
![\[P_{\text{JN-zaj}}=4 k_{\text{B}}T\Delta f\]](/images/math/6/3/4/634a973a440068cc792e939eb2d83b23.png)
ahol 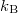 a Boltzmann-állandó,
a Boltzmann-állandó,  az abszolút hőmérséklet és
az abszolút hőmérséklet és  a sávszélesség.
a sávszélesség.
- A Méréstechnika tárgyban tanultak szerint egy
 ellenálláson eső feszültség szórásnégyzete egy
ellenálláson eső feszültség szórásnégyzete egy  sávszélességű frekvenciaablakban mérve a termikus zaj miatt
sávszélességű frekvenciaablakban mérve a termikus zaj miatt 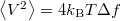 , így a termikus zaj teljesítménye
, így a termikus zaj teljesítménye 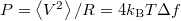 . A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon.
. A zaj-sávszélességről egy jó leírás található a http://en.wikipedia.org/wiki/Johnson-Nyquist\_noise oldalon.
Eszerint minél nagyobb az elvárt sávszélesség, annál nagyobb lesz a zaj teljesítménye is. A telekommunikációban a termikus zajteljesítmény nagyságára 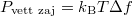 képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára
képletet használjuk, a 4-es faktor különbség oka, hogy egy valódi adó-vevő rendszerben csak a bejövő/kimenő feszültség fele esik a munkaellenálláson (a másik fele a jelet keltő/vevő egységben). Eszerint 300 K hőmérsékleten a zajteljesítmény nagyságára 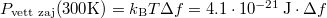 adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben
adódik, ami egy 50 Ohmos ellenálláson körülbelül 1 nV feszültségnek felel meg 1 Hz sávszélesség mellett, illetve dBm egységekben 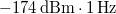 .
.
- A dBm egység definíciója:
![\setbox0\hbox{$P[\text{dBm}]=10\cdot \log_{10}(P/1\text{mW}).$}% \message{//depth:\the\dp0//}% \box0%](/images/math/c/a/d/cada73ee7df8a16390c26128fefd9511.png)
A nagyfrekvenciás méréstechnika alapproblémája tehát, hogy adott sávszélesség mellett minél jobb jel-zaj arányt érjünk el úgy, hogy a különböző információs csatornák frekvenciája különböző. Ennek megvalósítására adott vivőhullám-frekvenciára keverik rá az információt különböző modulációs módszerekkel. Az információt úgy kapjuk vissza, hogy szelektíven csak az adott vivőhullám körüli frekvenciára koncentrálunk és az itt megfigyelt jelet demoduláljuk. A továbbiakban bemutatjuk a különböző modulációs technikákat és azt, hogy milyen módszerrel lehetséges a frekvenciaszelektív mérés.
A jelmoduláció alapjai
A vivőhullám mint harmonikus rezgés általános alakja: ![\setbox0\hbox{$\psi(t)=A_{\text{c}} \cdot \exp\left[\mathrm{i}\left(2\pi f_{\text{c}} t+\phi_{\text{c}}\right)\right]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/b/3/b/b3b13ee0d818b0289badd6629a78272d.png) . Lehetőség van mindhárom paraméter (
. Lehetőség van mindhárom paraméter (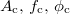 ) modulálására (itt
) modulálására (itt 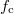 jelöli a vivőhullám/carrier frekvenciáját), amit amplitúdó- (AM), frekvencia- (FM), ill. fázismodulálásnak (PM) nevezünk. Itt csak az AM technikával foglalkozunk. Az AM jelet mutatja az 1. ábra.
jelöli a vivőhullám/carrier frekvenciáját), amit amplitúdó- (AM), frekvencia- (FM), ill. fázismodulálásnak (PM) nevezünk. Itt csak az AM technikával foglalkozunk. Az AM jelet mutatja az 1. ábra.
Az AM jelet felfoghatjuk úgy, hogy a vivőjelet a moduláló jellel összeszorozzuk. Amennyiben a moduláló jel is tiszta harmonikus hullám: 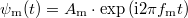 (itt az
(itt az  index a modulálásra vonatkozik), a trigonometrikus azonosságok alapján
index a modulálásra vonatkozik), a trigonometrikus azonosságok alapján
![\[\cos(\omega_1 t)\cos(\omega_2 t)=\frac{\cos\big( \left( \omega_1+\omega_2\right) t\big)+\cos\big( \left( \omega_1-\omega_2\right) t\big)}{2}\]](/images/math/6/8/6/6864fa18709c407bfac156d759c2994c.png)
látszik, hogy a két jel szorzata két szintén harmonikus hullám összege, melyek frekvenciája:  (feltéve, hogy
(feltéve, hogy 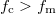 ). A későbbiekben bemutatjuk, hogyan valósítható meg a szorzás művelete, amit keverésnek is nevezünk. A jel demodulálása (azaz a lényeges információ előállítása) szintén szorzással valósítható meg: amennyiben az AM jelet újra beszorozzuk az
). A későbbiekben bemutatjuk, hogyan valósítható meg a szorzás művelete, amit keverésnek is nevezünk. A jel demodulálása (azaz a lényeges információ előállítása) szintén szorzással valósítható meg: amennyiben az AM jelet újra beszorozzuk az 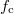 frekvenciájú jellel a kapott jelben 3 harmonikus hullám összege jelenik meg:
frekvenciájú jellel a kapott jelben 3 harmonikus hullám összege jelenik meg: 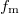 ,
, 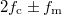 . Ezek közül értelemszerűen az első komponens az érdekes, a két másik nagyfrekvenciájú komponens kiszűrése (pl. aluláteresztő szűrővel) után az információt tartalmazó moduláló jel előáll. A tényleges kommunikációban a moduláló jel (pl. AM rádióadásban a továbbított hang) nem egyetlen harmonikus hullámból, hanem különböző frekvenciájú komponensek szuperpozíciójából áll. Látható, hogy ebben az esetben a demodulált jel az eredeti hangot adja vissza. Ezt a technikát nevezik szorzásos vagy \emph{heterodin} (angolul heterodyne) detektálásnak.
. Ezek közül értelemszerűen az első komponens az érdekes, a két másik nagyfrekvenciájú komponens kiszűrése (pl. aluláteresztő szűrővel) után az információt tartalmazó moduláló jel előáll. A tényleges kommunikációban a moduláló jel (pl. AM rádióadásban a továbbított hang) nem egyetlen harmonikus hullámból, hanem különböző frekvenciájú komponensek szuperpozíciójából áll. Látható, hogy ebben az esetben a demodulált jel az eredeti hangot adja vissza. Ezt a technikát nevezik szorzásos vagy \emph{heterodin} (angolul heterodyne) detektálásnak.
Korábban (kb. 50 évvel ezelőttig) az AM jelek demodulálását egyenirányítással (ún. detektoros vétellel) oldották meg (http://en.wikipedia.org/wiki/Envelope_detector). Ez azt használja ki, hogy az amplitúdómodulált vivőjelet egyenirányítva és a nagyfrekvenciás komponenst kiszűrve előáll a moduláló burkoló jel. Ezt a technikát nevezik \emph{burkoló detektoros} vételnek is. Ennek előnye, hogy a vevőegység és hangszóró nem igényel extra energiaforrást (bár a jel persze igen halk lesz) hanem az energiát a vivőjelből veszi. Mára a szorzásos módszer vált a rádiótechnikában egyeduralkodóvá a következő részben ismertetett okoknál fogva.
Frekvencia szelektív detektálás, mixerek
A burkoló detektoros demodulálás hátránya, hogy amennyiben több rádióadás van jelen egyszerre mindegyiket demodulálja, ezért nehéz egy tiszta jelet kapni. Ezen kicsit segíthet az, ha a vevő detektor előtt van egy sávszűrő, ami csak a kívánt vivőfrekvenciát és annak szűk tartományát engedi át. Ennek a megvalósításnak a hátránya, hogy a sávszűrő megépítése és különböző frekvenciákra hangolása nehézkes.
A heterodin detektálási technikában nincs szükség hangolható sávszűrőre, hanem csak egy fix aluláteresztő szűrőre. A kívánt vivőfrekvencia kiválasztását a demodulálásnál lekeveréshez használt frekvencia változtatásával érjük el. Az eddigiekben az a kérdés még nyitva maradt, hogyan érjük el az előző részben ismertetett, harmonikus hullámok összeszorzását.
Az összeszorzás eszköze a keverő vagy mixer. Ez egy olyan félvezető eszköz aminek az áram-feszültség karakterisztikája erősen nemlineáris, emiatt két ráadott váltakozóáramú jel szorzata jelenik meg rajta. A mixer sematikáját 2a. ábra mutatja, a portok elnevezéseinek jelöléseivel. A mixereket használhatjuk le- ill.\ felkeverőként is. Előbbihez az RF bemenetként és IF kimenetként funkcionál, míg utóbbihoz az IF a bemenet és RF-en van a felkevert kimenő jel. A 2b. ábra mutatja a mixert lekeverőként használva a frekvencia spektrumban milyen változás történik: az LO egy jól definiált frekvenciájú jel, míg az RF egy modulált, ezért szélesebb frekvenciaspektrumú jel. Az IF porton a két frekvencia különsége jelenik meg, ami jellegében az RF spektrum tulajdonságait hordozza. Felkeverés esetén pedig az LO bemenetre csatlakozik a jól definiált frekvenciájú vivőhullám-jel, az IF bemenetre csatlakoztatjuk az alacsonyfrekvenciás moduláló jelet, és az RF kimeneten jelenik meg az amplitúdómodulált szorzatjel.
A mixer egy lehetséges megvalósítását és működését szemléltetjük \aref{mixer_mukodes_fig}. ábrán. Amikor az LO feszültség olyan, hogy az \textbf{a}-\textbf{c} pontok között pozitív feszültség van (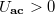 ), akkor a baloldali két dióda lezár, míg a jobboldali kettő nyitva van. Ekkor a \textbf{d} pont lebeg (feszültségét az RF port feszültsége adja) míg a \textbf{b} pont a földön van. Ezért az RF bemenetre adott feszültség közvetlenül, azonos előjellel megjelenik az IF kimeneten. Amikor (
), akkor a baloldali két dióda lezár, míg a jobboldali kettő nyitva van. Ekkor a \textbf{d} pont lebeg (feszültségét az RF port feszültsége adja) míg a \textbf{b} pont a földön van. Ezért az RF bemenetre adott feszültség közvetlenül, azonos előjellel megjelenik az IF kimeneten. Amikor (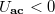 ), akkor a baloldali két dióda nyit ki, ezért a \textbf{d} pont lesz leföldelve, míg a jobboldali két dióda lezár, ezért ekkor az RF bemenetre adott feszültség -1 szerese jelenik meg az IF kimeneten.
), akkor a baloldali két dióda nyit ki, ezért a \textbf{d} pont lesz leföldelve, míg a jobboldali két dióda lezár, ezért ekkor az RF bemenetre adott feszültség -1 szerese jelenik meg az IF kimeneten.
Ezt a viselkedést szemlélteti a 3. ábra jobb oldali panele. A kapcsoló-mixer úgy viselkedik mintha az LO jel +1 és -1 közötti értékével szorzódna be az RF feszültség ami megjelenik az IF kimeneten. Az ábrán mutatott példában LO frekvenciája 20 MHz, RF frekvenciája 18 MHz és a szorzás után megjelenik az IF kimeneten egy alacsony (2 MHz-es) frekvenciával modulált 38 MHz-es jel. Ha ezt a jelet aluláteresztő szűrővel szürjük (példánkban numerikus csúszóátlagolást végeztünk) akkor jól látható az IF kimeneten megjelenő alacsony frekvencia. Ez a leírás egyben azt is megmutatja, hogy az LO feszültség nagyságától nem függ a kimeneti feszültség értéke, de az RF és IF feszültségek egymással arányosak (nem pontosan egyenlők mivel az eszköznek van egy kis vesztesége).
A Lock-in erősítő
A kétcsatornás fázisérzékeny egyenirányító vagy lock-in erősítő blokkdiagrammját a 4. ábra mutatja. Ez lényegében két lekeverő mixerből áll, az IF kimenetet aluláteresztő szűrők követik. A két csatorna azt jelenti, hogy a bejövő RF jelnek mérjük két komponensét: az egyik amelyik fázisban van az LO-val és a másik amelyik 90 fokkal eltolt fázisban van. Előfordulhatna ugyanis, hogy a bejövő RF jel fázisa 90 fokos szöget zár be az LO-éval, ezáltal az IF jel kisfrekvenciás komponense 0 lenne. A két mért csatorna miatt lehetőség van a két kimenet négyzetösszegének meghatározására: 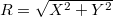 ami azért előnyős, mert a bejövő jel fázisa a belső oszcillátorhoz képest általában nem ismert, az
ami azért előnyős, mert a bejövő jel fázisa a belső oszcillátorhoz képest általában nem ismert, az  mennyiség azonban nem függ a fázistól.
mennyiség azonban nem függ a fázistól.
A gyakorlaton megismerkedünk a lock-in erősítő alapvető kezelésével, és azzal, hogy a segítségével az AM rádióadás közvetlenül demodulálható. Megjegyezzük, hogy a lock-in erősítő mint több milliós mérőeszköz használata a rádióadás vételére (amit egy filléres rádióval is megoldhatnánk) megmosolyogtató, azonban kiválóan alkalmas e műszer alapvető működésének demonstrációjára.
Nagyfrekvenciás jelek analízise, a Fourier transzformáció
A heterodin detektálás megismerése után ismételjük át, hogy hogyan határozható meg egy jel frekvenciatérbeli felbontása.
Egy $F(t)$ időfüggvény különböző frekvenciájú komponenseinek felbontását matematikailag a Fourier-transzformált segítségével adhatjuk meg: $$f(\omega)=\int_{-\infty}^{\infty} F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t.$$ Egy valós mérésnél a Fourier-transzformált függvényt csak közelítőleg tudjuk megadni, hiszen egyrészt véges ideig tart a mérésünk, másrészt a mérési adatok csak diszkrét időfelbontással álnak rendelkezésre. Először nézzük meg a véges idejű mérés hatását a Fourier-transzformáltra.
A véges idejű mérés megfelel annak, mintha az eredeti függvényt megszoroznánk a mérési intervallumnak megfelelő $W(t)$ ablakfüggvénnyel, és ezen szorzatfüggvény Fourier-transzformáltját számolnánk ki: $$f_W(\omega)=\int_{-\infty}^{\infty} W(t)\cdot F(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,$$ ahol a $W(t)$ függvény $|t|<T/2$ esetén $1/T$, ezen $T$ hosszúságú időintervallumon kívül pedig zérus. Megmutatható, hogy egy szorzatfüggvény Fourier-transzformáltja a két komponens Fourier-transzformáltjának a konvolúciója, azaz: $$ f_W(\omega)=\int_{-\infty}^{\infty} f(\omega ')w(\omega - \omega ')\frac{\mathrm{d}\omega}{2\pi},\ \ \ \ \mathrm{ahol}\ \ \ w(\omega)=\int_{-\infty}^{\infty} W(t)\mathrm{e}^{-i\omega t}\mathrm{d}t. $$ Nézzünk egy egyszerű példát, legyen $F(t)=A\cdot \exp(i\omega_0 t)$ egy harmonikus függvény, melynek a Fourier-transzformáltja egy Dirac-delta függvény: $f(\omega)=A\cdot 2\pi\delta(\omega-\omega_0)$. Véges idejű mérés esetén azonban a Fourier integrál értéke a fentiek alapján $f_W(\omega)=A\cdot w(\omega-\omega_0)$, azaz a harmonikus függvény Fourier-transzormáltjában egy valós mérés esetén a végtelenül keskeny Dirac-delta csúcs helyett az ablakfüggvény Fourier-transzormáltját látjuk az $\omega_0$ középfrekvenciához eltolva. A fent definiált \emph{téglalap ablak} esetén (azaz amikor $W(t)$ egy $T$ szélességű intervallumban konstans, azon kívül zérus, lásd 5a. ábra, kék folytonos vonal) az ablakfüggvény Fourier-transzformáltja $w(\omega)=(2/\omega T)\cdot \sin(\omega T/2)$, azaz $f_W(\omega)=\left(2/(\omega-\omega_0 ) T \right)\cdot \sin\left((\omega-\omega_0 ) T/2\right)$ (\ref{ablakfv_fig}b.\ ábra, kék folytonos vonal). A véges időintervallumra számolt Fourier-integrál is mutat egy határozott csúcsot az $\omega_0$ középfrekvencia körül, azonban ez a csúcs véges szélességű, ráadásul a csúcstól távolabb is oszcillációkat látunk a Fourier-transzformáltban, amit spektrális szivárgásnak nevezünk. Az $f_W(\omega)$ függvény $\omega_0$ melletti első zérushelyeinek a távolsága $4\pi/T$, így az $\omega_0$ körüli csúcs szélessége $\sim 2\pi/T$. Tehát az első fontos konklúzió, hogy {\bf véges időtartamú mérés esetén a jelünket a Fourier-térben csak véges, nagyságrendileg $\Delta \omega \approx 2\pi/T$ frekvenciafelbontással látjuk!}
Érdemes megjegyezni, hogy a fent említett téglalap ablak helyett választhatunk más ablakfüggvényt is, például $W(t)=\cos^2(t\pi/T)$ ún.\ Hanning-ablak esetén a mért jelben elnyomjuk a $|t|<T/2$ mintavételezési időablak széleihez közeli részeket (5a.\ ábra, piros szaggatott vonal). Ebben az esetben az $\omega_0$ körfrekvenciás jel Fourier-transzformáltjában $\omega_0$ körül egy még szélesebb csúcsot látunk (azaz a frekvenciafelbontás romlik), viszont az $\omega_0$-tól távolabbi oszcillációk amplitúdója (az ún.\ spektrális szivárgás) lecsökken (5b.\ ábra, piros szaggatott vonal).
Következő lépésként nézzük meg, hogy mi a hatása annak, hogy a jelünket nem folytonosan látjuk, hanem csak diszkrét mintavételezési időpontokban. Emiatt a jel Fourier-transzformáltját a folytonos integrál helyett kénytelenek vagyunk egy diszkrét összeggel, az ún.\ diszkrét Fourier-transzformálttal (DFT) közelíteni: $$ f_W(\omega)=\sum_{n=0}^{N-1} W(n\cdot \Delta t)F(n\cdot \Delta t) \mathrm{e}^{-i\omega n \Delta t}\Delta t, $$ ahol $\Delta t$ a szomszédos mérési pontok közötti idő, $N=T/\Delta t$ pedig a mintavételezett pontok száma. Az ún.\ Nyquist-Shannon mintavételezési törvény szerint {\bf $\Delta t$ sűrűségű mintavételezés esetén a jelet $\omega_\mathrm{max}=2\pi/2\Delta t$ maximális körfrekvenciáig tudjuk rekonstruálni}.
Könnyen belátható, hogy a diszkrét Fourier-transzformált fenti képlet szerinti kiértékelése $N$ mérési pont esetén $\sim N^2$ művelet ($\Delta \omega \approx 2\pi/N\Delta t$ frekvenciafelbontás és $\omega_\mathrm{max}=2\pi/2\Delta t$ maximális felbontható frekvencia esetén csak $\omega_\mathrm{max}/\Delta \omega\approx N$ diszkrét pontban érdemes kiértékelni a diszkrét Fourier-transzformáltat, és a definíció szerint egy adott frekvencián $~N$ művelet a szumma kiszámítása). Egy ügyes trükkel azonban jelentősen csökkenthető a számítási műveletek mennyisége. Megmutatható, hogy ha a mérési pontok száma kettő hatványa ($N=2^p$), és a frekvenciatérben $\omega_k=2\pi k/N\Delta t,\ \ \ k=0,1,...,N/2$ diszkrét körfrekvenciáknál értékeljük ki a Fourier-transzformáltat, akkor az ún. Fast Fourier Transform (FFT) algoritmus segítségével a számítási műveletek száma $N^2$-ről $N\log_2 N$-re csökken, ami nagy N esetén lényeges különbség.
A mérőműszerek jelentős része, így a laborgyakorlaton használt digitális oszcilloszkóp is az FFT algoritmus numerikus kiértékelése alapján határozza meg a mért jel spektrumát. A legtöbb esetben a műszer nem adja meg külön a spektrum valós és képzetes részét, hanem csak a Fourier-transzformált abszolút érték négyzetét látjuk. Ezen kívül a mérőműszerek általában a frekvencia, és nem a körfrekvencia függvényében adják meg a spektrumot, erre érdemes odafigyelni a mérés kiértékelésénél.
A Fourier transzformáció definiciójánál azt látjuk, hogy a Fourier spektrum komplex mennyiség. Erre azért van szükség, hogy a különböző frekvenciájú harmonikus tagok \emph{fázisát} is le tudjuk írni. Könnyen belátható, hogy amennyiben $F(t)$ páros függvény (pl. cos), akkor a Fourier spektrum tisztán valós, amennyiben pedig $F(t)$ páratlan függvény (pl. sin), akkor a Fourier spektrum tisztán képzetes. Tetszőleges $F(t)$ esetén pedig a Fourier spektrum tartalmaz valós és képzetes tagokat is\footnote{Ilyen értelemben a komplex jelölésnek az a szerepe, hogy a leírást rövidítse, egyébként kétkomponensű vektorokat kellene írnunk.}. Amennyiben a fázis ismerete nem lényeges és csak az egyes Fourier komponensek erősségére vagyunk kiváncsiak akkor a Fourier spektrum valós és képzetes részeinek négyzetösszegének gyökéből képezhetjük az ún. Fourier erősséget (\emph{Fourier magnitude}).
Egy kérdés azonban még nyitva maradt: amikor harmonikus rezgésről beszélünk gyakran mint cos, sin vagy $\mathrm{e}^{i\omega_0 t}$-ként hivatkozunk rá. Itt mi a komplex jelölés szerepe? Erre a rövid válasz az, hogy önmagában a cos vagy sin függvény nem adja meg a harmonikus rezgés frekvenciájának \emph{előjelét}. Első hallásra meglepő, hogy harmonikus rezgés frekvenciájának előjele van, azonban gondoljunk csak a mixeres lekeverésre: amennyiben RF frekvenciája kisebb mint az LO frekvenciája, a kapott IF jel alacsonyfrekvenciás komponensének fekvenciája \emph{negatív}. Az előjel elvesztésének bemutatására tekintsük először a $\cos\left( \omega_{\text{IF}}t\right)$ jelet, ennek \aref{FT_def}. képlet alapján a Fourier transzformáltja valós és tartalmaz $\pm \omega_{\text{IF}}$-nél is egy-egy pozitív csúcsot. Második példánkban tekintsük a $\sin\left( \omega_{\text{IF}}t\right)$ jelet, aminek Fourier transzformáltja képzetes és $\pm \omega_{\text{IF}}$-nél mutat egy-egy ellentétes előjelű csúcsot. Tehát egyik példában sem tudjuk a jel frekvenciájának előjelét egyértelműen meghatározni. Ezzel szemben a $\mathrm{e}^{-i\omega_{\text{IF}} t}$ Fourier transzformáltjának $\omega_{\text{IF}}$-nél (előjelhelyesen) van egy csúcsa\footnote{Azaz nincs csúcsa $-\omega_{\text{IF}}$-nél.}.
A $\mathrm{e}^{-i\omega_{\text{IF}} t}$ kifejezés valós és képzetes részei úgy viselkednek mint a trigonometrikus függvények definiciójakor használt egységkörön mozgó pont vetületei, ami foroghat pozitív és negatív körüljáráson is. Ezzel szemben külön-külön a cos és sin vetületek nem érzékenyek az egységkörön mozgó pont körüljárásának irányára.
Már csak azt a kérdést kell megválaszolnunk, hogy méréstechnikában hogyan tudjuk ezt a $\mathrm{e}^{-i\omega_{\text{IF}} t}$ komplex időfüggő mennyiséget előállítani a mért \emph{valós} jelekből. A válasz az, hogy a valós és képzetes részek a lock-in technikánál bemutatott kvadratúra detektálásból adódnak: azaz a bejövő jelet két, egymástól 90 fokban eltolt jellel keverjük le. Az így kapott két adatsort ($X(t)$ és $Y(t)$ \aref{LI_fig}. ábra jelöléseivel) \emph{tekintjük} a bejövő lekevert jel valós és képzetes részeinek: $\widetilde{X}(t)=X(t)+i Y(t)$. Az FT után szintén két adatsort kapunk \aref{FT_def}. képlet alapján:
$$
\widetilde{x}(\omega)=x(\omega)+i y(\omega)=\int_{-\infty}^{\infty} \widetilde{X}(t)\mathrm{e}^{-i\omega t}\mathrm{d}t,
$$
ezért ezt komplex vagy kétcsatornás Fourier transzformációnak nevezzük.
Ha a tagokat expliciten kiírjuk, akkor belátható, hogy e két adatsor a következőképpen adódik:
$$ x(\omega)=\int_{-\infty}^{\infty} X(t)\cos(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\sin(\omega t)\mathrm{d}t,\\ y(\omega)=\int_{-\infty}^{\infty} -X(t)\sin(\omega t)\mathrm{d}t+\int_{-\infty}^{\infty} Y(t)\cos(\omega t)\mathrm{d}t. $$
E két adatsor négyzetösszegének gyöke: $\sqrt{x(\omega)^2+y(\omega)^2}$ adja meg a különböző frekvenciájú komponensek erősségét a Fourier spektrumban. </wlatex>