„Folyadékok viszkozitásának mérése” változatai közötti eltérés

A Fizipedia wikiből
 
(2 szerkesztő 15 közbeeső változata nincs mutatva)
1. sor: 1. sor:
 
<wlatex>
 
<wlatex>
  
−
[[Kategória:Fizika BSC alapképzés]]
 
−
<!--[[Kategória:Fizika BSC alkalmazott fizika szakirány]]-->
 
−
<!--[[Kategória:Fizika BSC fizikus szakirány]]-->
 
−
<!--[[Kategória:Fizikus MSC alapképzés]]-->
 
−
<!--[[Kategória:Fizikus MSC alkalmazott fizika szakirány]]-->
 
−
<!--[[Kategória:Fizikus MSC kutatófizikus szakirány]]-->
 
−
<!--[[Kategória:Fizikus MSC nukleáris technika szakirány]]-->
 
−
<!--[[Kategória:Fizikus MSC orvosi fizika szakirány]]-->
 
 
[[Kategória:Mechanika]]  
 
[[Kategória:Mechanika]]  
 
<!--[[Kategória:Elektromosságtan]]-->  
 
<!--[[Kategória:Elektromosságtan]]-->  
24. sor: 16. sor:
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
−
[[Kategória:Fizika Tanszék]]
 
−
<!--[[Kategória:Elméleti Fizika Tanszék]]-->
 
−
<!--[[Kategória:Atomfizika Tanszék]]-->
 
−
<!--[[Kategória:Nukleáris Technikai Intézet]]-->
 
−
<!--[[Kategória:Matematika Intézet]]-->   
 
 
[[Kategória:Szerkesztő:Vankó]]
 
[[Kategória:Szerkesztő:Vankó]]
  
37. sor: 24. sor:
 
''Ennek érdekében:''
 
''Ennek érdekében:''
 
* összefoglaljuk a viszkozitással kapcsolatos elméletet,
 
* összefoglaljuk a viszkozitással kapcsolatos elméletet,
−
* ismertetjük a viszkozitás-mérés néhány módszerét,
+
* ismertetjük a viszkozitásmérés néhány módszerét,
 
* megmérjük néhány anyag viszkozitását,
 
* megmérjük néhány anyag viszkozitását,
 
* vizsgáljuk a folyadékok viszkozitásának hőmérsékletfüggését.
 
* vizsgáljuk a folyadékok viszkozitásának hőmérsékletfüggését.
 +
  
 
__TOC__
 
__TOC__
49. sor: 37. sor:
 
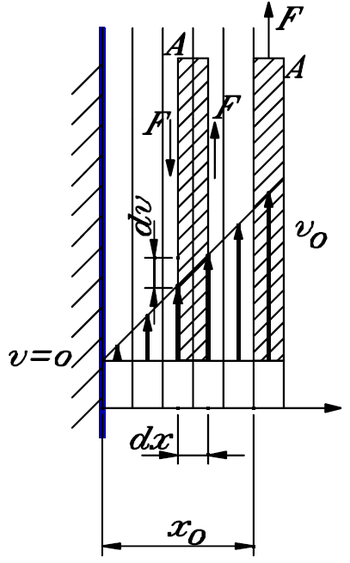
Ha a folyadékban egy álló felülethez közeli, $x_0$ távolságban levő, $A$ nagyságú, az előzővel párhuzamos felületet [[#fig:1|(1. ábra)]] $v_0$ sebességgel mozgatunk, akkor az alábbiakat tapasztaljuk:
 
Ha a folyadékban egy álló felülethez közeli, $x_0$ távolságban levő, $A$ nagyságú, az előzővel párhuzamos felületet [[#fig:1|(1. ábra)]] $v_0$ sebességgel mozgatunk, akkor az alábbiakat tapasztaljuk:
 
* Az $A$ nagyságú felület állandó $v_0$ sebességű mozgatásához állandó $F$ erő szükséges.
 
* Az $A$ nagyságú felület állandó $v_0$ sebességű mozgatásához állandó $F$ erő szükséges.
−
* Az álló és a mozgó felület közötti folyadék-részben a folyadék áramlási sebessége - $x_o$ kicsisége miatt - a felületekre merőleges $x$ távolság függvényében 0-tól $v_0$-ig gyakorlatilag lineárisan változik.
+
* Az álló és a mozgó felület közötti folyadékrészben a folyadék áramlási sebessége – $x_0$ kicsisége miatt – a felületekre merőleges $x$ távolság függvényében 0-tól $v_0$-ig gyakorlatilag lineárisan változik.
  
 
A jelenség magyarázata a kővetkező. A folyadék a vele érintkező szilárd felülethez rendszerint hozzátapad, és így a felülethez legközelebb eső folyadékrészecskék a felülettel együtt mozognak (vagy állnak). A fékezőerő így nem a folyadék és a szilárd felület között fellépő közönséges súrlódás, hanem az egyes folyadékrétegek között fellépő belső súrlódás következménye. Ez az erő a folyadékban fellépő molekuláris hatások következtében jön létre úgy, hogy a gyorsabban mozgó folyadék rétegek a szomszédos, lassabban mozgó rétegeket gyorsítani, az utóbbiak pedig az előzőket – és így közvetve a mozgó szilárd lemezt is – lassítani igyekeznek.
 
A jelenség magyarázata a kővetkező. A folyadék a vele érintkező szilárd felülethez rendszerint hozzátapad, és így a felülethez legközelebb eső folyadékrészecskék a felülettel együtt mozognak (vagy állnak). A fékezőerő így nem a folyadék és a szilárd felület között fellépő közönséges súrlódás, hanem az egyes folyadékrétegek között fellépő belső súrlódás következménye. Ez az erő a folyadékban fellépő molekuláris hatások következtében jön létre úgy, hogy a gyorsabban mozgó folyadék rétegek a szomszédos, lassabban mozgó rétegeket gyorsítani, az utóbbiak pedig az előzőket – és így közvetve a mozgó szilárd lemezt is – lassítani igyekeznek.
  
 
A vázolt jelenség kvantitatív vizsgálatából megállapítható, hogy a mozgatás irányában fekvő két szomszédos A felületű folyadékréteg között fellépő belső súrlódási erő [[#fig:1|(1. ábra)]] nagysága:
 
A vázolt jelenség kvantitatív vizsgálatából megállapítható, hogy a mozgatás irányában fekvő két szomszédos A felületű folyadékréteg között fellépő belső súrlódási erő [[#fig:1|(1. ábra)]] nagysága:
−
{{eq|F{{=}}\eta A\frac{\text{d} v}{\text{d} x},|eq:1|(1)}}
+
$$F=\eta A\frac{\text{d} v}{\text{d} x}$$
−
ahol $\frac{\text{d} v}{\text{d} x}$ a mozgásirányra merőleges sebességesés (sebesség-gradiens), $\eta$ a folyadék anyagi minőségétől függő belső súrlódási vagy viszkozitási tényező (szokás dinamikai viszkozitásnak nevezni, mértékegysége Pa s). Az [[#eq:1|(1)]] kifejezésből látható, hogy az áramló folyadékban az egymással érintkező rétegek között nyírófeszültség $(\tau)$ lép fel, melynek nagysága:
+
ahol $\text{d}v/\text{d}x$ a mozgásirányra merőleges sebességesés (sebesség-gradiens), $\eta$ a folyadék anyagi minőségétől függő belső súrlódási vagy viszkozitási tényező (szokás dinamikai viszkozitásnak nevezni, mértékegysége Pa s). A kifejezésből látható, hogy az áramló folyadékban az egymással érintkező rétegek között $(\tau)$ nyírófeszültség lép fel, melynek nagysága:
−
$$\tau=\frac{F}{A}=\eta \frac{\text{d} v}{\text{d} x}.$$
+
$$\tau=\frac{F}{A}=\eta\frac{\text{d}v}{\text{d}x}$$
−
A viszkozitás tehát azt adja meg, hogy egységnyi sebesség-gradiens esetén mekkora feszültség lép fel az egyes rétegek között. A tapasztalat szerint az anyagok viszkozitása függ a hőmérséklettől. Gázok esetében a növekvő hőmérséklettel $\eta$ növekszik, folyadékokban viszont csökken az alábbi tapasztalati tőrvény szerint:
+
A viszkozitás tehát azt adja meg, hogy egységnyi sebesség-gradiens esetén mekkora feszültség lép fel az egyes rétegek között. A tapasztalat szerint az anyagok viszkozitása függ a hőmérséklettől. Gázok esetében a növekvő hőmérséklettel $\eta$ növekszik, folyadékokban viszont csökken az alábbi tapasztalati törvény szerint:
−
$$\eta (T)=A\exp\left(\frac{B}{RT}\right).$$
+
$$\eta (T)=A\exp\left(\frac{B}{RT}\right)$$
 
Ez az Eyring-Andrade formula, ahol $A$ és $B$ a folyadékra jellemző állandók, $R$ pedig a gázállandó.  
 
Ez az Eyring-Andrade formula, ahol $A$ és $B$ a folyadékra jellemző állandók, $R$ pedig a gázállandó.  
  
67. sor: 55. sor:
 
===Belső súrlódási együttható mérése vékony csövön történő áramoltatással===
 
===Belső súrlódási együttható mérése vékony csövön történő áramoltatással===
  
−
Ha a mérendő folyadékot kis átmérőjű hengeres csövön, nem túl nagy nyomáskülönbség mellett - azaz nem túl nagy áramlási sebességgel - áramoltatjuk át, akkor az áramlás lamináris lesz. (Egy $r$ sugarú csőben lamináris a $\rho$ sűrűségű folyadék $v$ sebességű áramlása, ha a Reynolds szám $Re=\frac{\rho rv}{\eta}<1160$.) Ebben az esetben az $r$ sugarú, $l$ hosszúságú csövön $t$ idő alatt átáramló folyadéktérfogat a Hagen-Poiseuille-féle törvény szerint:
+
Ha a mérendő folyadékot kis átmérőjű hengeres csövön, nem túl nagy nyomáskülönbség mellett – azaz nem túl nagy áramlási sebességgel – áramoltatjuk át, akkor az áramlás lamináris lesz. (Egy $r$ sugarú csőben lamináris a $\rho$ sűrűségű folyadék $v$ sebességű áramlása, ha a Reynolds-szám $Re=\rho rv/\eta<1160$.) Ebben az esetben az $r$ sugarú, $l$ hosszúságú csövön $t$ idő alatt átáramló folyadéktérfogat a Hagen-Poiseuille-féle törvény szerint:
−
{{eq|v{{=}}\frac{\pi(p_1-p_2)}{8\eta l}r^4t,|eq:2|(2)}}
+
$$v=\frac{\pi(p_1-p_2)}{8\eta l}r^4t$$
−
ahol $p_1$ és $p_2$ a cső két végén a nyomás értéke. Tehát a $t$ idő alatt átáramlott folyadékmennyiség, a nyomáskülönbség, és a geometriai adatok $(r, l)$ ismeretében az $\eta$ viszkozitás [[#eq:2|(2)]] alapján meghatározható. A fenti összefüggésen alapul többek közt az Ostwald-féle kapilláris viszkoziméter.
+
ahol $p_1$ és $p_2$ a cső két végén a nyomás értéke. Tehát a $t$ idő alatt átáramlott folyadékmennyiség, a nyomáskülönbség, és a geometriai adatok ($r$, $l$) ismeretében az $\eta$ viszkozitás meghatározható. A fenti összefüggésen alapul többek közt az Ostwald-féle kapilláris viszkoziméter.
  
 
====Az Ostwald-féle kapilláris viszkoziméter====
 
====Az Ostwald-féle kapilláris viszkoziméter====
  
−
{{fig|Folyadékok_viszkozitásának_mérése_2.png|fig:2|2.ábra}}
+
{{fig2|Viszkozitas.png|fig:2|2.ábra}}
  
−
A mérőeszköz a [[#fig:2|2. ábrán]] látható. A mérést úgy végezzük, hogy a készülékbe töltött folyadékot a kapilláris szárú ágban levő $V$ térfogatú gömb fölé az "a" jelig szívatjuk. Ezután mérjük azt az időt, amely alatt a meniszkusz ettől a jeltől a gömb alatti "b" jelig süllyed. Ha a $\rho$ sűrűségű folyadék szintkülönbsége az eszköz két ágában kezdetben $h_l$, a végső pillanatban pedig $h_2$, akkor a kifolyás ideje alatt a közepes nyomás $p=\rho g\frac{h_1+h_2}{2}$, ahol $g$ a nehézségi gyorsulás. Abszolút méréshez a $V$, $r$, $l$, $h_1$ és $h_2$ ismerete szükséges. Relatív mérésnél elegendő, ha ugyanazon készülékben a $\rho$ sűrűségű vizsgálandó folyadék $t$ kifolyási idején kívül meghatározzuk egy ismert sűrűségű és viszkozitású ($\rho_0$ és $\eta0$) folyadék $t_0$ kifolyási idejét. Ezen az adatokból a viszkozitás az
+
A mérőeszköz a [[#fig:2|2. ábrán]] látható. A mérést úgy végezzük, hogy a készülékbe töltött folyadékot a kapilláris szárú ágban levő $V$ térfogatú gömb fölé az „a” jelig szívatjuk. Ezután mérjük azt az időt, amely alatt a meniszkusz ettől a jeltől a gömb alatti „b” jelig süllyed. Ha a $\rho$ sűrűségű folyadék szintkülönbsége az eszköz két ágában kezdetben $h_l$, a végső pillanatban pedig $h_2$, akkor a kifolyás ideje alatt a közepes nyomás $p=\rho g\left(h_1+h_2\right)/2$, ahol $g$ a nehézségi gyorsulás. Abszolút méréshez a $V$, $r$, $l$, $h_1$ és $h_2$ ismerete szükséges. Relatív mérésnél elegendő, ha ugyanazon készülékben a $\rho$ sűrűségű vizsgálandó folyadék $t$ kifolyási idején kívül meghatározzuk egy ismert sűrűségű és viszkozitású ($\rho_0$ és $\eta_0$) folyadék $t_0$ kifolyási idejét. Ezen adatokból a viszkozitás az
 
$$\frac{\eta}{\eta_0}=\frac{\rho t}{\rho_0t_0}$$
 
$$\frac{\eta}{\eta_0}=\frac{\rho t}{\rho_0t_0}$$
 
összefüggés alapján számítható.
 
összefüggés alapján számítható.
  
−
===Viszkozitásmérés Stokes törvénye alapján===
+
===Viszkozitásmérés a Stokes-törvény alapján===
  
 
Stokes törvénye értelmében az $\eta$ viszkozitású, homogén folyadékban egyenletes sebességgel haladó $r$ sugarú golyóra a mozgás irányával szemben
 
Stokes törvénye értelmében az $\eta$ viszkozitású, homogén folyadékban egyenletes sebességgel haladó $r$ sugarú golyóra a mozgás irányával szemben
−
{{eq|F{{=}}6\pi\eta rv|eq:3|(3)}}
+
$$F=6\pi\eta rv$$
 
nagyságú, a mozgást akadályozó erő hat. Folyadékban, nehézségi erő hatására függőlegesen eső golyó sebessége addig növekszik, míg a mozgást akadályozó erő egyenlő nem lesz a nehézségi erő és a felhajtóerő különbségével. Az erők egyensúlyának beállása után a golyó egyenletes sebességgel esik. Az erők egyensúlyát kifejező egyenlet:
 
nagyságú, a mozgást akadályozó erő hat. Folyadékban, nehézségi erő hatására függőlegesen eső golyó sebessége addig növekszik, míg a mozgást akadályozó erő egyenlő nem lesz a nehézségi erő és a felhajtóerő különbségével. Az erők egyensúlyának beállása után a golyó egyenletes sebességgel esik. Az erők egyensúlyát kifejező egyenlet:
−
$$6\pi\eta rv=\frac{4}{3}\pi r^3(\rho_\text{g}-\rho_\text{k})g,$$
+
$$6\pi\eta rv=\frac{4}{3}\pi r^3(\rho_g-\rho_k)g$$
−
ahol $\rho_\text{g}$ a golyó $\rho_\text{k}$ pedig a közeg sűrűsége, $r$ a golyó sugara, $v$ az egyenletes mozgás sebessége. A [[#eq:3|(3)]] kifejezés átrendezése és az $L$ hosszúságú út megtételéhez szükséges $t$ idő bevezetése után $\eta$-ra az alábbi összefüggést kapjuk:
+
ahol $\rho_g$ a golyó $\rho_k$ pedig a közeg sűrűsége, $r$ a golyó sugara, $v$ az egyenletes mozgás sebessége. A kifejezés átrendezése és az $L$ hosszúságú út megtételéhez szükséges $t$ idő bevezetése után $\eta$-ra az alábbi összefüggést kapjuk:
−
{{eq|\eta{{=}}\frac{2}{9}r^2(\rho_\text{g}-\rho_\text{k})g\frac{t}{L},|eq:4|(4)}}
+
$$\eta=\frac{2}{9}r^2(\rho_g-\rho_k)g\frac{t}{L}$$
 
melynek segítségével $t$ és $L$ mérése, valamint a többi paraméter ismerete esetén $\eta$ meghatározható.
 
melynek segítségével $t$ és $L$ mérése, valamint a többi paraméter ismerete esetén $\eta$ meghatározható.
  
−
A Stokes-törvény csak kis Reynolds számú ($Re<1$) lamináris áramlás esetére érvényes és csak akkor, ha a golyó végtelen kiterjedésűnek és homogénnek tekinthető közegben mozog. Ha a golyó egy $R$ sugarú függőleges henger belsejében esik, akkor a mozgást gátló erő az alábbiak szerint módosul:
+
A Stokes-törvény csak kis Reynolds-számú ($Re<1$) lamináris áramlás esetére érvényes és csak akkor, ha a golyó végtelen kiterjedésűnek és homogénnek tekinthető közegben mozog. Ha a golyó egy $R$ sugarú függőleges henger belsejében esik, akkor a mozgást gátló erő az alábbiak szerint módosul:
−
$$F=6\pi\eta rv\left(1+2.4\frac{r}{R}\right).$$ (9)
+
$$F=6\pi\eta rv\left(1+2,4\frac{r}{R}\right)$$
−
Ennek alapján a viszkozitást [[#eq:4|(4)]] helyett az alábbi formula szolgáltatja:
+
Ennek alapján a viszkozitást a korábbi helyett az alábbi formula szolgáltatja:
−
$$\eta=\frac{2}{9}r^2(\rho_\text{g}-\rho_\text{k})g\frac{t}{L\left(1+2.4\frac{r}{R}\right)}.$$ (10)
+
$$\eta=\frac{2}{9}r^2(\rho_g-\rho_k)g\frac{t}{L\left(1+2,4\frac{r}{R}\right)}$$
  
 
==Mérési feladatok==
 
==Mérési feladatok==
 +
 +
[[A méréshez rendelkezésre álló eszközök: Folyadékok viszkozitásának mérése|A méréshez rendelkezésre álló eszközök]]
  
 
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
 
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
 +
 +
*''A mérés három, összetartozó részből áll. Az olaj viszkozitását olajba ejtett apró golyók segítségével, a Stokes-törvény alapján mérik. Ez a mérés megadja az olaj viszkozitását szobahőmérsékleten. Az egyik Ostwald-féle viszkoziméterrel a szobahőmérsékletű olaj és a szobahőmérsékletű víz viszkozitásának arányát lehet megmérni. A másik Ostwald-viszkoziméterrel pedig a hideg víz viszkozitását lehet meghatározni a szobahőmérsékletű vízhez viszonyítva. Felhasználva az olaj viszkozitásának mért értékét meghatározható a szobahőmérsékletű víz viszkozitása, majd ebből a hideg víz viszkozitása a hőmérséklet függvényében. Ez alapján pedig már meghatározhatók az Eyring-Andrade formulában szereplő állandók''
 +
*''A hibaszámításban ennek megfelelően az egyes mérések hibáival kell tovább számolni a következő méréseknél.''
  
 
'''1.''' Mérje meg az étolaj viszkozitását a Stokes-törvény alapján!
 
'''1.''' Mérje meg az étolaj viszkozitását a Stokes-törvény alapján!
  
−
A mérés függőleges helyzetű üvegcsőben süllyedő golyók megfigyelésével történik. A golyót a folyadék felszínéről, a henger tengelye mentén óvatosan indítsa el! A mérést akkor kezdje, mikor az állandósult sebesség kialakult! Ez a folyadék felszíne alatt néhány cm-rel történik meg. A sebességmérést az edény alja fölött ugyanennyivel fejezze be! Mérje meg a golyók átmérőjét és tömegét, majd számítsa ki sűrűségüket! Az olaj sűrűségét úszó sűrűségmérővel határozza meg!
+
*''Mielőtt mérni kezd, becsülje meg (pusztán szemrevételezés alapján) egy kis golyó tömegét!''
 +
**''Körülbelül mekkora az átmérője? Ebből közelítő fejszámolással határozza meg a térfogatát!''
 +
**''Milyen anyagból lehet? (Olajban, vízben elsüllyed.) Körülbelül mekkora lehet a sűrűsége?''
 +
**''Mekkora egy golyó körülbelüli tömege? (Összehasonlításképp: az ékszerészmérleg mérési hibája legalább 0,01 g.)''
 +
*''Az olaj viszkozitásához mérni kell:''
 +
**''az olaj sűrűségét úszó sűrűségmérővel (használat után az olajat le kell törölni)''
 +
**''golyók sűrűségét: ehhez 100-200 db golyót kell leszámolni, és ékszerészmérleggel megmérni a tömegüket, valamint 10-20 golyó átmérőjét kell megmérni''
 +
**''cső átmérőjét tolómérővel (korrekció!)''
 +
**''azt a távolságot, amin a golyók esését mérik''
 +
**''beejtendő golyók (10-20 db) átmérőjét csavarmikrométerrel''
 +
**''esés idejét''
 +
A golyót a folyadék felszínéről, a henger tengelye mentén óvatosan indítsa el! A mérést akkor kezdje, mikor az állandósult sebesség kialakult! Ez a folyadék felszíne alatt néhány cm-rel történik meg. A sebességmérést az edény alja fölött ugyanennyivel fejezze be!
 +
*''Célszerű az egyes golyók mért átmérő és idő értéke alapján viszkozitást számolni, majd ezeket az eredményeket átlagolni. Miért jobb ez, mint az átlagos átmérőből és az átlagos esési időből számolni a viszkozitást?''
  
 
'''2.''' Viszkozitás mérése az Ostwald-féle módszer segítségével
 
'''2.''' Viszkozitás mérése az Ostwald-féle módszer segítségével
  
−
Határozza meg az Ostwald-féle módszer segítségével a víz viszkozitását szobahőmérséklet és 0 °C között víz és étolaj mintákon végzett mérésekkel! Ábrázolja a víz viszkozitását a hőmérséklet függvényében! Határozza meg az Eyring-Andrade formulában szereplő A és B paramétereket!
+
Határozza meg az Ostwald-viszkoziméterek segítségével a víz viszkozitását szobahőmérséklet és 0 °C között víz és étolaj mintákon végzett mérésekkel! Ábrázolja a víz viszkozitását a hőmérséklet függvényében! Határozza meg az Eyring-Andrade formulában szereplő $A$ és $B$ paramétereket!
 +
 
 +
Az Ostvald-féle viszkoziméterrel – a kapilláris adatainak hiányában – csak relatív méréseket lehet végezni. Az abszolút eredményekhez használja fel az étolaj viszkozitásának az 1. mérésben kapott értékét!
 +
 
 +
Az egyik eszköz segítségével előbb a desztillált vízzel mérje a kifolyási időt (szobahőmérsékleten, ötször-tízszer). Ezután a viszkozimétert alkohollal kétszer át kell öblíteni, és akváriummotorral levegőt átszívatva ki kell szárítani. (Ehhez kérje a mérésvezető segítségét!) Ezután olajjal feltöltve a kifolyási időket ismét határozza meg (legalább kétszer-háromszor)!
 +
*''Az Ostwald-viszkoziméterben a vizet a vékonyabb szárhoz csatlakozó műanyag csővel a felső jel fölé kell szívni, majd a lefolyási időt stopperrel mérni. Amennyiben a viszkoziméterben olaj van, felszívás helyett sűrített levegővel lehet a folyadékot felfújni (ha kell, kérjenek segítséget!)''
  
−
Az Ostvald-féle viszkoziméterrel – a kapilláris adatainak hiányában – csak relatív méréseket lehet végezni. Az abszolút eredményekhez használja fel az étolaj viszkozitásának az [[#Mérje meg az étolaj viszkozitását a Stokes-törvény alapján!|1. mérésben]] kapott értékét!
+
A másik (vékonyabb kapillárisú) eszközzel a desztillált víz kifolyási idejét mérje sok alkalommal, szobahőmérsékletről indulva, fokozatosan 0 °C-ig hűtve.
−
Az egyik eszköz segítségével előbb a desztillált víznél mérje a kifolyási időt (szobahőmérsékleten, legalább ötször), majd a viszkozimétert alkohollal kétszer át kell öblíteni, és akváriummotorral levegőt átszívatva ki kell szárítani. (Kérje a mérésvezető segítségét!) Ezután olajjal feltöltve a kifolyási időket ismét határozza meg! A másik eszköznél a desztillált víz kifolyási idejét mérje szobahőmérsékletről indulva, fokozatosan 0 °C-ig hűtve.  
+
*''Folyamatos felszívással-leengedéssel mérjék a lefolyási időt, miközben a főzőpohárban lévő vizet jég bedobásával és keveréssel folyamatosan hűtik. A keverő fordulatszámát ne állítsák túl nagyra, mert eltörheti a viszkozimétert.''
 +
*''Figyelem! A két viszkoziméter paraméterei eltérők!''
  
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2016. szeptember 7., 17:35-kori változata


A mérés célja:

  • elmélyíteni a viszkozitással kapcsolatos ismereteket,
  • ismertetni néhány viszkozitás mérési eljárást.

Ennek érdekében:

  • összefoglaljuk a viszkozitással kapcsolatos elméletet,
  • ismertetjük a viszkozitásmérés néhány módszerét,
  • megmérjük néhány anyag viszkozitását,
  • vizsgáljuk a folyadékok viszkozitásának hőmérsékletfüggését.


Tartalomjegyzék


Elméleti összefoglaló

1.ábra

Ha a folyadékban egy álló felülethez közeli, 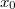\setbox0\hbox{$x_0$}% \message{//depth:\the\dp0//}% \box0% távolságban levő, \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% nagyságú, az előzővel párhuzamos felületet (1. ábra) 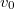\setbox0\hbox{$v_0$}% \message{//depth:\the\dp0//}% \box0% sebességgel mozgatunk, akkor az alábbiakat tapasztaljuk:

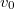  • Az \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% nagyságú felület állandó \setbox0\hbox{$v_0$}% \message{//depth:\the\dp0//}% \box0% sebességű mozgatásához állandó \setbox0\hbox{$F$}% \message{//depth:\the\dp0//}% \box0% erő szükséges.
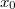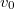  • Az álló és a mozgó felület közötti folyadékrészben a folyadék áramlási sebessége – \setbox0\hbox{$x_0$}% \message{//depth:\the\dp0//}% \box0% kicsisége miatt – a felületekre merőleges \setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0% távolság függvényében 0-tól \setbox0\hbox{$v_0$}% \message{//depth:\the\dp0//}% \box0%-ig gyakorlatilag lineárisan változik.

A jelenség magyarázata a kővetkező. A folyadék a vele érintkező szilárd felülethez rendszerint hozzátapad, és így a felülethez legközelebb eső folyadékrészecskék a felülettel együtt mozognak (vagy állnak). A fékezőerő így nem a folyadék és a szilárd felület között fellépő közönséges súrlódás, hanem az egyes folyadékrétegek között fellépő belső súrlódás következménye. Ez az erő a folyadékban fellépő molekuláris hatások következtében jön létre úgy, hogy a gyorsabban mozgó folyadék rétegek a szomszédos, lassabban mozgó rétegeket gyorsítani, az utóbbiak pedig az előzőket – és így közvetve a mozgó szilárd lemezt is – lassítani igyekeznek.

A vázolt jelenség kvantitatív vizsgálatából megállapítható, hogy a mozgatás irányában fekvő két szomszédos A felületű folyadékréteg között fellépő belső súrlódási erő (1. ábra) nagysága:

\[F=\eta A\frac{\text{d} v}{\text{d} x}\]

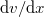ahol \setbox0\hbox{$\text{d}v/\text{d}x$}% \message{//depth:\the\dp0//}% \box0% a mozgásirányra merőleges sebességesés (sebesség-gradiens), \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% a folyadék anyagi minőségétől függő belső súrlódási vagy viszkozitási tényező (szokás dinamikai viszkozitásnak nevezni, mértékegysége Pa s). 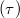A kifejezésből látható, hogy az áramló folyadékban az egymással érintkező rétegek között \setbox0\hbox{$(\tau)$}% \message{//depth:\the\dp0//}% \box0% nyírófeszültség lép fel, melynek nagysága:

\[\tau=\frac{F}{A}=\eta\frac{\text{d}v}{\text{d}x}\]

A viszkozitás tehát azt adja meg, hogy egységnyi sebesség-gradiens esetén mekkora feszültség lép fel az egyes rétegek között. A tapasztalat szerint az anyagok viszkozitása függ a hőmérséklettől. Gázok esetében a növekvő hőmérséklettel \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% növekszik, folyadékokban viszont csökken az alábbi tapasztalati törvény szerint:

\[\eta (T)=A\exp\left(\frac{B}{RT}\right)\]

Ez az Eyring-Andrade formula, ahol \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% a folyadékra jellemző állandók, \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% pedig a gázállandó.

Folyadékok viszkozitásának mérésére számos eljárás létezik. Az alábbiakban két mérési módszert mutatunk be.

Mérési módszerek

Belső súrlódási együttható mérése vékony csövön történő áramoltatással

Ha a mérendő folyadékot kis átmérőjű hengeres csövön, nem túl nagy nyomáskülönbség mellett – azaz nem túl nagy áramlási sebességgel – áramoltatjuk át, akkor az áramlás lamináris lesz. 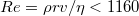(Egy \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% sugarú csőben lamináris a \setbox0\hbox{$\rho$}% \message{//depth:\the\dp0//}% \box0% sűrűségű folyadék \setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0% sebességű áramlása, ha a Reynolds-szám \setbox0\hbox{$Re=\rho rv/\eta<1160$}% \message{//depth:\the\dp0//}% \box0%.) Ebben az esetben az \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% sugarú, \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0% hosszúságú csövön \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% idő alatt átáramló folyadéktérfogat a Hagen-Poiseuille-féle törvény szerint:

\[v=\frac{\pi(p_1-p_2)}{8\eta l}r^4t\]

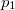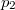ahol \setbox0\hbox{$p_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$p_2$}% \message{//depth:\the\dp0//}% \box0% a cső két végén a nyomás értéke. Tehát a \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% idő alatt átáramlott folyadékmennyiség, a nyomáskülönbség, és a geometriai adatok (\setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%) ismeretében az \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% viszkozitás meghatározható. A fenti összefüggésen alapul többek közt az Ostwald-féle kapilláris viszkoziméter.

Az Ostwald-féle kapilláris viszkoziméter

2.ábra

A mérőeszköz a 2. ábrán látható. A mérést úgy végezzük, hogy a készülékbe töltött folyadékot a kapilláris szárú ágban levő \setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0% térfogatú gömb fölé az „a” jelig szívatjuk. Ezután mérjük azt az időt, amely alatt a meniszkusz ettől a jeltől a gömb alatti „b” jelig süllyed. 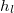Ha a \setbox0\hbox{$\rho$}% \message{//depth:\the\dp0//}% \box0% sűrűségű folyadék szintkülönbsége az eszköz két ágában kezdetben \setbox0\hbox{$h_l$}% \message{//depth:\the\dp0//}% \box0%, a végső pillanatban pedig 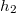\setbox0\hbox{$h_2$}% \message{//depth:\the\dp0//}% \box0%, akkor a kifolyás ideje alatt a közepes nyomás 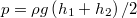\setbox0\hbox{$p=\rho g\left(h_1+h_2\right)/2$}% \message{//depth:\the\dp0//}% \box0%, ahol 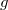\setbox0\hbox{$g$}% \message{//depth:\the\dp0//}% \box0% a nehézségi gyorsulás. 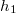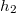Abszolút méréshez a \setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$l$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$h_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$h_2$}% \message{//depth:\the\dp0//}% \box0% ismerete szükséges. 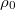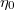Relatív mérésnél elegendő, ha ugyanazon készülékben a \setbox0\hbox{$\rho$}% \message{//depth:\the\dp0//}% \box0% sűrűségű vizsgálandó folyadék \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% kifolyási idején kívül meghatározzuk egy ismert sűrűségű és viszkozitású (\setbox0\hbox{$\rho_0$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$\eta_0$}% \message{//depth:\the\dp0//}% \box0%) folyadék \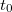setbox0\hbox{$t_0$}% \message{//depth:\the\dp0//}% \box0% kifolyási idejét. Ezen adatokból a viszkozitás az

\[\frac{\eta}{\eta_0}=\frac{\rho t}{\rho_0t_0}\]

összefüggés alapján számítható.

Viszkozitásmérés a Stokes-törvény alapján

Stokes törvénye értelmében az \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% viszkozitású, homogén folyadékban egyenletes sebességgel haladó \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% sugarú golyóra a mozgás irányával szemben

\[F=6\pi\eta rv\]

nagyságú, a mozgást akadályozó erő hat. Folyadékban, nehézségi erő hatására függőlegesen eső golyó sebessége addig növekszik, míg a mozgást akadályozó erő egyenlő nem lesz a nehézségi erő és a felhajtóerő különbségével. Az erők egyensúlyának beállása után a golyó egyenletes sebességgel esik. Az erők egyensúlyát kifejező egyenlet:

\[6\pi\eta rv=\frac{4}{3}\pi r^3(\rho_g-\rho_k)g\]

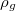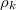ahol \setbox0\hbox{$\rho_g$}% \message{//depth:\the\dp0//}% \box0% a golyó \setbox0\hbox{$\rho_k$}% \message{//depth:\the\dp0//}% \box0% pedig a közeg sűrűsége, \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% a golyó sugara, \setbox0\hbox{$v$}% \message{//depth:\the\dp0//}% \box0% az egyenletes mozgás sebessége. A kifejezés átrendezése és az \setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0% hosszúságú út megtételéhez szükséges \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% idő bevezetése után \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0%-ra az alábbi összefüggést kapjuk:

\[\eta=\frac{2}{9}r^2(\rho_g-\rho_k)g\frac{t}{L}\]

melynek segítségével \setbox0\hbox{$t$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0% mérése, valamint a többi paraméter ismerete esetén \setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% meghatározható.

A Stokes-törvény csak kis Reynolds-számú (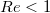\setbox0\hbox{$Re<1$}% \message{//depth:\the\dp0//}% \box0%) lamináris áramlás esetére érvényes és csak akkor, ha a golyó végtelen kiterjedésűnek és homogénnek tekinthető közegben mozog. Ha a golyó egy \setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0% sugarú függőleges henger belsejében esik, akkor a mozgást gátló erő az alábbiak szerint módosul:

\[F=6\pi\eta rv\left(1+2,4\frac{r}{R}\right)\]

Ennek alapján a viszkozitást a korábbi helyett az alábbi formula szolgáltatja:

\[\eta=\frac{2}{9}r^2(\rho_g-\rho_k)g\frac{t}{L\left(1+2,4\frac{r}{R}\right)}\]

Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
  • A mérés három, összetartozó részből áll. Az olaj viszkozitását olajba ejtett apró golyók segítségével, a Stokes-törvény alapján mérik. Ez a mérés megadja az olaj viszkozitását szobahőmérsékleten. Az egyik Ostwald-féle viszkoziméterrel a szobahőmérsékletű olaj és a szobahőmérsékletű víz viszkozitásának arányát lehet megmérni. A másik Ostwald-viszkoziméterrel pedig a hideg víz viszkozitását lehet meghatározni a szobahőmérsékletű vízhez viszonyítva. Felhasználva az olaj viszkozitásának mért értékét meghatározható a szobahőmérsékletű víz viszkozitása, majd ebből a hideg víz viszkozitása a hőmérséklet függvényében. Ez alapján pedig már meghatározhatók az Eyring-Andrade formulában szereplő állandók
  • A hibaszámításban ennek megfelelően az egyes mérések hibáival kell tovább számolni a következő méréseknél.

1. Mérje meg az étolaj viszkozitását a Stokes-törvény alapján!

  • Mielőtt mérni kezd, becsülje meg (pusztán szemrevételezés alapján) egy kis golyó tömegét!
    • Körülbelül mekkora az átmérője? Ebből közelítő fejszámolással határozza meg a térfogatát!
    • Milyen anyagból lehet? (Olajban, vízben elsüllyed.) Körülbelül mekkora lehet a sűrűsége?
    • Mekkora egy golyó körülbelüli tömege? (Összehasonlításképp: az ékszerészmérleg mérési hibája legalább 0,01 g.)
  • Az olaj viszkozitásához mérni kell:
    • az olaj sűrűségét úszó sűrűségmérővel (használat után az olajat le kell törölni)
    • golyók sűrűségét: ehhez 100-200 db golyót kell leszámolni, és ékszerészmérleggel megmérni a tömegüket, valamint 10-20 golyó átmérőjét kell megmérni
    • cső átmérőjét tolómérővel (korrekció!)
    • azt a távolságot, amin a golyók esését mérik
    • beejtendő golyók (10-20 db) átmérőjét csavarmikrométerrel
    • esés idejét

A golyót a folyadék felszínéről, a henger tengelye mentén óvatosan indítsa el! A mérést akkor kezdje, mikor az állandósult sebesség kialakult! Ez a folyadék felszíne alatt néhány cm-rel történik meg. A sebességmérést az edény alja fölött ugyanennyivel fejezze be!

  • Célszerű az egyes golyók mért átmérő és idő értéke alapján viszkozitást számolni, majd ezeket az eredményeket átlagolni. Miért jobb ez, mint az átlagos átmérőből és az átlagos esési időből számolni a viszkozitást?

2. Viszkozitás mérése az Ostwald-féle módszer segítségével

Határozza meg az Ostwald-viszkoziméterek segítségével a víz viszkozitását szobahőmérséklet és 0 °C között víz és étolaj mintákon végzett mérésekkel! Ábrázolja a víz viszkozitását a hőmérséklet függvényében! Határozza meg az Eyring-Andrade formulában szereplő \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$B$}% \message{//depth:\the\dp0//}% \box0% paramétereket!

Az Ostvald-féle viszkoziméterrel – a kapilláris adatainak hiányában – csak relatív méréseket lehet végezni. Az abszolút eredményekhez használja fel az étolaj viszkozitásának az 1. mérésben kapott értékét!

Az egyik eszköz segítségével előbb a desztillált vízzel mérje a kifolyási időt (szobahőmérsékleten, ötször-tízszer). Ezután a viszkozimétert alkohollal kétszer át kell öblíteni, és akváriummotorral levegőt átszívatva ki kell szárítani. (Ehhez kérje a mérésvezető segítségét!) Ezután olajjal feltöltve a kifolyási időket ismét határozza meg (legalább kétszer-háromszor)!

  • Az Ostwald-viszkoziméterben a vizet a vékonyabb szárhoz csatlakozó műanyag csővel a felső jel fölé kell szívni, majd a lefolyási időt stopperrel mérni. Amennyiben a viszkoziméterben olaj van, felszívás helyett sűrített levegővel lehet a folyadékot felfújni (ha kell, kérjenek segítséget!)

A másik (vékonyabb kapillárisú) eszközzel a desztillált víz kifolyási idejét mérje sok alkalommal, szobahőmérsékletről indulva, fokozatosan 0 °C-ig hűtve.

  • Folyamatos felszívással-leengedéssel mérjék a lefolyási időt, miközben a főzőpohárban lévő vizet jég bedobásával és keveréssel folyamatosan hűtik. A keverő fordulatszámát ne állítsák túl nagyra, mert eltörheti a viszkozimétert.
  • Figyelem! A két viszkoziméter paraméterei eltérők!


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Folyadékok_viszkozitásának_mérése&oldid=19098”