„Termikus neutronfluxus meghatározása aktivációs módszerrel” változatai közötti eltérés
(Új oldal, tartalma: „<wlatex> __TOC__ == BEVEZETÉS == Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása …”) |
|||
| (egy szerkesztő 13 közbeeső változata nincs mutatva) | |||
| 5. sor: | 5. sor: | ||
== BEVEZETÉS == | == BEVEZETÉS == | ||
| − | Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása megfelelő számlálórendszer segítségével mérhető. A keletkező ''fajlagos aktivitás'' | + | Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása megfelelő számlálórendszer segítségével mérhető. A keletkező ''fajlagos aktivitás''<ref>A besugárzott anyag egy atomjára [vagy tömegegységére] vonatkoztatott aktivitás.</ref> a besugárzás helyén uralkodó neutronfluxustól és a besugárzott anyag ''aktivációs hatáskeresztmetszeté''től függ. A mérés célja a neutronfluxus meghatározása. Szigorúan véve azonban ''nincs olyan módszer, amely lehetővé tenné a neutronfluxus közvetlen mérését.'' Legfeljebb arról lehet szó, hogy a neutronfluxusra a mért fajlagos aktivitásból valamilyen feltevések mellett többé-kevésbé pontos becslést adjunk. Amilyen pontosan ismerjük az aktivációs hatáskeresztmetszetet, olyan pontosan tudjuk a neutronfluxust meghatározni. Minthogy számos olyan anyag van, melyeknek aktivációs hatáskeresztmetszete más-más módon függ a neutronenergiától, ezzel a módszerrel a neutronok energia szerinti eloszlásáról is nyerhetünk némi információt. |
A jelen mérés keretében aktivációs detektorok felhasználásával fogjuk a termikus neutronfluxus értékét közelítőleg meghatározni a BME oktatóreaktorának aktív zónájában. A mérés két részből áll: a termikus neutronfluxus abszolút értékének becslése és helyfüggésének vizsgálata. A mérés elvének megértéséhez előbb a reaktorelmélet számos tételét kell megismernünk. Ezek részletesebben megtalálhatók az [1-4] kézikönyvekben. | A jelen mérés keretében aktivációs detektorok felhasználásával fogjuk a termikus neutronfluxus értékét közelítőleg meghatározni a BME oktatóreaktorának aktív zónájában. A mérés két részből áll: a termikus neutronfluxus abszolút értékének becslése és helyfüggésének vizsgálata. A mérés elvének megértéséhez előbb a reaktorelmélet számos tételét kell megismernünk. Ezek részletesebben megtalálhatók az [1-4] kézikönyvekben. | ||
| 13. sor: | 13. sor: | ||
===Neutronspektrum, neutronfluxus eloszlása termikus reaktorokban=== | ===Neutronspektrum, neutronfluxus eloszlása termikus reaktorokban=== | ||
| − | Maghasadásban gyors neutronok keletkeznek, energia-eloszlásuk az 1. ábrán látható. Termikus reaktorokban a gyors neutronok - elsősorban a moderátor atommagjaival való ütközések révén - fokozatosan lelassulnak, és | + | Maghasadásban gyors neutronok keletkeznek, energia-eloszlásuk az 1. ábrán látható. Termikus reaktorokban a gyors neutronok - elsősorban a moderátor atommagjaival való ütközések révén - fokozatosan lelassulnak, és a 2. ábrán sematikusan bemutatott neutronspektrum alakul ki. Legyen az ${E}$ és ${E+dE}$ közé eső energiájú neutronok sűrűsége a reaktor ${\underline r}$ pontjának közelében ${n(\underline r,E)dE}$. Ennek felhasználásával a ''neutronfluxus'' definíciója: |
| − | a 2. ábrán sematikusan bemutatott | + | |
| − | + | ||
| − | definíciója: | + | |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi(\underline r, E) = vn(\underline r,E) \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi(\underline r, E) = vn(\underline r,E), \]</latex></div> |
| align = "right" | <span id="eq2"> (1) </span> | | align = "right" | <span id="eq2"> (1) </span> | ||
|} | |} | ||
| 31. sor: | 28. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi(\underline r, E) = \frac{E}{(kT)^2}\exp\Bigg\{-\frac{E}{kT} \Bigg\} \qquad \qquad E \leq E_{th} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi(\underline r, E) = \frac{E}{(kT)^2}\exp\Bigg\{-\frac{E}{kT} \Bigg\}, \qquad \qquad E \leq E_{th} \]</latex></div> |
| align = "right" | <span id="eq2"> (2) </span> | | align = "right" | <span id="eq2"> (2) </span> | ||
|} | |} | ||
| − | ahol ${E_{th}}$ a termikus tartomány - többé-kevésbé önkényesen megválasztott - felső határa (általában 0,625 eV), ${k}$ a Boltzmann-állandó és ${T}$ a termikus neutronspektrumot jellemző, hőmérséklet dimenziójú mennyiség. Általában '' | + | ahol ${E_{th}}$ a termikus tartomány - többé-kevésbé önkényesen megválasztott - felső határa (általában 0,625 eV), ${k}$ a Boltzmann-állandó és ${T}$ a termikus neutronspektrumot jellemző, hőmérséklet dimenziójú mennyiség.<ref>Általában ''neutronhőmérséklet''nek szoktuk nevezni, amely némileg magasabb, mint a reaktor abszolút hőmérséklete.</ref> |
{| | {| | ||
| 41. sor: | 38. sor: | ||
|} | |} | ||
| − | Amikor ''termikus | + | Amikor ''termikus neutronfluxusról'' beszélünk, ezen az alábbi integrált értjük: |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(\underline r) = \int\limits_{0}^{E_{th}}\Phi(\underline r,E)dE \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(\underline r) = \int\limits_{0}^{E_{th}}\Phi(\underline r,E)dE, \]</latex></div> |
| align = "right" | <span id="eq2"> (3) </span> | | align = "right" | <span id="eq2"> (3) </span> | ||
|} | |} | ||
| 55. sor: | 52. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(\underline r) = v.n_{th}(\underline r) \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(\underline r) = v.n_{th}(\underline r), \]</latex></div> |
| align = "right" | <span id="eq2"> (3a) </span> | | align = "right" | <span id="eq2"> (3a) </span> | ||
|} | |} | ||
| 70. sor: | 67. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(x,y,z) = \Phi_{th}(0,0,0)\cos\Bigg(\frac{\pi x}{a}\Bigg)\cos\Bigg(\frac{\pi | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(x,y,z) = \Phi_{th}(0,0,0)\cos\Bigg(\frac{\pi x}{a}\Bigg)\cos\Bigg(\frac{\pi y}{b}\Bigg)\cos\Bigg(\frac{\pi z}{c}\Bigg) \]</latex></div> |
| align = "right" | <span id="eq2"> (2) </span> | | align = "right" | <span id="eq2"> (2) </span> | ||
|} | |} | ||
| − | ahol ${a}$, ${b}$ és ${c}$ rendre az aktív zónának a tényleges ${a’}$, ${b’}$ és ${c’}$ fizikai méretekhez képest az ún. ''extrapolációs | + | ahol ${a}$, ${b}$ és ${c}$ rendre az aktív zónának a tényleges ${a’}$, ${b’}$ és ${c’}$ fizikai méretekhez képest az ún. ''extrapolációs távolsággal'' megnövelt méretei.<ref>A reaktorelmélet alapjául szolgáló diffúzióegyenlet határfeltételei szerint a reaktor tényleges felületét az extrapolációs távolsággal kijjebb tolva kapott felületen (az ún. ''extrapolált határfelület''en) kell megkövetelni a fluxus eltűnését. Az extrapolációs távolság értéke vízzel moderált reaktorokban néhány mm. Mérésünk szempontjából nincs jelentősége.</ref> |
Ha tehát a termikus neutronfluxust valamely ${x = x_{0}}$, ${y = y_{0}}$ helyen a ${z}$ függvényében | Ha tehát a termikus neutronfluxust valamely ${x = x_{0}}$, ${y = y_{0}}$ helyen a ${z}$ függvényében | ||
| 92. sor: | 89. sor: | ||
|} | |} | ||
| − | A reaktorok többsége azonban nem csupasz, hanem az aktív zónát ún. ''reflektor'' veszi körül, amely az aktív zónából kiszökő neutronokat részben visszaszórja | + | A reaktorok többsége azonban nem csupasz, hanem az aktív zónát ún. ''reflektor'' veszi körül, amely az aktív zónából kiszökő neutronokat részben visszaszórja<ref>Innen ered a reflektor neve.</ref> A kiszökő neutronok többsége a termikusnál nagyobb energiájú, ún. ''epitermikus'' neutron, amelyek a reflektorban termikus energiára lelassulnak. Mivel az ilyen energiájú neutronok szabad úthossza kisebb, mint az epitermikus neutronoké, a termikus neutronfluxusnak a reflektorban helyi maximuma alakul ki. Ezt a jelenséget ''reflektorpúp''nak nevezzük, amely víz reflektor esetében mindig kialakul, viszont grafit reflektor esetében általában nem. A 4. ábrán összehasonlítjuk a termikus neutronfluxusnak csupasz és reflektált reaktorban a ${z}$ tengely mentén kialakuló eloszlását. |
| − | + | {| | |
| + | | <span id="fig:4">[[Fájl: FizLab5_TNF_041.jpg|közép|bélyegkép|300px|4.ábra: Termikus neutronfluxus eloszlása egy csupasz és egy reflektált reaktor z koordinátája mentén]]</span> | ||
| + | |} | ||
Mivel a reflektor lecsökkenti az aktív zónából kiszökő neutronok számát, a reflektált | Mivel a reflektor lecsökkenti az aktív zónából kiszökő neutronok számát, a reflektált | ||
| − | reaktor kritikus tömege kisebb, mint az azonos összetételű csupasz reaktoré. A különbséget a ''reflektor-megtakarítás''sal vesszük figyelembe, amelyet a következőképpen definiáljuk. A reflektált reaktor aktív zónájában a reflektortól bizonyos távolságban ugyanolyan alakú térbeli eloszlás alakul ki, mint csupasz reaktorban. Az aktív zónának ezt a részét ''aszimptotikus tartomány''nak nevezzük. Téglatest alakú aktív zónában ezt az eloszlást tehát szintén a (2) képlet adja meg, de most az ${a}$, ${b}$ és ${c}$ mennyiségek a tényleges ${a’}$, ${b’}$ és ${c’}$ méreteknél lényegesen nagyobbak. A különbséget nevezzük reflektor-megtakarításnak. Például, a ${z}$ irányban vett reflektor-megtakarítást a | + | reaktor kritikus tömege kisebb, mint az azonos összetételű csupasz reaktoré. A különbséget a ''reflektor-megtakarítás''sal vesszük figyelembe, amelyet a következőképpen definiáljuk. A reflektált reaktor aktív zónájában a reflektortól bizonyos távolságban ugyanolyan alakú térbeli eloszlás alakul ki, mint csupasz reaktorban. Az aktív zónának ezt a részét ''aszimptotikus tartomány''nak nevezzük. Téglatest alakú aktív zónában ezt az eloszlást tehát szintén a (2) képlet adja meg, de most az ${a}$, ${b}$ és ${c}$ mennyiségek a tényleges ${a’}$, ${b’}$ és ${c’}$ méreteknél ''lényegesen'' nagyobbak. A különbséget nevezzük reflektor-megtakarításnak. Például, a ${z}$ irányban vett reflektor-megtakarítást a |
{| width = "100%" | {| width = "100%" | ||
| 108. sor: | 107. sor: | ||
képlettel definiáljuk. (Az ${x}$ és ${y}$ irányú reflektor-megtakarítás definíciója hasonló.) Mindezt | képlettel definiáljuk. (Az ${x}$ és ${y}$ irányú reflektor-megtakarítás definíciója hasonló.) Mindezt | ||
| − | az | + | az 4. ábrán illusztrájuk. Az aktív zóna belsejében kialakuló cos-eloszlást a reflektorban folytatva, a kapott fluxus az aktív zónán kívül, a reflektor belsejében válik zérussá. Ennek a pontnak az aktív zóna határától mért távolsága a reflektor-megtakarítás. Értéke a szokásos víz moderátoros és víz reflektoros reaktorokban 7÷9 cm.<ref>A reflektor-megtakarítást nem szabad összetéveszteni az extrapolációs távolsággal, hiszen az utóbbi a ''csupasz reaktornak a vákuummal határos'' felületén, az előbbi pedig az ''aktív zónának a reflektorral határos felületén'' van definiálva. Értékük is jelentősen eltér: a reflektor-megtakarítás sokkal nagyobb, mint az extrapolációs távolság.</ref> |
| − | |||
===Makroszkópikus eloszlás mérése aktivációs módszerrel=== | ===Makroszkópikus eloszlás mérése aktivációs módszerrel=== | ||
| 116. sor: | 114. sor: | ||
====A mérés elve==== | ====A mérés elve==== | ||
| − | Ha egy aktivációs detektort az ${\underline r}$ helyen besugározunk, akkor abban az időegység alatt felaktiválódott atomok számát, a '' | + | Ha egy aktivációs detektort az ${\underline r}$ helyen besugározunk, akkor abban az időegység alatt felaktiválódott atomok számát, a ''reakciósebesség''et az |
{| width = "100%" | {| width = "100%" | ||
| 125. sor: | 123. sor: | ||
|} | |} | ||
| − | integrál fejezi ki, ahol ${\sigma_{d}(E)}$ a detektoranyag mikroszkopikus ''aktivációs hatáskeresztmetszete'' | + | integrál fejezi ki, ahol ${\sigma_{d}(E)}$ a detektoranyag mikroszkopikus ''aktivációs hatáskeresztmetszete''<ref>Az aktivációs hatáskeresztmetszet általában a befogási hatáskeresztmetszet. Vannak azonban eltérések is. Amikor például a detektor hasadóanyag, és a hasadási termékek összaktivitását mérjük, az aktivációs hatáskeresztmetszet a hasadási hatáskeresztmetszettel azonos.</ref> és ${N_{d}}$ a detektorban levő aktiválható atommagok teljes száma. A gyakorlatban csak (5) szerinti reakciósebességeket lehet mérni, de a fluxust magát nem. Bizonyos feltételezésekkel azonban a mért reakciósebességekből következtethetünk a fluxusra is. Ennek érdekében definiáljuk az ''átlagos aktivációs hatáskeresztmetszet''et: |
{| width = "100%" | {| width = "100%" | ||
| 167. sor: | 165. sor: | ||
|} | |} | ||
| − | Ha az aktiválás elég sokáig tart, az aktív magok száma eléri az ${R(\underline r) | + | Ha az aktiválás elég sokáig tart, az aktív magok száma eléri az ${R(\underline r)/\lambda}$ telítési értéket. Ha azonban a besugárzás egy véges ${t_{a}}$ ideig tart, az aktivitás a telítési értéknél kisebb: |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \lambda N(\underline r,t_{a}) = R(\underline r)(1-\exp(-\lambda t_{a})) \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \lambda N(\underline r,t_{a}) = R(\underline r)(1-\exp(-\lambda t_{a})). \]</latex></div> |
| align = "right" | <span id="eq2"> </span> | | align = "right" | <span id="eq2"> </span> | ||
|} | |} | ||
| 179. sor: | 177. sor: | ||
aktivitás exponenciálisan csökken: | aktivitás exponenciálisan csökken: | ||
| − | Ezek az összefüggések még nem veszik figyelembe, hogy a neutronfluxus a besugárzott anyagban pontról pontra változhat. Ha a besugárzott minta formája a szokás szerinti fólia, amelynek a vastagsága nem elhanyagolható, akkor belsejében bekövetkező neutronabszorpció miatt az átlagos neutronfluxus (${\Phi_{th}}$) kisebb, mint a fólia felszínen uralkodó fluxusnak ${\Phi^{ | + | {| width = "100%" |
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ A(\underline r,t) = R(\underline r)(1-exp(-\lambda t_{a}))exp(-\lambda t). \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (10) </span> | ||
| + | |} | ||
| + | |||
| + | Ezek az összefüggések még nem veszik figyelembe, hogy a neutronfluxus a besugárzott anyagban pontról pontra változhat. Ha a besugárzott minta formája a szokás szerinti fólia, amelynek a vastagsága nem elhanyagolható, akkor belsejében bekövetkező neutronabszorpció miatt az átlagos neutronfluxus (${\overline\Phi_{th}}$) kisebb, mint a fólia felszínen uralkodó fluxus (${\Phi^{0}_{th}}$). Ezt az effektust nevezzük ''önárnyékolás''nak. a (7) és (8) képletekben szereplő fluxusnak ${\Phi^{0}_{th}}$ felel meg. Tekintve, hogy a mért aktivitás alapján erre az utóbbira kívánunk következtetni, az önárnyékolást a | ||
{| width = "100%" | {| width = "100%" | ||
| 185. sor: | 190. sor: | ||
| width = "10%" | | | width = "10%" | | ||
| width = "80%" | <div class="texdisplay"><latex display >\[G = \frac{\overline\Phi{th}}{\Phi^{o}_{th}} \]</latex></div> | | width = "80%" | <div class="texdisplay"><latex display >\[G = \frac{\overline\Phi{th}}{\Phi^{o}_{th}} \]</latex></div> | ||
| − | | align = "right" | <span id="eq2"> | + | | align = "right" | <span id="eq2"> </span> |
|} | |} | ||
| 193. sor: | 198. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[G = \frac{1-2E_{3}(d\Sigma_{t})}{d\Sigma_{t}} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[G = \frac{1-2E_{3}(d\Sigma_{t})}{d\Sigma_{t}}, \]</latex></div> |
| align = "right" | <span id="eq2"> (11) </span> | | align = "right" | <span id="eq2"> (11) </span> | ||
|} | |} | ||
| 204. sor: | 209. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ A(\underline r,t) = G\Phi^{0}_{th}(\underline r,t)\overline\sigma_{d}N_{d}(1-\exp(-\lambda t_{a}))\exp(-\lambda t) \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ A(\underline r,t) = G\Phi^{0}_{th}(\underline r,t)\overline\sigma_{d}N_{d}(1-\exp(-\lambda t_{a}))\exp(-\lambda t). \]</latex></div> |
| align = "right" | <span id="eq2"> (12) </span> | | align = "right" | <span id="eq2"> (12) </span> | ||
|} | |} | ||
| − | |||
| − | |||
====A termikus neutronfluxus becslése a besugárzott detektor aktivitásának ismeretében==== | ====A termikus neutronfluxus becslése a besugárzott detektor aktivitásának ismeretében==== | ||
| 217. sor: | 220. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ vn(v)dv = \Phi(E)dE \qquad \qquad E=\frac{mv^2}{2} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ vn(v)dv = \Phi(E)dE, \qquad \qquad E=\frac{mv^2}{2}, \]</latex></div> |
| align = "right" | <span id="eq2"> </span> | | align = "right" | <span id="eq2"> </span> | ||
|} | |} | ||
| 226. sor: | 229. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ v_{0} = \sqrt\frac{2kT}{m} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ v_{0} = \sqrt\frac{2kT}{m}, \]</latex></div> |
| align = "right" | <span id="eq2"> (13a) </span> | | align = "right" | <span id="eq2"> (13a) </span> | ||
|} | |} | ||
| 235. sor: | 238. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \overline v = \frac{2}{\sqrt\pi}v_{0} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \overline v = \frac{2}{\sqrt\pi}v_{0}. \]</latex></div> |
| align = "right" | <span id="eq2"> (13b) </span> | | align = "right" | <span id="eq2"> (13b) </span> | ||
|} | |} | ||
| 247. sor: | 250. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \overline\sigma_{d} = \frac{\int\limits_{0}^{\infty}\Phi(\underline r,E)\frac{C}{v}dE}{\int\limits_{0}^{\infty}\Phi(\underline r,E)dE} = \frac{C\int\limits_{0}^{\infty}n(\underline r,E)dE}{\int\limits_{0}^{\infty}vn(\underline r,E)dE} = \frac{C}{\overline v} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \overline\sigma_{d} = \frac{\int\limits_{0}^{\infty}\Phi(\underline r,E)\frac{C}{v}dE}{\int\limits_{0}^{\infty}\Phi(\underline r,E)dE} = \frac{C\int\limits_{0}^{\infty}n(\underline r,E)dE}{\int\limits_{0}^{\infty}vn(\underline r,E)dE} = \frac{C}{\overline v}, \]</latex></div> |
| align = "right" | <span id="eq2"> (14) </span> | | align = "right" | <span id="eq2"> (14) </span> | ||
|} | |} | ||
| − | ahol ${C = v_{0}\sigma(v_{0})}$ állandó. | + | ahol ${C = v_{0}\sigma(v_{0})}$ állandó. A (14) képletben kihasználtuk, hogy ${\Phi(\underline r,E) = vn(\underline r,E)}$. Ha a ${v_{0}}$ = 2200 m/s-hoz tartozó hatáskeresztmetszetet ${\sigma_{0}}$ = ${\sigma(v_{0}})$-val jelöljük, a (13) képletek alapján beláthatjuk, hogy |
| − | A (14) képletben kihasználtuk, hogy ${\Phi(\underline r,E) = vn(\underline r,E)}$. Ha a ${v_{0}}$ = 2200 m/s-hoz tartozó hatáskeresztmetszetet ${\sigma_{0}}$ = ${\sigma(v_{0}}$-val jelöljük, a (13) képletek alapján beláthatjuk, hogy | + | |
{| width = "100%" | {| width = "100%" | ||
| 280. sor: | 282. sor: | ||
| ${A_{d}}$ || - az aktiválódó izotóp tömegszáma | | ${A_{d}}$ || - az aktiválódó izotóp tömegszáma | ||
|- | |- | ||
| − | | ${L}$ || = 6,0221*10<sup>23</sup> ( | + | | ${L}$ || = 6,0221*10<sup>23</sup> (Avogadro szám) |
|} | |} | ||
| − | Az eddigi képletek megadják a (12) egyenletben szereplő minden mennyiség értékét, tehát a termikus neutronfluxust a mért ${A(\underline r,t)}$ aktivitás alapján ki tudjuk számítani, ha ismerjük a termikus neutronspektrumot jellemző ${T}$ hőmérsékletet, a detektor ${\sigma_{0}}$ és ${\sigma_{t}}$ | + | Az eddigi képletek megadják a (12) egyenletben szereplő minden mennyiség értékét, tehát a termikus neutronfluxust a mért ${A(\underline r,t)}$ aktivitás alapján ki tudjuk számítani, ha ismerjük a termikus neutronspektrumot jellemző ${T}$ hőmérsékletet, a detektor ${\sigma_{0}}$ és ${\sigma_{t}}$ hatáskeresztmetszeteit, továbbá jogos az a feltételezés, hogy a detektor ''csak'' a termikus neutronok hatására aktiválódik. |
| − | hatáskeresztmetszeteit, továbbá jogos az a feltételezés, hogy a detektor ''csak'' a termikus neutronok hatására aktiválódik. | + | |
| − | Ha a detektor besugárzása olyan helyen történik, ahol jelentős epitermikus fluxus is jelen van, és/vagy a detektor epitermikus aktivációs hatáskeresztmetszete a termikus aktivációs hatáskeresztmetszet mellett jelentős, akkor a nyert aktivitás egy részéért az epitermikus neutronok felelősek. Emiatt egy korrekcióval meg kell határozni, hogy a létrehozott aktivitásnak mekkora része származik a termikus neutronfluxustól. Erre az ad lehetőséget, hogy a kadmium neutronabszorpciós hatáskeresztmetszete termikus energiákon igen nagy ( | + | Ha a detektor besugárzása olyan helyen történik, ahol jelentős epitermikus fluxus is jelen van, és/vagy a detektor epitermikus aktivációs hatáskeresztmetszete a termikus aktivációs hatáskeresztmetszet mellett jelentős, akkor a nyert aktivitás egy részéért az epitermikus neutronok felelősek. Emiatt egy korrekcióval meg kell határozni, hogy a létrehozott aktivitásnak mekkora része származik a termikus neutronfluxustól. Erre az ad lehetőséget, hogy a kadmium neutronabszorpciós hatáskeresztmetszete termikus energiákon igen nagy (5. ábra), az epitermikus tartományban pedig elhanyagolható. Ha tehát a detektort megfelelő vastagságú kadmiummal borítva sugározzuk be, akkor a burkolat a termikus neutronokat gyakorlatilag teljesen kiszűri, így a detektor aktivitása csak a 0,4÷0,7 eV<ref>Ez az ún. ''kadmium-levágási energia'': a kadmium hatáskeresztmetszetét ez alatti neutronenergiákra gyakorlatilag végtelennek, a felettiekre pedig nullának vesszük. Nyilvánvaló, hogy a levágási energia függ a kadmiumborítás vastagságától.</ref> feletti epitermikus neutronoktól származik. Két azonos detektort alkalmazva, az egyiket csupaszon, másikat kadmium burkolatban (azonos körülmények között) besugározva, a termikus aktivitás egyszerűen nyerhető: |
{| width = "100%" | {| width = "100%" | ||
| 305. sor: | 306. sor: | ||
|} | |} | ||
| + | Szokás definiálni az úgynevezett kadmium-arányt, amely a csupasz és a kadmium burkolatú detektorok aktivitásának hányadosa: | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ R_{Cd} = \frac{A_{cs}}{A_{Cd}}. \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (18) </span> | ||
| + | |} | ||
| + | |||
| + | (17) és (18) felhasználásával a termikus neutronok által indukált aktivitás és az összes neutron által indukált aktivitás hányadosa a következőképpen írható: | ||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \frac{A_{th}}{A_{cs}} = 1-\dfrac{1}{R_{Cd}}. \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (18) </span> | ||
| + | |} | ||
| + | |||
| + | A már korábban említett ${1/v}$ ''hatás-keresztmetszetű'' detektoranyagok esetében a kadmium-arány értéke jellemzően nagy ($R_{Cd}>>1$), amiből (19) alapján az következik, hogy ilyen anyagoknál az epitermikus neutronok járuléka a teljes aktivitásban elhanyagolható a termikus neutronok járulékához képest. | ||
Végeredményben a következő képletet használjuk a termikus fluxus becslésére: | Végeredményben a következő képletet használjuk a termikus fluxus becslésére: | ||
| 311. sor: | 331. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \Phi_{th}(\underline r) = \frac{A_{cs}(\underline r,t)-A_{Cd}(\underline r,t)}{N_{d}\overline\sigma_{d}G(1-\exp(-\lambda t_{a}))\exp(-\lambda t)}, \]</latex></div> |
| align = "right" | <span id="eq2"> (18) </span> | | align = "right" | <span id="eq2"> (18) </span> | ||
|} | |} | ||
| 317. sor: | 337. sor: | ||
ahol a nevezőben szereplő mennyiségeket rendre a (13), (16), (6) és (11) képletek alapján számítjuk ki. | ahol a nevezőben szereplő mennyiségeket rendre a (13), (16), (6) és (11) képletek alapján számítjuk ki. | ||
| − | + | {| | |
| − | + | | <span id="fig:6">[[Fájl: FizLab5_TNF_06.jpg|közép|bélyegkép|300px|5.ábra: ${\sigma_{c}}$ változása a neutronenergia függvényében <sup>164</sup>Dy, <sup>197</sup>Au és <sup>113</sup>Cd esetében]]</span> | |
| + | |} | ||
| − | A | + | A 5. ábra szerint ilyen anyag a diszprózium <sup>164</sup>Dy izotópja, amelynek a befogási hatáskeresztmetszete 1 eV-ig gyakorlatilag 1/v-nek tekinthető. 1 eV felett a hatáskeresztmetszet gyorsan csökken, 100 eV környékén pedig rezonanciái is vannak, de a kadmium levágási energia feletti tartományban bekövetkező reakciók a teljes aktiválódásnak egy százalékát sem teszik ki. Aktiválódást követően ebben a következő reakciók játszódnak le: |
| 328. sor: | 349. sor: | ||
A gyakorlatban az utolsó, 2,35 órás felezési idejű bomlásból származó ${\beta}$-részecskéket szoktuk megszámlálni. Ennek a mérésnek megvan az a hátránya, hogy általában nem ismert a számláló-berendezés hatásfoka, így gyakorlatilag nem tudjuk meghatározni az ${A(\underline r,t)}$ aktivitás abszolút értékét. Erre való tekintettel a diszpróziummal való mérés csak relatív információt szolgáltat: a neutronfluxus abszolút értékét nem, legfeljebb csak térfüggésének az alakját tudjuk meghatározni. | A gyakorlatban az utolsó, 2,35 órás felezési idejű bomlásból származó ${\beta}$-részecskéket szoktuk megszámlálni. Ennek a mérésnek megvan az a hátránya, hogy általában nem ismert a számláló-berendezés hatásfoka, így gyakorlatilag nem tudjuk meghatározni az ${A(\underline r,t)}$ aktivitás abszolút értékét. Erre való tekintettel a diszpróziummal való mérés csak relatív információt szolgáltat: a neutronfluxus abszolút értékét nem, legfeljebb csak térfüggésének az alakját tudjuk meghatározni. | ||
| − | A termikus neutronfluxus abszolút értékének a meghatározása az arany aktiválása révén lehetséges. A <sup>197</sup>Au izotóp befogási hatáskeresztmetszete szintén a | + | A termikus neutronfluxus abszolút értékének a meghatározása az arany aktiválása révén lehetséges. A <sup>197</sup>Au izotóp befogási hatáskeresztmetszete szintén a 5. ábrán látható. Neutronokkal való besugárzás hatására az aranyban az alábbi reakciósor játszódik le: |
| 334. sor: | 355. sor: | ||
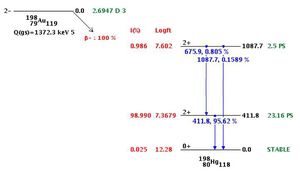
| − | Amint a | + | Amint a 6. ábrán látható, a <sup>198</sup>Au 64,68 órás felezési idejű bomlásban egyidejűleg ${\beta}$ és ${\gamma}$ részecskék is keletkeznek. (Pontosabban a ${\beta}$ bomlások 95,62 %-át egy 411,8 keV-os ${\gamma}$-foton kibocsátása is követi.) Így koincidencia számláló segítségével az arany abszolút aktivitása |
meghatározható. | meghatározható. | ||
| 342. sor: | 363. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ n_{\beta} = \eta_{\beta}A \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ n_{\beta} = \eta_{\beta}A; \]</latex></div> |
| align = "right" | <span id="eq2"> (19a) </span> | | align = "right" | <span id="eq2"> (19a) </span> | ||
|} | |} | ||
| 349. sor: | 370. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ n_{\gamma} = \eta_{\gamma}k_{\gamma}A \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ n_{\gamma} = \eta_{\gamma}k_{\gamma}A; \]</latex></div> |
| align = "right" | <span id="eq2"> (19b) </span> | | align = "right" | <span id="eq2"> (19b) </span> | ||
|} | |} | ||
| 360. sor: | 381. sor: | ||
|} | |} | ||
| − | ahol ${\eta_{\beta}}$ | + | ahol ${\eta_{\beta}}$ ill. ${\eta_{\gamma}}$ a béta-, ill. a gamma-detektorok hatásfoka, ${k_{\gamma}}$ a ${\gamma}$-vonal gyakorisága és ${A}$ a fóliában másodpercenként bekövetkező bomlások száma, azaz a minta aktivitása. Ezekből felírható: |
{| width = "100%" | {| width = "100%" | ||
| 371. sor: | 392. sor: | ||
Látható, hogy a minta aktivitása a hatásfokok ismerete nélkül nyerhető. | Látható, hogy a minta aktivitása a hatásfokok ismerete nélkül nyerhető. | ||
| − | + | {| | |
| + | | <span id="fig:7">[[Fájl: FizLab5_TNF_07.jpg|közép|bélyegkép|300px|6.ábra: A <sup>198</sup>Au bomlási sémája [5]]]</span> | ||
| + | |} | ||
A mérőberendezés tehát egy béta- és egy gamma- szcintillációs detektorból, két egycsatornás analizátorból (differenciál-diszkriminátor), három számlálóból és egy koincidencia áramkörből áll. A detektorok jele erősítés után az egycsatornás analizátorokra érkezik, melyek segítségével mind a ${\beta}$-, mind a ${\gamma}$-, spektrumból kiválasztható a kívánt tartomány. (Ez a háttér csökkentése érdekében fontos.) Az ÉS | A mérőberendezés tehát egy béta- és egy gamma- szcintillációs detektorból, két egycsatornás analizátorból (differenciál-diszkriminátor), három számlálóból és egy koincidencia áramkörből áll. A detektorok jele erősítés után az egycsatornás analizátorokra érkezik, melyek segítségével mind a ${\beta}$-, mind a ${\gamma}$-, spektrumból kiválasztható a kívánt tartomány. (Ez a háttér csökkentése érdekében fontos.) Az ÉS | ||
| 379. sor: | 402. sor: | ||
A mérésnél figyelembe kell venni, hogy a béta-detektor valamennyire érzékeny a gamma-sugárzásra is. Ez az ún. ''béta-detektor gamma-érzékenysége'', mely úgy határozható meg, hogy a mintára béta-abszorbenst (műanyag lapot) helyezünk a béta-detektor felőli oldalon. Az így kapott ${n_{\beta\gamma}}$ számlálási sebesség a ${\beta}$ csatornán, a béta-detektor gammaérzékenysége. | A mérésnél figyelembe kell venni, hogy a béta-detektor valamennyire érzékeny a gamma-sugárzásra is. Ez az ún. ''béta-detektor gamma-érzékenysége'', mely úgy határozható meg, hogy a mintára béta-abszorbenst (műanyag lapot) helyezünk a béta-detektor felőli oldalon. Az így kapott ${n_{\beta\gamma}}$ számlálási sebesség a ${\beta}$ csatornán, a béta-detektor gammaérzékenysége. | ||
| − | Egy másik korrekciót a véletlen koincidenciák miatt kell alkalmazni. Az ${n_{v\textrm{é}l}}$ azaz a véletlen koincidenciák időegységre jutó száma: | + | Egy másik korrekciót a véletlen koincidenciák miatt kell alkalmazni. Az ${n_{v\textrm{é}l}}$ azaz a ''véletlen koincidenciák'' időegységre jutó száma: |
{| width = "100%" | {| width = "100%" | ||
| 402. sor: | 425. sor: | ||
sebesség a béta abszorbens alkalmazásakor (ez magában foglalja a ${h_{\beta}}$ béta-háttér értéket is), ${n_{\beta,\gamma,ko}}$ a koincidencia számlálási sebesség az abszorbens alkalmazásakor, a vesszős mennyiségek pedig rendre a korrigált béta, gamma és koincidencia számlálási sebességek. | sebesség a béta abszorbens alkalmazásakor (ez magában foglalja a ${h_{\beta}}$ béta-háttér értéket is), ${n_{\beta,\gamma,ko}}$ a koincidencia számlálási sebesség az abszorbens alkalmazásakor, a vesszős mennyiségek pedig rendre a korrigált béta, gamma és koincidencia számlálási sebességek. | ||
| − | A ${\tau}$ felbontási idő az általában alkalmazott "ÉS" típusú koincidencia körök esetében a koincidencia kör bemeneteire adott jelek hosszának összege. Mivel a bemenetekre az egycsatornás analizátorokból érkeznek a jelek, amelyek szabványos 0,5 ${\mu}$s hosszúságú logikai (TTL) impulzusok, a felbontási idő 0,5 | + | A ${\tau}$ felbontási idő az általában alkalmazott "ÉS" típusú koincidencia körök esetében a koincidencia kör bemeneteire adott jelek hosszának összege. Mivel a bemenetekre az egycsatornás analizátorokból érkeznek a jelek, amelyek szabványos 0,5 ${\mu}$s hosszúságú logikai (TTL) impulzusok, a felbontási idő 0,5 μs-nak tekinthető. (19c) és (20) alapján könnyen belátható, hogy |
{| width = "100%" | {| width = "100%" | ||
| 411. sor: | 434. sor: | ||
|} | |} | ||
| − | teljesülése esetén lenne a véletlen koincidenciák száma azonos a valódi koincidenciákéval. Ehhez azonban esetünkben 1 MBq aktivitású forrásra lenne szükség. Mivel az alkalmazott forrás aktivitása ennél több nagyságrenddel kisebb, ezért | + | teljesülése esetén lenne a véletlen koincidenciák száma azonos a valódi koincidenciákéval. Ehhez azonban esetünkben 1 MBq aktivitású forrásra lenne szükség. Mivel az alkalmazott forrás aktivitása ennél több nagyságrenddel kisebb, ezért ${n_{v\textrm{é}l}}$ a legtöbb praktikus esetben elhanyagolható. |
| − | Az <sup>197</sup>Au aktivációs hatáskeresztmetszete a termikus neutronenergiák tartományában közelítőleg az ${1/v}$ törvényt követi, a rezonanciatartományban azonban számos rezonanciacsúcsa van ( | + | Az <sup>197</sup>Au aktivációs hatáskeresztmetszete a termikus neutronenergiák tartományában közelítőleg az ${1/v}$ törvényt követi, a rezonanciatartományban azonban számos rezonanciacsúcsa van (5. ábra). A legnagyobb rezonancia 4,47 eV-nál lép fel, ahol ${\sigma}$c = 9890 barn. Ezért a (17) szerinti kadmiumkorrekciónak itt nagy szerepe van. Ezért a fenti módszerrel egy Cd-burkolattal és egy anélkül besugárzott fólia aktivitását is meghatározzuk. |
Az I. táblázat összefoglalja a termikus neutronfluxus abszolút értékének meghatározásához elvégzendő méréseket. | Az I. táblázat összefoglalja a termikus neutronfluxus abszolút értékének meghatározásához elvégzendő méréseket. | ||
| 433. sor: | 456. sor: | ||
| "csupasz fólia" || ${n_{\beta}}$ || ${n_{\gamma}}$ || ${n_{ko}}$ || ${n_{\beta\gamma}}$ || - || ${n_{\beta\gamma,ko}}$ | | "csupasz fólia" || ${n_{\beta}}$ || ${n_{\gamma}}$ || ${n_{ko}}$ || ${n_{\beta\gamma}}$ || - || ${n_{\beta\gamma,ko}}$ | ||
|- | |- | ||
| − | | Cd-os fólia | + | | Cd-os fólia || ${n_{\beta}}$ || ${n_{\gamma}}$ || ${n_{ko}}$ || ${n_{\beta\gamma}}$ || - || ${n_{\beta\gamma,ko}}$ |
|- | |- | ||
| fólia nélkül || - || ${h_{\gamma}}$ || - || - || - || - | | fólia nélkül || - || ${h_{\gamma}}$ || - || - || - || - | ||
| 441. sor: | 464. sor: | ||
====A termikus neutronfluxus térfüggésének meghatározása==== | ====A termikus neutronfluxus térfüggésének meghatározása==== | ||
| − | A diszprózium detektor aktivitása a fentiek szerint a termikus neutronfluxussal arányos, ezért az aktivitás mérése során nyert beütésszámok közvetlenül felhasználhatók a termikus neutronfluxus térbeli eloszlásának a kísérleti meghatározásához. Ha a reaktor különböző ${\underline{r}}$ pontjaiban besugárzott detektorok különbözők (más a térfogatuk, tömegük stb.), ezt ''kalibrációs tényezők''kel kell figyelembe venni. Erre nincs szükség, ha aktiválandó mintaként huzalt használunk, és a huzal egyes szakaszainak az aktivitását külön megmérjük. Hallgatólagosan feltételezzük, hogy a huzal átmérője, Dy-tartalma stb. a huzal mentén végig azonos. A mérés folyamán azonban a minta aktivitása folyamatosan csökken, amit a mérésnél kompenzálni kell, vagy a kiértékelés során bomláskorrekciót kell alkalmazni. A gyakorlat során az első megoldást alkalmazzuk. | + | A diszprózium detektor aktivitása a fentiek szerint a termikus neutronfluxussal arányos, ezért az aktivitás mérése során nyert beütésszámok közvetlenül felhasználhatók a termikus neutronfluxus térbeli eloszlásának a kísérleti meghatározásához. Ha a reaktor különböző ${\underline{r}}$ pontjaiban besugárzott detektorok különbözők (más a térfogatuk, tömegük stb.), ezt ''kalibrációs tényezők''kel kell figyelembe venni. Erre nincs szükség, ha aktiválandó mintaként huzalt használunk, és a huzal egyes szakaszainak az aktivitását külön megmérjük.<ref>Hallgatólagosan feltételezzük, hogy a huzal átmérője, Dy-tartalma stb. a huzal mentén végig azonos.</ref> A mérés folyamán azonban a minta aktivitása folyamatosan csökken, amit a mérésnél kompenzálni kell, vagy a kiértékelés során bomláskorrekciót kell alkalmazni. A gyakorlat során az első megoldást alkalmazzuk. |
A detektor aktivitása az egyes mérések kezdeti időpontjában a (12) formula szerint írható. Abban az esetben, amikor a minta aktivitása nem nagy a mérőberendezés holtidejéhez képest, a mérőberendezés által szolgáltatott ${I(t)}$ ''számlálási sebesség'' (intenzitás) arányos a minta aktivitásával: | A detektor aktivitása az egyes mérések kezdeti időpontjában a (12) formula szerint írható. Abban az esetben, amikor a minta aktivitása nem nagy a mérőberendezés holtidejéhez képest, a mérőberendezés által szolgáltatott ${I(t)}$ ''számlálási sebesség'' (intenzitás) arányos a minta aktivitásával: | ||
| 448. sor: | 471. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ I(t) = \eta A(\underline r,t) \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ I(t) = \eta A(\underline r,t), \]</latex></div> |
| align = "right" | <span id="eq2"> (23) </span> | | align = "right" | <span id="eq2"> (23) </span> | ||
|} | |} | ||
| 457. sor: | 480. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}I(t')dt' \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}I(t')dt'. \]</latex></div> |
| align = "right" | <span id="eq2"> </span> | | align = "right" | <span id="eq2"> </span> | ||
|} | |} | ||
| 465. sor: | 488. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}\eta A(\underline r,t')\textrm{e}^{\lambda t'}dt' = \frac{\eta A(\underline r,t)(1-\textrm{e}^{ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}\eta A(\underline r,t')\textrm{e}^{-\lambda t'}dt' = \frac{\eta A(\underline r,t)(1-\textrm{e}^{\lambda t_{m}})}{\lambda} \approx \eta A(\underline r,t)t_{m}, \]</latex></div> |
| align = "right" | <span id="eq2"> (24) </span> | | align = "right" | <span id="eq2"> (24) </span> | ||
|} | |} | ||
| 490. sor: | 513. sor: | ||
|} | |} | ||
| − | függvény értékét kell meghatározni minden egyes adatpontra. Ennek érdekében a | + | függvény értékét kell meghatározni minden egyes adatpontra. Ennek érdekében a ${t_{m}}$ értékét a mérés kezdetén megfelelő értéken rögzítjük, és a huzal minden egyes pontjának mérésekor rögzítjük a mérés befejezésének időponját. Ennek felhasználásával a (26) szerinti korrekciót a <sup>165</sup>Dy felezési idejének ismeretében tudjuk számolni ([6] alapján 2,334±0,001 óra). |
==A mérési feladat== | ==A mérési feladat== | ||
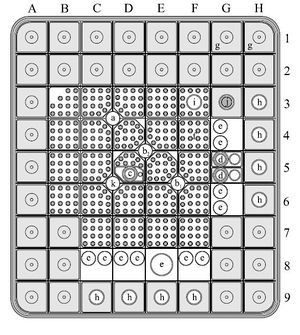
| − | A gyakorlat során az aktív zóna E6 pozíciójában (ld. | + | A gyakorlat során az aktív zóna E6 pozíciójában (ld. 7.ábra), függőleges egyenes mentén határozzuk meg a termikus neutronfluxus relatív eloszlását az előzőekben leírt módszerrel, majd ennek ismeretében a függőleges irányú reflektor-megtakarítást. A méréshez 10% Dy-ot tartalmazó, Dy-Al ötvözetből készült huzalt használunk. A termikus neutronfluxus abszolút értékét Au fólia felaktiválása révén határozzuk meg. |
==A méréshez szükséges eszközök, anyagok== | ==A méréshez szükséges eszközök, anyagok== | ||
| 514. sor: | 537. sor: | ||
===A huzalaktivitás mérésének elve és a mérőberendezés leírása=== | ===A huzalaktivitás mérésének elve és a mérőberendezés leírása=== | ||
| − | A termikus neutronfluxus térbeli eloszlásának meghatározására Dy-Al ötvözetből készült huzalt használunk. A huzal hossza mentén a helyfüggő aktivitást a huzalaktivitásmérő berendezéssel határozzuk meg. Mivel a huzal a z axiális koordináta mentén helyezkedik el, a (25)-ben szereplő ${B(\underline r,t)}$ helyett most ${B(z,t)}$-t írunk. A huzalaktivitásmérő berendezés a következő részekből áll: | + | A termikus neutronfluxus térbeli eloszlásának meghatározására Dy-Al ötvözetből készült huzalt használunk. A huzal hossza mentén a helyfüggő aktivitást a huzalaktivitásmérő berendezéssel határozzuk meg. Mivel a huzal a ${z}$ axiális koordináta mentén helyezkedik el, a (25)-ben szereplő ${B(\underline r,t)}$ helyett most ${B(z,t)}$-t írunk. A huzalaktivitásmérő berendezés a következő részekből áll: |
* fogasléccel ellátott tartósín, amelyben a huzalt rögzítjük | * fogasléccel ellátott tartósín, amelyben a huzalt rögzítjük | ||
| 524. sor: | 547. sor: | ||
* számítógép megfelelő adatgyűjtő szofverrel (GenieMot) | * számítógép megfelelő adatgyűjtő szofverrel (GenieMot) | ||
| − | + | {| | |
| + | | <span id="fig:8">[[Fájl: FizLab5_TNF_08.jpg|közép|bélyegkép|300px|7.ábra: Az aktív zóna keresztmetszete]]</span> | ||
| + | |} | ||
a - automata szabályzórúd; b1, b2 - biztonságvédelmi rudak; c - gyors csőposta; d - | a - automata szabályzórúd; b1, b2 - biztonságvédelmi rudak; c - gyors csőposta; d - | ||
| 537. sor: | 562. sor: | ||
Az előkészületek során a mérőhuzalt a plexi besugárzó tartórúd vájatába helyezzük. A plexi moderációs tulajdonságai hasonlítanak a vízéhez, így az aktív zóna fluxuseloszlásának zavarása csekély. | Az előkészületek során a mérőhuzalt a plexi besugárzó tartórúd vájatába helyezzük. A plexi moderációs tulajdonságai hasonlítanak a vízéhez, így az aktív zóna fluxuseloszlásának zavarása csekély. | ||
| − | A besugárzó rudat az operátor az álló reaktor E6 (D5-el szomszédos) pozíciójába helyezi, majd elvégzi a besugárzást. A besugárzás közben a D5 pozicióban lévő csőpostában a Dy fóliát is felaktiváljuk. Tekintettel arra, hogy Dy-Al ötvözettel dolgozunk, az Al zavaró aktivitásának lecsengése érdekében a besugárzás után a mintákat legalább 20 percig pihentetni kell. (Az alumínium felezési ideje 2,24 perc.) Ezután a huzalt a tartórúdból kivesszük, és a huzalaktivitás-mérő berendezés tartósínjébe helyezzük. A mérés során a <sup>165</sup>Dy bomlásából származó ${\beta^{-}}$ | + | A besugárzó rudat az operátor az álló reaktor E6 (D5-el szomszédos) pozíciójába helyezi, majd elvégzi a besugárzást. A besugárzás közben a D5 pozicióban lévő csőpostában a Dy fóliát is felaktiváljuk. Tekintettel arra, hogy Dy-Al ötvözettel dolgozunk, az Al zavaró aktivitásának lecsengése érdekében a besugárzás után a mintákat legalább 20 percig pihentetni kell. (Az alumínium felezési ideje 2,24 perc.) Ezután a huzalt a tartórúdból kivesszük, és a huzalaktivitás-mérő berendezés tartósínjébe helyezzük. A mérés során a <sup>165</sup>Dy bomlásából származó ${\beta^{-}}$ részeket detektáljuk. |
| − | A ${\beta}$- mérőfej segítségével először a Cd-burkolattal és anélkül besugárzott Dy fóliákat mérjük meg. A beütésszámok összehasonlításával meggyőződünk róla, hogy a valóban igaz a feltételezés, hogy az aktvitásnak csak elhanyagolhatóan csekély része származik az epitermikus neutronok által kiváltott reakciókból. Így a „csupaszon” besugárzott huzal aktivitás-eloszlása valóban a termikus fluxus eloszlását fogja visszaadni. | + | A ${\beta}$-mérőfej segítségével először a Cd-burkolattal és anélkül besugárzott Dy fóliákat mérjük meg. A beütésszámok összehasonlításával meggyőződünk róla, hogy a valóban igaz a feltételezés, hogy az aktvitásnak csak elhanyagolhatóan csekély része származik az epitermikus neutronok által kiváltott reakciókból. Így a „csupaszon” besugárzott huzal aktivitás-eloszlása valóban a termikus fluxus eloszlását fogja visszaadni. |
Ezután tartósínt az induló pozícióba toljuk, majd a számítógépen beállítjuk a mérési pontokat és a mérési időt. Szintén be kell állítani azt a spektrum tartományt, amelyben a beütésszámok összegzésre kerülnek. A mérés végén egy ASCII filet kapunk, amelynek sorai tartalmazzák a pozíciót, a megadott mérési idő alatt kapott beütésszámot a kiválasztott spektrum tartományban, valamint az adott pozícióban végzett mérés befejezésének időpontját. | Ezután tartósínt az induló pozícióba toljuk, majd a számítógépen beállítjuk a mérési pontokat és a mérési időt. Szintén be kell állítani azt a spektrum tartományt, amelyben a beütésszámok összegzésre kerülnek. A mérés végén egy ASCII filet kapunk, amelynek sorai tartalmazzák a pozíciót, a megadott mérési idő alatt kapott beütésszámot a kiválasztott spektrum tartományban, valamint az adott pozícióban végzett mérés befejezésének időpontját. | ||
| 552. sor: | 577. sor: | ||
===A termikus neutronfluxus relatív eloszlásának kiértékelése=== | ===A termikus neutronfluxus relatív eloszlásának kiértékelése=== | ||
| − | Az egyes pontokban mért beütésszámokon (26) alapján el kell végezni a bomlási idő korrekciót. Az így kapott korrigált adatpontok helyfüggése a termikus neutronfluxuseloszlás helyfüggésével arányos (vö. (25)). Ábrázoljuk a mérési pontokat grafikusan, majd a mért görbe középső szakaszára (3) képlet szerinti koszinusz függvényt illesztve, határozzuk meg az axiális reflektor-megtakarítást a (4) képlet alapján! Erre a feladatra általában megfelelő illesztő programra van szükség. | + | Az egyes pontokban mért beütésszámokon (26) alapján el kell végezni a bomlási idő korrekciót. Az így kapott korrigált adatpontok helyfüggése a termikus neutronfluxuseloszlás helyfüggésével arányos (vö. (25)). Ábrázoljuk a mérési pontokat grafikusan, majd a mért görbe középső szakaszára (3) képlet szerinti koszinusz függvényt illesztve, határozzuk meg az axiális reflektor-megtakarítást a (4) képlet alapján!<ref> Erre a feladatra általában megfelelő illesztő programra van szükség.</ref> |
====A relatív fluxusmérés hibaszámítása==== | ====A relatív fluxusmérés hibaszámítása==== | ||
| 561. sor: | 586. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ D^{2}(B_{i}) = M(B_{i}) \approx B_{i} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ D^{2}(B_{i}) = M(B_{i}) \approx B_{i}. \]</latex></div> |
| align = "right" | <span id="eq2"> (27) </span> | | align = "right" | <span id="eq2"> (27) </span> | ||
|} | |} | ||
| − | Ez a közelítő képlet ugyanazzal a feltétellel érvényes, mint maga az egész mérési módszer: mind a holtidő, mind a hattér hatása elhanyagolható. A holtidő korrekciójának legegyszerűbb módja, ha a | + | Ez a közelítő képlet ugyanazzal a feltétellel érvényes, mint maga az egész mérési módszer: mind a holtidő, mind a hattér hatása elhanyagolható. A holtidő korrekciójának legegyszerűbb módja, ha a ${t_{m}}$ mérési időt élő időben (live time) adjuk meg. Ekkor is ügyelni kell azonban, hogy lehetőleg a legnagyobb beütésszámoknál se haladja meg a holtidő a néhány %-ot. |
===A termikus neutronfluxus abszolút értékének hibaszámítása=== | ===A termikus neutronfluxus abszolút értékének hibaszámítása=== | ||
| − | A termikus neutronfluxus abszolút értékének a hibaszámítása lényegesen bonyolultabb feladat, mint a relatív eloszlásé. Mindenekelőtt két fajta hibát kell megkülönböztetnünk: ''statisztikus'' és ''szisztematikus'' hiba. A matematikai statisztikában ezeknek a fogalmaknak a neve: szórás, illetve torzítás. A fent használt | + | A termikus neutronfluxus abszolút értékének a hibaszámítása lényegesen bonyolultabb feladat, mint a relatív eloszlásé. Mindenekelőtt két fajta hibát kell megkülönböztetnünk: ''statisztikus'' és ''szisztematikus'' hiba.<ref>A matematikai statisztikában ezeknek a fogalmaknak a neve: ''szórás'', illetve ''torzítás''. A fent használt elnevezések csak köznyelviek, és a matematikában nem elfogadottak.</ref> |
| − | elnevezések csak köznyelviek, és a matematikában nem elfogadottak. | + | |
''Statisztikus hiba becslése'' | ''Statisztikus hiba becslése'' | ||
| 579. sor: | 603. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ D^{2}A = (n_{\beta}+n_{\beta\gamma})\Big(\frac{ | + | | width = "80%" | <div class="texdisplay"><latex display >\[ D^{2}A = (n_{\beta}+n_{\beta\gamma})\Big(\frac{n'_{\gamma}}{n'_{ko}}\Big)^{2}+(n_{\gamma}+h_{\gamma})\Big(\frac{n'_{\beta}}{n'_{ko}}\Big)^{2}+(n_{ko}+n_{\beta\gamma,ko})\Big(\frac{n'_{\beta}n'_{\gamma}}{{n{^{'}_{ko}}^2 }}\Big)^{2} \]</latex></div> |
| align = "right" | <span id="eq2"> (28) </span> | | align = "right" | <span id="eq2"> (28) </span> | ||
|} | |} | ||
| 588. sor: | 612. sor: | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ r(A) = \frac{D(A)}{A} = \sqrt {\frac{(n_{\beta}+n_{\beta\gamma})}{{n'_{\beta}}^2}+\frac{(n_{\gamma}+h_{\gamma})}{{n'_{\gamma}}^2}} = \sqrt {r^{2}(n'_{\beta})+r^{2}(n'_{\gamma})+r^{2}(n'_{ko})} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ r(A) = \frac{D(A)}{A} = \sqrt {\frac{(n_{\beta}+n_{\beta\gamma})}{{n'_{\beta}}^2}+\frac{(n_{\gamma}+h_{\gamma})}{{n'_{\gamma}}^2}+\frac{(n_{ko}+n_{\beta\gamma,ko})}{{n'_{ko}}^2}} = \sqrt {r^{2}(n'_{\beta})+r^{2}(n'_{\gamma})+r^{2}(n'_{ko})} \]</latex></div> |
| align = "right" | <span id="eq2"> (29) </span> | | align = "right" | <span id="eq2"> (29) </span> | ||
|} | |} | ||
| − | Az egyes beütésszámok relatív szórásai tehát összeadódnak. Mivel a három mért érték közül az ${n'_{ko}}$ várhatóan nagyságrendileg kisebb a másik kettőnél, ez fogja legjobban befolyásolni az aktivitás statisztikus hibáját. A mérési időt ezért úgy kell megválasztani, hogy már az ${n'_{ko}} | + | Az egyes beütésszámok relatív szórásai tehát összeadódnak. Mivel a három mért érték közül az ${n'_{ko}}$ várhatóan nagyságrendileg kisebb a másik kettőnél, ez fogja legjobban befolyásolni az aktivitás statisztikus hibáját. A mérési időt ezért úgy kell megválasztani, hogy már az ${n'_{ko}}$ is elegendően nagy legyen. |
| − | ${N_{d}}$ kivételével a (18) képletben szereplő többi mennyiség számított mennyiség, amelyek hibája szisztematikus hibának minősül (lásd alább). ${N_{d}}$ ismeretének a pontossága gyakorlatilag megegyezik a fóliák ${M}$ tömegének a pontosságával (vö. (16) képlet). A csupasz és kadmiumborítású fólia tömege lehet eltérő is. Ebben az esetben a hibaszámítási képlet jóval bonyolultabb. Az egyszerűség kedvéért feltételezzük, hogy tömegeik azonosak. Ennek alapján a termikus neutronfluxus relatív szórása: | + | ${N_{d}}$ kivételével a (18) képletben szereplő többi mennyiség számított mennyiség, amelyek hibája szisztematikus hibának minősül (lásd alább). ${N_{d}}$ ismeretének a pontossága gyakorlatilag megegyezik a fóliák ${M}$ tömegének a pontosságával (vö. (16) képlet).<ref>A csupasz és kadmiumborítású fólia tömege lehet eltérő is. Ebben az esetben a hibaszámítási képlet jóval bonyolultabb. Az egyszerűség kedvéért feltételezzük, hogy tömegeik azonosak.</ref>Ennek alapján a termikus neutronfluxus relatív szórása: |
{| width = "100%" | {| width = "100%" | ||
|- | |- | ||
| width = "10%" | | | width = "10%" | | ||
| − | | width = "80%" | <div class="texdisplay"><latex display >\[ \frac{D(\Phi_{th})}{\Phi_{th}} \approx \sqrt {\frac{D^{2}(M)}{M^{2}} + \frac{D^{2}(A_{CS})+D^{2}(A_{Cd})} {(A_{CS}-A_{Cd})}} \]</latex></div> | + | | width = "80%" | <div class="texdisplay"><latex display >\[ \frac{D(\Phi_{th})}{\Phi_{th}} \approx \sqrt {\frac{D^{2}(M)}{M^{2}} + \frac{D^{2}(A_{CS})+D^{2}(A_{Cd})} {(A_{CS}-A_{Cd})}}. \]</latex></div> |
| align = "right" | <span id="eq2"> (30) </span> | | align = "right" | <span id="eq2"> (30) </span> | ||
|} | |} | ||
| 607. sor: | 631. sor: | ||
A (30) alatti statisztikus hiba a mérés gondos végrehajtásával akár 1÷2%-ra is leszorítható. Nehezebb csökkenteni a szisztematikus hibákat, amelyek értéke akár 10% nagyságrendű is lehet. Ezek közül a legfontosabbak: | A (30) alatti statisztikus hiba a mérés gondos végrehajtásával akár 1÷2%-ra is leszorítható. Nehezebb csökkenteni a szisztematikus hibákat, amelyek értéke akár 10% nagyságrendű is lehet. Ezek közül a legfontosabbak: | ||
| − | * A G önárnyékolási tényező nehezen számolható mennyiség. Ennek oka egyrész az, hogy a (11) képlet csak közelítő (különösen a kadmiumborítású fólia esetében), másrészt bonyolult kiszámítani a képletben szereplő ${\sigma_{t}}$ hatáskeresztmetszetet. | + | * A ${G}$ önárnyékolási tényező nehezen számolható mennyiség. Ennek oka egyrész az, hogy a (11) képlet csak közelítő (különösen a kadmiumborítású fólia esetében), másrészt bonyolult kiszámítani a képletben szereplő ${\sigma_{t}}$ hatáskeresztmetszetet. |
| − | * Hasonlóan sok feltevésre van szükség a (18) képletben szereplő ${\overline v}$ | + | * Hasonlóan sok feltevésre van szükség a (18) képletben szereplő ${\overline v}$ ${\overline\sigma_{d}}$ szorzat számításhoz. Néhány példa a felmerülő problémákra: csak számításból ismerjük a (14) képletbe helyettsítendő neutronspektrumot, az arány hatáskeresztmetszét csak véges pontossággal ismerjük, stb. |
* A (18) képlet nevezőjében szereplő ${\lambda}$ bomlási állandót csak véges pontossággal ismerjük. Ennek hatása azonban legfeljebb ezrelékes nagyságrendű (pl. a <sup>198</sup>Au felezési ideje [6] alapján: 2,6948±0,0012 nap). További pontatlanság, hogy a ${t_{a}}$-t tartalmazó aktiválási tényező feltételezi, hogy az aktiválás kezdetén a minta pillanatszerűen kerül a besugárzási pozícióba, majd onnan vissza. Ez korrigálható, ha a (8) helyett egy olyan differenciálegyenletet oldunk meg, amely figyelembe veszi a neutronfluxus tényleges időfüggését a minta mozgatása során. Azonban ha az aktiválás ideje 10 s vagy hosszabb, akkor ez a korrekció 1% alatt van. | * A (18) képlet nevezőjében szereplő ${\lambda}$ bomlási állandót csak véges pontossággal ismerjük. Ennek hatása azonban legfeljebb ezrelékes nagyságrendű (pl. a <sup>198</sup>Au felezési ideje [6] alapján: 2,6948±0,0012 nap). További pontatlanság, hogy a ${t_{a}}$-t tartalmazó aktiválási tényező feltételezi, hogy az aktiválás kezdetén a minta pillanatszerűen kerül a besugárzási pozícióba, majd onnan vissza. Ez korrigálható, ha a (8) helyett egy olyan differenciálegyenletet oldunk meg, amely figyelembe veszi a neutronfluxus tényleges időfüggését a minta mozgatása során. Azonban ha az aktiválás ideje 10 s vagy hosszabb, akkor ez a korrekció 1% alatt van. | ||
| 623. sor: | 647. sor: | ||
# Milyen összefüggés van a huzal aktivitásának helyfüggése és a termikus fluxus axiális eloszlása között? | # Milyen összefüggés van a huzal aktivitásának helyfüggése és a termikus fluxus axiális eloszlása között? | ||
# Hogyan határozzuk meg a termikus neutronfluxus abszolút értékét? | # Hogyan határozzuk meg a termikus neutronfluxus abszolút értékét? | ||
| − | # A termikus neutronfluxus abszolút értékének meghatározásakor milyen statisztikus és | + | # A termikus neutronfluxus abszolút értékének meghatározásakor milyen statisztikus és szisztematikus hibák lépnek fel? |
| − | szisztematikus hibák lépnek fel? | + | |
==Irodalom== | ==Irodalom== | ||
| 640. sor: | 663. sor: | ||
[7] Szatmáry Zoltán: Mérések kiértékelése, egyetemi jegyzet, BME Természettudományi | [7] Szatmáry Zoltán: Mérések kiértékelése, egyetemi jegyzet, BME Természettudományi | ||
| + | |||
| + | ==Külső hivatkozások== | ||
| + | |||
| + | A Neutron aktivációs analitika laborjegyzet forrása elérhető a [http://www.reak.bme.hu/uploads/media/06_thflux_huzal_koinc_SzM.pdf] linken. | ||
| + | |||
| + | ==Lábjegyzetek== | ||
| + | |||
| + | <references /> | ||
A lap jelenlegi, 2018. február 12., 17:53-kori változata
Tartalomjegyzék[elrejtés] |
BEVEZETÉS
Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása megfelelő számlálórendszer segítségével mérhető. A keletkező fajlagos aktivitás[1] a besugárzás helyén uralkodó neutronfluxustól és a besugárzott anyag aktivációs hatáskeresztmetszetétől függ. A mérés célja a neutronfluxus meghatározása. Szigorúan véve azonban nincs olyan módszer, amely lehetővé tenné a neutronfluxus közvetlen mérését. Legfeljebb arról lehet szó, hogy a neutronfluxusra a mért fajlagos aktivitásból valamilyen feltevések mellett többé-kevésbé pontos becslést adjunk. Amilyen pontosan ismerjük az aktivációs hatáskeresztmetszetet, olyan pontosan tudjuk a neutronfluxust meghatározni. Minthogy számos olyan anyag van, melyeknek aktivációs hatáskeresztmetszete más-más módon függ a neutronenergiától, ezzel a módszerrel a neutronok energia szerinti eloszlásáról is nyerhetünk némi információt.
A jelen mérés keretében aktivációs detektorok felhasználásával fogjuk a termikus neutronfluxus értékét közelítőleg meghatározni a BME oktatóreaktorának aktív zónájában. A mérés két részből áll: a termikus neutronfluxus abszolút értékének becslése és helyfüggésének vizsgálata. A mérés elvének megértéséhez előbb a reaktorelmélet számos tételét kell megismernünk. Ezek részletesebben megtalálhatók az [1-4] kézikönyvekben.
ELMÉLETI ÖSSZEFOGLALÁS
Neutronspektrum, neutronfluxus eloszlása termikus reaktorokban
Maghasadásban gyors neutronok keletkeznek, energia-eloszlásuk az 1. ábrán látható. Termikus reaktorokban a gyors neutronok - elsősorban a moderátor atommagjaival való ütközések révén - fokozatosan lelassulnak, és a 2. ábrán sematikusan bemutatott neutronspektrum alakul ki. Legyen az 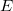 és
és 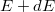 közé eső energiájú neutronok sűrűsége a reaktor
közé eső energiájú neutronok sűrűsége a reaktor  pontjának közelében
pontjának közelében 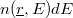 . Ennek felhasználásával a neutronfluxus definíciója:
. Ennek felhasználásával a neutronfluxus definíciója:
![\[ \Phi(\underline r, E) = vn(\underline r,E), \]](/images/math/b/d/f/bdf89af1ba6058963fde882c685486fa.png) |
(1) |
ahol  az
az 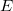 energiájú neutron sebessége. A neutronspektrumnak mérésünk szempontjából
legfontosabb része a termikus spektrum, amely jó közelítéssel a Maxwell-eloszlással írható le:
energiájú neutron sebessége. A neutronspektrumnak mérésünk szempontjából
legfontosabb része a termikus spektrum, amely jó közelítéssel a Maxwell-eloszlással írható le:
![\[ \Phi(\underline r, E) = \frac{E}{(kT)^2}\exp\Bigg\{-\frac{E}{kT} \Bigg\}, \qquad \qquad E \leq E_{th} \]](/images/math/8/f/3/8f37fc2bf5599ac1688d3e8b5ba59d10.png) |
(2) |
ahol 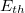 a termikus tartomány - többé-kevésbé önkényesen megválasztott - felső határa (általában 0,625 eV),
a termikus tartomány - többé-kevésbé önkényesen megválasztott - felső határa (általában 0,625 eV), 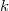 a Boltzmann-állandó és
a Boltzmann-állandó és 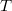 a termikus neutronspektrumot jellemző, hőmérséklet dimenziójú mennyiség.[2]
a termikus neutronspektrumot jellemző, hőmérséklet dimenziójú mennyiség.[2]
Amikor termikus neutronfluxusról beszélünk, ezen az alábbi integrált értjük:
![\[ \Phi_{th}(\underline r) = \int\limits_{0}^{E_{th}}\Phi(\underline r,E)dE, \]](/images/math/e/1/5/e1542918faffaa34ed99c068aceb942d.png) |
(3) |
amelyet gyakran a
![\[ \Phi_{th}(\underline r) = v.n_{th}(\underline r), \]](/images/math/6/3/e/63e9991f94e3c89dc1b0231a8e3adb7e.png) |
(3a) |
alakban írunk fel, ahol 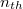 a termikus neutronoknak az
a termikus neutronoknak az  helyvektorú pont körüli sűrűsége és
helyvektorú pont körüli sűrűsége és  a termikus neutronok átlagos sebessége (lásd alább).
a termikus neutronok átlagos sebessége (lásd alább).
A termikus neutronfluxus térbeli változása függ a reaktor alakjától és belső felépítésétől. Téglatest alakú, csupasz (reflektor nélküli) reaktorban (3. ábra) a termikus neutronfluxus térbeli eloszlását a reaktorelmélet szerint az alábbi összefüggés adja meg:
![\[ \Phi_{th}(x,y,z) = \Phi_{th}(0,0,0)\cos\Bigg(\frac{\pi x}{a}\Bigg)\cos\Bigg(\frac{\pi y}{b}\Bigg)\cos\Bigg(\frac{\pi z}{c}\Bigg) \]](/images/math/e/3/d/e3d6e8c0c2ef20e5276b4a71e591850e.png) |
(2) |
ahol  ,
, 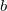 és
és  rendre az aktív zónának a tényleges
rendre az aktív zónának a tényleges 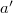 ,
, 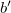 és
és 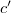 fizikai méretekhez képest az ún. extrapolációs távolsággal megnövelt méretei.[3]
fizikai méretekhez képest az ún. extrapolációs távolsággal megnövelt méretei.[3]
Ha tehát a termikus neutronfluxust valamely 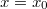 ,
, 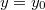 helyen a
helyen a  függvényében
tekintjük, a
függvényében
tekintjük, a
![\[ \Phi_{th}(x_{0},y_{0,}z) = \Phi_{0}\cos\Bigg(\frac{\pi z}{c}\Bigg) = \Phi_{0}\varphi(z) \]](/images/math/8/5/3/85328303990c5b9c4d58590dd568664e.png) |
(3) |
eloszlást kapjuk. Ez a cos-alakú axiális eloszlás egyébként érvényes henger alakú reaktor esetében is, ha a henger tengelye egybeesik a koordinátarendszer  tengelyével.
tengelyével.
A reaktorok többsége azonban nem csupasz, hanem az aktív zónát ún. reflektor veszi körül, amely az aktív zónából kiszökő neutronokat részben visszaszórja[4] A kiszökő neutronok többsége a termikusnál nagyobb energiájú, ún. epitermikus neutron, amelyek a reflektorban termikus energiára lelassulnak. Mivel az ilyen energiájú neutronok szabad úthossza kisebb, mint az epitermikus neutronoké, a termikus neutronfluxusnak a reflektorban helyi maximuma alakul ki. Ezt a jelenséget reflektorpúpnak nevezzük, amely víz reflektor esetében mindig kialakul, viszont grafit reflektor esetében általában nem. A 4. ábrán összehasonlítjuk a termikus neutronfluxusnak csupasz és reflektált reaktorban a  tengely mentén kialakuló eloszlását.
tengely mentén kialakuló eloszlását.
Mivel a reflektor lecsökkenti az aktív zónából kiszökő neutronok számát, a reflektált
reaktor kritikus tömege kisebb, mint az azonos összetételű csupasz reaktoré. A különbséget a reflektor-megtakarítással vesszük figyelembe, amelyet a következőképpen definiáljuk. A reflektált reaktor aktív zónájában a reflektortól bizonyos távolságban ugyanolyan alakú térbeli eloszlás alakul ki, mint csupasz reaktorban. Az aktív zónának ezt a részét aszimptotikus tartománynak nevezzük. Téglatest alakú aktív zónában ezt az eloszlást tehát szintén a (2) képlet adja meg, de most az  ,
, 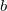 és
és  mennyiségek a tényleges
mennyiségek a tényleges 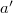 ,
, 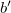 és
és 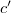 méreteknél lényegesen nagyobbak. A különbséget nevezzük reflektor-megtakarításnak. Például, a
méreteknél lényegesen nagyobbak. A különbséget nevezzük reflektor-megtakarításnak. Például, a  irányban vett reflektor-megtakarítást a
irányban vett reflektor-megtakarítást a
![\[ 2\lambda_{z} = c-c' \]](/images/math/c/1/8/c18bfd2b4d24605a5ef91f4eb2428aeb.png) |
(4) |
képlettel definiáljuk. (Az  és
és 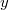 irányú reflektor-megtakarítás definíciója hasonló.) Mindezt
az 4. ábrán illusztrájuk. Az aktív zóna belsejében kialakuló cos-eloszlást a reflektorban folytatva, a kapott fluxus az aktív zónán kívül, a reflektor belsejében válik zérussá. Ennek a pontnak az aktív zóna határától mért távolsága a reflektor-megtakarítás. Értéke a szokásos víz moderátoros és víz reflektoros reaktorokban 7÷9 cm.[5]
irányú reflektor-megtakarítás definíciója hasonló.) Mindezt
az 4. ábrán illusztrájuk. Az aktív zóna belsejében kialakuló cos-eloszlást a reflektorban folytatva, a kapott fluxus az aktív zónán kívül, a reflektor belsejében válik zérussá. Ennek a pontnak az aktív zóna határától mért távolsága a reflektor-megtakarítás. Értéke a szokásos víz moderátoros és víz reflektoros reaktorokban 7÷9 cm.[5]
Makroszkópikus eloszlás mérése aktivációs módszerrel
A mérés elve
Ha egy aktivációs detektort az  helyen besugározunk, akkor abban az időegység alatt felaktiválódott atomok számát, a reakciósebességet az
helyen besugározunk, akkor abban az időegység alatt felaktiválódott atomok számát, a reakciósebességet az
![\[ R(\underline r) = N_{d}\int\limits_{0}^{\infty}\Phi(\underline r,E)\sigma_{d}(E)dE \]](/images/math/d/a/a/daaec1b54bba18e807862579537a915f.png) |
(5) |
integrál fejezi ki, ahol 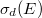 a detektoranyag mikroszkopikus aktivációs hatáskeresztmetszete[6] és
a detektoranyag mikroszkopikus aktivációs hatáskeresztmetszete[6] és 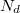 a detektorban levő aktiválható atommagok teljes száma. A gyakorlatban csak (5) szerinti reakciósebességeket lehet mérni, de a fluxust magát nem. Bizonyos feltételezésekkel azonban a mért reakciósebességekből következtethetünk a fluxusra is. Ennek érdekében definiáljuk az átlagos aktivációs hatáskeresztmetszetet:
a detektorban levő aktiválható atommagok teljes száma. A gyakorlatban csak (5) szerinti reakciósebességeket lehet mérni, de a fluxust magát nem. Bizonyos feltételezésekkel azonban a mért reakciósebességekből következtethetünk a fluxusra is. Ennek érdekében definiáljuk az átlagos aktivációs hatáskeresztmetszetet:
![\[ \overline\sigma_{d} = \frac{\int\limits_{0}^{\infty}\Phi(\underline r,E)\sigma_{d}(E)dE}{\int\limits_{0}^{\infty}\Phi(\underline r,E)dE} \]](/images/math/2/4/8/2484048369fecaa89f5faf4ee2fecf6f.png) |
(6) |
Ez a mennyiség szigorúan véve függ attól az  helytől, ahol a besugárzás történik, hiszen
a
helytől, ahol a besugárzás történik, hiszen
a 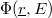 spektrum is változhat helyről helyre. A reaktorelmélet szerint azonban az aszimptotikus tartományban ez a függés elhanyagolható. Ilyen értelemben beszélhetünk átlagos aktivációs hatáskeresztmetszetről, és hagyhatjuk el a helyfüggés feltüntetését.
spektrum is változhat helyről helyre. A reaktorelmélet szerint azonban az aszimptotikus tartományban ez a függés elhanyagolható. Ilyen értelemben beszélhetünk átlagos aktivációs hatáskeresztmetszetről, és hagyhatjuk el a helyfüggés feltüntetését.
Vannak detektorok, amelyek hatáskeresztmetszete csak a termikus neutronokra számottevő, ezért ezeket termikus detektoroknak nevezzük. Egy ilyen detektorra érvényes, hogy
![\[ R(\underline r) = \Phi_{th}(\underline r)\overline\sigma_{d}N_{d} \]](/images/math/b/3/6/b360f9d78632b7214752941a16b891eb.png) |
(7) |
ahol 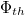 a termikus neutronfluxus (vö. (3) egyenletek).
a termikus neutronfluxus (vö. (3) egyenletek).
A besugárzás során az aktív magok 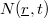 számának időbeli változását a keletkezés és a bomlás különbsége adja meg:
számának időbeli változását a keletkezés és a bomlás különbsége adja meg:
![\[ \frac{dN(\underline r,t)}{dt} = \Phi_{th}(\underline r)\overline\sigma_{d}N_{d}-\lambda N(\underline r,t) \]](/images/math/c/6/3/c6369074e3ad967972014482c2697656.png) |
(8) |
ahol 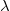 a keletkezett aktív magok bomlási állandója, t pedig az aktiválás kezdete óta eltelt idő. A besugárzás kezdetén a besugárzandó anyag általában inaktív, tehát
a keletkezett aktív magok bomlási állandója, t pedig az aktiválás kezdete óta eltelt idő. A besugárzás kezdetén a besugárzandó anyag általában inaktív, tehát 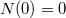 . Ekkor a fenti ifferenciálegyenlet megoldása (7) figyelembevételével:
. Ekkor a fenti ifferenciálegyenlet megoldása (7) figyelembevételével:
![\[ N(\underline r,t) = \frac{R(\underline r)}{\lambda}(1-\exp(-\lambda t)) \]](/images/math/6/4/a/64a87582d8df3ba8b41c9552742b235a.png) |
(9) |
Ha az aktiválás elég sokáig tart, az aktív magok száma eléri az 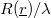 telítési értéket. Ha azonban a besugárzás egy véges
telítési értéket. Ha azonban a besugárzás egy véges 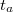 ideig tart, az aktivitás a telítési értéknél kisebb:
ideig tart, az aktivitás a telítési értéknél kisebb:
![\[ \lambda N(\underline r,t_{a}) = R(\underline r)(1-\exp(-\lambda t_{a})). \]](/images/math/9/f/2/9f22d747a8c09e97a6304d309d503a0e.png) |
A besugárzás befejezése utáni eltelik 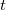 idő, amíg az aktivitást megmérjük. Ez alatt a mérhető
aktivitás exponenciálisan csökken:
idő, amíg az aktivitást megmérjük. Ez alatt a mérhető
aktivitás exponenciálisan csökken:
![\[ A(\underline r,t) = R(\underline r)(1-exp(-\lambda t_{a}))exp(-\lambda t). \]](/images/math/0/6/6/0669d5c67f6f1e5636b83650ea89d8c7.png) |
(10) |
Ezek az összefüggések még nem veszik figyelembe, hogy a neutronfluxus a besugárzott anyagban pontról pontra változhat. Ha a besugárzott minta formája a szokás szerinti fólia, amelynek a vastagsága nem elhanyagolható, akkor belsejében bekövetkező neutronabszorpció miatt az átlagos neutronfluxus (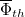 ) kisebb, mint a fólia felszínen uralkodó fluxus (
) kisebb, mint a fólia felszínen uralkodó fluxus (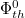 ). Ezt az effektust nevezzük önárnyékolásnak. a (7) és (8) képletekben szereplő fluxusnak
). Ezt az effektust nevezzük önárnyékolásnak. a (7) és (8) képletekben szereplő fluxusnak 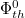 felel meg. Tekintve, hogy a mért aktivitás alapján erre az utóbbira kívánunk következtetni, az önárnyékolást a
felel meg. Tekintve, hogy a mért aktivitás alapján erre az utóbbira kívánunk következtetni, az önárnyékolást a
![\[G = \frac{\overline\Phi{th}}{\Phi^{o}_{th}} \]](/images/math/4/d/b/4dbbdb288f2da6b405243a187a2ef16b.png) |
önárnyékolási tényezővel vesszük figyelembe. Ha a detektor vastagsága 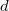 , makroszkopikus totális hatáskeresztmetszete
, makroszkopikus totális hatáskeresztmetszete 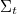 , akkor izotróp neutronfluxus-eloszlás esetén a reaktorelmélet szerint
, akkor izotróp neutronfluxus-eloszlás esetén a reaktorelmélet szerint 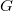 a következő formulával közelíthető:
a következő formulával közelíthető:
![\[G = \frac{1-2E_{3}(d\Sigma_{t})}{d\Sigma_{t}}, \]](/images/math/3/1/1/311518e4ac87ea79c86d26d49f963e4d.png) |
(11) |
ahol 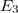 a harmadrendű exponenciális-integrál függvény.
a harmadrendű exponenciális-integrál függvény.
Végül fentiek összevonásával a detektor aktivitásának időfüggvénye:
![\[ A(\underline r,t) = G\Phi^{0}_{th}(\underline r,t)\overline\sigma_{d}N_{d}(1-\exp(-\lambda t_{a}))\exp(-\lambda t). \]](/images/math/1/1/e/11e4ef77b9595878e316972bafd52fb0.png) |
(12) |
A termikus neutronfluxus becslése a besugárzott detektor aktivitásának ismeretében
A termikus neutronfluxusnak az energiától való függését a (2) alatti függvény adja meg, amely 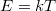 -nél veszi fel a maximumát. (Emlékeztetőül megjegyezzük, hogy
-nél veszi fel a maximumát. (Emlékeztetőül megjegyezzük, hogy 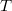 a neutronhőmérséklet (vö. (2) képlet).) Ez a függvény az alábbi egyszerű kapcsolatban van a termikus neutronok sebességeloszlásával:
a neutronhőmérséklet (vö. (2) képlet).) Ez a függvény az alábbi egyszerű kapcsolatban van a termikus neutronok sebességeloszlásával:
![\[ vn(v)dv = \Phi(E)dE, \qquad \qquad E=\frac{mv^2}{2}, \]](/images/math/c/0/a/c0a799a87873d3cec05d9f2cf76bab48.png) |
ahol 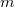 a neutron tömege. Az így kapott sebességeloszlás szerinti legvalószínűbb sebesség:
a neutron tömege. Az így kapott sebességeloszlás szerinti legvalószínűbb sebesség:
![\[ v_{0} = \sqrt\frac{2kT}{m}, \]](/images/math/b/e/3/be3c19cce7cb406428dc5775720cc934.png) |
(13a) |
amint könnyen levezethetjük. Vegyük észre, hogy ez éppen az 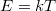 energiának megfelelő sebesség. Az átlagos sebesség azonban ettől eltér:
energiának megfelelő sebesség. Az átlagos sebesség azonban ettől eltér:
![\[ \overline v = \frac{2}{\sqrt\pi}v_{0}. \]](/images/math/8/2/1/8213c63ab36014a2eb8972cef1bb9283.png) |
(13b) |
Szobahőmérsékleten 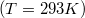
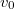 = 2200 m/s, amely az
= 2200 m/s, amely az 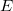 = 0,0253 eV energiának felel
meg.
= 0,0253 eV energiának felel
meg.
Termikus detektorok esetében az átlagos aktivációs hatáskeresztmetszet (6) szerinti képletébe a termikus spektrumot kell írni. Ez egyszerű eredményre vezet az ún. 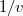 hatás-keresztmetszetű detektoranyagok esetében. Ekkor ugyanis (6) így írható:
hatás-keresztmetszetű detektoranyagok esetében. Ekkor ugyanis (6) így írható:
![\[ \overline\sigma_{d} = \frac{\int\limits_{0}^{\infty}\Phi(\underline r,E)\frac{C}{v}dE}{\int\limits_{0}^{\infty}\Phi(\underline r,E)dE} = \frac{C\int\limits_{0}^{\infty}n(\underline r,E)dE}{\int\limits_{0}^{\infty}vn(\underline r,E)dE} = \frac{C}{\overline v}, \]](/images/math/c/c/8/cc8e74813fa38e45935c25c6fd6ab998.png) |
(14) |
ahol 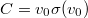 állandó. A (14) képletben kihasználtuk, hogy
állandó. A (14) képletben kihasználtuk, hogy 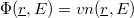 . Ha a
. Ha a 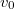 = 2200 m/s-hoz tartozó hatáskeresztmetszetet
= 2200 m/s-hoz tartozó hatáskeresztmetszetet 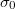 =
= 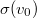 -val jelöljük, a (13) képletek alapján beláthatjuk, hogy
-val jelöljük, a (13) képletek alapján beláthatjuk, hogy
![\[ \overline\sigma_{d}(T) = \sigma_{0}\frac{\sqrt\pi}{2}\sqrt\frac{293K}{T} \]](/images/math/1/a/1/1a11eeccb93ca4b2b1ebc39ecf5b2ea5.png) |
(15) |
A besugárzott mintában levő atommagok 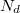 számának számítása:
számának számítása:
![\[ N_{d} = \frac{M\alpha L}{A_{d}} \]](/images/math/3/2/e/32e527e8b90e007ab428bca3b52c4df3.png) |
(16) |
ahol
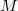 |
- a minta tömege (g) |
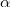 |
- a detektoranyag aktiválódó izotópjának előfordulási gyakorisága |
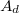 |
- az aktiválódó izotóp tömegszáma |
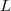 |
= 6,0221*1023 (Avogadro szám) |
Az eddigi képletek megadják a (12) egyenletben szereplő minden mennyiség értékét, tehát a termikus neutronfluxust a mért 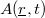 aktivitás alapján ki tudjuk számítani, ha ismerjük a termikus neutronspektrumot jellemző
aktivitás alapján ki tudjuk számítani, ha ismerjük a termikus neutronspektrumot jellemző 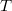 hőmérsékletet, a detektor
hőmérsékletet, a detektor 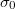 és
és 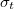 hatáskeresztmetszeteit, továbbá jogos az a feltételezés, hogy a detektor csak a termikus neutronok hatására aktiválódik.
hatáskeresztmetszeteit, továbbá jogos az a feltételezés, hogy a detektor csak a termikus neutronok hatására aktiválódik.
Ha a detektor besugárzása olyan helyen történik, ahol jelentős epitermikus fluxus is jelen van, és/vagy a detektor epitermikus aktivációs hatáskeresztmetszete a termikus aktivációs hatáskeresztmetszet mellett jelentős, akkor a nyert aktivitás egy részéért az epitermikus neutronok felelősek. Emiatt egy korrekcióval meg kell határozni, hogy a létrehozott aktivitásnak mekkora része származik a termikus neutronfluxustól. Erre az ad lehetőséget, hogy a kadmium neutronabszorpciós hatáskeresztmetszete termikus energiákon igen nagy (5. ábra), az epitermikus tartományban pedig elhanyagolható. Ha tehát a detektort megfelelő vastagságú kadmiummal borítva sugározzuk be, akkor a burkolat a termikus neutronokat gyakorlatilag teljesen kiszűri, így a detektor aktivitása csak a 0,4÷0,7 eV[7] feletti epitermikus neutronoktól származik. Két azonos detektort alkalmazva, az egyiket csupaszon, másikat kadmium burkolatban (azonos körülmények között) besugározva, a termikus aktivitás egyszerűen nyerhető:
![\[ A_{th} = A_{cs}-A_{Cd} \]](/images/math/9/c/c/9cc0c7661a8a801d0e2bb6b99f77ba4a.png) |
(17) |
ahol
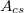 |
- a csupasz detektor aktivitása |
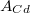 |
- a kadmium burkolatú detektor aktivitása |
Szokás definiálni az úgynevezett kadmium-arányt, amely a csupasz és a kadmium burkolatú detektorok aktivitásának hányadosa:
![\[ R_{Cd} = \frac{A_{cs}}{A_{Cd}}. \]](/images/math/9/2/6/926d29978d6cd13a33c84ae9756e3b27.png) |
(18) |
(17) és (18) felhasználásával a termikus neutronok által indukált aktivitás és az összes neutron által indukált aktivitás hányadosa a következőképpen írható:
![\[ \frac{A_{th}}{A_{cs}} = 1-\dfrac{1}{R_{Cd}}. \]](/images/math/9/c/0/9c0fd3b897b038ce43c9b1f819abd31d.png) |
(18) |
A már korábban említett 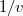 hatás-keresztmetszetű detektoranyagok esetében a kadmium-arány értéke jellemzően nagy (
hatás-keresztmetszetű detektoranyagok esetében a kadmium-arány értéke jellemzően nagy (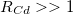 ), amiből (19) alapján az következik, hogy ilyen anyagoknál az epitermikus neutronok járuléka a teljes aktivitásban elhanyagolható a termikus neutronok járulékához képest.
), amiből (19) alapján az következik, hogy ilyen anyagoknál az epitermikus neutronok járuléka a teljes aktivitásban elhanyagolható a termikus neutronok járulékához képest.
Végeredményben a következő képletet használjuk a termikus fluxus becslésére:
![\[ \Phi_{th}(\underline r) = \frac{A_{cs}(\underline r,t)-A_{Cd}(\underline r,t)}{N_{d}\overline\sigma_{d}G(1-\exp(-\lambda t_{a}))\exp(-\lambda t)}, \]](/images/math/3/9/a/39a9f88da943144a911557cf76a84108.png) |
(18) |
ahol a nevezőben szereplő mennyiségeket rendre a (13), (16), (6) és (11) képletek alapján számítjuk ki.
A 5. ábra szerint ilyen anyag a diszprózium 164Dy izotópja, amelynek a befogási hatáskeresztmetszete 1 eV-ig gyakorlatilag 1/v-nek tekinthető. 1 eV felett a hatáskeresztmetszet gyorsan csökken, 100 eV környékén pedig rezonanciái is vannak, de a kadmium levágási energia feletti tartományban bekövetkező reakciók a teljes aktiválódásnak egy százalékát sem teszik ki. Aktiválódást követően ebben a következő reakciók játszódnak le:
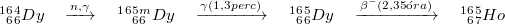
A gyakorlatban az utolsó, 2,35 órás felezési idejű bomlásból származó 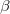 -részecskéket szoktuk megszámlálni. Ennek a mérésnek megvan az a hátránya, hogy általában nem ismert a számláló-berendezés hatásfoka, így gyakorlatilag nem tudjuk meghatározni az
-részecskéket szoktuk megszámlálni. Ennek a mérésnek megvan az a hátránya, hogy általában nem ismert a számláló-berendezés hatásfoka, így gyakorlatilag nem tudjuk meghatározni az 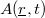 aktivitás abszolút értékét. Erre való tekintettel a diszpróziummal való mérés csak relatív információt szolgáltat: a neutronfluxus abszolút értékét nem, legfeljebb csak térfüggésének az alakját tudjuk meghatározni.
aktivitás abszolút értékét. Erre való tekintettel a diszpróziummal való mérés csak relatív információt szolgáltat: a neutronfluxus abszolút értékét nem, legfeljebb csak térfüggésének az alakját tudjuk meghatározni.
A termikus neutronfluxus abszolút értékének a meghatározása az arany aktiválása révén lehetséges. A 197Au izotóp befogási hatáskeresztmetszete szintén a 5. ábrán látható. Neutronokkal való besugárzás hatására az aranyban az alábbi reakciósor játszódik le:
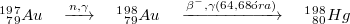
Amint a 6. ábrán látható, a 198Au 64,68 órás felezési idejű bomlásban egyidejűleg 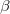 és
és 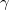 részecskék is keletkeznek. (Pontosabban a
részecskék is keletkeznek. (Pontosabban a 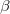 bomlások 95,62 %-át egy 411,8 keV-os
bomlások 95,62 %-át egy 411,8 keV-os 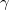 -foton kibocsátása is követi.) Így koincidencia számláló segítségével az arany abszolút aktivitása
meghatározható.
-foton kibocsátása is követi.) Így koincidencia számláló segítségével az arany abszolút aktivitása
meghatározható.
Ehhez egy olyan berendezést használunk, melynek egy szcintillációs béta- és egy szintén szcintillációs gamma-detektora van. A béta- és a gamma-csatornák kimenő jelei egy-egy számlálóra, ill. egy koincidenciakör két bemenetére csatlakoznak. Így regisztrálásra kerül a béta-részecskék és a gamma-fotonok száma, valamint az adott mérési idő alatt bekövetkező koincidencia események száma. Jelölje a 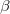 -részecskék másodpercenkénti számát
-részecskék másodpercenkénti számát 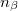 ill. a gamma-fotonokét
ill. a gamma-fotonokét 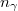 , a koincidencia eseményekét
, a koincidencia eseményekét 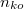 . Ezen adatokkal felírhatók a következő összefüggések:
. Ezen adatokkal felírhatók a következő összefüggések:
![\[ n_{\beta} = \eta_{\beta}A; \]](/images/math/a/e/7/ae71606ac81f1f97eb1854a4b83aa8ad.png) |
(19a) |
![\[ n_{\gamma} = \eta_{\gamma}k_{\gamma}A; \]](/images/math/1/c/f/1cfbf7ce40e526ae32aab99d4a85937b.png) |
(19b) |
![\[ n_{k0} = \eta_{\beta}\eta_{\gamma}k_{\gamma}A \]](/images/math/8/7/5/87565e5c50d6f2170638b9ad5c6db183.png) |
(19c) |
ahol 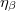 ill.
ill. 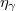 a béta-, ill. a gamma-detektorok hatásfoka,
a béta-, ill. a gamma-detektorok hatásfoka, 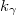 a
a 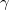 -vonal gyakorisága és
-vonal gyakorisága és 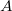 a fóliában másodpercenként bekövetkező bomlások száma, azaz a minta aktivitása. Ezekből felírható:
a fóliában másodpercenként bekövetkező bomlások száma, azaz a minta aktivitása. Ezekből felírható:
![\[ A(Bq) = \frac{n_{\beta}n_{\gamma}}{n_{ko}} \]](/images/math/3/5/5/355163f76dd8a1415629039f38bd88bd.png) |
(20) |
Látható, hogy a minta aktivitása a hatásfokok ismerete nélkül nyerhető.
A mérőberendezés tehát egy béta- és egy gamma- szcintillációs detektorból, két egycsatornás analizátorból (differenciál-diszkriminátor), három számlálóból és egy koincidencia áramkörből áll. A detektorok jele erősítés után az egycsatornás analizátorokra érkezik, melyek segítségével mind a 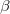 -, mind a
-, mind a 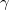 -, spektrumból kiválasztható a kívánt tartomány. (Ez a háttér csökkentése érdekében fontos.) Az ÉS
kapunak is nevezett koincidencia kör (legalább) két bemenettel és egy kimenettel rendelkezik. A kimeneten csak akkor jelenik meg impulzus, ha bemeneteire egy időben érkeznek jelek. Természetesen ki kell kötni, hogy milyen időkülönbségű legyen a jelek időbeli egybeesése: az a
-, spektrumból kiválasztható a kívánt tartomány. (Ez a háttér csökkentése érdekében fontos.) Az ÉS
kapunak is nevezett koincidencia kör (legalább) két bemenettel és egy kimenettel rendelkezik. A kimeneten csak akkor jelenik meg impulzus, ha bemeneteire egy időben érkeznek jelek. Természetesen ki kell kötni, hogy milyen időkülönbségű legyen a jelek időbeli egybeesése: az a  időtartam, amelynél rövidebb időn belül érkező jeleket a koincidencia-berendezés még egy időben érkezőnek észlel, az adott berendezés felbontási ideje. A három számlálóból kettő közvetlenül az egycsatornás analizátorok kimenetére kötve az
időtartam, amelynél rövidebb időn belül érkező jeleket a koincidencia-berendezés még egy időben érkezőnek észlel, az adott berendezés felbontási ideje. A három számlálóból kettő közvetlenül az egycsatornás analizátorok kimenetére kötve az 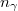 -t, és az
-t, és az 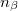 -t, a harmadik pedig az
-t, a harmadik pedig az 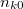 -t számolja. A számlálók össze vannak
hangolva, vagyis egyszerre indíthatók és azonos ideig számlálnak.
-t számolja. A számlálók össze vannak
hangolva, vagyis egyszerre indíthatók és azonos ideig számlálnak.
A mérésnél figyelembe kell venni, hogy a béta-detektor valamennyire érzékeny a gamma-sugárzásra is. Ez az ún. béta-detektor gamma-érzékenysége, mely úgy határozható meg, hogy a mintára béta-abszorbenst (műanyag lapot) helyezünk a béta-detektor felőli oldalon. Az így kapott 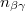 számlálási sebesség a
számlálási sebesség a 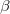 csatornán, a béta-detektor gammaérzékenysége.
csatornán, a béta-detektor gammaérzékenysége.
Egy másik korrekciót a véletlen koincidenciák miatt kell alkalmazni. Az 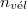 azaz a véletlen koincidenciák időegységre jutó száma:
azaz a véletlen koincidenciák időegységre jutó száma:
![\[ n_{v\textrm{é}l} = 2\tau n_{\beta}n_{\gamma} \]](/images/math/6/9/e/69e35013d9aa16e0e6a04466e7f38ab6.png) |
(21) |
ahol  a koincidencia berendezés feloldási ideje,
a koincidencia berendezés feloldási ideje, 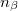 ill.
ill. 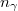 a béta ill. gamma csatornán a
számlálási sebességek. Ezek alapján a fólia aktivitása:
a béta ill. gamma csatornán a
számlálási sebességek. Ezek alapján a fólia aktivitása:
![\[ A = \frac {(n_{\beta}-n_{\beta\gamma})(n_{\gamma}-h_{\gamma})}{n_{ko}-n_{v\textrm{é}l}-n_{\beta,\gamma,ko}} = \frac{n'_{\beta}n'_{\gamma}}{n'_{ko}} \]](/images/math/c/5/2/c52f5cbd9b7ca739a40888307c7bd967.png) |
(22) |
Ahol 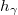 a gamma-háttér számlálási sebessége (cps),
a gamma-háttér számlálási sebessége (cps), 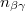 a béta ágon mért számlálási
sebesség a béta abszorbens alkalmazásakor (ez magában foglalja a
a béta ágon mért számlálási
sebesség a béta abszorbens alkalmazásakor (ez magában foglalja a 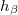 béta-háttér értéket is),
béta-háttér értéket is), 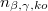 a koincidencia számlálási sebesség az abszorbens alkalmazásakor, a vesszős mennyiségek pedig rendre a korrigált béta, gamma és koincidencia számlálási sebességek.
a koincidencia számlálási sebesség az abszorbens alkalmazásakor, a vesszős mennyiségek pedig rendre a korrigált béta, gamma és koincidencia számlálási sebességek.
A  felbontási idő az általában alkalmazott "ÉS" típusú koincidencia körök esetében a koincidencia kör bemeneteire adott jelek hosszának összege. Mivel a bemenetekre az egycsatornás analizátorokból érkeznek a jelek, amelyek szabványos 0,5
felbontási idő az általában alkalmazott "ÉS" típusú koincidencia körök esetében a koincidencia kör bemeneteire adott jelek hosszának összege. Mivel a bemenetekre az egycsatornás analizátorokból érkeznek a jelek, amelyek szabványos 0,5 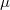 s hosszúságú logikai (TTL) impulzusok, a felbontási idő 0,5 μs-nak tekinthető. (19c) és (20) alapján könnyen belátható, hogy
s hosszúságú logikai (TTL) impulzusok, a felbontási idő 0,5 μs-nak tekinthető. (19c) és (20) alapján könnyen belátható, hogy
![\[ A = \frac {1}{2\tau} \]](/images/math/e/6/4/e649bec8305a82ddcd9f9d3e96acec65.png) |
teljesülése esetén lenne a véletlen koincidenciák száma azonos a valódi koincidenciákéval. Ehhez azonban esetünkben 1 MBq aktivitású forrásra lenne szükség. Mivel az alkalmazott forrás aktivitása ennél több nagyságrenddel kisebb, ezért 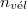 a legtöbb praktikus esetben elhanyagolható.
a legtöbb praktikus esetben elhanyagolható.
Az 197Au aktivációs hatáskeresztmetszete a termikus neutronenergiák tartományában közelítőleg az 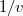 törvényt követi, a rezonanciatartományban azonban számos rezonanciacsúcsa van (5. ábra). A legnagyobb rezonancia 4,47 eV-nál lép fel, ahol
törvényt követi, a rezonanciatartományban azonban számos rezonanciacsúcsa van (5. ábra). A legnagyobb rezonancia 4,47 eV-nál lép fel, ahol 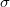 c = 9890 barn. Ezért a (17) szerinti kadmiumkorrekciónak itt nagy szerepe van. Ezért a fenti módszerrel egy Cd-burkolattal és egy anélkül besugárzott fólia aktivitását is meghatározzuk.
c = 9890 barn. Ezért a (17) szerinti kadmiumkorrekciónak itt nagy szerepe van. Ezért a fenti módszerrel egy Cd-burkolattal és egy anélkül besugárzott fólia aktivitását is meghatározzuk.
Az I. táblázat összefoglalja a termikus neutronfluxus abszolút értékének meghatározásához elvégzendő méréseket.
A termikus neutronfluxus abszolút értékének koincidencia
módszerrel történő meghatározásához elvégzendő mérések
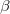 árnyékolás nélkül árnyékolás nélkül
|
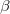 árnyékolással árnyékolással
| |||||
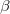 |
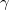 |
koincidencia | 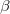 |
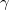 |
koincidencia | |
| "csupasz fólia" | 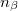 |
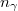 |
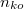 |
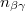 |
- | 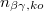
|
| Cd-os fólia | 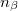 |
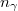 |
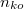 |
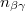 |
- | 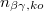
|
| fólia nélkül | - | 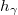 |
- | - | - | - |
A termikus neutronfluxus térfüggésének meghatározása
A diszprózium detektor aktivitása a fentiek szerint a termikus neutronfluxussal arányos, ezért az aktivitás mérése során nyert beütésszámok közvetlenül felhasználhatók a termikus neutronfluxus térbeli eloszlásának a kísérleti meghatározásához. Ha a reaktor különböző  pontjaiban besugárzott detektorok különbözők (más a térfogatuk, tömegük stb.), ezt kalibrációs tényezőkkel kell figyelembe venni. Erre nincs szükség, ha aktiválandó mintaként huzalt használunk, és a huzal egyes szakaszainak az aktivitását külön megmérjük.[8] A mérés folyamán azonban a minta aktivitása folyamatosan csökken, amit a mérésnél kompenzálni kell, vagy a kiértékelés során bomláskorrekciót kell alkalmazni. A gyakorlat során az első megoldást alkalmazzuk.
pontjaiban besugárzott detektorok különbözők (más a térfogatuk, tömegük stb.), ezt kalibrációs tényezőkkel kell figyelembe venni. Erre nincs szükség, ha aktiválandó mintaként huzalt használunk, és a huzal egyes szakaszainak az aktivitását külön megmérjük.[8] A mérés folyamán azonban a minta aktivitása folyamatosan csökken, amit a mérésnél kompenzálni kell, vagy a kiértékelés során bomláskorrekciót kell alkalmazni. A gyakorlat során az első megoldást alkalmazzuk.
A detektor aktivitása az egyes mérések kezdeti időpontjában a (12) formula szerint írható. Abban az esetben, amikor a minta aktivitása nem nagy a mérőberendezés holtidejéhez képest, a mérőberendezés által szolgáltatott 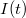 számlálási sebesség (intenzitás) arányos a minta aktivitásával:
számlálási sebesség (intenzitás) arányos a minta aktivitásával:
![\[ I(t) = \eta A(\underline r,t), \]](/images/math/4/b/0/4b06e9b5b21526f9d3bfa08ea06ad368.png) |
(23) |
ahol 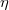 - számlálóberendezés hatásfoka. A mérés folyamán nem ezt az intenzitást, hanem valamely véges
- számlálóberendezés hatásfoka. A mérés folyamán nem ezt az intenzitást, hanem valamely véges 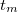 mérési idő alatti összes beütésszámot lehet megkapni:
mérési idő alatti összes beütésszámot lehet megkapni:
![\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}I(t')dt'. \]](/images/math/0/d/3/0d3ebbe159f9e98315c5bd8dabea39dd.png) |
Tekintve, hogy a számlásái sebesség a mérés közben csökken, ezt így írhatjuk:
![\[ B(\underline r,t) = \int\limits_{t}^{t+t_{m}}\eta A(\underline r,t')\textrm{e}^{-\lambda t'}dt' = \frac{\eta A(\underline r,t)(1-\textrm{e}^{\lambda t_{m}})}{\lambda} \approx \eta A(\underline r,t)t_{m}, \]](/images/math/e/f/8/ef8747eea4fe17ab4da6d612a222df61.png) |
(24) |
ahol a közelítő egyenlőség arra a (gyakori) esetre vonatkozik, amikor a mérési idő a bomláshoz képest rövid, vagyis, amikor 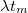
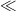 1.
1.
A mérés során kapott beütésszámok a (12) és (24) formulák összevonása révén hozhatók kapcsolatba a termikus neutronfluxussal:
![\[ B(\underline r,t) = \Phi_{th}(\underline r,t) \Bigg\{\frac{G\overline\sigma_{d}N_{d}(1-\textrm{e}^{-\lambda t_{a}}}{\lambda} \Bigg\}\textrm{e}^{-\lambda t}(1-\textrm{e}^{\lambda t_{m})} \]](/images/math/8/d/2/8d2eb991ad88be542e3a4af9ce603cb5.png) |
(25) |
A kapcsos zárójelben szereplő kifejezés a huzal minden pontjára azonos. Ahhoz, hogy a beütésszámokból a termikus neutronfluxussal arányos értékeket kapjunk, az
![\[ F(t_{m},t) = (1-\textrm{e}^{-\lambda t_{m}})\textrm{e}^{-\lambda t} \]](/images/math/1/2/4/124577725fdb42d4415b7e2d4ec2e58b.png) |
(26) |
függvény értékét kell meghatározni minden egyes adatpontra. Ennek érdekében a 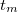 értékét a mérés kezdetén megfelelő értéken rögzítjük, és a huzal minden egyes pontjának mérésekor rögzítjük a mérés befejezésének időponját. Ennek felhasználásával a (26) szerinti korrekciót a 165Dy felezési idejének ismeretében tudjuk számolni ([6] alapján 2,334±0,001 óra).
értékét a mérés kezdetén megfelelő értéken rögzítjük, és a huzal minden egyes pontjának mérésekor rögzítjük a mérés befejezésének időponját. Ennek felhasználásával a (26) szerinti korrekciót a 165Dy felezési idejének ismeretében tudjuk számolni ([6] alapján 2,334±0,001 óra).
A mérési feladat
A gyakorlat során az aktív zóna E6 pozíciójában (ld. 7.ábra), függőleges egyenes mentén határozzuk meg a termikus neutronfluxus relatív eloszlását az előzőekben leírt módszerrel, majd ennek ismeretében a függőleges irányú reflektor-megtakarítást. A méréshez 10% Dy-ot tartalmazó, Dy-Al ötvözetből készült huzalt használunk. A termikus neutronfluxus abszolút értékét Au fólia felaktiválása révén határozzuk meg.
A méréshez szükséges eszközök, anyagok
A mérés elvégzéséhez a reaktoron és a radioaktív minták kezeléséhez, méréséhez szükséges eszközökön kívül szükség van a huzalaktivitás-mérő berendezésre is. Mivel ez egyedi célműszer, működését részletesen ismertetjük.
A méréshez szükséges eszközök, anyagok listája
- reaktor + mintaszállító csőposta berendezés
- plexi tartórúd a huzal számára
- koincidencia mérőberendezés
- huzalaktivitás-mérő berendezés
- Dy-Al ötvözetből készült huzal
- Dy-Al ötvözetből készült fólia
- Au fóliák
- Al és Cd kapszulák a fóliák számára
- sugárvédelmi felszerelés (gumikesztyű, csipesz stb.)
A huzalaktivitás mérésének elve és a mérőberendezés leírása
A termikus neutronfluxus térbeli eloszlásának meghatározására Dy-Al ötvözetből készült huzalt használunk. A huzal hossza mentén a helyfüggő aktivitást a huzalaktivitásmérő berendezéssel határozzuk meg. Mivel a huzal a  axiális koordináta mentén helyezkedik el, a (25)-ben szereplő
axiális koordináta mentén helyezkedik el, a (25)-ben szereplő 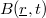 helyett most
helyett most 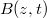 -t írunk. A huzalaktivitásmérő berendezés a következő részekből áll:
-t írunk. A huzalaktivitásmérő berendezés a következő részekből áll:
- fogasléccel ellátott tartósín, amelyben a huzalt rögzítjük
- ólomtorony, amelyen keresztül tolható a huzaltartó sín
- szcintillációs β-mérőfej az ólomtoronyba illesztve, alatta rézből készült kollimátor, hogy a huzalnak csak egy pár mm-es darabját „lássa”
- léptetőmotor, amely gondoskodik a sín továbbításáról a detektor alatt
- léptetőmotor vezérlőegység USB porton keresztül számítógéphez csatlakoztatva
- digitális spektrum-analizátor (Canberra DSA1000) a
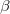 -mérőfej jeleinek feldolgozására, szintén a számítógéphez csatlakoztatva
-mérőfej jeleinek feldolgozására, szintén a számítógéphez csatlakoztatva
- számítógép megfelelő adatgyűjtő szofverrel (GenieMot)
a - automata szabályzórúd; b1, b2 - biztonságvédelmi rudak; c - gyors csőposta; d - termikus csőposták; e - függőleges besugárzó csatornák vízben; f - fűtőelem-kazetták; g - grafit reflektorelemek; h - függőleges besugárzó csatornák grafitban; i - függőleges besugárzó csatorna fűtőelem-kazettában; j - neutron-forrás; k - kézi szabályzórúd.
A mérés menete
A termikus neutronfluxus relatív eloszlásának mérése
Az előkészületek során a mérőhuzalt a plexi besugárzó tartórúd vájatába helyezzük. A plexi moderációs tulajdonságai hasonlítanak a vízéhez, így az aktív zóna fluxuseloszlásának zavarása csekély.
A besugárzó rudat az operátor az álló reaktor E6 (D5-el szomszédos) pozíciójába helyezi, majd elvégzi a besugárzást. A besugárzás közben a D5 pozicióban lévő csőpostában a Dy fóliát is felaktiváljuk. Tekintettel arra, hogy Dy-Al ötvözettel dolgozunk, az Al zavaró aktivitásának lecsengése érdekében a besugárzás után a mintákat legalább 20 percig pihentetni kell. (Az alumínium felezési ideje 2,24 perc.) Ezután a huzalt a tartórúdból kivesszük, és a huzalaktivitás-mérő berendezés tartósínjébe helyezzük. A mérés során a 165Dy bomlásából származó 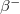 részeket detektáljuk.
részeket detektáljuk.
A 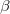 -mérőfej segítségével először a Cd-burkolattal és anélkül besugárzott Dy fóliákat mérjük meg. A beütésszámok összehasonlításával meggyőződünk róla, hogy a valóban igaz a feltételezés, hogy az aktvitásnak csak elhanyagolhatóan csekély része származik az epitermikus neutronok által kiváltott reakciókból. Így a „csupaszon” besugárzott huzal aktivitás-eloszlása valóban a termikus fluxus eloszlását fogja visszaadni.
-mérőfej segítségével először a Cd-burkolattal és anélkül besugárzott Dy fóliákat mérjük meg. A beütésszámok összehasonlításával meggyőződünk róla, hogy a valóban igaz a feltételezés, hogy az aktvitásnak csak elhanyagolhatóan csekély része származik az epitermikus neutronok által kiváltott reakciókból. Így a „csupaszon” besugárzott huzal aktivitás-eloszlása valóban a termikus fluxus eloszlását fogja visszaadni.
Ezután tartósínt az induló pozícióba toljuk, majd a számítógépen beállítjuk a mérési pontokat és a mérési időt. Szintén be kell állítani azt a spektrum tartományt, amelyben a beütésszámok összegzésre kerülnek. A mérés végén egy ASCII filet kapunk, amelynek sorai tartalmazzák a pozíciót, a megadott mérési idő alatt kapott beütésszámot a kiválasztott spektrum tartományban, valamint az adott pozícióban végzett mérés befejezésének időpontját.
A termikus neutronfluxus abszolút értékének meghatározása
Két azonos méretű és tömegű arany fóliát sugárzunk be - egy csupaszt és egy kadmiumos borításút - a reaktor D5 pozíciójában elhelyezkedő besugárzó csatornában. A polietilén besugárzó tokba zárt fóliákat a besugárzó csatornához csatlakozó mintaszállító csőposta rendszer segítségével juttatjuk az üzemelő reaktorba. A besugárzás befejezésének időpontját jegyezzük fel, és mérjük meg az egyes fóliák aktivitásának méréséig eltelt
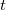 időt. A koincidencia számláló-berendezés segítségével megmérjük a minták aktivitását, amelyek megfelelnek a (17)-ben szereplő
időt. A koincidencia számláló-berendezés segítségével megmérjük a minták aktivitását, amelyek megfelelnek a (17)-ben szereplő 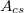 és
és 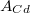 értékeknek.
értékeknek.
A mérések kiértékelése
A termikus neutronfluxus relatív eloszlásának kiértékelése
Az egyes pontokban mért beütésszámokon (26) alapján el kell végezni a bomlási idő korrekciót. Az így kapott korrigált adatpontok helyfüggése a termikus neutronfluxuseloszlás helyfüggésével arányos (vö. (25)). Ábrázoljuk a mérési pontokat grafikusan, majd a mért görbe középső szakaszára (3) képlet szerinti koszinusz függvényt illesztve, határozzuk meg az axiális reflektor-megtakarítást a (4) képlet alapján![9]
A relatív fluxusmérés hibaszámítása
A valószínűség-elméletből tudjuk, hogy a beütésszámok a Poisson-eloszlást követik. Ebből következik, hogy az egyes beütésszámok szórásnégyzete megegyezik a várható értékükkel. Az utóbbiakat magukkal a beütésszámokkal közelítjük, tehát általában igaz, hogy
![\[ D^{2}(B_{i}) = M(B_{i}) \approx B_{i}. \]](/images/math/7/d/1/7d1f9956d7a54761e4bd72ec4663edc1.png) |
(27) |
Ez a közelítő képlet ugyanazzal a feltétellel érvényes, mint maga az egész mérési módszer: mind a holtidő, mind a hattér hatása elhanyagolható. A holtidő korrekciójának legegyszerűbb módja, ha a 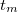 mérési időt élő időben (live time) adjuk meg. Ekkor is ügyelni kell azonban, hogy lehetőleg a legnagyobb beütésszámoknál se haladja meg a holtidő a néhány %-ot.
mérési időt élő időben (live time) adjuk meg. Ekkor is ügyelni kell azonban, hogy lehetőleg a legnagyobb beütésszámoknál se haladja meg a holtidő a néhány %-ot.
A termikus neutronfluxus abszolút értékének hibaszámítása
A termikus neutronfluxus abszolút értékének a hibaszámítása lényegesen bonyolultabb feladat, mint a relatív eloszlásé. Mindenekelőtt két fajta hibát kell megkülönböztetnünk: statisztikus és szisztematikus hiba.[10]
Statisztikus hiba becslése
Élve azzal a feltételezéssel, hogy a beütésszámok Poisson-eloszlásúak, a (22) alapján számított aktivitások szórásnégyzetét a hibaterjedés ismert képlete (pl. [6]) alapján 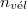 elhanyagolása után a következőképpen írhatjuk fel:
elhanyagolása után a következőképpen írhatjuk fel:
![\[ D^{2}A = (n_{\beta}+n_{\beta\gamma})\Big(\frac{n'_{\gamma}}{n'_{ko}}\Big)^{2}+(n_{\gamma}+h_{\gamma})\Big(\frac{n'_{\beta}}{n'_{ko}}\Big)^{2}+(n_{ko}+n_{\beta\gamma,ko})\Big(\frac{n'_{\beta}n'_{\gamma}}{{n{^{'}_{ko}}^2 }}\Big)^{2} \]](/images/math/8/4/5/8451bfa137044c6e80ac963f433fe472.png) |
(28) |
Ebből a relatív szórás a következőképpen adódik:
![\[ r(A) = \frac{D(A)}{A} = \sqrt {\frac{(n_{\beta}+n_{\beta\gamma})}{{n'_{\beta}}^2}+\frac{(n_{\gamma}+h_{\gamma})}{{n'_{\gamma}}^2}+\frac{(n_{ko}+n_{\beta\gamma,ko})}{{n'_{ko}}^2}} = \sqrt {r^{2}(n'_{\beta})+r^{2}(n'_{\gamma})+r^{2}(n'_{ko})} \]](/images/math/0/a/2/0a22516361ec59fa68bd48df50160603.png) |
(29) |
Az egyes beütésszámok relatív szórásai tehát összeadódnak. Mivel a három mért érték közül az 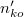 várhatóan nagyságrendileg kisebb a másik kettőnél, ez fogja legjobban befolyásolni az aktivitás statisztikus hibáját. A mérési időt ezért úgy kell megválasztani, hogy már az
várhatóan nagyságrendileg kisebb a másik kettőnél, ez fogja legjobban befolyásolni az aktivitás statisztikus hibáját. A mérési időt ezért úgy kell megválasztani, hogy már az 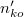 is elegendően nagy legyen.
is elegendően nagy legyen.
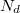 kivételével a (18) képletben szereplő többi mennyiség számított mennyiség, amelyek hibája szisztematikus hibának minősül (lásd alább).
kivételével a (18) képletben szereplő többi mennyiség számított mennyiség, amelyek hibája szisztematikus hibának minősül (lásd alább). 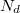 ismeretének a pontossága gyakorlatilag megegyezik a fóliák
ismeretének a pontossága gyakorlatilag megegyezik a fóliák 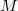 tömegének a pontosságával (vö. (16) képlet).[11]Ennek alapján a termikus neutronfluxus relatív szórása:
tömegének a pontosságával (vö. (16) képlet).[11]Ennek alapján a termikus neutronfluxus relatív szórása:
![\[ \frac{D(\Phi_{th})}{\Phi_{th}} \approx \sqrt {\frac{D^{2}(M)}{M^{2}} + \frac{D^{2}(A_{CS})+D^{2}(A_{Cd})} {(A_{CS}-A_{Cd})}}. \]](/images/math/f/2/2/f22ba5d042298776be6a380f65420084.png) |
(30) |
Szisztematikus hiba
A (30) alatti statisztikus hiba a mérés gondos végrehajtásával akár 1÷2%-ra is leszorítható. Nehezebb csökkenteni a szisztematikus hibákat, amelyek értéke akár 10% nagyságrendű is lehet. Ezek közül a legfontosabbak:
- A
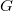 önárnyékolási tényező nehezen számolható mennyiség. Ennek oka egyrész az, hogy a (11) képlet csak közelítő (különösen a kadmiumborítású fólia esetében), másrészt bonyolult kiszámítani a képletben szereplő
önárnyékolási tényező nehezen számolható mennyiség. Ennek oka egyrész az, hogy a (11) képlet csak közelítő (különösen a kadmiumborítású fólia esetében), másrészt bonyolult kiszámítani a képletben szereplő 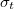 hatáskeresztmetszetet.
hatáskeresztmetszetet.
- Hasonlóan sok feltevésre van szükség a (18) képletben szereplő
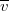
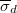 szorzat számításhoz. Néhány példa a felmerülő problémákra: csak számításból ismerjük a (14) képletbe helyettsítendő neutronspektrumot, az arány hatáskeresztmetszét csak véges pontossággal ismerjük, stb.
szorzat számításhoz. Néhány példa a felmerülő problémákra: csak számításból ismerjük a (14) képletbe helyettsítendő neutronspektrumot, az arány hatáskeresztmetszét csak véges pontossággal ismerjük, stb.
- A (18) képlet nevezőjében szereplő
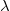 bomlási állandót csak véges pontossággal ismerjük. Ennek hatása azonban legfeljebb ezrelékes nagyságrendű (pl. a 198Au felezési ideje [6] alapján: 2,6948±0,0012 nap). További pontatlanság, hogy a
bomlási állandót csak véges pontossággal ismerjük. Ennek hatása azonban legfeljebb ezrelékes nagyságrendű (pl. a 198Au felezési ideje [6] alapján: 2,6948±0,0012 nap). További pontatlanság, hogy a 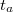 -t tartalmazó aktiválási tényező feltételezi, hogy az aktiválás kezdetén a minta pillanatszerűen kerül a besugárzási pozícióba, majd onnan vissza. Ez korrigálható, ha a (8) helyett egy olyan differenciálegyenletet oldunk meg, amely figyelembe veszi a neutronfluxus tényleges időfüggését a minta mozgatása során. Azonban ha az aktiválás ideje 10 s vagy hosszabb, akkor ez a korrekció 1% alatt van.
-t tartalmazó aktiválási tényező feltételezi, hogy az aktiválás kezdetén a minta pillanatszerűen kerül a besugárzási pozícióba, majd onnan vissza. Ez korrigálható, ha a (8) helyett egy olyan differenciálegyenletet oldunk meg, amely figyelembe veszi a neutronfluxus tényleges időfüggését a minta mozgatása során. Azonban ha az aktiválás ideje 10 s vagy hosszabb, akkor ez a korrekció 1% alatt van.
Végeredményben látjuk, hogy a számos szisztematikus hiba miatt a neutronfluxus méréséről valójában nem beszélhetünk. Amiről szó lehet, az a neturonfluxus közelítő meghatározása, de ennek eredménye erősen függ a kiértékelésben tett feltevésektől.
Ellenőrző kérdések
- Mi a termikus neutronfluxus?
- Mi a különbség az extrapolációs távolság és a reflektor-megtakarítás között?
- Mi az átlagos aktivációs hatáskeresztmetszet?
- Mi a szerepe az önárnyékolási tényezőnek, és hogyan határozzuk meg?
- Hogyan becsüljük a termikus neutronfluxust mért aktivitások alapján?
- Milyen összefüggés van a huzal aktivitásának helyfüggése és a termikus fluxus axiális eloszlása között?
- Hogyan határozzuk meg a termikus neutronfluxus abszolút értékét?
- A termikus neutronfluxus abszolút értékének meghatározásakor milyen statisztikus és szisztematikus hibák lépnek fel?
Irodalom
[1] G.I.Bell, S.Classtone: Nuclear Reactor Theory, New York etc., Van Nostrand Reinhold (1973) (Alapos, áttekintő elméleti munka)
[2] J.J. Duderstadt, L.J. Hamilton: Nuclear Reactor Analysis, Wiley and Sons (1976).
[3] Szatmáry Zoltán: Bevezetés a reaktorfizikába, Akadémiai Kiadó, Budapest (2000)
[4] Csom Gyula: Atomerőművek üzemtana I., A reaktorfizika és –technika alapjai, Műegyetemi Kiadó (1997)
[5] NuDat 2 adatbázis, National Nuclear Data Center, Brookhaven National Laboratory, http://www.nndc.bnl.gov/nudat2/
[6] Jagdish K. Tuli: Nuclear Wallet Cards, National Nuclear Data Center, Brookhaven National Laboratory, Upton, New York, U.S.A. (2000)
[7] Szatmáry Zoltán: Mérések kiértékelése, egyetemi jegyzet, BME Természettudományi
Külső hivatkozások
A Neutron aktivációs analitika laborjegyzet forrása elérhető a [1] linken.
Lábjegyzetek
- ↑ A besugárzott anyag egy atomjára [vagy tömegegységére] vonatkoztatott aktivitás.
- ↑ Általában neutronhőmérsékletnek szoktuk nevezni, amely némileg magasabb, mint a reaktor abszolút hőmérséklete.
- ↑ A reaktorelmélet alapjául szolgáló diffúzióegyenlet határfeltételei szerint a reaktor tényleges felületét az extrapolációs távolsággal kijjebb tolva kapott felületen (az ún. extrapolált határfelületen) kell megkövetelni a fluxus eltűnését. Az extrapolációs távolság értéke vízzel moderált reaktorokban néhány mm. Mérésünk szempontjából nincs jelentősége.
- ↑ Innen ered a reflektor neve.
- ↑ A reflektor-megtakarítást nem szabad összetéveszteni az extrapolációs távolsággal, hiszen az utóbbi a csupasz reaktornak a vákuummal határos felületén, az előbbi pedig az aktív zónának a reflektorral határos felületén van definiálva. Értékük is jelentősen eltér: a reflektor-megtakarítás sokkal nagyobb, mint az extrapolációs távolság.
- ↑ Az aktivációs hatáskeresztmetszet általában a befogási hatáskeresztmetszet. Vannak azonban eltérések is. Amikor például a detektor hasadóanyag, és a hasadási termékek összaktivitását mérjük, az aktivációs hatáskeresztmetszet a hasadási hatáskeresztmetszettel azonos.
- ↑ Ez az ún. kadmium-levágási energia: a kadmium hatáskeresztmetszetét ez alatti neutronenergiákra gyakorlatilag végtelennek, a felettiekre pedig nullának vesszük. Nyilvánvaló, hogy a levágási energia függ a kadmiumborítás vastagságától.
- ↑ Hallgatólagosan feltételezzük, hogy a huzal átmérője, Dy-tartalma stb. a huzal mentén végig azonos.
- ↑ Erre a feladatra általában megfelelő illesztő programra van szükség.
- ↑ A matematikai statisztikában ezeknek a fogalmaknak a neve: szórás, illetve torzítás. A fent használt elnevezések csak köznyelviek, és a matematikában nem elfogadottak.
- ↑ A csupasz és kadmiumborítású fólia tömege lehet eltérő is. Ebben az esetben a hibaszámítási képlet jóval bonyolultabb. Az egyszerűség kedvéért feltételezzük, hogy tömegeik azonosak.
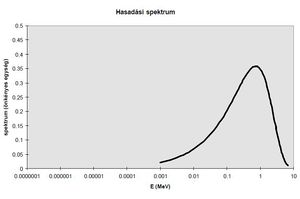
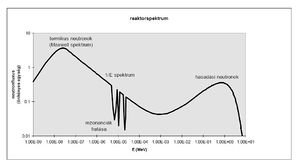
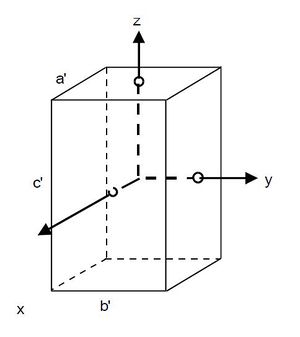
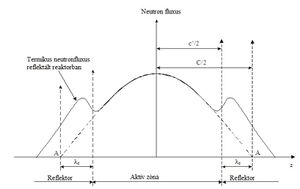
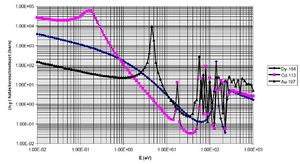
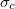 változása a neutronenergia függvényében 164Dy, 197Au és 113Cd esetében
változása a neutronenergia függvényében 164Dy, 197Au és 113Cd esetében