„3. Mérés: RC-körök vizsgálata” változatai közötti eltérés
a |
a |
||
| 52. sor: | 52. sor: | ||
| Egy $L$ induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg: | | Egy $L$ induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg: | ||
| − | $$ U=L\frac{dI}{dt} $$ | + | $$ U=L\frac{dI}{dt}. $$ |
Az időben harmonikusan változó áramot ismét komplex alakban adjuk meg | Az időben harmonikusan változó áramot ismét komplex alakban adjuk meg | ||
| 92. sor: | 92. sor: | ||
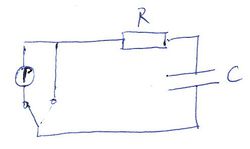
| Az ábrán látható soros RC körrel vizsgálhatjuk egy $C$ kapacitású kondenzátor feltöltődését és kisülését. Ha hosszú időn keresztül véges $U$ feszültséget kapcsolunk a körre a kondenzátor feltöltődik. Ezt követően, t=0 időpillanatban a kapcsolót átkapcsolva rövidre zárjuk az áramkört, azaz a bemeneti pontok azonos feszültségre kerülnek: | | Az ábrán látható soros RC körrel vizsgálhatjuk egy $C$ kapacitású kondenzátor feltöltődését és kisülését. Ha hosszú időn keresztül véges $U$ feszültséget kapcsolunk a körre a kondenzátor feltöltődik. Ezt követően, t=0 időpillanatban a kapcsolót átkapcsolva rövidre zárjuk az áramkört, azaz a bemeneti pontok azonos feszültségre kerülnek: | ||
| − | $$ U_R+U_C=0 $$ | + | $$ U_R+U_C=0. $$ |
Ekkor a kondenzátor fegyverzetein tárolt töltések átáramlanak az ellentétes fegyverzetre, hogy az új egyensúly elérését követően nulla feszültség essen a bemeneten (és a kondenzátoron is). Ezt az áramot például a fenti egyenlet deriválásával számíthatjuk ki: | Ekkor a kondenzátor fegyverzetein tárolt töltések átáramlanak az ellentétes fegyverzetre, hogy az új egyensúly elérését követően nulla feszültség essen a bemeneten (és a kondenzátoron is). Ezt az áramot például a fenti egyenlet deriválásával számíthatjuk ki: | ||
| − | $$ \frac{dU_R}{dt}+\frac{dU_C}{dt}=R\frac{dI}{dt}+\frac{I}{C}=0 $$ | + | $$ \frac{dU_R}{dt}+\frac{dU_C}{dt}=R\frac{dI}{dt}+\frac{I}{C}=0. $$ |
Tehát az áramkörben folyó időfüggő áram az alábbi differenciálegyenletet elégíti ki: | Tehát az áramkörben folyó időfüggő áram az alábbi differenciálegyenletet elégíti ki: | ||
| − | $$ \frac{dI}{dt}=-\frac{I}{RC} $$ | + | $$ \frac{dI}{dt}=-\frac{I}{RC}. $$ |
Az $RC$ szorzat láthatóan idő dimenziójú, érdemes bevezetni a $\tau$=$RC$ időállandót. Az exponenciális függvény kielégíti a fenti egyenletet, hiszen deriváltja szintén exponenciális: | Az $RC$ szorzat láthatóan idő dimenziójú, érdemes bevezetni a $\tau$=$RC$ időállandót. Az exponenciális függvény kielégíti a fenti egyenletet, hiszen deriváltja szintén exponenciális: | ||
| 117. sor: | 117. sor: | ||
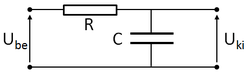
| Megvizsgálhatjuk a soros RC kör harmonikus meghajtásra adott válaszát is. Például a meghajtó $U_{be}$ feszültség $U_{ki}$=$U_C$ kondenzátor feszültségre gyakorolt hatását. Az eszközökön eső feszültség a meghajtó feszültséggel lesz egyenlő: | | Megvizsgálhatjuk a soros RC kör harmonikus meghajtásra adott válaszát is. Például a meghajtó $U_{be}$ feszültség $U_{ki}$=$U_C$ kondenzátor feszültségre gyakorolt hatását. Az eszközökön eső feszültség a meghajtó feszültséggel lesz egyenlő: | ||
| − | $$ U_R+U_C=U_{be} $$ | + | $$ U_R+U_C=U_{be}. $$ |
Az impedanciáról tanultakat felhasználva | Az impedanciáról tanultakat felhasználva | ||
| − | $$ U_{be}=RI+Z_CI $$ | + | $$ U_{be}=RI+Z_CI, $$ |
| − | $$ U_{ki}=Z_CI=\frac{Z_C}{R+Z_C}U_{be}=\frac{1}{i\omega RC+1}U_{be}=\frac{1}{i\omega\tau+1}U_{be}$$ | + | $$ U_{ki}=Z_CI=\frac{Z_C}{R+Z_C}U_{be}=\frac{1}{i\omega RC+1}U_{be}=\frac{1}{i\omega\tau+1}U_{be}. $$ |
| [[File:RC.png|250px|thumb|right|Soros RC kör]] | | [[File:RC.png|250px|thumb|right|Soros RC kör]] | ||
| 131. sor: | 131. sor: | ||
| Az amplitúdók arányát és a fáziskülönbséget az alábbi arány számításával határozhatjuk meg: | | Az amplitúdók arányát és a fáziskülönbséget az alábbi arány számításával határozhatjuk meg: | ||
| − | $$ \frac{U_{ki}}{U_{be}}=\frac{\vert U_{ki}\vert}{\vert U_{be}\vert} e^{\varphi_{ki}-\varphi_{be}} $$ | + | $$ \frac{U_{ki}}{U_{be}}=\frac{\vert U_{ki}\vert}{\vert U_{be}\vert} e^{\varphi_{ki}-\varphi_{be}}. $$ |
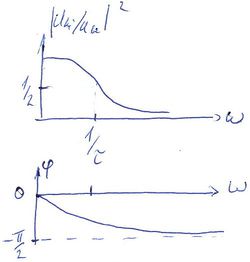
Az amplitúdóarányt az alábbi Lorentz görbe adja meg: | Az amplitúdóarányt az alábbi Lorentz görbe adja meg: | ||
| − | $$ \frac{\vert U_{ki}\vert^2}{\vert U_{be}\vert^2}=\frac{1}{1+(\omega\tau)^2} $$ | + | $$ \frac{\vert U_{ki}\vert^2}{\vert U_{be}\vert^2}=\frac{1}{1+(\omega\tau)^2}. $$ |
Tehát 1/$\tau$ körfrekvencia alatt a feszültség nagyrészt a kapacitáson esik, míg nagyobb frekvenciákon az impedanciája és a rajta eső feszültség is lecsökken. A fáziskülönbséghez a komplex szám fázisát kell meghatározni: | Tehát 1/$\tau$ körfrekvencia alatt a feszültség nagyrészt a kapacitáson esik, míg nagyobb frekvenciákon az impedanciája és a rajta eső feszültség is lecsökken. A fáziskülönbséghez a komplex szám fázisát kell meghatározni: | ||
| 143. sor: | 143. sor: | ||
A fázisszöget a képzetes és valós rész hányadosa adja meg: | A fázisszöget a képzetes és valós rész hányadosa adja meg: | ||
| − | $$ tg(\varphi)=-\omega\tau $$ | + | $$ tg(\varphi)=-\omega\tau. $$ |
| [[File:RC_trans.jpg|250px|thumb|right|Amplitúdóarány és fáziskülönbség frekvencia függése soros RC körben.]] | | [[File:RC_trans.jpg|250px|thumb|right|Amplitúdóarány és fáziskülönbség frekvencia függése soros RC körben.]] | ||
|} | |} | ||
A lap 2019. december 6., 11:34-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Időben harmonikusan változó jel
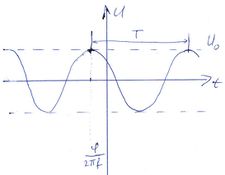
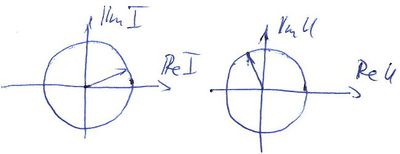
Lineáris áramkörök és harmonikusan változó áram és feszültség jelek részletes tárgyalását lásd a Kisérleti Fizika 1 kurzus rezgésekről szóló fejezetében [1]. A fontosabb mennyiségeket és összefüggéseket alább összefoglaljuk. Az ábrán egy  periodus idővel változó, periodus idővel változó,  =1/ =1/ frekvenciájú feszültség jel látható. Ha a jel amplitúdója frekvenciájú feszültség jel látható. Ha a jel amplitúdója  és fázisa és fázisa  , az időfüggést az alábbi alakban adhatjuk meg: , az időfüggést az alábbi alakban adhatjuk meg:
![\[ U(t)=U_0cos(2\pi ft+\varphi).\]](/images/math/9/6/e/96eab080ec8a57c04dc37fbab0d08b88.png) Hasznos még bevezetni a körfrekvenciát ![\[ U(t)=U_0e^{i(\omega t+\varphi)}=U_0e^{i\varphi} e^{i\omega t}.\]](/images/math/8/a/d/8add4dcdf3c333d2eb2d49999df631c7.png) A harmonikusan változó feszültség a komplex síkon egy |
Lineáris áramköri elemek
Lineáris áramköri elemek esetén az áthajtott áramot és az elemen eső feszültséget vagy azok deriváltjait lineáris összefüggés kapcsolja össze. Legegyszerűbb ilyen elem az ohmikus ellenállás:
![\[ U=RI \]](/images/math/0/6/3/063b550b153e506421bd709bd6808ca7.png) Az ellenálláson áthaladó áramot az alábbi komplex alakban adhatjuk meg ![\[ I=I_0e^{i\omega t}, \]](/images/math/b/d/b/bdb488bc3e2778d55a33d3ef116d5107.png) melyből kiszámíthatjuk a rajta eső feszültsége: ![\[ Ue^{i\omega t}=RI_0e^{i\omega t}. \]](/images/math/0/d/8/0d8fb867d5d69c2aac8c45bdf2fdc5e9.png) Tehát az áram és a feszültség fázisa azonos az amplitúdokat pedig a |
Egy  induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg: induktivitással jellemezhető tekercs esetén a tekercs kapocsain mérhető feszültséget az alábbi képlet adja meg:
![\[ U=L\frac{dI}{dt}. \]](/images/math/9/7/9/9794a92a5bdf42258d2b83d9675f7712.png) Az időben harmonikusan változó áramot ismét komplex alakban adjuk meg ![\[ I=I_0e^{i\omega t}, \]](/images/math/b/d/b/bdb488bc3e2778d55a33d3ef116d5107.png) melyből a tekercs kapcsain mérhető feszültség: ![\[ Ue^{i\omega t}=i\omega LI_0e^{i\omega t}. \]](/images/math/3/6/a/36a36501bee526a2533ccf5e17cae0e5.png) Tehát a feszültség fázisa |
A  kapacitással jellemezhető kondenzátor esetén ismert, hogy kapacitással jellemezhető kondenzátor esetén ismert, hogy
![\[ Q=CU. \]](/images/math/e/c/3/ec33c1bde7608b580162804655742f21.png) Ezt az összefüggést deriválva és átrendezve a korábbiakhoz hasonló alakú kifejezést kapunk: ![\[ \frac{dU}{dt}=\frac{1}{C}I, \]](/images/math/9/3/a/93ad8959bee68c81cbf1f05351c1ae71.png) hiszen a kondenzátor eltolási árama a töltésváltozással egyenlő. A komplex feszültség-áram összefüggés az alábbi alakot ölti: ![\[ Ue^{i\omega t}=\frac{1}{i\omega C}I_0e^{i\omega t}. \]](/images/math/8/d/b/8db535ea01ab073f095b45769b5e1dea.png) Tehát a feszültség fázisa - |
Soros RC kör
Az ábrán látható soros RC körrel vizsgálhatjuk egy  kapacitású kondenzátor feltöltődését és kisülését. Ha hosszú időn keresztül véges kapacitású kondenzátor feltöltődését és kisülését. Ha hosszú időn keresztül véges  feszültséget kapcsolunk a körre a kondenzátor feltöltődik. Ezt követően, t=0 időpillanatban a kapcsolót átkapcsolva rövidre zárjuk az áramkört, azaz a bemeneti pontok azonos feszültségre kerülnek: feszültséget kapcsolunk a körre a kondenzátor feltöltődik. Ezt követően, t=0 időpillanatban a kapcsolót átkapcsolva rövidre zárjuk az áramkört, azaz a bemeneti pontok azonos feszültségre kerülnek:
![\[ U_R+U_C=0. \]](/images/math/f/9/2/f92916ad79dcf03962b342ea5ef14a5c.png) Ekkor a kondenzátor fegyverzetein tárolt töltések átáramlanak az ellentétes fegyverzetre, hogy az új egyensúly elérését követően nulla feszültség essen a bemeneten (és a kondenzátoron is). Ezt az áramot például a fenti egyenlet deriválásával számíthatjuk ki: ![\[ \frac{dU_R}{dt}+\frac{dU_C}{dt}=R\frac{dI}{dt}+\frac{I}{C}=0. \]](/images/math/2/5/5/25571c744682373fb7c8bf67a588c02b.png) Tehát az áramkörben folyó időfüggő áram az alábbi differenciálegyenletet elégíti ki: ![\[ \frac{dI}{dt}=-\frac{I}{RC}. \]](/images/math/7/8/d/78def24c4d11e83455fbde7b363d2c8d.png) Az ![\[ I=I_0e^{-t/\tau}, \]](/images/math/7/9/8/798aac8af6f3d136b9b4089061c3fa64.png) ahol ![\[ Q=\int_0^\infty I_0e^{-t/\tau}dt= -I_0\tau e^{-\infty/\tau}+I_0\tau e^{0/\tau}=I_0\tau. \]](/images/math/9/5/6/956b6c0727da6a80217e96e229de95cf.png) |
Megvizsgálhatjuk a soros RC kör harmonikus meghajtásra adott válaszát is. Például a meghajtó 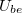 feszültség feszültség 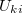 = =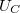 kondenzátor feszültségre gyakorolt hatását. Az eszközökön eső feszültség a meghajtó feszültséggel lesz egyenlő: kondenzátor feszültségre gyakorolt hatását. Az eszközökön eső feszültség a meghajtó feszültséggel lesz egyenlő:
![\[ U_R+U_C=U_{be}. \]](/images/math/d/e/2/de224daba9e1bd0a6f32c4496f62a106.png) Az impedanciáról tanultakat felhasználva ![\[ U_{be}=RI+Z_CI, \]](/images/math/4/e/f/4ef90b2d8c6b5e3a91924c1c906f8660.png) ![\[ U_{ki}=Z_CI=\frac{Z_C}{R+Z_C}U_{be}=\frac{1}{i\omega RC+1}U_{be}=\frac{1}{i\omega\tau+1}U_{be}. \]](/images/math/7/0/9/7094d09710c2c8225257126e927e7743.png) |
Az amplitúdók arányát és a fáziskülönbséget az alábbi arány számításával határozhatjuk meg:
![\[ \frac{U_{ki}}{U_{be}}=\frac{\vert U_{ki}\vert}{\vert U_{be}\vert} e^{\varphi_{ki}-\varphi_{be}}. \]](/images/math/c/3/b/c3bcf984773979bc2e242816c48ed759.png) Az amplitúdóarányt az alábbi Lorentz görbe adja meg: ![\[ \frac{\vert U_{ki}\vert^2}{\vert U_{be}\vert^2}=\frac{1}{1+(\omega\tau)^2}. \]](/images/math/6/7/4/674a57cc6ab0f9f042b690a9ae1a21cc.png) Tehát 1/ ![\[ \frac{U_{ki}}{U_{be}}=\frac{1-i\omega\tau}{1+(\omega\tau)^2}. \]](/images/math/f/c/0/fc0759a8a4503fd115b04efe38250c06.png) A fázisszöget a képzetes és valós rész hányadosa adja meg: ![\[ tg(\varphi)=-\omega\tau. \]](/images/math/1/f/5/1f5efc73acdf1bec4f0ecc19fde4041a.png) |
Mérési feladatok
1. Feladat A próbapanelen állítsunk össze egy  =10 k
=10 k ellenállásból és az ismeretlen
ellenállásból és az ismeretlen  kapacitású kondenzártorból (barna áramköri elem) álló soros kapcsolást.
kapacitású kondenzártorból (barna áramköri elem) álló soros kapcsolást. 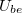 bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre
bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre  =1 kHz frekvenciájú,
=1 kHz frekvenciájú, 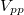 =1 V-os szinusz jelet. A bemeneti és a kondenzátoron eső
=1 V-os szinusz jelet. A bemeneti és a kondenzátoron eső 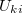 kimeneti feszültséget kapcsoljuk a mérőkártya AI 0+, AI 0- és AI 1+, AI 1- csatlakozói közé. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást valamint a triggert.
kimeneti feszültséget kapcsoljuk a mérőkártya AI 0+, AI 0- és AI 1+, AI 1- csatlakozói közé. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást valamint a triggert.
Rögzítsük mindkét csatornán a feszültség időfüggését, majd az oszcilloszkóp program STOP gombjának megnyomasa után, a LOG gomb segítségével mentsük el a mért jelalakokat. Az IGOR segítségével olvassuk be a jeleket. (A loadwaves/tweaks menu beállításai: az összes elválasztó jelet ki kell pipálni, date format: year.month.day, line containing column label: 2, first line containing data: 5.) A data/change wave scaling menüvel állítsuk be az időtengely lépésközét. (Figyelem az oszcilloszkóp időalapjának változtatásával változik a skálázás is!) Illesszünk szinusz görbét, és az illesztésből határozzuk meg a két jel amplitúdójának arányát, illetve a fázisuk különbséget. Számítsuk ki az ismeretlen  kapacitást és becsüljük meg a mérés hibáját. Végezzük el a fenti mérést 100 Hz-en, 330 Hz-en, 3.3 kHz-en és 10 kHz-en is. A mért amplitúdó arányokat és fáziskülönbségeket a frekvencia logaritmusának függvényében ábrázoljuk. Miért nevezik ezt a kapcsolást aluláteresztő szűrőnek?
kapacitást és becsüljük meg a mérés hibáját. Végezzük el a fenti mérést 100 Hz-en, 330 Hz-en, 3.3 kHz-en és 10 kHz-en is. A mért amplitúdó arányokat és fáziskülönbségeket a frekvencia logaritmusának függvényében ábrázoljuk. Miért nevezik ezt a kapcsolást aluláteresztő szűrőnek?
2. Feladat Vizsgáljuk tovább a fenti áramkört! A bemeneti pontokra  =100 Hz frekvenciájú négyszögjelet kapcsoljunk. Az oszcilloszkóp beállítása után, mentsük el a kimeneti jelet. A kisülési görbékre exponenciális függvényt illesztve határozzuk meg az időállandót, majd számítsuk ki a
=100 Hz frekvenciájú négyszögjelet kapcsoljunk. Az oszcilloszkóp beállítása után, mentsük el a kimeneti jelet. A kisülési görbékre exponenciális függvényt illesztve határozzuk meg az időállandót, majd számítsuk ki a  kapacitás értékét ezzel a módszerrel is.
kapacitás értékét ezzel a módszerrel is.
 =2
=2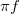 . Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
. Az időbeli változást leíró differenciál egyenletek könnyebb kezeléséhez érdemes bevezetni az alábbi komplex változót, melynek valós része adja a mérhető jelet:
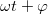 állandó szögsebességgel fordul körbe.
állandó szögsebességgel fordul körbe.
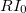 összefüggéssel számolhatjuk ki.
összefüggéssel számolhatjuk ki.
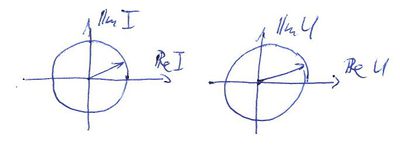
 -vel eltolódik az áramhoz képest, az amplitúdokat pedig a
-vel eltolódik az áramhoz képest, az amplitúdokat pedig a 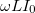 összefüggéssel számolhatjuk ki. Érdemes bevezetni az ellenálláshoz hasonló fogalmat, az impedanciát. Ez a komplex mennyiség lineáris áramkörökben megadja a feszülség és az áram komplex arányát. Induktivitás esetén
összefüggéssel számolhatjuk ki. Érdemes bevezetni az ellenálláshoz hasonló fogalmat, az impedanciát. Ez a komplex mennyiség lineáris áramkörökben megadja a feszülség és az áram komplex arányát. Induktivitás esetén 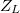 =
=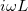 .
.
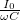 összefüggéssel számolhatjuk ki. A kondenzátorhoz tartozó impedancia
összefüggéssel számolhatjuk ki. A kondenzátorhoz tartozó impedancia 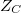 =
=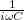 .
.
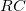 szorzat láthatóan idő dimenziójú, érdemes bevezetni a
szorzat láthatóan idő dimenziójú, érdemes bevezetni a  =
=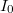 később meghatározandó állandó. (Ellenőrizzük, hogy ez a függvény valóban megoldása a fenti differenciálegyenletnek!) Az integrálási állandó meghatározásához használjuk fel, hogy t=0 idő pillanatban ismert
később meghatározandó állandó. (Ellenőrizzük, hogy ez a függvény valóban megoldása a fenti differenciálegyenletnek!) Az integrálási állandó meghatározásához használjuk fel, hogy t=0 idő pillanatban ismert  =
=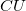 töltést tárolt. A kapcsoló átfordítása után átfolyó töltésmennyiségnek egyenlőnek kell lennie a tárolt töltéssel:
töltést tárolt. A kapcsoló átfordítása után átfolyó töltésmennyiségnek egyenlőnek kell lennie a tárolt töltéssel: