„RLC körök mérése” változatai közötti eltérés
| 195. sor: | 195. sor: | ||
| width="250pt" | <div class="texdisplay"><latex display >\[ \begin{array}{rcl} \mathbf{U}_L & = & \mathbf{I}j\omega L \\ \\ \mathbf{U}_R & = & \mathbf{I}R \\ \\ \mathbf{U}_C & = & \mathbf{I}/j\omega C \end{array} \]</latex></div> | | width="250pt" | <div class="texdisplay"><latex display >\[ \begin{array}{rcl} \mathbf{U}_L & = & \mathbf{I}j\omega L \\ \\ \mathbf{U}_R & = & \mathbf{I}R \\ \\ \mathbf{U}_C & = & \mathbf{I}/j\omega C \end{array} \]</latex></div> | ||
|} | |} | ||
| + | |||
| + | ==Mérési feladatok== | ||
| + | |||
| + | 1. Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget $\omega$ függvényében! Ábrázolja a $20\textrm{lg}(U_{ki}/U_{be})$ - $\textrm{lg}(\omega/\omega_0)$ függvényt! Ugyanitt ábrázolja a számításból adódó értékeket is. ($U_{be} = 1 \textrm{V}$, $\omega_0 = 1/RC$, a feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!) | ||
| + | |||
| + | 2. Állítson össze aluláteresztő szűrőt tekercs felhasználá-sával. Végezze el az 1. pont szerinti feladatokat! Itt $\omega_0 = R/L$ legyen! | ||
| + | |||
| + | 3. Állítson össze felüláteresztő szűrőt kondenzátor felhasználásával! A feladatokat az 1. pont szerint végezze el! Itt $\omega_0 = 1/RC$ legyen! | ||
| + | |||
| + | 4. Állítson össze felüláteresztő szűrőt tekercs felhasználásával. A feladatokat az 1. pont szerint végezze el! Itt $\omega_0 = R/L$ legyen! | ||
| + | |||
| + | 5. Állítson össze kettős T-szűrőt! Mérje a kimenő feszült-séget $\omega$ függvényében! Ábrázolja $20\textrm{lg}(U_{ki}/U_{be})$-t $\textrm{lg}(\omega/\omega_0)$ függvényében! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!) | ||
| + | |||
| + | 6. Mérje meg mindkét aktív szűrő kimenő feszültségét $\omega$ függvényében! Ábrázolja a $20\textrm{lg}(U_{ki}/U_{be})$ - $\textrm{lg}(\omega/\omega_0)$ függvényt! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!) | ||
| + | |||
| + | 7. Állítson össze soros rezgőkört! ($R$ külön elemként legyen bekötve!) A frekvencia függvényében mérje meg $U_R$, $U_L$, és $U_C$ értékeit! Számítsa ki és ábrázolja a körben folyó áramot és az eredő impedanciát $\omega$ függvényében és határozza meg $\omega_0$-t. | ||
| + | |||
| + | Megjegyzések: A méréshez szükséges alkatrészek egy átlátszó plexidobozban találhatók, banánhüvelyes kivezetésekkel. Az alkatrészek értékei a dobozról leolvashatók. Az egyes mérési feladatok elvégzésekor a mérési pontokat úgy válasszuk meg, hogy ahol jelentős a kimenő jel változása, ott sűrűbben, ahol kisebb, ott ritkábban helyezkedjenek el! | ||
A lap 2012. február 10., 20:24-kori változata
Szerkesztés alatt!
Tartalomjegyzék[elrejtés] |
A mérés célja:
-megismerkedni a leggyakrabban használt frekvenciafüggő áramköri elemekkel és az ezekből felépülő szelektív áramkörökkel.
Ennek érdekében:
-áttekintjük a váltakozó áramú hálózatok reaktáns elemeinek tulajdonságait és néhány egyszerű szűrő és egy rezgőkör frekvenciafüggő viselkedését; -méréseket végzünk a fent említett hálózatokon.
Elméleti összefoglaló
Tekercs
A tekercsben indukálódó feszültséget az
![\[ u(t) = L \frac{\textrm{d} i(t)}{\textrm{d} t} \]](/images/math/b/9/7/b9710f6c92cb97243f2b7ac6041c2968.png) |
(1) |
egyenlet írja le. Szinuszos gerjesztés [ 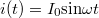 ] esetén
] esetén
![\[ u(t) = L \omega I_0 \textrm{cos}\omega t, \]](/images/math/0/3/5/035e8061307b0fb1e88ab24eea483f20.png) |
(2) |
ami a következő alakba is írható:
![\[ u(t) = L \omega I_0 \textrm{sin}( \omega t + 90^\circ ), \]](/images/math/f/1/c/f1c9d1f12cf58ff6ee685253d1a0780f.png) |
(3) |
tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest. A jelenség magyarázata a Lenz-törvényen alapul.
Kondenzátor
A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:
![\[ i(t) = C \frac{\textrm{d} u(t)}{\textrm{d} t}. \]](/images/math/3/a/5/3a59cf6674a1e812bd6efebb50d10387.png) |
(4) |
Szinuszos gerjesztés [ 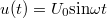 ] esetén:
] esetén:
![\[ i(t) = C \omega U_0 \textrm{cos}\omega t, \]](/images/math/2/4/9/249f0a17c4e98375ef0b67a874a7fd59.png) |
(5) |
ami a fentiekhez hasonlóan a következő alakba írható:
![\[ i(t) = C \omega U_0 \textrm{sin}( \omega t + 90^\circ ), \]](/images/math/3/8/7/38735ee3e3c4984f666b1b322710f6f7.png) |
(6) |
azaz a kondenzátor árama 90°-ot siet a feszültségéhez képest. Magyarázata az, hogy először áram folyik, így töltések kerülnek a lemezekre, és ezek hozzák létre a feszültséget. Gyakran szükséges a kondenzátor feszültségének ismerete, ami (4) alapján az alábbiak szerint számítható:
![\[ u(t) = \frac{1}{C} \int i(t)\textrm{d}t . \]](/images/math/6/7/0/670d10edef033c504ff445211a4ae29e.png) |
(7) |
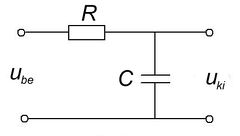
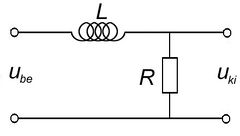
Aluláteresztő szűrő
Írjuk fel az 1.a és 1.b ábrákon látható kapcsolások kimenő feszültségeit! (A vastag betűs mennyiségek komplex változók,  a képzetes egység.)
a képzetes egység.)
![\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1}{1 + j\omega RC} \end{array} \]](/images/math/b/7/c/b7c626c15eb78b040394ba7114fd43ac.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{R}{R + j\omega L} \\ \\ \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{1}{1 + j\omega L/R} \end{array} \]](/images/math/8/d/5/8d535a5d400eee015ae924bfc0899e45.png) |
A kimeneti és bemeneti feszültségek hányadosa a hálózatra jellemző, frekvenciafüggő kifejezés.
![\[ \frac{\mathbf{U}_{ki}}{\mathbf{U}_{be}} = \frac{1}{1 + j\omega RC} \]](/images/math/b/4/a/b4ac9a1d7d323374047107f0f4c351ef.png) |
![\[ \frac{\mathbf{U}_{ki}}{\mathbf{U}_{be}} = \frac{1}{1 + j\omega L/R} \]](/images/math/b/d/8/bd868eaf7f755a0d4b16d6196eceb5e8.png) |
(8) |
A két (8) kifejezés formailag azonos, tehát a két kapcsolás azonos jellegű viselkedést mutat. Ameddig 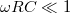 vagy
vagy 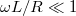 , a kifejezések értéke 1, ha
, a kifejezések értéke 1, ha 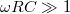 vagy
vagy 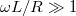 , a hányados értéke
, a hányados értéke 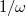 szerint csökken. Ez azt jelenti, hogy adott
szerint csökken. Ez azt jelenti, hogy adott  ,
,  és
és  esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.
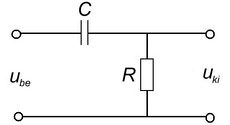
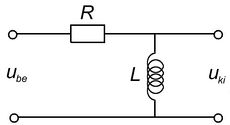
Felüláteresztő szűrő
A 2.a és a 2.b ábrákon látható kapcsolásokat leíró egyenletek az előző pontban követett eljárás alapján az alábbiak szerint alakulnak.
![\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{R}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{ki}}{\mathbf{U}_{be}} & = & \frac{1}{1 + 1/j\omega RC} \end{array} \]](/images/math/e/6/6/e669f6954b5a319f927877a2718d09c3.png) |
![\[ \begin{array}{rcl} \mathbf{U}_{ki} & = & \mathbf{U}_{be} \frac{j\omega L}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{ki}}{\mathbf{U}_{be}} & = & \frac{1}{1 + R/j\omega L} \end{array} \]](/images/math/2/9/8/298063be4f4115fe576ac7cfac5f7f4a.png) |
(9) |
A kifejezésekből jól látszik, hogy a kapcsolások a kisfrekvenciás jeleket nem engedik a kimenetre, míg a nagyfrekvenciás jelek csillapítás nélkül jelennek meg a kimeneti pontokon.
Sávzáró szűrő
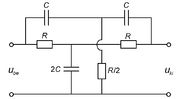
Alul és felüláteresztő szűrők egymás után kapcsolásával és az áteresztési tartományok helyes megválasztásával előállítható olyan szűrő, amelyik csak egy meghatározott tartományban csillapítja a jelet. Az ilyen kapcsolást nevezik sávzáró szűrőnek. Ennek egy realizálása a kettős T szűrő, a 3. ábrán látható.
A kapcsolás részletes elemzése nélkül is megállapítható, hogy alacsony frekvenciákon a hosszági ellenállásokon, magas frekvenciákon a hosszági kondenzátorokon jut jel a kimenetre.
Sáváteresztő szűrő
Az 1.5 pontban leírtak alapján alul- és felüláteresztő szűrőkből összeállítható olyan kapcsolás is, amely csak egy meghatározott tartományban engedi át a jeleket. Ezek a sáváteresztő szűrök.
Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. műveleti erősítő) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.
Soros rezgőkör
Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (4. ábra).
A hálózat eredő impedanciája:
![\[ \mathbf{Z}(\omega) = R + j\omega L + 1/j\omega C \]](/images/math/9/d/6/9d6af5d312b9e43f456f36075669994e.png) |
(10) |
Az impedancia abszolút értéke és fázisszöge:
![\[ Z(\omega) = \sqrt{R^2 + (\omega L-1/\omega C)^2} , \]](/images/math/d/8/3/d8390aabf94076fa241a14a1292e587b.png) |
![\[ \textrm{tan}\phi = \frac{\omega L - 1/\omega C}{R} \]](/images/math/f/2/5/f2518becda23a81cee59ffcc238878d6.png) |
A körben folyó áram:
![\[ I(\omega) = \frac{U_{be}}{\sqrt{R^2 + (\omega L-1/\omega C)^2}} \]](/images/math/6/3/d/63d66ef8473ad020971f6bda056bebc0.png) |
(11) |
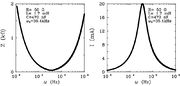
A 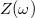 és
és 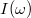 függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (5. ábra).
függvényeket ábrázolva a kapcsolás jellegzetes tulajdonságaira derül fény (5. ábra).
Látható, hogy az eredő impedanciának 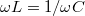 esetén az
esetén az
![\[ \omega_0 = \frac{1}{\sqrt{LC}} \]](/images/math/7/1/0/7103f4ab2b02728bc54093dd64f2299c.png) |
(12) |
körfrekvencián minimuma van, értéke valós, a veszteségi ellenállással egyezik meg. A jelenséget rezonanciának,  -t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, úgynevezett áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.
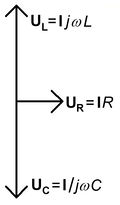
Ez az áram - kis veszteségi ellenállást feltételezve - igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymással 180°-os szöget zárnak be, abszolút értékük megegyezik, hiszen azonos áram folyik át rajtuk (6. ábra).
-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián a körben folyó áram értéke maximális, úgynevezett áramrezonancia alakul ki. A bemeneti feszültség és a körben folyó áram közötti fázisszög az impedancia fázisszöge, ebben az esetben nulla.
Ez az áram - kis veszteségi ellenállást feltételezve - igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymással 180°-os szöget zárnak be, abszolút értékük megegyezik, hiszen azonos áram folyik át rajtuk (6. ábra).
![\[ \begin{array}{rcl} \mathbf{U}_L & = & \mathbf{I}j\omega L \\ \\ \mathbf{U}_R & = & \mathbf{I}R \\ \\ \mathbf{U}_C & = & \mathbf{I}/j\omega C \end{array} \]](/images/math/c/6/4/c647c10d0048963efd42fa691670fac4.png) |
Mérési feladatok
1. Állítson össze aluláteresztő szűrőt kondenzátor felhasználásával! Mérje meg a kimenő feszültséget  függvényében! Ábrázolja a
függvényében! Ábrázolja a 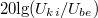 -
- 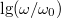 függvényt! Ugyanitt ábrázolja a számításból adódó értékeket is. (
függvényt! Ugyanitt ábrázolja a számításból adódó értékeket is. (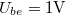 ,
, 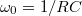 , a feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
, a feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
2. Állítson össze aluláteresztő szűrőt tekercs felhasználá-sával. Végezze el az 1. pont szerinti feladatokat! Itt 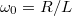 legyen!
legyen!
3. Állítson össze felüláteresztő szűrőt kondenzátor felhasználásával! A feladatokat az 1. pont szerint végezze el! Itt 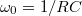 legyen!
legyen!
4. Állítson össze felüláteresztő szűrőt tekercs felhasználásával. A feladatokat az 1. pont szerint végezze el! Itt 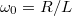 legyen!
legyen!
5. Állítson össze kettős T-szűrőt! Mérje a kimenő feszült-séget  függvényében! Ábrázolja
függvényében! Ábrázolja 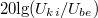 -t
-t 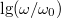 függvényében! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
függvényében! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
6. Mérje meg mindkét aktív szűrő kimenő feszültségét  függvényében! Ábrázolja a
függvényében! Ábrázolja a 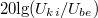 -
- 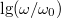 függvényt! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
függvényt! (A feszültségeket multiméterrel mérje és oszcilloszkópon ellenőrizze!)
7. Állítson össze soros rezgőkört! ( külön elemként legyen bekötve!) A frekvencia függvényében mérje meg
külön elemként legyen bekötve!) A frekvencia függvényében mérje meg 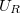 ,
, 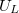 , és
, és 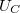 értékeit! Számítsa ki és ábrázolja a körben folyó áramot és az eredő impedanciát
értékeit! Számítsa ki és ábrázolja a körben folyó áramot és az eredő impedanciát  függvényében és határozza meg
függvényében és határozza meg  -t.
-t.
Megjegyzések: A méréshez szükséges alkatrészek egy átlátszó plexidobozban találhatók, banánhüvelyes kivezetésekkel. Az alkatrészek értékei a dobozról leolvashatók. Az egyes mérési feladatok elvégzésekor a mérési pontokat úgy válasszuk meg, hogy ahol jelentős a kimenő jel változása, ott sűrűbben, ahol kisebb, ott ritkábban helyezkedjenek el!