„Mágneses momentum mérése vibrációs magnetométerrel” változatai közötti eltérés
Lenk (vitalap | szerkesztései) |
Lenk (vitalap | szerkesztései) |
||
| 43. sor: | 43. sor: | ||
amelynek alakja abból adódik, hogy a mágneses tér a momentumra forgatónyomatékot gyakorolhat. Tegyük fel, hogy a mágneses teret egy „g” görbével jellemezhető hurokban folyó „I” áram határozza meg. Egy vákuumban lévő $(\mathbf{B = \mu_0 \cdot H})$ hurok által keltett tér a Biot-Savart-törvény szerint: | amelynek alakja abból adódik, hogy a mágneses tér a momentumra forgatónyomatékot gyakorolhat. Tegyük fel, hogy a mágneses teret egy „g” görbével jellemezhető hurokban folyó „I” áram határozza meg. Egy vákuumban lévő $(\mathbf{B = \mu_0 \cdot H})$ hurok által keltett tér a Biot-Savart-törvény szerint: | ||
| − | {{eq|\mathbf{H(r)} {{=}} I \cdot \oint_g | + | {{eq|\mathbf{H(r)} {{=}} I \cdot \oint_g d \mathbf{r'} \times \mathbf{(r-r')}\mathbf{r-r'} |eq:4|(4)}}{{=}} I \cdot \mathbf{H^e}|eq:4|(4)}} |
A lap 2012. november 13., 21:30-kori változata
A mérés célja:
A mérés célja megismerkedni egy makroszkopikus minta mágneses dipólmomentumának mérésével, valamint megvizsgálni egy lágymágneses anyag momentumának változását a külső mágnesező tér függvényében. A külső mágneses teret egyenáramú gerjesztő tekerccsel hozzuk létre, amely a különböző mintákban eltérő mágneses dipólmomentumot kelt. A mágneses térerősség mértéke a gerjesztő tekercs áramával szabályozható. Az ily módon felmágnesezett minta közelébe helyezett másik tekercsben (mérőtekercs) a dipólmomentum tere mágneses fluxust hoz létre. Ha a mintát a mérőtekercshez képest mozgatjuk, a tekercsben fluxusváltozás lép föl, ami feszültséget indukál. Az indukált feszültség értékéből a minta mágneses momentuma meghatározható. A mérési összeállítás akkor optimális, ha az elemek paramétereinek megválasztása révén (tekercsek alakja, minta helye stb.) a mért feszültség arányos a mágneses momentummal, valamint értéke a lehető legnagyobb.
Tartalomjegyzék[elrejtés] |
Szerkesztés alatt!
Elméleti összefoglaló
Elméleti alapok
Egy H mágneses térerősségvektorral jellemzett térben lévő közegben kialakuló B mágneses indukció a következő összefüggéssel írható le:
![\[\mathbf{B} = \mathbf{\mu_0}(\mathbf{H} + \mathbf{M})\]](/images/math/b/4/6/b46df8b3cd38e5d41df42cc6dce78d26.png)
ahol M a mágneses dipólmomentum sűrűség vektor vagy mágnesezettségi vektor. Egy makroszkópikus méretű, „V” térfogatú test mágneses momentuma (m) a következő térfogati integrálással kapható meg:
![\[\mathbf{m} = \mathbf{\int \limits_V M} dV\]](/images/math/7/9/f/79f9b1b9902cbbce6875e5da74854bd3.png)
A mérés során az m(H) függvényt szeretnénk meghatározni. A mérés a mágneses indukció jelenségén alapul, vagyis mindenekelőtt meg kell határoznunk a bevezetőben említett mérőtekercsben indukált „U” feszültség és az m mágneses momentum közötti kapcsolatot. Az alábbiakban kivonatosan bemutatjuk a keresett összefüggés levezetését. Kiindulásul a Maxwell-egyenleteket alkalmazzuk kvázistacionárius közelítésben, azaz az időben változó terek okozta sugárzást elhanyagoljuk. A levezetés kulcsgondolata szerint először összehasonlítjuk egy „I” áramjárta tekercs mágneses terébe helyezett m mágneses dipólus energiáját azzal az energiával, amit ugyanez a dipólus tárol ugyanebben a tekercsben az általa létrehozott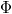 
fluxus által. Így megkapjuk a 
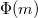összefüggést. Mivel a fluxusnál az indukált feszültség sokkal egyszerűbben mérhető, mozgatni fogjuk a mintát, és meghatározzuk a keresett U(m) összefüggést.
A mérés elve
Először egy külső H mágneses térben lévő m dipólus energiáját (W1) írjuk föl skalárszorzat formájában:
![\[W_1 = -\mathbf{m \cdot H}\]](/images/math/1/2/e/12ea215cf38955e9d8fbbc94494a3b9b.png)
amelynek alakja abból adódik, hogy a mágneses tér a momentumra forgatónyomatékot gyakorolhat. Tegyük fel, hogy a mágneses teret egy „g” görbével jellemezhető hurokban folyó „I” áram határozza meg. Egy vákuumban lévő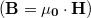 
hurok által keltett tér a Biot-Savart-törvény szerint:
![\[\mathbf{H(r)} = I \cdot \oint_g d \mathbf{r'} \times \mathbf{(r-r')}\mathbf{r-r'} \]](/images/math/6/6/0/660a4e3a9eba385005c4edbe587877a5.png)
Mérési feladatok
Mágneses momentum mérése vibrációs magnetométerrel
