„Mágneses momentum mérése vibrációs magnetométerrel” változatai közötti eltérés
Lenk (vitalap | szerkesztései) a |
Lenk (vitalap | szerkesztései) a |
||
| 74. sor: | 74. sor: | ||
===A vibrációs magnetométer=== | ===A vibrációs magnetométer=== | ||
A Biot-Savart törvény itt nem részletezett alkalmazásával meg lehet győződni róla, hogy a 2. ábrán látható kettős mérőhurok elrendezés alkalmas a $\frac{\partial H_z^e}{\partial z} {{=}} const$. feltételnek megfelelő mágneses tér előállítására, és ne felejtsük el, hogy így az induktivitás kölcsönössége, azaz az ekvivalenciánk alapján ideális mérőhuroknak/-tekercsnek is. A levezetésben csak a két ellentétes körüljárású áramhurok terének z komponensét kell meghatározni a z tengely mentén, majd annak megfelelő deriváltját képezni. Ez a z = 0 „középpontban” és annak z << d kis környezetében az ábra jelöléseit felhasználva az alábbi alakot ölti: | A Biot-Savart törvény itt nem részletezett alkalmazásával meg lehet győződni róla, hogy a 2. ábrán látható kettős mérőhurok elrendezés alkalmas a $\frac{\partial H_z^e}{\partial z} {{=}} const$. feltételnek megfelelő mágneses tér előállítására, és ne felejtsük el, hogy így az induktivitás kölcsönössége, azaz az ekvivalenciánk alapján ideális mérőhuroknak/-tekercsnek is. A levezetésben csak a két ellentétes körüljárású áramhurok terének z komponensét kell meghatározni a z tengely mentén, majd annak megfelelő deriváltját képezni. Ez a z = 0 „középpontban” és annak z << d kis környezetében az ábra jelöléseit felhasználva az alábbi alakot ölti: | ||
| + | {{eq|\frac{\partial H_z^e}{\partial z} {{=}} - \frac{3\cdot R^2\cdot d}{\left(R^2+d^2\right)^{5/2}}|eq:13|(13)}} | ||
| + | amely valóban állandó (z-től független). Maximális értékét megfelelő R/d arány mellett veszi fel, melyet az R = áll. feltételes szélsőérték keresésével határozhatunk meg. Ennek eredménye: | ||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
A lap 2013. február 6., 08:15-kori változata
A mérés célja:
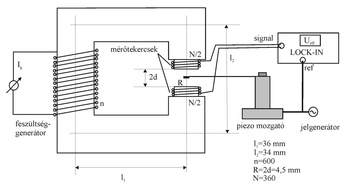
A mérés célja megismerkedni egy makroszkopikus minta mágneses dipólmomentumának mérésével, valamint megvizsgálni egy lágymágneses anyag momentumának változását a külső mágnesező tér függvényében. A külső mágneses teret egyenáramú gerjesztő tekerccsel hozzuk létre, amely a különböző mintákban eltérő mágneses dipólmomentumot kelt. A mágneses térerősség mértéke a gerjesztő tekercs áramával szabályozható. Az ily módon felmágnesezett minta közelébe helyezett másik tekercsben (mérőtekercs) a dipólmomentum tere mágneses fluxust hoz létre. Ha a mintát a mérőtekercshez képest mozgatjuk, a tekercsben fluxusváltozás lép föl, ami feszültséget indukál. Az indukált feszültség értékéből a minta mágneses momentuma meghatározható. A mérési összeállítás akkor optimális, ha az elemek paramétereinek megválasztása révén (tekercsek alakja, minta helye stb.) a mért feszültség arányos a mágneses momentummal, valamint értéke a lehető legnagyobb.
Tartalomjegyzék[elrejtés] |
Szerkesztés alatt!
Elméleti összefoglaló
Elméleti alapok
Egy H mágneses térerősségvektorral jellemzett térben lévő közegben kialakuló B mágneses indukció a következő összefüggéssel írható le:
![\[\mathbf{B} = \mathbf{\mu_0}(\mathbf{H} + \mathbf{M})\]](/images/math/b/4/6/b46df8b3cd38e5d41df42cc6dce78d26.png)
ahol M a mágneses dipólmomentum sűrűség vektor vagy mágnesezettségi vektor. Egy makroszkópikus méretű, „V” térfogatú test mágneses momentuma (m) a következő térfogati integrálással kapható meg:
![\[\mathbf{m} = \mathbf{\int \limits_V M} dV\]](/images/math/7/9/f/79f9b1b9902cbbce6875e5da74854bd3.png)
A mérés során az m(H) függvényt szeretnénk meghatározni. A mérés a mágneses indukció jelenségén alapul, vagyis mindenekelőtt meg kell határoznunk a bevezetőben említett mérőtekercsben indukált „U” feszültség és az m mágneses momentum közötti kapcsolatot. Az alábbiakban kivonatosan bemutatjuk a keresett összefüggés levezetését. Kiindulásul a Maxwell-egyenleteket alkalmazzuk kvázistacionárius közelítésben, azaz az időben változó terek okozta sugárzást elhanyagoljuk. A levezetés kulcsgondolata szerint először összehasonlítjuk egy „I” áramjárta tekercs mágneses terébe helyezett m mágneses dipólus energiáját azzal az energiával, amit ugyanez a dipólus tárol ugyanebben a tekercsben az általa létrehozott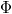 
fluxus által. Így megkapjuk a 
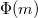összefüggést. Mivel a fluxusnál az indukált feszültség sokkal egyszerűbben mérhető, mozgatni fogjuk a mintát, és meghatározzuk a keresett U(m) összefüggést.
A mérés elve
Először egy külső H mágneses térben lévő m dipólus energiáját (W1) írjuk föl skalárszorzat formájában:
![\[W_1 = -\mathbf{m \cdot H}\]](/images/math/1/2/e/12ea215cf38955e9d8fbbc94494a3b9b.png)
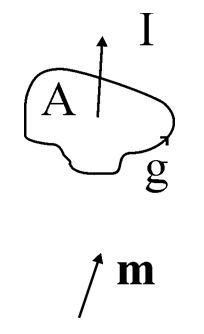
amelynek alakja abból adódik, hogy a mágneses tér a momentumra forgatónyomatékot gyakorolhat. Tegyük fel, hogy a mágneses teret egy „g” görbével jellemezhető hurokban folyó „I” áram határozza meg. Egy vákuumban lévő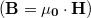 
hurok által keltett tér a Biot-Savart-törvény szerint:
![\[\mathbf{H(r)} = I \cdot \oint_g \frac{d\mathbf{r'}\times{}\left(\mathbf{r-r'}\right)}{{\left\vert{}\mathbf{r-r'}\right\vert{}}^3} = I \cdot \mathbf{H^e}\]](/images/math/c/d/1/cd16687f6610fa3c07ca9dbdb8f1cb67.png)
ahol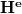 
-vel jelöltük az egységnyi áram által keltett mágneses térerősséget, amely csupán a geometriától függ. Ezt behelyettesítve (3)-ba a következőt kapjuk:
![\[W_1 = - \mathbf{m} \cdot \mathbf{H^e} \cdot I\]](/images/math/b/4/5/b45dd952b7bcae0b71d9271261998e63.png)
Másodszor azt nézzük meg, hogy mekkora az energiája az m mágneses momentum keltette B mágneses indukciójú térben található „A” felületű vezető huroknak, melyben „I” áram folyik:
![\[W_2 = I \cdot \Phi /2\]](/images/math/4/d/5/4d565d26dc3707fd70443b0075e0934f.png)
ahol 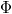a hurokban fellépő mágneses indukciófluxus:
![\[\Phi = \int_A \mathbf{B} d\mathbf{A}\]](/images/math/b/1/1/b11e49fae8bdcd453f1702beeaf9a833.png)
 |
Amennyiben az „I” árammal H térerősséget létrehozó, valamint a Φ fluxust tartalmazó hurok és a mágneses momentum egy és ugyanaz mind a két esetben, az előbbi energiakifejezéseknek egyenlőnek kell lenniük:
![\[W_1 = W_2 \qquad \to \qquad -\mathbf{m} \cdot \mathbf{H}^e \cdot I = \frac{I\cdot \Phi}{2}\]](/images/math/0/3/4/034d034565bf92e9fa4c87894218c93b.png)
ahol I-vel egyszerűsíthetünk, így a mágneses fluxus a hurokban:
![\[\Phi = 2\cdot \mathbf{m} \cdot \mathbf{H}^e\]](/images/math/4/a/3/4a34c51e66f5105e585e0187f4503d75.png)
Most azt az esetet vizsgáljuk meg, amikor a mágneses dipólust mozgatjuk a mérőhurokhoz képest. Ekkor a geometria változása fluxusváltozást eredményez, amely a mérőtekercsben indukált feszültséget (U) hoz létre:
![\[U(t) = - \frac{d \Phi }{dt} = -\frac{d \Phi }{d \mathbf{r} } \cdot \frac{d \mathbf{r} }{dt} = -2 \cdot grad \left(\mathbf{m} \cdot \mathbf{H} ^e\right) \cdot \frac{d \mathbf{r} }{dt}\]](/images/math/9/a/6/9a60ad45b1609be35320d422970cf017.png)
A fenti összefüggésben az idő (t) szerinti deriválást a láncszabály alapján mindjárt átalakítottuk hely szerinti deriválásra, ahol r a dipólus helyvektorát jelenti. Az m a végső mérendő mennyiség, értékét a gerjesztő tekercs árama határozza meg, ami egy mérési pontban időben állandó. Ha a dipólus mozgástartománya kicsi a gerjesztő tekercs jellemző méreteihez képest, m értéke a mozgás során helyfüggetlen is, mivel kis helyváltoztatás során a gerjesztő tekercs mágneses tere állandó. A mágneses momentum épp ezért kiemelhető a gradiensből, ahol így csak H^e marad. Ha a mérési elrendezés geometriája olyan, hogy H^e-nek, m-nek és a helyvektor dr megváltozásának csak azonos irányú komponense van, és a koordináta rendszerünket úgy vesszük fel, hogy a z-tengelye ebbe az irányba mutat, akkor a fenti mennyiségek helyettesíthetők H_z^e, m_z ill. dz komponenseikkel. Ekkor a fenti kifejezés a következőre egyszerűsödik:
![\[U(t) = -2\cdot m_z \cdot \frac{\partial H_z^e}{\partial z}\cdot \frac{dz}{dt}\]](/images/math/0/2/e/02e2838b570f730fa22fb6ae0da3371a.png)
A dipólus mozgatása során fellépő indukált feszültség tehát akkor mérhető könnyen, ha időben vagy állandó, vagy harmonikusan változik. Az előbbihez a dipólus egyenes vonalú egyenletes mozgását kellene biztosítani a helytől lineárisan függő Hze esetén, ami nehezen kivitelezhető. Kézenfekvő tehát a dipólus „z0” amplitudójú, ω körfrekvenciájú szinuszos rezgetése. Ekkor a fenti összefüggés a következő alakot ölti:
![\[U(t) = -2\cdot m_z \cdot \frac{\partial H_z^e}{\partial z}\cdot z_0\cdot \omega \cos(\omega t)\]](/images/math/b/f/9/bf9956cabb602f179f780da32f64c2e9.png)
Látható, hogy a legnagyobb indukált feszültséget akkor kapjuk, ha a minta mozgása gyors, valamint ha az egységnyi áram által indukált mágneses tér gyorsan változik a hellyel. Ebben az esetben akkor lesz az indukált feszültség arányos m-el, ha H_z^e hely szerinti változása a mozgás tartományában első rendben állandó, azaz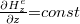 
. A feladat tehát egy ilyen mérőhurok geometriát találni.
 |
A vibrációs magnetométer
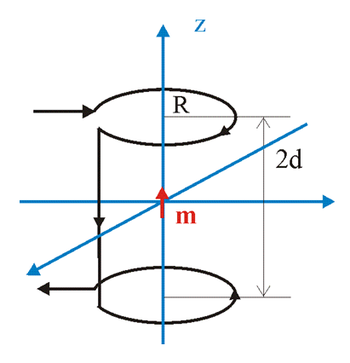
A Biot-Savart törvény itt nem részletezett alkalmazásával meg lehet győződni róla, hogy a 2. ábrán látható kettős mérőhurok elrendezés alkalmas a 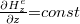. feltételnek megfelelő mágneses tér előállítására, és ne felejtsük el, hogy így az induktivitás kölcsönössége, azaz az ekvivalenciánk alapján ideális mérőhuroknak/-tekercsnek is. A levezetésben csak a két ellentétes körüljárású áramhurok terének z komponensét kell meghatározni a z tengely mentén, majd annak megfelelő deriváltját képezni. Ez a z = 0 „középpontban” és annak z << d kis környezetében az ábra jelöléseit felhasználva az alábbi alakot ölti:
\[\frac{\partial H_z^e}{\partial z} = - \frac{3\cdot R^2\cdot d}{\left(R^2+d^2\right)^{5/2\]
amely valóban állandó (z-től független). Maximális értékét megfelelő R/d arány mellett veszi fel, melyet az R = áll. feltételes szélsőérték keresésével határozhatunk meg. Ennek eredménye:
 |
 |
 |
Mérési feladatok
PDF formátum
Mágneses momentum mérése vibrációs magnetométerrel
