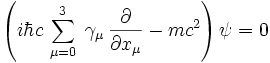„Szilárdtestfizika” változatai közötti eltérés
| (egy szerkesztő 2 közbeeső változata nincs mutatva) | |||
| 16. sor: | 16. sor: | ||
== A szilárd anyagok elektromos vezetésének kvantummechanikai alapjai == | == A szilárd anyagok elektromos vezetésének kvantummechanikai alapjai == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== A fémek szabadelektron-elmélete === | === A fémek szabadelektron-elmélete === | ||
| 304. sor: | 140. sor: | ||
Az előző fejezetben bemutatott fizikai meggondolások alapján a Fermi–Dirac eloszlásfüggvényre egy „lekerekített lépcsőfüggvény” várható (ld. [[#abra323|ábra]]). Ennek megfelelően, a szigorú elméleti számítások eredményeként a következő összefüggés adódik: | Az előző fejezetben bemutatott fizikai meggondolások alapján a Fermi–Dirac eloszlásfüggvényre egy „lekerekített lépcsőfüggvény” várható (ld. [[#abra323|ábra]]). Ennek megfelelően, a szigorú elméleti számítások eredményeként a következő összefüggés adódik: | ||
| − | $$ f^{FD} (E,T) = \frac{1}{\left[ \exp\left( \frac{E - E_F}{kT} \right) \right]} $$ | + | $$ f^{FD} (E,T) = \frac{1}{\left[ \exp\left( \frac{E - E_F}{kT} \right) + 1 \right]} $$ |
Az $E_F$ paraméter neve ''Fermi-energia''. Látható, hogy $f^{FD}(E_F, T) = 0,5$. Ábrázolva a függvényt különböző hőmérsékleteken az alábbi görbék adódnak: | Az $E_F$ paraméter neve ''Fermi-energia''. Látható, hogy $f^{FD}(E_F, T) = 0,5$. Ábrázolva a függvényt különböző hőmérsékleteken az alábbi görbék adódnak: | ||
| 363. sor: | 199. sor: | ||
Látható tehát, hogy [[#eq3|(3)]] második része úgy írható, hogy | Látható tehát, hogy [[#eq3|(3)]] második része úgy írható, hogy | ||
| − | $$ n(f) = af^2 \frac{1}{\exp(hf/kT) - 1} = g(f) \frac{1}{\exp(hf/kT)} \equiv g(f)\cdot f^{\rm foton}(f,T). $$ | + | $$ n(f) = af^2 \frac{1}{\exp(hf/kT) - 1} = g(f) \frac{1}{\exp(hf/kT) - 1} \equiv g(f)\cdot f^{\rm foton}(f,T). $$ |
Összevetve ezt az elektrongáz esetén látottakkal, az $E = hf$ energiájú fotonállapotok betöltöttségét a | Összevetve ezt az elektrongáz esetén látottakkal, az $E = hf$ energiájú fotonállapotok betöltöttségét a | ||
| 704. sor: | 540. sor: | ||
érték adódik. | érték adódik. | ||
| − | <small><b>Megjegyzés</b>. A valódi érték ennek a fele, azaz $0.045 \, {\rm eV}$ | + | <small><b>Megjegyzés</b>. A valódi érték ennek a fele, azaz $0.045 \, {\rm eV}$. A különbség abból adódik, hogy a ${\rm Si}$ háttér valójában nem folytonos közeg. A kristályrács kvantummechanikai hatását is figyelembe kell venni. Erre szolgál az ''effektív tömeg'' fogalma. Ez hozza be e hiányzó $0.5$-ös faktort. A részleteket az MSc szinten tárgyaljuk majd.</small> |
Mivel a szilícium esetén a tiltott sáv szélessége $1,1 \, {\rm eV}$, így valójában azt kaptuk, hogy a kötött állapotok energiaszintjei a vezetési sáv alja alatt, ahhoz nagyon közel, a tiltott sávban helyezkednek el. | Mivel a szilícium esetén a tiltott sáv szélessége $1,1 \, {\rm eV}$, így valójában azt kaptuk, hogy a kötött állapotok energiaszintjei a vezetési sáv alja alatt, ahhoz nagyon közel, a tiltott sávban helyezkednek el. | ||
A lap jelenlegi, 2011. szeptember 1., 14:15-kori változata
Tartalomjegyzék[elrejtés] |
|
|

|
|
|
|
A szilárd anyagok elektromos vezetésének kvantummechanikai alapjai
A fémek szabadelektron-elmélete
A fémek jól vezetik az elektromos áramot. Tehát az elektromos áramot alkotó elektronok viszonylag „könnyedén” tudnak mozogni a fém belsejében. A fémes kötés ugyanis úgy alakul ki, hogy a fématomok egyesülésekor a vegyérték elektronok „közössé válnak”. Ez azt jelenti, hogy nincsenek a fémet alkotó atomokhoz kötve, hanem azokról mintegy „leszakadva” a fém teljes makroszkopikus térfogatában mozoghatnak. Első közelítésként azt mondjuk, hogy a fém elektronjai ún. szabadelektron gázt alkotnak.
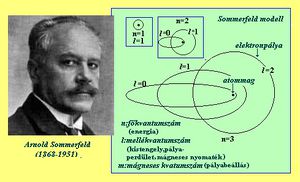
Az elkövetkezőkben a nagyszámú (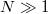 ) elektront tartalmazó szabadelektron gáz kvantummechanikai tárgyalásával foglalkozunk. Ezt a modellt már pár évvel a Schrödinger-egyenlet felfedezése (1926) után Arnold Sommerfeld dolgozta ki (1927/28). Egyszerű volta ellenére választ tudott adni egy-két olyan mérési tapasztalatra (kontakt potenciál, fémek fajhője stb), amelyek magyarázatánál a klasszikus fizika csődöt mondott.
) elektront tartalmazó szabadelektron gáz kvantummechanikai tárgyalásával foglalkozunk. Ezt a modellt már pár évvel a Schrödinger-egyenlet felfedezése (1926) után Arnold Sommerfeld dolgozta ki (1927/28). Egyszerű volta ellenére választ tudott adni egy-két olyan mérési tapasztalatra (kontakt potenciál, fémek fajhője stb), amelyek magyarázatánál a klasszikus fizika csődöt mondott.
Ennek a modellnek a lényege a következő. A fém vezetési elektronjai a fémrácsot alkotó iontörzsek terében mozognak, ugyanakkor egymással is kölcsönhatásban vannak. Ezt az igen bonyolultnak tűnő kvantummechanikai problémát alkalmas modellválasztással egyszerűen meg lehet oldani.
Tekintsük bármelyik fémelektront. Ez egyrészt az iontörzsekkel, másrészt a többi elektronnal van kölcsönhatásban. Vegyünk egyszerűségképpen egy egy-vegyértékű fémet! Ekkor az iontörzsek száma megegyezik a fémes kötést létrehozó elektronok  számával. Tehát bármelyik elektront tekintve a pozitív töltésű iontörzsek és a többi, negatív töltésű elektron száma gyakorlatilag megegyezik (
számával. Tehát bármelyik elektront tekintve a pozitív töltésű iontörzsek és a többi, negatív töltésű elektron száma gyakorlatilag megegyezik (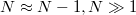 ), ezért semlegesítik egymást. Tehát az elektron szabadon mozoghat az egész fém belsejében. Ugyanakkor tapasztalati tény, hogy normál körülmények között az elektron nem lép ki a fémből. Ezt úgy tudjuk modellezni, hogy az elektront egy potenciáldobozban lévőnek tekintjük. A doboz mérete a fém makroszkopikus méretével egyezik meg és az egyszerűség végett legyen kocka alakú.
), ezért semlegesítik egymást. Tehát az elektron szabadon mozoghat az egész fém belsejében. Ugyanakkor tapasztalati tény, hogy normál körülmények között az elektron nem lép ki a fémből. Ezt úgy tudjuk modellezni, hogy az elektront egy potenciáldobozban lévőnek tekintjük. A doboz mérete a fém makroszkopikus méretével egyezik meg és az egyszerűség végett legyen kocka alakú.
Az elektron pályaállapotait tehát egy dobozba zárt elektron Schrödinger-egyenlete határozza meg. Az előzőekben ezt az egyenletet már megoldottuk. Eszerint egy pályaállapot három kvantumszámmal (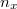 ,
, 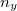 ,
, 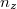 ) jellemezhető. Az energiaszinteket pedig e három kvantumszám négyzetösszege határozza meg, azaz
) jellemezhető. Az energiaszinteket pedig e három kvantumszám négyzetösszege határozza meg, azaz
![\[ E = \frac{\hbar^2}{8mL^2} \left( n_x^2 + n_y^2 + n_z^2 \right). \]](/images/math/1/a/9/1a9589ff1b7cc7d4155aaafb81df3594.png)
Az is láttuk, hogy a pályaállapotok degeneráltak, azaz egy energiaszinthez több különböző állapot tartozik. Ezeket a pályaállapotokat kell a Pauli-elv szerint az  számú elektronnal betölteni úgy, hogy minden pályaállapotba maximum két elektron lehet ellentétes spinnel. Mivel az
számú elektronnal betölteni úgy, hogy minden pályaállapotba maximum két elektron lehet ellentétes spinnel. Mivel az  nagyon nagy (Avogadro számnyi!), ezért a betöltött állapotok majd mindegyike relatíve magas energiaszintekhez fog tartozni. Ez azt jelenti, hogy betöltött energiaszintek relatív „távolsága” (azaz a relatív kvantáltság) igen kicsi lesz. Ennek bizonyítása egydimenziós doboz esetén igen egyszerű. Az eredmény pedig triviálisan általánosítható a háromdimenziós modellre is. Az energiaszintek közötti relatív távolság tehát
nagyon nagy (Avogadro számnyi!), ezért a betöltött állapotok majd mindegyike relatíve magas energiaszintekhez fog tartozni. Ez azt jelenti, hogy betöltött energiaszintek relatív „távolsága” (azaz a relatív kvantáltság) igen kicsi lesz. Ennek bizonyítása egydimenziós doboz esetén igen egyszerű. Az eredmény pedig triviálisan általánosítható a háromdimenziós modellre is. Az energiaszintek közötti relatív távolság tehát
![\[ \frac{\Delta E_n}{E_n} = \frac{E_{n+1} - E_n}{E_n} = \frac{(n+1)^2 - n^2}{n^2} = \frac{2n-1}{n^2} \to 0, \quad \text{ha} \quad n\to\infty, \]](/images/math/f/4/0/f407335eaa3a7576f5490428503e3cc8.png)
azaz az energiaszintek kvantáltsága mintegy „eltűnik”. Így folytonos energiaskálára ( ) térhetünk át. Ekkor a degeneráció foka helyett bevezetjük a
) térhetünk át. Ekkor a degeneráció foka helyett bevezetjük a 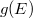 állapotsűrűség fogalmát. Eszerint a
állapotsűrűség fogalmát. Eszerint a 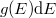 azon elektronállapotok számát jelenti, amelyeknek az energiája az
azon elektronállapotok számát jelenti, amelyeknek az energiája az 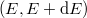 tartományba esik. A Pauli-elv szerint minden pályaállapothoz két spin-állapot is tartozik. Tehát a teljes (spinpálya)
tartományba esik. A Pauli-elv szerint minden pályaállapothoz két spin-állapot is tartozik. Tehát a teljes (spinpálya) 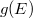 állapotsűrűség az
állapotsűrűség az 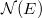 pályaállapot-sűrűség kétszerese lesz:
pályaállapot-sűrűség kétszerese lesz:
![\[ g(e) = 2{\cal N}(E). \]](/images/math/3/6/4/3644ba6012ded02d1c6c3c3ea3b8ec9f.png)
Határozzuk meg az 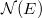 pályaállapot-sűrűséget a potenciáldobozba zárt elektron esetén! Minden pályaállapotot három kvantumszám (
pályaállapot-sűrűséget a potenciáldobozba zárt elektron esetén! Minden pályaállapotot három kvantumszám (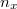 ,
, 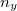 ,
, 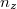 ) határoz meg. Ezért egy
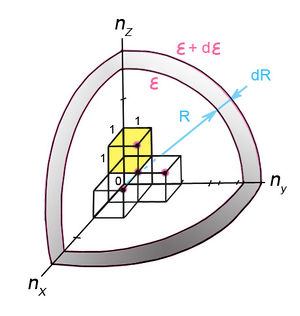
) határoz meg. Ezért egy 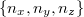 koordinátarendszerben (azaz a kvantumszámok „terében”) egy pályaállapotot egy pont fog reprezentálni. Az ezen állapothoz tartozó energia értéke
koordinátarendszerben (azaz a kvantumszámok „terében”) egy pályaállapotot egy pont fog reprezentálni. Az ezen állapothoz tartozó energia értéke 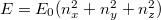 lesz. Látható, hogy a kvantumszámok terében az összes
lesz. Látható, hogy a kvantumszámok terében az összes  energiájú állapot egy
energiájú állapot egy  sugarú gömbön helyezkedik el, hiszen
sugarú gömbön helyezkedik el, hiszen
![\[ n_x^2 + n_y^2 + n_z^2 = \frac{E}{E_0} \equiv R^2. \]](/images/math/e/5/7/e576ac1f5e50e13c077be73148033b1e.png)
Tekintsük azokat az állapotokat, amelyek energiája az 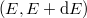 tartományba esik! Mivel a kvantumszámok értéke csak pozitív szám lehet, így az ezen állapotokat reprezentáló pontok egy gömbhéj nyolcadban vannak. Mivel az
tartományba esik! Mivel a kvantumszámok értéke csak pozitív szám lehet, így az ezen állapotokat reprezentáló pontok egy gömbhéj nyolcadban vannak. Mivel az 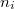 kvantumszámok csak (pozitív) egész számokat vehetnek fel, ezért minden egyes egységnyi térfogatban csak egy reprezentáns pont van. Ezért az
kvantumszámok csak (pozitív) egész számokat vehetnek fel, ezért minden egyes egységnyi térfogatban csak egy reprezentáns pont van. Ezért az 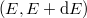 tartományban lévő állapotok száma megegyezik az említett gömbhéj-nyolcad térfogatával:
tartományban lévő állapotok száma megegyezik az említett gömbhéj-nyolcad térfogatával:
![\[ {\cal N} (E) \, {\rm d} E = \frac{4\pi}{8} R^2 \, {\rm d} R. \]](/images/math/d/d/3/dd35c531dff969a3d1ed8a80d747876a.png)
Mivel pedig látható, hogy
![\[ R = \frac{\sqrt{E}}{\sqrt{E_0}} \quad \text{és} \quad {\rm d}R = \frac{1}{2\sqrt{E_0}} \frac{1}{\sqrt{E}} {\rm d} E, \]](/images/math/b/4/a/b4ab22bc9b880edddfa32a26163af924.png)
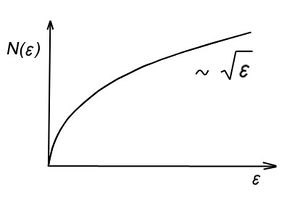
a pályaállapot sűrűségre az adódik, hogy:
![\[ {\cal N}(E) \sim \sqrt{E}. \]](/images/math/4/b/2/4b20708ff3e9a414d1b6047e2bc9e26a.png)
A Sommefeld-féle fémmodell szerint tehát a „potenciáldoboz-állapotokat kell”  darab elektronnal betölteni. Eredményül megkapjuk az elektronok energia szerinti eloszlását. Az ezt megadó függvényt
darab elektronnal betölteni. Eredményül megkapjuk az elektronok energia szerinti eloszlását. Az ezt megadó függvényt 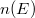 -vel fogjuk jelölni. Eszerint az
-vel fogjuk jelölni. Eszerint az 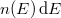 megadja azon elektronok számát, amelyeknek az energiája az
megadja azon elektronok számát, amelyeknek az energiája az 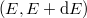 tartományban van. Az elektronok
tartományban van. Az elektronok 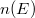 eloszlásfüggvényének a meghatározása
eloszlásfüggvényének a meghatározása 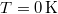 esetén (azaz alapállapotban) igen egyszerű. A Pauli-elv szerint ugyanis minden spin-pálya állapotban maximum egyetlen elektron lehet. Ezért az alapállapoti elektrongázban egy bizonyos energiaszint alatt minden állapot be van töltve, fölötte pedig minden állapot üres lesz. Ezt az energiaszintet
esetén (azaz alapállapotban) igen egyszerű. A Pauli-elv szerint ugyanis minden spin-pálya állapotban maximum egyetlen elektron lehet. Ezért az alapállapoti elektrongázban egy bizonyos energiaszint alatt minden állapot be van töltve, fölötte pedig minden állapot üres lesz. Ezt az energiaszintet 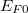 -val jelöljük és Fermi-energiának nevezzük. Mivel a betöltött állapotok száma éppen
-val jelöljük és Fermi-energiának nevezzük. Mivel a betöltött állapotok száma éppen  kell, hogy legyen, így ez a feltétel a Fermi-szintet egyértelműen meghatározza.
kell, hogy legyen, így ez a feltétel a Fermi-szintet egyértelműen meghatározza.
Eredményül tehát az adódik, hogy az 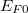 érték alatt
érték alatt 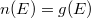 és fölötte
és fölötte 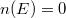 . Ha a fém hőmérséklete emelkedik (
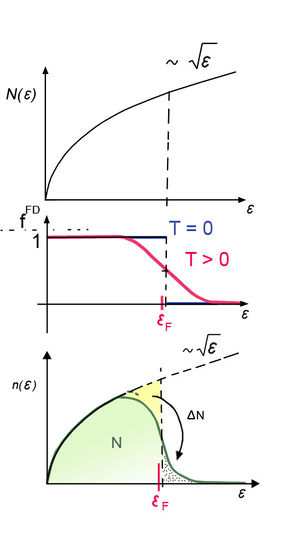
. Ha a fém hőmérséklete emelkedik (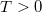 ), akkor az elektronok magasabb energiaszintre kell, hogy kerüljenek. A Pauli-elv miatt ez csak úgy lehetséges, ha a Fermi-szint közelében lévő elektronok a Fermi-szint fölé jutnak, majd az így üresen maradt állapotok egy részét a mélyebb energiaszintről származó elektronok töltik be. Azaz végül is a Fermi-energia környékén lévő állapotok csak részben lesznek beöltve (ld. ábra).
), akkor az elektronok magasabb energiaszintre kell, hogy kerüljenek. A Pauli-elv miatt ez csak úgy lehetséges, ha a Fermi-szint közelében lévő elektronok a Fermi-szint fölé jutnak, majd az így üresen maradt állapotok egy részét a mélyebb energiaszintről származó elektronok töltik be. Azaz végül is a Fermi-energia környékén lévő állapotok csak részben lesznek beöltve (ld. ábra).
Az állapotok betöltöttségét egy 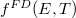 függvénnyel lehet megadni:
függvénnyel lehet megadni:
![\[ n(E) = g(E) f^{FD}(E,T). \]](/images/math/9/2/7/92731e3b30b77fafd64b8d6a91273bf8.png) |
(2) |
Az 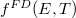 -t Fermi–Dirac-féle eloszlásfüggvénynek hívjuk. Az előzőek szerint
-t Fermi–Dirac-féle eloszlásfüggvénynek hívjuk. Az előzőek szerint 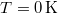 hőmérsékleten ez egy „lépcsőfüggvény” kell, hogy legyen. Véges
hőmérsékleten ez egy „lépcsőfüggvény” kell, hogy legyen. Véges  hőmérsékleten az eloszlásfüggvény kissé „lekerekedik”. A változás azonban az
hőmérsékleten az eloszlásfüggvény kissé „lekerekedik”. A változás azonban az 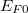 értéknek csak körülbelül a
értéknek csak körülbelül a 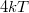 nagyságú környezetére korlátozódik. Az elmondottakat kvalitatív szemléltetését az ábrán mutattuk be.
nagyságú környezetére korlátozódik. Az elmondottakat kvalitatív szemléltetését az ábrán mutattuk be.
További elemi ismereteket (a matematikai részletek mellőzésével) a következő fejezetben találhatunk.
Érdemes megvizsgálni azt, hogy az imént kapott 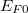 érték a „hétköznapi” energiákhoz képest mekkora. Az összehasonlítást azonban nem az energiaskálán, hanem a nála sokkal szemléletesebb hőmérséklet skálán fogjuk elvégezni. Erre szolgál a Fermi hőmérséklet (
érték a „hétköznapi” energiákhoz képest mekkora. Az összehasonlítást azonban nem az energiaskálán, hanem a nála sokkal szemléletesebb hőmérséklet skálán fogjuk elvégezni. Erre szolgál a Fermi hőmérséklet (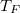 ) fogalma.
) fogalma.
Ismeretes, hogy a klasszikus ideális gáz átlagenergiája, az ekvipartíció törvénye szerint, a gáz hőmérsékletével arányos. A 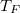 Fermi hőmérsékleten értjük annak az ideális gáznak a hőmérsékletét, amelynek az átlagenergiája megegyezik a nulla Kelvin fokos elektrongáz átlagenergiájával. Azaz
Fermi hőmérsékleten értjük annak az ideális gáznak a hőmérsékletét, amelynek az átlagenergiája megegyezik a nulla Kelvin fokos elektrongáz átlagenergiájával. Azaz
![\[ kT_F \approx E_{F0}. \]](/images/math/c/3/5/c35eae90774b08fe15bc7fceb25e886e.png)
A fémek esetén 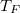 kb. 10 000 Kelvinnek adódik (összehasonlításul, a napkorona hőmérséklete kb. 6000 Kelvin). Tehát a Pauli-elvből adódó Fermi-energia a klasszikus fizikai energiaskálán meglehetősen nagy érték. Ez azt is jelenti, hogy ha a fém hőmérséklete (pár száz fokkal) megemelkedik, akkor a vezetési elektronjainak az átlagenergiája relatíve alig változik. Tehát a szobahőmérsékletű fém vezetési elektronjait nulla Kelvin fokos elektrongáznak lehet tekinteni, ugyanis a 300 Kelvin sokkal kisebb mint a 10 000 Kelvin!
kb. 10 000 Kelvinnek adódik (összehasonlításul, a napkorona hőmérséklete kb. 6000 Kelvin). Tehát a Pauli-elvből adódó Fermi-energia a klasszikus fizikai energiaskálán meglehetősen nagy érték. Ez azt is jelenti, hogy ha a fém hőmérséklete (pár száz fokkal) megemelkedik, akkor a vezetési elektronjainak az átlagenergiája relatíve alig változik. Tehát a szobahőmérsékletű fém vezetési elektronjait nulla Kelvin fokos elektrongáznak lehet tekinteni, ugyanis a 300 Kelvin sokkal kisebb mint a 10 000 Kelvin!
Mint azt már az imént említettük [ld. (2)], az elektronok 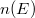 energia szerinti eloszlását a
energia szerinti eloszlását a 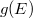 állapotsűrűség függvény és az
állapotsűrűség függvény és az 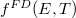 Fermi–Dirac eloszlásfüggvény szorzata adja meg. Az előzőekből következik, de a részletes számítás is azt bizonyítja, hogy a
Fermi–Dirac eloszlásfüggvény szorzata adja meg. Az előzőekből következik, de a részletes számítás is azt bizonyítja, hogy a  hőmérsékletű szabad elektrongáz
hőmérsékletű szabad elektrongáz 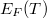 Fermi energiája a „hétköznapi” hőmérsékleti tartományban gyakorlatilag
Fermi energiája a „hétköznapi” hőmérsékleti tartományban gyakorlatilag 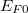 értékűnek vehető. Ez fizikailag azt jelenti, hogy csak azok az elektronok kerülhetnek magasabb energiájú állapotba (azok gerjesztődnek), amelyeknek a kezdeti energiája a Fermi szint közelében volt. A
értékűnek vehető. Ez fizikailag azt jelenti, hogy csak azok az elektronok kerülhetnek magasabb energiájú állapotba (azok gerjesztődnek), amelyeknek a kezdeti energiája a Fermi szint közelében volt. A  hőmérsékleten a gerjesztett elektronok
hőmérsékleten a gerjesztett elektronok 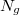 száma az
száma az  összelektron-számnak csak a töredéke, közelítőleg a
összelektron-számnak csak a töredéke, közelítőleg a 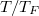 hányada. A
hányada. A  hőmérsékletű elektrongáz energiája tehát az alapállapoti energiától csak kevéssé (
hőmérsékletű elektrongáz energiája tehát az alapállapoti energiától csak kevéssé (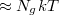 -vel) tér el. Ez azt is jelenti, hogy fémekben az elektronok fajhője elhanyagolható az iontörzsek fajhőjéhez képest. A Dulong-Petit törvénynek tehát ez a kvantummechanikai magyarázata.
-vel) tér el. Ez azt is jelenti, hogy fémekben az elektronok fajhője elhanyagolható az iontörzsek fajhőjéhez képest. A Dulong-Petit törvénynek tehát ez a kvantummechanikai magyarázata.
A fémek szabadelektron-modellje túl egyszerű ahhoz, hogy a szilárd testek elektromos tulajdonságait részleteiben is leírja. Láttuk, hogy a fémelektronok dinamikai viselkedése csak az 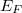 Fermi-szint környezetében számít. Szabadelektron gázról lévén szó, könnyen meghatározható a Fermi szinthez tartozó elektronállapotok
Fermi-szint környezetében számít. Szabadelektron gázról lévén szó, könnyen meghatározható a Fermi szinthez tartozó elektronállapotok 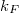 Fermi hullámszáma és az ehhez tartozó
Fermi hullámszáma és az ehhez tartozó 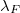 (Fermi) hullámhossz is. Ez utóbbira az adódik, hogy gyakorlatilag az atomi rácstávolsággal egyezik meg. Ugyanakkor ismeretes az is, hogy a fémek fizikai tulajdonságait éppen a Fermi-szint közelében lévő elektronok dinamikai tulajdonságai határozzák meg. Ez pedig azt jelenti, hogy pont ezen elektronok szempontjából nem hanyagolható el az atomi rácsszerkezet jelenléte. Így tehát a szabadelektron-modellünket tovább kell fejleszteni.
(Fermi) hullámhossz is. Ez utóbbira az adódik, hogy gyakorlatilag az atomi rácstávolsággal egyezik meg. Ugyanakkor ismeretes az is, hogy a fémek fizikai tulajdonságait éppen a Fermi-szint közelében lévő elektronok dinamikai tulajdonságai határozzák meg. Ez pedig azt jelenti, hogy pont ezen elektronok szempontjából nem hanyagolható el az atomi rácsszerkezet jelenléte. Így tehát a szabadelektron-modellünket tovább kell fejleszteni.
Ennek egyik lehetséges útja az, hogy valami módon figyelembe vesszük azt is, hogy a szilárd test atomjai térben szabályosan (kristályrácsot alkotva) helyezkednek el.
Ennek a szabályos rendnek az elektronokra gyakorolt hatása már az egydimenziós modellben is megnyilvánul. Minden, e jelenségkörrel kapcsolatos fogalom már itt is megjelenik. Didaktikai előnye ugyanakkor az, hogy matematikailag könnyen kezelhető és így a modell viszonylag egyszerűen végigszámolható.
A Fermi–Dirac eloszlásfüggvény
Ebben a fejezetben kissé részletesebben foglalkozunk az állapotok betöltésének a problémájával igen sok részecskét (elektront) tartalmazó rendszerek esetén. A korrekt megoldást először Enrico Fermi (olasz) és Paul Adrien Maurice Dirac (angol) fizikus dolgozta ki. Innen adódik a címbeli elnevezés is.
Tekintsünk egy nagyon sok elektron tartalmazó rendszert (pl. egy makroszkopikus méretű szilárd testet, azaz fémet, félvezetőt, vagy szigetelőt). Tegyük fel, hogy az elektronállapotokat valamilyen módon sikerült már meghatároznunk. A következőkben azt fogjuk megvizsgálni, hogy egy adott  hőmérsékleten ezek az állapotok hogyan vannak betöltve elektronokkal.
hőmérsékleten ezek az állapotok hogyan vannak betöltve elektronokkal.
Mint azt már tudjuk, a „betöltési szabályt” a Pauli-elv adja meg (TK: 1089. oldal). A háromdimenziós potenciáldoboz példáján láttuk, hogy az elektronállapotok általában olyanok, hogy több állapot is van, amelynek az energiája ugyanakkora. Ezt neveztük degenerációnak. Mivel a most tárgyalandó rendszerünk nagyon nagyszámú részecskét (elektront) tartalmaz (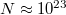 ), így a viszonylag magas
), így a viszonylag magas 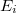 energiaszintek is be lesznek töltve. Mint azt már tudjuk, ez azt jelenti, hogy a lehetséges energiaszintek közötti távolság igen kicsi lesz magához az energiaszinthez képest. Azaz az energiaszintek „relatív kvantáltsága” elhanyagolhatóan kicsi lesz és így folytonos
energiaszintek is be lesznek töltve. Mint azt már tudjuk, ez azt jelenti, hogy a lehetséges energiaszintek közötti távolság igen kicsi lesz magához az energiaszinthez képest. Azaz az energiaszintek „relatív kvantáltsága” elhanyagolhatóan kicsi lesz és így folytonos  energiaskálán dolgozhatunk. Ez éppen megfelel a korrespondencia elvnek. Azaz makroszkopikus energiákon visszakapjuk a klasszikus mechanika folytonos energiaskáláját.
energiaskálán dolgozhatunk. Ez éppen megfelel a korrespondencia elvnek. Azaz makroszkopikus energiákon visszakapjuk a klasszikus mechanika folytonos energiaskáláját.
Ekkor a degeneráció fogalma helyett be lehet vezetni a 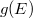 ún. spinpálya-állapotsűrűséget. Gyakran, ha ez nem okoz félreértést, egyszerűen csak állapotsűrűséget mondunk. Ez azt jelenti, hogy a
ún. spinpálya-állapotsűrűséget. Gyakran, ha ez nem okoz félreértést, egyszerűen csak állapotsűrűséget mondunk. Ez azt jelenti, hogy a 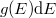 kifejezés megadja az
kifejezés megadja az 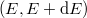 tartományba tartozó spinpálya-állapotok számát. A
tartományba tartozó spinpálya-állapotok számát. A 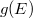 spinpálya-állapotok száma az
spinpálya-állapotok száma az 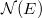 pályaállapotok számának a kétszerese, hiszen egy adott (pálya)állapotban az elektron spinje kétféle lehet (
pályaállapotok számának a kétszerese, hiszen egy adott (pálya)állapotban az elektron spinje kétféle lehet (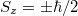 ).
).
Az előzőekben már bevezettük az elektronok energia szerinti eloszlását megadó 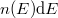 kifejezést is. Ez (definíció szerit) megadja azon elektronok számát, amelyeknek az energiája (
kifejezést is. Ez (definíció szerit) megadja azon elektronok számát, amelyeknek az energiája ( hőmérsékleten) az
hőmérsékleten) az 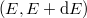 energiatartományba esik. Láttuk azt is, hogy ennek nyilvánvalóan függni kell attól is, hogy hány állapot van, amely elektronnal betölthető. Azaz formálisan felírtuk, hogy
energiatartományba esik. Láttuk azt is, hogy ennek nyilvánvalóan függni kell attól is, hogy hány állapot van, amely elektronnal betölthető. Azaz formálisan felírtuk, hogy
![\[ n(E) = g(E) \cdot f^{FD}(E,T). \]](/images/math/c/1/2/c1217099ddf85baf32cebd43a84e9c4c.png)
A Pauli-elv miatt nyilvánvaló, hogy
![\[ 0 \leq f^{FD}(E,T) \leq 1. \]](/images/math/0/b/2/0b2d7f8ffad6b031183c305b89558bc7.png)
Az elektronok energia szerinti eloszlását  hőmérsékleten tehát az
hőmérsékleten tehát az 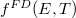 függvény határozza meg. Ezt először E. Fermi és P. A. M. Dirac határozta meg, ezért Fermi–Dirac eloszlásfüggvénynek nevezzük (erre utal az „FD” index is).
függvény határozza meg. Ezt először E. Fermi és P. A. M. Dirac határozta meg, ezért Fermi–Dirac eloszlásfüggvénynek nevezzük (erre utal az „FD” index is).
Természetesen, a részletes és matematikailag egzakt levezetéstől a BSc kurzusban el kell tekintenünk, erre csak az MSc tanulmányokban kerülhet majd sor. Az egzakt matematikai formula azonban igen szemléletes eredményt ad, ezért könnyen elfogadható lesz, a statisztikus fizika elméleti hátterének az ismerete nélkül is.
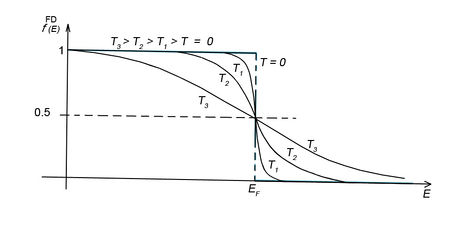
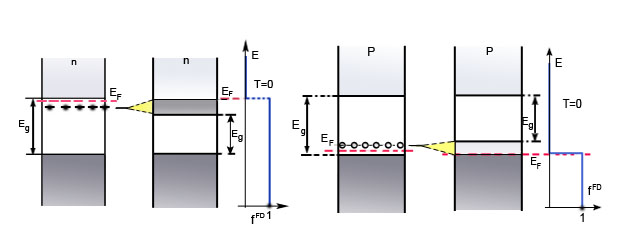
Az előző fejezetben bemutatott fizikai meggondolások alapján a Fermi–Dirac eloszlásfüggvényre egy „lekerekített lépcsőfüggvény” várható (ld. ábra). Ennek megfelelően, a szigorú elméleti számítások eredményeként a következő összefüggés adódik:
![\[ f^{FD} (E,T) = \frac{1}{\left[ \exp\left( \frac{E - E_F}{kT} \right) + 1 \right]} \]](/images/math/0/7/2/072bb19a4b41fffd378737a1c71cc7be.png)
Az 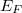 paraméter neve Fermi-energia. Látható, hogy
paraméter neve Fermi-energia. Látható, hogy 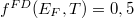 . Ábrázolva a függvényt különböző hőmérsékleteken az alábbi görbék adódnak:
. Ábrázolva a függvényt különböző hőmérsékleteken az alábbi görbék adódnak:
Látható, hogy magas energiaszintek esetén (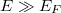 ) éppen a klasszikus statisztikus mechanikában tanult Maxwel-féle eloszláshoz jutunk (TK: 500. oldal, 20c-43. feladat):
) éppen a klasszikus statisztikus mechanikában tanult Maxwel-féle eloszláshoz jutunk (TK: 500. oldal, 20c-43. feladat):
![\[ \lim_{\varepsilon\ll \varepsilon_F} f^{FD}(E,T) = \text{állandó}\cdot\exp\left( -\frac{E}{kT} \right) = f^{MB}(E,T). \]](/images/math/0/f/a/0fabdfbc278e11d2d3a355426b858779.png)
Ez azért megnyugtató, mert így teljesül a korrespondencia-elv. Azaz az elektronok „kvantumstatisztikája” határesetben (magas energiaszinteken) visszaadja a klasszikus fizikában (tömegpontok esetén) tapasztalt eredményeket.
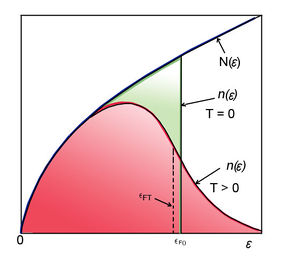
Az 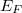 paraméter fizikai tartalmának a megértése nagyon lényeges. Ezért ezt egy egyszerű elektron-rendszer példáján keresztül próbáljuk tisztázni. Legyen ez a már részletesen is tárgyalt szabadelektron gáz (ld. ábra).
paraméter fizikai tartalmának a megértése nagyon lényeges. Ezért ezt egy egyszerű elektron-rendszer példáján keresztül próbáljuk tisztázni. Legyen ez a már részletesen is tárgyalt szabadelektron gáz (ld. ábra).
Mint azt láttuk, szabadelektron gáz esetén az állapotsűrűségét a 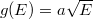 függvény adja meg. Ha a rendszer alapállapotban van, azaz a hőmérséklete
függvény adja meg. Ha a rendszer alapállapotban van, azaz a hőmérséklete 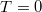 Kelvin, akkor az állapotok betöltöttségét megadó
Kelvin, akkor az állapotok betöltöttségét megadó 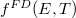 Fermi–Dirac eloszlásfüggvény egy lépcsőfüggvény lesz, hiszen látható, hogy
Fermi–Dirac eloszlásfüggvény egy lépcsőfüggvény lesz, hiszen látható, hogy
![\[ \lim_{T\to 0} f^{FD} (E,T) = \lim_{T\to 0} \frac{1}{\exp\left( \frac{E - E_F}{kT} \right) + 1} = \begin{cases} 1, & \text{ha $E\leq E_F$}, \\ 0, & \text{ha $E \geq E_F$}. \end{cases} \]](/images/math/8/a/f/8af3ded9dcfb63c75b0da15e396fa2bc.png)
Ez azt jelenti, hogy alapállapotban az elektronok az 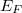 energiaszintig minden állapotot betöltenek, azon felül pedig minden állapot üres lesz. Természetesen pontosan ezt vártuk a Pauli-elv alapján is. Nyilvánvaló, hogy az
energiaszintig minden állapotot betöltenek, azon felül pedig minden állapot üres lesz. Természetesen pontosan ezt vártuk a Pauli-elv alapján is. Nyilvánvaló, hogy az 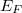 Fermi-energia értéke abból kell, hogy kiadódjon, hogy az állapotokat betöltő elektronok száma éppen
Fermi-energia értéke abból kell, hogy kiadódjon, hogy az állapotokat betöltő elektronok száma éppen  .
.
Ha növekszik a rendszer hőmérséklete, akkor ez azt jelenti, hogy az elektronok az alacsonyabb energiájú állapotokból magasabb energiájú állapotokba jutnak. Ez tükröződik az 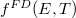 eloszlásfüggvény alakjában is. Fermi energiának most azt az
eloszlásfüggvény alakjában is. Fermi energiának most azt az 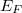 energiaszintet hívjuk, amelynél az eloszlásfüggvény az 1/2 értéket vesz fel.
energiaszintet hívjuk, amelynél az eloszlásfüggvény az 1/2 értéket vesz fel.
Az eloszlásfüggvény „szimmetrikus” a Fermi szint környezetében. Ez azt jelenti, hogy ha a 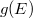 állapotsűrűség állandó volna, akkor a hőmérséklet emelkedésével az
állapotsűrűség állandó volna, akkor a hőmérséklet emelkedésével az 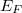 Fermi-szint alatt kiürülő állapotok száma éppen megegyezne az
Fermi-szint alatt kiürülő állapotok száma éppen megegyezne az 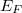 fölött betöltődő állapotok számával. Az elektronok
fölött betöltődő állapotok számával. Az elektronok  száma tehát nem változna, ahogyan annak lennie is kell. Ha a
száma tehát nem változna, ahogyan annak lennie is kell. Ha a 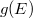 állapotsűrűség (mint a mi példánkban is) egy monoton növekvő függvény, akkor a Fermi-szintet csökkenteni kell ahhoz, hogy a kiürülő és az újonnan betöltődő állapotok száma megegyezzen. Azaz ahhoz, hogy az
állapotsűrűség (mint a mi példánkban is) egy monoton növekvő függvény, akkor a Fermi-szintet csökkenteni kell ahhoz, hogy a kiürülő és az újonnan betöltődő állapotok száma megegyezzen. Azaz ahhoz, hogy az  összelektronszám állandó maradjon az kell, hogy az
összelektronszám állandó maradjon az kell, hogy az 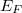 függjön a hőmérséklettől. Jelen esetben az
függjön a hőmérséklettől. Jelen esetben az 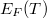 csökkenjen az alapállapotban (
csökkenjen az alapállapotban (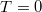 ) adódott
) adódott 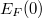 -hoz képest. Megmutatható, hogy ez a hőmérsékletfüggés a szabadelektron gáz esetén olyan kicsi, hogy nyugodtan elhanyagolható, így a Fermi-szintet (szobahőmérsékletű tartományban) állandónak vehetjük, azaz
-hoz képest. Megmutatható, hogy ez a hőmérsékletfüggés a szabadelektron gáz esetén olyan kicsi, hogy nyugodtan elhanyagolható, így a Fermi-szintet (szobahőmérsékletű tartományban) állandónak vehetjük, azaz 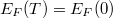 .
.
Ezek után megadható a szabadelektron gázban az elektronok energia szerinti eloszlása. A tárgyaltak szerint adódik tehát, hogy
![\[ n(E) {\rm d}E = a\sqrt{E} f(E,T) \, {\rm d}E = a\sqrt{E} \frac{1}{\exp\left( \frac{E - E_F}{kT} \right) + 1} \, {\rm d}E. \]](/images/math/0/9/3/0936c8d8612763bd9f2df923c19e428d.png)
Ez tehát megadja azon elektronok számát, amelyek energiája  hőmérsékleten
hőmérsékleten  és
és 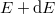 közé esik.
közé esik.
Fotonokból álló rendszer (a fotongáz)
A fentiekben bevezetett 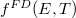 eloszlásfüggvényből adódó
eloszlásfüggvényből adódó 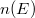 matematikai alakja nagyon hasonlít a feketetest sugárázásakor megismert formulához (TK: 1026. oldal). Láttuk, hogy a
matematikai alakja nagyon hasonlít a feketetest sugárázásakor megismert formulához (TK: 1026. oldal). Láttuk, hogy a  hőmérsékletű (fekete) test által, az
hőmérsékletű (fekete) test által, az  és
és 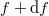 frekvenciatartományban kisugárzott elektromágneses hullámok összenergiáját az alábbi formula adta meg:
frekvenciatartományban kisugárzott elektromágneses hullámok összenergiáját az alábbi formula adta meg:
![\[ u(f) \, {\rm d}f = a \frac{hf^3}{\exp(hf / kT) - 1} \, {\rm d}f. \]](/images/math/d/4/b/d4b311b1bf743274404dc6935b4e4245.png)
A kellő összehasonlítás végett írjuk át ezt olyan alakba, amelyik fizikai tartalmát tekintve azonos a szabadelektron gáz esetén kapottal. A térben lévő 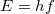 energiájú fotonok
energiájú fotonok 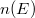 számának eloszlása könnyen definiálható a fent megadott
számának eloszlása könnyen definiálható a fent megadott 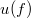 segítségével, hiszen írható, hogy
segítségével, hiszen írható, hogy
![\[ u(f) = hf\cdot n(f), \quad \text{azaz} \quad n(f) = af^2\frac{1}{\exp(hf/kT) - 1}. \]](/images/math/d/9/9/d99285148992c23e457b17166bc3c05c.png) |
(3) |
Mint azt a hullámtani ismereteink alapján tudjuk, egy (térbeli) síkhullámot az alábbi matematikai függvény ad meg:
![\[ \Psi({\bf r}, t) = A \sin({\bf kr} - \omega t). \]](/images/math/c/3/8/c387db181dde3d5301f86b8f27ea8d4b.png)
Azaz egy (hullám)állapotot a 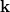 hullámszám-vektor jellemez, ahol
hullámszám-vektor jellemez, ahol 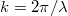 . Az elektromágneses hullámok esetén
. Az elektromágneses hullámok esetén 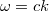 . Látható tehát, hogy minden olyan
. Látható tehát, hogy minden olyan 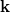 , amelynek a nagysága ugyanakkora, egyforma
, amelynek a nagysága ugyanakkora, egyforma  frekvenciájú hullámot ad meg. Azaz a különböző irányba haladó, de azonos hullámhosszú hullámok frekvenciája megegyezik. Ugyanakkor a „különböző irányba való haladás” különböző hullámállapotot (idegen szóval módust) is jelent. Így van értelme annak a kérdésnek, hogy vajon hány (hullám)állapot van, amelynek a frekvenciája megegyezik?
frekvenciájú hullámot ad meg. Azaz a különböző irányba haladó, de azonos hullámhosszú hullámok frekvenciája megegyezik. Ugyanakkor a „különböző irányba való haladás” különböző hullámállapotot (idegen szóval módust) is jelent. Így van értelme annak a kérdésnek, hogy vajon hány (hullám)állapot van, amelynek a frekvenciája megegyezik?
Erre könnyen lehet válaszolni, hiszen azon állapotok száma, amelyeknek a frekvenciája  és
és 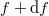 , egy
, egy  sugarú és
sugarú és 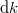 vastagságú gömbhéj térfogatával kell, hogy arányos legyen. Mivel pedig
vastagságú gömbhéj térfogatával kell, hogy arányos legyen. Mivel pedig 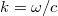 , valamint
, valamint 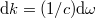 , adódik, hogy
, adódik, hogy
![\[ g(\omega){\rm d}\omega \sim \omega^2 {\rm d}\omega, \quad \text{azaz} \quad g(f){\rm d}f \sim f^2{\rm d} f. \]](/images/math/c/e/9/ce9ffe17aa6a1b12f2cd287f7df7d51b.png)
Látható tehát, hogy (3) második része úgy írható, hogy
![\[ n(f) = af^2 \frac{1}{\exp(hf/kT) - 1} = g(f) \frac{1}{\exp(hf/kT) - 1} \equiv g(f)\cdot f^{\rm foton}(f,T). \]](/images/math/d/1/a/d1aa2c3b1aa08db9da67a8e8e96aa947.png)
Összevetve ezt az elektrongáz esetén látottakkal, az 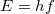 energiájú fotonállapotok betöltöttségét a
energiájú fotonállapotok betöltöttségét a
![\[ f^{\rm foton}(E,T) = \frac{1}{\exp(E/kT) - 1} \]](/images/math/4/0/1/401e12ca2ac75e43bb9fd38ead5aa405.png)
függvénnyel lehet definiálni. Ez már alkalmas arra, hogy összehasonlítsuk a jól ismert 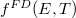 Fermi–Dirac-féle eloszlásfüggvénnyel. Mivel
Fermi–Dirac-féle eloszlásfüggvénnyel. Mivel 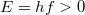 , ezért
, ezért 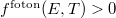 , amint annak lennie is kell.
, amint annak lennie is kell.
„Alacsony” frekvenciákon (ha 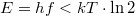 ) az adódik, hogy
) az adódik, hogy 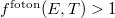 , ami azt jelenti, hogy egy adott „fotonállapotban” (módusban) több foton is lehet. A fotonokra tehát nem érvényes a Pauli-elv!
, ami azt jelenti, hogy egy adott „fotonállapotban” (módusban) több foton is lehet. A fotonokra tehát nem érvényes a Pauli-elv!
Mivel az 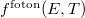 kifejezés ezen matematikai alakját (a statisztikus fizika elvei alapján) Satyendra Nath Bose és Albert Einstein határozták meg, ezért ezt Bose–Einstein-féle eloszlásfüggvénynek szokták nevezni.
kifejezés ezen matematikai alakját (a statisztikus fizika elvei alapján) Satyendra Nath Bose és Albert Einstein határozták meg, ezért ezt Bose–Einstein-féle eloszlásfüggvénynek szokták nevezni.
Érdemes összehasonlítani a megismert eloszlásfüggvényeket. Ezek mindegyike különböző statisztikai meggondolásokat tartalmaznak, amelyeknek jól definiált fizikai alapjuk van. Ezekkel és az igen fontos és érdekes további részletekkel, valamint a lehetséges fizikai alkalmazásokkal azonban már csak az MSc Fizika kurzusban fogunk megismerkedni.
Célszerű lesz az eloszlásfüggvényeket egy közös matematikai alakban felírni:
![\[ f^X (E,T) = \frac{1}{\exp\left( \frac{E - E_0}{kT} \right) + \delta}, \]](/images/math/1/3/2/13278aea6f1c17f07de1ab0b708e0f55.png)
ahol
| Fermi–Dirac eloszlás esetén | 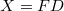
|
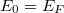
|
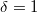 , ,
|
| Bose–Einstein eloszlás esetén | 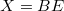
|
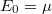
|
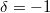 , ,
|
| Maxwell–Boltzmann eloszlás esetén | 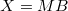
|
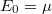
|
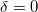 . .
|
(Természetesen az 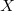 csak egy jelölő index, amely az egyes eloszlásfüggvényeket különbözteti meg egymástól.)
csak egy jelölő index, amely az egyes eloszlásfüggvényeket különbözteti meg egymástól.)
A közös formulában megjelenő 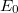 paramétert kémiai potenciálnak hívjuk. Az elnevezés jogosságának megértetése igen messze vezetne, ezért ezzel nem is próbálkozunk. Fogadjuk el ezt csupán egy „családnévnek” és ne firtassuk az eredetét!
paramétert kémiai potenciálnak hívjuk. Az elnevezés jogosságának megértetése igen messze vezetne, ezért ezzel nem is próbálkozunk. Fogadjuk el ezt csupán egy „családnévnek” és ne firtassuk az eredetét!
Amint azt láttuk, a fotonok a Bose–Einsten statisztikát követik. Az is kiderült, hogy ebben az esetben 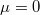 kell, hogy legyen.
kell, hogy legyen.
Megjegyzés. Azt tapasztaljuk, hogy vannak olyan fizikai rendszerek, amelyek esetén a  egy véges érték. Ekkor azonban az
egy véges érték. Ekkor azonban az 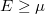 feltételnek is teljesülnie kell, hiszen az eloszlásfüggvény soha nem lehet negatív! Ugyanis „negatív számú részecskéről” beszélni teljesen értelmetlen dolog lenne! Az evvel kapcsolatos további ismereteket az MSc Fizika tantárgy tartalmazza.
feltételnek is teljesülnie kell, hiszen az eloszlásfüggvény soha nem lehet negatív! Ugyanis „negatív számú részecskéről” beszélni teljesen értelmetlen dolog lenne! Az evvel kapcsolatos további ismereteket az MSc Fizika tantárgy tartalmazza.
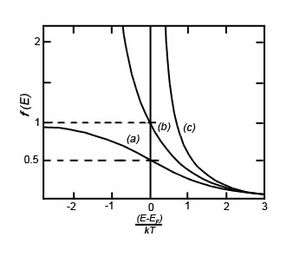
A közös 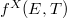 függvényt célszerű lesz úgy felrajzolni, hogy a vízszintes tengely mentén az
függvényt célszerű lesz úgy felrajzolni, hogy a vízszintes tengely mentén az 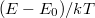 értéket mérjük fel. Az eredményt az alábbi ábrán mutattuk be, ahol (a) a Fermi–Dirac, (b) a Maxwell–Boltzmann és (c) a Bose–Einstein statisztika eloszlásfüggvényét jelenti.
értéket mérjük fel. Az eredményt az alábbi ábrán mutattuk be, ahol (a) a Fermi–Dirac, (b) a Maxwell–Boltzmann és (c) a Bose–Einstein statisztika eloszlásfüggvényét jelenti.
Látható, hogy nagy energiákon mindhárom függvény ugyanúgy viselkedik, azaz mind a két kvantumstatisztika átmegy a klasszikus Maxwell–Boltzmann statisztikába. Alacsony energiákon az eltérések igen karakterisztikussá válnak.
- A Pauli-elvet egyedül csak a Fermi–Dirac statisztika teljesíti!

A Stagg Field Stadion (1927-ben) |
Enrico Fermi (1901-1954)
Nobel-díj (1938): „az újabb radioaktív elemek neutron besugárzással történő létrehozásáért és a lassú neutronokkal előidézett magreakciók felfedezéséért”. Rómában született. Egyetemi diplomáját és doktorátusát (20 évesen!) Pisában szerezte meg. 1924-től a római egyetem Fizika Intézetének a tanára, majd igazgatója lett. 1938-ban (Nobel-díja átvétele után) az USA-ba emigrált. A Columbia Egyetem és a Chicago Egyetem tanára lett. Vezetése alatt itt (a Stagg Field stadion lelátója alatt) épült meg a világ első működő atomreaktora. A (grafit rudakkal) szabályozott láncreakció indult el. Ezzel a „második tűzgyújtással” kezdetét vette az „Atomkorszak”. A II. világháború alatt Los Alamosban részt vett az atombomba előállításában. Halála után a Chicagoi Egyetem Fizika Intézet neve: lett. Tiszteletére a 100-as rendszámú mesterséges elemet Fermiumnak nevezték el. |

A Dirac-egyenlet: |
Paul Adrien Maurice Dirac (1902-1984)
Nobel-díj 1933 (Schrödingerrel megosztva): „az atomelmélet új és gyümölcsöző megfogalmazásáért.” Az angliai Bristolban született. A város egyetemének villamosmérnöki karán tanult, de doktorátusát (Cambridge-ben) már elméleti fizikából szerezte. 1929-32-ig Wisconsin, Michigan, Princeton USA egyetemei hívták meg. 1937-ben feleségül vette (a magyar származású Nobel-díjas) Wigner Jenő nővérét 1932-69 között Cambridge-ben Newton matematikai tanszékének professzora volt. Ezután az USA-ba költözött, hogy idősebb nővére közelében élhessen. Utolsó évtizedeit a Floridai Állami Egyetem (Tallahassee) professzoraként élte le. Legfőbb érdeme az elektronok relativisztikus hullámegyenletének a megalkotása. Ennek egyenes következménye az elektronspin megjelenése a (linearizált) egyenletben. A kapott energiaspektrum alapján megjósolta pozitron létezését, valamint az (elektron-pozitron) párképződést és az annihilációt is. Ennek kapcsán névéhez fűződik az antirészecskék világának a megsejtése is. Őt tekintjük a Kvantumelektrodinamika megalapozójának is. Egy villamosmérnök számára nevét a Dirac-delta őrzi. |

|
Satyendra Nath Bose (1894-1974)
Az indiai Kalkuttában született. 1921-től a Calcutta University Fizika Tanszékén dolgozott. 1924-ben írt cikkében a Planck-féle sugárzási törvény klasszikus fizikai fogalmakra történő utalás nélküli levezetését adta meg. A kezdeti visszautasítások után a cikkét közvetlenül Einsteinnek küldte el. Ő rögtön felismerte az eredmény jelentőségét. Maga fordította le német nyelvre és Bose nevében beküldte a kor vezető rangos fizikai folyóiratához, a Zeitschrift für Physik-hez. A cikk megjelenésének köszönhetően ezután Bose Európába látogatott. Itt olyan neves fizikusokkal dolgozhatott, mint Louis de Broglie, Marie Curie és A. Einstein. Bár Nobel-díjat nem kapott, a róla elnevezett Bose–Einstein statisztika révén minden fizikus- és mérnökhallgató megismeri a nevét. Ezzel örökre beírta magát a Fizika tudományába |
A félvezetők energiasáv szerkezete és az elektronika alapjai
A (kovalens) kémiai kötés egyszerű kvantummechanikai modellje
A kovalens kémiai kötésről már a középiskolai (sőt az általános iskolai) Kémia tantárgyban szó volt. Ennek a fejezetnek az egyik célja, hogy megteremtse a kapcsolatot az eddig tárgyalt kvantummechanikai ismereteink és a kémiában tanultak között.
Két atom között létrejövő kovalens kémiai kötés fizikai lényegét már egydimenziós modellen is szemléltetni tudjuk.
Megjegyzés. Tudatosan olyan modellt választottunk, amely elég egyszerű ahhoz, hogy viszonylag kis erővel numerikusan is végigszámolható legyen, ugyanakkor elegendően „bonyolult” ahhoz, hogy a kívánt effektust leírja. (Azaz követtük az „Occam borotvája” elvet, amely a modellalkotás egyik igen fontos ismeretelméleti eszköze.) Természetesen, magát a számolást nem hajtjuk végre, de megadjuk azon a gondolatmenetet, amelyet követve a numerikus számításokat bárki elvégezheti (még a BSc szak szintjén is).
Megtanultuk már, hogy milyen az atomok (elektron)konfigurációja, azaz miképpen töltik be az elektronok a lehetséges állapotokat. (TK: 1090. oldal) A Pauli-elv segítségével az atomok elektronszerkezete megkonstruálható.
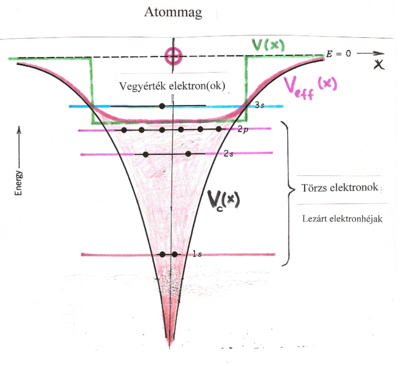
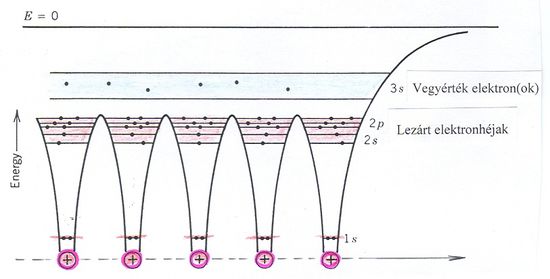
A teljesen betöltött héjak (lezárt héjak) alkotják az iontörzset. A részben betöltött (al)héjak (nyílt héjak) elektronjait vegyérték elektronoknak nevezzük. Ennek oka az, hogy ha az atom kölcsönhatásba lép egy másik atommal (pl. vegyülés történik), akkor a folyamat során az iontörzsek gyakorlatilag változatlanok maradnak. Ugyanis a zárt héj „feltöréséhez” viszonylag „nagy” energia kell (TK: 1092. oldal). Azaz a vegyület kialakulásában csak a (nyílt héjon lévő) vegyérték elektronok vesznek részt, legalábbis a „természetes” körülmények között. A vegyérték elektronok (a Pauli-elv miatt) csak a lezárt héjak feletti energiaszinteket foglalhatják el. Ezt úgy „modellezhetjük”, mintha a vegyérték elektron egy 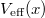 potenciálgödörbe lenne bezárva, melynek első energiaszintje éppen a nyílt héj energiaszintje. Egydimenziós, kvalitatív modell esetén ez egy „négyszögletes potenciálgödörrel” jellemezhető. Mindezt a következő ábrán szemléltettük.
potenciálgödörbe lenne bezárva, melynek első energiaszintje éppen a nyílt héj energiaszintje. Egydimenziós, kvalitatív modell esetén ez egy „négyszögletes potenciálgödörrel” jellemezhető. Mindezt a következő ábrán szemléltettük.
A négyszögletes potenciálgödörhöz (vagy potenciálvölgyhöz) akkor jutunk, ha a 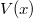 potenciális energia olyan, hogy egy
potenciális energia olyan, hogy egy  hosszúságú szakaszon állandó, azon kívül pedig ennél nagyobb, szintén állandó értékű. Azaz például
hosszúságú szakaszon állandó, azon kívül pedig ennél nagyobb, szintén állandó értékű. Azaz például
![\[ V(x) = \begin{cases} V_0 & \text{ha $x\notin L$}, \\ V_0 - V_L & \text{ha $x\in L$}. \end{cases} \]](/images/math/7/5/b/75b9731fe6263ea965c4a664470fc084.png)
Itt a potenciálgödör „mélységét” a 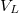 , a szélességét az
, a szélességét az  adja meg. Ebben az igen egyszerű modellben ez a két paraméter definiálja az elektron fizikai környezetét. Természetesen a potenciális energia „nulla szintje” akárhol megválasztható, azaz a
adja meg. Ebben az igen egyszerű modellben ez a két paraméter definiálja az elektron fizikai környezetét. Természetesen a potenciális energia „nulla szintje” akárhol megválasztható, azaz a 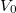 érték bármekkora lehet. A következő ábrán az atomoknál megszokott módon a
érték bármekkora lehet. A következő ábrán az atomoknál megszokott módon a 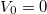 esetet mutattuk be. A matematikai formulák egyszerűsítése végett gyakran élünk a
esetet mutattuk be. A matematikai formulák egyszerűsítése végett gyakran élünk a 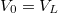 választással. A későbbiekben is ezt fogjuk használni.
választással. A későbbiekben is ezt fogjuk használni.
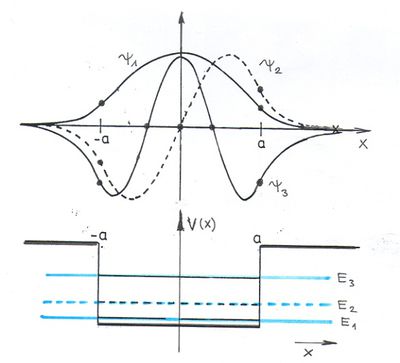
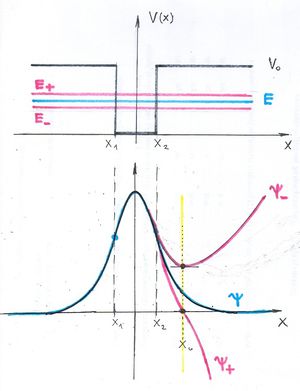
Az ábra alapján látható, hogy kötött állapotról csak akkor beszélhetünk, ha a részecske  energiájára fennáll, hogy
energiájára fennáll, hogy 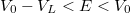 . A klasszikus mozgás tartománya tehát az
. A klasszikus mozgás tartománya tehát az  hosszúságú szakasz. A Schrödinger-egyenlet megoldása nélkül, pusztán az általános ismereteink alapján fel tudjuk rajzolni a hullámfüggvények várható alakját:
hosszúságú szakasz. A Schrödinger-egyenlet megoldása nélkül, pusztán az általános ismereteink alapján fel tudjuk rajzolni a hullámfüggvények várható alakját:
Mint azt tudjuk, az állapotfüggvények „egy púpú”, „két púpú” stb. függvények lesznek.
Azért választottunk ilyen egyszerű modellt, hogy bemutassuk azt, hogy a tárgyalásra kerülő jelenség numerikusan is végigszámolható. Ha a modellre jellemző paramétereket „ügyesen” választjuk meg, akkor (a modellen belül) „reális” számszerű eredményeket kaphatunk. A szükséges matematikai formulákhoz a Schrödinger-egyenlet felírásával jutunk. Ez szinte minden elemi Kvantummechanika könyvben benne van. A megoldás elvi menetét az előzőekben már részletesen mi is megtárgyaltuk. Mivel amúgy is eléggé „durva” modellről van szó, a „kvantitatív” (számszerű) tárgyalásnak jelen esetben nem sok értelme lenne. Elegendő „csak” kvalitatív eredményekre szorítkoznunk. Azaz be szeretnénk látni, hogy egy ilyen elnagyolt modell esetén is „létrejön” a kémiai kötés két atom között.
Az egyszerűség végett legyen ebben az „atomban” csupán csak egy (vegyérték) elektron, amelynek energiáját jelöljük 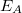 -val. Legyen ez most éppen az
-val. Legyen ez most éppen az 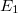 alapállapoti energia. Az elektron az ennek megfelelő állapotban van.
alapállapoti energia. Az elektron az ennek megfelelő állapotban van.
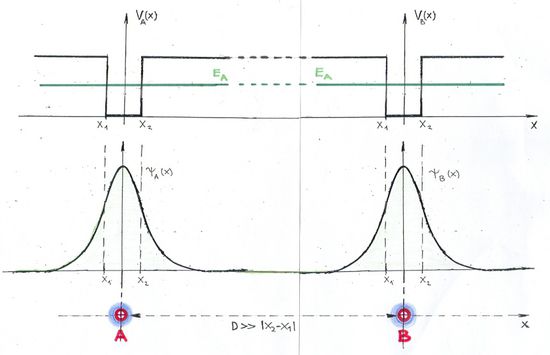
Tekintsünk két atomot ( és
és  ), amelyek egymástól nagyon nagy távolságra vannak. Ekkor a két vegyérték elektron állapotfüggvénye (
), amelyek egymástól nagyon nagy távolságra vannak. Ekkor a két vegyérték elektron állapotfüggvénye (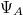 és
és 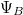 ) nem „fedi át” egymást (azaz az „elektronfelhők nem zavarják egymást”), így két független atomunk van. Mindkettőben az elektron energiája ugyanakkora, nevezetesen
) nem „fedi át” egymást (azaz az „elektronfelhők nem zavarják egymást”), így két független atomunk van. Mindkettőben az elektron energiája ugyanakkora, nevezetesen 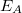 . Szemléltetés:
. Szemléltetés:
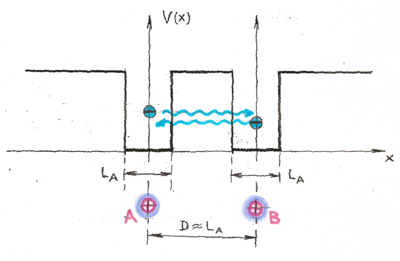
Közelítsük egymáshoz a két atomot! Tovább egyszerűsödik a modellünk, ha a két vegyérték elektron közötti Coulomb-taszítástól eltekintünk. Ekkor az atomok közelítésekor mindkét elektron csak az iontörzsekkel lép kölcsönhatásba. Mint azt láttuk, ezek szerkezete elégé stabil és így a „vegyülés során” a potenciálgödrök alakja nem változik. Ha a két „atom” elegendően közel kerül egymáshoz, akkor a (vegyérték) elektronok (pl. alagúteffektussal, TK: 1063. oldal) „átjuthatnak” a két atomot elválasztó potenciálgáton és így mind a két atomhoz tartozni fognak. Azaz ekkor a két atomot már egy kvantummechanikai rendszernek kell tekinteni.
A Coulomb-taszítás hiánya miatt a két elektron egymástól függetlenül vizsgálható. Ezt úgy tudjuk modellezni, hogy bármelyik elektron ugyanazt a „kettős potenciálvölgyet” fogja érzékelni. Ez durva modellnek tűnik ugyan, de a kvalitatív fizikai eredmények lényegén nem változtat. Ugyanakkor a „számolást” igen leegyszerűsíti.
Az egydimenziós Schrödinger-egyenlet általános matematikai tulajdonságainak az ismeretében könnyen felrajzolhatjuk a lehetséges állapotfüggvényeket. Ezeket, mivel most már az 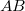 molekulában lévő elektronok lehetséges állapotait adja meg, molekulapályáknak szoktuk nevezni és (jelen esetben)
molekulában lévő elektronok lehetséges állapotait adja meg, molekulapályáknak szoktuk nevezni és (jelen esetben) 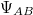 –vel fogjuk jelölni.
–vel fogjuk jelölni.
Ezeket az állapotokat veheti fel aztán a molekulában lévő (most összesen) két darab elektron. Természetesen ezen molekulapályák „betöltésénél” is alkalmaznunk kell az atomok elektronszerkezeténél megismert Pauli-elvet!
Látható, hogy a rendszer a két (egyforma) atommagot összekötő egyenes szakasz ( ) felezősíkjára nézve tükörszimmetrikus. Legyen a
) felezősíkjára nézve tükörszimmetrikus. Legyen a  szakasz felezőpontja
szakasz felezőpontja 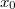 ! Ekkor az említett tükörszimmetria matematikai kifejezése a következő:
! Ekkor az említett tükörszimmetria matematikai kifejezése a következő:
![\[ V(x_0 - x) = V(x - x_0). \]](/images/math/c/8/a/c8a9f588962880dc7dc3390f543cfa29.png)
Ez azt jelenti, hogy ha a rendszert tükrözzük a felező síkra, akkor fizikailag valójában „nem történik semmi”. Így nem változhat meg a rendszerben lévő elektronok valószínűségi eloszlása sem. Tehát:
![\[ \left| \Psi_{AB}(x_0 - x) \right|^2 = \left| \Psi_{AB}(x - x_0) \right|^2. \]](/images/math/5/2/7/527b826ce406d15b3ef161a5ec05fbb9.png)
Ebből viszont az következik, hogy
![\[ \Psi_{AB}(x_0 - x) = \pm \Psi_{AB}(x - x_0). \]](/images/math/7/e/9/7e91826e5194ba8ef6c5740bb4218c0b.png)
Látható tehát, hogy a molekulapályákat megadó állapotfüggvények (az 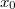 szimmetriapontra nézve) vagy páros, vagy pedig páratlan függvények lehetnek. Ennek megfelelően az
szimmetriapontra nézve) vagy páros, vagy pedig páratlan függvények lehetnek. Ennek megfelelően az 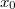 pontban nyilvánvalóan teljesül az alábbi két feltétel:
pontban nyilvánvalóan teljesül az alábbi két feltétel:
![\[ \begin{cases} \Psi_{AB}(x_0) = 0, & \text{ha páratlan függvényről van szó, és} \\ \left. \frac{\rm d}{{\rm d}x} \Psi_{AB}(x) \right|_{x_0} = 0 & \text{ha páros függvényről van szó.} \end{cases} \]](/images/math/2/9/5/29554343160cd47c1344a959af1a2de2.png)
Akinek a megadott szimmetria kifejezés idegennek tűnik, az éljen az 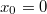 választással, és akkor már a középiskolás matematikából ismerős összefüggéseket kap.
választással, és akkor már a középiskolás matematikából ismerős összefüggéseket kap.
A lehetséges molekulapályák a Schrödinger-egyenlet általános (matematikai) tulajdonságai alapján megkonstruálhatók, és közben megkapjuk az állapotokhoz tartozó energiaszintek értékét is. A molekulapályák meghatározásának igen egyszerű a módja. A megoldás a fentiekben tárgyalt szimmetria kihasználásán, nevezetesen az állapotfüggvények 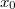 szimmetriapontban mutatott viselkedésén alapszik (ld. előző formula).
szimmetriapontban mutatott viselkedésén alapszik (ld. előző formula).
Tekintsük először a szabad atom imént definiált egydimenziós (potenciálgödör) modelljét! A Kvantummechanika részben láttuk, hogy egydimenziós kötött állapot esetén a lehetséges állapotfüggvények megkeresése az igen szemléletes „próbálgatásos módszerrel” történhet.
Tegyük fel, hogy sikerült megoldanunk a Schrödinger-egyenletet és megkaptuk az  alapállapoti energiaszintet és az ehhez tartozó
alapállapoti energiaszintet és az ehhez tartozó 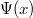 állapotfüggvényt. Látható, hogy az
állapotfüggvényt. Látható, hogy az 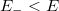 nem lesz az atomban lévő elektron „jó” energiaszintje. Ez igen személetesen megérthető. Mivel
nem lesz az atomban lévő elektron „jó” energiaszintje. Ez igen személetesen megérthető. Mivel 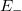 valamivel kisebb, mint a „jó”
valamivel kisebb, mint a „jó”  energia, ezért a potenciálgödörben az elektron impulzusa kisebb, a hozzá tartozó lokális de Broglie-hullámhossz nagyobb, tehát a
energia, ezért a potenciálgödörben az elektron impulzusa kisebb, a hozzá tartozó lokális de Broglie-hullámhossz nagyobb, tehát a 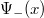 hullámfüggvény lassabban fog változni, mint a
hullámfüggvény lassabban fog változni, mint a 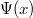 . De ez azt jelenti, hogy (
. De ez azt jelenti, hogy (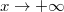 esetén) nem tart a zérushoz. Így nem képezhető belőle egy valószínűségsűrűség-függvény. Teljesen hasonló a helyzet
esetén) nem tart a zérushoz. Így nem képezhető belőle egy valószínűségsűrűség-függvény. Teljesen hasonló a helyzet 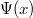 esetében.
esetében.
Ekkor azonban a gödör belsejében a lokális impulzus megnő, és így a de Broglie-hullámhossz lecsökken, ezért a 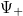 a
a 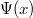 -hez képest gyorsabban fog változni. Ezért aztán a klasszikusan tiltott tartományban véges távolságon belül eléri az
-hez képest gyorsabban fog változni. Ezért aztán a klasszikusan tiltott tartományban véges távolságon belül eléri az  tengelyt, aminek következtében (
tengelyt, aminek következtében (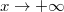 esetén) „elszáll” a végtelenbe. Azaz nem lesz „jó” állapotfüggvény! Mindezt már megtárgyaltuk a hullámfüggvények általános matematikai viselkedésének a vizsgálatakor. Lásd ábra.
esetén) „elszáll” a végtelenbe. Azaz nem lesz „jó” állapotfüggvény! Mindezt már megtárgyaltuk a hullámfüggvények általános matematikai viselkedésének a vizsgálatakor. Lásd ábra.
A bemutatott „effektus” igen jól használható a kétatomos molekulapályák kvalitatív meghatározására. Ennek egy olyan (szimmetriameggondolásokon alapuló) „módját” választjuk, amelynél elkerülhető a Schrödinger-egyenlet teljes megoldása és ugyanakkor igen szemléletes.
Tekintsük az iménti atomi potenciálvölgyet és válasszunk ki egy 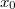 pontot a jobboldali „klasszikusan tiltott” tartományban. Ez lesz majd az
pontot a jobboldali „klasszikusan tiltott” tartományban. Ez lesz majd az 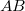 molekula szimmetriasíkjának a helye, azaz az
molekula szimmetriasíkjának a helye, azaz az  és a
és a  atommagot összekötő
atommagot összekötő  egyenes szakasz felezőpontja.
egyenes szakasz felezőpontja.
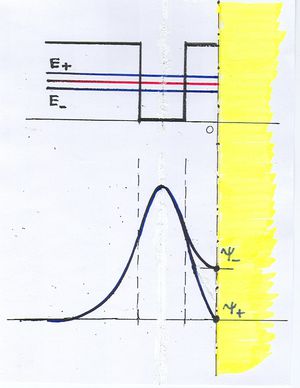
Emeljük meg az energiát arra az 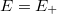 energia szintre amikor a hozzátartozó hullámfüggvényre teljesül, hogy
energia szintre amikor a hozzátartozó hullámfüggvényre teljesül, hogy 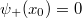 . Ezek után csökkentsük le az energiát egy olyan
. Ezek után csökkentsük le az energiát egy olyan 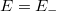 értékre, amikor a hullámfüggvénynek az
értékre, amikor a hullámfüggvénynek az 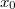 pontban vízszintes érintője van, azaz a deriváltja kielégíti a
pontban vízszintes érintője van, azaz a deriváltja kielégíti a 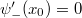 összefüggést.
összefüggést.
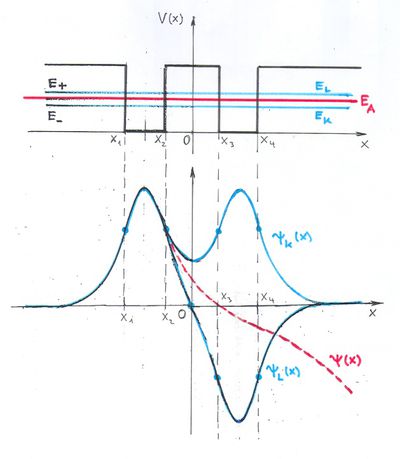
„Takarjuk ki” a kapott ábra 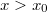 részét, majd tükrözzük az egészet az
részét, majd tükrözzük az egészet az 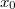 pontra. A művelet elvégzése után megkapjuk a keresett molekulapályákat, hiszen
pontra. A művelet elvégzése után megkapjuk a keresett molekulapályákat, hiszen
![\[ \Psi_{-}(x)\to\Psi_K(x), \quad \Psi_{+}\to\Psi_L(x), \quad \Psi_{AB} = \begin{cases} \Psi_K & \text{páros függvény} \\ \Psi_L & \text{páratlan függvény} \end{cases} \]](/images/math/0/b/4/0b487bba9ad440a60521607afc60492a.png)
Az alkalmazott „geometriai” módszer lényegéből adódik, hogy az így „megkonstruált” („összeszabott”) függvények a (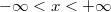 ) tartományban mindenhol kielégítik a Schrödinger-egyenletet, valamint pontosan teljesítik a hullámfüggvényekre kirótt általános követelményeket, azaz a Born-féle definícióval megtalálási valószínűségsűrűség-függvényeket adnak. Természetesen most az
) tartományban mindenhol kielégítik a Schrödinger-egyenletet, valamint pontosan teljesítik a hullámfüggvényekre kirótt általános követelményeket, azaz a Born-féle definícióval megtalálási valószínűségsűrűség-függvényeket adnak. Természetesen most az 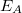 energiaszinthez tartozó hajdani
energiaszinthez tartozó hajdani 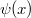 atomi állapotfüggvény „nem lesz jó”, hiszen a másik atom hatására „elszáll a
atomi állapotfüggvény „nem lesz jó”, hiszen a másik atom hatására „elszáll a 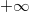 -be”.
-be”.
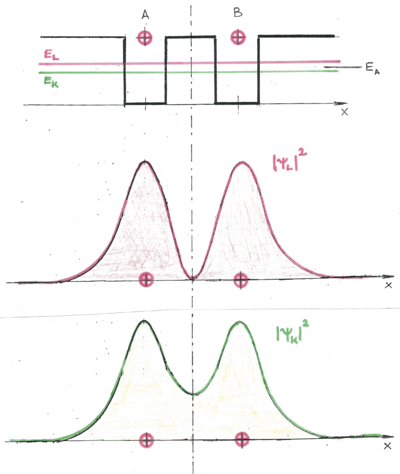
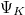 állapot esetén a
állapot esetén a 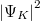 a két atom közötti térben (a potenciálgátban) véges értékű, azaz az elektron itt véges valószínűséggel megtalálható. Szemléletesen szólva az elektron mintegy összetartja a két iontörzset. Ezért ez egy ún. kötőpálya lesz. A
a két atom közötti térben (a potenciálgátban) véges értékű, azaz az elektron itt véges valószínűséggel megtalálható. Szemléletesen szólva az elektron mintegy összetartja a két iontörzset. Ezért ez egy ún. kötőpálya lesz. A 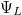 állapot esetén a
állapot esetén a 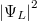 a potenciálgát középpontjában (most
a potenciálgát középpontjában (most 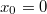 ) zérus értékű, ezért ez nem hozhat létre kötést. Ezt hívják lazítópályának.
) zérus értékű, ezért ez nem hozhat létre kötést. Ezt hívják lazítópályának.
Megjegyzés. Látható, hogy mind a kötő, mind pedig a lazító molekulapályák a molekulát alkotó két atom 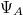 és
és 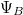 atompályáiból alkalmas lineáris kombinációval közelítőleg létrehozhatók (szuperpozíció elve!), hiszen:
atompályáiból alkalmas lineáris kombinációval közelítőleg létrehozhatók (szuperpozíció elve!), hiszen:
![\[ \Psi_K \approx \Psi_A + \Psi_B, \quad \text{valamint} \quad \Psi_L \approx \Psi_A - \Psi_B. \]](/images/math/3/e/7/3e756ca4b96c1d7f164d7cf7bf3e29b9.png)
Ennek nagyon hasznos és szemléletes következményeit majd az MSc szintű Fizika tantárgyban fogjuk megtárgyalni. Az elmondottakhoz még csak annyit kell hozzátennünk, hogy a középiskolai Kémia órákon a „molekulakötéseknél” előkerült  és
és 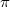 pályák esetén is ugyanerről van szó!
pályák esetén is ugyanerről van szó!
Általánosságban is elmondhatjuk, hogy két atom közelítésekor a szabad atomi energiaszint két közeli energiaszintre hasad fel. Az alacsonyabb energiájú a kötőpályákat, a magasabb energiájú a lazítópályákat adja.
![\[ \begin{cases} E_{+} \equiv E_L > E_A & \text{$\Psi_L(x)$, lazító pálya}, \\ E_{-} \equiv E_K < E_A & \text{$\Psi_K(x)$ kötő pálya}. \end{cases} \]](/images/math/9/2/8/928b48e092cbf10f6d408d6d866a194d.png)
Az „energiasáv szerkezet” kialakulásának fizikai okai
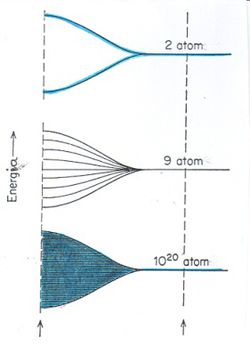
Maradva továbbra is az egydimenziós modellnél, az előzőekben elmondottak alapján „könnyen elfogadható” az, hogy ha  darab egyforma atomot helyezünk el egy egyenes mentén (és így lépnek egymással kölcsönhatásba), akkor az atomi energiaszintek
darab egyforma atomot helyezünk el egy egyenes mentén (és így lépnek egymással kölcsönhatásba), akkor az atomi energiaszintek  részre hasadnak fel.
részre hasadnak fel.
A „felhasadás mértéke” nagyon kicsi az atomi energiaszintek közötti (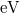 -nyi) különbségekhez képest. Ezért, ha
-nyi) különbségekhez képest. Ezért, ha 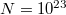 nagyságrendű, akkor a felhasadt energiaszintek közötti távolság nagyságrendje
nagyságrendű, akkor a felhasadt energiaszintek közötti távolság nagyságrendje 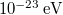 körül van, ami gyakorlatilag „folytonosnak” tekinthető. Így szemléletesen azt mondjuk, hogy az atomi energiaszintek energiasávokká alakulnak.
körül van, ami gyakorlatilag „folytonosnak” tekinthető. Így szemléletesen azt mondjuk, hogy az atomi energiaszintek energiasávokká alakulnak.
A sávokat „tiltott energiatartományok”, ún. tiltott energiasávok (angol szóval gap-ek) választják el egymástól. Ha a felhasadás mértéke akkora, hogy a sávok egymásba nyúlnak, akkor sávátfedésről beszélünk.
Természetesen egy valódi, háromdimenziós kristályban a dolog kissé bonyolultabb. Ezen a szinten azonban ez az elvi lényeget nem érinti. Ennek matematikailag precíz és fogalmaiban árnyalt tanulmányozása azonban már csak az MSc kurzus keretei között lehetséges. Itt meg kell elégednünk az eddig bemutatott „kvalitatív képekkel”.
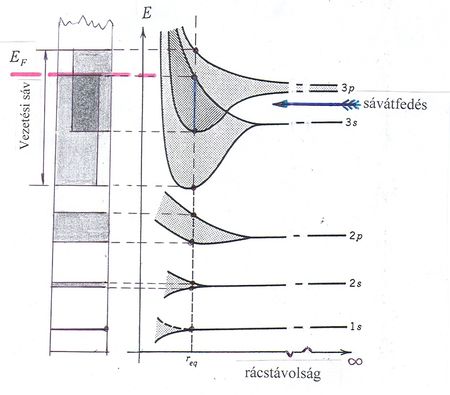
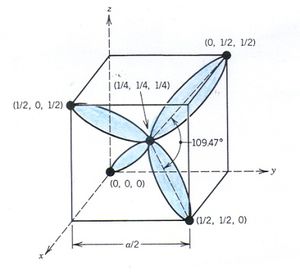
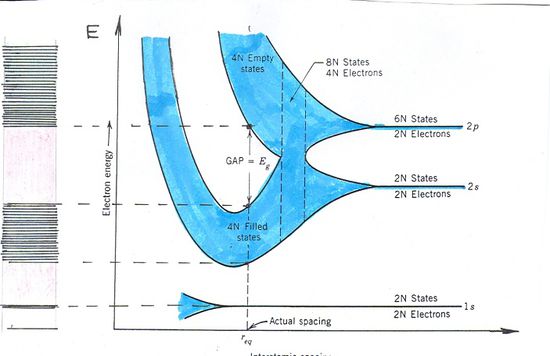
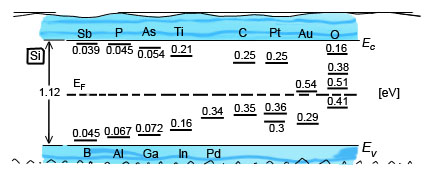
A szilícium kristályban a négy vegyértékű 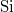 atomok ún. gyémántrácsban kristályosodnak. Ekkor a szomszédos atomok a fenti ábrán bemutatott formációban helyezkednek el. Az atomi vegyérték elektronok
atomok ún. gyémántrácsban kristályosodnak. Ekkor a szomszédos atomok a fenti ábrán bemutatott formációban helyezkednek el. Az atomi vegyérték elektronok  illetve
illetve  állapotúak. Az elemek periódusos rendszerének a magyarázatánál láttuk, hogy az elektronok közötti kölcsönhatás miatt az
állapotúak. Az elemek periódusos rendszerének a magyarázatánál láttuk, hogy az elektronok közötti kölcsönhatás miatt az  és a
és a  állapotokhoz tartozó energiák kissé eltérnek egymástól. Ezen energiaszintek „sávokká történő” felhasadása látható a fenti ábrán.
állapotokhoz tartozó energiák kissé eltérnek egymástól. Ezen energiaszintek „sávokká történő” felhasadása látható a fenti ábrán.
Megjegyzés. A háromdimenziós részletes elméleti számítások szerint továbbra is fennáll az, hogy egy adott energiasávhoz tartozó (pálya)állapotok száma éppen a rácsban lévő atomok  számával egyezik meg. Ezek közül azonban soknak ugyanaz lesz az energiája (ebben pl. különbözik az egydimenziós esettől). Ez a körülmény azonban a Pauli-elv teljesülésekor nem játszik szerepet. Hiszen ez az elv az állapotok betöltésére vonatkozik és ez nem függ attól, hogy ezek az állapotok milyen energiákhoz tartoznak.
számával egyezik meg. Ezek közül azonban soknak ugyanaz lesz az energiája (ebben pl. különbözik az egydimenziós esettől). Ez a körülmény azonban a Pauli-elv teljesülésekor nem játszik szerepet. Hiszen ez az elv az állapotok betöltésére vonatkozik és ez nem függ attól, hogy ezek az állapotok milyen energiákhoz tartoznak.
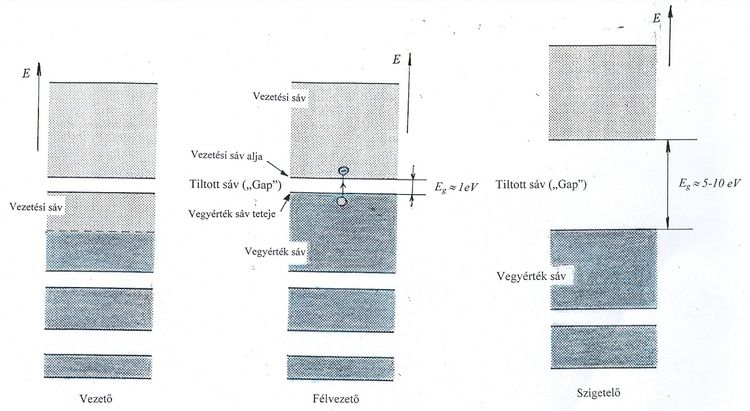
Az energiasávok egymáshoz képesti elhelyezkedéséből következtethetünk az illető szilárd test elektromos vezetési tulajdonságaira is.
Azok az elemek, amelyeknek az atomjai páratlan számú vegyérték elektronnal rendelkeznek, biztosan elektromos vezetők lesznek. Ennek a kvalitatív magyarázata könnyen megérthető. Mint azt már említettük, minden energiasávhoz  darab pályaállapot tartozik. A Pauli-elv miatt minden pályaállapotot maximum két elektron tölthet be (ellentétes spinnel). Erre azt szoktuk mondani, hogy „egy energiasávban éppen
darab pályaállapot tartozik. A Pauli-elv miatt minden pályaállapotot maximum két elektron tölthet be (ellentétes spinnel). Erre azt szoktuk mondani, hogy „egy energiasávban éppen 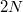 darab elektronnak van hely”. Mármost minket elsősorban az érdekel, hogy a kristályban lévő elektronok energiája mekkora. A meghonosodott szóhasználat szerint azt akarjuk tudni, hogy „az elektronok az egyes energiasávokat hogyan töltik be?” Erre választ kapunk, ha tudjuk, hogy az elektronok a lehetséges állapotokat miként töltik be.
darab elektronnak van hely”. Mármost minket elsősorban az érdekel, hogy a kristályban lévő elektronok energiája mekkora. A meghonosodott szóhasználat szerint azt akarjuk tudni, hogy „az elektronok az egyes energiasávokat hogyan töltik be?” Erre választ kapunk, ha tudjuk, hogy az elektronok a lehetséges állapotokat miként töltik be.
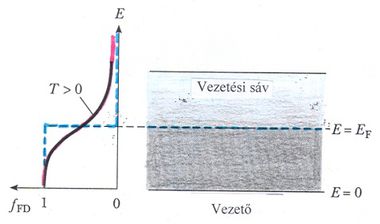
Ezen „energiacentrikus” szemlélet igen egyszerű, és ugyanakkor jól használható képet ad a szilárd test minket érdeklő (elsősorban elektromos és optikai) tulajdonságok megértéséhez. Tehát, ha atomonként páratlan számú vegyérték elektron vesz részt a kristály kialakulásában, akkor az állapotok betöltése után a „legfelső” még betöltésre kerülő energiasáv csak félig lesz feltöltve elektronokkal. Ezért, ha külső elektromos teret kapcsolunk a kristályra, akkor ezek az elektronok magasabb energiaszintre tudnak kerülni, azaz az elektromos tér hatására növekszik a kristálybeli kinetikus energiájuk. Ezt makroszkopikusan úgy észleljük, hogy a kristály vezeti az elektromos áramot. Ezért a félig (részlegesen) betöltött sávot vezetési sávnak hívjuk.
További, precíz részletekkel az MSc tanulmányainkban fogunk foglalkozni.
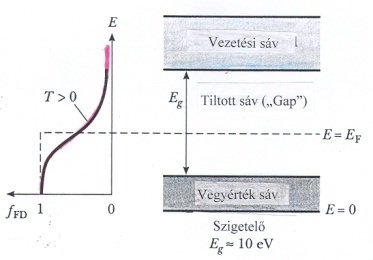
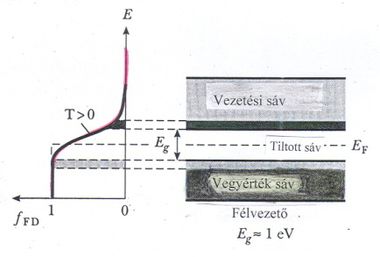
Az előzőek alapján azt várjuk, hogy a páros vegyértékű kristályok energiasávjai (alapállapotban) teljesen betöltöttek lesznek. Ha a tiltott sáv elegendően nagy (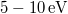 ), akkor a betöltött sávban lévő elektronok még szobahőmérsékleten sem rendelkeznek annyi energiával, hogy „átugorják” a tiltott sávot. Hiszen pl. szobahőmérsékleten (
), akkor a betöltött sávban lévő elektronok még szobahőmérsékleten sem rendelkeznek annyi energiával, hogy „átugorják” a tiltott sávot. Hiszen pl. szobahőmérsékleten (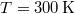 ) a termikus mozgásra jellemző átlagos energia
) a termikus mozgásra jellemző átlagos energia 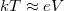 , és ez sokkal kisebb, mint a már említett
, és ez sokkal kisebb, mint a már említett 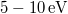 . Így a legfelső (teljesen) betöltött sávot követő energiasáv üres lesz. Ha külső elektromos teret kapcsolunk a kristályra, akkor az elektronok energiája nem tud megnövekedni. Energetikailag mintegy „bezárva maradnak” a sávokba. Így a rendszer egészét tekintve „nem történik semmi”. Makroszkopikus skálán ez úgy jelentkezik, hogy a külső elektromos tér semmilyen hatással nincsen a kristályra. Azaz a kristály szigetelőként viselkedik. A teljesen betöltött sávokat vegyérték sávnak (sokszor valenciasávnak) nevezzük (utalva a vegyérték elektronokkal való betöltöttségre).
. Így a legfelső (teljesen) betöltött sávot követő energiasáv üres lesz. Ha külső elektromos teret kapcsolunk a kristályra, akkor az elektronok energiája nem tud megnövekedni. Energetikailag mintegy „bezárva maradnak” a sávokba. Így a rendszer egészét tekintve „nem történik semmi”. Makroszkopikus skálán ez úgy jelentkezik, hogy a külső elektromos tér semmilyen hatással nincsen a kristályra. Azaz a kristály szigetelőként viselkedik. A teljesen betöltött sávokat vegyérték sávnak (sokszor valenciasávnak) nevezzük (utalva a vegyérték elektronokkal való betöltöttségre).
A várakozásunkkal ellentétben azonban vannak páros vegyértékű atomokból felépülő vezetők is. Ennek oka is szemléletesen megérthető. Ha ugyanis az atomi energiaszintek felhasadása olyan nagy, hogy a felhasadt sávok egymásba nyúlnak, akkor nem alakulhat ki tiltott sáv. Ez a már említett sávátfedés jelensége. Ekkor a keletkező új (eredő) sáv csak részlegesen lesz betöltve elektronokkal. Így a helyzet ugyanaz lesz, mint a fémek esetében volt. Tehát (páros vegyértékű) elektromos vezető alakul ki. Emiatt az átfedett sávot most is vezetési sávnak hívjuk.
Ha a sávfelhasadás mértéke olyan, hogy a „gap” mérete kb. 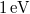 lesz, akkor az eddigiekhez képest egy új jelenséggel találkozunk. Alapállapotban (makroszkopikusan ez a
lesz, akkor az eddigiekhez képest egy új jelenséggel találkozunk. Alapállapotban (makroszkopikusan ez a 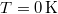 -es esetet jelenti) az elektront tartalmazó (valencia-, vegyérték) sávok mindegyike teljesen be van töltve. Ha emeljük a kristály hőmérsékletét, akkor a legfelső vegyérték sávban lévő elektronok egy kis hányada át tudja ugorni a tiltott sávot. Így elektronok kerülnek az eddig üres vezetési sávba. Ezek a külső elektromos térre ugyanúgy reagálnak, mint azt már a fémeknél megbeszéltük. Mivel viszonylag kevés az ilyen módon gerjesztett elektronok száma, így a kevés töltéshordozó csak kis áramot jelenthet. Azaz a kristály „enyhe” vezetőképességgel fog rendelkezni. Az ilyen anyagokat szerkezeti félvezetőknek nevezzük.
-es esetet jelenti) az elektront tartalmazó (valencia-, vegyérték) sávok mindegyike teljesen be van töltve. Ha emeljük a kristály hőmérsékletét, akkor a legfelső vegyérték sávban lévő elektronok egy kis hányada át tudja ugorni a tiltott sávot. Így elektronok kerülnek az eddig üres vezetési sávba. Ezek a külső elektromos térre ugyanúgy reagálnak, mint azt már a fémeknél megbeszéltük. Mivel viszonylag kevés az ilyen módon gerjesztett elektronok száma, így a kevés töltéshordozó csak kis áramot jelenthet. Azaz a kristály „enyhe” vezetőképességgel fog rendelkezni. Az ilyen anyagokat szerkezeti félvezetőknek nevezzük.
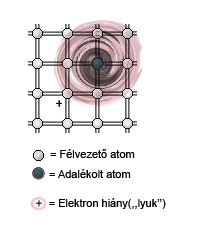
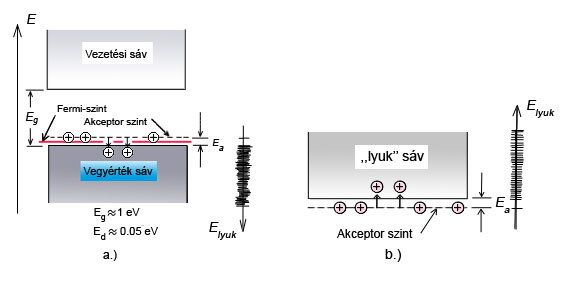
Ha külső elektromos teret kapcsolunk a félvezetőre, akkor nem csak a vezetési sávban lévő elektronok reagálnak erre, hanem a vegyérték sáv elektronjai is. Ugyanis a külső elektromos tér hatására ezek az elektronok is magasabb energiaszintre képesek kerülni, hiszen az alacsonyabb energiájú betöltött állapotokból az elektronok a magasabb energiájú üres állapotokba juthatnak. Azaz a vegyérték sávban az „üres állapotok” mintegy „lefelé vándorolnak” az energiaskálán. Tudjuk, hogy a vegyérték sávban lehetséges, betölthető állapotok száma 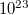 körül van. Szobahőmérsékleten ezeknek csak a töredéke üres. Egy
körül van. Szobahőmérsékleten ezeknek csak a töredéke üres. Egy 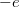 (negatív) töltésű elektron eltávolítása a rendszerből ekvivalens egy
(negatív) töltésű elektron eltávolítása a rendszerből ekvivalens egy 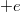 (pozitív töltés) hozzáadásával. Ezért a betöltött állapotok elektronjai együttes hatásukban úgy viselkednek, mintha néhány pozitív töltésű részecske lenne jelen a félvezetőben. Ezeket a pozitív töltésű részecskéket lyukaknak nevezzük. Azt mondjuk, hogy ha felkerül egy elektron a vezetési sávba, akkor egy lyukat hagy hátra a vegyérték sávban. A vezetésben pedig mind az elektronok, mind pedig a lyukak részt vesznek.
(pozitív töltés) hozzáadásával. Ezért a betöltött állapotok elektronjai együttes hatásukban úgy viselkednek, mintha néhány pozitív töltésű részecske lenne jelen a félvezetőben. Ezeket a pozitív töltésű részecskéket lyukaknak nevezzük. Azt mondjuk, hogy ha felkerül egy elektron a vezetési sávba, akkor egy lyukat hagy hátra a vegyérték sávban. A vezetésben pedig mind az elektronok, mind pedig a lyukak részt vesznek.
A hőmérséklet emelésével növekedni fog a vezetési sávban lévő elektronok és a vegyérték sávban lévő lyukak száma, hiszen egyre több elektronnak lesz elegendő energiája ahhoz, hogy a tiltott sávot átugorja. A félvezetők vezetőképessége tehát 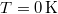 -en zérus (hiszen üres a vezetési sáv). A hőmérséklet emelkedésével pedig a vezetési töltéshordozók (elektronok és lyukak) számának növekedése miatt a vezetőképesség is nőni fog. Mindezeket a kísérleti eredmények számszerűen is fényesen igazolják.
-en zérus (hiszen üres a vezetési sáv). A hőmérséklet emelkedésével pedig a vezetési töltéshordozók (elektronok és lyukak) számának növekedése miatt a vezetőképesség is nőni fog. Mindezeket a kísérleti eredmények számszerűen is fényesen igazolják.
Az elektronállapotok betöltöttsége és így a vezetési elektronok  számának a kvantitatív számítása az
számának a kvantitatív számítása az 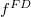 Fermi–Dirac-féle eloszlásfüggvény segítségével történik. Ehhez ismerni kell még az állapotoknak az energiaszintek szerinti
Fermi–Dirac-féle eloszlásfüggvény segítségével történik. Ehhez ismerni kell még az állapotoknak az energiaszintek szerinti 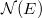 eloszlását is. Ezt állapotsűrűségnek hívják. Ezzel írható, hogy:
eloszlását is. Ezt állapotsűrűségnek hívják. Ezzel írható, hogy:
![\[ n(E) = {\cal N}(E) f^{FD} (E,T). \]](/images/math/0/9/1/091b830caa7a5d911d33d0e970157f4b.png)
Az Elektronika c. tantárgyban ez az összefüggés számtalanszor fog szerepelni.
Az 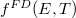 Fermi–Dirac-féle eloszlásfüggvény jellegzetességeit az előző fejezetben vázlatosan már megtárgyaltuk. A jelen estben történő alkalmazása így semmi gondot nem jelenthet.
Fermi–Dirac-féle eloszlásfüggvény jellegzetességeit az előző fejezetben vázlatosan már megtárgyaltuk. A jelen estben történő alkalmazása így semmi gondot nem jelenthet.
Az elmondottaknak megfelelően az előző ábrán a megbeszélt betöltési viszonyok Fermi–Dirac-függvény szerinti magyarázatát láthatjuk. Az állapotsűrűség és az 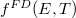 eloszlásfüggvény pontos ismeretében a töltéshordozók számát elegendő pontossággal, numerikusan is meg tudjuk határozni.
eloszlásfüggvény pontos ismeretében a töltéshordozók számát elegendő pontossággal, numerikusan is meg tudjuk határozni.
Az elméleti modell(ek) helyességét a tervezett félvezető alkatrészek kellően pontos működése egyértelműen igazolja.
Adalékolt félvezetők
Eddig szerkezeti félvezetőkkel foglalkoztunk. Ez egy homogén félvezető egykristályt jelentett. 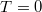 Kelvin fokos hőmérsékleten a félvezetőben csak olyan elektron van, amelynek az állapota a vegyérték sáv valamelyik energiaszintjéhez tarozik és nincsen olyan vegyérték sávhoz tartozó állapot, amelyet elektron ne venne fel. Ugyanakkor olyan elektron nincsen a rendszerben, amelynek energiája a vezetési sáv valamelyik energiaszintjével egyezne meg.
Kelvin fokos hőmérsékleten a félvezetőben csak olyan elektron van, amelynek az állapota a vegyérték sáv valamelyik energiaszintjéhez tarozik és nincsen olyan vegyérték sávhoz tartozó állapot, amelyet elektron ne venne fel. Ugyanakkor olyan elektron nincsen a rendszerben, amelynek energiája a vezetési sáv valamelyik energiaszintjével egyezne meg.
Mint azt már az előzőekben megbeszéltük, ez a mondat precíz ugyan, de túl körülményes és hosszú. Ezért kialakult egy „szóhasználat” (egy „szakzsargon”) amelyet mondani szoktunk. Így az előbbi állítás röviden így hangzik: a vegyérték sáv állapotai mind be vannak töltve és a vezetési sáv minden állapota üres. Vagy még rövidebben: a vegyérték sáv teljesen tele van és a vezetési sáv üres. A továbbiakban ez utóbbi szóhasználattal fogunk élni.
Ha az alapállapotban lévő (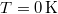 ) rendszerhez hozzáadnánk egy elektront, akkor az csak a vezetési sávba kerülhetne, hiszen a vegyérték sávban már nincsen több hely (hiszen az alapállapotban teljesen tele van).
) rendszerhez hozzáadnánk egy elektront, akkor az csak a vezetési sávba kerülhetne, hiszen a vegyérték sávban már nincsen több hely (hiszen az alapállapotban teljesen tele van).
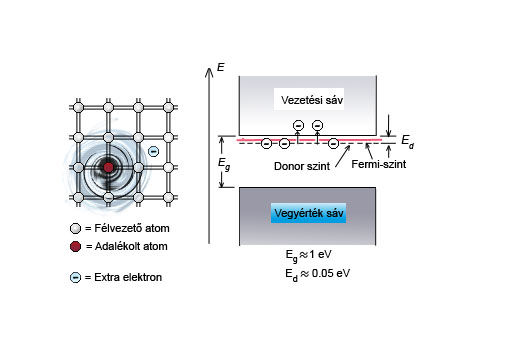
A vezetési elektronok számát azonban a gyakorlatban ilyen módon megnövelni nem tudjuk, mert így a félvezető kristály eredő elektromos töltése megváltozna. A kristály feltöltődne, ami makroszkopikus szinten is éreztetné nem kívánatos hatásait. Az ötlet azonban nem elvetendő és egy egyszerű „trükkel” megvalósítható. Eszerint az elektronnal együtt adjunk egy protont is a rendszerhez! Ezt legegyszerűbben úgy érhetjük el, hogy egy szilícium (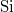 ) atomot pl. egy foszfor (
) atomot pl. egy foszfor (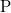 ) atomra cserélünk ki. Ezt nevezzük adalékolásnak (néha szennyezésnek).
) atomra cserélünk ki. Ezt nevezzük adalékolásnak (néha szennyezésnek).
Hasonlítsuk össze a két atom elektronszerkezetét!
![\[ {\rm Si}(14): (1s)^2 (2s)^2 (2p)^6 | (3s)^2 (3p)^2 \]](/images/math/3/0/e/30efdd4255cc0d7b75a8dd3c903240be.png)
![\[ {\rm P}(15): (1s)^2 (2s)^2 (2p)^6 | (3s)^2 (3p)^3 \]](/images/math/8/c/2/8c28c322cbfc30368e865acdac6010b0.png)
A kétféle atom elektronszerkezetéből látszik, hogy az iontörzsük felépítése teljesen azonos, nevezetesen 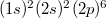 . A vegyérték elektronok állapotai is egyformák, csak számuk különböző (4 és 5). Joggal feltételezhetjük (ismerve a protonok és az atomok egymáshoz viszonyított méretét), hogy a kétféle iontörzs mérete gyakorlatilag megegyezik. Tehát ez az „atomcsere” elhanyagolható rácsdeformációt fog okozni.
. A vegyérték elektronok állapotai is egyformák, csak számuk különböző (4 és 5). Joggal feltételezhetjük (ismerve a protonok és az atomok egymáshoz viszonyított méretét), hogy a kétféle iontörzs mérete gyakorlatilag megegyezik. Tehát ez az „atomcsere” elhanyagolható rácsdeformációt fog okozni.
Mivel ezáltal a kristályba egy többlet elektron került, a foszfor atomokat donor atomoknak nevezzük. A többletelektron neve a donor elektron. (Donor = valamit adó.)
A foszfor atom környezetében azonban a fizikai viszonyok megváltoznak. Ennek oka az, hogy a foszfor iontörzs a környezetéhez képest egy protonnyi (pozitív) töltéstöbblettel rendelkezik. Ez az első pillanatra bonyolultnak tűnő rendszer egy egyszerű „hidrogénszerű modellel” közelítőleg egészen jól leírható.
Tekintsük ugyanis a szilícium kristályt folytonos (kontinuum) közegnek. Ekkor a foszfor atom helyén egy pontszerű pozitív (többlet)töltés fog megjelenni. A foszfor atom ötödik (többlet) vegyérték (donor) elektronja pedig ennek a terében kötött állapotba fog kerülni. Ha a donor elektron energiája elegendően nagy, akkor az „leszakadva” a pozitív ponttöltéstől, attól nagyon „eltávolodik”. Ha az elektron olyan messze került a pozitív töltéstől, hogy annak hatása már elhanyagolható, akkor ő már csak a tiszta szilícium kristályt érzékeli maga körül. Az elektron ekkor a szilícium kristályban immáron „szabadon” fog mozogni és így részt vesz a kristály elektromos vezetésében. De mint tudjuk ebben az esetben az energiájának a szilícium kristály vezetési sávjába kell esnie.
Mindebből következik, hogy a foszfor atom jelenléte a szilícium kristályban úgy modellezhető, mint egy (folytonos) szilícium közegben lévő hidrogén atom, amelynek ionizációs energiaszintje (a vákuum szint helyett) a szilícium kristály vezetési sávjának az alja.
Nyilvánvalóan, ennek a hidrogén atomnak az elektronja is érzékeli azt, hogy ő egy szilícium kristályba van „beágyazva”. Például úgy, hogy az elektromos töltése polarizálja a környezetében lévő kristályt, amit a szilícium dielektromos állandóján keresztül lehet figyelembe venni. Mindez azt jelenti, hogy a foszfor atom körül kialakuló kötött állapotok energiaszintjeit úgy kell meghatározni, hogy a hidrogén atom energiaszintjeit megadó összefüggésbe a vákuum 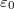 dielektromos állandója helyett a szilícium
dielektromos állandója helyett a szilícium 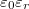 dielektromos állandóját írjuk.
dielektromos állandóját írjuk.
Megjegyzés. A részletesebb modell szerint a kristályrács jelenléte egy összetett kvantummechanikai kölcsönhatás révén is megnyilvánul. Ezt az elektron „tömegének” a módosításával tudunk figyelembe venni (ezt nevezzük effektív tömeg közelítésnek). A részleteket azonban csak az MSc kurzuson fogjuk tárgyalni.
Tanultuk, hogy a hidrogén atom kötött elektronjának a lehetséges energiaszintjeit a következő formula adja meg (TK: 1051. és 1078. oldal):
![\[ E_n = -\frac{m{\rm e}^4}{8h^2\varepsilon_0^2} \frac{1}{n^2} = -\frac{13,6 \, {\rm eV}}{n^2}, \quad \text{ahol} \quad n = 1,2,3,... . \]](/images/math/9/b/b/9bb23926b82a8c51cb8ead4b79397435.png)
Innen látszik, hogy az 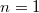 -hez tartozó alapállapotú elektronnak
-hez tartozó alapállapotú elektronnak 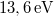 -nyi energiát kell felvennie ahhoz, hogy az energiája elérje vákuum szintet jelentő
-nyi energiát kell felvennie ahhoz, hogy az energiája elérje vákuum szintet jelentő 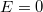 energiaszintet (ekkor
energiaszintet (ekkor 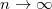 ). A szilicium kristályba ágyazott hidrogén atom modell esetén az energiaszinteket (a megadott módosítással) az
). A szilicium kristályba ágyazott hidrogén atom modell esetén az energiaszinteket (a megadott módosítással) az
![\[ E_n = -\frac{m{\rm e}^4}{8h^2 \varepsilon_0^2} \frac{1}{\varepsilon_r} \frac{1}{n^2} = -\frac{13,6 \, {\rm eV}}{\varepsilon_r^2} \frac{1}{n^2} \]](/images/math/9/f/3/9f31256fea450f8fcdebebfb169d7295.png)
kifejezés adja meg. Mivel szilícium esetén 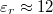 , így az ionizációs energiára
, így az ionizációs energiára
![\[ \frac{13,6}{12^2} \, {\rm eV} = 0,09 \, {\rm eV} \]](/images/math/2/f/5/2f5c35108484cdafb471250bc55aac69.png)
érték adódik.
Megjegyzés. A valódi érték ennek a fele, azaz 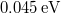 . A különbség abból adódik, hogy a
. A különbség abból adódik, hogy a 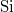 háttér valójában nem folytonos közeg. A kristályrács kvantummechanikai hatását is figyelembe kell venni. Erre szolgál az effektív tömeg fogalma. Ez hozza be e hiányzó
háttér valójában nem folytonos közeg. A kristályrács kvantummechanikai hatását is figyelembe kell venni. Erre szolgál az effektív tömeg fogalma. Ez hozza be e hiányzó 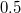 -ös faktort. A részleteket az MSc szinten tárgyaljuk majd.
-ös faktort. A részleteket az MSc szinten tárgyaljuk majd.
Mivel a szilícium esetén a tiltott sáv szélessége 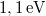 , így valójában azt kaptuk, hogy a kötött állapotok energiaszintjei a vezetési sáv alja alatt, ahhoz nagyon közel, a tiltott sávban helyezkednek el.
, így valójában azt kaptuk, hogy a kötött állapotok energiaszintjei a vezetési sáv alja alatt, ahhoz nagyon közel, a tiltott sávban helyezkednek el.
Alapállapotban (0 Kelvin hőmérsékleten) tehát az adalékolt félvezetők elektronszerkezete úgy néz ki, hogy a vegyérték sáv teljesen tele van, a vezetési sáv teljesen üres és a (donor) elektronok a foszfor atomok környezetében kötött állapotban vannak. Már nagyon kis hőmérsékletemelkedésre a kötött állapotban lévő donor elektronok leszakadnak a donor atomokról és felkerülnek a vezetési sávba. Sikerült tehát megnövelni a vezetésben résztvevő elektronok („n” típusú, negatív töltéshordozók) számát. Ezért ezt a félvezetőt n-típusú félvezetőnek szoktuk hívni.
Számoljuk ki a donor atomot modellező hidrogén atom „méretét”. Az ezt jellemző adat lehet az első Bohr-sugár. Mint azt láttuk, vákuumban lévő hidrogén atom esetében ez (TK: 1050. oldal)
![\[ r_n = a_0 n^2, \quad \text{ahol} \quad a_0 = \frac{h^2}{\pi n {\rm e}^2} \varepsilon_0 = 0,0529 \, {\rm nm}. \]](/images/math/3/9/d/39dd343347c4b46886183610843b2e94.png)
Ha most a megbeszéltek szerint a dielektromos állandó helyére 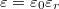 -t írunk, akkor azt kapjuk eredményül, hogy a „modell hidrogén” atomunk sugara kb. 12-szer akkora, mint egy szabad hidrogén atomé. Tételezzük fel, hogy a kristályrácsban az atomok távolsága a szabad hidrogén atom sugarának kb. 3–4-szerese. Ebből az következik, hogy a szilícium kristályban lévő hidrogénszerű atom kb. 60 db. kristályatomot foglal magába. Ez a modell kiindulásául szolgáló „folytonos anyag” feltételezésével nagyjában összhangban van.
-t írunk, akkor azt kapjuk eredményül, hogy a „modell hidrogén” atomunk sugara kb. 12-szer akkora, mint egy szabad hidrogén atomé. Tételezzük fel, hogy a kristályrácsban az atomok távolsága a szabad hidrogén atom sugarának kb. 3–4-szerese. Ebből az következik, hogy a szilícium kristályban lévő hidrogénszerű atom kb. 60 db. kristályatomot foglal magába. Ez a modell kiindulásául szolgáló „folytonos anyag” feltételezésével nagyjában összhangban van.
Teljesen hasonló a helyzet akkor, ha egy szilícium atomot pl. egy alumínium (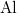 ) atomra cserélünk ki.
) atomra cserélünk ki.
![\[ {\rm Al}(13): \quad (1s)^2 (2s)^2 (2p)^6 | (3s)^2 (3p)^1. \]](/images/math/2/a/3/2a3fc5c8b9f562888aaa8c219c05206d.png)
Most a rendszerből elvettünk egy elektront és egy protont is. Ezért az alumínium atomot akceptor atomnak, a kristályt akceptor félvezetőnek nevezzük. (Akceptor = valamit elfogadó, itt elvevő.) Az egy elektron elvétele azt jelenti, hogy a vegyérték sávban egy üres hely jelenik meg. Megmutatható (MSc kurzus) hogy a vegyérték sáv elektronjainak együttes viselkedése (az elektron hiány miatt) egyetlen, pozitív töltésű részecskeként írható le. Ennek a „fiktív részecskének” a neve lyuk. Ez a pozitív lyuk lép kölcsönhatásba a hiányzó protont modellező negatív ponttöltéssel.
Akceptor atom adalékolása esetén a kötött állapotok számítása pontosan úgy történik, mint a donor adalékolás esetén volt. A „negatív töltésű mag” terében a pozitív lyuk kötött állapotba kerül, amelynek az energiaszintjei a tiltott sávban lévő, „vegyérték sáv feletti” energiaszintekként jelennek meg.
Az elektronok eloszlása a vegyérték sávban fizikailag ekvivalens a lyukak eloszlásával a lyuk sávban. Azért, hogy ne kellejen külön mindig egy „lyuk sávot” is felrajzolni (ez egy „kényelmi szempont”) a lyukak energia szerinti eloszlásának a szemléltetésére továbbra is az elektronok vegyérték sávját fogjuk használni. Azaz a vegyérték sáv be nem töltött állapotait fogjuk a lyukakkal azonosítani.
Tehát pl. alapállapotban (amikor a vegyérték sáv minden állapota be van töltve elektronnal) azt mondjuk, hogy „a vegyérték sávban nincsen egy lyuk sem”. Azaz a lyukmodell alapján a lyuk szempontjából nézve a vegyérték sáv teljesen „üres”. A lyukak a negatív töltésű rögzített „mag” körül kötött állapotban vannak. Azaz a lyukak betöltik az akceptor nívókat.
A rendszer hőmérsékletének emelkedésével nő a rendszer energiája. A lyukak leszakadnak a „negatív magokról” és szabaddá válnak, azaz újabb szabad lyukak („p” típusú, pozitív töltéshordozók) jelennek meg amelyek részt vesznek félvezető elektromos vezetésében. Ezért ezt a félvezetőt p-típusú félvezetőnek szoktuk nevezni. Az elektronok nyelvén ez azt jelenti, hogy a vegyérték sávból elektronok „ugranak fel az akceptor nívóra” (ld. fenti ábra). Ennek megfelelően a vegyérték sávban üres állapotok keletkeznek. Ez a lyukmodellben azt jelenti, hogy a lyukak felkerültek a „lyuk sávba”, de ehelyett azt szoktuk mondani, hogy „lyukak jelentek meg a vegyérték sávban” (ld. fenti ábra). Tovább növelve a hőmérsékletet, a vegyérték sávot újabb elektronok hagyják el, azaz újabb lyukak jelennek meg és vesznek részt a vezetésben.
A lyukak és az elektronok számát (többek között) a Fermi–Dirac eloszlásfüggvény segítségével tudjuk numerikusan is meghatározni. További praktikus, számítás-technikai részletekkel a szakmai tantárgyaknál illetve az MSc Fizika kurzusban találkozhatunk.
Az alábbi két táblázatban a legfontosabb adalékolt félvezető adatokat mutatjuk be.
Szilícium kristály esetén:
Gallium-Arzenid kristály esetében pedig:
A félvezető alapú elektronikai alkatrészekben lejátszódó jelenségek fizikai alapja az ún. p-n átmenet. Ez úgy állítható elő, hogy egy p-típusú és egy n-típusú félvezetőt szorosan „összeillesztünk”. A kialakult struktúra elektronszerkezete a következő gondolatmenettel érthető meg.
A szilárd testek energia-sávszerkezetének tárgyalásakor nem beszéltünk arról, hogy milyen fizikai viszonyok uralkodnak a félvezető szélénél. Mivel az elektronok „önmaguktól” nem lépnek ki a szilárd anyagból ezt úgy modellezhetjük, hogy az elektronok egy potenciálgödörben vannak. A potenciálgödör valójában az elektron potenciális energia függvényét jelenti. Ebben a „potenciálgödörben” lévő elektronok lehetséges energiaszintjei a tanult „sávokba” rendeződnek. A potenciálgödör „teteje” a vákuum szintet jelenti.
Ha a p-típusú és az n-típusú félvezető felület egymástól nagyon távol van, akkor szükségképpen a vákuumszintjük megegyezik.
Ha két félvezető elegendően közel kerül egymáshoz, akkor a két felület egy potenciálgátat fog alkotni. A vákuumszintek egyenlősége miatt a vezetési sáv egy  energiaszintjén a p oldalon sokkal kevesebb elektron van, mint az n oldalon. Így (mivel az elektronok egyforma valószínűséggel mennek „jobbra” vagy „balra”) elektronok lépnek át az n-típusú félvezetőből a p-típusúba.
energiaszintjén a p oldalon sokkal kevesebb elektron van, mint az n oldalon. Így (mivel az elektronok egyforma valószínűséggel mennek „jobbra” vagy „balra”) elektronok lépnek át az n-típusú félvezetőből a p-típusúba.
Ennek következtében az érintkező felület két oldala között töltésmegosztás keletkezik, amely potenciálkülönbséget hoz létre a két félvezető között, és ez csökkenti az eredeti Fermi-szintek közötti különbséget.
Ez a töltésmegosztás addig folytatódik, ameddig a rendszer egyensúlyi állapotba nem jut, azaz két Fermi szint egyenlő nem lesz. Ugyanis egyetlen kvantummechanikai rendszerről lévén szó, csak egyetlen Fermi szint lehet. Mivel az átment elektronok 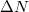 száma sokkal kisebb mint a két félvezetőben lévő elektronok (
száma sokkal kisebb mint a két félvezetőben lévő elektronok (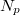 és
és 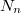 ) száma, ezért a Fermi-szintnek a saját energiasávjukhoz viszonyított helyzete gyakorlatilag nem változik meg. A (pozitív, illetve a negatív) többlettöltések (a dielektrikumoknak megfelelően) a határoló felület környezetében oszlanak el. A kialakult térfogati töltéssűrűség alakítja ki az eredő elektromos teret és így az elektronok potenciális energia függvényét. A kialakult energiaviszonyokat az alábbi ábrán szemléltettük. A szokásoknak megfelelően ezen egy
) száma, ezért a Fermi-szintnek a saját energiasávjukhoz viszonyított helyzete gyakorlatilag nem változik meg. A (pozitív, illetve a negatív) többlettöltések (a dielektrikumoknak megfelelően) a határoló felület környezetében oszlanak el. A kialakult térfogati töltéssűrűség alakítja ki az eredő elektromos teret és így az elektronok potenciális energia függvényét. A kialakult energiaviszonyokat az alábbi ábrán szemléltettük. A szokásoknak megfelelően ezen egy 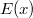 függvényt ábrázoltunk, ahol
függvényt ábrázoltunk, ahol  a p-n átmenetre merőleges irányt jelenti.
a p-n átmenetre merőleges irányt jelenti.
Megjegyzés. Általában az  -et nem szokták kiírni, ezért mi sem tesszük. Az
-et nem szokták kiírni, ezért mi sem tesszük. Az 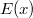 közelítő kiszámítására az Elektronika tantárgy kereteiben kerül sor.
közelítő kiszámítására az Elektronika tantárgy kereteiben kerül sor.
Az elektronok energia szerinti eloszlását a Fermi–Dirac eloszlásfüggvény határozza meg.
Ha beállt a termikus egyensúly, akkor már nincsen töltésáramlás. Ennek az az oka, hogy az adott energiájú elektronok sűrűsége „mindkét oldalon” ugyanakkora. Ezt az ábrán úgy szimbolizáljuk, hogy egy adott energiaszintre mindkét oldalon ugyanannyi elektront és lyukat rajzoltunk.
Kapcsoljunk a p oldalra pozitív és az n oldalra negatív feszültséget. Ekkor a p-n ,átmenetben egy olyan („külsőnek” nevezett) 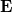 elektromos tér alakul ki, amely a p-től az n irányába mutat! Így az elektronok vezetési sávbeli energiaszintjei az n oldalon a magasabb energiák irányába tolódnak el. Ezáltal az n oldali betöltött energiaszintek a p oldali csak kevéssé betöltött (mondhatni üres) energiaszintekkel kerülnek azonos nívóra. Ezáltal az n oldali „többségi” töltéshordozók (ezek most az elektronok) átmennek a p oldalra. Így egy erős
elektromos tér alakul ki, amely a p-től az n irányába mutat! Így az elektronok vezetési sávbeli energiaszintjei az n oldalon a magasabb energiák irányába tolódnak el. Ezáltal az n oldali betöltött energiaszintek a p oldali csak kevéssé betöltött (mondhatni üres) energiaszintekkel kerülnek azonos nívóra. Ezáltal az n oldali „többségi” töltéshordozók (ezek most az elektronok) átmennek a p oldalra. Így egy erős  (diffúziós) áram indul meg. Ez folyamatosan fennmarad, hiszen az áramkörből állandóan pótlódnak a töltések. Ezt a jelenséget nyitásnak nevezzük. Az ábráról az is leolvasható, hogy ugyanez az effektus igaz a vegyérték sávban lévő pozitív töltéshordozókra azaz a lyukakra is. Ugyanis a „nyitó irányú” tér hatására a p oldalon többségben lévő lyukak átáramlanak az n oldalra, ezzel is növelve a nyitó áram nagyságát. A teljes áram tehát a (többségi töltéshordozókból) elektronokból és lyukakból fog állni. A p-n átmenetre kapcsolt
(diffúziós) áram indul meg. Ez folyamatosan fennmarad, hiszen az áramkörből állandóan pótlódnak a töltések. Ezt a jelenséget nyitásnak nevezzük. Az ábráról az is leolvasható, hogy ugyanez az effektus igaz a vegyérték sávban lévő pozitív töltéshordozókra azaz a lyukakra is. Ugyanis a „nyitó irányú” tér hatására a p oldalon többségben lévő lyukak átáramlanak az n oldalra, ezzel is növelve a nyitó áram nagyságát. A teljes áram tehát a (többségi töltéshordozókból) elektronokból és lyukakból fog állni. A p-n átmenetre kapcsolt  feszültséget nyitó feszültségnek, a folyó áramot nyitó irányú áramnak hívjuk. Mindezt az alábbi ábrán szemléltettük.
feszültséget nyitó feszültségnek, a folyó áramot nyitó irányú áramnak hívjuk. Mindezt az alábbi ábrán szemléltettük.
Ha most az n oldalra kapcsoljuk a pozitív és a p oldalra a negatív feszültséget, akkor (az ellenkező irányú 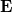 elektromos tér hatására) az n oldalon lévő elektronok energiája lecsökken. Ezáltal az p oldali kevéssé betöltött energiaszintek az n oldali (gyakorlatilag) üres energiaszintekkel kerülnek azonos nívóra. Ezáltal a p oldali „kisebbségi” töltéshordozók (ezek most is az elektronok) átmennek az n oldalra. Azaz egy igen kicsi
elektromos tér hatására) az n oldalon lévő elektronok energiája lecsökken. Ezáltal az p oldali kevéssé betöltött energiaszintek az n oldali (gyakorlatilag) üres energiaszintekkel kerülnek azonos nívóra. Ezáltal a p oldali „kisebbségi” töltéshordozók (ezek most is az elektronok) átmennek az n oldalra. Azaz egy igen kicsi  áram lép csak fel. Ez szintén folyamatosan fennmarad. Ezt a jelenséget zárásnak nevezzük. A p-n átmenetre kapcsolt ilyen irányú
áram lép csak fel. Ez szintén folyamatosan fennmarad. Ezt a jelenséget zárásnak nevezzük. A p-n átmenetre kapcsolt ilyen irányú  feszültséget záró feszültségnek, a folyó kicsi áramot pedig záró irányú áramnak hívjuk. Hasonlóan magyarázható a vegyérték sávban lévő kisebbségi lyukak áramlása is.
feszültséget záró feszültségnek, a folyó kicsi áramot pedig záró irányú áramnak hívjuk. Hasonlóan magyarázható a vegyérték sávban lévő kisebbségi lyukak áramlása is.
A tárgyalt p-n átmenet az ún. félvezető dióda.
A jellegzetes 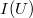 dióda (karakterisztika) függvény matematikai formában történő meghatározására szintén az Elektronika tantárgy bevezető fejezeteiben kerül majd sor. Az elmondottak alapján kialakuló dióda karakterisztikát az alábbi ábra szemlélteti.
dióda (karakterisztika) függvény matematikai formában történő meghatározására szintén az Elektronika tantárgy bevezető fejezeteiben kerül majd sor. Az elmondottak alapján kialakuló dióda karakterisztikát az alábbi ábra szemlélteti.
Ha most tovább növeljük a záró feszültséget, akkor egy igen érdekes effektussal találkozhatunk:
Elegendően nagy feszültség esetén ugyanis a p oldal vegyérték sávja az n oldal vezetési sávjával energetikailag azonos szintre kerül. Így az igen sok elektront tartalmazó p oldali vegyérték sávot az igen kevés elektront tartalmazó n oldali vezetési sávtól csak egy keskeny potenciálgát választja el. Nyilvánvaló, hogy ez a „meredeken megdőlt” tiltott sáv annál keskenyebb, minél nagyobb a záró irányú feszültség. Ez a tiltott sáv az elektron számára „ugyanolyan” tartományt jelent, mintha egy „klasszikusan tiltott tartomány” volna. Azaz egy potenciálgátként funkcionál. Ezen a gáton az elektronok alagút effektussal átjuthatnak. Így (mivel igen sok elektronunk van ezeken az energiaszinteken) egy igen erős, ún. letörési áram indul el. Ezt a jelenséget felfedezőjéről Zener-effektusnak nevezik.
Az alábbi ábrán bemutatunk egy valódi mért Zener 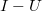 karakterisztikát is a nagyságrendi adatok érzékeltetése végett.
karakterisztikát is a nagyságrendi adatok érzékeltetése végett.
Az erősen adalékolt félvezetők és technikai alkalmazásai
Az alagút dióda
Clarence Zeners 1934-ben ajánlotta először egy olyan effektus kísérleti létrehozását, amelyben igen erős (belső) elektromos tér hatására az elektronok a vegyérték sávból a tiltott sávon keresztül a vezetési sávba jutnak. Ő volt az első, aki kiszámította ennek az „átugrásnak” a valószínűségét.
Az effektus kísérleti megvalósítása kb. 30 évet váratott magára. 1957-ben Leo Esaki kísérleti úton igazolta Zener elméleti jóslatát. Kísérleteit a Sony Co. laboratóriumában, Galliummal és Arzénnel erősen adagolt Germániummal végezte. Az eredményei alapján fejlesztette ki a róla elnevezett tunnel diodáts.
Munkássága elismeréseként 1973-ban elnyerte a fizikai Nobel-díjat. (Mindezt az alagúteffektus kapcsán már elmondtuk.)
A következőkben erről az effektusról lesz szó. Mi történik, ha az adalékolás mértékét erősen megnöveljük?
Egy bizonyos „szennyezési” koncentráció felett az adalékolt atomok olyan közel kerülnek egymáshoz, hogy kölcsönhatásba lépnek egymással. Az előzőekben láttuk, hogy egy (szerkezeti) félvezetőbe ágyazott idegen (adalékolt) atom körüli „kötött állapot térbeli mérete” jócskán megnő. Így az adalékolt atomok közötti kölcsönhatás könnyebben létrejön. Ekkor (az előzőekben már bemutatott effektus miatt) a kötött állapotok energiaszintjei sávokká hasadnak fel. Ez a sáv aztán „egybeolvad” a vezetési illetve a vegyérték sávval, mintegy kiszélesítve azt. A Fermi-szint ekkor adalékolt atomok sávja és a félvezető sáv elválasztó határán van.
Az alábbi ábrán mind a donor, mind pedig az akceptor nívók sávvá szélesedését mutatjuk be. (Ezt gyakran a szennyezési nívók elfajulásának is nevezik.)
Természetesen ezekből a félvezetőkből is csinálhatunk egy p-n átmenetet. Így jutunk el az Esaki-féle alagút diodához. A „szokványos” p-n átmeneteknél alkalmazott záró- és nyitó irányú feszültségeket kell alkalmazni most is.
Kapcsoljunk záró feszültséget a diodánkra. Mint az az alábbi ábrán látható, egy igen erős, záró irányú alagút áram (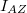 ) indul el.
) indul el.
Ennek oka nyilvánvalóan az, hogy a vegyérték sáv sok elektront tartalmazó energiaszintjei a vezetési sáv majdnem üres energianívóival kerülnek egy szintre. A „tiltott sáv jelentette” viszonylag keskeny potenciálgáton az elektronok könnyen „átalagutaznak”. (A jelenség fizikai lényege „ugyanaz”, mint ami a Zener effektusnál volt.)
Kis nyitó irányú feszültségek esetén egy igen erős (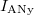 ) alagút áram lép fel (ld. b. ábra).
) alagút áram lép fel (ld. b. ábra).
Ennek oka az, hogy a vegyérték sáv üres energiazónája (amely a sávvá szélesedett akceptor nívókból áll) az energiaskálán mintegy „fedésbe” kerül a vezetési sáv betöltött energiazónájával (azaz a donor nívók sávjával). A maximális alagútáram természetesen a maximális „átfedés” esetén lép fel.
Tovább növelve a nyitófeszültséget, a sávok egyre jobban eltolódnak és a kívánt „átfedés” lassan megszűnik. Így az alagútáram csökkeni kezd majd meg is szűnik. A diódán azonban továbbra is folyik egy igen kicsiny 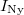 áram, hiszen a többségi töltéshordozók (a véges
áram, hiszen a többségi töltéshordozók (a véges  hőmérséklet miatt) már megjelentek a magasabb energiaszinteken is (lásd c. ábra, fennebb).
hőmérséklet miatt) már megjelentek a magasabb energiaszinteken is (lásd c. ábra, fennebb).
Még tovább növelve a nyitófeszültséget, ez a nyitó irányú 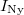 áram is növekedni fog. A helyzet pontosan ugyanaz, mint az a „hagyományos” p-n átmenetnél volt (ld. d. ábra, fennebb). Így a mostani nyitóirányú
áram is növekedni fog. A helyzet pontosan ugyanaz, mint az a „hagyományos” p-n átmenetnél volt (ld. d. ábra, fennebb). Így a mostani nyitóirányú 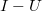 függvény is ugyanolyan jellegűvé válik, mint amilyent már láttunk a „normális” diodáknál.
függvény is ugyanolyan jellegűvé válik, mint amilyent már láttunk a „normális” diodáknál.
A teljes „áram-feszültség” karakterisztikát a fenti ábra mutatja. Az 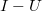 függvény jellegzetessége az a negatív ellenállású tartomány, amelyik a nyitó irányban lép fel akkor, amikor a növekvő nyitófeszültség ellenére az áram csökken. Pontosan ez a jelenség adja az alagút dióda technikai különlegességét. A karakterisztikának ezt a tartományát pl. „gyorsműködésű” oszcillátorok készítésére szokták felhasználni.
függvény jellegzetessége az a negatív ellenállású tartomány, amelyik a nyitó irányban lép fel akkor, amikor a növekvő nyitófeszültség ellenére az áram csökken. Pontosan ez a jelenség adja az alagút dióda technikai különlegességét. A karakterisztikának ezt a tartományát pl. „gyorsműködésű” oszcillátorok készítésére szokták felhasználni.
Fénykibocsátó diódák
Az erősen adalékolt p-n átmenetek másik, igen fontos alkalmazási területe a fénykibocsátó félvezetők. Ezek lehetnek
a.) egyszerű fényforrások (LED = Light Emitting Diode) vagy
b.) koherens fényt szolgáltató félvezető LASER-ek.
Az alapeffektus mindkettőnél lényegében ugyanaz, „csak” a megvalósító félvezető és a kiegészítő „struktúra” más. A részleteket az Elektronika tantárgy idevonatkozó fejezeteiből tudhatjuk majd meg. Itt most csak a jelenség fizikai lényegét tudjuk bemutatni, annak is a „sávszerkezetből adódó” (energetikai) részletét.
A LED működési elve az energiasáv-ábra alapján érthető meg.
Ha a nyitó irányú feszültség elegendően nagy, akkor (szemléletesen szólva) a vegyérték sáv üres zónája és a vegyérték sáv betöltött donor sávja a p-n átmenet  tartományában kerül egymással „térbeli átfedésbe”. Ez azt jelenti, hogy a p és az n típusú félvezetőket elválasztó (térbeli) átmeneti tartományban elektronok és lyukak halmozódnak fel. Mivel ezek a tér egy adott térfogatában együtt vannak jelen, így egymással kölcsönhatásba lépve „rekombinálódnak”. Azaz az „állapotok” nyelvén mondva, az
tartományában kerül egymással „térbeli átfedésbe”. Ez azt jelenti, hogy a p és az n típusú félvezetőket elválasztó (térbeli) átmeneti tartományban elektronok és lyukak halmozódnak fel. Mivel ezek a tér egy adott térfogatában együtt vannak jelen, így egymással kölcsönhatásba lépve „rekombinálódnak”. Azaz az „állapotok” nyelvén mondva, az  tartományban lévő elektronok a vezetési sávból visszaugranak a vegyérték sáv üres állapotaiba, így csökkentve a rendszer energiáját. Az elektronok az energiájukat egy foton kibocsátásával „vesztik el”. Ezáltal elektronok és lyukak tűnnek el az
tartományban lévő elektronok a vezetési sávból visszaugranak a vegyérték sáv üres állapotaiba, így csökkentve a rendszer energiáját. Az elektronok az energiájukat egy foton kibocsátásával „vesztik el”. Ezáltal elektronok és lyukak tűnnek el az  zónából. Erre mondjuk azt, hogy „egy elektron-lyuk pár egy foton kibocsátásával rekombinálódott”. A rekombinációk egymástól függetlenül zajlanak le.
zónából. Erre mondjuk azt, hogy „egy elektron-lyuk pár egy foton kibocsátásával rekombinálódott”. A rekombinációk egymástól függetlenül zajlanak le.
A folyamat állandósul, hiszen a fellépő nyitóáram állandóan gondoskodik az újabb elektron-lyuk párok megjelenéséről az  zónában. (Ezt a folyamatot injektálásnak nevezi a szakirodalom.) Amíg a megfelelő nyitófeszültég be van kapcsolva, a dióda fényt bocsát ki. A fény frekvenciáját a sávszélesség, a nyitófeszültség és a hőmérséklet (azaz a sávok betöltöttsége) együttesen (de nem egyforma mértékben) határozza meg. A részletek megértse azonban már túlhaladja egy BSc Fizika kurzus kereteit, hiszen mint az bizonyára látszik, komolyabb félvezető-(szilárdtest)-fizikai ismereteket igényel.
zónában. (Ezt a folyamatot injektálásnak nevezi a szakirodalom.) Amíg a megfelelő nyitófeszültég be van kapcsolva, a dióda fényt bocsát ki. A fény frekvenciáját a sávszélesség, a nyitófeszültség és a hőmérséklet (azaz a sávok betöltöttsége) együttesen (de nem egyforma mértékben) határozza meg. A részletek megértse azonban már túlhaladja egy BSc Fizika kurzus kereteit, hiszen mint az bizonyára látszik, komolyabb félvezető-(szilárdtest)-fizikai ismereteket igényel.
Megjegyzés. A p-n átmenet térbeli  tartományát kiürített rétegnek nevezik. Az amúgy igen „szemléletes” elnevezés részletes fizikai okait az MSc fizika kurzus tárgyalja majd. De az Elektronika tantárgy idevonatkozó részeinél is lesz van szó.
tartományát kiürített rétegnek nevezik. Az amúgy igen „szemléletes” elnevezés részletes fizikai okait az MSc fizika kurzus tárgyalja majd. De az Elektronika tantárgy idevonatkozó részeinél is lesz van szó.
A félvezető LASER működési elvét az energiasáv-ábra alapján lehet elmagyarázni.
Mind a LED, mind pedig a LASER esetén az elemi fény-effektust az „elektron-lyuk párok” rekombinációja szolgáltatja. Nyilvánvaló azonban, hogy amíg a LED esetén a spontán emisszió, addig a LASER esetén az „indukált emisszió” a domináló effektus.
A LASER működés alapelveinél tanultak értelmében, a félvezetőben valami módon egy ún. „inverz populációt” kell létrehozni. Erre elvileg a LED-nél látott  réteghez hasonló tartomány lehetne alkalmas. Ennek technikai megvalósítsa azonban (a LASER működés biztosításának a követelménye miatt) már komplikáltabb feladat. A (bonyolult) elméleti ismereteknek a hiányában fogadjuk el tényként az alábbiakat.
réteghez hasonló tartomány lehetne alkalmas. Ennek technikai megvalósítsa azonban (a LASER működés biztosításának a követelménye miatt) már komplikáltabb feladat. A (bonyolult) elméleti ismereteknek a hiányában fogadjuk el tényként az alábbiakat.
A félvezető lézerek (egy lehetséges) felépítése a következő. 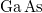 (gallium-arzenid) kristály p illetve n típusú
(gallium-arzenid) kristály p illetve n típusú 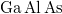 (gallium-alumínium-arzenid) réteg között „helyezkedik” el. Ezt az ún. rétegszerkezetet (szendvics szerkezetet) ma már rutinszerűen létre lehet hozni az ún. epitaxiális rétegnövesztés technológiájának az alkalmazásával. Ennek az a lényege, hogy a megadott struktúrát (alakzatot) atomi rétegenként lehet létrehozni, így a különböző félvezető típusú tartományokat csupán csak atomrácsnyi szélességű átmenetek választják el egymástól. Így a
(gallium-alumínium-arzenid) réteg között „helyezkedik” el. Ezt az ún. rétegszerkezetet (szendvics szerkezetet) ma már rutinszerűen létre lehet hozni az ún. epitaxiális rétegnövesztés technológiájának az alkalmazásával. Ennek az a lényege, hogy a megadott struktúrát (alakzatot) atomi rétegenként lehet létrehozni, így a különböző félvezető típusú tartományokat csupán csak atomrácsnyi szélességű átmenetek választják el egymástól. Így a 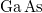 réteg igen jól lokalizált lesz.
réteg igen jól lokalizált lesz.
Ez a réteg (itt nem részletezhető elvi okok miatt) már alkalmas arra, hogy benne a szükséges inverz populáció létrejöjjön.
A 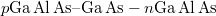 „hármas réteget” egy p-n átmenetnek is tekinthetjük. Ha reá nyitó feszültséget kapcsolunk, akkor a
„hármas réteget” egy p-n átmenetnek is tekinthetjük. Ha reá nyitó feszültséget kapcsolunk, akkor a 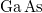 rétegben inverz populáció alakul ki.
rétegben inverz populáció alakul ki.
A LASER effektus létrejöttéhez minden körülmény rendelkezésre áll. Mindez az energiasáv ábrán látható (ld. fennebb).
Az indukált emisszió létrejöttéhez szükséges „optikai rezonátort” a 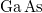 „külső felületén” alakítják ki. Sokszor ez nem is igényel külön tehnológiát, mert a
„külső felületén” alakítják ki. Sokszor ez nem is igényel külön tehnológiát, mert a 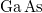 félvezető törésmutatója elég nagy (kb. 2-3), és így a felület kristálysikja elegendően jó visszaverő felületet szolgáltat. Természetesen vigyázni kell a felület kellő megmunkálására.
félvezető törésmutatója elég nagy (kb. 2-3), és így a felület kristálysikja elegendően jó visszaverő felületet szolgáltat. Természetesen vigyázni kell a felület kellő megmunkálására.
Így tehát ez a 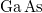 réteg lesz az az aktív tartomány, amelyben az elektronok, a lyukak és a fotonok kölcsönható keveréke a LASER effektust produkálni fogja.
réteg lesz az az aktív tartomány, amelyben az elektronok, a lyukak és a fotonok kölcsönható keveréke a LASER effektust produkálni fogja.